Predicting crystalline lens fall caused by accommodation from changes in wavefront error

Abstract

PURPOSE

To illustrate and develop a method for estimating crystalline lens decentration as a function of accommodative response using changes in wavefront error and show the method and limitations using previously published data (2004) from 2 iridectomized monkey eyes so that clinicians understand how spherical aberration can induce coma, in particular in intraocular lens surgery.

SETTINGS

College of Optometry, University of Houston, Houston, USA.

DESIGN

Evaluation of diagnostic test or technology.

METHODS

Lens decentration was estimated by displacing downward the wavefront error of the lens with respect to the limiting aperture (7.0 mm) and ocular first surface wavefront error for each accommodative response (0.00 to 11.00 diopters) until measured values of vertical coma matched previously published experimental data (2007). Lens decentration was also calculated using an approximation formula that only included spherical aberration and vertical coma.

RESULTS

The change in calculated vertical coma was consistent with downward lens decentration. Calculated downward lens decentration peaked at approximately 0.48 mm of vertical decentration in the right eye and approximately 0.31 mm of decentration in the left eye using all Zernike modes through the 7th radial order. Calculated lens decentration using only coma and spherical aberration formulas was peaked at approximately 0.45 mm in the right eye and approximately 0.23 mm in the left eye.

CONCLUSIONS

Lens fall as a function of accommodation was quantified noninvasively using changes in vertical coma driven principally by the accommodation-induced changes in spherical aberration. The newly developed method was valid for a large pupil only.

According to the Helmholtz theory of accommodation,¹ ciliary muscle contraction releases zonular tension around the lens equator, allowing the lens equatorial diameter to decrease, the lens thickness to increase, and the lens anterior surface to become more steeply curved. Although there are other theories of accommodation,^2-4 the Helmholtz theory is by far the most consistent with experimental data.^5-11

An interesting feature of the Helmholtz theory is that when an eye accommodates, the lens is free to fall. The lens is free to fall assuming the head is in an upright position because zonular tension is relaxed and the larger density of the crystalline lens allows it to move within the constraints of the intraocular accommodative system. That the lens does fall is supported directly and indirectly by several studies. For example, Glasser and Kaufman⁹ showed that the apparent image of lens opacity fell 300 μm with accommodation by analyzing the video images of a lens opacity observed in a cynomolgus monkey during centrally stimulated maximum accommodation. Indirect evidence that the lens falls with accommodation is seen in studies by Takeda et al.¹² and Atchison et al.,¹³ who found that accommodative responses vary as a function of vertical gaze direction. They observed that downward gaze provided a larger accommodative response than upward gaze or primary gaze. They inferred that the decreased zonular tension enabled the lens to fall forward, increasing the dioptric power of the system. More recently, He et al.¹⁴ reported that the lens wobbles more after saccadic eye movements in the presbyopic eye when the eye attempts to accommodate. The wobble is present even though there is no actual change in power of the crystalline lens, supporting the notion that the act of trying to accommodate releases tension on the zonules regardless of whether the lens can still change shape.

To our knowledge, no study has provided an estimation of lens fall as a function of the accommodative response. However, authors report increasing change in the wavefront error in the eye over a large (8.0 mm) aperture, which is consistent with the lens falling with increasing accommodation. Here, the focus will be on the data of Vilupuru et al.,¹⁵ who found in monkey eyes increasing negative spherical aberration and negative vertical coma with increasing accommodation while horizontal coma remained essentially stable.

By calculating lens fall through wavefront error, the study can serve as a good example of the interaction between spherical aberration, coma, and decentration. It is important for clinicians, in particular cataract surgeons, to understand this interaction when implanting different types of intraocular lenses (IOLs).

Overall, the purpose of this paper is to (1) provide an intuitive narrative illustrating the underlying principles of calculating lens fall from changes in wavefront error with increasing accommodation, (2) explicitly present the quantitative approach for extracting estimates of lens fall as a function of accommodation from measured changes in coma using whole-eye wavefront error measurements through the 7th radial order or only spherical aberration, (3) show the application of these methods using the data of Vilupuru et al.¹⁵ to estimate lens fall as a function of accommodation, (4) discuss the limitations of the approach and future applications, and (5) show how a displaced IOL with spherical aberration can induce coma.

MATERIALS AND METHODS

In this study, it was assumed that (1) changes in vertical coma with increasing accommodation are not due to the crystalline lens becoming increasingly pear shaped, (2) aberrations in the anterior optical surface of the eye (here the anterior surface of a contacted lens) and the internal optics lie in the same plane and there is no contact lens or whole-eye positional changes during accommodation, (3) changes in vertical coma are due to lens fall as opposed to lens tilt or to the lens changing shape in a nonuniform manner (eg, becoming pear shaped), and (4) the center of the pupil remains fixed with accommodation. The limitations imposed by these assumptions on the calculations of lens fall will be addressed in the discussion.

Intuitive Narrative of the Underlying Principles

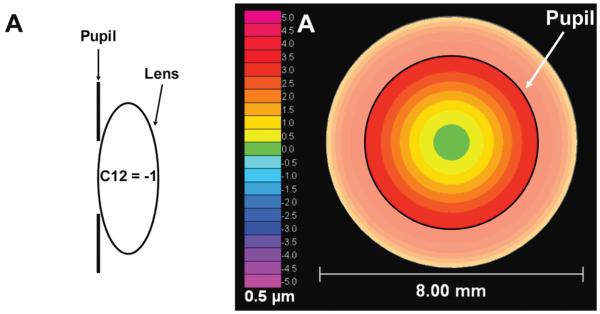
To understand the underlying principles, consider a simple optical system consisting only of an entrance pupil (say 5.0 mm) and a wavefront error with only spherical aberration (−1.0 μm) that has been well defined over a larger area (say 8.0 mm), as shown in Figure 1, A.

Figure 1.

A and B: An entrance pupil (black circle), say 5.0 mm, superimposed on a wavefront error map that is smaller than the diameter (8.0 mm) of an optical element (eg, the crystalline lens). Here, the wavefront error is only spherical aberration of −1 μm over an 8.0 mm diameter. In A, the wavefront error of the optical element is centered on the entrance pupil and rotationally symmetric. In B, the optical element has fallen 1.0 mm with respect to the entrance pupil. As a result, the measured aberrations through the entrance pupil will change becoming nonrotationally symmetric. In C, changes in each Zernike coefficient values in micrometers (2nd to 4th order) due to this drop were calculated within the 5.0 mm entrance of pupil (WFE = wavefront error).

Consider what happens to the wavefront error measured through the pupil if the underlying wavefront error moves (ie, crystalline lens falls) with respect to the pupil, as in Figure 1, B. Notice that the measured wavefront error through the pupil is different (ie, it is no longer rotationally symmetric around the center of the pupil) in these 2 cases even though the underlying wavefront remained constant. (Note: Shifting the wavefront error with respect to the center of the pupil is the same as shifting the center of the pupil with respect to the wavefront error except the movements in a fixed-coordinate system are opposite in direction.) After the shift, there is a change in the measured aberration over the 5.0 mm pupil even though optical properties over the full 8.0 mm diameter are unchanged. Figure 1, C, shows the change in measured wavefront error as a function of Zernike mode induced by the fall of the wavefront error with respect to the pupil. Notice that the amount of spherical aberration (C12) did not change, the amount of negative vertical coma (C7) increased, and there was no change in horizontal coma (C8). This is exactly what will happen if an IOL with spherical aberration is displaced.

These effects are not new. It is well known that such movement of the wavefront error with respect to the entrance pupil will induce systematic and predictable changes in the measured wavefront error.^16-18 This study capitalized on these known effects to calculate the estimate the degree to which the crystalline lens falls with accommodation. The systematic nature of these changes is easy to see in the Zernike expansion representation of the wavefront error (Figure 2).

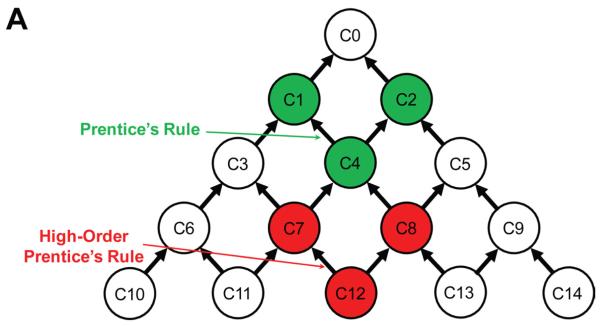
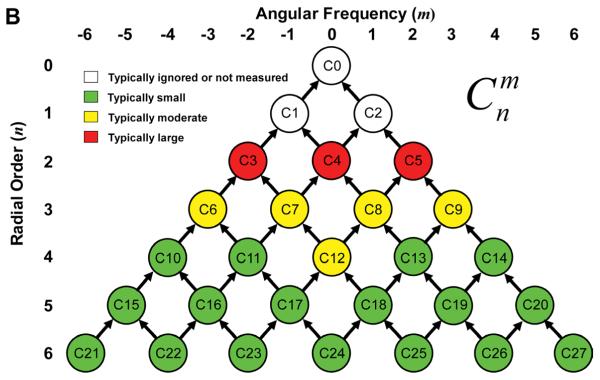
Figure 2.

A and B: The circles in represent Zernike mode coefficients for the fitted wavefront error over the entrance pupil. Codes within each circle represent the ANSI standard³¹ single-index numbering for each Zernike mode. B: Corresponding radial order and angular frequency enable double-index numbering. Arrows represent how each mode influences other modes if the wavefront error shifts with respect to the pupil. A: The dark green circles show Prentice’s rule; that is, a shift of the pupil will cause the sphere (defocus) component (C4) in the optical system (eg, glasses or a change in crystalline lens power) to induce prism (C1 and C2). The red circles A show a corresponding HOA effect between spherical aberration (C12) and the coma terms (C7 and C8). B: Measured aberrations that are typically ignored (white circles), are typically small in magnitude (green circles), are typically moderate in magnitude (yellow circles), and are typically large in magnitude (red circles) in normal monkey eyes and human eyes.

Each circle in Figure 2, A and B, represents 1 of the Zernike modes. The arrows indicate how each Zernike mode influences other modes as the location of the underlying wavefront translates relative to the entrance aperture. The arrows were determined by an analytical algorithm derived by Dai¹⁹ in which he converted Zernike coefficients to Taylor coefficients. The derived equation provides the interaction relationship between the terms of interest after decentration. Each mode can only influence modes in a lower radial order and never influence modes of a higher radial order.

If the lens falls and mode C12 (spherical aberration) is not zero, the fall will cause C12 to feed directly into the coma terms (red circles in Figure 2, A) and then indirectly to other lower-order terms on up the tree. If the movement is only downward the change in coma will be directly loaded into vertical coma (C7) and from coma into astigmatism mode (C5) and defocus (C4), as previously shown in Figure 1, C. This change in coma is analogous to the induced change in prism when an eye looks through a spectacle lens in a location away from the optical axis of the lens (dark green circles in Figure 2, A) as described by Prentice’s rule. As such, the induced change in coma caused by a placement shift of the spherical aberration is a “high-order Prentice’s rule” for the influence of spherical aberration on coma and other aberrations on up the Zernike tree.

Figure 2, B, shows pictorially why the analysis focuses on the interactions between spherical aberration (C12) and coma (C7 and C8). Typically, C0, C1, and C2 (white circles in Figure 2, B) are not measured because these modes do not affect image quality. The C3, C4, and C5 aberrations are lower order and if the individual has a significant spherocylindrical error, they are usually large compared with all other aberrations. For the unaccommodated eye, the higher-order aberrations (HOAs) that are typically moderate in magnitude (yellow circles in Figure 2, B) are trefoil (C7 and C9), coma (C7 and C8), and spherical aberration (C12).²⁰ These aberrations are cannot be corrected with standard spectacle lenses. As the eye accommodates C4 (ie, defocus) increases in a positive direction and C12 (spherical aberration) becomes increasingly negative.^15,21-25 Note that C12 (spherical aberration) is the only 4th-order radial aberration that is moderately large and also changes with accommodation,^15,21-25 making the impact of spherical aberration on coma a marker of lens fall.

To illustrate the fundamental principles used to quantify crystalline lens fall, consider a more complex multiple component system consisting of a cornea and crystalline lens (Figure 3). In this model, the corneal optics are fixed with respect to the pupil and the lens optics are not. Each component (cornea and lens) has a wavefront error of its own; together, the errors define the wavefront error in the eye. For simplicity, consider the wavefront error in both the cornea and lens to lie in the plane of the entrance pupil, as is commonly done for the eye.^16,26 Under this set of assumptions, the eye’s wavefront error is the sum of the corresponding modes in the 2 subcomponents.

Figure 3.

An accommodating crystalline lens that falls will induce a change in wavefront error in a predictable manner dependent on the wavefront error present in the lens at each level of accommodation and the amount of crystalline lens fall.

In Figure 3, as the eye accommodates, the crystalline lens moves down with respect to the center of the pupil while the corneal optics remains fixed with respect to the center of the pupil. For the purpose of this illustrative model, assume that before any movement, all Zernike coefficients for the lens are zero except for spherical aberration (C12 = −1) and that all Zernike coefficients for the cornea are fixed (ie, do not change as the lens falls). In this case, only the location of lens spherical aberration changes. Now assume that the eye accommodates to a new stimulus value and falls some small amount. In this illustrative model, as the lens falls, the downward movement will change the value of vertical coma (C7) depending on the amount of movement and magnitude of the spherical aberration (C12) and will not alter the magnitude of C12 itself. Furthermore, if the lens falls straight down, horizontal coma (C8) will remain unchanged. The same order of events will happen if other HOAs are involved. That is, each aberration will feed up the pyramid, as shown in Figure 2.

It is known that the largest change (by far) in HOAs with accommodation is an increase in negative in spherical aberration (C12) dependent on the magnitude of accommodation.^15,21-25 If the pupil is large enough, movement of C12 will directly induce a change in coma and indirectly induce a change in modes farther up the pyramid. Several studies^21,23-25 have shown that other modes in the 4th radial order (C10, C11, C13, and C14) as well as higher radial orders are only minimally, if at all, changed as the eye accommodates in both monkeys and humans. These considerations make change in coma a particularly sensitive metric of lens movement.

Quantitative Approach

Several studies^18,19,27-29 introduced a different algorithm to scale, translate, or rotate Zernike expansions. Comastri et al.¹⁸ present conversion formulas for scaling changes in each coefficient of the Zernike polynomial up to 7th radial order for horizontal shifts in the pupil center in an optical system with a known wavefront error. Although their formulas were only for horizontal shift of the optics with respect to the limiting aperture, clockwise rotation of 90 degrees using the matrix put forward by Guirao et al.²⁷ can make the Comastri et al.¹⁸ conversion formulas applicable to downward decentration and the calculation of the resulting change in vertical coma as follows:

$$\begin{array}{cc}\hfill & C{7}^{\prime }={\left(\frac{r^{\prime }}{r}\right)}^{3}C7+2\sqrt{5}\left(\frac{d}{r}\right){\left(\frac{r^{\prime }}{r}\right)}^{3}C11+2\sqrt{10}\left(\frac{d}{r}\right){\left(\frac{r^{\prime }}{r}\right)}^{3}C12\hfill \\ \hfill & +5\sqrt{6}{\left(\frac{d}{r}\right)}^2{\left(\frac{r^{\prime }}{r}\right)}^{3}C16+2\sqrt{6}\left[\left(\frac{15}{2}\right){\left(\frac{d}{r}\right)}^2{\left(\frac{r^{\prime }}{r}\right)}^3+{\left(\frac{r^{\prime }}{r}\right)}^5-{\left(\frac{r^{\prime }}{r}\right)}^3\right]C17\hfill \\ \hfill & +10\sqrt{7}{\left(\frac{d}{r}\right)}^2{\left(\frac{r^{\prime }}{r}\right)}^{3}C22+2\sqrt{7}\left[20{\left(\frac{d}{r}\right)}^3{\left(\frac{r^{\prime }}{r}\right)}^3+6\left(\frac{d}{r}\right){\left(\frac{r^{\prime }}{r}\right)}^5-5\left(\frac{d}{r}\right){\left(\frac{r^{\prime }}{r}\right)}^3\right]C23\hfill \\ \hfill & +2\sqrt{14}\left[15{\left(\frac{d}{r}\right)}^3{\left(\frac{r^{\prime }}{r}\right)}^3+6\left(\frac{d}{r}\right){\left(\frac{r^{\prime }}{r}\right)}^5-5\left(\frac{d}{r}\right){\left(\frac{r^{\prime }}{r}\right)}^3\right]C24\hfill \\ \hfill & +35\sqrt{2}{\left(\frac{d}{r}\right)}^4{\left(\frac{r^{\prime }}{r}\right)}^{3}C29+3\sqrt{2}\left[\left(\frac{175}{3}\right){\left(\frac{d}{r}\right)}^4{\left(\frac{r^{\prime }}{r}\right)}^3+28{\left(\frac{d}{r}\right)}^2{\left(\frac{r^{\prime }}{r}\right)}^5-20{\left(\frac{d}{r}\right)}^2{\left(\frac{r^{\prime }}{r}\right)}^3\right]C30\hfill \\ \hfill & +2\sqrt{2}\left[175{\left(\frac{d}{r}\right)}^4{\left(\frac{r^{\prime }}{r}\right)}^3+126{\left(\frac{d}{r}\right)}^2{\left(\frac{r^{\prime }}{r}\right)}^5+7{\left(\frac{r^{\prime }}{r}\right)}^7-90{\left(\frac{d}{r}\right)}^2{\left(\frac{r^{\prime }}{r}\right)}^3-12{\left(\frac{r^{\prime }}{r}\right)}^5+5{\left(\frac{r^{\prime }}{r}\right)}^3\right]C31\hfill \end{array}$$ (1)

where C7 and C7′ are pre-fall and post-fall vertical coma, respectively; r and r’ are pre-fall and post-fall aperture sizes, respectively (ie, pupil radii 4.0 mm and 3.5 mm in the calculation, respectively); and d is the lens fall amount. Because all the Zernike coefficients are known, d can be solved, for example, using a symbol function in Matlab (The Mathworks Inc.).

To evaluate the influence of aberrations in the 5th, 6th, and 7th radial orders on spherical aberration and in turn on vertical coma changes during lens movement, all other higher-order Zernike terms except for C12 were omitted, reducing the equation 1 to

$$C{7}^{\prime }={\left(\frac{r^{\prime }}{r}\right)}^{3}C7+2\sqrt{10}\left(\frac{d}{r}\right){\left(\frac{r^{\prime }}{r}\right)}^{3}C12$$ (2)

Lens fall, d, calculated from equations 1 and 2 can then be compared to determine the relative importance of including the influence of all Zernike modes in the 4th radial order and higher. The difference in the results of the 2 equations (1 and 2) reflects the influence of aberrations in the 5th, 6th, and 7th radial orders.

To apply both equations, an estimate of the internal aberrations (primarily due to the crystalline lens) was calculated using the method of Artal el al.¹⁶ for each level of accommodation in both eyes. In this method, the crystalline lens wavefront error is estimated by subtracting the corneal aberrations (estimated by the corneal first surface) from the whole eye measurement made at each level of accommodation.

Whole-Eye Wavefront Error

Vilupuru et al.¹⁵ report a whole-eye wavefront error over an 8.0 mm diameter in 2 iridectomized eyes of 1 monkey measured as a function of accommodation induced by Edinger-Westphal stimulation. Wavefront errors were measured with a purpose-built Hartmann-Shack wavefront sensor and expressed in the recommended standard form for the ophthalmic use of the Zernike expansion first proposed in an Optical Society of America meeting,³⁰ which later became the American National Standards Institute, Inc. notation (ANSI Z80.28-2004) up to the 10th radial order.³¹

First-Surface Wavefront Error

In the Vilupuru et al.¹⁵ study, the monkey wore a rigid contact lens to avoid evaporation of tear film from the eye during the course of the accommodation experiment. Because the contact lens first surface replaces the corneal first surface, it is the contact lens first surface that defines the aberrations in the first surface of the contact lens–eye system.

The contact lens first surface aberration was measured using a Keratron videokeratographer (Optikon 2000 SpA). The aberrations were expressed in ANSI standard Zernike coefficients to the 10th radial order over an 8.0 mm diameter, and it was assumed that the measurement axis of the videokeratographer and whole-eye wavefront error measurement were coincident.

Crystalline Lens Wavefront Error Estimation

An estimate of the crystalline lens wavefront error was made as follows:

$$\text{Crystalline}\text{lens}\text{wavefront}\text{error}=\text{Whole}\text{eye}\text{wavefront}\text{error}-\text{Contact}\text{lens}\text{first}\text{surface}\text{wavefront}\text{error}$$ (3)

Verification of Modeling the Optical Consequences of a Falling Crystalline Lens

A custom C++ program (designed by Raymond A. Applegate, OD, PhD, and Jason D. Marsack, PhD, and developed by Sarver and Associates, Inc.) was used to model the aberration result of a 2-component optical system in which 1 component is fixed with respect to the limiting aperture (the corneal first surface) and the second component shifts with respect to limiting aperture. It is assumed that both optical components exist in the same optical plane. The program first shifts the center of the moving wavefront error to the new location of interest with respect to the center of the systems pupil and then densely resamples the shifted wavefront error over the pupil and refits the normalized Zernike expansion using a least-squares criterion. Once the new set of Zernike terms has been calculated for the shifted optical component, the terms can be added 1 by 1 to the Zernike fit of the fixed optical component. The program was applied to independently verify the results calculated from equation 1.

RESULTS

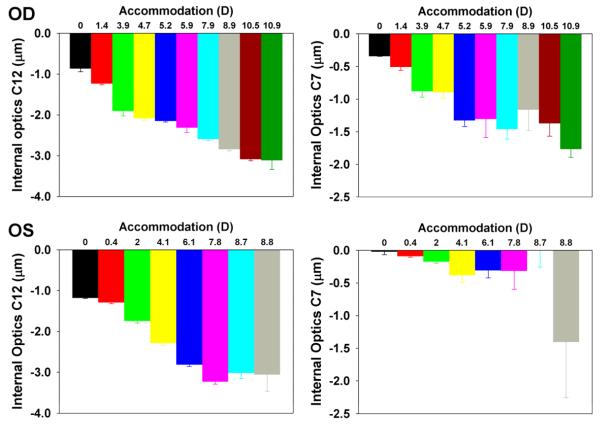
Figure 4 shows the spherical aberration (C12) and vertical coma (C7) of internal optics calculated from equation 3 as a function of accommodation. In both eyes, C12 (spherical aberration) became more and more negative with accommodation. The same trend holds true for C7. However, the left eye showed a less systematic change than the right eye, in particular for C7.

Figure 4.

Magnitude of C12 and C7 of internal optics as a function of accommodation in diopters in the right and left eye of the study monkey (The whole-eye wavefront data are from Vilupuru et al.¹⁵). As the accommodation goes up, C12 and C7 generally became more and more negative.

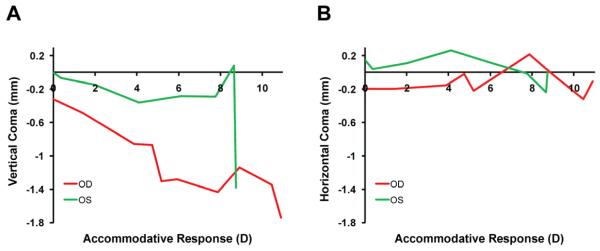
Figure 5 replots vertical coma and horizontal coma as a function of the accommodative response in the right eye and left eye. Unlike vertical coma, horizontal coma fails to show systematic changes with an increase in accommodative response. The maximum changes in horizontal coma are small and nonsystematic as a function of accommodation compared with those of vertical coma (1.42 μm and 1.46 μm) in both eyes, implying that the crystalline lens falls straight down with accommodation.

Figure 5.

Whole eye vertical (C7) and horizontal (C8) coma in micrometers as a function of accommodative response in diopters in both eyes of the study monkey. The red trace represents the right eye (OD) and the green trace represents, the left eye (OS).

Figure 6 shows the estimated downward movement of the lens as a function of the accommodative response calculated from equations 1 and 2. The analysis shows that the lens fell gradually between 0.00 D and 5.00 diopters (D) of accommodative response in both eyes. In the right eye, the lens apparently stopped falling between 5.00 D and 6.00 D. The left eye behaved similarly except for a large increase in lens fall at the maximum level of accommodation.

Figure 6.

Estimated fall of the crystalline lens as a function of accommodative response in the right eye (OD) and the left eye (OS) in the study monkey. Solid symbols are estimations using the full equation 1 and the open symbols, using only spherical aberration (equation 2). The maximal lens falls are indicated by solid arrows (equation 1) and open arrows (equation 2) (SA = spherical aberration).

DISCUSSION

We report a new way to noninvasively estimate lens fall as a function of accommodation from changes in the measured wavefront error of the eye. Glasser and Kaufman⁹ report an apparent maximum lens fall of 300 μm in monkey eyes under accommodative stimulus conditions similar to those used with the 2 eyes of 1 monkey investigated here. Apparent fall of the lens was viewed through the cornea. To appropriately compare the Glasser and Kaufman data⁹ with our estimates of lens fall, the apparent fall must be converted to an actual fall. To make this conversion, a schematic monkey eye put forward by Lapuerta and Schein³² was built in Zemax software (Zemax Development Corp.) and a ray tracing was performed to estimate the actual fall given the measured apparent fall. This correction showed the actual fall to be 230 μm. Although there are not enough cross-sectional data to estimate the variability in lens fall between subjects, we suspect that the differences between lens falls may be due to differences in the circumlental space that defines the available space in which the lens can fall and the specific biomechanical properties of the accommodative apparatus in each eye.

Two equations were used to estimate lens fall from accommodation-induced changes in wavefront error. Both equations showed that the lenses fell. In the right eye, the 2 estimates of maximum fall were similar in magnitude (480 μm and 450 μm), while in the left eye calculated the 2 estimates were different (310 μm and 230 μm). The reasons for this difference are not readily apparent from the limited sample of eyes tested to date.

Four key assumptions were made in this study. First, we assumed that changes in vertical coma are not due to the lens becoming more and more pear shaped during accommodation. Although we cannot rule out this possibility, to our knowledge there is no reported evidence that the lens becomes pear shaped during accommodation. Although it is possible that the lens-shape change might cause a change in coma, several human studies^21,23-25 did not show systematic changes in coma as a function of accommodation over small apertures.

Second, we assumed aberrations in the anterior cornea and the internal optics lie on the same plane and anterior corneal optics remain constant. Results from Artal et al.¹⁶ show that good compensation for aberrations between anterior cornea optics and internal optics based on the single-plane model. In addition to direct measurement (videokeratography), they indirectly measured aberrations in the anterior corneal surface using water-filled goggles to eliminate corneal first-surface optics. The 2 methods gave similar results, supporting the validity of the single-plane model. Like Artal et al.’s study,¹⁶ corneal wavefront error was well compensated for by the internal optics aberrations obtained in the current study, indirectly supporting the validity of a single-plane model. It is possible that eye movement or movement of the contact lens caused the changes in vertical coma as opposed to accommodation, per se. This is unlikely in Vilupuru et al.’s experiment¹⁵ because the monkey eyes were kept open and fixed by sutures to avoid potential eye movement. Because blinking was eliminated, it is reasonable to assume that the hard contact lens remained stable once it was placed on the eye.

Third, we assumed that changes in vertical coma were caused by lens tilt accompanied or not accompanied by lens decentration during accommodation. Lens positive tilt (upper lens tilts forward) around the horizontal axis during accommodation has been reported in primates³³ and averaged 1.22 degrees. To evaluate the role tilt may have, we built a schematic monkey eye model³² with aberration¹⁵ in Zemax software. Decentration or tilt of the crystalline lens was in turn modeled to explore the relative effects each has on vertical coma. Decentration induced changes in vertical coma were proportional to the amount of decentration and the magnitude of the spherical aberration of the internal optics. Lens tilt–induced changes in vertical coma varied, principally due to factors other than spherical aberrations, in particular, the magnitude of defocus (C4) of the internal optics. Nevertheless, lens decentration (between 0.0 mm and 0.5 mm) induced a more profound effect on vertical coma than lens tilt (0 to 2 degrees). As a consequence, lens tilt, if present, is a relatively minor confounding factor in the calculation of lens fall, leading to slightly larger estimates of lens fall than actually occurred.

Fourth, variations in pupil location can induce changes in vertical coma. Although a potential issue that would need to be controlled for in eyes with an iris, in the Vilupuru et al. study¹⁵ the monkey’s eyes were iridectomized and the instrumentation and the head of the monkey were fixed in space with respect to each other.

The less systematic change in vertical coma in the left eye as opposed to the right is puzzling. In particular, the positive shift in coma between 7.8 D and 8.7 D followed by a large negative shift is hard to explain. Perhaps the circumlental space was smaller in the left eye. If the lens stopped falling, this could explain why vertical coma did not become more negative at larger accommodative states while spherical aberration did. The positive shift is harder to explain; until more data are collected, we have no good explanation. A monkey study³⁴ using goniovideography and Scheimpflug imaging also suggests for unknown reasons that some of the monkey lens did not fall during accommodation. A better understanding of the physiologic aspect of accommodation in the future might help explain the individual variability.

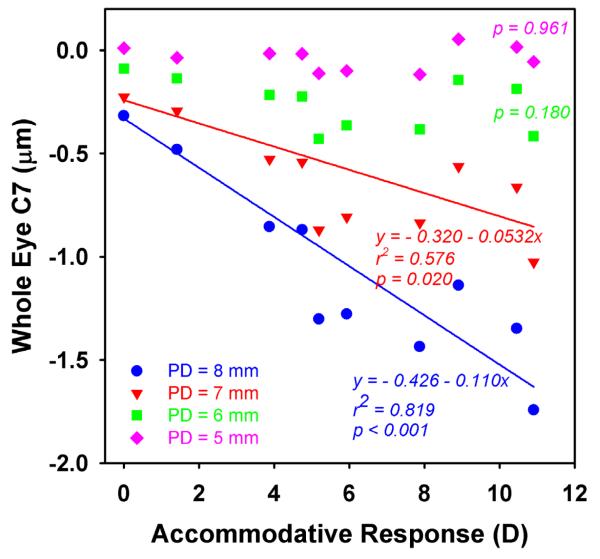
When measuring over smaller pupil diameters, several studies^21,23-25 found no significant changes in vertical coma during accommodation in humans. This is not surprising given the smaller pupil diameter used in these studies. If the pupil diameter is small, the impact of spherical aberration on coma is markedly reduced. As it is shown in Figure 7, the original whole-eye vertical coma magnitude with an 8.0 mm pupil increased in the negative direction systematically and significantly with accommodation. When vertical coma was rescaled to a pupil diameter of 6.0 mm or 5.0 mm, the changes were not statistically significant. In other words, if Vilupuru et al.¹⁵ measured wavefront error with a smaller pupil, say 6.0 mm, the change in vertical coma would likely be similar to the changes reported in the human studies^21,23-25 when the pupil diameter was smaller than 6.0 mm. The impact of pupil diameter can be seen in equations 1 and 2, in which the scaling factor for pupil diameter is

$${\left(\frac{r^{\prime }}{r}\right)}^3$$

Thus, a large pupil diameter (at least 6.0 mm) is required to apply these methods to quantify estimates of lens fall during accommodation. However, it is also possible that unlike in primates,^9,34 the human crystalline lens cannot fall during accommodation because of the anatomic and physiologic differences between the humans and non-human primates.

Figure 7.

Rescaled data for whole-eye vertical coma in the right eye in (PD). Vertical coma becomes increasingly negative with accommodation with pupil diameters of 8.0 mm (P < .001) and 7.0 mm (P = .020) but with for pupil diameters of 6.0 mm and 5.0 mm.

As can be seen in equation 2, these findings support the recent report³⁵ that aberration-free aspheric IOLs are less likely than a spherical IOL or a spherical aberration-correcting IOL to induce coma when decentration and tilt occur. Clinician must pay particular attention to this kind of induced coma, especially for patients who have relatively larger physiologic pupil diameters.

In conclusion, we report a noninvasive method to quantify crystalline lens decentration as a function of accommodative response using measured changes in vertical coma that are driven principally by the accommodation-induced changes in spherical aberration. In 2 eyes, the estimated amount of lens fall was 480 μm and 310 μm.