Abstract
The objective of this study is to investigate the effects of respiratory motion (RM) on defect detection in Tc-99m sestamibi myocardial perfusion SPECT (MPS) using a phantom population that includes patient variability. Three RM patterns are included, namely breath-hold, slightly enhanced normal breathing, and deep breathing. For each RM pattern, six 4-D NCAT phantoms were generated, each with anatomical variations. Anterior, lateral and inferior myocardial defects with different sizes and contrasts were inserted. Noise-free SPECT projections were simulated using an analytical projector. Poisson noise was then added to generate noisy realizations. The projection data were reconstructed using the OS-EM algorithm with 1 and 4 subsets/iteration and at 1, 2, 3, 5, 7, and 10 iterations. Short-axis images centered at the centroid of the myocardial defect were extracted, and the channelized Hotelling observer (CHO) was applied for the detection of the defect. The CHO results show that the value of the area under the receiver operating characteristics (ROC) curve (AUC) is affected by the RM amplitude. For all the defect sizes and contrasts studied, the highest or optimal AUC values indicate maximum detectability decrease with the increase of the RM amplitude. With no respiration, the ranking of the optimal AUC value in decreasing order is anterior then lateral, and finally inferior defects. The AUC value of the lateral defect drops more severely as the RM amplitude increases compared to other defect locations. Furthermore, as the RM amplitude increases, the AUC values of the smaller defects drop more quickly than the larger ones. We demonstrated that RM affects defect detectability of MPS imaging. The results indicate that developments of optimal data acquisition methods and RM correction methods are needed to improve the defect detectability in MPS.
Index Terms: Mathematical observer, myocardial perfusion SPECT, phantom population, channelized Hotelling observer (CHO)
I. Introduction
It has been demonstrated that respiratory motion (RM) may cause image artifacts and affect clinical diagnoses in myocardial perfusion SPECT (MPS) [1], [2]. Respiratory motion involves the movements of the heart, diaphragm, lungs and thoracic cage as well as abdominal organs such as the liver and spleen. During normal breathing, heart motion in humans is about 10 mm along the head-to-foot direction. Studies have demonstrated that artifacts from RM in MPS usually appear as a reduction in regional image intensity in the area of the inferior and anterior walls of the left ventricle and that this causes false-positive results [1], [3], [4]. With the advent of multi-modality imaging, co-registered anatomical X-ray CT images can be used in combination with SPECT images for localization and attenuation correction. In SPECT/CT, the major contributions of RM to artifacts involve two aspects. First, the emission data is acquired over the whole respiratory period and this may lead to image blurring. Second, the CT transmission data acquired at a specific phase of the respiratory cycle may not match that of the emission data, and will therefore not reflect the true effect of attenuation of this data. The image artifacts and quantitative errors caused by such a mismatch have been reported [5]–[7]. Results from these studies indicate that free breathing and post-exhalation breath-hold provides higher registration accuracy than a post-inhalation breath-hold protocol [6]. Artifacts due to image mismatch have also been observed in PET/CT cardiac studies [8]–[10]. Many correction methods for RM have been proposed for MPS [11]–[13]. The effects of RM on image non-uniformity and the resulting false-positive diagnoses have been widely investigated in MPS studies. However, reports on the effects of RM on myocardial defect detection in MPS images are limited.
The effects of RM on defect detection task in MPS are complicated. Respiratory motion induces artifacts in normal MPS images. If an artifact results in uptake reduction in a region where a myocardial defect is located, this defect will become more visible and more easily detected. On the other hand, RM causes image blurring that decreases the image contrast and thus degrades defect detection.
In this study, we used a set of phantoms with anatomical variations and a mathematical observer to evaluate the RM effects on defect detection. It has been shown that the channelized Hotelling observer (CHO) [14]–[16] with appropriate channels can predict the human observer performance in defect detection tasks [17]–[20]. In particular, CHO is a linear observer which models the linear nature of human perception in low contrast detection tasks, and the channel mechanism models the frequency selective features of human visual system [16]. In addition, another advantage of CHO study is that, despite the long computer processing time involved, it is less difficult and costly to conduct than a human observer study.
In this study, we investigated factors that may affect myocardial defect detection in Tc-99m sestamibi MPS images. These factors include RM amplitude, defect location, defect size, and defect contrast.
II. Methods
A. Phantoms
The 4-D NCAT phantom has the ability to model the 3-D activity and attenuation distributions of various anatomical features and organs and both cardiac and RM [21], [22]. It has the ability to model. In this study, we focused on the effects of RM and cardiac motion due to the beating heart was not modeled and its effect was not evaluated. Since ventricular diastole represents a large portion of the cardiac cycle, we set the cardiac phase to be in the middle of the diastolic phase during respiration.
We simulated three RM patterns, namely breath-hold (BH), and slightly enhanced normal breathing (NB) and deep breathing (DB) with maximum diaphragm motion amplitude of 2 cm and 4 cm, respectively, to cover a wide range of RM. It should be noted that DB with maximum diaphragm motion amplitude rarely occurs in clinical studies. The RM was modeled in both cranial-and-caudal and dorsal-and-ventral directions and included the motions of the liver, the heart, the stomach, and the spleen in the 4-D NCAT phantom. The liver is set to move forward during inspiration at an amount equal to the anteroposterior expansion of the chest, then back to its original position during expiration, and up and down with the diaphragm. In addition, the motions of heart and liver are set equal in both amplitude and phase in the 4-D NCAT phantom.
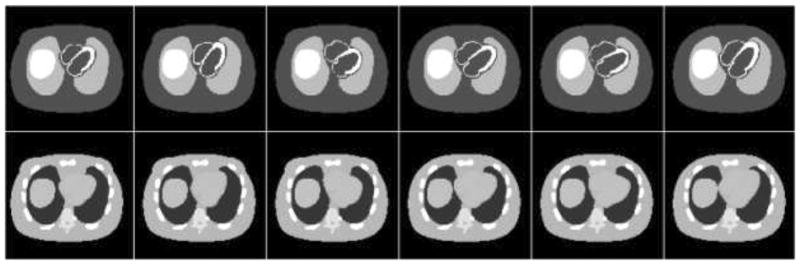
The respiratory period simulated included 2 seconds for inspiration and 3 seconds for expiration [22]. Sixteen uniformly spaced temporal frames were generated throughout a respiratory cycle. For each of the three RM patterns, six 4-D NCAT phantoms (3 males and 3 females) were generated, each with a different anatomy. The anatomical parameters of the phantoms were randomly sampled from the distributions obtained from the Emory PET thorax model database [23], [24]. By doing so, we modeled realistically model patient anatomical variability among a patient population [23]. The distribution of radioactivity concentration in different organs was set to model that of a typical clinical Tc-99m sestamibi MPS study [25]. Sample transaxial slices of the activity and attenuation distributions from each of the six 4-D NCAT phantoms are shown in Fig. 1. The matrix size used to generate the 3-D NCAT phantoms was 128×128×128, with a pixel size and slice thickness of 0.31 cm. Regional myocardial perfusion defects were simulated on the anterior, lateral, and inferior walls of the left ventricle myocardium. The size of the defects was 60° in the circumferential dimension and 2 cm, 1.5 cm and 1 cm in longitudinal size; the contrasts used were 15% (15% uptake reduction compared to normal wall uptake), 11.25% and 7.5%. Fig. 2 shows sample short-axis reconstructed MPS images with and without the myocardial defects.
Fig. 1.
Sample transaxial slices of activity (top row) and attenuation (bottom row) distributions from each of the 4-D NCAT phantoms (from left to right column) represent anatomical variations among a patient population.
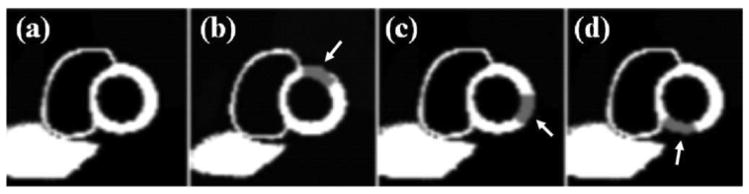
Fig. 2.
Sample simulated short-axis MPS images (a) without a myocardial perfusion defect, (b) with an anterior defect, (c) with a lateral defect, and (d) with an inferior defect. The arrows indicate defect locations. Defect contrast and size have been enhanced for the display.
B. Projection Data Simulation
Projection data was simulated from the 4-D NCAT phantoms with attenuation, scatter, and detector-collimator response using an analytical projector. They were generated from the activity distribution and its corresponding attenuation map for each of the 16 time frame of the respiratory cycle.
A typical clinical stress MPS imaging protocol using a dual-headed SPECT system was used in the simulation. Sixty-four projections were acquired from the rotation of a dual-headed SPECT system over a 180° arc, from 45° right anterior oblique (RAO) to 45° left posterior oblique (LPO). The acquisition time was 20 seconds per projection for the stress study assuming a same-day rest/stress protocol. Four respiratory cycles were included in each projection. The projections of all time frames over the respiratory cycle were summed to generate the average emission data. A low-energy high resolution (LEHR) parallel collimator with thickness of 2.4 cm hole diameter of 1.2 mm was used in the simulation. The intrinsic resolution of the detector modeled was 0.4 cm. The distance from the center-of-rotation to the collimator face (radius-of-rotation) was 20 cm.
A total of 64 noise-free projections with a matrix size of 128×128 were simulated and then collapsed to a 64×64 matrix. To adjust the difficulty of the myocardial defection detection task for the highest possible statistical power in the ROC analysis of the CHO study, the total number of detected counts was set to 64 000 for a 3.1 mm slice through the center of the heart, a count level that is about 1/3 of that found in typical MPS studies. Poisson noise fluctuations were then added to the noise-free projections to generate a total of 30 noisy realizations.
C. Image Reconstruction and Processing
The simulated noisy projection data were reconstructed using the OS-EM algorithm with 12 different subset and iteration settings. They were 1 and 4 (number of subsets)/iteration at 1, 2, 3, 5, 7, and 10 iterations. Note that the 1 subset/iteration results in 64 projections/subset and is equivalent to the ML-EM algorithm. The 4 subsets/iteration resulted in 16 projections/subset and 4 updates per iteration.
The averaged attenuation distribution over the 16 respiratory time frames was used in the image reconstruction. Compensations for attenuation, scatter, and collimator-detector response were implemented. The dimension of the reconstructed images is 64×64×64 with a pixel width and slice thickness of 0.63 cm. The 3-D reconstructed images were then re-sliced to short-axis (SA) images and a single slice, containing the centroid of the myocardial defect, was extracted. The SA images were then processed with a low-pass Butterworth filter using parameters found to be optimal in similar SPECT studies, i.e., an order of 5 and a cutoff frequency of 0.15 pixel−1 [26], [27]. A 32×32 image containing the myocardium was extracted and rescaled to 256-level grayscale for use in the CHO study.
D. Implementation of the Channelized Hotelling Observer (CHO)
The channel model used for CHO was four octave-wide rotationally symmetric frequency channels [27]. Fig. 3 shows the four frequency domain channels and their spatial domain counterparts, shifted to a specific defect location. For every defect location, the center of the spatial domain template was moved to the position of the defect centroid. This was performed by taking the inverse Fourier transform of the frequency domain channel following a phase shift. Then by taking the inner product of each SA image with the spatial domain template of each channel, a four-element feature vector was obtained. We define a data treatment as a combination of given RM amplitude, defect location, size and contrast, and update number of the image reconstruction method. Half of the defect-present and defect-absent feature vector pairs for each data treatment were used as the training set to obtain one trained CHO, which was then tested with the remaining half of feature vectors. The test statistics (rating values) were further analyzed to determine the AUC value using the ROCKIT program [28], which uses a maximum likelihood estimation to fit a bi-normal ROC curve.
Fig. 3.
Images of the four frequency-domain channels (top row) and shifted spatial-domain templates (bottom row) corresponding to a specific defect location used in the CHO study.
The AUC values at different updates for any specific data treatment evaluated were plotted as a function of the number of updates, based on the evaluation of the myocardial defect detection performance for that data treatment. We name this plot an AUC curve. The highest or optimal AUC value of the resulting AUC curve, which is denoted as mAUC, was used as the performance index for that data treatment. The difference in the AUC curves between different data treatments was defined as the AUC difference curve, which was then used to estimate the magnitude of the difference between these data treatments.
III. Results
A. Effect of Respiratory Motion Amplitude
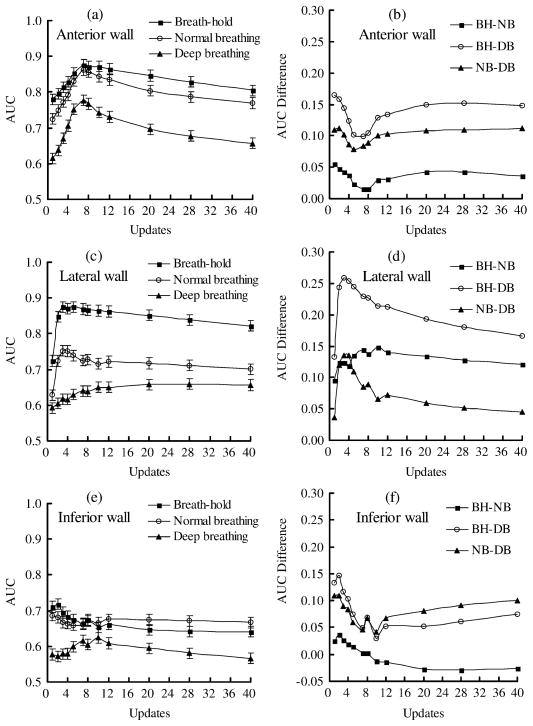
Since the RM effects on myocardial defect detection depend on defect location [1], [3], [4], it is necessary to analyze the defect detectability at each location separately. Images of all defect sizes and defect contrasts for a specific RM amplitude and defect location were included when estimating the AUC value using that data treatment. Fig. 4 shows the AUC (left column) and AUC difference (right column) curves for the effects of RM amplitude on the detection of defect at the anterior (a),(b), lateral (c),(d), and inferior (e),(f) region of the left ventricular walls.
Fig. 4.
The AUC (left column) and AUC difference (right column) curves for the the effects of respiratory motion amplitude on the myocardial defect located at the anterior (a), (b), the lateral (c), (d), and the inferior (e), (f) walls. Error bars show the standard deviation. The acronyms in the figure legends are BH: breath hold; NB: normal breathing; and DB: deep breathing.
In the anterior wall, the ranking of performance, in the order of decreasing AUC, is BH, NB, and DB for all updates (Fig. 4(a)). The mAUCs of BH and NB are very close in value and are considerably higher than that of the DB. Fig. 4(b) shows the AUC difference curves obtained using the defects on the anterior wall.
The ranking data treatments in defect detection on the lateral wall is similar to that on the anterior wall (Fig. 4(c)), but the decrease in AUC values for both BH to NB and BH to DB are much more prominent compared to the anterior wall. The AUC difference curves show that the difference in BH-NB is larger than for NB-DB (Fig. 4(d)). This suggests that the effect of NB is higher on the lateral wall, and is less on the anterior wall.
It was found that the AUC value of DB is lower than that of BH and NB for all updates for defect detection on the inferior wall, and the difference between BH and NB is less obvious (Fig. 4(e), (f)). In some updates, the AUC value of the NB is slightly higher than that of the BH. This may suggest that the artifact of decrease image intensity due to RM plays a relatively more important role in this situation. However, the mAUC of the BH is still higher than that of the NB. These results indicated that the performance of myocardial defect detection is affected by the RM amplitude.
An apparent reduction in count density of the bulls-eye polar map due to RM in both anterior and inferior walls relative to that of lateral wall has been observed in previous study [29]. This is an undesirable effect since it affects the performance of the defect detection task. Our results showed a limited effect of normal respiration on the detection of defects on the anterior wall. This can be attributed to the two cancelling effects of RM. The superimposition of a cold artifact on the defect to be detected seems to improve the defect detection on defect-present images but also seems to cause more false positive decisions on defect-absent images.
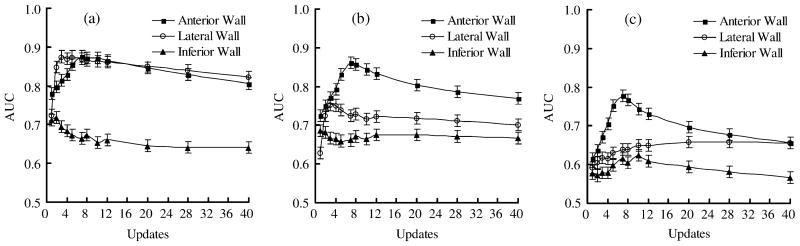
B. Effect of Defect Location
To demonstrate the effects of defect location, the AUC curves shown in Fig. 4 were rearranged and presented for each RM pattern in Fig. 5 showing the AUC curves of the different defect locations of BH (a), NB (b), and DB (c). For all RM amplitudes, the mAUC corresponds to defect detection on the anterior wall is higher than or close to that of the lateral wall, and is considerably higher than that of the inferior wall. The differences between the AUC curves of the anterior and lateral wall are small for BH, but are more prominent for the NB and DB. The mAUC of the lateral wall is higher than that of the inferior wall for all RM patterns.
Fig. 5.
The AUC curves for different defect locations of (a) breath-hold (BH), (b) normal breathing (NB), and (c) deep breathing (DB) as a function of update number. Error bars show the standard deviation.
Note that defect detection on the inferior wall is considerably lower than that on other locations for the BH pattern. This can be attributed to the fact that the inferior wall region is affected more severely by scattering from surrounding organs such as the liver and spleen compared to the other wall regions. Thus, the effectiveness of the compensations for attenuation and scatter may be different in the different wall locations and may decrease the overall detection performance in the inferior wall compared to that of the other defect locations of breath-hold pattern. Further studies are required to investigate this issue.
From these results, it is suggested that the lateral wall is more sensitive to respiration compared to the other locations.
C. Effects of Defect Size
The evaluation of the effects of defect size was based on a defect contrast of 15%. Table I shows the mAUC and mAUC difference between RM amplitudes of different defect sizes at three locations. For a defect size of 2 cm on the anterior wall, the mAUC difference between BH and NB is less prominent, which means that for defect of this size, normal respiration does not affect defect detection on the anterior wall. However, the mAUC decreases considerably as we move from NB to DB. On the lateral wall, NB decreases the detection performance at this size of defect, while DB makes detection significantly more difficult. Similar results were observed on the inferior wall.
TABLE I.
mAUC and mAUC Difference Between Respiratory Motion Patterns of Defect Size 2 cm, 1.5 cm, and 1 cm at the Defect
| Defect size | Anterior wall | Lateral wall | Inferior wall | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| mAUC | BH | NB | DB | BH | NB | DB | BH | NB | DB | |
| 2 cm | 0.944 | 0.942 | 0.877 | 0.936 | 0.840 | 0.681 | 0.928 | 0.853 | 0.712 | |
| 1.5 cm | 0.918 | 0.788 | 0.754 | 0.863 | 0.853 | 0.701 | 0.768 | 0.745 | 0.708 | |
| 1 cm | 0.872 | 0.758 | 0.701 | 0.806 | 0.740 | 0.675 | 0.741 | 0.706 | 0.688 | |
| mAUC difference | BH-NB | NB–DB | BH-DB | BH-NB | NB–DB | BH-DB | BH-NB | NB–DB | BH-DB | |
| 2 cm | 0.002 | 0.065 | 0.067 | 0.096 | 0.159 | 0.255 | 0.075 | 0.141 | 0.216 | |
| 1.5 cm | 0.130 | 0.034 | 0.164 | 0.010 | 0.152 | 0.162 | 0.023 | 0.037 | 0.060 | |
| 1 cm | 0.114 | 0.057 | 0.171 | 0.066 | 0.065 | 0.131 | 0.035 | 0.018 | 0.053 | |
BH: Breath-hold, NB: Normal breathing, DB: Deep breathing.
If the defect size is decreased to 1.5 cm, which is closer to the displacement distance of the heart along the body-axis as well as the system spatial resolution, the effect of RM on the anterior wall becomes more apparent. The mAUC is decreased from 0.918 (BH) to 0.788 (NB) then to 0.754 (DB). In the lateral wall, the mAUC of the BH and NB is very close and that of the DB is lower than the other two. The only obvious difference observed was between BH and DB on the inferior wall.
For defects of 1 cm in size, the difference in mAUC between the RM amplitudes is obvious for the anterior and lateral walls and is less prominent for the inferior wall. This indicates that RM has more significant effects on the detection of smaller defects than on the detection of larger defects on the anterior and left walls; this difference is less significant in the inferior wall.
D. Effect of Defect Contrast
The comparison of defect contrast was based on a defect size of 2 cm in order to allow easier discrimination. The mAUC and mAUC difference between the RM patterns using different contrasts and at three locations are shown in Table II. For an anterior defect whose contrast is 15%, the mAUC difference between BH and NB is less obvious. Normal respiration does not affect the detection performance of an anterior defect of this contrast, but DB will affect it. For a lateral and or inferior defect of this contrast, both NB and DB will influence defect detection. If the defect contrast is decreased to 11.25%, the differences between the mAUCs of BH and NB are smaller in all locations, but DB will affect the detection of anterior and lateral defects. The effect of RM on the defect detection on the inferior wall is not apparent at this level of contrast. For a defect contrast of 7.5%, the difference in mAUC between the different RM patterns is small for all defect locations, which may be due to defect detection at this level of contrast is difficult.
TABLE II.
mAUC and mAUC Difference Between Respiratory Motion Patterns of Defect Contrast 15%, 11.25%, and 7.5% at the Defect Locations
| Defect contrast | Anterior wall | Lateral wall | Inferior wall | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| mAUC | BH | NB | DB | BH | NB | DB | BH | NB | DB | |
| 15% | 0.944 | 0.942 | 0.877 | 0.936 | 0.840 | 0.681 | 0.928 | 0.853 | 0.712 | |
| 11.25% | 0.864 | 0.825 | 0.766 | 0.791 | 0.754 | 0.668 | 0.676 | 0.663 | 0.654 | |
| 7.5% | 0.800 | 0.776 | 0.752 | 0.689 | 0.667 | 0.649 | 0.651 | 0.612 | 0.611 | |
| mAUC difference | BH-NB | NB–DB | BH-DB | BH-NB | NB–DB | BH-DB | BH-NB | NB–DB | BH-DB | |
| 15% | 0.002 | 0.065 | 0.067 | 0.096 | 0.159 | 0.255 | 0.075 | 0.141 | 0.216 | |
| 11.25% | 0.039 | 0.059 | 0.098 | 0.037 | 0.086 | 0.123 | 0.013 | 0.009 | 0.022 | |
| 7.5% | 0.024 | 0.024 | 0.048 | 0.022 | 0.018 | 0.040 | 0.039 | 0.001 | 0.040 | |
BH: Breath-hold, NB: Normal breathing, DB: Deep breathing. Note.
IV. Discussion and Conclusion
Respiratory motion that occurs during MPS studies commonly degrades image quality. Although the heterogeneity in the bull’s-eye polar map caused by RM in normal uniform myocardial perfusion in MPS images is known [29], its effect on defect detection in MPS images is less well known.
Many factors related to respiration affect myocardial defect detection in MPS images. Image blurring caused by RM is an undesirable effect and it decreases the detectability of normal perfusion defects and makes the detection task more difficult. Respiration motion induced cold regional artifact increases false positive decisions from normal MPS images and thus is also an undesirable effect. In contrast, the superimposition of a RM induced artifact on the defect to be detected may make the defect more visible and easier to be detected. Most previous studies have focused on RM induced artifacts on normal MPS images and have shown that it has the greatest effects in the anterior and inferior defects. We used defect absent and defect present images to show the effects of RM on MPS. The tradeoff of these factors may partially explain the difference in results between previous studies and this study.
In this study, we investigated the effects of RM on defect detection in MPS in terms of RM magnitude as well as the size, location and contrast of the myocardial defect using a simulated mathematical observer study. It was shown that the effects of RM on defect detection are related to both the RM pattern and the defect location. The detection of defects on the anterior wall is shown to be more tolerant of normal respiration compared to the lateral and inferior walls. This advantage disappears during deep breathing. The ranking of defect detection in order of decreasing performance among these three wall regions is anterior, lateral, and inferior for all RM patterns. It has also been shown that the decrease in detection performance caused by RM for a specific defect size and contrast is affected by the defect location. For example, normal respiration has no obvious effect on the detection of a 2 cm-sized anterior defect, but the effect becomes apparent in the lateral and inferior walls. For a smaller 1.5 cm-sized defect, normal respiration will affect anterior defect detection but not that on the lateral wall.
There were some limitations in this study. First, the number of phantoms used in this study was limited. Modeling more variations in activity and anatomical distributions will make the simulation more realistic. Second, heart motion due to beating was not included in this study. The diastolic phase may represent a large portion of the cardiac cycle, but it is not all of it. Furthermore, the present study is limited by the fact that it is a computer simulation and although useful in understanding RM effect on MPS, it may not be necessarily translate directly to clinical situation. Further experimental and clinical investigations are therefore needed.
We concluded that RM has considerable influence on the defect detection task performance in MPS. Optimization of the data acquisition method and development of motion correction methods for RM are therefore needed in order to improve defect detection in MPS images.
Acknowledgments
This work was supported in part by the NSC96-2320-B-010-018-MY3, VGHUST Joint Research Program, Tsou’s Foundation Grant VGHUST96-G7-1, and US DHHS NIH Research Grant R01 EB168.
Contributor Information
Yu-Wen Yang, Email: ywyang98@ms25.hinet.net, Department of Biomedical Imaging and Radiological Sciences, National Yang-Ming University, Taipei, Taiwan.
Jyh-Cheng Chen, Email: jcchen@ym.edu.tw, Department of Biomedical Imaging and Radiological Sciences, National Yang-Ming University, Taipei, Taiwan.
Xin He, Email: xinhe@jhmi.edu, Department of Radiology, Johns Hopkins Medical Institute, Baltimore, MD 21218 USA.
Shyh-Jen Wang, Email: jwshyh@vghtpe.gov.tw, Department of Nuclear Medicine, Taipei Veterans General Hospital, Taipei, Taiwan.
Benjamin M. W. Tsui, Email: btsui1@jhmi.edu, Department of Radiology, Johns Hopkins Medical Institute, Baltimore, MD 21218 USA.
References
- 1.Tsui BMW, Segars WP, Lalush DS. Effects of upward creep and respiratory motion in myocardial SPECT. IEEE Trans Nucl Sci. 2000 Jun;47:1192–1195. [Google Scholar]
- 2.Segars WP, Tsui BMW. Study of the efficacy of respiratory gating in myocardial SPECT using the new 4-D NCAT phantom. IEEE Trans Nucl Sci. 2002 Jun;49:675–679. [Google Scholar]
- 3.Cho K, Kumiata SI, Okada S, Kumazaki T. Development of respiratory gated myocardial SPECT system. J Nucl Cardiol. 1999;6:20–28. doi: 10.1016/s1071-3581(99)90061-2. [DOI] [PubMed] [Google Scholar]
- 4.Pitman A, Kalff V, Van Every B, Risa B, Barnden L, Kelly M. Contributions of subdiaphragmatic activity, attenuation, and diaphragmatic motion to inferior wall artifact in attenuation-corrected Tc-99m myocardial perfusion SPECT. J Nucl Cardiol. 2005;12:401–409. doi: 10.1016/j.nuclcard.2005.04.010. [DOI] [PubMed] [Google Scholar]
- 5.Fricke H, Fricek E, Weise R, Kammeier A, Lindner O, Burchert W. A method to remove artifacts in attenuation-corrected myocardial perfusion SPECT introduced by misalignment between emission scan and CT-derived attenuation maps. J Nucl Med. 2004;45:1619–1625. [PubMed] [Google Scholar]
- 6.Utsunomiya D, et al. Object-specific attenuation correction at SPECT/CT in thorax: optimization of respiratory protocol for image registration. Radiology. 2005;237:662–669. doi: 10.1148/radiol.2372041387. [DOI] [PubMed] [Google Scholar]
- 7.Goetze S, Brown TL, Lavely WC, Zhang Z, Bengel FM. Attenuation correction in myocardial perfusion SPECT/CT: Effects of misregistration and value of reregistration. J Nucl Med. 2007 Jul;48:1090–1095. doi: 10.2967/jnumed.107.040535. [DOI] [PubMed] [Google Scholar]
- 8.Pan T, et al. Attenuation correction of PET cardiac data with low-dose average CT in PET/CT. Med Phys. 2006;33:3931–3938. doi: 10.1118/1.2349843. [DOI] [PubMed] [Google Scholar]
- 9.Le Meunier L, Maass-Moreno R, Carrasquillo J, Dieckmann W, Bacharach S. PET/CT imaging: Effect of respiratory motion on apparent myocardial uptake. J Nucl Cardiol. 2006;13:821–830. doi: 10.1016/j.nuclcard.2006.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Alessio AM, Kohlmyer S, Branch K, Chen G, Caldwell J, Kinahan P. Cine CT for attenuation correction in cardiac PET/CT. J Nucl Med. 2007;48:794–801. doi: 10.2967/jnumed.106.035717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bruyant PP, King MA, Pretorius PH. Correction of the respiratory motion of the heart by tracking of the center of mass of thresholded projections: A simulation study using the dynamic MCAT phantom. IEEE Trans Nucl Sci. 2002 Oct;49:2159–2166. [Google Scholar]
- 12.Beach RD, et al. Feasibility of stereo-infrared tracking to monitor patient motion during cardiac SPECT imaging. IEEE Trans Nucl Sci. 2004 Oct;51:2693–2698. doi: 10.1109/TNS.2004.835786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kovalski G, Israel O, Keidar Z, Frenkel A, Sachs J, Azhari H. Correction of heart motion due to respiration in clinical myocardial perfusion SPECT scans using respiratory gating. J Nucl Med. 2007;48:630–636. doi: 10.2967/jnumed.106.037390. [DOI] [PubMed] [Google Scholar]
- 14.Barrett HH, Yao J, Rolland JP, Myers KJ. Model observers for the assessment of image quality. Proc Natl Acad Sci. 1993;90:9758–9765. doi: 10.1073/pnas.90.21.9758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Abbey CK, Barrett HH, Eckstein MP. Practical issues and methodology in assessment of image quality using model observers. Proc SPIE. 1997;3032:182–194. [Google Scholar]
- 16.Myers KJ, Barrett HH. Addition of a channel mechanism to the ideal observer model. J Opt Soc Amer A. 1987;4:2447–2457. doi: 10.1364/josaa.4.002447. [DOI] [PubMed] [Google Scholar]
- 17.Gifford HC, Wells RG, King MA. A comparison of human observer LROC and numerical observer ROC for tumor detection in SPECT images. IEEE Trans Nucl Sci. 1999 Aug;46(4):1032–1037. [Google Scholar]
- 18.Wollenweber SD, Tsui BMW, Lalush DS, Frey EC, LaCroix KJ, Gullberg GT. Comparison of hotelling observer models and human observers in defect detection from myocardial SPECT imaging. IEEE Trans Nucl Sci. 1999 Dec;46(6):2098–2103. [Google Scholar]
- 19.Narayanan MV, et al. Optimization of iterative reconstructions of Tc-sestamibi cardiac SPECT studies using numerical observers. IEEE Trans Nucl Sci. 2002 Oct;49:2355–2360. [Google Scholar]
- 20.Gilland KL, Tsui BMW, Qi Y, Gullberg GT. Comparison of channelized hotelling and human observers in determining optimum OS-EM reconstruction parameters for myocardial SPECT. IEEE Trans Nucl Sci. 2006 Jun;53:1200–1204. [Google Scholar]
- 21.Segars WP, Lalush DS, Tsui BMW. A realistic spline-based dynamic heart phantom. IEEE Trans Nucl Sci. 1999 Jun;46:503–506. [Google Scholar]
- 22.Segars WP, Lalush DS, Tsui BMW. Modeling respiratory mechanics in the MCAT and spline-based MCAT phantoms. IEEE Trans Nucl Sci. 2001 Feb;48:89–97. [Google Scholar]
- 23.He X, Frey EC, Links JM, Gilland KL, Segars WP, Tsui BMW. A mathematical observer study for the evaluation and optimization of compensation methods for myocardial SPECT using a phantom population that realistically models patient variability. IEEE Trans Nucl Sci. 2004 Feb;51:218–224. [Google Scholar]
- 24.Barclay AB, Eisner RL, DiBella EV. Emory PET Thorax Model Database. [Online]. Available: http://www.emory.edu/CRL/abb/thoraxmodel/Contents.html.
- 25.LaCroix KJ, Tsui BM, Frey EC, Jaszczak RJ. Receiver operating characteristic evaluation of iterative reconstruction with attenuation correction in 99 mTc-sestamibi myocardial SPECT images. J Nucl Med. 2000;41:502–513. [PubMed] [Google Scholar]
- 26.Sankaran S, Frey EC, Gilland KL, Tsui BMW. Optimum compensation method and filter cutoff frequency in myocardial SPECT: A human observer study. J Nucl Med. 2002;43:432–438. [PubMed] [Google Scholar]
- 27.Frey EC, Gilland KL, Tsui BMW. Application of task-based measures of image quality to optimization and evaluation of three-dimensional reconstruction-based compensation methods in myocardial perfusion SPECT. IEEE Trans Med Imag. 2002 Sep;21(9):1040–1050. doi: 10.1109/TMI.2002.804437. [DOI] [PubMed] [Google Scholar]
- 28.ROCKIT. ROC Analysis Software; University of Chicago: [Online]. Available: http://home.uchicago.edu/~junji/KRL_HP/KRL_ROC/software_index.htm. [Google Scholar]
- 29.Pitman AG, Kalff V, Van Every B, Risa B, Barnden LR, Kelly MJ. Effect of mechanically simulated diaphragmatic respiratory motion on myocardial SPECT processed with and without attenuation correction. J Nucl Med. 2002;43:1259–1267. [PubMed] [Google Scholar]