Quantifying the impact of fixed effects modeling of clusters in multiple imputation for cluster randomized trials

Abstract

In cluster randomized trials (CRTs), identifiable clusters rather than individuals are randomized to study groups. Resulting data often consist of a small number of clusters with correlated observations within a treatment group. Missing data often present a problem in the analysis of such trials, and multiple imputation (MI) has been used to create complete data sets, enabling subsequent analysis with well-established analysis methods for CRTs. We discuss strategies for accounting for clustering when multiply imputing a missing continuous outcome, focusing on estimation of the variance of group means as used in an adjusted t-test or ANOVA. These analysis procedures are congenial to (can be derived from) a mixed effects imputation model; however, this imputation procedure is not yet available in commercial statistical software. An alternative approach that is readily available and has been used in recent studies is to include fixed effects for cluster, but the impact of using this convenient method has not been studied. We show that under this imputation model the MI variance estimator is positively biased and that smaller ICCs lead to larger overestimation of the MI variance. Analytical expressions for the bias of the variance estimator are derived in the case of data missing completely at random (MCAR), and cases in which data are missing at random (MAR) are illustrated through simulation. Finally, various imputation methods are applied to data from the Detroit Middle School Asthma Project, a recent school-based CRT, and differences in inference are compared.

1 Introduction

In cluster randomized trials (CRTs), identifiable clusters of subjects (e.g. clinics, communities, or schools) rather than individuals are randomized to study groups, while the outcomes of interest are observed on individuals within each cluster. Resulting data often consist of a small number of clusters, each containing a relatively larger number of subjects, and within each cluster observations are likely to be correlated. Usually the resulting intraclass correlation (ICC) is small, with typical values in the 0.05 to 0.001 range (Murray and Blitstein, 2003), but even small values can lead to large variance inflation factors and cannot be ignored (Donner and Klar, 2000; Murray, 1998). Typical analysis methods for CRTs include t-tests adjusted to account for the ICC and mixed model ANOVA/ANCOVA.

Multiple imputation (MI) has been used in practice for handling missing data in cluster randomized trials. An advantage of MI is that the standard analysis approaches developed for CRTs can be used without modification. It is known in the statistical community that the correct multiple imputation model in cluster randomization is one that accounts for the clustering through mixed effects. Imputations under the mixed effects model are congenial (in the sense of Meng, 1994) to an analysis that does account for the clustering within study groups, that is, the analysis procedure can be derived from the imputation model. However, there is concern that practitioners do not understand what constitutes a congenial imputation model in the context of CRTs (D. M. Murray, personal communication, 2010). While it is well known by practitioners that using fixed effects for clusters (i.e. dummy variables indicating cluster membership) in analysis models leads to inflated type I error, the impact of using this type of model for imputation has not been studied.

This paper describes the effects of imputing data from cluster randomized trials (CRTs) using a model with fixed effects for cluster on subsequent analyses in which clusters are appropriately modeled as random effects. We restrict attention to a continuous outcome in a balanced design, and throughout we assume that the mean is correctly specified and focus on the impact of model misspecification on the MI variance estimator. We derive an expression for the bias of the MI variance estimator when data are missing completely at random (MCAR). Through simulation we compare the fixed effects for cluster imputation model to one that ignores clusters, as well as a model that uses random effects for cluster, under both an MCAR mechanism with available covariates as well as a missing at random (MAR) mechanism.

There are several examples of CRTs that have used mixed effects models for analysis, but fixed effects for clusters in imputation. One example is in the Community Youth Development Study (CYDS), which includes an extended nested cohort CRT evaluating the effectiveness of a prevention system designed to reduce adolescent substance abuse (Hawkins et al., 2008; Brown et al., 2009; Hawkins et al., 2009). Twenty-four communities in seven states were matched within state and randomized to receive either the intervention or control condition. Details on recruitment methods and study design are available elsewhere (Brown et al., 2009). Analysis models included complex multi-level hierarchical models that properly captured the nested structure of the data (Brown et al., 2009). However, imputation in this study used NORM software (Schafer, 2000), which uses a multivariate normal model to generate imputations and cannot accommodate random effects. Brown et al. (2009, p.362) state that they used “dummy-coded indicators of community membership (to preserve the nested structure of the data).” This language suggests that the authors wanted to incorporate the clustering into the imputation model, but were not aware of the proper way to do so.

Another example of a CRT using fixed effects imputation is the Detroit Middle School Asthma Project (DMSAP), an extended nested cohort CRT assessing two in-school interventions to enhance management of asthma over a three year time period (Clark et al., 2010). Nineteen middle schools were randomized to one of three study arms: control (six schools), program one (seven schools), and program two (six schools). Details on the methods used to identify and enroll students with probable asthma are available elsewhere (Clark et al., 2010). Linear and nonlinear mixed models were used for analysis. Imputation was performed with IVEWARE (Raghunathan et al., 2001), a SAS-callable software that uses sequential regression imputation and cannot incorporate random effects. The authors used “dummy variables for school to incorporate the clustered design” (Clark et al., 2010, p.84). As in the CYDS, the intention of preserving the hierarchical structure was there, but software limitations did not allow for a congenial imputation model. In particular, IVEWARE was chosen due to its ability to handle the continuous, binary, multicategory, and count variables that were all subject to missingness in a non-monotone pattern.

Imputation methods in current commercial software only allow for fixed effects for clusters, for example proc mi in SAS (SAS Institute Inc., 2004) or mi impute in Stata (Stata Press, 2009). Analysts wanting to incorporate cluster effects must use fixed effects for clusters even when subsequent analyses would not use this model. Examples of additional recent CRTs that used multiple imputation include French et al. (2005), Pate et al. (2005), and Ganz et al. (2005). Details of the imputation procedures used were not given, but since each study used SAS for analysis it is likely that they used SAS for the imputations as well, and thus were forced to either include fixed effects for clusters or ignore them altogether.

The only software that we are aware of that allows use of mixed effects models for imputation is PAN (Schafer, 2008), available as a package in R (R Development Core Team, 2009). Details on the MCMC imputation method used in PAN can be found in Schafer (1997). However, R is not widely used outside of the statistical community and is less likely to be used by practitioners designing and analyzing CRTs than the more widely available commercial alternatives. In addition, PAN uses a multivariate linear mixed effects model, so categorical data must be treated as multivariate normal in imputations, which can lead to bias (Horton et al., 2003).

The effect of ignoring the clusters in CRTs was studied by Taljaard et al. (2008). They evaluated imputation strategies for CRT data via simulation, assuming missingness was completely at random (MCAR). They concluded that if the ICC is small (<0.005), ignoring the clusters may yield acceptable Type I error, but if ICCs are larger, ignoring the clustering will lead to severe inflation of the Type I error. The authors compared results from ignoring clusters to several alternate imputation methods, most notably a mixed effects imputation model with random effects for cluster. Taljaard et al. did not evaluate the approach using fixed effects for clusters.

In the context of clustered data from sample surveys, Reiter et al. (2006) compared fixed and mixed effects imputation strategies when survey data were missing at random (MAR). Fixed and mixed effects imputation strategies had similar performance for most scenarios. The methods only differed when there were no population stratum or cluster effects, with the fixed effects imputation resulting in inflated variance estimates. While both survey data and CRT data can be clustered, the effect of the clustering on analyses is usually appreciably less in survey data (Scott and Holt, 1982). In survey data, one generally assumes that the ICC for covariates is similar in magnitude to the ICC for the outcome variable. This is in contrast to CRT data, where the ICC of the key covariate of interest (treatment group) is exactly one. Thus the findings in Reiter et al. cannot be automatically extended to data from CRTs.

This article is organized as follows. Section 2 reviews methods for analysis of data from CRTs and their extension to a multiple imputation analysis. In Section 3 we describe the fixed effects for cluster imputation model. In Section 4 we derive an analytical expression for the bias of the multiple imputation variance estimator under MCAR when imputing with a fixed effects model. In Section 5 we use a simulation study to evaluate the bias when covariates are available under MCAR as well as under MAR, and compare to alternate imputation models. In Section 6 we illustrate differences in inference under different imputation models using data from the Detroit Middle School Asthma Study. Some concluding remarks and suggestions for future research are provided in Section 7.

2 Variance Estimation for CRTs

2.1 Complete Data

We now review existing results for analysis of CRTs (Murray, 1998). Assume we have a balanced design post-test only CRT with l = 1, 2 treatment groups, each consisting of j = 1, …, k clusters with i = 1, …, m individuals per cluster. The outcome y_ijl for subject i in cluster j in treatment group l is assumed to follow the model,

$$\begin{array}{c}\hfill y_{\mathit{\text{ijl}}}={\mu }_l+b_{\mathit{\text{jl}}}+e_{\mathit{\text{ijl}}},\hfill \\ \hfill b_{\mathit{\text{jl}}}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}N(0,\rho {\sigma }^2)\hfill \\ \hfill e_{\mathit{\text{ijl}}}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}N(0,(1-\rho ){\sigma }^2),\hfill \end{array}$$ (1)

where b_jl ⊥ e_ijl and ρ is the intraclass correlation. The variance of the mean for study group l is then given by:

$$\text{Var}({\overline{y}}_{··l})=\frac{{\sigma }^2}{\mathit{\text{km}}}[1+(m-1)\rho ],$$ (2)

where ${\overline{y}}_{··l}={\displaystyle {\sum }_{j=1}^k}{\displaystyle {\sum }_{i=1}^m}{y}_{\mathit{\text{ijl}}}/\mathit{\text{km}}$.

An ANOVA partitioning of variance is used to estimate σ² and ρ. The mean squares between clusters (MSC) and within (MSW) clusters are given by,

$$\begin{array}{cc}\mathit{\text{MSW}}=\frac{{\displaystyle {\sum }_{l=1}^2}{\displaystyle {\sum }_{j=1}^k}{\displaystyle {\sum }_{i=1}^m}{(y_{\mathit{\text{ijl}}}-{\overline{y}}_{·\mathit{\text{jl}}})}^2}{2k(m-1)}\hfill & \mathit{\text{MSC}}=\frac{{\displaystyle {\sum }_{l=1}^2}{\displaystyle {\sum }_{j=1}^k}m{({\overline{y}}_{·\mathit{\text{jl}}}-{\overline{y}}_{··l})}^2}{2(k-1)}\hfill \end{array}.$$ (3)

Estimates of σ² and ρ are then given by,

$$\begin{array}{cc}{\hat{\sigma }}^2=\frac{\mathit{\text{MSC}}-\mathit{\text{MSW}}}{m}+\mathit{\text{MSW}}\hfill & \hat{\rho }=\frac{\mathit{\text{MSC}}-\mathit{\text{MSW}}}{\mathit{\text{MSC}}+(m-1)\mathit{\text{MSW}}}.\hfill \end{array}$$ (4)

Plugging (3) and (4) into (2) yields the estimator for the variance of a group mean.

These variance estimates are used directly when comparing two group means with a two-sample t-test adjusted to reflect the ICC (Donner and Klar, 2000). The test is given by

$$T=\frac{{\overline{y}}_{··2}-{\overline{y}}_{··1}}{\sqrt{\frac{2{\hat{\sigma }}^2}{\mathit{\text{km}}}[1+(m-1)\hat{\rho }]}}~t_{2(k-1)}.$$ (5)

Substituting (4) into (5) yields an alternate expression for the estimated variance of the difference in means, V̂(ȳ_··2 − ȳ_··1) = 2 × MSC/km.

Several other analysis methods are available for comparing two group means in the post-test only CRT design. One could first calculate the cluster means and apply the standard two-sample t-test to the cluster means. Alternatively one could use a mixed-effects ANOVA model (Murray, 1998). A non-parametric option is to use a permutation test on the cluster means, where treatment assignments are permuted (Feng et al., 2001). For balanced designs with no covariates these approaches are all identical (Donner and Klar, 1994).

For the purpose of this paper we focus on estimating the variance of a single group mean, since this is used directly in the adjusted t-test. Overestimating the variance would lead to conservative tests, and underestimating the variance would inflate Type I error.

2.2 Incomplete Data

Suppose now that some subjects in each cluster are missing the outcome. If the data are missing completely at random (MCAR), a complete case analysis is valid, but may be inefficient (Little and Rubin, 2002). In addition, an interesting feature of CRTs is that singly imputing the corresponding cluster mean for a missing response also leads to valid inference under MCAR (Taljaard et al., 2008). This result is intuitive with the two-stage analysis that first calculates cluster means and then performs a t-test on the means. Clearly the cluster means are unchanged by this type of imputation, so the subsequent t-test whose degrees of freedom depend on the number of clusters, not the number of subjects, is valid. If data are missing at random (MAR) the complete case analysis and thus singly imputing the cluster means may be invalid (Little and Rubin, 2002).

An alternative method to handle incomplete data in CRTs is to multiply impute the missing values. First proposed by Rubin (1978), multiple imputation (MI) involves performing D ≥ 2 independent imputations to create D complete data sets that are each analyzed with standard methods and estimates combined over the D completed data sets. Unlike a complete case analysis, multiple imputation is valid when data are MAR (in addition to MCAR), assuming the multiple imputation model correctly includes variables associated with response propensity (Little and Rubin, 2002).

For multiply imputed CRT data, estimates of the l^th group mean and its variance would be obtained as follows. Let the mean of group l in imputed data set d be denoted ${\overline{y}}_{··l}^{(d)}$ and let W^(d) be its estimated variance using Equation (2). These D estimates are then combined to obtain the MI mean estimate and MI variance estimate. The overall group mean estimate is given by the average of the D mean estimates,

$${\hat{\theta }}_D=\frac{1}{D}{\displaystyle \sum _{d=1}^D}{\overline{y}}_{··l}^{(d)}.$$ (6)

The estimated variance of θ̂_D is the sum of the average within-imputation variance and the between-imputation variance. The average within-imputation variance is

$${\overline{W}}_D=\frac{1}{D}{\displaystyle \sum _{d=1}^D}{W}^{(d)}$$

and the between-imputation variance is

$$B_D=\frac{1}{D-1}{\displaystyle \sum _{d=1}^D}{({\overline{y}}_{··l}^{(d)}-{\hat{\theta }}_D)}^2.$$

The total variance of θ̂_D is the sum of these expressions, with a bias correction for the finite number of multiply imputed data sets,

$${\hat{V}}_D=\hat{V}({\hat{\theta }}_D)={\overline{W}}_D+\frac{D+1}{D}{B}_D.$$ (7)

The adjusted t-test (for a single group mean) under multiple imputation is then given by

$$T=\frac{{\hat{\theta }}_D-{\theta }_D}{\sqrt{{\hat{V}}_D}}~t_{\nu }.$$

For CRTs, the complete data degrees of freedom are small, since it is based on the number of clusters not the total number of subjects. For this reason the usual formula for the degrees of freedom ν for multiply imputed data,

$$\nu =(D-1){(1+\frac{D}{D+1}\frac{{\overline{W}}_D}{B_D})}^2,$$

is not appropriate. When the completed data sets have limited degrees of freedom, a refinement to the ν is recommended (Barnard and Rubin, 1999; Little and Rubin, 2002),

$${\nu }^{*}={({\nu }^{-1}+{\hat{\nu }}_{\mathit{\text{obs}}}^{-1})}^{-1}$$

where

$${\hat{\nu }}_{\mathit{\text{obs}}}=\left(\frac{{\overline{W}}_D}{{\hat{V}}_D}\right)\left(\frac{{\nu }_{\mathit{\text{com}}}+1}{{\nu }_{\mathit{\text{com}}}+3}\right){\nu }_{\mathit{\text{com}}}$$

and ν_com are the degrees of freedom for the complete data test (i.e., 2(k − 1)).

3 Fixed Effects Imputation Model for CRTs

Creation of the multiply imputed values is a key step in a multiple imputation analysis. We assume that the imputer uses a parametric regression model, though we expect that these results would extend to imputation via a non-parametric method such as hot deck with the approximate Bayesian bootstrap (Rubin and Schenker, 1986). Using widely available commercial software the only method for incorporating cluster effects is to include indicators for cluster in a regression imputation model. Letting I(·) denote the indicator function that takes the value 1 when the contained expression is true and 0 otherwise, one way to write the fixed effects regression model is,

$$y_{\mathit{\text{ijl}}}={\displaystyle \sum _{g=1}^2}{\displaystyle \sum _{c=1}^k}{\alpha }_{\mathit{\text{cg}}}I(c=j,g=l)+X_{\mathit{\text{ijl}}}\beta +e_{\mathit{\text{ijl}}}.$$ (8)

In this model the unknown parameters {α_cg} allow a different intercept for each cluster c nested within treatment group g, X_ijl is a vector of additional covariates included in the regression model, β is a vector of unknown regression coefficients, and e_ijl ~ N(0, ϕ²) is residual error. We use ϕ² to distinguish this variance from that of the data generation model described in Section 2.1.

To make the imputation “proper” in the sense of Rubin (1987), imputations are generated in a two-step process. First, values for the regression coefficients α, β, and ϕ² are drawn from their observed-data posterior distributions. Second, random draws of the missing y_ijl are created conditional on the drawn values of the parameters. This type of stochastic regression imputation is available in SAS (proc mi) and other software. The details of the imputation method for data from CRTs with no covariates and fixed effects for cluster is given in Appendix A.1.

There is an inherent discrepancy between this imputation model and the analysis model, and we can write both models (omitting any additional covariates X) in ANOVA form for direct comparison. We use tildes to denote random effects.

$$\begin{array}{cc}\text{Imputation model}:\hfill & y_{\mathit{\text{ijl}}}=\mu +G_l+C_{\mathit{\text{jl}}}+{\tilde{e}}_{\mathit{\text{ijl}}}\hfill \\ \hfill \text{Analysis model}:& y_{\mathit{\text{ijl}}}=\mu +G_l+{\tilde{C}}_{\mathit{\text{jl}}}+{\tilde{e}}_{\mathit{\text{ijl}}}\hfill \end{array}$$

For both models the observed value y_ijl is expressed as a function of the grand mean (μ), the effect of the lth group (G_l), the effect of the j^th cluster within the lth group (C_jl or C̃_jl), and residual error (ẽ_ijl). In order to account for the positive ICC, the analysis model includes the cluster effect as a random effect. However, the fixed effect imputation model incorporates the cluster effect as a fixed effect.

4 MCAR, No Covariates

We begin by examining the simplest case, where data are missing completely at random and there are no additional covariates for inclusion in the imputation model. We assume that the data have the (balanced) form described in Section 2.1. For simplicity we assume that the follow-up rate π in each cluster is the same, and treat sample sizes as fixed (i.e. number of respondents in each cluster = mπ = fixed). Multiple imputation proceeds using the model (8) with fixed effects for cluster and no additional covariates, which effectively imputes for each missing observation the mean of the cluster to which the observation belongs, plus random error. Assume a total of D imputed data sets are created.

We focus on estimation of a single group mean and its variance. The expected value of the MI mean estimator for group l as D → ∞ is E(θ̂_D) = E[ȳ_··l] = μ_l, and thus is unbiased under MCAR. However, the MI variance estimator is biased. As shown in Appendix A.2., as D → ∞, the variance of the point estimator θ̂_D is given by,

$$\text{Var}({\hat{\theta }}_D)=[1+(m\pi -1)\rho ]{\sigma }^2/\mathit{\text{km}}\pi$$ (9)

while the mean of the multiple imputation variance estimator V̂_D is given by,

$$\mathrm{E}[{\hat{V}}_D]=[1+(m\pi -1)\rho ]{\sigma }^2/\mathit{\text{km}}\pi +2(1-\pi )(1-\rho ){\sigma }^2/\mathit{\text{km}}\pi .$$ (10)

The bias of the multiple imputation variance estimator is then given by,

$$\mathrm{E}({\hat{V}}_D)-\text{Var}({\hat{\theta }}_D)=2(1-\pi )(1-\rho ){\sigma }^2/\mathit{\text{km}}\pi .$$

The bias is always positive and the MI variance estimator overestimates true variance. Smaller cluster size m, smaller number of clusters k, and a greater amount of nonresponse (smaller π) lead to larger bias. In addition, smaller ρ leads to greater bias. To visualize the bias as a function of these parameters, we rewrite in terms of relative bias as:

$$\text{Relative Bias}=\frac{\mathrm{E}({\hat{V}}_D)-\text{Var}({\hat{\theta }}_D)}{\text{Var}({\hat{\theta }}_D)}=\frac{2(1-\pi )(1-\rho )}{1+(m\pi -1)\rho }$$

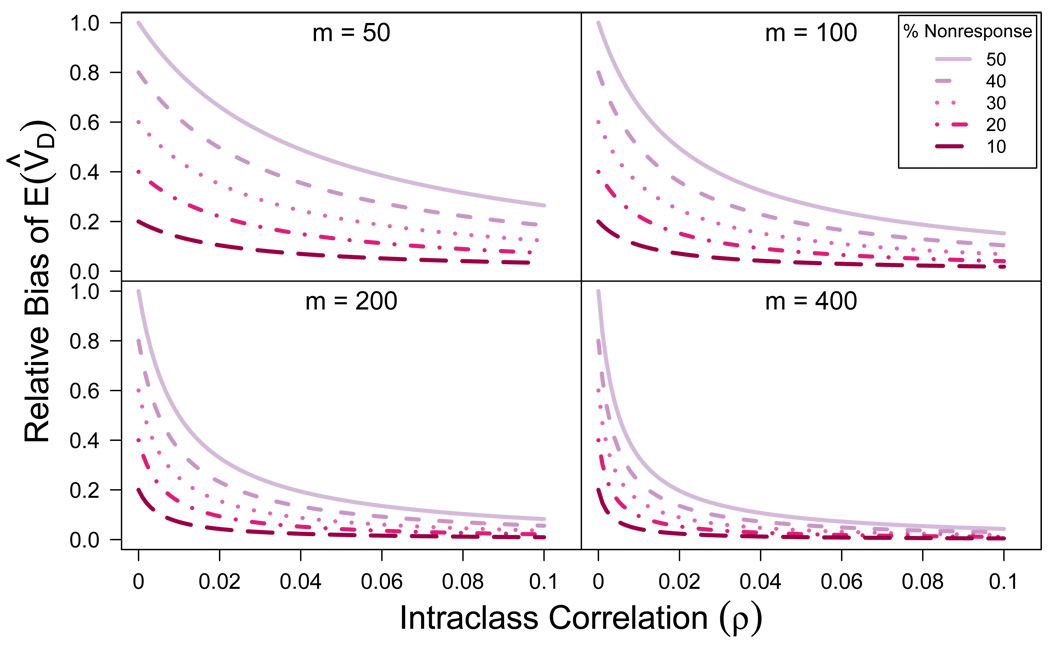
From this equation we see that the relative bias does not depend on the number of clusters k, but does still depend on cluster size, response rate, and ICC. Plots of the relative bias as a function of ICC (ρ) for various combinations of cluster size m and nonresponse rate (1 − π) are shown in Figure 1. The largest bias is at ρ = 0, when the relative bias is 2(1 − π), and as ρ → 1, the bias goes to zero.

Figure 1.

Relative bias of the MI variance estimator as a function of ICC (ρ) for various combinations of cluster size m and nonresponse rate (1 − π)

It seems startling at first that smaller ICCs lead to larger overestimation. We would tend to think that as the ICC tends to zero, an imputation method that treats cluster members as independent (i.e. no random effects) would perform better. However, if we think of the imputation with fixed effects as fixing the cluster means at the observed values, we are forcing the imputed values to cluster around these means. Thus the imputation artificially inflates the ICC for the imputed observations. As ρ → 0 the variance of the mean of the observed values approaches the variance under independence, but by imputing under the fixed effects model we force apart the means of the imputed data. This increases the between-cluster variability, inflating the ICC, and overestimating the estimated variance of the mean.

5 MAR and MCAR with Covariates

Next we investigate more realistic situations where covariate information is available to aid in the imputation, both under MCAR and MAR. Performance of the MI variance estimator was evaluated for these situations with a Monte Carlo study. As in Section 4 we restrict attention to estimating the mean of a single group, so the subscript l is dropped in the remainder of this section. All simulations were performed using the software package R (R Development Core Team, 2009).

5.1 Simulation Study: Data Generation

Since the results from MCAR with no covariates showed that smaller cluster sizes led to worse performance of the MI variance estimator, we chose m = 50 subjects for each of k = 20 clusters. For each subject i in cluster j a single covariate X was generated as x_ij ~ N(0, 1), independently for i = {1, …, m}, j = {1, …, k}. We fixed σ² = 100 and generated the outcome Y from y_ij = 10 + τσx_ij + b_j + e_ij where b_j ~ N(0, ρσ²) is the cluster-level error and e_ij ~ N(0, (1 − τ² − ρ)σ²) is the subject-level error.

Parameters varied in generating the data included the unconditional ICC of Y, ρ = (0.001, 0.005, 0.01, 0.05, 0.1, 0.5), and the correlation between the outcome Y and covariateX, τ = (0, 0.3, 0.5, 0.7, 0.9). Though CRTs rarely have ICCs above 0.1 (Murray and Blitstein, 2003), the value of ρ = 0.5 was included to evaluate relative performance of the methods in the extreme. When the unconditional ICC is this large, the data generation model does not allow τ = 0.9, so this one combination is excluded from the simulation. When τ = 0, X provides no extra information about Y, and as τ → 1 the strength of X as a predictor of Y increases. There are two types of ICCs to consider due to the introduction of the covariate X. The conditional ICC is the ratio of between-cluster variance to total variance conditional on X; while the unconditional ICC is the same ratio, integrating over X. For the purposes of our simulation we focused on the unconditional ICC, since the analysis goal is estimating the unconditional mean of Y; we note that the two quantites are (obviously) closely related.

Once data were created for a specified τ and ρ, missing values were imposed by generating the response indicator r_ij according to a logistic regression model,

$$\text{logit}(P(r_{\mathit{\text{ij}}}=0|y_{\mathit{\text{ij}}},x_{\mathit{\text{ij}}}))={\alpha }_0+{\alpha }_1{x}_{\mathit{\text{ij}}}$$ (11)

The intercept α₀ was chosen so that E(r_ij) = 0.7, giving an expected 30% nonresponse rate. We generated missingness under two different mechanisms based on the value of α₁: (a) MCAR: α₁ = 0, (b) MAR: α₁ = 1. We also evaluated the intermediate value of α₁ = 0.5; resulting conclusions were the same and results are not shown.

5.2 Simulation Study: Imputation Methods

We compared the performance of three multiple imputation models. All three methods included a fixed effect for the covariate X, but varied in how they incorporated cluster effects. The first model used fixed effects for cluster (as in (8) and Section 4). Alternative models included a naive model that ignored clusters and a model with random effects for clusters, which matched the data generation model. The MICE package in R (van Buuren and Groothuis-Oudshoorn, 2010) was used for the fixed effects for cluster imputation and the imputation ignoring clusters; the PAN package (Schafer, 2008) was used for mixed effects imputation. Details on the MCMC imputation method used in PAN can be found in Schafer (1997); briefly, it uses an MCMC algorithm to simulate draws from the posterior distribution of the parameters and then imputes missing values conditional on the drawn parameter values. For our simulation we selected non-informative priors for regression parameters, diffuse inverse-Wishart priors for variance components, and allowed a burn-in period of 1,000 iterations before imputing on every 100th iteration.

For a given τ, ρ, and α₁ the simulation proceeded as follows. First we generated a sample of size k × m = 1, 000 for the covariate X and then generated Y given X. Nonresponse indicators for each observation were independently drawn from a Bernoulli distribution with probabilities according to (11) and values were then deleted to create the respondent data set. We then separately performed each type of multiple imputation with D = 10. For each method, the MI estimator of the overall mean of Y (θ̂_D) and its variance (V̂_D) were calculated using (6) and (7). This entire process was repeated 1,000 times for each parameter combination and results were averaged over the 1,000 replicates.

Performance of the MI estimators was summarized as follows. The average MI variance estimate was taken to be the average of 1,000 point estimates of V̂_D. This was compared to the empirical variance of the MI mean, defined as the variance of the 1,000 point estimates of θ̂_D, using the ratio V̂_D/θ̂_D. In order to obtain an estimate of the simulation error for this ratio we generated interval estimates using the bootstrap (Efron, 1994), since each set of 1,000 replicates only provided a single point estimate of the ratio. Five hundred bootstrap samples were drawn from the set of 1,000 pairs of estimates (θ̂_D, V̂_D) and the empirical and estimated variance were recalculated. The 2.5th to 97.5th percentiles of the resulting bootstrap distribution are provided together with the point estimates. In addition to evaluating the ratio of estimated to empirical variance, coverage properties of a nominal 95% interval were also evaluated for each of the three imputation methods.

5.3 Simulation Study: Results

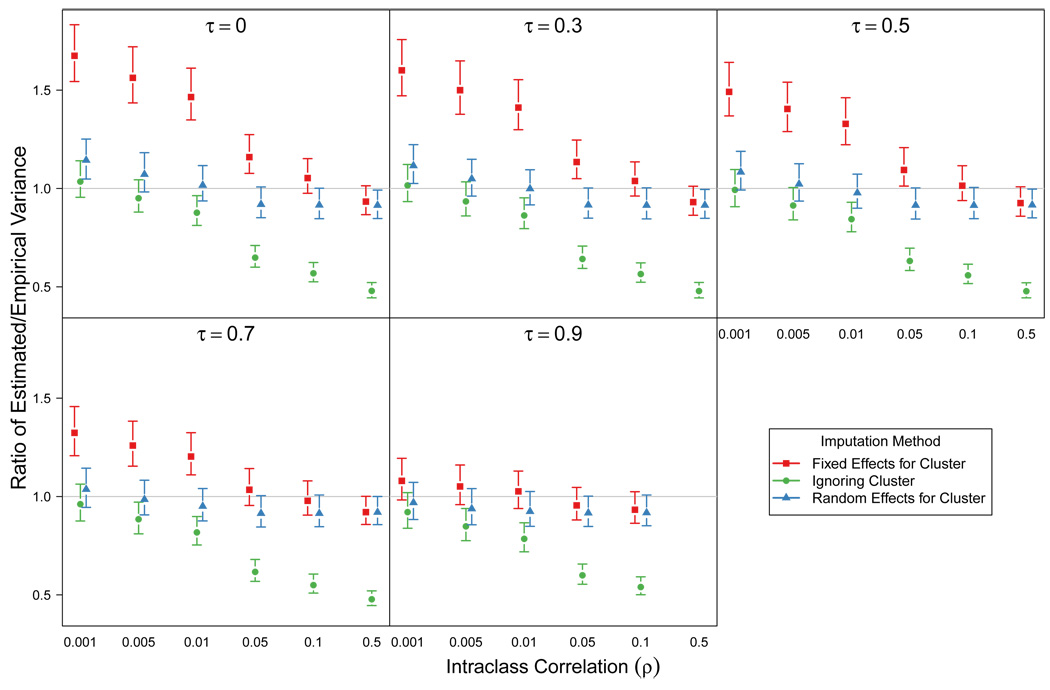
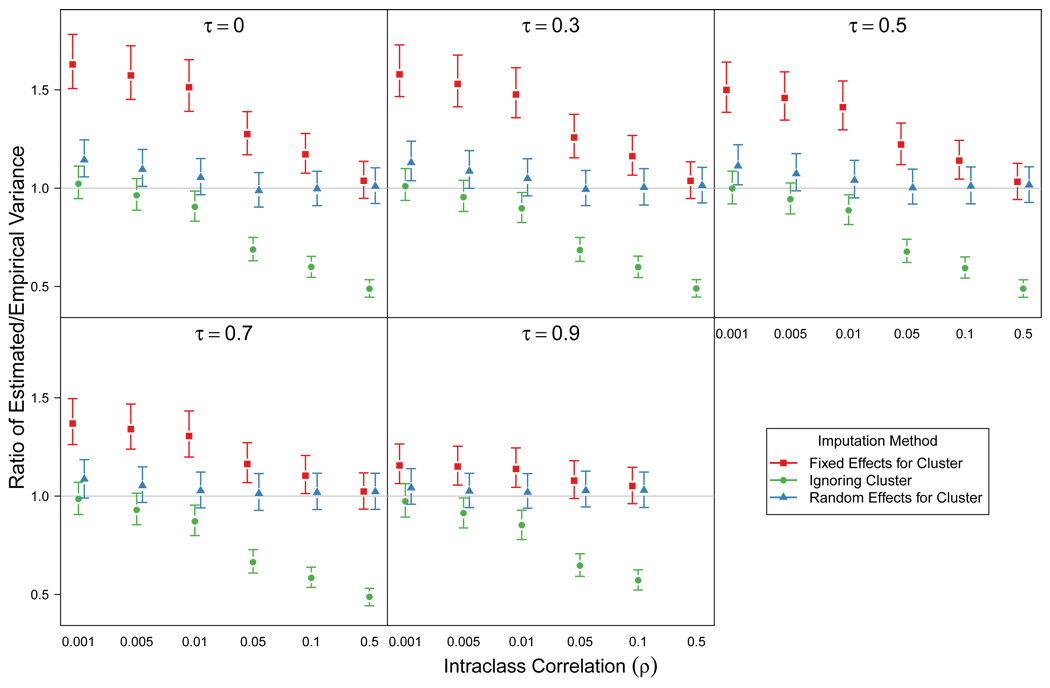
Point estimates of the ratio of estimated to empirical MI variance and bootstrap intervals for all three imputation methods are seen in Figure 2 for MCAR and Figure 3 for MAR. In comparing the two sets of figures, we see that the difference between the MCAR and the MAR mechanisms is slight. It appears that whether X actually drives missingness is not the important factor; since in both cases we condition on X in the imputations the two situations are very similar.

Figure 2.

MCAR mechanism: Ratio of average MI variance estimate to empirical variance of the MI mean estimator as a function of unconditional ICC (ρ) and correlation between outcome and covariate (π). Lines are bootstrapped 95% intervals (2.5th to 97.5th percentiles) to show simulation error. Results from 1,000 replicates for each parameter combination.

Figure 3.

MAR mechanism: Ratio of average MI variance estimate to empirical variance of the MI mean estimator as a function of unconditional ICC (ρ) and correlation between outcome and covariate (τ). Lines are bootstrapped 95% intervals (2.5th to 97.5th percentiles) to show simulation error. Results from 1,000 replicates for each parameter combination.

The performance of the fixed effects for cluster imputation method can be summarized as follows. When τ = 0, the covariate doesn’t inform Y and the situation is similar to that in Section 4 (MCAR with no covariates). The most severe overestimation of the variance is at ρ = 0 and this bias decreases as ρ increases. As τ → 1, the strength of the covariate as a predictor of Y increases and the overestimation of the MI variance is less pronounced. However, even when X is extremely highly correlated with Y(τ = 0.9) there is still some overestimation of variance for the lowest values of ρ. In the exaggerated (for CRTs) case of ρ = 0.5, the results from a fixed effects for cluster imputation method are indistinguishable from the results from the random effects for cluster imputation method.

Intuitively, we can think of the effect of τ as follows. For a given unconditional ICC ρ, the conditional ICC ρ_y·x will be larger than ρ, assuming X explains some of the total variance of Y. In the imputation model with fixed effects for clusters, since we condition on X we are misspecifying the conditional ICC of Y. For a given unconditional ICC, larger τ leads to larger unconditional ICC, and since we have seen that the overestimation of variance is actually less severe for higher ICC values, the overestimation of variance will be less pronounced for larger τ.

In contrast to the fixed effects for cluster model, the imputation model that ignores clusters performs poorly for large values of ρ and underestimates the true MI variance. This agrees with results for type I error in previous studies (Taljaard et al., 2008). The strength of the covariate does not affect the performance of this imputation method; the underestimation is similar for all values of τ.

The final method, using random effects for cluster, is undoubtedly the best method in this simulation. There is slight overestimation of variance for the smallest value of ρ and with an uninformative covariate, but for all other scenarios the ratio is approximately 1. For this method we are both imputing and analyzing the data with the same model, which is also the data generation model, so this result is not a surprise. Clearly this method would be the recommended method for practitioners were software readily available.

Over and underestimation of variance can also be seen when examining coverage of nominal 95% intervals. Empirical coverage for each method is shown in Table 1 for both MCAR and MAR mechanisms. As expected, imputation with fixed effects for cluster leads to overcoverage for small ρ, while ignoring clusters leads to undercoverage for large ρ. These results highlight the errors in inference that may result from these types of imputation models; either a decrease in power (fixed effects for cluster) or an increase in type I error (ignoring clusters). Coverage is at or near nominal for the random effects imputation method for all values of ρ and τ.

Table 1.

Empirical coverage of nominal 95% interval for three imputation methods: FIX = Fixed cluster effects; IGN = Ignoring clusters; RAN = Random cluster effects. Results from 1,000 replicates for each combination of correlation between outcome Y and covariate X (τ), unconditional ICC of Y (ρ), and missingness mechanisms (MCAR, MAR).

		MCAR			MAR
τ	ρ	FIX	IGN	RAN	FIX	IGN	RAN
0.0	0.001	99.2	97.2	97.4	98.9	96.9	97.7
	0.005	99.0	96.3	97.0	99.0	96.4	97.5
	0.01	99.0	96.0	97.0	98.5	95.9	96.9
	0.05	97.3	91.3	94.7	98.0	93.2	95.9
	0.1	96.3	89.7	94.2	97.2	90.2	95.6
	0.5	94.6	83.8	94.7	96.3	85.6	95.8
0.3	0.001	99.0	96.9	97.4	99.1	96.8	97.7
	0.005	98.6	96.5	96.6	99.1	96.4	96.9
	0.01	98.6	95.7	96.1	98.9	95.4	96.6
	0.05	96.7	91.0	94.5	97.5	93.1	96.0
	0.1	96.0	88.7	94.3	96.7	90.7	96.0
	0.5	94.6	83.7	94.7	95.9	85.7	95.8
0.5	0.001	98.9	96.5	96.7	98.5	96.6	97.2
	0.005	98.7	96.0	95.9	98.7	96.2	96.4
	0.01	97.9	95.1	95.8	98.5	95.2	96.2
	0.05	96.4	90.3	94.8	97.1	92.7	96.2
	0.1	95.9	87.7	94.6	96.5	90.4	96.3
	0.5	94.4	84.1	94.3	95.6	85.5	95.5
0.7	0.001	98.4	96.1	96.5	97.7	96.4	97.1
	0.005	98.1	94.6	96.3	98.1	95.4	96.4
	0.01	97.7	94.4	95.8	97.8	94.3	95.8
	0.05	95.9	89.3	94.8	96.9	91.0	96.3
	0.1	95.2	87.0	94.8	96.5	89.2	96.2
	0.5	94.1	83.5	94.1	95.6	85.1	95.6
0.9	0.001	96.4	94.8	94.8	97.2	96.1	96.3
	0.005	96.1	93.9	94.8	96.7	94.7	96.0
	0.01	96.2	92.8	94.9	96.2	93.9	95.4
	0.05	94.9	88.6	94.8	96.6	90.1	95.5
	0.1	94.5	86.2	94.3	96.3	87.4	95.7

Bolded values are below 1.96 simulation standard errors.

Italicized values are above 1.96 simulation standard errors.

6 Illustration using DMSAP Data

We now illustrate the effect that uncongenial imputation can have on CRT data using data from the Detroit Middle School Asthma Project (DMSAP), introduced in Section 1. In particular we compare the fixed effects for cluster imputation model to an imputation model that ignores cluster, a mixed effects imputation model with random effects for cluster, and a complete case analysis. All imputation and analysis strategies were implemented in R.

We restricted attention to outcome measures on the child interview at the 12-month follow-up, which include previously validated measures of asthma-related quality of life (QOL) (Juniper et al., 1996), psychological development (Eccles et al., 1991), and peer support (Zimet et al., 1988). Each of the three measures are obtained via a series of questions on Likert scales, with the final score taken as the average score. Quality of life scores range from 1 to 7, with higher scores indicating higher asthma-related QOL; psychological development scores range from 1 to 5, with higher scores indicating more autonomy demonstrated by the child; peer support scores range from 1 to 7 with higher scores indicating higher levels of social support. Histograms of residuals from regression models for complete cases indicated approximate normality for all three outcomes.

For use as predictors in the imputation models we used the baseline value of each outcome, as well as demographic variables hypothesized to be related to these outcomes: age, gender, race, reporting a doctor’s diagnosis of asthma, and asthma severity level. These variables were used in the original imputation analysis of the DMSAP data set. Since the DMSAP data have a “swiss-cheese” pattern of missingness, with scattered item nonresponse in addition to the large amount of unit nonresponse, we took children with complete data at baseline on these selected variables as our analysis sample, n=1144, 89% of the total sample. Of these, 336 (29%) were missing the follow-up QOL score, 336 (29%) were missing the follow-up psychological development score, and 337 (29%) were missing the follow-up peer support score. In this data set there were k = 38 clusters with an average cluster size of m̄ = 30 (range: 15–59).

For each of the three selected 12-month outcome measures, we separately performed multiple imputation using a model with fixed effects for cluster, a model ignoring cluster, and a model with a random intercept for cluster. A total of 10 multiply imputed data sets were generated with each of the methods for each outcome. For each outcome we also performed a complete case analysis.

Resulting inference from the imputed data sets was summarized as follows. First we calculated the estimate of ICC resulting from each imputation method by combining estimates over the 10 multiply imputed data sets as in Section 2.2. We calculated both the unconditional ICC as in (4) and the ICC conditional on the variables used in the imputation, estimated using variance components estimates from a mixed effects model with random effect for clusters. To examine the effect of the various imputation methods on inference we then performed an adjusted t-test to estimate the effect of intervention 1 compared to control. Comparisons of intervention 2 to control were also performed; results were similar and are not shown.

6.1 Results

The resulting ICC values are presented in Table 2. For all three outcomes, and for both unconditional and conditional ICCs, the ICC under fixed cluster effects imputation is larger than that under random effects imputation. The inflation is most severe for the psychological development outcome; under the random effects model the ICCs are smallest for this outcome (0.016, 0.018) and are inflated approximately 80% above this when imputing with fixed effects for cluster. For both types of ICCs, the smaller the ICC the larger the relative overestimation of this ICC by the fixed cluster effect method.

Table 2.

Estimates of ICC for three outcome measures using different imputation strategies, Detroit Middle School Asthma Project data (n = 1144).

Outcome	Imputation Method	Unconditional ICC	Increase over RE imputation	Conditional ICC	Increase over RE imputation
QOL	Fixed cluster effects	0.049	+55%	0.084	+32%
	Ignoring clusters	0.012	−63%	0.030	−53%
	Random cluster effects	0.032		0.064
	Complete cases	0.026		0.059
Psych. Devel.	Fixed cluster effects	0.028	+78%	0.033	+80%
	Ignoring clusters	−0.001	−109%	0.002	−89%
	Random cluster effects	0.016		0.018
	Complete cases	0.000		0.000
Peer Support	Fixed cluster effects	0.048	+26%	0.048	+37%
	Ignoring clusters	0.019	−50%	0.007	−80%
	Random cluster effects	0.038		0.035
	Complete cases	0.034		0.000

RE: Random effects, QOL: Quality of Life, Psych. Devel.: Psychological Development

Conversely, the imputation model that ignores cluster drastically reduces estimates of ICC compared to the random effects model. More severe underestimation is evident with smaller ICCs. The complete case ICCs tend to be smaller than the random effects imputation, though not as small as the imputation that ignores clusters. However, missingness is likely at random for the DMSAP data (MAR), not completely at random (MCAR), so the complete case estimates are suspect and are merely included for comparative purposes.

Table 3 displays results from the adjusted t-tests of the effect of intervention 1 compared to control. The intervention did not appear to have a strong impact on any of the three outcome measures; the estimates of the intervention effects are small and similar under all four analysis methods. There are, however, differences in the precision of the estimates and resulting p-values. For all three outcomes the same pattern emerges as with the ICCs; variances are larger for the fixed effects for cluster imputation than for the random effects imputation, which are in turn larger than those under the imputation that ignores clusters. For the psychological development outcome, if we use the random effects imputation the result is a borderline p-value (p = 0.06). However, under fixed effects for cluster imputation the p-value is well outside even the borderline significance range (p = 0.18). We note this primarily to demonstrate how the deflated variances from the fixed cluster effects imputation might directly impact inferences; in this case all the estimated intervention effects are small and below clinical significance and so would not be considered significant even with borderline p-values.

Table 3.

Results from adjusted t-tests for the intervention 1 effect under different imputation strategies, Detroit Middle School Asthma Project data (n = 1144).

Outcome	Imputation Method	Estimated Mean Difference	Estimated Variance	Increase over RE imputation	p-value
QOL	Fixed cluster effects	0.19	0.024	+38%	0.23
	Ignoring clusters	0.21	0.013	−23%	0.08
	Random cluster effects	0.22	0.017		0.11
	Complete cases	0.22	0.018		0.11
Psych. Devel.	Fixed cluster effects	0.12	0.0078	+44%	0.18
	Ignoring clusters	0.14	0.0043	−21%	0.04
	Random cluster effects	0.15	0.0054		0.06
	Complete cases	0.14	0.0044		0.05
Peer Support	Fixed cluster effects	−0.10	0.0096	+20%	0.29
	Ignoring clusters	−0.10	0.0057	−28%	0.19
	Random cluster effects	−0.11	0.0080		0.22
	Complete cases	−0.08	0.0081		0.37

RE: Random effects, QOL: Quality of Life, Psych. Devel.: Psychological Development

As an astute reviewer pointed out, some of the difference in p-values for the fixed versus random effects imputation methods is due to differing variance estimates, but some is also due to the difference in point estimates (for example, 0.12 versus 0.15 for the psychological development outcome). In order to eliminate the possibility that an “unlucky” set of imputations was driving differences between methods, we repeated the entire MI process an additional 10 times. On average, the point estimates from the two methods were identical. The resulting range of p-values for the psychological development outcome was 0.10–0.19 for the fixed effects imputation and 0.05–0.15 for the random effects imputation, and the p-value from fixed effects imputation was larger than that from random effects imputation in nine of ten repetitions. The patterns seen in Tables 2 and 3 and described above were also seen in all of the repetitions of the MI process.

7 Summary

Cluster randomized trials can have high rates of nonresponse and multiple imputation is often an attractive solution. The correct multiple imputation model is one that accounts for the clustering through random effects; however, most software assumes independent observations. Previous work has shown that ignoring the clustering can lead to increase Type I error. In this paper we have shown that multiply imputing CRT data with a model that incorporates clustering using fixed effects for cluster can lead to severe overestimation of variance of group means, and that the overestimation is more severe for small cluster sizes and small ICCs. The overestimation of variance leads to a decrease in power, which is especially dangerous for CRTs which are often underpowered. With strong covariate information one can reduce bias in the MI variance estimator, though extremely strong covariates are not always available.

Our results were obtained under the simple case of a balanced post-test only design with continuous variables. This allowed us to vary systematically the key elements of the problem, namely the cluster size, ICC, and covariate strength. It seems unlikely that more complex scenarios, such as unbalanced designs and mixed covariate types will lead to different conclusions, though this is admittedly a possibility. A key feature of the simulations that will be an area for future work is the lack of clustering on the covariates X. We assumed that observations X were independent for all subjects, while in CRTs it is likely that there will be clustering in the covariates in addition to the outcomes. We hypothesize that the poor performance of the fixed effects for cluster imputation model might be abated if some of the clustering in the (partially unobserved) outcome can be explained by the (fully observed) covariate, and future work is needed in this area. Other areas that merit attention are extension to both categorical outcomes and cluster-level covariates, both of which are ubiquitous in CRTs. In the context of categorical outcomes, Yucel and colleagues (Yucel and Raghunathan, 2006; Zhao and Yucel, 2009) have developed a software called SHRIMP that uses hierarchical models to perform sequential regression imputation, in a manner similar to IVEWARE. This method has not been widely used in practice, but it seems promising for CRTs where the analysis models themselves are hierarchical models, and thus congeniality of imputation and analysis models would be achievable. The performance of this method in the CRT setting merits attention, especially since the method would allow for non-monotone patterns of missingness and mixed type outcome variables.

Appendix

A.1. Imputation procedure with fixed effects for cluster

We assume without loss of generality that the first r subjects in each cluster are the respondents. Following the notation of Kim (2004) we can write the imputation procedure for the imputation model given in (8) with no covariates X as follows.

• [M1]
  For each repetition of the imputation procedure, d = 1, …, D, draw

  $${\varphi }_{(d)}^{*2}|{\mathrm{y}}_{\mathrm{r}}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}(2\mathit{\text{kr}}-2k){\hat{\varphi }}_r^2/{\chi }_{2\mathit{\text{kr}}-2k}^2$$

  where ${\hat{\varphi }}_r^2={\displaystyle {\sum }_{l=1}^2}{\displaystyle {\sum }_{j=1}^k}{\displaystyle {\sum }_{i=1}^r}{(y_{\mathit{\text{ijl}}}-{\overline{y}}_{·\mathit{\text{jl}}})}^2/(2\mathit{\text{kr}}-2k)$ is the estimate of residual variance using respondent data only, and y_r denotes the vector of respondent outcomes.
• [M2]
  Draw the cluster means for j = 1, …, k and l = 1, 2 as

  $${\alpha }_{\mathit{\text{jl}}(d)}^{*}|{\mathrm{y}}_{\mathrm{r}},{\varphi }_{(d)}^{*2}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}N({\overline{y}}_{·\mathit{\text{jl}}},{\varphi }_{(d)}^{*2}/r)$$
• [M3]
  For each missing unit i = r + 1, …, m in the 2k clusters, draw

  $$e_{\mathit{\text{ijl}}(d)}^{**}|{\alpha }_{\mathit{\text{jl}}(d)}^{*},{\varphi }_{(d)}^{*2}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{~}N(0,{\varphi }_{(d)}^{*2})$$

Then $y_{\mathit{\text{ijl}}(d)}^{**}={\alpha }_{\mathit{\text{jl}}(d)}^{*}+e_{\mathit{\text{ijl}}(d)}^{**}$ is the imputed value associated with unit i in cluster j and treatment group l for the d^th repetition of the imputation.

A.2. Variance of the multiple imputation point estimate

The proof of (9) and (10) is similar to Kim (2004), who proves the finite sample bias for non-clustered data under a congenial regression imputation model. We assume a different population model as given by (1), and ignore the finite sample corrections.

Under (1) and MCAR,

$$\text{Cov}(y_{\mathit{\text{ijl}}},y_{i\prime j\prime l\prime (d)}^{**})=\{\begin{array}{cc}[1+(r-1)\rho ]{\sigma }^2/r\hfill & \text{if}j=j\prime ,l=l\prime \hfill \\ 0\hfill & \text{if}j\ne j\prime \text{ or }l\ne l\prime \hfill \end{array}$$ (12)

and

$$\text{Cov}(y_{\mathit{\text{ijl}}(d)}^{**},y_{i\prime j\prime l(s)}^{**})=\{\begin{array}{cc}[1+(r-1)\rho ]{\sigma }^2/r+(1-\rho ){\sigma }^2(1+r^{-1})\hfill & \text{if}i=i\prime ,j=j\prime ,d=s\hfill \\ [1+(r-1)\rho ]{\sigma }^2/r+(1-\rho ){\sigma }^2/r\hfill & \text{if}i\ne i\prime ,j=j\prime ,d=s\hfill \\ [1+(r-1)\rho ]{\sigma }^2/r\hfill & \text{if}i\ne i\prime ,j=j\prime ,d\ne s\hfill \\ 0\hfill & \text{if}j\ne j\prime \text{ or }l\ne l\prime \hfill \end{array}$$ (13)

where, as in Kim (2004), the expectations are taken over the joint distribution of (1) and the imputation [M1–M3] with fixed respondent indices. The proof of (12) and (13) follows Kim (2004) and is omitted here for space considerations; details are available from the author upon request. We note that in Kim (2004) there is a small sample correction, λ, which for our case would be λ = 2k(r −1)/[2k(r − 1) − 2]. Since 2kr is the total number of respondents over all clusters and treatment groups, and this is generally large for cluster randomized trials, we assume that λ ≈ 1 and so the finite sample correction is omitted.

Note that ${\hat{\theta }}_D=D^{-1}{\displaystyle {\sum }_{d=1}^D}{\overline{y}}_{··l}^{(d)}\text{ and the }{\overline{y}}_{··l}^{(d)},d=1,\dots ,D$ are identically distributed. Thus,

$$\text{Var}({\hat{\theta }}_D)=(1-D^{-1})\text{Cov}({\overline{y}}_{··l}^{(1)},{\overline{y}}_{··l}^{(2)})+D^{-1}V({\overline{y}}_{··l}^{(1)})$$

By (12) and (13) we have,

$$\begin{array}{cc}\text{Cov}({\overline{y}}_{··l}^{(1)},{\overline{y}}_{··l}^{(2)})\hfill & ={(\mathit{\text{km}})}^{-2}\text{Cov}({\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=1}^r}{y}_{\mathit{\text{ijl}}}+{\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=r+1}^m}{y}_{\mathit{\text{ijl}}(1)}^{**},{\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=1}^r}{y}_{\mathit{\text{ijl}}}+{\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=r+1}^m}{y}_{\mathit{\text{ijl}}(2)}^{**})\hfill \\ \hfill & ={(\mathit{\text{km}})}^{-2}\{\mathit{\text{kr}}[1+(r-1)\rho ]{\sigma }^2+2k(m-r)[1+(r-1)\rho ]{\sigma }^2+k{(m-r)}^2[1+(r-1)\rho ]{\sigma }^2/r\}\hfill \\ \hfill & =[1+(r-1)\rho ]{\sigma }^2/\mathit{\text{kr}}\hfill \end{array}$$

which has the form of (2) with r replacing m. We also have,

$$\begin{array}{cc}\text{Var}({\overline{y}}_{··l}^{(1)})\hfill & =\text{Var}({\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=1}^r}{y}_{\mathit{\text{ijl}}}+{\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=r+1}^m}{y}_{\mathit{\text{ijl}}(1)}^{**})\hfill \\ \hfill & ={(\mathit{\text{km}})}^{-2}\{\mathit{\text{kr}}[1+(r-1)\rho ]{\sigma }^2+2k(m-r)[1+(r-1)\rho ]{\sigma }^2+k{(m-r)}^2[1+(r-1)\rho +(1-\rho )]{\sigma }^2/r+k(m-r)(1-\rho ){\sigma }^2\}\hfill \\ \hfill & =[1+(r-1)\rho ]{\sigma }^2/\mathit{\text{kr}}+(m-r)(1-\rho ){\sigma }^2/\mathit{\text{kmr}}\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\text{Var}({\hat{\theta }}_D)\hfill & =(1-D^{-1})[1+(r-1)\rho ]{\sigma }^2/\mathit{\text{kr}}+D^{-1}\{[1+(r-1)\rho ]{\sigma }^2/\mathit{\text{kr}}+(m-r)(1-\rho ){\sigma }^2/\mathit{\text{kmr}}\}\hfill \\ \hfill & =[1+(r-1)\rho ]{\sigma }^2/\mathit{\text{kr}}+D^{-1}(m-r)(1-\rho ){\sigma }^2/\mathit{\text{kmr}}\hfill \end{array}$$

Plugging in r = mπ and taking the limit as D → ∞ yields the result in (9).

To obtain E[V̂_D], we note that for a single imputation, the estimate W^(d) = MSC^(d)/km as noted in Section 2.1, where MSC^(d) is the mean squares between clusters for the d^th imputed data set. In addition, since the clusters are independent, $\text{Var}({\overline{y}}_{·\mathit{\text{jl}}}^{(d)})=k\text{Var}({\overline{y}}_{··l}^{(d)})$. Thus from (3) we have that,

$$\begin{array}{cc}\mathrm{E}[W^{(d)}]=\mathrm{E}[{\mathit{\text{MSC}}}^{(d)}/\mathit{\text{km}}]\hfill & =\mathrm{E}\left[\frac{{\displaystyle {\sum }_{l=1}^2}{\displaystyle {\sum }_{j=1}^k}m{({\overline{y}}_{·\mathit{\text{jl}}}^{(d)}-{\overline{y}}_{··l}^{(d)})}^2}{2\mathit{\text{km}}(k-1)}\right]\hfill \\ \hfill & =\frac{{\displaystyle {\sum }_{l=1}^2}m[{\displaystyle {\sum }_{j=1}^k}\text{Var}({\overline{y}}_{·\mathit{\text{jl}}}^{(d)})-k\text{Var}({\overline{y}}_{··l}^{(d)})]}{2\mathit{\text{km}}(k-1)}\hfill \\ \hfill & =\frac{2m[k^2\text{Var}({\overline{y}}_{··l}^{(d)})-k\text{Var}({\overline{y}}_{··l}^{(d)})]}{2\mathit{\text{km}}(k-1)}=\text{Var}({\overline{y}}_{··l}^{(d)})\hfill \\ \hfill & =[1+(r-1)\rho ]{\sigma }^2/\mathit{\text{kr}}+(m-r)(1-\rho ){\sigma }^2/\mathit{\text{kmr}}\hfill \end{array}$$ (14)

Also, since the ${\overline{y}}_{··l}^{(d)}$ are i.i.d.,

$$\begin{array}{cc}\mathrm{E}[B_D]\hfill & =\text{Var}({\overline{y}}_{··l}^{(1)})-\text{Cov}({\overline{y}}_{··l}^{(1)},{\overline{y}}_{··l}^{(2)})\hfill \\ \hfill & =(m-r)(1-\rho ){\sigma }^2/\mathit{\text{kmr}}\hfill \end{array}$$ (15)

Since as D → ∞, V̂_D = W^(d) + B_D, summing (14) and (15) and plugging in r = mπ yields the result in (10).