Abstract
In 1980 DSA provided a real time series of digitally processed angiographic images that facilitated and reduced the risk of angiographic procedures. This technique has become an enabling technology for interventional radiology. Initially it was hoped that intravenous DSA could eliminate the need for arterial injections. However the 2D nature of the images resulted in overlap of vessels and repeat injections were often required. Ultimately the use of smaller arterial catheters and reduced iodine injections resulted in significant reduction in complications. During the next two decades time resolved MR DSA angiographic methods were developed that produced time series of 3D images. These 4D displays were initially limited by tradeoffs in temporal and spatial resolution when acquisitions obeying the Nyquist criteria were employed. Then substantial progress was made in the implementation of undersampled non-Cartesian acquisitions such as VIPR and constrained reconstruction methods such as HYPR, which removed this tradeoff and restored SNR usually lost by accelerated techniques. Recently, undersampled acquisition and constrained reconstruction have been applied to generate time series of 3D x-ray DSA volumes reconstructed using rotational C-arm acquisition completing a 30 year evolution from DSA to 4D DSA. These 4D DSA volumes provide a flexible series of roadmaps for interventional procedures and solve the problem of vessel overlap for intravenous angiography. Full time-dependent behavior can be visualized in three dimensions. When a biplane system is used, 4D fluoroscopy is also possible, enabling the interventionalist to track devices in vascular structures from any angle without moving the C-arm gantrys. Constrained reconstruction methods have proved useful in a broad range of medical imaging applications, where substantial acquisition accelerations and dose reductions have been reported.
Keywords: constrained reconstruction, undersampled acquisition, accelerated imaging, HYPR, VIPR, MR-DSA, 4D x-ray DSA
INTRODUCTION
In this paper, we focus on the development of time resolved angiography that has recently benefitted from the use of undersampled sub-Nyquist acquisition and constrained reconstruction. This has occurred within the context of magnetic resonance imaging and, more recently, the same approach has facilitated the completion of a 30-year transition from the initially introduced x-ray DSA technique to a full 4D implementation of DSA presently under investigation. We will also briefly mention applications of constrained reconstruction in other areas of medical imaging.
The examples presented in this review are admittedly focused on the methods with which we are most familiar, for example, the HYPR method.1, 2 The field of constrained reconstruction is rapidly evolving and for many purposes algorithms more recent than HYPR may provide improved reconstructions especially in situations involving less sparse image volumes or motion.3, 4, 5
EARLY CONTRIBUTIONS IN X-RAY
Subtraction angiography was first implemented with film by Ziedses des Plantes in 1934 in a thesis6 that introduced both film-subtraction and geometrical tomography.
The transition to real time DSA grew out of attempts to perform k-edge subtraction experiments. For this purpose a real time digital video image processor (DVIP) was constructed for rapid combination of acquired image data7 without the need to re-expose the subject as had been the case with early analog storage tube8 implementations used for energy subtraction imaging.9, 10
As the DVIP was being applied to 3-spectrum K-edge imaging, experiments in off-line computer reconstruction of time-dependent angiographic subtraction imaging was reported by Ovitt et al. at the University of Arizona.11 Related work was also reported in pediatric cardiology by Brennecke and Heintzen at the Kiel Kinderklinic.12 These time subtraction experiments produced greater SNR and were easier to implement than the energy subtraction experiments being conducted at the University of Wisconsin. Realizing this, the DVIP apparatus was adapted for time subtraction angiography. The result was the development of the first real time DSA system that led to the commercial introduction of DSA at the 1980 RSNA.
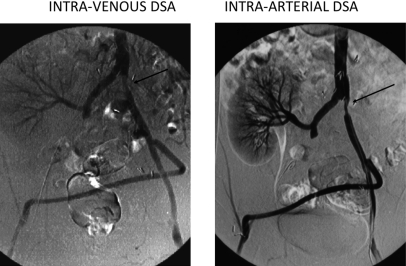
Within 2 years there were more than 30 companies making DSA apparatus. Much of the enthusiasm was based on the hope that DSA could be done with intravenous iodine injections. However, although several convincing images were shown by the major academic institutions, in time it was realized that better image quality could be more consistently obtained using small intra-arterial catheters with reduced amounts of iodine. Figure 1 shows an early comparison of intravenous vs intra-arterial DSA. In spite of the trend back to intra-arterial injection, the advent of DSA resulted in a marked decrease in angiographic complication rates due to the use of decreased iodine doses, smaller catheters, and decreased examination times.13
Figure 1.
Comparison of IV and intra-arterial DSA. Intravenous angiography was sensitive to soft tissue motion and marginal iodine contrast. Intra-arterial DSA permitted the use of smaller catheters and smaller amounts of iodine and resulted in reduced complication rates.
As can be seen in Fig. 1, motion is an inherent problem even in intra-arterial DSA.
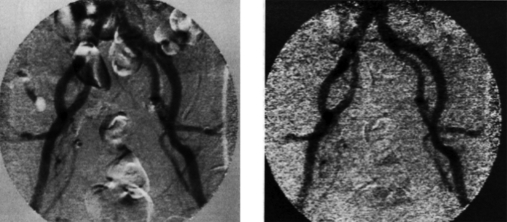
In an attempt to solve this problem, Brody14 implemented a hybrid energy∕time subtraction technique in which tissue subtracted images taken before and after contrast injection were subtracted to produce DSA images without soft tissue artifacts. Figure 2 shows a typical example of this type of image. Because the time subtraction follows energy subtraction and tissue cancellation, problems associated with soft tissue motion are eliminated. However due to the need for a second order subtraction, the SNR is significantly degraded relative to time subtraction.
Figure 2.
Brody’s hybrid energy—time subtraction method for tissue cancelled DSA. This technique was introduced as a product but was abandoned due to excessive image noise.
This method was introduced briefly as a commercial product but was not widely used due to limited SNR. It is interesting to note that had recent constrained reconstruction techniques such as HYPR1, 2 been available at that time, the second order time-energy image might have been widely adopted.
At this point we turn our attention to developments in time resolved MR angiography. The 4D DSA technique presented later in this paper was inspired by a series of developments in MR as well as continued developments in rotational 3D DSA.15, 16, 17
CARTESIAN KEYHOLE AND TRICKS
During the 1990’s considerable development of time resolved MR intravenous angiographic methods emerged. Because of the flexibility with which k-space could be sampled and the dominance of the central portion of k-space in determining image contrast, methods for time resolved 3D MR angiography developed quickly. The Keyhole method of Van Vaals et al.18 provided low spatial frequency dynamic information but had the disadvantage that high spatial frequencies were only sampled once at the end of the contrast injection. These were added to an ongoing time series of low spatial frequency acquisitions to provide detail. The result was that high spatial frequency information appeared prematurely. Later Korosec et al.19 introduced the TRICKS technique in which high spatial frequencies were sampled throughout the examination, but less often than the low spatial frequencies. In TRICKS the time frames are formed by adding an interpolated set of high spatial frequencies to the low spatial frequency information. TRICKS is currently the standard method for time resolved 3D MR angiographic studies and has been implemented in similar form by several MR manufacturers.
A number of faster methods have been developed using sub-Nyquist undersampled radial acquisition. Progress has also been made in combining Cartesian acquisition with parallel imaging20, 21, 22 to produce substantial improvements in temporal and spatial resolution. However, these still await commercial implementation.
In 1995 Rasche et al.23 employed undersampled radial acquisition for MR catheter tracking. Later Scheffler and Henning24 used the same approach to implement small field of view MR imaging. The basic principle is that when radial acquisition is undersampled there is a radius within the point spread function in which spatial resolution is preserved and streaking artifacts are absent. Beyond this, streaks begin to appear and can communicate with distant portions of the image. The radius of the streak-free zone increases as sampling is increased.
In 2000 Peters et al.25 observed that for the case of 2D MR angiography the undersampled radial technique could be used for full field of view MR angiography. This is a result of the sparsity of the angiographic data set which provides relatively few sources of streaks. Using this technique, undersampling factors of 4–6 relative to full Nyquist sampling were well tolerated and provided significantly improved spatial resolution in the phase encoding direction for the same imaging time.
Figure 3 shows early results from Peters in which a resolution phantom was scanned twice using radial sampling and conventional Cartesian phase encoding. The same number of radial projections and phase encodings were used. With radial sampling, the increased resolution in the phase encoding (L-R) direction is achieved in the same scan time. It is well known that in radial sampling the center of k-space is sampled to a higher degree than the outer portion. It is the undersampling of the outer portion that leads to the artifacts.
Figure 3.
Comparison of resolution phantom using Cartesian phase encoding (left) and 4x undersampled radial acquisition (right) in same scan time. The Cartesian spatial resolution in the phase encoding direction is inferior to that of the radial acquisition.
Soon after this Barger et al.26 reported an undersampled 3D technique called VIPR in which the origins of k-space trajectories are distributed over the surface of a sphere in k-space and pass through the center of k-space. In this case undersampling artifacts are distributed in three rather than two dimensions and undersampling factors of 30–40 are well tolerated.
Figure 4 shows a 3D phase contrast acquisition using a phase contrast implementation of VIPR (PC-VIPR) with a factor of 36 angular undersampling.
Figure 4.
PC VIPR images obtained with an undersampling factor of 36. PC VIPR provides flow information in addition to anatomical information. Courtesy of Kevin Johnson.
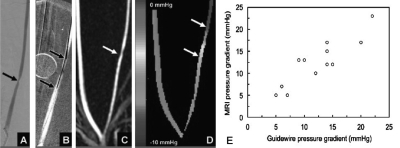
The increase in acquisition speed provided by this approach has resulted in an order of magnitude decrease in phase contrast voxel size and has led to the development of PC∕VIPR techniques for measurements of pressure gradients and wall sheer stress in small vessels.27, 28, 29, 30, 31 Figure 5 adapted from Lum et al.27 shows pressure gradient measurements that provide a new diagnostic tool for assessment of stenotic disease.
Figure 5.
(a) 46% stenosis in a 2.6 mm left common carotid artery in a pig. (b). Pressure transducer measurement that found a 6 mm Hg pressure drop. (C) PC VIPR angiogram. (d) Pressure map indicating a 7 mm Hg pressure drop. Adapted from Lum et al. (e) Comparison of MR and guidewire pressure measurements.
In a Radiology editorial32 commenting on the Lum paper, Martin Prince stated that “in the future, our entire approach to vascular assessment may change, starting with analyzing pressure gradient maps….”
PC VIPR measurements of pressure gradients were initially successful in the cranial circulation.33 PC VIPR use in imaging renal arteries has recently been reported by Francois et al.34 VIPR has also been used successfully for coronary angiography35 nonbreath hold pediatric cardiac imaging,36 musculoskeletal imaging,37, 38 peripheral angiography,38 and floating table angiography.39
ANGIOGRAPHY USING COMBINED RADIAL UNDERSAMPLING AND CONSTRAINED RECONSTRUCTION
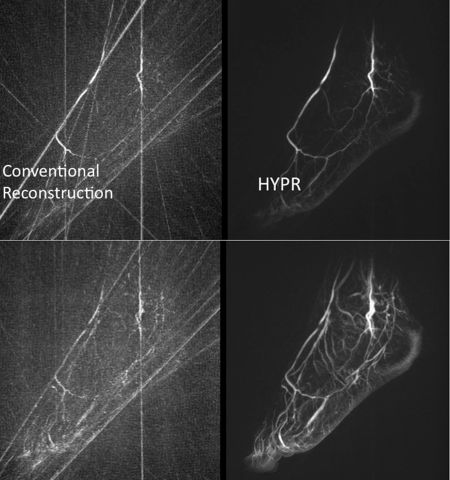
One of the potential drawbacks of accelerated undersampled data acquisition is loss of SNR and, in the case of radial acquisition, streak artifacts. Constrained reconstruction techniques have been developed to deal with these problems. Examples of this include the RIGR40 technique introduced by Lauterbur and Liang more than 20 years ago and the more recent KT Blast technique.41 These constrained reconstruction techniques are characterized by the use of a training image that provides information about the general configuration of vessels but which typically contains no temporal information. This training image is a high SNR image with few artifacts and is typically used to constrain the reconstruction of highly undersampled time frames. For example, in the HYPR technique,1, 2 as applied to radially acquired time frames, a composite image is formed by summing some or all of the time frames in a series of interleaved radial acquisitions. Without applying the constraint the individual time frames are noisy and streak ridden. The composite image contains few streaks because it is well sampled and has high SNR. Following HYPR processing, the individual time frames have greatly reduced streaks and have SNR equivalent to the composite image. An example of this is illustrated in Fig. 6, which compares conventional filtered back projection images to the HYPR result. The images were undersampled by a factor of 50.42 The increased quality of the HYPR time frames is due to the use of all the data acquired during the scan to construct each time frame. In the conventional reconstruction only the limited amount of data actually acquired during each time frame is used.
Figure 6.
Comparison of conventional filtered back projection reconstruction and HYPR reconstruction using 16 projections per time frame in a “stack of stars” geometry. The Nyquist requirement was 800 projections. From Wieben (Ref. 42).
Even when radial acquisition is used the limited time available during the first pass of contrast can result in undersampling streaks and inadequate signal to noise ratio. The combination of radial undersampling and HYPR processing can greatly decrease the previous tradeoff required between spatial and temporal resolution. HYPR reduces streak artifacts and provides an SNR characteristic of a much longer acquisition while preserving temporal resolution. Several iterative variations of HYPR have recently been reported and are useful in situations where sparsity is limited.3, 4, 5
The two most common radial acquisition modes for time resolved contrast angiography are the “stack of stars” (SOS) acquisition in which radial acquisition is employed in plane and phase encoding is used through plane, and the VIPR acquisition which is a 3D radial acquisition. VIPR is best suited to large spherelike volumes, whereas the SOS acquisition can be used for good advantage in the legs where oblong volumes do not require as much phase encoding.
The tradeoff between spatial and temporal resolution can be almost completely eliminated using a method employing two separate acquisitions. This so-called hybrid HYPR acquisition mode43, 44 uses a several minute acquisition to form a high spatial resolution, high SNR image that contains no temporal information. This is used as the composite image in the HYPR process and can be a phase contrast, contrast-enhanced, time of flight, or noncontrast inflow image. These long acquisitions provide various kinds of contrast that can be emphasized in the processed time series. During a separate acquisition a series of highly undersampled time frames are acquired. These are convolved to produce weighting images that determine which vessels in the high resolution, high SNR composite are present in the resulting time frames. Due to the sparsity of the angiographic data set, this can be done while maintaining the intrinsic temporal information inherent in the contrast inflow.
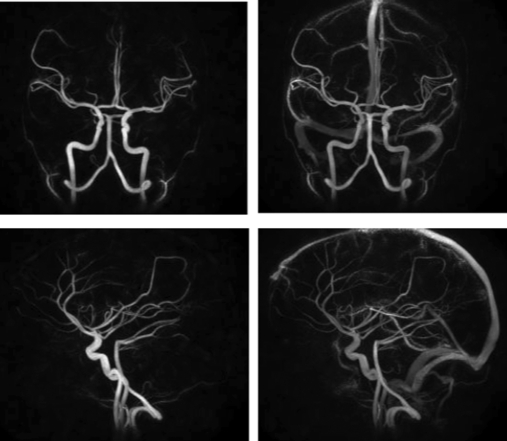
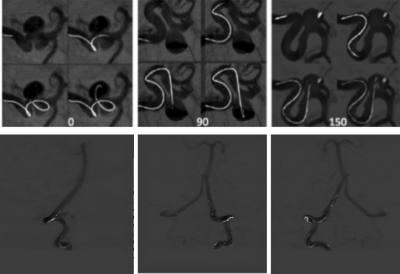
Figure 7 shows an example of a hybrid phase contrast HYPR∕VIPR acquisition in which the angular undersampling factor was approximately 800. The spatial resolution is 0.69 mm isotropic and the temporal aperture for the time resolved data is 0.75 s.
Figure 7.
Selected Hybrid phase contrast HYPR/ VIPR time frames. The contrast-enhanced time frames were acquired with an angular undersampling factor of 800.
The sensitivity of this method is illustrated in Fig. 8, where images have been obtained using 1 cc of gadolinium.
Figure 8.
Hybrid phase contrast HYPR /VIPR images obtained with 1 cc of gadolinium contrast. The use of small amounts of contrast improves artery/vein separation.
4D DSA; COMPLETING A 30 YEAR CIRCLE
The beginnings of practical time resolved angiography began with the introduction of x-ray DSA in 1980. Although time resolved information was available with rapid film changers, the process involved considerable delay for film development, involved considerable risk due to the need to leave catheters in place for long times and generally required more contrast material and larger catheters than those needed for DSA. The film approach was cumbersome for the purposes of interventional x-ray angiography, which greatly accelerated after the introduction of DSA. However, the hope of doing all of x-ray angiography with intravenous injections was not realized due to many factors including overlap of vessels, which often necessitated reinjection with alternate projections. Because of the limitations imposed by the fact that the DSA time frames were two dimensional, the use of arterial injections was adopted. Because smaller catheters and less contrast were possible, coupled with immediate availability of subtracted images, reduction of complications by a factor of 4–8 were reported.13
Prior to the reconstruction of 3D rotational DSA using CT-like reconstructions with flat panel systems45 Kruger et al.46, 47, 48 implemented a tomosynthetic DSA mode using a circular tomographic motion and temporal filtration. This provided the first 4D DSA capability in the form of a time series of planes generated by tomosynthesis. They also simulated the generation of full CT angiographic reconstructions.49
More recently, Badea et al.50 reported on tomographic DSA in which a series of injections were used to generate information at several projection angles. Pollmann et al.51 reported on complete CT angiographic time series using a small rapidly rotating gantry using complete angular data sets resulting in a frame rate equal to the gantry rotation speed.
The lessons learned in connection with constrained reconstruction of undersampled MRA data sets suggest methods that can be applied to x-ray DSA to provide a time series of 3D images.
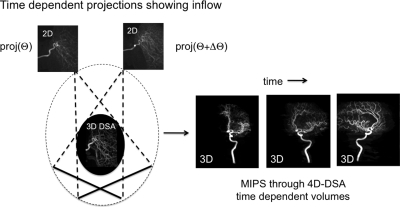
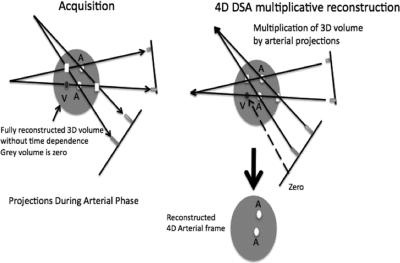
Once a high resolution, high SNR 3D vascular volume is reconstructed, this can be used as an image constraint for the reconstruction of 4D time frames. This is analogous to the hybrid MRA approach in which two separate acquisitions are used to form the time frames. In the case of 4D DSA, intrinsically high resolution projection data are available during the C-arm rotation and only a single injection is required. The temporal information inherent in the projections obtained in the course of obtaining data for the 3D angiogram can be embedded in the 3D volume using just one or two projections. This results in the generation of 3D volumes at the projection frame rate, typically 30 s, when one projection is used with some degradation of temporal resolution for a small minority of voxels when two projections are used. The basic idea is illustrated in Fig. 9.
Figure 9.
Schematic of the 4D DSA reconstruction using two projections per 3D time frame. Following multiplication by the first projection, streaks appear when the volume is viewed in directions not along the projection direction. These are removed by the second multiplication.
The data acquisition and reconstruction are shown in more detail in Fig. 10.
Figure 10.
Illustration of the data acquisition and multiplicative reconstruction step for 4D DSA. For each time frame two projections and the reconstructed 3D DSA volume are used. In the gray areas where vessels are not present the volume is zero. Where the detected rays cross the vessels in the 3D volume signal is deposited in the backprojection step (circles) Where the 3D volume is zero the multiplication produces zero signal (squares). In arterial phase projections, veins are still zero and the projection multiplies the vein in the 3D DSA volume by zero.
The use of two projections is needed to remove streak artifacts that would occur if only a single projection were backprojected. In the multiplication process, if there is any background signal outside of the vessels this will result in signal being deposited outside the vessels. When multiplication is repeated from another angle the streaks enjoy only a single multiplication at each angle and have significantly less signal than within the vessel, where substantial signal was present for both multiplications. Following the sequential multiplications a square root transform is typically applied to restore the proper vessel signal. Angular separations of 30°–60° are typically used.
Although this reconstruction differs in many ways from the hybrid MRA method there are some similarities, particularly with respect to the transferring of the spatial resolution and SNR of the 3D DSA volume, which integrates signal from all projections, into the individual 4D DSA time frames. This is in part accomplished by convolving the individual projections before casting them through the time independent 3D DSA volume. The 4D DSA time frame temporal resolution is determined by the projection frame rate. Even when two projections are used, the majority of voxels in the sparse angiographic space have a temporal resolution characterized by the projection frame rate, typically 30∕s. However for voxels that line up with another voxel in a projected ray, the temporal resolution degrades to that of the time between the two projections, typically 0.5 s.
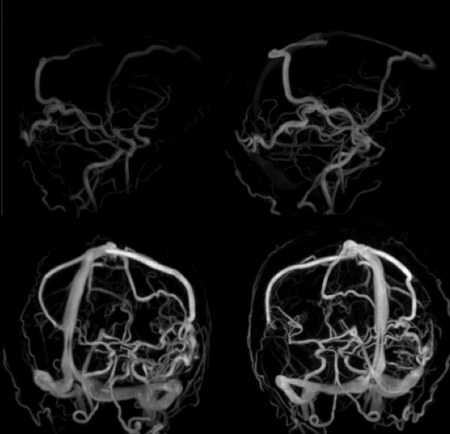
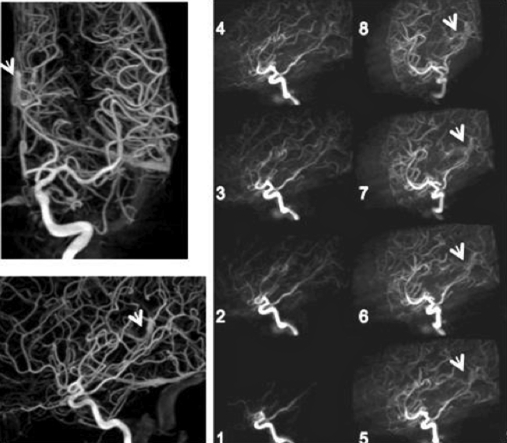
Figure 11 shows a comparison of the 3D rotational DSA volumes (left) used to reconstruct the 4D DSA time frames and MIPS through selected volumes evolving in time (right). In this case early filling of the Vein of Galen is shown. One time frame volume was generated for each of 248 acquired projection angles.
Figure 11.
Early filling of the vein of Galen. Two projections from a 3D DSA (left) and MIPS through a 4D DSA(right) derived by using two of the 220 projections used to form the 3D volume. Dynamic filling of the vascular structures is clearly seen on the rotating 4D DSA volume as indicated by the arrows
The acquisition of projection data can be continued in multiple sweeps of the C-arm during the single injection. During inflow, significant variations in contrast could result in an inconsistent projection set for reconstruction of the 3D DSA time independent image volume. In this case the projections obtained during the second or third sweep can be used to define the 3D vascular volume used to reconstruct the 4D DSA time frames.
It should be mentioned that the 4D DSA images shown in this paper were all reconstructed at low resolution, typically 2563 due to memory limitations of the computer used for reconstruction. Additionally calibration corrections for C-arm rotational imperfections were not included. Image quality is expected to improve when these and a number of additional corrections are made.
Temporal curves obtained from the 4D-DSA time frames agree very well with the curves obtained directly from the 2D projections. For the purposes of obtaining quantitative flow information the 3D rotational DSA volume is binarized before the multiplicative projection processing.
Comparing to the most advanced hybrid MRA methods that provide temporal apertures of 0.5–0.75 s, 4D-DSA frames are formed rates of about 30 s−1. The temporal aperture for the vast majority of voxels in the sparse angiographic data set is 1∕30 s degrading to about 0.5 s for those voxels that are in the shadow of vessels in the second projection typically occurring 30°–60° later in the sweep. The spatial resolution in hybrid MRA provides voxel sizes of about (0.69 mm)3 = 0.33 mm3. With a 5123 4D DSA reconstruction over 20 cm FOV the voxel size should be 0.06 mm3. This remains to be validated and is subject to making accurate corrections for the C-arm trajectory.
4D FLUOROSCOPY
During interventional procedures where it may be desired, for example, to place a device in an aneurysm, it is sometimes not possible for the C-Arm to provide an adequate view angle due to physical restrictions even when biplane fluoroscopy is available. In some cases the intervention is aborted, and the patient is sent to surgery. When a biplane fluoroscopy system is used, it is possible to embed the fluoroscopic information in the 3D DSA data volume and then to display the fluoroscopy procedure from any desired angle without moving the gantry. This should ensure that an adequate angular view can be obtained. Figure 12 show examples from procedures involving catheter and coil placements. These images were generated using matlab in a postprocessing mode. However current GPU processing technology will permit real time fluoroscopy provided that registration of the 3D DSA volume and the ongoing fluoroscopy projections is maintained.
Figure 12.
4D fluoroscopic views created at several angles without gantry motion. Top row, coil placement in aneurysm. Bottom row-catheter tracking. Images were generated in matlab at reduced resolution. The 4D fluoroscopic mode requires biplane fluoroscopy.
TIME∕ENERGY SUBTRACTED 4D DSA
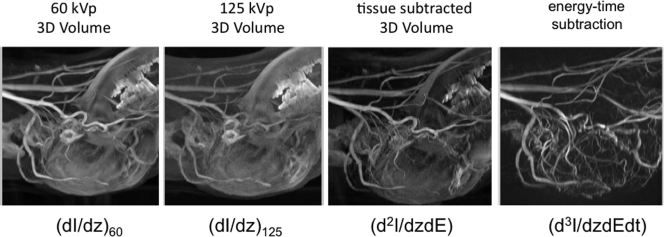
Soft tissue motion can be a problem when intravenous angiography is attempted with conventional time subtraction DSA. Preliminary experiments have been carried using the tomographic extension of hybrid energy∕time subtraction method proposed by Brody.14 This represents the d3I∕dEdtdz term in Ref. 52. In this case dual energy tissue or bone subtraction is typically done in each projection before the normal 4D DSA algorithm is applied. For the results presented in Fig. 13 two sequential acquisitions at 60 and 125 kVp were done using identical injection parameters. Ultimately a rapid energy switching at each projection should be used.5
Figure 13 shows the post-contrast tomographic reconstructions at each energy, a tissue subtracted volume and the time∕energy subtracted volume obtained following the additional temporal subtraction of tissue–subtracted precontrast images. Once the time∕energy subtracted time independent 3D volume is reconstructed, temporal frames may be reconstructed using time-energy subtracted projections and the same multiplicative algorithm used in the time subtraction case (point 14). This mode should permit the extension of the 4D DSA method to regions such as the chest and abdomen, where soft tissue motion is present.
Figure 13.
Progression of images involved in the formation of the time/energy subtracted CT angiographic volume. Shown are MIPs through the 3D DSA volumes at 60 and 125 kVp, a tissue subtracted MIP at one point in time, and a time-energy 4D DSA MIP. Note that unlike the previous mode introduced by Brody (Ref. 14) signal to noise ratio is adequate. The derivatives refer to the image classification scheme defined in Ref. 52.
DISCUSSION
This paper traces the development of time resolved angiography starting with the introduction of DSA and progressing through the developments in x-ray, CT, and MRI that eventually suggested the 4D DSA method described here. Important work leading to this development included the development of C-arm based 3D x-ray DSA which, when implemented with current flat panel detector systems, provides time independent angiographic images of exquisite spatial resolution. The generation of high frame rate 3D angiographic volumes was facilitated by reconstruction techniques designed for highly undersampled radial data sets and the use of constrained reconstruction. The development of 4D DSA is just one example of combining what has been learned in several related imaging fields, in this case CT, MRI, and x-ray imaging, where related acquisition and reconstruction principles can be adapted across modalities.
A general research philosophy that we would recommend to our younger colleagues when considering a potential imaging application is certainly to build on the good work that others have done but to always ask the question “how would I do this if I could start all over again.” Sometimes modalities advance incrementally, often due to commercial development requirements, and it is too expensive to completely back up and start over. In the case of 4D DSA, much has been built on the fine work that has occurred in CT reconstruction and the development of C-arm based cone beam acquisition. In the case of VIPR MRI, the sparsity of the angiographic data set was exploited to produce undersampling factors close to 1000 permitting new applications such as the measurement of pressure gradients and wall shear stress that required large reductions in voxel size. The hybrid HYPR∕VIPR approach has decoupled spatial and temporal resolution, eliminating a long- standing tradeoff. These are examples in which we have suggested backing up a few decades to the time when Cartesian MRI acquisition was chosen over Lauterbur’s original radial acquisition due to several existing factors including gradient limitations. It is interesting to note that the HYPR method is related to the constrained reconstruction approach introduced by Webb et al.40 more than 20 years ago. The applications of constrained reconstruction have extended to a wide range of medical imaging applications involving image series including several parameters in addition to time. Concurrent with the development of HYPR and its associated methods has been the introduction of compressed sensing algorithms53 and, in the case of MRI, parallel imaging54, 55, 56 which can be used to provide complementary gains in acceleration and artifact reduction. Minimization of various image norms, data consistency constraints and the use of constraining images are being combined to further improve temporal resolution in several imaging areas and to reduce radiation dose.57, 58 A new sampling theorem introduced by Candes59 provides an explanation for why it has been possible to obtain high resolution, high SNR MR angiograms with factors approaching 1000. The addition of parallel imaging and compressed sensing should provide another factor of 10 or so.
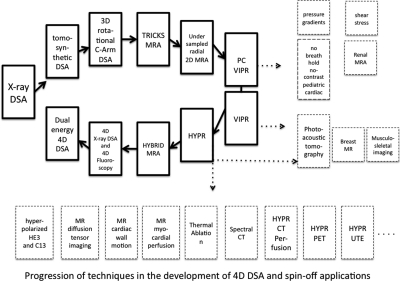
Figure 14 shows the progression of techniques related to time resolved angiography as well as applications in other areas of medical imaging that have benefitted form undersampled acquisition and HYPR reconstruction. The outlined boxes show the progression of techniques, beginning with x-ray DSA, moving to MRA and back to 4D DSA. Following the introduction of DSA, Kruger generated time resolved tomosynthetic DSA planes that helped to resolve the vessel overlap problem.46, 47, 48 The development of true CT nontime resolved DSA reconstructions with good quality flat panel systems was an important step. Following that, a series of techniques that could be called MR DSA were developed based initially on view sharing but eventually on highly undersampled radial acquisitions. The addition of HYPR and the introduction of hybrid HYPR MRA led to the very large acceleration factors illustrated in this paper. Ultimately the use of constrained reconstruction in the case of x-ray C-arm data using a full sweep volume as a constraint permitted the generation of 3D time frames using a factor of more than 100 fewer projections per time frame than normally required for the conventional reconstruction of a 3D volume.
Figure 14.
Progression of techniques in the development of 4D DSA and several accelerated or dose reduced medical imaging applications that have emerged as a result of the use of undersampled acquisition and/or constrained reconstruction.
As illustrated earlier, HYPR and VIPR led to a number of spin-off applications where undersampling artifacts and radiation dose can be reduced. The mathematical explanation for why techniques such as VIPR were able to provide large acceleration factors is provided by the Candes theorem, which demands the kind of signal sparsity and artifact randomness that VIPR MRA provides.
The commercial implementation of many of the techniques discussed in this paper will take a long time, 4D DSA being a probable exception. Although it is one thing to make a technique work in a university laboratory, a large and expensive engineering commitment must be made to bring these techniques to reliable commercial products. A case in point is the present dominance of TRICKS and related techniques that were introduced in 1998. In spite of the fact that some of the MRA techniques discussed here offer orders of magnitude improvement in voxel size and temporal resolution, the introduction of this technology may be painfully slow.
CONCLUSIONS
The use of undersampled acquisition and constrained reconstruction has produced significant improvements in the spatial and temporal resolution of time resolved angiography and provides new opportunities in several areas of medical imaging. In MRI the increased spatial and temporal resolution have led the way to new quantitative flow applications and improved diagnostic capabilities. In CT perfusion, the application of HYPR has produced considerable dose reductions. In positron tomography the increased SNR provided by HYPR can reduce dose requirements and lead to improved single voxel time-activity curves. Other applications that have benefitted from these techniques are listed in connection with Fig. 14.60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71 Application of reconstruction with undersampled data sets and constrained reconstruction in x-ray DSA has completed the transition to a full 4D modality which should expand the role of DSA in diagnosis and intervention with the possibility of substantial dose reduction.
ACKNOWLEDGMENTS
The authors wish to acknowledge the many collaborators who provided illustrations of their work in this area. Kevin Johnson, Yijing Wu, Pat Turski, Kang Wang, Oliver Wieben and Ben Landgraf contributed MR results. The work in 4D DSA has been done primarily in collaboration with Charlie Strother. Kevin Royalty and Kari Pulfer have helped with data acquisition and Dan Consigny has been responsible for animal preparation. MR applications have been achieved with partial support from GE Healthcare and 4D DSA data acquisition has been facilitated by Siemens.
References
- Mistretta C. A., Wieben O., Velikina J., Block W., Perry J., Wu Y., Johnson K., and Wu Y., “Highly constrained backprojection for time-resolved MRI,” Magn. Reson. Med. 55, 30–40 (2006). 10.1002/mrm.v55:1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson K. M., Velikina J., Wu Y., Kecskemeti S., Wieben O., and Mistretta C. A., “Improved waveform fidelity using local HYPR reconstruction (HYPR LR),” Magn. Reson. Med. 59(3), 456–462 (2008). 10.1002/mrm.v59:3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Halloran R. L., Wen Z., Holmes J. H., and Fain S. B., “Iterative reconstruction of time-resolved images using highly constrained back-projection (HYPR),” Magn. Reson. Med. 59, 132–139 (2008). 10.1002/mrm.v59:1 [DOI] [PubMed] [Google Scholar]
- Samsonov A. A., Wieben O., and Block W. F., “HYPRIT: Generalized HYPR reconstruction by iterative estimation,” Abstract, ISMRM Workshop on Non-Cartesian MRI Sedona, Arizona (2007).
- Griswold M.et al. , “More optimal HYPR reconstructions using a combination of HYPR and conjugate-gradient minimization,” Abstract, 18th International Workshop on MR Angiography, Basel, Switzerland (2006).
- Ziedses Des Plantes B. G., “Planigraphieen subtractie. Röntgenographische differentiatie methoden thesis,” Kemink en Zoon, Utrecht, 1934, p. 112.
- Kruger R. A., Mistretta C. A., Lancaster J., Houk T. L., Goodsitt M. M., Riederer S. J., Hicks J., Sackett J. F., Crummy A. B., and Flemming D., “A digital video image processor for real-time subtraction imaging,” Opt. Eng. 17(6), 652–657 (1978). [Google Scholar]
- Crummy A. B., Mistretta C. A., Cline R., Terry W., Ort M. G., Kelcz F., and Cameron J. R., “An inexpensive storage system for selective catheterization procedures,” Radiology 110, 369–372 (1973). 10.1148/110.2.3 79 [DOI] [PubMed] [Google Scholar]
- Crummy A. B., Mistretta C. A., Ort M. G., Kelcz F., Cameron J. R., and Siedband M. P., “Absorption edge fluoroscopy using quasi-monoenergetic x-ray beams,” Invest. Radiol. 8, 402–412 (1973). [PubMed] [Google Scholar]
- Kelcz F. and Mistretta C. A., “Absorption edge fluoroscopy using a 3-spectrum technique,” Med. Phys. 3(3), 159–168 (1977). 10.1118/1.594219 [DOI] [PubMed] [Google Scholar]
- Ovitt T. W. et al. , “Development of a digital subtraction system for intravenous angiography,” Proc. SPIE, 206, 183–189 (1979). [Google Scholar]
- Brennecke R.et al. , “Computerized video-image preprocessing with applications to cardio-angiographic roentgen-image series,” in Digital Image Processing, edited by Nagel H. H (Springer-Verlag, Berlin, 1977), pp. 244–262. [Google Scholar]
- Waugh J. R. and Sacharias N., “Arteriographic complications in the DSA era,” Radiology 182, 243–246 (1992). [DOI] [PubMed] [Google Scholar]
- Brody W. R., “Hybrid subtraction for improved arteriography,” Radiology 141(3), 828–831 (1981). [DOI] [PubMed] [Google Scholar]
- Fahrig R., Fox A. J., Lownie S., and Holdsworth D. W., “Use of a C-arm system to generate true three-dimensional computed rotational angiograms: preliminary in vitro and in vivo results,” AJNR Am J Neuroradiol. 18(8), 1507–1514 (1997). [PMC free article] [PubMed] [Google Scholar]
- Fahrig R., Moreau M., and Holdsworth D. W., “Three-dimensional computed tomographic reconstruction using a C-arm mounted XRII: Correction of image intensifier distortion,” Med. Phys. 24(7), 1097–10106 (1997) 10.1118/1.598013 [DOI] [PubMed] [Google Scholar]
- Fahrig R. and Holdsworth D. W., “Three-dimensional computed tomographic reconstruction using a C-arm mounted XRII: Image-based correction of gantry motion non-idealities,” Med. Phys. 27, 30–38 (2000). 10.1118/1.598854 [DOI] [PubMed] [Google Scholar]
- Van Vaals J. et al. , “Keyhole method for accelerating imaging of contrast agent uptake,” J. Magn. Reson. Imaging 3, 671–675 (1993). 10.1002/jmri.v3:4 [DOI] [PubMed] [Google Scholar]
- Korosec F. R., Frayne R., Grist T. M., and Mistretta C. A., “Time-resolved contrast-enhanced 3D MR angiography,” Magn. Reson. Med. 36, 345–351 (1996). 10.1002/mrm.v36:3 [DOI] [PubMed] [Google Scholar]
- Haider C. R., Glockner J., Stanson A. W., and Reiderer S., “Peripheral vasculature: High temporal- and spatial-resolution three-dimensional contrast-enhnaced MR Angiography,” Radiology 253, 831–843 (2009). 10.1148/radiol.2533081744 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson C. P., Haider C. R., Borish E. A., Glockner J. F., and Riederer S. J., “Time-resolved bolus chase MR angiography with real-time triggering of table motion,” Magn. Reson. Med. 64, 629–637 (2010). 10.1002/mrm.22537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K.et al. , “Interleaved variable density sampling with ARC parallel imaging and Cartesian HYPR for dynamic MR angiography,” Proceedings of the Joint Annual Meeting of ISMRM-ESMRMB (abstract), Stockholm, 2010.
- Rasche V., deBoer R. W., Holz D., and Proska R., “Continuous radial acquisition for dynamic MRI,” Magn. Reson. Med. 34, 754–761 (1995). 10.1002/mrm.v34:5 [DOI] [PubMed] [Google Scholar]
- Scheffler K. and Hennig J., “Reduced circular field of view imaging,” Magn. Reson. Med. 40, 474–480 (1998). 10.1002/mrm.v40:3 [DOI] [PubMed] [Google Scholar]
- Peters D. C. et al. , Undersampled projection reconstruction applied to MR angiography,” Magn. Reson. Med. 43(1), 91–101 (2000). [DOI] [PubMed] [Google Scholar]
- Barger A. V., Block W. F., Toropov Y., Grist T. M., and Mistretta C. A., “Time-resolved contrast-enhanced imaging with isotropic resolution and broad coverage using an undersampled 3D projection trajectory,” Magn. Reson. Med. 48, 297–305 (2002). 10.1002/mrm.v48:2 [DOI] [PubMed] [Google Scholar]
- Lum D. P., Johnson K. M., Paul R. K., Turk A. S., Consigny D. W., Grinde J. R., Mistretta C. A., and Grist T. M., “Measurement of trans-stenotic pressure gradients in swine: Comparison between retrospective ECG-gated 3D phase-contrast MRA and endovascular pressure-sensing guidewires,” Radiology 245, 751–760 (2007). 10.1148/radiol.2453061946 [DOI] [PubMed] [Google Scholar]
- Moftakhar R., Aagaard-Kienitz B., Johnson K. M., Turski P. A., Consigny D., Grinde J., Turk A. S., Niemann D. B., and Mistretta C. A., “Non-invasive measurement of intra-aneurysmal pressure and flow velocity using phase contrast vastly undersampled projection imaging (PC VIPR),” AJNR Am. J. Neuroradiol. 28(9), 1710–1714 (2007). 10.3174/ajnr.A0648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turk A. S., Johnson K. M., Niemann L. D., Aagaard-Kienitz B., Consigny D., Grinde J., Turski P., Haughton V., and Mistretta C. A., “Physiological and anatomic assessment of a canine artery stenosis model with phase contrast with vastly undersampled isotropic projection imaging,” AJNR Am. J. Neuroradiol. 28, 111–115 (2007). 10.3174/ajnr.A0713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bley T. A., Johnson K. M., Francois C. J., Reeder S. B., Schiebler M., Landgraf B., Consigny D. W., Grist T. M., and Wieben O., “Non-invasive assessment of transstenotic pressure gradients in porcine renal artery stenoses using phase contrast MRA,” Radiology (2010). [DOI] [PMC free article] [PubMed]
- Bieging E. T., Frydrychowicz A., Landgraf B. R., Johnson K. M., Wieben O., and François C. J., “In vivo 3-dimensional magnetic resonance wall shear stress estimation in ascending aortic dilatation,” J. Magn. Reson. Imaging 33(3), 589–597 (2011). 10.1002/jmri.22485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prince M. R., “Science to practice: Is there a replacement for percentage stenosisn characterizing occlusive vascular disease?,” Radiology 245(3) 617–618 (2007). 10.1148/radiol.2453071331 [DOI] [PubMed] [Google Scholar]
- Chang W., Landgraf B., Johnson K. M., Kecskemeti S., Wu Y., Velikina J., Rowley H., Wieben O., Mistretta C., and Turski P., “Velocity measurements in the middle cerebral arteries of healthy volunteers using 3D radial phase-contrast HYPRFlow: Comparison with transcranial doppler sonography and 2D phase-contrast MR imaging,” AJNR Am J Neuroradiol. 32(1), 54–59 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francois C. J., Lum D. P., Johnson K. M., Landgraf B. R., Bley T. A., Reeder S. B., Schiebler M. L., Grist T. M., and Wieben O., “Renal arteries: Isotropic, high-spatial-resolution, unenhanced MR angiography with three-dimensional radial phase contrast,” Radiology 258(1), 254–260 (2011). 10.1148/radiol.10100443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie J., Lai P., Bhat H., and Li D. J., “Whole-heart coronary magnetic resonance angiography at 3.0T using short-TR steady-state free precession, vastly undersampled isotropic projection reconstruction,” Magn. Reson. Imaging 31(5), 1230–1235 (2010). 10.1002/jmri.22140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frydrychowicz A., Landgraf B., Wieben O., and Francois C. J., “Images in cardiovascular medicine. Scimitar syndrome: Added value by isotropic flow-sensitive four-dimensional magnetic resonance imaging with PC-VIPR (phase-contrast vastly undersampled isotropic projection reconstruction),” Circulation 121, e434–6 (2010). 10.1161/CIRCULATIONAHA.109.931857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kijowski R., Blankenbaker D. G., Klaers J. L., Shinki K., De A. A. Smet, and Block W. F., “Vastly undersampled isotropic projection steady-state free precession imaging of the knee: Diagnostic performance compared with conventional MR,” Radiology 251(1), 185–194. (2009). 10.1148/radiol.2511081133 [DOI] [PubMed] [Google Scholar]
- Du J., Carroll T. J., Brodsky E., Lu A., Grist T. M., Mistretta C. A., and Block W. F., “Contrast-enhanced peripheral magnetic resonance angiography using time-resolved vastly undersampled isotropic projection reconstruction,” J. Magn. Reson. Imaging 20(5), 894–900 (2004). 10.1002/jmri.v20:5 [DOI] [PubMed] [Google Scholar]
- Fain S. B., Browning F. J., Polzin J. A., Du J., Zhou Y., Block W. F., Grist T. M., and Mistretta C. A., “Floating table isotropic projection (FLIPR) acquisition: A time-resolved 3D method for extended field-of-view MRI during continuous table motion,” Magn. Reson. Med. 52(5), 1093–10102 (2004). 10.1002/mrm.v52:5 [DOI] [PubMed] [Google Scholar]
- Webb A. G., Liang Z. P., Magin R. I., and Lauterbur P. C., “Applications of reduced encoding MR imaging with generalized series reconstruction (RIGR),” J. Magn. Reson. Imaging 3(6), 925–928 (1993). 10.1002/jmri.v3:6 [DOI] [PubMed] [Google Scholar]
- Tsao J., Boesiger P., and Pruessmann K. P., “k-t BLAST and k-t SENSE: Dynamic MRI with high frame rate exploiting spatiotemporal correlations,” Magn. Reson. Med. 50(5), 1031–1042 (2003). 10.1002/mrm.v50:5 [DOI] [PubMed] [Google Scholar]
- Wieben O., Velikina J., Block W. F., Perry J., Wu Y., Johnson K. M., Wu Y., Korosec F. R., and Mistretta C. A., “Highly constrained back projection (HYPR): Theory and potential applications,” 14th Proceedings of the ISMRM (Seattle, Washington, DC, 2006), p. 688.
- Velikina J. V., Johnson K. M., Wu Y. J., Turski P. A., and Mistretta C. A., “PC HYPR FLOW,” Magn. Reson. Imaging 31, 447–456 (2010). 10.1002/jmri.22035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y. et al. , “Fast whole-brain 4D contrast-enhanced MR angiography with velocity encoding using undersampled radial acquisition and highly constrained projection reconstruction: Image-quality assessment in volunteer subjects,” AJNR Am. J. Neuroradiol. 32, E47–E50 (2011). 10.3174/ajnr.A2022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahrig R., Ganguly A., Starman J., and Strobel N., “C-arm CT with XRIIs and digital flat panels: A review,” Invited Paper at SPIE 49th Annual Meeting, Denver, Colorado, 5535 (2004).
- Kruger R. A., Nelson J. A., Ghosh-Roy D., Miller F. J., Anderson R. E., and Liu P. L., “Dynamic tomographic DSA using temporal filtration,” Radiology 147, 863–867 (1983). [DOI] [PubMed] [Google Scholar]
- Anderson R. E., Kruger R. A., Sherry P. G., Nelson J. A., and Liu P. Y., “Tomographic DSA using temporal filtration. Initial neurovascular applications,” AJNR 5, 277–280 (1984). [PMC free article] [PubMed] [Google Scholar]
- DeVries N., Miller F. J., Wojtowycz M. M., Brown P. R., Yandow D. R., Nelson J. A., and Kruger R. A., “Tomographic digital subtraction angiography: Initial clinical studies using tomosynthesis,” Radiology 157, 239–241 (1985). [DOI] [PubMed] [Google Scholar]
- Ning R. and Kruger R. A., “Computer simulation of image intensifier-based CTdetector: Vascular application,” Med. Phys. 15(2), 188–192 (1988). 10.1118/1.596250 [DOI] [PubMed] [Google Scholar]
- Badea C. T., Hedlund L. W., Lin M. D., Boslego J. S. Mackel, Samei E., Allan G., and Johnson G. A., “Tomographic digital subtraction angiography for lung perfusion estimation in Rodents,” Med. Phys. 34(5), 1546–1555 (2007). 10.1118/1.2717384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollmann S. I., Norley C. J. D., Pelz D. M., Lownie S. P, and Holdsworth D. W., “Four dimensional intravenous cone-beam computed tomographic subtraction angiography: In vitro study of feasibility,” Invest. Radiol. 43(11), 753–761 (2008). 10.1097/RLI.0b013e3181812c4c [DOI] [PubMed] [Google Scholar]
- Mistretta C. A., “The use of a general description of the radiological transmission image for categorizing imaging enhancement procedures,” Opt. Eng. 13(2), 134–137 (1974). [Google Scholar]
- Lustig M., Donoho D., and Pauly J. M., “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magn. Reson. Med. 58, 1182–1195 (2007). 10.1002/mrm.v58:6 [DOI] [PubMed] [Google Scholar]
- Sodickson D. K., Griswold M. A., and Jakob P. M., “SMASH imaging,” Magn. Reson. Imaging Clin. N Am. 7(2), 237–254 (1999). [PubMed] [Google Scholar]
- Pruessmann K. P., Weiger M., Scheidegger M. B., and Boesiger P., “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med. 42(5), 952–962 (1999). [DOI] [PubMed] [Google Scholar]
- Griswold M. A., and Jakob P. M., Heidemann R. M., Nittka M., Jellus V., Wang J., Kiefer B., and Haase A., “Generalized autocalibrating partially parallel acquisitions (GRAPPA),” Magn. Reson. Med. 47(6), 1202–1210, (2002). 10.1002/mrm.v47:6 [DOI] [PubMed] [Google Scholar]
- Chen G. H., Tang J., and Leng S., “Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets,” Med. Phys. 35(2), 660–663 (2008). 10.1118/1.2836423 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J., Hsieh J., and Chen G. H., “Temporal resolution improvement in cardiac CT using PICCS (TRI-PICCS): Performance studies,” Med. Phys. 37(8), 4377–4388 (2010). 10.1118/1.3460318 [DOI] [PubMed] [Google Scholar]
- Candes E. J., Romberg J., and Tao T., “Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information,” IEEE Trans. Inf. Theory 52(2), 489–509 (2006). 10.1109/TIT.2005.862083 [DOI] [Google Scholar]
- Mistretta C. A., “Undersampled radial MR acquisition and highly constrained back projection (HYPR) reconstruction: Potential medical imaging applications in the post-Nyquist era,” Magn. Reson. Imaging 29(3), 501–516 (2009). 10.1002/jmri.21683 [DOI] [PubMed] [Google Scholar]
- Wang K., Du J., O’Halloran R., Fain S., Kecskemeti S., Wieben O., Johnson K. M., and Mistretta C., “Ultrashort TE spectroscopic imaging (UTESI) using complex highly-constrained backprojection with local reconstruction (HYPR LR),” Magn. Reson. Med. 62(1), 127–134 (2009). 10.1002/mrm.21986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K., “Application of Accelerated Acquisition and highly constrained reconstruction methods to MR,” Ph.D. thesis, Department of Medical Physics, University of Wisconsin, Madison, 2010. [Google Scholar]
- Holmes J. H., O’Halloran R. L., Brodsky E. K., Bley T. A., Francois C. J., Velikina J. V., Sorkness R. L., Busse W. W., and Fain S. B., “Three dimensional imaging of ventilation dynamics in asthmatics using multi-echo projection acquisition with constrained reconstruction,” Magn. Reson. Med. 62(6), 1543–1556 (2009). 10.1002/mrm.22150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christian B. T., Vandehey N. T., Floberg J. M., and Mistretta C. A., “Dynamic PET denoising with HYPR processing,” J. Nucl. Med. 51, 1147–1154 (2010). 10.2967/jnumed.109.073999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson C. J., Connett J. M., Schwarz S. W., Rocque P. A., Guo L. W., Philpott G. W., Zinn K. R., Meares C. F., and Welch M. J., “Copper-64-labeled antibodies for PET imaging,” J. Nucl. Med. 33, 1685–1691 (1992). [PubMed] [Google Scholar]
- Herzog H., Tellman L., Qaim S. M., Spellerberg S., Schmid A., and Coenen H. H., “PET quantitation and imaging of the non-pure positron-emitting iodine isotope 124I,” Appl. Radiat. Isot. 56, 673–679 (2002). 10.1016/S0969-8043(01)00283-4 [DOI] [PubMed] [Google Scholar]
- Floberg J. M.et al. , “Improving SNR in dynamic PET imaging of copper-64 and iodine-124 using HYPR,” Proceedings of the 2009 ISNM Meeting. Toronto, Canada
- Supanich M. P., Rowley H. A., Turk A. S., Hsieh J., Speidel M., Pulfer Supanich1 K., Chen G. H., and Mistretta C. A., “Low radiation dose neurovascular HYPR CT: Combined CT perfusion and time-resolved CT angiography from a single dynamic injection,” Abstract, RSNA (2007).
- Liu X., Primak A. N., Krier J. D., Yu L., Lerman L. O., and McCollough C. H., “Accurate, in vivo determination of renal perfusion and hemodynamics using HYPR noise reduction and a ten-fold decrease in radiation dose,” Abstract, RSNA (2008). [DOI] [PMC free article] [PubMed]
- Ertel D., Brauweiler R., Speidel M. A., Mistretta C. A., and Kalender W. A., Accurate, “In vivo determination of renal perfusion and hemodynamics using HYPR noise reduction and a ten-fold decrease in radiation dose,” Abstract, RSNA (2008).
- Krissak R., Mistretta C. A., Henzler T., Reichert M., Schoenberg S. O., and Fink C., “Noise reduction and image quality improvement of low Dose and ultra low dose brain perfusion CT by using the HYPR algorithm,” Poster Number: LL-NRS-SU3A, RSNA, 2010. [DOI] [PMC free article] [PubMed]