Nonrigid PET motion compensation in the lower abdomen using simultaneous tagged-MRI and PET imaging

Abstract

Purpose: We propose a novel approach for PET respiratory motion correction using tagged-MRI and simultaneous PET-MRI acquisitions.Methods: We use a tagged-MRI acquisition followed by motion tracking in the phase domain to estimate the nonrigid deformation of biological tissues during breathing. In order to accurately estimate motion even in the presence of noise and susceptibility artifacts, we regularize the traditional HARP tracking strategy using a quadratic roughness penalty on neighboring displacement vectors (R-HARP). We then incorporate the motion fields estimated with R-HARP in the system matrix of an MLEM PET reconstruction algorithm formulated both for sinogram and list-mode data representations. This approach allows reconstruction of all detected coincidences in a single image while modeling the effect of motion both in the emission and the attenuation maps. At present, tagged-MRI does not allow estimation of motion in the lungs and our approach is therefore limited to motion correction in soft tissues. Since it is difficult to assess the accuracy of motion correction approaches in vivo, we evaluated the proposed approach in numerical simulations of simultaneous PET-MRI acquisitions using the NCAT phantom. We also assessed its practical feasibility in PET-MRI acquisitions of a small deformable phantom that mimics the complex deformation pattern of a lung that we imaged on a combined PET-MRI brain scanner.Results: Simulations showed that the R-HARP tracking strategy accurately estimated realistic respiratory motion fields for different levels of noise in the tagged-MRI simulation. In simulations of tumors exhibiting increased uptake, contrast estimation was 20% more accurate with motion correction than without. Signal-to-noise ratio (SNR) was more than 100% greater when performing motion-corrected reconstruction which included all counts, compared to when reconstructing only coincidences detected in the first of eight gated frames. These results were confirmed in our proof-of-principle PET-MRI acquisitions, indicating that our motion correction strategy is accurate, practically feasible, and is therefore ready to be tested in vivo.Conclusions: This work shows that PET motion correction using motion fields measured with tagged-MRI in simultaneous PET-MRI acquisitions can be made practical for clinical application and that doing so has the potential to remove motion blur in whole-body PET studies of the torso.

INTRODUCTION

Complex, nonrigid respiratory motion degrades the spatial resolution of PET studies, creating distorted images due to motion blurring and artifacts due to mismatches between the emission and the transmission data. As the spatial resolution of clinical PET scanners improves, losses of image quality due to motion become a major limitation of the diagnostic accuracy of clinical cardiac^{1, 2} and oncology PET studies.^{3, 4, 5}

Respiratory gating^{6, 7, 8} is sometimes used to reduce motion blurring in thoracic clinical PET imaging. Such acquisition strategy assumes that organ motion is periodic and therefore consists in binning events into different sinograms corresponding to different states of motion of the chest in order to reduce motion blurring within image frames. As the duration of the gated frames is reduced, so is the effect of motion, allowing accurate quantification of the tracer in small structures. The trade-off is that as the motion effect is reduced, the signal-to-noise (SNR) ratio of the gated reconstruction worsens since it contains a fraction of all counts, which ultimately reduces its diagnostic power.⁸ In addition, uncompensated motion during acquisition of attenuation data may cause artifacts in the reconstruction, even in gated acquisition strategies, a fact that is usually ignored.

To overcome these limitations, approaches have been designed to reconstruct a single PET image containing all detected coincidences while incorporating motion estimates in the PET reconstruction process. In brain imaging, involuntary rigid-body motion of the head can be accurately tracked using optical or infrared cameras synchronized to the PET acquisition.^{9, 10, 11, 12, 13} However, tracking external markers does not allow estimation of the nonrigid deformation of the chest and internal organs. Up to the present day, virtually all nonrigid motion correction methods are based on image-based registration algorithms acting on a gated CT acquisition performed shortly before or after the PET acquisition.^{14, 15, 16} Such techniques are rarely used clinically, however, because they are not accurate in regions that appear uniform on CT images, e.g., the myocardium and the liver. Perhaps more importantly, the use of additional CT measurements significantly increases the patient radiation exposure. This renders such approaches inappropriate to apply in practice and may severely limit the number of CT gated frames and therefore the accuracy of the estimated motion fields. Another approach, which avoids increasing the patient radiation exposure, consists in estimating respiratory motion fields by applying image-registration algorithms to respiratory gated MRI images.^{17, 18, 19, 20} Applied concurrently to the PET acquisition, such techniques could potentially yield more accurate motion correction than in PET-CT, thanks to the improved soft tissue contrast of MR imaging. However, like the PET-CT registration techniques mentioned above, they would also necessarily have limited accuracy in uniform regions without T1, T2 or proton density contrast. Finally, several groups have proposed estimating nonrigid motion fields from the PET data itself. Methods have been developed that attempt motion estimation from the PET data simultaneously with the reconstruction procedure²¹ and as a separate step from reconstructed gated images.^{22, 23, 24} It is not clear yet that such approaches yield accurate motion estimates because of poor statistics within the PET frames, poor spatial resolution of the PET data, and uniform PET signal within organs that move significantly during respiration, e.g., the myocardium and the liver.

Ideally, respiratory PET motion correction should (i) not increase the patient radiation exposure; (ii) be accurate in uniform regions like the liver and the myocardium and (iii) not significantly increase the acquisition and processing time. Ongoing technological developments in simultaneous PET-MR imaging^{25, 26, 27} offer the promise of more ideal PET motion correction by using motion sensitive MR pulse sequences that are accurate in regions with no PET, CT, T1, T2, and proton density contrast and do not increase the patient radiation exposure. Velocity encoded phase contrast MRI (VEPC-MRI) allows estimation of velocity vectors for every pixel of an MRI image by subtracting two phase images acquired with different velocity encoding gradients but otherwise identical acquisition parameters.^{28, 29} Tagged-MRI is another MRI technique that allows estimation of the complex deformation of biological tissues by superimposing a regular tagging pattern on the object magnetization distribution^{30, 31, 32, 33, 34} (for a review of MR-based motion estimation approaches, see Ref. 35). Both tagged-MRI and VEPC-MRI are established techniques that have been used extensively to quantify myocardial motion^{31, 32, 33, 34} and measure blood flow,^{28, 29} but, to our knowledge, these have not yet been used to motion correction PET data acquired simultaneously with the MRI acquisition. This is becoming feasible and practical as whole-body combined PET-MRI scanners are being developed by several medical device manufacturers, and prototypes have already been installed.^{36, 37} Note that tagged-MRI and VEPC-MRI are fundamentally different from MR motion estimation via intensity-based image registration^{17, 18, 19, 20} since they are intrinsically sensitive to motion (i.e., their accuracy does not depend on the presence of T1 or T2 contrast).

In this work, we propose estimation of nonrigid motion fields using a tagged-MRI acquisition performed simultaneously with the PET acquisition, using a combined PET-MRI scanner. We chose to use tagged-MRI rather than VEPC-MRI to estimate motion fields because tagged-MRI directly yields the displacement vectors that are needed to motion correct the PET data, whereas VEPC-MRI estimates velocity vectors that are tangent to the trajectory of material points. This MRI-motion tracking technique (i) does not increase the patient radiation exposure, (ii) is accurate in uniform regions without CT, PET, T1, T2, and proton density contrast, and (iii) does not significantly increase the PET acquisition time since both the PET and MRI datasets are acquired concurrently. A limitation of tagged-MRI (and VEPC-MRI) is that it does not allow estimation of motion in the lungs. Our approach is therefore only capable of correcting for motion in soft tissues like the kidneys or the liver.

We propose incorporating these motion fields into the system matrix of an iterative PET reconstruction algorithm, allowing reconstruction of a single image containing all detected counts while at the same time correcting the raw data for detector sensitivity, random and scatter coincidences, and motion in the attenuation map. This approach is general and can be applied to correct PET acquisitions for breathing and cardiac motion; however, we focus in this work on respiratory motion correction. Since it is difficult to objectively assess the accuracy of motion correction approaches in vivo, we explored the accuracy of the proposed method using numerical simulations and assessed its practical feasibility in proof-of-principle physical acquisitions of a small deformable phantom imaged on a prototype combined PET-MRI brain scanner. Future studies will be dedicated to assessing the approach in vivo in both animals and humans.

We describe our tagged-MRI motion estimation strategy in Sec. 2, and the incorporation of these motion estimates in the PET reconstruction in Sec. 3. We then explore the accuracy of our motion correction approach using numerical simulations of PET and tagged-MRI acquisitions in Sec. 4. Finally, we show a proof-of-principle study of the proposed approach in simultaneous PET-MRI acquisitions using a combined PET-MRI scanner and a deformable phantom mimicking the complex, cyclical deformation of a lung.

MOTION ESTIMATION USING TAGGED-MRI

To estimate respiratory nonrigid motion fields we propose using a tagged-MRI acquisition (C-SPAMM) performed simultaneously with the PET acquisition followed by motion tracking in the phase domain (R-HARP).

Complementary spatial modulation of magnetization

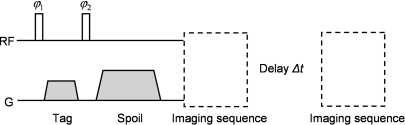
Spatial modulation of magnetization (SPAMM) is a motion sensitive MRI pulse sequence, the time diagram of which is shown in Fig. 1.

Figure 1.

Schematic representation of a 1D 1-1 SPAMM encoding sequence followed by two imaging sequences separated by a time evolution Δt.The image data acquired after the evolution time Δt show tag lines that have deformed with the object and have faded with the local T1 constant.

It is possible to show that the longitudinal component of the magnetization vector following a SPAMM sequence follows a sinusoidal pattern in the direction of the tagging gradient. The wave vector of this spatial sine wave is equal to k =γGτ, where γ is the proton gyromagnetic ratio, G is the tagging gradient, and τ is its duration.^{30, 31} Therefore, acquiring MRI data after a spoiled SPAMM sequence yields images that are the superposition of the object magnetization distribution and the sinusoidal tagging pattern.^{32, 33}

Since the sinusoidal tagging pattern created by a SPAMM sequence deforms with the patient during respiration, gating a SPAMM + readout acquisition reveals the complex deformation of tissues during breathing. It is important to note that the sinusoidal pattern created by a SPAMM sequence is visible even in uniform regions without T1, T2, and proton density contrast. In contrast with nonrigid motion estimation using registration algorithms applied to gated CT, PET and∕or anatomical MRI frames, respiratory gated tagged-MRI therefore has the advantage of yielding accurate motion estimates even in uniform regions like the liver and the myocardium. Since tagged-MRI acquisitions are used to track motion and not to image the T1, T2, and proton density contrast of the chest tissues, two independent SPAMM acquisitions can be performed using opposite second flip angle (i.e., a first dataset is acquired using ϕ₂ and a second with −ϕ₂) and subtracted in order to isolate the sinusoidal tagging pattern on reconstructed amplitude images³¹ (C-SPAMM). Note that C-SPAMM can create not only 1D but also 2D and 3D tagging patterns by using more than one gradient direction in the sequence shown in Fig. 1. Finally, tagging can be performed along any logical axis; however we assume herein, without loss of generality, that 3D tagging is performed along the x, y, and z axes.

Regularized harmonic phase motion tracking

Dense motion fields can be estimated from a gated tagged-MRI acquisition by tracking the C-SPAMM tagging pattern either on the phase or amplitude reconstructed images. In the amplitude domain, estimation of motion fields requires detecting the tag lines in every motion frame^{38, 39} and interpolating the displacement of physical points located between tags.^{40, 41, 42} Such a process is typically time-consuming and generally requires human intervention to correct mistakes in the feature detection step.³⁸ In contrast, tracking motion in the phase domain does not require detecting the tag lines and is therefore faster, more robust, and does not require human intervention.³⁴ Another important advantage of using phase instead of amplitude images is that the phase is intrinsically scaled to [−π, +π] independent of the MRI readout sequence and the organ imaged. This reduces the variability of the pixel intensities to be tracked and considerably simplifies the motion tracking procedure.

We propose tracking motion in the phase domain using the HARmonic Phase (HARP) algorithm originally proposed by Osman et al.³⁴ for quantifying myocardial motion (the phase in question is the harmonic phase obtained by Fourier transform of the reconstructed magnitude image, not the phase of the MRI signal itself which is affected by other effects, such as main field inhomogeneities and flow). The first step in HARP consists of filtering the tagging patterns in the x, yand z directions in order to remove residual contributions of the object magnetization to the phase images, and to isolate the local deformation of tissues along the x, y and z directions. Such filtering is most easily performed in k-space where the 3D tagging pattern consists of six peaks located on each side of the center of k-space on the υ_x, υ_y and υ_z frequency axes.³⁴ The distance between each peak and the center of k-space is inversely proportional to the frequency of the tagging pattern, so that increasing the frequency of the tagging pattern makes it easier to filter it in k-space. However, increasing the tagging frequency also reduces the maximum amplitude that can be tracked. In practice, the tagging frequency depends mainly on the amplitude of the motion imaged and the temporal resolution of the tagged-MRI acquisition and should therefore be optimized for specific applications.

Since the harmonic phase of a material point is a constant of motion, local deformations between the reference (acquired at time t) and a subsequent phase image (acquired at time t +Δt) can be estimated pixel-by-pixel by minimizing the following phase difference³⁴:

$$\psi (\mathbf{d})=\parallel \varphi (\mathbf{x},t)-\varphi (\mathbf{x}+\mathbf{d},t+\Delta t)\parallel {}^2$$ (1)

where d is the displacement vector of the material point located at x at time t in the reference frame and ϕ(x,t) = (ϕ_x(x,t), ϕ_y(x,t), ϕ_z(x,t))’ is the phase vector at location x and time t combining information about the tissue deformation in the x, y and z directions (this is a vector with nine components, i.e., three for each phase image). This HARmonic Phase tracking procedure (HARP) is well-posed as long as the amplitude of the displacement vector d is smaller than the period of the tagging pattern.³⁴ Equation 1 was initially proposed to track myocardial motion. When tracking motion across the chest, which is more challenging because of the greater variations of the magnetic susceptibility and the complex structure of motion fields in the torso, it is useful to regularize the motion tracking procedure by penalizing large variations of the displacement field across neighboring pixels

$$\psi ({\mathbf{d}}_1,\dots ,{\mathbf{d}}_M)={\displaystyle \sum _{i=1}^M{\parallel \phi (x,t)=\phi (x_i+{\mathbf{d}}_i,t+\Delta t\parallel }^2+\beta {\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j\in N(i)}{\alpha }_{ij}{\parallel {\mathbf{d}}_i-{\mathbf{d}}_j\parallel }^2,}}}$$ (2)

where M is the number of pixels in the phase images, N(i) denotes the set of pixels located in the neighborhood of pixel i, α_ij is a weight greater for pixels close to i(∑_j∈N(i)α_ij=1), and β is a parameter controlling the strength of the roughness penalty. Herein, we refer to the motion estimation procedure based on the minimization of Eq. 2 as Regularized-HARP (R-HARP).

In regions with little MRI signal, such as the lungs, the harmonic phase is random and does not contain useful motion information. To prevent these arbitrary phase values from biasing the motion estimation at other locations (because of the roughness penalty), we masked the regions of the phase images with little MRI signal in the minimization procedure of Eq. 2. Note that such masks can be obtained simply by adding the two C-SPAMM acquisitions, instead of subtracting them, and thresholding the resulting amplitude image.

MOTION-CORRECTED PET RECONSTRUCTION

Once the motion fields between consecutive motion frames have been estimated, they can be incorporated in the system matrix of a PET reconstruction algorithm, allowing reconstruction of all the detected coincidences into a single reference frame. Motion corrected list-mode MLEM PET reconstruction algorithms (MC-EM) have been proposed and are all of the form^{14, 15, 16, 22, 43}

$${\rho }_i^{(a+1)}=\frac{{\rho }_i^{(a)}}{{\tilde{s}}_i}\sum _{n=1}^N\frac{{\tilde{a}}_{\mathit{ni}}(f_n)}{{\sum }_{j=1}^M{\tilde{a}}_{\mathit{nj}}(f_n){\rho }_j^{(a)}},$$ (3)

where N is the number of detected coincidences, f_n is the motion frame in which coincidence n was detected, and ρ is the vector of pixel intensities to be estimated in the reference frame. In Eq. 3, ${\tilde{\alpha }}_{\mathit{ni}}(f_n)$ is the “moved” system matrix combining the system matrix and the motion warping operator registering the frame f_n to the reference frame

$$\tilde{\mathbf{A}}(f_n)=\mathbf{A}\mathbf{\Phi }(f_n),$$ (4)

where A is the K × M system matrix whose general element a_ki is the probability that a coincidence emitted from pixel i is detected in line of response (LOR) k and Φ(f_n) is the M × M motion operator deforming the reference image to the deformed image in frame f_n [Note that we do not propose rebinning the coincidences of the list-mode file in sinograms corresponding to the different MRI motion frames. Instead, the MRI motion frames in which coincidences are detected are determined before reconstruction using an external gating signal––in this study an analogue signal from the pressure transducer attached to the phantom (see Sec. 4B1), and the entire list file is reconstructed at once using Eq. 3]. These motion or warping operators are simply the interpolation matrices allowing computation of the pixel intensities in the deformed frames from the knowledge of pixel intensities in the reference frame. They can be computed using motion fields by simple linear interpolation.¹⁶ In Eq. 3, ${\tilde{s}}_i$ is the “moved” detection sensitivity of pixel i calculated by backprojecting the moved system matrices $\tilde{\mathbf{A}}(f)f=1\dots F$, where F is the number of motion frames, along all the LORs of the scanner and summing the sensitivity images corresponding to each frame. The calculation of sensitivity images in list-mode reconstruction of PET data is very time consuming,⁴⁴ so that in practice F should not be too large in order to reduce computation time. Note that a sinogram version of Eq. 3 is simply obtained by replacing the loop over N, the number of events in the list file, by a double loop over K, the number of sinogram bins, and F (in this case events detected in different motion frames must be binned in different sinograms).

As pointed out by Lamare et al.,^{14, 15} frame-dependent attenuation correction can be modeled in $\tilde{\mathbf{A}}(f_n)$ by computing attenuation correction factors (ACF) based on the attenuation maps deformed in every motion frame. Such maps can simply be obtained by deforming the attenuation map in the reference frame using the motion interpolation matrices Φ(f_n). The nonuniform attenuation map in the reference frame can itself be estimated directly from the MRI data using atlas registration-based techniques.^{45, 46, 47, 48, 49} Detector sensitivity correction factors and other motion-independent correction factors can be included in the static system matrix. Finally, scatter and random corrections can be implemented as additive terms in the denominator of Eq. 3. Since the spatial distributions of scatter and random coincidences vary slowly and do not depend strongly on the activity distribution, they can be assumed, to first approximation, to be independent of the respiratory motion frame and can therefore be computed for the average respiratory cycle using established techniques, e.g., the delayed window or the single photons technique for random estimation and the single scatter simulation for scatter estimation.^{50, 51, 52}

EVALUATION IN SIMULTANEOUS PET-MRI SIMULATIONS AND ACQUISITIONS

Simultaneous PET-MRI simulations

As a first evaluation step, we assessed the accuracy of our correction approach using numerical simulations of the PET and tagged-MRI acquisitions. Such simulations were useful to evaluate the accuracy of the motion estimation and image reconstruction procedures in the presence of noise in both the PET and tagged-MRI dataset since they allowed comparison with the ground truth.

Phantom

For both the PET and MRI simulations, we modeled a breathing patient using the NCAT phantom.⁵³ We modeled a 4 s respiratory cycle divided into 16 frames of 250 ms each. Activity and attenuation maps as well as the reference motion fields registering each of the 15 moved frames to the first, reference frame, were obtained using the NCAT program.

MRI simulation

Tagged-MRI simulations were performed using the open source MRI simulator SIMRI (Ref. ⁵⁴), which we modified to model motion of the object during the tagged-MRI sequence. Relaxation was modeled at 3T using the standard features of SIMRI and T1, T2, and proton density maps obtained using the NCAT anthropomorphic phantom⁵³ as well as published tissue values.⁵⁵ We modeled a 3D 1-1 C-SPAMM sequence with ϕ₁ = 45°, ϕ₂ = ±45° and a tagging period of 2 cm in the x, y, and z directions. After tagging, the entire spin-state model (magnetization vector field, T1, T2, and proton density scalar maps) was moved according to the reference motion fields for each frame. A 2D gradient echo readout was modeled with TR = 100 ms, TE = 10 ms, and α = 10° (perfect slice selection and perfect recovery of the longitudinal magnetization were assumed in this simulation). All of the 16 frames modeled were simulated, so that the timing resolution of this tagged-MRI simulation was 250 ms per frame. Since T1 fading of the tag lines is significant after ∼1 s in biological tissues at 3T, a fresh tagging pattern was created every four frames in order to avoid complete disappearance of the tag lines at the end of the cycle (i.e., a C-SPAMM sequence was performed immediately before acquiring the MRI signal for frames #1, 5, 9, and 13).

Three levels of random Gaussian noise were added to the simulated k-space data with energies (equal to σ², where σ is the standard deviation of the Gaussian noise distribution) equal to 5%, 15%, and 25% of the total data energy (equal to ${\Sigma }_{i=1}^M\left|K_i\right|{}^2∕M$, where k_i is the complex value of k-space sample i and M is the number of k-space samples). For each frame, three tagging peaks containing motion information in the x, y, and z directions were filtered as explained in Sec. 2B using 3D parallelepipedic hard rectangular filters extending along the half x, y, and z axes, respectively, that were smoothed by a 3D Hamming window. These peaks were reconstructed on a 128 (x) × 128 (y) × 64 (z) image matrix and their harmonic phase was extracted. Phase images pertaining to the same tagging segment (As explained above, a fresh tagging pattern was created before imaging the frames #1, 5, 9, and 13. The simulation was therefore divided in four segments corresponding to the groups of frames 1–4, 5–8, 9–12, and 13–16) were registered using R-HARP with values of the regularization parameter β ranging from 10⁻¹ to 10⁴ by increment of 10 as well as without regularization (β = 0). Since HARP is only capable of estimating small displacements,³⁴ we registered consecutive phase images within each segment. Total motion fields registering each frame to the first, reference frame, were obtained by summing the consecutive motion fields using tri-linear interpolation (interpolation was used in this summation step because the displacement vectors of a motion field generally do not land in the centers of pixels of the subsequent motion field. For example, when computing a combined motion field a → c it is necessary to first move each points of the Cartesian grid according to a → b and then to move these new points, which are not positioned on a Cartesian grid anymore, according to b → c by interpolating the field b → c at these new locations). Since this interpolation process necessarily introduced some error in the estimation of the total motion fields, the total number of summations was minimized by registering early motion frames backward (1 ← 2 ← 3 … ← 9) and late frames forward (10 → 11 → … → 16 → l).

PET simulation

Activity maps corresponding to each frames were obtained by adding six tumors to the NCAT activity map (three in the liver and a bone tumor in the sternum), blurring it with an isotropic 3D Gaussian filter with full width at half maximum (FWHM) equal to 4 mm and deforming it in the 16 motion frames modeled using the known NCAT motion fields. Note that the NCAT phantom allows only phase-based binning (frames of constant duration) and not amplitude-based binning (constant amplitude variation between frames), which better reflects the motion of internal organs. This was not a serious limitation in our study however because we used 16 frames, which is enough to capture the fastest movement of the chest during normal breathing (eight frames are more routinely used in clinic). Moreover, phase-based binning is better adapted to motion sensitive MRI acquisition strategies, which are most easily implemented for sets of frames with constant duration. These activity maps were projected into sinograms while modeling attenuation using the reference attenuation maps deformed in every frame. Ten noise realizations were simulated by adding a random Poisson noise to these noise-free attenuated sinograms, corresponding to the detection of 60 000 coincidences per slice per frame. These were finally summed two by two, yielding a total of eight sinograms corresponding to eight motion frames, in order to model intraframe motion in the PET data (as explained in Sec. 2B, the number of PET frames should be kept reasonably small in order to reduce the sensitivity image computation time).

These sinograms were reconstructed into a single PET image in the reference frame using the ordered-subset, sinogram version of the MC-EM algorithm described in Sec. 2 with five iterations and ten subsets. Motion correction was performed within the reconstruction algorithm using both the reference motion fields and the motion fields estimated with R-HARP. The first frame was also reconstructed without motion correction. We evaluated the performance of our motion correction approach for quantifying tumor activity by measuring contrast recovery coefficients in the hot tumors, defined as

$$\mathrm{CRC}=\frac{{\lambda }_{\mathrm{hot}}∕{\lambda }_{\mathrm{bkg}}}{c},$$ (5)

where λ_hot and λ_bkg are the mean values of region of interests (ROI) drawn on the hot tumor and the background, respectively, and c is the reference contrast of the hot tumor. We also measured the signal-to-noise ratio in these tumors, defined as

$$\mathrm{SNR}=\frac{{\lambda }_{\mathrm{hot}}-{\lambda }_{\mathrm{bkg}}}{\sqrt{{\sigma }_{\mathrm{hot}}^2+{\sigma }_{\mathrm{bkg}}^2}},$$ (6)

where λ_hot and λ_bkg are the average of the hot tumor and background ROIs computed over the ROI pixels and the ten noise realizations and σ_hot and σ_bkg are the average standard deviation of pixel intensities in the hot and background ROIs, computed over the ten noise realizations.

Simultaneous PET-MRI acquisitions

As a second evaluation step, we imaged a small deformable phantom mimicking the complex deformation pattern of a lung using a combined PET-MRI brain scanner. Although this phantom is a much simplified model of a lung, this study, which is preliminary to future in vivo animal and human testing, allowed us to show the feasibility of the proposed approach and to explore issues relative to its practical implementation.

Deformable PET-MRI phantom

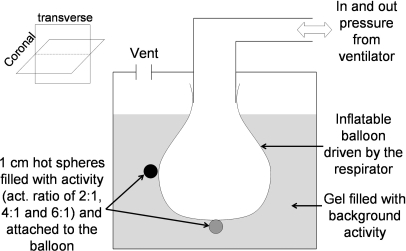
We have built a small deformable MRI-compatible phantom mimicking the cyclical, nonrigid motion of a lung. As shown in Fig. 2, this phantom consisted of a balloon inflated cyclically by a ventilator (Harvard Apparatus, Holliston MA) with a period of about 1 s, to which were attached five hollow spheres (Data Spectrum Corporation) filled with¹⁸ FDG with activity to background ratio of 2:1 (two spheres), 4:1 (two spheres), and 6:1 (one sphere). The balloon was filled with air and immersed in a radioactive (FDG) gel solution of methylcellulose powder well mixed in water with a thick, but not solid, consistency in order to reduce flow artifacts in the tagged-MRI acquisition. The total activity in the phantom at imaging time was 0.2 mCi. Pressure in the balloon was tracked using a pressure transducer, which created TTL pulse at the beginning of every motion cycle. This pulse was then sent to the MRI scanner to trigger the tagged-MRI acquisition and was written as a trigger event in the PET list-mode stream.

Figure 2.

Schematic representation of our deformable PET-MRI phantom (height = 15 cm; diameter = 12.2 cm).

We imaged this phantom on a prototype combined PET-MRI brain scanner at the Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston MA. This system is composed of a Siemens 3T Magnetom TIM Trio MRI scanner inside of which is inserted an MRI-compatible BrainPET 1 Siemens scanner operating simultaneously with the MRI scanner. This 3D PET system is made of 32 detector cassette modules of six 12 × 12 LSO, 2.5 × 2.5 × 20 mm³ crystal arrays each read out by a 3 × 3 array of APDs (axial∕transaxial FOV: 19.25 cm∕32 cm, energy resolution: 15% at 511 keV, energy window: 400–650 keV, spatial resolution at 1 cm off center: 2.1 mm FWHM). PET and MRI data were acquired simultaneously and were processed offline.

Motion estimation using tagged-MRI

Tagging in the three spatial directions was performed in one direction at a time using a 1D 1-1 C-SPAMM pulse sequence with ϕ₁ = 45° and ϕ₂ = ±45° and a tagging period of 8 mm. Tagged-MRI images were acquired using a 2D gradient echo sequence with TR = 0.8 s, TE = 2.4 ms, and α = 15°. Since the motion cycle period was shorter than the T1 relaxation constant of the gel, the imaging volume was tagged only once at the beginning of each cycle. An entire volume was acquired for each motion frame by permuting the order of the z slices acquisition in different motion cycles. This multiphase∕multislice acquisition strategy resulted in the acquisition of a 4D tagged volume with as many slices as motion frames, i.e., 32 in this work.

x, y, and z phase volumes were extracted from these 32 tagged volumes at every frame and were interpolated on 1 mm isotropic 128 × 128 × 128 volume grids using cubic B-splines. The motion fields between these 32 consecutive motion frames were estimated using R-HARP with values of the regularization parameter β ranging from 10⁻² to 10³ by increment of 10. Consecutive early frames were registered backward (1 ← 2,…, 16 ← 17) and late frames were registered forward (21 → 22,…, 32 → 1) and then summed using an tri-linear interpolation technique in order to obtain the motion fields between each of the motion frames and the first, reference frame (1 ← 2, 1 ← 3…) while minimizing the number of interpolation steps.

Acquisition and reconstruction of list-mode PET data with quantitative corrections

The list-mode PET data was acquired simultaneously with the MRI acquisition. Valid prompt and delayed coincidences, and time triggers (from the main clock of the scanner) and gating triggers (from the pressure monitoring unit described in Sec. 4B1) were written in the list-mode stream. Fifteen list-mode files corresponding to 5 min acquisitions each were acquired, yielding 15 independent noise realizations of the phantom. The prompt (random) detection rate was ∼233 000 (∼23 000) coincidences per second at the beginning and ∼130 000 (∼9300) coincidences per second at the end of the acquisition.

These 15 list-mode files were reconstructed independently with and without motion correction using the time-ordered subset list-mode version of the MC-EM algorithm shown in Eq. 3 (the same number of coincidences were reconstructed in all these files in order to allow direct comparison of the image intensities without scaling). Reconstructions were fully 3D with a maximum ring difference of 40 crystals, 16 subsets and four iterations, on a 128 × 128 × 128 image grid with 2 mm isotropic resolution. As explained in Sec. 3, the computing time for calculating the moved sensitivity image increases linearly with the number of motion frames F. Although 32 frames were available from the tagged-MRI acquisitions, we divided the PET motion cycle in only eight frames in order to reduce reconstruction time (these PET frames corresponded to the MRI time frames #1, 5, 9, 13, 17, 21, and 25). The attenuation map in the first, reference frame was obtained by assigning μ_air= 0 cm⁻¹ outside of the phantom and μ_water= 0.096 cm⁻¹ inside the phantom. Attenuation from the MRI transmit and receive coils was also corrected.

As explained in Sec. 3, random and scatter corrections were performed by assuming that the distribution of random and scatter coincidences in different motion frames did not change significantly. Moreover, both random and scatter corrections were performed using 2D correction sinograms which is equivalent to assuming that the distribution of random and scatter coincidences is the same in the direct and cross planes of the brainPET scanner. Random correction was performed using the delayed window technique⁵⁰ (since a decreasing amount of activity was imaged in consecutive list-mode acquisitions, a random sinogram was computed for every list-mode file). Scatter correction was performed using the single scatter simulation (SSS)⁵² with 263 diffusion centers per liter on a sinogram grid of size 64 (transax.) × 64 (angle) × 10 (slice) covering a FOV of 36 cm diameter and an axial FOV of 19.25 cm and using a single iteration. This sinogram was interpolated to the full size sinogram of the brainPET scanner (263 × 192 × 44, same FOV and axial FOV) while accounting for the arc effect. A scatter sinogram was computed only once for the first noise realization but was scaled to every list-mode acquisition independently by fitting the tails of the scatter distribution to the coincidences detected outside of the patient after subtracting the random sinogram from the prompt sinogram.

RESULTS

Simultaneous PET-MRI simulations

Motion estimation using tagged-MRI

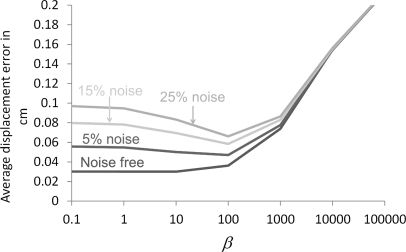
Figure 3 shows the average error of motion fields estimation using R-HARP as a function of the noise level in the tagged-MRI simulation and the regularization parameter β (the average error was defined as $\langle err\rangle =\frac{1}{N\times F}{\displaystyle {\sum }_{i-1}^N{\displaystyle {\sum }_{f=1}^F\left\{\right|d_{x,f,i}^{\text{est}}-d_{x,f,i}^{\text{ref}}}}|+|d_{y,f,i}^{\text{est}}-d_{y,f,i}^{\text{ref}}|+|d_{z,i}^{\text{est}}-d_{z,f,i}^{\text{ref}}\left|\right\}$, where N is the number of pixels, F is the number of frames, and d^est and d^ref denote the estimated and reference motion fields). As expected, increasing the noise level in the tagged-MRI acquisition increased the error of the motion field estimation for all values of the regularization parameter β. We note however that the smallest estimation error was reached for the same value of β at all noise levels. Moreover, the error associated with this optimal value of the regularization parameter varied only from 0.04 to 0.07 cm when increasing the noise level from 5% to 25%. These results indicate that our regularization of the HARP algorithm using a quadratic roughness penalty is adequate to estimate the complex, nonrigid motion fields due to breathing in the presence of Gaussian noise in the tagged-MRI acquisition.

Figure 3.

Average error of motion fields estimated using R-HARP as a function of the noise level and the regularization parameter β.

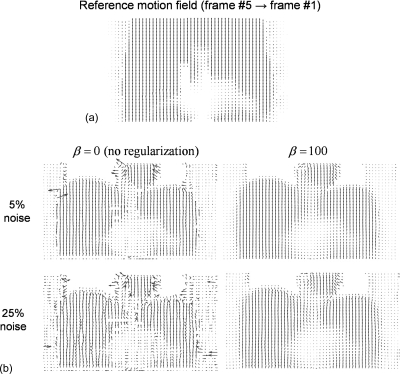
Figure 4 shows the motion field registering frame #5 to frame #1 (reference frame) estimated with R-HARP using the tagged-MRI simulations with 5% and 25% noise and with and without regularization. As noted above, using a single value of the regularization parameter β yielded accurate estimates of the motion fields both at low (5%) and high (25%) noise levels.

Figure 4.

(a) Reference motion field between the MRI frames #5 (end inspiration) and #1 (end expiration, reference frame) in the coronal view. (b) Motion fields estimated with R-HARP using the tagged-MRI simulations with 5% and 25% noise levels with and without regularization. As explained in Sec. 2B, our motion tracking procedure was masked in the lungs where little MRI signal was detected. Motion fields are shown in the coronal view and deformation vectors are in pixel units divided by five in this figure.

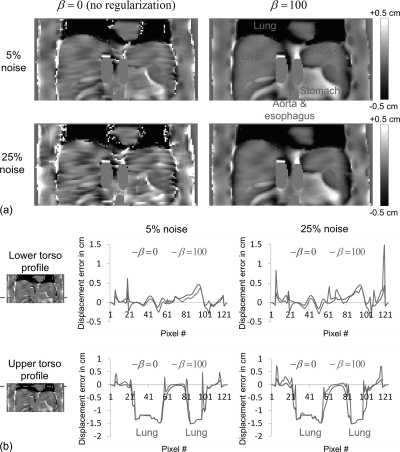
Figure 5 shows motion field estimation error maps and profiles corresponding to the fields shown in Fig. 4. These images show that motion tracking with R-HARP was accurate almost everywhere in the simulated torso except in regions surrounding the ribs and the interface between sliding and fixed structures in the thoracic cage (e.g., interface liver∕soft tissues in contact with the ribs). This is due to the short T2 constant of bone causing a rapid decay of the MR signal in these structures and to the fact that the reference motion field was discontinuous at the interface between sliding organs. Like Fig. 4, Fig. 5 also shows that regularizing the HARP algorithm using a quadratic prior yielded accurate motion estimation at all noise level in regions with significant MRI signal.

Figure 5.

(a) Motion field estimation error maps of the registration frame #5 → frame #1 with and without regularization using the tagged-MRI simulations with 5% and 25% noise levels. (b) Lower torso and upper torso profiles through these error maps. The estimation error is the greatest in the lungs, where it is in fact equal to the opposite of the reference displacement, since motion is not estimated in these regions.

Motion corrected PET reconstruction

Figure 6 shows simulated PET images reconstructed with our MRI-based motion correction (MRI-based MC, tagged-MRI simulation with 15% noise, regularization with β = 100), with motion correction using the reference motion fields (reference MC), without motion correction (no MC) and using only events detected in the first of eight frame (frame #1). Figure 7 shows contrast recovery coefficients (mean CRC ± standard deviation computed over ten noise realizations) and signal to noise ratio (SNR computed over ten noise realizations) in the six simulated tumors on images obtained with the same reconstruction strategies.

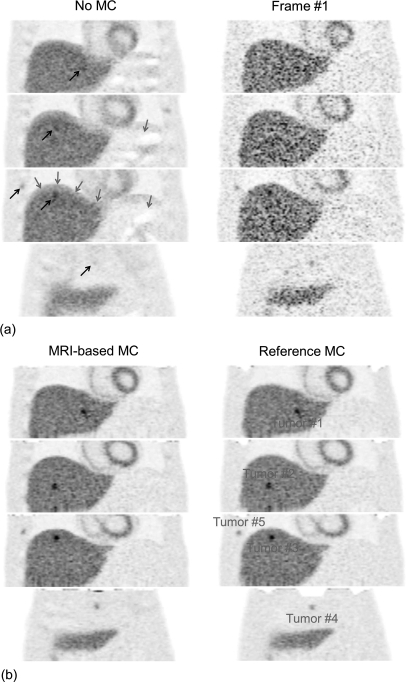
Figure 6.

Simulated PET images in the coronal view reconstructed with (MRI-based MC) and without motion correction (No MC) and using only events from the first frame (Frame #1). Also shown are images corrected using the reference motion fields (Reference MC), which represents the best achievable performance of our method at this noise level. Grey arrows show artifacts on the uncorrected image due to attenuation∕emission mismatches. Black arrows show regions of the uncorrected image with significant motion blurring.

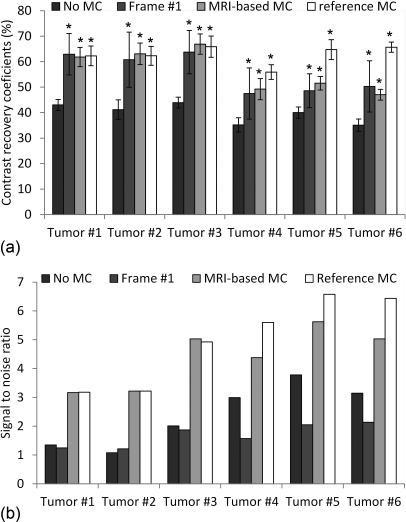
Figure 7.

(a) Contrast recovery coefficients (average CRC ± standard deviation computed over ten noise realizations) of the six simulated tumors measured on images reconstructed with the no MC, frame #1 and MRI-based MC strategies. Also shown are CRC values measured on images corrected using the reference motion fields. A star indicates a CRC value significantly greater than with no MC (p < 10⁻³). (b) Signal-to-noise ratio (computed over ten noise realizations) in the six tumors reconstructed with the no MC, frame #1 and MRI-based MC and the reference motion correction approaches.

Incorporating motion fields estimated with tagged-MRI in the PET reconstruction procedure clearly reduced motion blurring, yielding much clearer delineation of the liver and the myocardium and better recovery of the activity in small tumors. Our motion correction method yielded significantly greater contrast recovery of the hot small tumors than when not correcting for motion (MRI-based MC vs no MC). On the other hand, reconstructing all the counts yielded significantly greater SNR than when only reconstructing coincidences detected in the first frame (MRI-based MC vs frame #1). The SNR was also greater with MRI-based MC than with no MC because of the better recovery of the small tumor signal with MRI-based MC.

We note that modeling motion both in the emission and the attenuation maps removed artifacts due to emission∕attenuation mismatches that were particularly visible in the dome of the liver in the absence of motion correction. The contrast recovery coefficients of tumors #4 (in the sternum), #5 (right rib), and #6 (left rib) were significantly lower with MRI-based MC with than the best possible motion correction (reference MC) because of the difficulty of estimating motion fields in or around bone structures as explained in Sec. 5A1 and Fig. 5. We note however that, for all tumors, the differences between MRI-based MC and frame #1 CRCs were not significant, while the SNR was systematically greater with MRI-based MC than with frame #1. CRCs were also consistently greater with MRI-based MC than with no MC, even in the tumors #4, #5, and #6.

Simultaneous PET-MRI acquisitions

Motion estimation using tagged-MRI

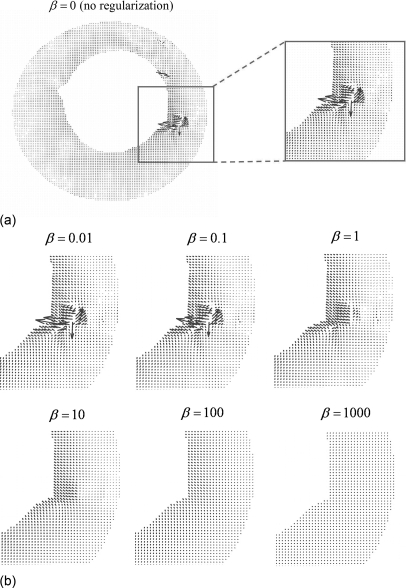
Figure 8 shows motion fields registering the acquired MRI frames #11 and #10 estimated with R-HARP with different values of the regularization parameter β. The presence of a sphere with a short T2 relaxation constant introduced a systematic error in the motion field estimation at this location. We chose a value of the regularization parameter β that was large enough to regularize such artifacts (β ≥ 1) but not so large that it significantly affected the overall structure of the motion field (β ≤ 10). In an effort to more quantitatively determine the optimal value of the regularization parameter, we also examined the maximum value of the Jacobian determinant |J| of the motion field over all pixels and motion frames as a function of β. The Jacobian determinant represents the local volume change and since the gel in our phantom is incompressible, a perfect motion estimation procedure should in theory yield |J| = 1 everywhere within the gel. Because of the presence of artifacts in the phase images, we found that even large values of β yielded values of |J| slightly different from unity in these regions; however, most of the reduction in its maximum value across the phantom was achieved for β = 10 with little further reduction using greater values.

Figure 8.

Motion fields estimated with R-HARP with the regularization parameter β ranging from 10⁻² to 10³ by increments of 10. In this figure, images are in the coronal view and displacement vectors are in pixel unit.

Motion correction of list-mode PET data

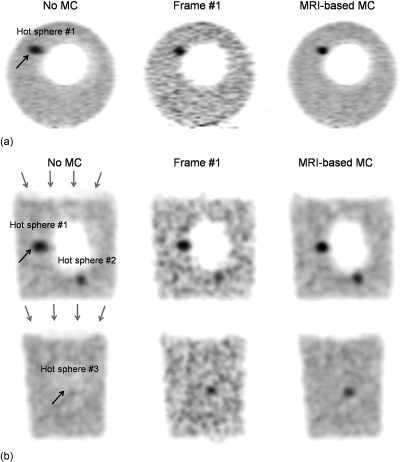
Figure 9 shows PET images of the deformable phantom reconstructed with our MRI-based motion correction (MRI-based MC) using β = 10 and without motion correction (no MC) as well as by reconstructing coincidences detected in the first PET motion frame only (frame #1). These images indicate that MRI-based motion correction allowed recovery of the intrinsic spatial resolution of the scanner that was otherwise degraded by motion (black arrows) and eliminated artifacts caused by attenuation∕emission mismatches due to motion (red arrows). Our motion correction strategy also increased the detectability of the hot tumor #3 compared to both the no MC and the frame #1 strategies as measured by the SNR. Indeed, this tumor was barely visible in the no MC strategy because it was blurred over several slices due to motion, while in the frame #1 reconstruction strategy its detectability was reduced by the presence of high background noise.

Figure 9.

PET images of the deformable PET-MRI phantom reconstructed using our MRI-based motion correction approach (MRI-based MC), without motion correction (no MC) as well as by reconstructing only events detected in the first PET motion frame (Frame #1). Reconstructed images are shown in the coronal (a) and the transaxial views (b) and are identically scaled. Grey arrows show artifacts on the uncorrected image due attenuation∕emission mismatches. Black arrows show regions of the uncorrected image with significant motion blurring.

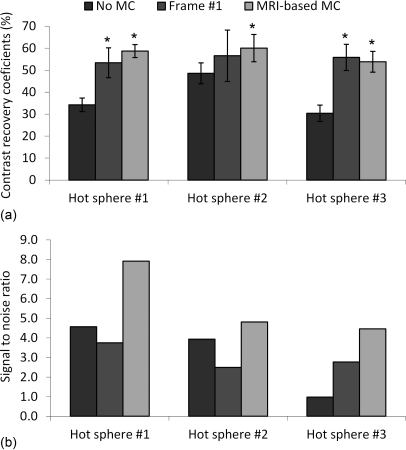
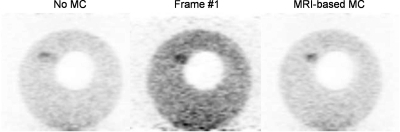
Figure 10 shows contrast recovery coefficients (CRC) and SNR in the three most visible spheres of images of the deformable phantom reconstructed with the MRI-based MC, no MC, and frame #1 strategies. Hot spheres CRCs were systematically greater with MRI-based MC and frame #1 than with no MC since loss of spatial resolution due to motion caused a reduction of the apparent activity level in these small tumors (CRCs were smaller than 100% even when performing motion correction because of partial volume effect). Figure 11 shows standard deviation images corresponding to reconstruction of the deformable PET-MRI phantom with the no MC, frame #1 and the MRI-based MC strategies. Like Fig. 10, these images show that reconstructing all coincidences in a single reference motion frame reduces the variance of the reconstructed images compared to when using only the fraction of coincidences detected in the first motion frame.

Figure 10.

(a) Contrast recovery coefficients (average CRC ± standard deviation computed over 15 noise realizations) of the three hottest spheres attached to our deformable phantom, measured on images reconstructed with the no MC, frame #1 and MRI-based MC strategies. A star indicates a CRC value significantly greater than with no MC (p < 10⁻³). (b) Signal-to-noise ratio (computed over 15 noise realizations) within the three hottest spheres estimated on images reconstructed with the no MC, frame #1 and MRI-based MC strategies.

Figure 11.

Standard deviation images computed over 15 noise realizations of the deformable PET-MRI phantom list-mode data reconstructed with the MRI-based MC, frame #1 and no MC strategies. Images are shown in the coronal view and are identically scaled on this figure.

As noted before, SNRs of small tumors were higher with MRI-based MC and no MC than with frame #1 because this gating strategy only allowed reconstructing a fraction of all counts and therefore increased noise. Although both MRI-based MC and no MC allowed reconstruction of all counts in a single image, SNRs were systematically greater with MRI-based MC than no MC as well since correcting for motion increased the PET signal in these small tumors.

DISCUSSION

In this work, we have presented a PET motion correction strategy based on the incorporation of motion fields measured with tagged-MRI in the system matrix of a PET iterative reconstruction algorithm. Although motion sensitive MRI pulse sequences like velocity encoded phase contrast MRI (VEPC-MRI) and tagged-MRI are established techniques routinely used in the clinic, to our knowledge, this work represents the first published report describing the use of such techniques for motion correction of PET data. The main advantages of our strategy over CT-based motion correction approaches are that (i) it does not increase the patient’s radiation exposure, (ii) it is accurate even in uniform regions without CT, PET, T1, T2, and proton density contrast, and (iii) it can be performed concurrently with the PET acquisition (instead of sequentially as in PET-CT imaging). Although combined PET-MRI scanners are not yet commercially available, they are currently being developed by several medical devices manufacturers, and prototypes have already been installed.^{36, 37}

We proposed using tagged-MRI to estimate nonrigid respiratory motion fields across the chest instead of VEPC-MRI because tagged-MRI directly yields displacement vectors whereas VEPC-MRI estimates velocity vectors that are tangent to the trajectory of material points. From such motion fields, interpolation matrices can be computed that allow warping of the PET image from the reference frame into the different moved motion frames. These interpolation matrices can in turn be incorporated in the system matrix of an MLEM reconstruction of the PET data allowing reconstruction of all detected coincidences into a single image while correcting for motion both in the emission and attenuation maps. This algorithm can be formulated both for sinogram and list-mode representations and requires that coincidences are binned in gated sinograms (sinogram representation) or that trigger events are included in the list-mode stream indicating the beginning of every motion cycle (list-mode representation). As with other motion-corrected PET reconstruction approaches, a limitation of this reconstruction strategy is that it involves computing F sensitivity images, where F is the number of motion frames, which is very time consuming in practice when reconstructing list-mode data.⁴⁴ As a practical matter, the number of motion frames should therefore be chosen so as to minimize reconstruction time while yielding frames short enough so that intraframe motion is negligible.

In this work we used a 1-1 C-SPAMM strategy both in numerical simulations and physical acquisitions to nonselectively tag the entire volume before imaging. Higher order binomial C-SPAMM sequences can also be used in order to create a sharper tagging pattern; however, such pulses are longer, and, since the shape of the tagging pattern is not crucial when tracking motion in the phase domain, it is unlikely that they will yield more accurate motion field estimates. We chose to process the tagged-MRI images obtained using this 1-1 C-SPAMM tagging strategy in the phase rather than in the amplitude domain. The main advantage of this technique, called HARmonic Phase tracking³⁴ (HARP), is that it is fast and avoids the need for automatically detecting the tag lines, which is difficult in practice and usually requires human intervention.³⁸ As explained in Sec. 2B, a limitation of this approach is that it requires that the tagging period be greater than the maximum displacement. Slowly varying tagging patterns can capture larger motion but are also more difficult to filter out because the distance between the center of k-space to the tagging peaks is inversely proportional to the tagging period. In practice, the tagging period should therefore be optimized for specific applications. Our numerical simulation results indicate that a tagging period of 2 cm used concurrently with a gating acquisition containing F = 16 motion frames allows accurate estimation of nonrigid motion fields with HARP due to patient breathing.

HARP was originally developed for quantifying myocardial motion.³⁴ Since the end goal of this work is to correct PET acquisitions for breathing motion, which is more challenging because of the greater variations of the magnetic susceptibility and the complex structure of motion fields in the torso, we regularized the HARP motion tracking procedure using a quadratic roughness penalty penalizing large variations of the displacement field across neighboring pixels. Our simulation results show that adding such a quadratic regularization scheme to HARP (R-HARP) allows accurate estimation of motion fields due to patient breathing, even in the presence of noise and artifacts in the phase images. Like most other motion estimation strategies, a limitation of R-HARP is that it does not allow estimation of motion in regions with little MRI signal, such as the lungs. We have therefore masked out such regions in the motion tracking procedure in order to prevent the random values of the harmonic phase in the lungs from introducing bias at other locations because of the roughness penalty. Such masks were simply obtained in all motion frames by adding two complementary SPAMM acquisitions, instead of subtracting them like in C-SPAMM, and segmenting the resulting amplitude image. Doing so yielded accurate estimation of the motion fields everywhere but in the lungs, even in regions that were very close to the lung boundaries (i.e., in the dome of the liver in simulations and in the small hot spheres attached to the balloon in physical acquisitions).

Because it is difficult to objectively evaluate motion correction approaches in vivo, we have evaluated the accuracy and practical feasibility of our motion correction approach in numerical simulations of a breathing patient and in physical acquisitions of a small deformable phantom using a prototype combined PET-MRI brain scanner. These proof-of-principle simulations and acquisition studies demonstrate that tagged-MRI based PET motion correction is accurate in regions with significant MRI signal, even in uniform regions, and can be practically implemented on a real system with a complex block-based PET structure and a nonideal MRI scanner. Moreover, our PET-MRI simulations indicate that the spatial and time resolution of the tagged-MRI acquisition do not need to be very high (we simulated 3 mm isotropic and 250 ms spatial and temporal resolutions, respectively) in order to accurately motion correct the PET data. Small hot tumor contrast (CRC) and signal-to-noise ratio (SNR) were significantly better when performing MRI-based motion correction using these parameters than when not performing motion correction and when reconstructing only one of eight motion frames alone. These results were confirmed in physical acquisitions, where low-noise, high-contrast, and artifact-free PET images were reconstructed from list-mode data with detector sensitivity and frame dependent motion and attenuation corrections in the system matrix. These results show that the proposed approach is accurate and feasible, and is therefore ready to be tested in vivo.

Future work will include testing of the proposed approach in vivo both in animals and humans using brain and whole body combined PET-MRI scanners. In practice, there will be two ways of gating both the list-mode PET and the MRI acquisition: (i) by using an external signal, e.g., a respiratory belt, or (ii) by interleaving navigator echoes within the tagged-MRI acquisition. The use of navigator echoes to monitor the state of respiration of the patient is well established²⁰ and would preclude the need for additional hardware, e.g., a respiratory belt. Note that both gating strategies mentioned above monitor the state of respiration of the patient with a time resolution greater than that actually needed to perform the motion correction. However, finer temporal resolution of the gating signal could prove very useful for analyzing the specific breathing pattern of the subject imaged. This, in turn, would allow detection of abnormally deep and shallow breaths, which should be removed from the study. Even in the subset of normal breaths, there might be some variability in the amplitude and direction of local displacement vectors, which could affect the motion estimation. Some degree of immunity of our approach to this problem is provided by the fact that it only requires estimation of motion fields on a coarse grid (∼5 mm spatial resolution) so the average displacement vector in each of these large voxels should be relatively constant over several periods of the breathing cycle. It was not possible to study the capability of our approach to handle abnormally deep of shallow breaths, nor the variability of normal breaths, in this study since we imaged a regularly beating phantom. This problem is outside of the scope of this paper, and we will address it in a separate publication using in vivo studies.

Application of the proposed approach to in vivo data acquired in humans and animal will also require estimation of an attenuation map in the reference frame from MRI images using, for example, atlas-based techniques.^{45, 46, 47, 48, 49} Such a process will most likely require acquiring extra proton density, T1 or T2 weighted MRI images in addition to the tagged MRI data used for motion correction, because it might prove difficult in practice to filter out the tagging pattern of C-SPAMM images while preserving adequate spatial resolution for accurate attenuation correction. The motion correction procedure methods presented in this work is, of course, applicable concurrently to any attenuation map estimation method. The authors acknowledge the difficulty of applying such approaches in vivo however, especially in the lungs where the attenuation coefficient can vary considerably spatially and between patients, and will dedicate future work on MR-based attenuation correction especially as it is applied concurrently to motion correction.