The importance of tissue segmentation for dose calculations for kilovoltage radiation therapy

Abstract

Purpose: The aim of this work was to evaluate the effect of tissue segmentation on the accuracy of Monte Carlo (MC) dose calculations for kilovoltage radiation therapy, which are commonly used in preclinical radiotherapy studies and are also being revisited as a clinical treatment modality. The feasibility of tissue segmentation routinely done on the basis of differences in tissue mass densities was studied and a new segmentation scheme based on differences in effective atomic numbers was developed.Methods: MC dose calculations in a cylindrical mouse phantom with small cylindrical inhomogeneities consisting of 34 ICRU-44 tissues were performed using the EGSnrc∕BEAMnrc and DOSXYZnrc codes. The dose to tissue was calculated for five different kilovoltage beams currently used in small animal radiotherapy: a microCT 120 kV beam, two 225 kV beams filtered with either 4 mm of Al or 0.5 mm of Cu, a heavily filtered 320 kV beam, and a ¹⁹²Ir beam. The mean doses to the 34 ICRU-44 tissues as a function of tissue mass density and effective atomic number and beam energy were studied. A treatment plan for an orthotopic lung tumor model was created, and the dose distribution was calculated for three tissue segmentation schemes using 4, 8, and 39 tissue bins to assess the significance of the simulation results for kilovoltage radiotherapy.Results: In our model, incorrect assignment of adipose tissue to muscle caused dose calculation differences of 27%, 13%, and 7% for the 120 kV beam and the 225 kV beams filtered with 4 mm Al and 0.5 mm Cu, respectively. For the heavily filtered 320 kV beam and a ¹⁹²Ir source, potential dose calculation differences due to tissue mis-assignment were below 4%. There was no clear relationship between the dose to tissue and its mass density for x-ray beams generated by tube potentials equal or less than 225 kV. A second order polynomial fit approximated well the absorbed dose to tissue as a function of effective atomic number for these beams. In the mouse study, the 120 kV beam dose to bone was overestimated by 100% and underestimated by 10% for the 4 and 8-tissue segmentation schemes compared to the 39-tissue segmentation scheme, respectively. Dose to adipose tissue was overestimated by 30% and underestimated by 10%, respectively. In general, organ at risk (OAR) doses were overestimated in the 4-tissue and the 8-tissue segmentation schemes compared to the 39-tissue segmentation.Conclusions: Tissue segmentation was shown to be a key parameter for dose calculations with kilovoltage beams used in small animal radiotherapy when an x-ray tube with a potential ≤225 kV is used as a source. A new tissue segmentation scheme with 39 tissues based on effective number differences derived from mass density differences has been implemented.

INTRODUCTION

Preclinical laboratory studies are vital to understand cancer radiobiology and to develop and validate radiation therapies prior to clinical translation. Irradiation of laboratory animal models of cancer helps to understand the responses of tumors and normal tissues to various radiation delivery techniques, as well as their complex dose-response relationships. In this report we investigate the accuracy of dose calculations for small animal radiotherapy, a key factor in the execution of laboratory radiotherapy studies with maximal scientific and translational significance.

Formerly, simple single beam irradiation techniques were used for laboratory research in radiotherapy.^{1, 2} However with the development of conformal radiotherapy, intensity modulated radiation therapy, and image-guided radiation therapy, new conformal small animal radiation therapy systems simulating clinical dose delivery methods have been designed.^{3, 4, 5, 6, 7} While systems developed at Princess Margaret Hospital and John Hopkins University use 225 kV x-ray tubes for irradiation of small animals, preclinical radiation therapy at Washington University, originally done with a ¹⁹²Ir source, has been recently conducted with a 320 kV x-ray tube. At Stanford University, a kilovoltage (kV) GE eXplore Locus microCT scanner (GE Healthcare, London, Ontario, Canada) has been modified for delivery of therapeutic doses to small animals.^{6, 8}

In order to efficiently study biological effects of radiotherapy, the delivered dose must be calculated with high accuracy. All dedicated conformal small animal radiotherapy systems described above utilize kV photon beams for which the TMR-based dose calculation method is not accurate because it does not account for tissue inhomogeneities. For kV photon beams, the dose to high atomic number tissues such as bones will be elevated compared to soft tissue due to the importance of the photoelectric effect in these tissue types for this photon energy range. The Monte Carlo (MC) technique is potentially the most accurate method for dose calculation in these cases.

In the EGSnrc∕DOSXYZnrc MC dose calculation code,⁹ each voxel of the CT image of the subject receiving radiotherapy is converted into its mass density and tissue type. For treatments with megavoltage beams, mass density is the crucial parameter that dictates the accuracy of dose calculations¹⁰ and may be the only parameter that is needed for MC dose calculations.¹¹ The conversion of CT numbers into mass or electron densities has been studied extensively.^{12, 13, 14} However, the conversion of CT numbers into tissue types for kV beam dose calculations has not yet been thoroughly investigated. Zhou et al.¹⁵ reported that 47 bones types should be used if the dose from a 120 kV beam is to be calculated with 2% accuracy. The bone types are segmented based on mass densities derived from CT numbers. The effects of tissue inhomogeneities for a brachytherapy ¹⁹²Ir source have been previously studied.^{16, 17} A breast cancer case study demonstrated dose overestimation to all structures by more than 5% compared to the TG-43 dose calculation formalism.¹⁶ In an esophageal case, a 15% underestimation of dose to sternum bone was shown.¹⁷ However, more research must be performed t o similarly evaluate dose calculations in soft tissues. The CT numbers of various soft tissue types are similar, and precise tissue segmentation based on CT number differences is not possible.

Bazalova et al.¹⁰ recently presented that tissue segmentation for MC dose calculations can be improved by the use of dual-energy CT (DECT) based material extraction. CT images acquired at two different voltages are analyzed, and the effective atomic numbers and electron or mass densities of each voxel are calculated based on a parameterization of the linear attenuation coefficient. It was also reported that incorrect tissue assignment could result in 4.2% error in dose calculation for a 250 kV beam. The dose calculation errors due to tissue mis-assignment are expected to be larger for lower energy photon beams. The purpose of this work is to investigate the effect of tissue segmentation on the accuracy of Monte Carlo dose calculations (MCDC) for kV photon beams currently used for small animal radiotherapy.

MATERIALS AND METHODS

All MC simulations were performed in the EGSnrc (Refs. ^{18, 19}) MC codes. Photon beams were modeled using the BEAMnrc (Ref. ²⁰) code, and all dose calculations were run in the DOSXYZnrc (Ref. ⁹) code. The dependence of the absorbed dose on the mass density (p) and the effective atomic number (Z) for various ICRU-44 (Ref. ²¹) human tissues (Table Table I.) was studied with a cylindrical mouse phantom. Simulations were run for four different kV photon beam energies that are currently used in small animal radiotherapy research. The microCT scanner utilizes a 120 kV x-ray beam filtered with 2.5 mm of Al. Two other systems are using a 225 kV x-ray beam that can be further modified using additional filtration with the two extreme cases being 4 mm of Al and 0.5 mm of Cu. The absorbed dose to this phantom was also calculated for heavily filtered 320 kV beam and a ¹⁹²Ir source, as has been employed at Washington University for small animal studies.

Table 1.

The values of mass density (ρ) and effective atomic number (Z)^a for 34 ICRU-44 tissues. Tissue used in the 4-tissue and 8-tissue small animal dose calculations are italicized.

Medium	P g∕cm3	Z
Lung (inf.)	0.260	7.879
Adipose	0.950	6.670
Skeleton-yellow marrow	0.980	6.559
Cell nucleus	1.000	8.167
Breast	1.020	7.271
Skeleton-red marrow	1.030	7.266
GI tract	1.030	7.710
Lymph	1.030	7.837
Pancreas	1.040	7.699
Testis	1.040	7.816
Brain	1.040	7.878
Thyroid	1.050	7.710
Ovary	1.050	7.843
Muscle	1.050	7.848
Kidney	1.050	7.840
Lung (def.)	1.050	7.879
Heart	1.060	7.806
Blood	1.060	7.825
Liver	1.060	7.866
Spleen	1.060	7.872
Eye lens	1.070	7.541
Skin	1.090	7.627
Skeleton-cartilage	1.100	8.329
Skeleton-spongiosa	1.180	10.678
Skeleton-sacrum	1.290	11.407
Skeleton-vert. column (D6,L3)	1.330	11.742
Skeleton-femur	1.330	12.087
Skeleton-ribs (2,6)	1.410	12.224
Skeleton-vert. column (C4)	1.420	12.271
Skeleton-humerus	1.460	12.612
Skeleton-ribs (10)	1.520	12.760
Skeleton-cranium	1.610	13.129
Skeleton-mandible	1.680	13.332
Skeleton-cortical bone	1.920	13.978

^aZ, where w_i is fraction by weight of element i with atomic number 22 Z_i²² (Ref. ²²).

MicroCT x-ray beam

MicroCT 120 kV treatment beams filtered with 2.5 mm of aluminum and shaped to various sizes by a two-stage collimator were previously modeled in the BEAMnrc code and compared to depth dose curves and beam profiles measured with EBT Gafchromic films.⁸ MC simulations were optimized and a library of phase-space files for treatment beams with diameters up to 30 mm was generated. The 5 mm diameter beam phase-space file was used for dose calculations using the DOSXYZnrc code in this work.

225 kV x-ray beams

Two 225 kV x-ray treatment beams were modeled with two filtrations: a 4 mm Al filter and a 0.5 mm Cu filter. The tube itself was modeled as a 20°-tilted tungsten anode struck by an incident 225 keV electron beam, with the emitted x-ray beam filtered by either of the two filters just below the x-ray tube output window. Similar to the overall geometry of the JHU system,⁴ the x-rays were shaped to a (5 × 5) mm beam using a 1-in.-thick brass block located at 30 cm from the 3 mm diameter focal spot. The source to isocenter distance was set to 35 cm. Two phase-space files were produced for the two Al-filtered and Cu-filtered beams and used for dose calculation in the next step of the study.

320 kV beam

The 320 kV beam was simulated with a 20°-tilted tungsten anode and a 320 keV electron beam. The photon beam was extensively filtered with 1.5 mm Pb, 5 mm Sn, 1 mm Cu, and 4 mm Al to generate a beam with half-value layer of 4.6 mm Cu.⁷ The beam was subsequently collimated with a 7-mm-thick tungsten block to a (5 × 5) mm beam at 15 cm from the focal spot. The source-to-isocenter distance was set to 30 cm.

To produce the phase space files for the 225 kV and the 320 kV sources, all processes relevant to low energy electron and photon interactions, such as electron impact ionization, bound Compton scattering, and Rayleigh scattering, were included in the simulations. Directional Bremsstrahlung splitting of 1 × 10⁶ was used for all x-ray beam simulations. The NIST Bremsstrahlung cross-section and the XCOM photon cross-section database were used.

¹⁹²Ir

The ¹⁹²Ir beam was modeled using a bare spectrum²³ and rectangular parallel beams. Beams of this spectrum were conformed to (5 × 5) mm fields and directed onto the phantom.

Phantom dose calculations

Dose deposited in a 2 cm diameter cylindrical mouse phantom consisting of muscle tissue and a single, central 5 mm diameter heterogeneity (Fig. 1) was calculated using a (0.2 × 0.2 × 0.2) mm grid. The heterogeneity was varied between 34 ICRU-44 (Ref. ²¹) tissues and used the densities listed in Table Table I.. Dose was calculated for each phantom setup using each of the x-ray beams described above. The resolution used is double that of typical microCT images with (0.1 × 0.1 × 0.1) mm³ voxels and balances dose calculation accuracy for small animal subjects with computation time. The treatment plan applied to the phantom consisted of five isocentric equally distributed beams. The mean dose to the tissue heterogeneity was calculated for each simulated case.

Figure 1.

Dose distribution calculated for five uniformly spaced 5 mm diameter 120 kV beams filtered with 2.5 mm of Al in a 2 cm diameter phantom with a 5 mm cortical bone heterogeneity: the isocenter axial (a), coronal (b), and sagittal slices (c).

Due to the low photon energies electrons were not transported, which significantly shortened the dose calculation time and resulted in dose calculation differences of less than 5% and 20% in the first layer of surface voxels for the 120 kV beam and ¹⁹²Ir, respectively. Negligible differences were observed at larger depths for all beams. The dose differences in the tissue inhomogeneity for simulations with ECUT set at 0.516 and 1.511 MeV (no electron transport) were within statistical uncertainties of the simulations for all beams investigated in the study. A photon splitting number of 100 was used. The statistical dose calculation uncertainties did not exceed 1% in the high dose regions for all dose calculations. All MC simulations were run on a 2 × 3 GHz Quad-Core Intel Xeon machine with 4 GB memory.

Relationships between the absorbed dose D and mass density and effective atomic number for the 34 tissue types were investigated.

Based on the relationship between the absorbed dose and the effective atomic number for the 120 kV beam, a new tissue set TS2% required to achieve 2% dose calculation accuracy for this beam was derived. New tissue types with the required effective atomic numbers were created from the ICRU data set as follows. The elemental composition of the new tissues was linearly interpolated from the two neighboring ICRU tissues. The content of hydrogen (for Z < 8) and calcium (for Z > 8) was, however, modified to achieve the required effective atomic number. The mass density of the new tissue was also a linearly interpolated based on the two neighboring ICRU tissues. The TS2% tissue set with 92 tissues was used to derive tissues for small animal dose calculations.

Small animal dose calculations

The effect of tissue assignment was assessed by simulating treatment of a mouse with an orthotopic lung tumor with all studied beams. The treatment plan consisted of nine equally weighted 9 and 10 mm large beams uniformly spread between 150° and 230°, and the prescribed dose to the target was 5 Gy. A CT number to mass density (ρ) calibration curve (ρ = 1.034 × HU∕1000 + 1.040 for HU < 0 and p = 0.224 × HU∕l000 + 1.040 for HU ≥ 0) was created with an electron density CT phantom (CIRS, Norfolk, VI). Three tissue segmentation schemes with 4, 8, and 39 tissue types were applied. Due to the lack of mouse tissue composition data in the literature, human ICRU-44 tissues were used. However, it is expected that mouse bone densities are lower than human bone densities.²⁴ In the first segmentation scheme, only four tissues commonly employed in MC simulations were used in the simulation: air (CT numbers from −1000 to −820), lung (−820 to −340), muscle (−340 to 280), and cortical bone (280–3100). In the second simulation, 8 tissue types that can be relatively easily segmented in usually noisy microCT images were used. Adipose tissue (−340 to −100) was added between the lung and muscle tissue, and the bone material from the 4-tissue segmentation scheme was split into four bone materials––spongiosa (280–1200), ribs (2,6) (1200–2100), cranium (2100–2900), and cortical bone (2900–3100). The bone material bins are 0.2 g∕cm³ wide and the representative tissue type was selected from the center of each bin (Tables Table I. and Table II.).

Table 2.

CT number and mass density ranges for the 4-tissue and 8-tissue segmentation schemes.

CT number
−1000	−820	−340	−70	0	280	1200	2100	3000
4-tissue seg.	Air	Lung	Muscle		Cortical bone
8-tissue seg.	Air	Lung	Adipose	Muscle	Cranium	Spongiosa	Ribs (2,6)	Cortical
39-tissue seg.	Air	8 × 0.1 g∕cm3			30 × 0.02 g∕cm3
0	0.19	0.7	0.97	1.0	1.1	1.5	1.7
mass density (g∕cm3)

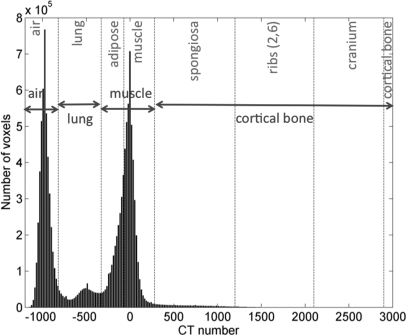
The third segmentation scheme with 39 tissue types was derived from the 120 kV TS2% segmentation based on differences in effective atomic numbers. Figure 2 represent a histogram of CT numbers for the entire mouse microCT data volume. The soft tissue peak around 0 HU can be fitted with a Gaussian with a standard deviation of 97 HU that corresponds to the noise in the data set. It is therefore reasonable to assume that 97 HU can be resolved in tissue segmentation. According to the calibration curve segments, 97 HU correspond to 0.1 and 0.02 g∕cm³ for ρ < 1 g∕cm³ and ρ ≥ 1 g∕cm³, respectively.

Figure 2.

Histogram of CT numbers with the corresponding 4-tissue (in blue) and 8-tissue (in red) material assignment of the microCT data set. Dashed lines define air, lung, adipose, muscle, spongiosa, ribs (2,6), cranium, and cortical bone as used in the 8-tissue segmentation model. Adipose and muscle are combined into muscle and spongiosa, ribs (2,6), cranium, and cortical bone are combined into cortical bone in the 4-tissue segmentation model.

It was found out that 92 tissue types are needed to achieve 2% dose calculation accuracy. Ideally, all 92 TS2% tissue types should be used in dose calculations with 120 kV beams. However, in order to resolve soft tissues for the TS2% segmentation scheme, CT image noise of less than 5 HU is required.

Due to the 97 HU image noise in our data set, the tissue types used for small animal dose calculations were selected from TS2% in the following way (Figure 3). For each mass density bin of the mouse data (open triangles), the respective effective atomic number was calculated using the ICRU tissue data set (squares). If the mass density bin contained ICRU tissues, the effective atomic number of the bin was calculated as the mean of the mass density of the ICRU tissues in the bin. If there were no ICRU tissues present in the mass density bin, the effective atomic number of the bin was interpolated based on the two neighboring ICRU tissues.

Figure 3.

Demonstration of tissue segmentation for lower (a) and higher (b) effective atomic number (Z) intervals in small animal dose calculations using 39 tissue types. Z is plotted as a function of mass density for ICRU tissues (squares), for tissue types required to achieve 2% dose calculation accuracy for a 120 kV beam based on Z differences (circles), and for the center of bins for segmentation with 0.02 g∕cm³ mass density bins (open triangles). Tissue types used for dose calculations are shown in closed triangles and separated by solid lines.

In the next step, the mouse tissue types defined by effective atomic numbers (closed triangles) were segmented using the TS2% segmentation scheme (circles) based on nearest neighbor interpolation. Due to the image noise of 97 HU (or 0.02 g∕cm³ for ρ ≥ 1 g∕cm³), some TS2% bins with Z < 12.0 were combined into a single effective atomic number bin based on mass density differences [Fig. 3a]. For example, the 1.17 g∕cm³ mass density bin (Z = 10.40) encompasses six TS2% bins with Z in the range between 10.14 and 10.57. On the other hand, some mass density bins for Z > 12.0 were combined into a single effective atomic number bin [Fig. 3b]. For example, the 1.49 and 1.51 g∕cm³ mass density bins are two resolvable tissue types, which can be combined into one TS2% atomic number based tissue type (Z = 12.72). In summary, due to the image noise and the ability to combine tissues based on mass density, the Ninety-two 2% effective atomic number materials were reduced to 39 effective atomic number bins. With this segmentation limited by the noise in CT images, the maximum difference between two neighboring soft tissues is 10%.

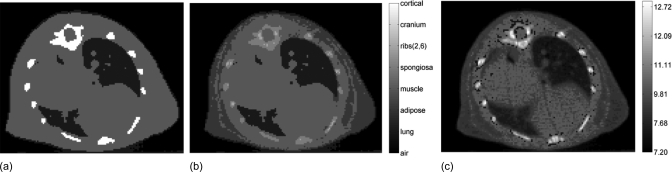
Mass densities of each voxel were identical for all tissue segmentation schemes. Adipose tissue segmentation was performed based on differences in CT numbers and by visual assessment. Due to partial volume artifacts, the interface between lung and soft tissue was incorrectly assigned to adipose tissue when simple thresholding was used; therefore, these voxels were manually assigned to be soft tissue. Tissue maps of the isocentric slice for all three tissue segmentation schemes are shown in Fig. 4.

Figure 4.

Tissue segmentation with 4 tissues (a), 8 tissues (b), and 39 tissues based on effective atomic number differences (c).

RESULTS

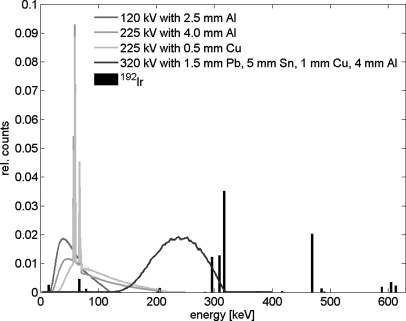
All phase-space files were calculated in 5 h and contained more than 1 × 10⁶ particles. The energy spectra of the photon beams investigated in this study are plotted in Fig. 5. The mean energies for the 120 kV beam and the 225 kV beams filtered with 4 mm of Al and 0.5 mm of Cu were 55, 77, and 92 keV, respectively. The mean energy for the 320 kV beam and the ¹⁹²Ir source were 237 and 346 keV, respectively. Dose calculations in the DOSXYZnrc code were optimized resulting in dose calculation times of less than 30 min for phantom simulations and less than 4 h for small animal simulations.

Figure 5.

Spectral distributions of the photon beams investigated in the study. The 120 kV beam is a circular beam of 5 mm in diameter and the 225 kV beams and the 320 kV beam are (5 × 5) mm rectangular beams. The ¹⁹²Ir spectrum is the bare spectrum.

The results of the dose calculations are plotted and summarized in the following sections.

All doses are normalized to dose to muscle with density of muscle (Table Table I.).

Dependence of dose to tissue on mass density

120 kV x-ray beam

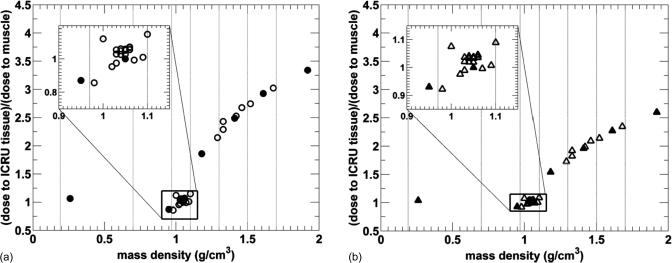
The mean doses for the 34 ICRU-44 tissues as a function of the mass density for the microCT 120 kV beam filtered with 2.5 mm Al are plotted in Fig. 6. Due to the material composition of each soft tissue, a nonlinear relationship between the absorbed dose and mass density of all tissues is evident.

Figure 6.

Relative dose to tissue as a function of tissue mass density for 34 ICRU tissues from a 120 kV beam with <E> = 55 keV. Tissues used in 4-tissue and 8-tissue model small animal dose calculations are plotted with filled symbols and vertical lines indicated.

The relative absorbed doses for soft tissues with mass densities between 0.95 and 1.15 g∕cm³ encompassed by the black rectangle are between 0.69 and 1.15. Figure 6 also demonstrates there is a relationship between the absorbed dose and mass density for tissues with mass density higher than 1.2 g∕cm³, even though some nonlinearities due to material composition are still present. Statistical uncertainties of <1.4% are not plotted for clarity.

225 kV x-ray beams

The results for the 225 kV beam filtered with 4 mm of Al and 0.5 mm Cu are presented in Figs. 7a, 7b, respectively. A comparable distribution of points for soft tissues in the rectangle is seen for both 225 kV beams, it also resembles the distribution of doses from the 120 kV beam in Fig. 6. However, the spread of doses for these tissues is different, being from 0.87 to 1.15 for the 4 mm Al filtered beam and from 0.93 to 1.09 for the 0.5 mm Cu filtered beam. The dose-width of the spread is observed to decrease with increasing mean x-ray energy, as expected.

Figure 7.

Relative dose to tissue as a function of tissue mass density for 34 ICRU tissues from a 225 kV beam filtered by 4 mm of Al with <E> = 77 keV (a) and 0.5 mm of Cu with <E> = 92 keV (b). Tissues used in 4-tissue and 8-tissue model small animal dose calculations are plotted with filled symbols and vertical lines indicated the tissue segmentation ranges. Statistical uncertainties of <1.4% are not plotted for clarity.

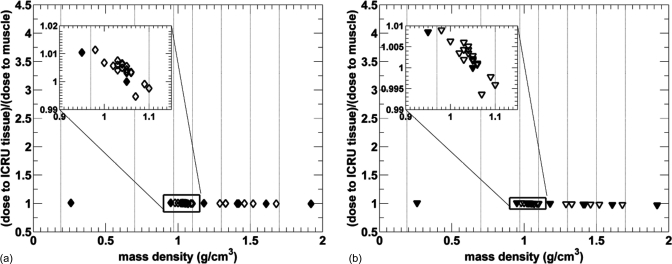
320 kV beam

Figure 8a represents the results of the dose calculation for a heavily filtered 320 kV beam with the mean energy of 237 keV. Unlike for the previous beam energies, the absorbed dose only slightly decreases with increasing tissue density for all studied beams. The rectangle encompassing soft tissues shows that the dose differences for all soft tissues are within 2%. The maximum dose difference for all tissues is also within 2%.

Figure 8.

Relative dose to tissue as a function of tissue mass density for 34 ICRU tissues from irradiation with an extensively filtered 320 kV beam with <E> = 237 keV (a) and a ¹⁹²Ir source with <E> = 346 keV (b). Tissues used in 4-tissue and 8-tissue model small animal dose calculations are plotted with filled symbols and vertical lines indicated the tissue segmentation ranges. Statistical uncertainties of <1.4% are not plotted for clarity.

¹⁹²Ir source

The dose to tissue as a function of mass density from a ¹⁹²Ir source is plotted in Fig. 8b. Similarly to the heavily filtered 320 kV beam, the absorbed dose only slightly decreases with increasing mass density; the spread of all studied tissues is within 4%. This is in agreement with the mass energy absorption coefficients for human tissues at 346 keV listed in the NIST database.²⁵ Note that the spread of absorbed doses for soft tissues in the rectangle is less than 2%.

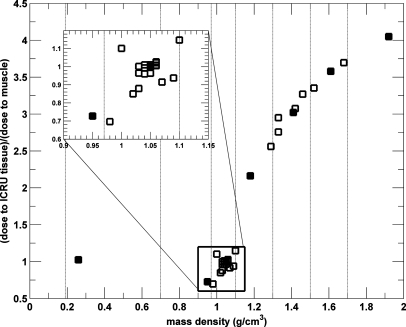
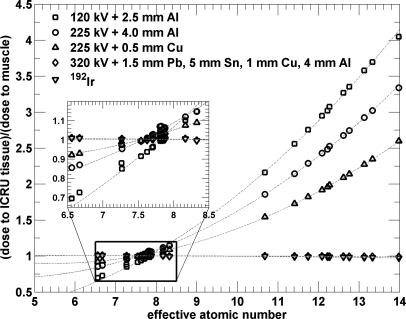
Dependence of dose to tissue on effective atomic number

The photoelectric effect is strongly dependent on the effective atomic number and is the dominant interaction for the sources modeled with potentials ≤225 kV. The absorbed dose for the 34 ICRU-44 tissues as a function of the tissue effective atomic number for all studied beams is plotted in Fig. 9. A strong relationship between the mean absorbed dose and the effective atomic number for all ICRU-44 tissues for all beams is apparent. The relationship between the absorbed dose in a tissue and the effective atomic number of the tissue can be very well approximated by a second order polynomial (Fig. 9). The R² values of the polynomial fits are larger than 0.99 for the 120 kV and both 225 kV beams and they are 0.90 for the 320 kV and ¹⁹²Ir beam. The inset in Fig. 9 shows that the fit match the data points to within 5%. The absorbed dose for the 320 kV beam and the ¹⁹²Ir source decreases, albeit slightly, as both a function of the mass density and the effective atomic number of tissues for these beam energies.

Figure 9.

Relative dose to tissue as a function of tissue effective atomic number for 34 ICRU tissues from irradiation with photon beams used for conformal small animal radiation therapy. The quadratic fits are plotted with dashed lines.

Based on the quadratic fit, a tissue set TS2% for the 120 kV beam was created. New tissue types with the appropriate effective numbers were generated so that the dose calculation differences due to tissue mis-assignment are less than 2%. It was found that 92 tissue types were needed for the relevant 6.5–14.0 effective atomic number range. However, for the small animal study these 92 types were reduced to 39 effective atomic number bins due to the 97 HU noise in microCT images.

Small animal dose calculations

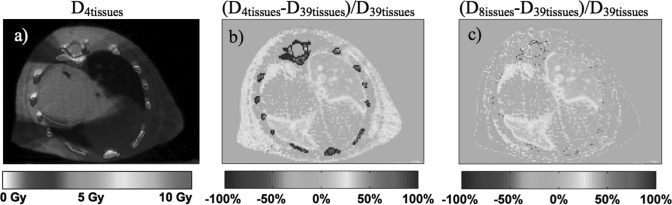
The results from the small animal dose calculations with the 120 kV beam using the 4, 8, and 39-tissue segmentation schemes for a target dose of 5 Gy are presented in Fig. 10. The dose distribution for the 4-tissue segmentation scheme is presented in Fig. 10a. The dose difference maps (D_4tissues −D_39tissues)∕D_39tissues and (D_8tissues−D_39tissues)∕D_39tissues are shown in Figs. 10b, 10c, respectively. These simulations utilize the tissue segmentations presented in Fig. 4.

Figure 10.

Monte Carlo dose distribution for an orthotopic lung tumor with the standard 4-tissue segmentation scheme (a) for a 120 kVp plan. The percentage difference maps (D_4tissues−D_39tissues)∕D_39tissues and (D_8tissues−D_39tissues)∕D_39tissues are shown in (b) and (c), respectively. The PTV is delineated in red.

When the 4-tissue segmentation is used, large dose differences up to 100% compared to the 39-tissue segmentation schemes can be seen in the ribs. Due to the assignment of ribs to cortical bone in the 4-tissue segmentation scheme, the dose calculated in the bone is 10.7 Gy, whereas it is between 4.8 Gy and 5.1 Gy in the 39-tissue segmentation scheme in which the ribs were assigned to tissues with effective atomic numbers of 10.75 − 11.89. The dose to the ribs is 4.5 Gy in the 8-tissue calculation in which the ribs were assigned to spongiosa and ribs (2,6). This results in up to 15% differences from the 39-tissue segmentation scheme. The results of Figs. 10b, 10c also demonstrate that in comparison with the 39-tissue segmentation scheme the dose to adipose is overestimated by approximately 30% using the 4-tissuse segmentation and underestimated by 10% using the 8-tissue segmentation. When adipose is assigned as muscle in the 4-tissue segmentation scheme, the dose to the subcutaneous adipose tissue on the right side is calculated to be 6.1 Gy. The dose to the same adipose tissue is 4.2 Gy and 4.7 Gy for the 8-tissue and 39-tissue segmentation schemes, respectively. These large dose calculations differences are expected based on the phantom simulations presented in Fig. 6. The mean right lung dose differences between the 39-tissue segmentation and both the 4-tissue and 8-tissue segmentation schemes are 10%. It can also be seen that there are no significant dose differences in the PTV in between the three segmentation schemes. However, finer tissue segmentation causes dose inhomogeneities in the PTV when the 39-tissue segmentation scheme is used.

For the 225 kV beam filtered with 4 mm Al the dose differences between the 4-tissue and 39-tissue segmentation schemes are −70% in the ribs, 10% in the right subcutaneous adipose tissue, and 7% in the lung. When the 8-tissue segmentation scheme is used, the differences for the same beam are −11% in the ribs, −6% in the right subcutaneous adipose tissue, and 7% in the lung. The differences for the 225 kV beam filtered with 0.5 mm Cu are lower in all tissues. The dose differences in the ribs are −57% and −7% for the 4-tissue and 8-tissue segmentation schemes.

There are no significant dose differences for the 320 kV beam and the ¹⁹²Ir beam between these two different tissue segmentation schemes.

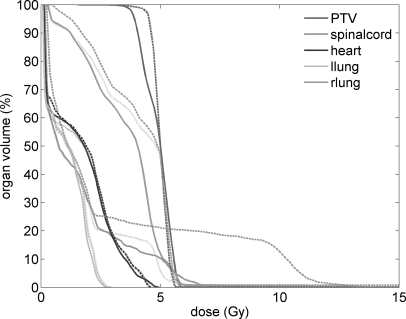
Dose volume histograms (DVH) for the PTV and organs at risk (OARs) are plotted in Fig. 11. The DVHs for the PTV are nearly identical for the 4-tissue and 8-tissue segmentation schemes. Differences in the 39-tissue segmentation scheme PTV are due to the fine tissue segmentation, and they show a 0.6 Gy (13%) dose difference to the PTV D90. There are significant differences in the DVHs of OARs. The largest difference is observed for the spinal cord where the maximum dose is 12 Gy in the 4-tissue segmentation scheme whereas it is 6 and 7 Gy in the 8-tissue and 39-tissue segmentation schemes, respectively. The dose to right lung is the lowest in the 39-tissue segmentation scheme, with a D₅₀ of 4.0 Gy. In the 4-tissue and 8-tissue segmentation schemes, the D₅₀ is 4.9 and 4.8 Gy, corresponding to 23% and 20% differences, respectively. In general, for a similar PTV coverage, the 4-tissue and the 8-tissue segmentation schemes overestimate the dose to critical organs compared to the 39-tissue segmentation.

Figure 11.

DVH for the PTV, the spinal cord, the heart and the left and the right lung for 120 kVp dose calculations with the 39-tissue segmentation scheme (solid curves), with the 4-tissue segmentation scheme (dashed curves), and with the 8-tissue segmentation scheme (dotted curves).

DISCUSSION

This study shows that incorrect tissue segmentation can result in large dose calculation differences for kilovoltage photon beams. The dose calculation differences due to different tissue segmentation schemes increase with decreasing energy of the beam. Currently, tissue segmentation in CT images is done based on differences in CT numbers or mass densities. In our model using a centrally located 5 mm diameter inhomogeneity in a 2 cm diameter phantom, various tissue segmentation schemes could result in various dose differences in soft tissues.

The simple 4-tissue segmentation scheme with air, lung, soft tissue, and cortical bone is still being implemented for kilovoltage beam dose calculations.²⁶ In this segmentation scheme, adipose tissue is incorrectly assigned to muscle tissue. Our model predicts that the dose calculation difference could be as high as 27%, 13% and 7%, (normalized to dose to muscle) for the 120 kV beam and the two 225 kV beams filtered with 4 mm Al and 0.5 mm Cu, respectively. Adipose tissue and yellow marrow (ρ = 0.98 g∕cm³) with mass densities of approximately 1.00 g∕cm³ contain a higher fraction of hydrogen that causes the tissues to have a significantly lower effective atomic number (∼6.5 compared to ∼7.8 and larger for soft tissues). The predominant interaction at these energies is the photoelectric effect with the linear attenuation coefficient being Z⁴ dependent.²⁷ The strong Z-dependence results in significant differences of the absorbed doses to adipose tissue or yellow marrow compared to the absorbed dose to muscle tissue.

Even larger dose calculation differences can occur when adipose tissue (ρ = 0.95 g∕cm³) is incorrectly assigned as cartilage tissue (ρ = 1.10 g∕cm³). This could happen if tissues are segmented based on differences in mass densities with 0.15 g∕cm³ or wider bins, both tissue types fall into the same bin, and the bin is represented by one of the two tissue types. The dose calculation differences could then be as high as 36%, 24%, and 14% (normalized to dose to cartilage) for the 120 kV beam, the 4 mm Al filtered and 0.5 mm Cu filtered 225 kV beams, respectively. Note that based on the CT number to mass density calibration curve presented in this work 0.15 g∕cm³ bin width corresponds to image noise of 454 HU. If tissues are segmented at the limit of image noise levels as suggested in this work, this worst-case scenario is unlikely.

The predominant photon interaction for human tissues using the heavily filtered 320 kV beam and a ¹⁹²Ir source is Compton scattering, with mass energy absorption coefficient nearly independent of mass density and effective atomic number.²⁸ An incorrect assignment of tissues would therefore not result in significant differences in dose calculation for these photon beams.

Note that the inflated lung point with mass density of 0.26 g∕cm³ can be easily segmented in CT images and is generally not of concern. The dose calculation differences in small animal tissues could also depend on the beam arrangement and small animal anatomy. The second order polynomial fit of the absorbed dose as a function of effective atomic number is a good approximation for the studied beams. Photoelectric effect cross-section decreases with Z⁴ and Compton interaction cross-section depends only on Z. Based on observation of Figs. 67, a second-order polynomial fit was a logical choice. Higher order polynomials could be used for lower beam energies, however, the R² values of the fits were excellent for all x-ray beams with tube potentials ≤225 kV when second order polynomials were used.

The polynomial fits were used to create a new set of 92 tissues in which the 120 kV beam dose differences between two neighboring tissue types are within 2%. The doses to the new tissues in the TS2% segmentation scheme agree with the 120 kV polynomial fit to within 2%. Due to the high noise in the presented microCT images, the 92 tissue types were reduced to 39 tissues. If higher quality CT images are available, a larger number of materials can be segmented. In order to use all 92 tissue types and achieve 2% dose calculation accuracy for the 120 kV beam, the noise in CT images needs to be less than 5 HU.

It was found that 69 and 53 materials are required for an effective atomic number based scheme with 2% accuracy for the 225 kV beams filtered with 4 mm Al and 0.5 mm Cu, respectively. Due to the CT image noise levels of 97 HU in our small animal data set, these have to be reduced to 38 and 29 tissue types, respectively. If the CT images noise levels are equal or less than 13 and 22 HU, all 69 and 53 materials can be used and dose calculation differences less than 2% for the 225 kV beams filtered with 4 mm Al and 0.5 mm Cu, respectively, can be achieved.

Dose for higher energy beams can be also calculated with the 92-tissue segmentation scheme derived for the 120 kV beam, which due to image noise was reduced to 39 tissue types as discussed in the previous section. For lower energy beams, a new tissue set to achieve 2% dose calculation accuracy must be derived.

The small animal study shows that for a similar PTV coverage, the dose to OARs can be affected by the choice of tissue segmentation scheme. The importance of bone assignment is also shown in the small animal study. Dose calculation results with different tissue segmentation schemes for bone tissues can be significantly different. Based on mass density differences, mouse ribs were segmented as cortical bone and mostly as spongiosa in the 4-tissue and 8-tissue segmentation schemes, respectively [Figs. 4a, 4b]. They were not assigned as human ribs due to the fact that mouse bone density is lower than bone density of human tissues. Whereas according to previously published data,²⁴ mouse femur has an average density of approximately 1.1 g∕cm³, the average density of human femur is 1.33 g∕cm³. Moreover, based on the CT number to mass density calibration curve, the maximum mass density of the entire mouse CT dataset is 1.7 g∕cm³. The density of human cortical bone is 1.92 g∕cm³. We assume that due to the finer tissue segmentation scheme, the dose calculation with 39 tissue types is more accurate; however, rigorous comparison with physical dosimetry will be needed to validate this claim.

Based on the small animal simulations, cortical bone (or the default ICRPBONE521ICRU) should not be used as the representative bone material in tissue segmentations for mouse MC dose calculations with kilovoltage beams. Cortical bone, however, might be present in other small animals used for radiotherapy preclinical studies, such as rats or rabbits.

Due to the high effective atomic number of bone tissues, dose to bone is an important issue of small animal radiation therapy when kilovoltage beams are used. Figure 9 demonstrates that the dose to cortical bone (Z = 14) is 4.0, 3.3, and 2.6 times higher than the dose to muscle for the 120 kV beam, 225 kV beam filtered with 4 mm of Al and 0.5 mm of Cu, respectively. The dose to bone is slightly less than to the dose to muscle when the 320 kV beam or a ¹⁹²Ir source is used. It has been shown, however, that single radiation doses up to 30 Gy do not cause a significant effect on bone mineral density and fragility of small animal bones.²⁹

The dose D for each tissue type was normalized to dose to muscle with the density of muscle. Doses to muscle with the density of each ICRU-44 tissue were also calculated and used for normalization, however, maximum differences of 5% from the former normalization were found. This suggests that the calculated dose differences are due to differences in tissue compositions.

The results of the study suggest that unlike in megavoltage radiotherapy, kilovoltage small animal radiotherapy treatment planning using MC simulations should segment the subject using the differences in the atomic numbers rather than mass densities. This could be achieved by dual-energy microCT (DEmCT) imaging. MicroCT images are acquired at two different tube voltages and the mass density and the effective atomic number can be calculated based on an approximation of the linear attenuation coefficient. Though this approach is possible for clinical CT images, microCT images suffer from significantly higher noise (noise for muscle tissue of 50–100 HU in microCT images shown here as opposed to <10 HU in clinical CT images) and DEmCT is more challenging.

CONCLUSIONS

It has been demonstrated that tissue segmentation is one of the key steps in Monte Carlo treatment planning for small animal radiotherapy with kilovoltage beams. With our model employing a small centrally located tissue inhomogeneity we have shown that whereas tissue segmentation is not crucial for a heavily filtered 320 kV beam and a ¹⁹²Ir source, the conventional approach to tissue segmentation based on mass density differences of tissues does not yield acceptable dose calculations results for beams generated by x-ray tubes with potentials equal or less than 225 kV. If tissue segmentation is not properly handled and for example adipose is incorrectly assigned as muscle tissue, dose calculation differences in a 5 mm diameter inhomogeneity up to 27%, 13%, and 7% for a 120 kV x-ray beam and for 225 kV x-ray beams filtered with 4 mm Al and 0.5 mm Cu, respectively, can occur. Such large dosimetric uncertainties could render current small animal radiotherapy approaches practically meaningless, especially if PTV or OARs contained mis-assigned tissues.

It has been shown that there is a strong relationship between the absorbed dose to tissue and the effective atomic number of the tissue for all studied beams. We suggest that the effective atomic number of each voxel should be used for tissue segmentation for Monte Carlo dose calculations when x-ray beams with tube potentials equal or less than 225 kV are used. The choice of number of tissues needed for segmentation depends on the required dose calculation accuracy and the energy of the treatment beam, and it can be limited by the noise in the CT data set.

We present a method for tissue segmentation with 39 tissue types derived from the relationship between the absorbed dose, the effective atomic number, and the mass density of ICRU tissues. Differences in dose distributions between three segmentation schemes for a small animal treatment have demonstrated that doses to OARs could be overestimated with the common 4-tissue segmentation scheme and easily implementable 8-tissue segmentation scheme compared to the more accurate 39-tissue segmentation scheme.