Abstract
The availability of high-throughput parallel methods for sequencing microbial communities is increasing our knowledge of the microbial world at an unprecedented rate. Though most attention has focused on determining lower-bounds on the  -diversity i.e. the total number of different species present in the environment, tight bounds on this quantity may be highly uncertain because a small fraction of the environment could be composed of a vast number of different species. To better assess what remains unknown, we propose instead to predict the fraction of the environment that belongs to unsampled classes. Modeling samples as draws with replacement of colored balls from an urn with an unknown composition, and under the sole assumption that there are still undiscovered species, we show that conditionally unbiased predictors and exact prediction intervals (of constant length in logarithmic scale) are possible for the fraction of the environment that belongs to unsampled classes. Our predictions are based on a Poissonization argument, which we have implemented in what we call the Embedding algorithm. In fixed i.e. non-randomized sample sizes, the algorithm leads to very accurate predictions on a sub-sample of the original sample. We quantify the effect of fixed sample sizes on our prediction intervals and test our methods and others found in the literature against simulated environments, which we devise taking into account datasets from a human-gut and -hand microbiota. Our methodology applies to any dataset that can be conceptualized as a sample with replacement from an urn. In particular, it could be applied, for example, to quantify the proportion of all the unseen solutions to a binding site problem in a random RNA pool, or to reassess the surveillance of a certain terrorist group, predicting the conditional probability that it deploys a new tactic in a next attack.
-diversity i.e. the total number of different species present in the environment, tight bounds on this quantity may be highly uncertain because a small fraction of the environment could be composed of a vast number of different species. To better assess what remains unknown, we propose instead to predict the fraction of the environment that belongs to unsampled classes. Modeling samples as draws with replacement of colored balls from an urn with an unknown composition, and under the sole assumption that there are still undiscovered species, we show that conditionally unbiased predictors and exact prediction intervals (of constant length in logarithmic scale) are possible for the fraction of the environment that belongs to unsampled classes. Our predictions are based on a Poissonization argument, which we have implemented in what we call the Embedding algorithm. In fixed i.e. non-randomized sample sizes, the algorithm leads to very accurate predictions on a sub-sample of the original sample. We quantify the effect of fixed sample sizes on our prediction intervals and test our methods and others found in the literature against simulated environments, which we devise taking into account datasets from a human-gut and -hand microbiota. Our methodology applies to any dataset that can be conceptualized as a sample with replacement from an urn. In particular, it could be applied, for example, to quantify the proportion of all the unseen solutions to a binding site problem in a random RNA pool, or to reassess the surveillance of a certain terrorist group, predicting the conditional probability that it deploys a new tactic in a next attack.
Introduction
A fundamental problem in microbial ecology is the “rare biosphere” [1] i.e. the vast number of low-abundance species in any sample. However, because most species in a given sample are rare, estimating their total number i.e.  -diversity is a difficult task [2], [3], and of dubious utility [4], [5]. Although parametric and non-parametric methods for species estimation show some promise [6], [7], microbial communities may not yet have been sufficiently deeply sampled [8] to test the suitability of the models or fit their parameters. For instance, human-skin communities demonstrate an unprecedented diversity within and across skin locations of same individuals, with marked differences between specimens [9].
-diversity is a difficult task [2], [3], and of dubious utility [4], [5]. Although parametric and non-parametric methods for species estimation show some promise [6], [7], microbial communities may not yet have been sufficiently deeply sampled [8] to test the suitability of the models or fit their parameters. For instance, human-skin communities demonstrate an unprecedented diversity within and across skin locations of same individuals, with marked differences between specimens [9].
In an environment composed of various but an unknown number of species, let  be the proportion in which a certain species
be the proportion in which a certain species  occurs. Samples from microbial communities may be conceptualized as sampling–with replacement–different colored balls from an urn. The urn represents the environment where samples are taken: soil, gut, skin, etc. The balls represent the different members of the microbial community, and each color is a uniquely defined operational taxonomic unit.
occurs. Samples from microbial communities may be conceptualized as sampling–with replacement–different colored balls from an urn. The urn represents the environment where samples are taken: soil, gut, skin, etc. The balls represent the different members of the microbial community, and each color is a uniquely defined operational taxonomic unit.
In the non-parametric setting, the urn is composed by an unknown number of colors occurring in unknown relative proportions. In this setting, the  -diversity of the urn [10] corresponds to the cardinality of the set
-diversity of the urn [10] corresponds to the cardinality of the set 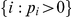 . Although various lower-confidence bounds for this parameter have been proposed in the literature [11]–[14], tight lower-bounds on
. Although various lower-confidence bounds for this parameter have been proposed in the literature [11]–[14], tight lower-bounds on  -diversity are difficult in the non-parametric setting because a small fraction of the urn could be composed by a vast number of different colors [15]. Motivated by this, we shift our interest to predicting instead the fraction of balls with a color unrepresented in the first
-diversity are difficult in the non-parametric setting because a small fraction of the urn could be composed by a vast number of different colors [15]. Motivated by this, we shift our interest to predicting instead the fraction of balls with a color unrepresented in the first  observations from the urn. This is the unobservable random variable:
observations from the urn. This is the unobservable random variable:
where  denote the sequence of colors observed when sampling
denote the sequence of colors observed when sampling  balls from the urn. Notice how
balls from the urn. Notice how 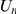 depends both on the specific colors observed in the sample, and the unknown proportions of these colors in the urn. This quantity is very useful to assess what remains unknown in the urn. For instance, the probability of discovering a new color with one additional observation is precisely
depends both on the specific colors observed in the sample, and the unknown proportions of these colors in the urn. This quantity is very useful to assess what remains unknown in the urn. For instance, the probability of discovering a new color with one additional observation is precisely 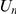 , and the mean number of additional observations to discover a new color is
, and the mean number of additional observations to discover a new color is 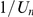 . We note that
. We note that 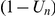 corresponds to what is called the conditional coverage of a sample of size
corresponds to what is called the conditional coverage of a sample of size  in the literature. For this reason, we refer to
in the literature. For this reason, we refer to 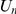 as the conditional uncovered probability of the sample.
as the conditional uncovered probability of the sample.
The expected value of 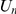 is given by:
is given by:
Unlike the conditional uncovered probability of the sample, 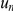 is a parameter that depends on the unknown urn composition but not on the specific colors observed in the sample. Interest in the above quantities or related ones has ranged from estimating the probability distribution of the keys used in the Kenngruppenbuch (the Enigma cipher book) in World War II [16], to assessing the confidence that an iterative procedure with a random start has found the global maximum of a given function [17], to predicting the probability of discovering a new gene by sequencing additional clones from a cDNA library [18]. We note that
is a parameter that depends on the unknown urn composition but not on the specific colors observed in the sample. Interest in the above quantities or related ones has ranged from estimating the probability distribution of the keys used in the Kenngruppenbuch (the Enigma cipher book) in World War II [16], to assessing the confidence that an iterative procedure with a random start has found the global maximum of a given function [17], to predicting the probability of discovering a new gene by sequencing additional clones from a cDNA library [18]. We note that 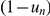 is called the expected coverage of the sample in the literature.
is called the expected coverage of the sample in the literature.
Various predictors of 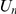 and estimators of
and estimators of 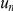 have been proposed in the literature. These are mostly based on a user-defined parameter
have been proposed in the literature. These are mostly based on a user-defined parameter 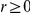 and the statistics
and the statistics 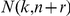 ,
, 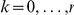 ; defined as the number of colors observed
; defined as the number of colors observed 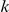 -times, when
-times, when  additional balls are sampled from the urn.
additional balls are sampled from the urn.
Turing and Good [19] proposed to estimate 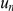 using the biased statistic
using the biased statistic 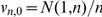 . Posteriorly, Robbins [20] proposed to predict
. Posteriorly, Robbins [20] proposed to predict 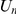 using
using
| (1) |
which he showed to be unbiased for 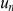 and to satisfy the inequality
and to satisfy the inequality 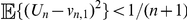 . Despite the possibly small quadratic variation distance between
. Despite the possibly small quadratic variation distance between 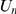 and Robbins' estimator, and as illustrated by the plots on the left side of Fig. 1, when using Robbins' estimator to predict
and Robbins' estimator, and as illustrated by the plots on the left side of Fig. 1, when using Robbins' estimator to predict 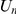 sequentially with
sequentially with  (to assess the quality of the predictions at various depths in the sample), we observe that unusually small or large values of
(to assess the quality of the predictions at various depths in the sample), we observe that unusually small or large values of 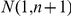 may offset subsequent predictions of
may offset subsequent predictions of 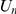 . In fact, as seen on the right-hand plots of the same figure, an offset prediction is usually followed by another offset prediction of the same order of magnitude, even
. In fact, as seen on the right-hand plots of the same figure, an offset prediction is usually followed by another offset prediction of the same order of magnitude, even 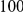 observations later (correlation coefficient of green clouds,
observations later (correlation coefficient of green clouds, 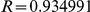 and
and 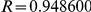 on top- and bottom-right plots).
on top- and bottom-right plots).
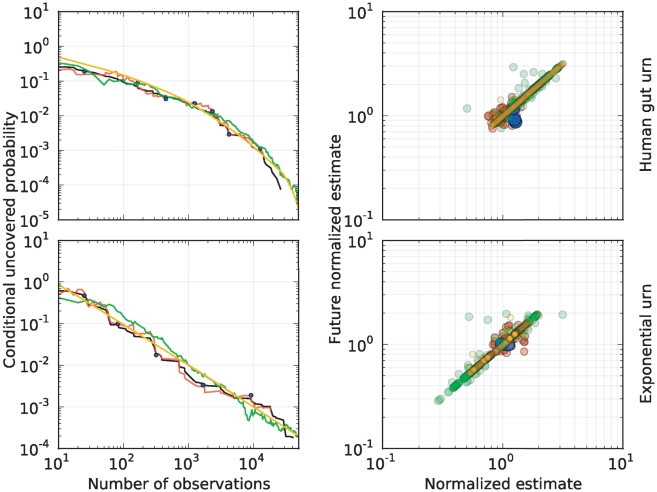
Figure 1. Point predictions in a human-gut and exponential urn.
Plots associated with a human-gut (top-row) and exponential urn (bottom-row). Left-column, sequential predictions of the conditional uncovered probability (black), as a function of the number  of observations, using Robbins' estimator in equation (1) (green), Starr's estimator in equation (2) (orange), and the Embedding algorithm (blue, red), over a same sample of size
of observations, using Robbins' estimator in equation (1) (green), Starr's estimator in equation (2) (orange), and the Embedding algorithm (blue, red), over a same sample of size 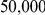 from each urn. Starr's estimator was implemented keeping
from each urn. Starr's estimator was implemented keeping 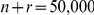 . Blue predictions correspond to consecutive outputs of the Embedding algorithm in Table 1, which was reiterated until exhausting the sample using the parameter
. Blue predictions correspond to consecutive outputs of the Embedding algorithm in Table 1, which was reiterated until exhausting the sample using the parameter 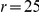 . Red predictions correspond to outputs of the algorithm each time a new species was discovered. Right-column, correlation plots associated with consecutive predictions of the conditional uncovered probability (normalized by its true value at the point of prediction), under the various methods. The green and orange clouds correspond to pairs of predictions, 100-observations apart, using Robbins' and Starr's estimators, respectively. Blue and red clouds correspond to pairs of consecutive outputs of the Embedding algorithm, following the same coloring scheme than on the left plots. Notice how the red and blue clouds are centered around
. Red predictions correspond to outputs of the algorithm each time a new species was discovered. Right-column, correlation plots associated with consecutive predictions of the conditional uncovered probability (normalized by its true value at the point of prediction), under the various methods. The green and orange clouds correspond to pairs of predictions, 100-observations apart, using Robbins' and Starr's estimators, respectively. Blue and red clouds correspond to pairs of consecutive outputs of the Embedding algorithm, following the same coloring scheme than on the left plots. Notice how the red and blue clouds are centered around 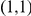 , indicating the accuracy of our methodology in a log-scale. Furthermore, the green and orange clouds show a higher level of correlation than the blue and red clouds, indicating that our method recovers more easily from previously offset predictions. In each urn, our predictions used the
, indicating the accuracy of our methodology in a log-scale. Furthermore, the green and orange clouds show a higher level of correlation than the blue and red clouds, indicating that our method recovers more easily from previously offset predictions. In each urn, our predictions used the 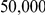 observations and a HPP with intensity one–simulated independently from the urn–to predict sequentially the uncovered probability of the first part of the sample. See Fig. 4 for the associated rank curve in each urn.
observations and a HPP with intensity one–simulated independently from the urn–to predict sequentially the uncovered probability of the first part of the sample. See Fig. 4 for the associated rank curve in each urn.
Subsequently, for each 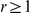 , Starr [21] proposed to predict
, Starr [21] proposed to predict 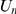 using
using
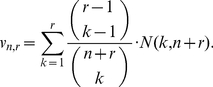 |
(2) |
Even though 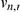 is the minimum variance unbiased estimator of
is the minimum variance unbiased estimator of 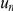 based on
based on  additional observations from the urn [22], Starr showed that
additional observations from the urn [22], Starr showed that 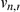 may be strongly negatively correlated with
may be strongly negatively correlated with 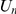 when
when 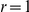 (note that Starr's and Robbins' estimators are identical when
(note that Starr's and Robbins' estimators are identical when 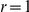 ). Furthermore, the sequential prediction of
). Furthermore, the sequential prediction of 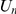 via Starr's estimator is affected by issues similar to Robbins' estimator, which is also illustrated in Fig. 1, even when the parameter
via Starr's estimator is affected by issues similar to Robbins' estimator, which is also illustrated in Fig. 1, even when the parameter  is set as large as possible, namely
is set as large as possible, namely 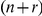 is equal to the sample size (correlation coefficient of orange clouds,
is equal to the sample size (correlation coefficient of orange clouds, 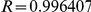 and
and 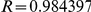 on top- and bottom-right, respectively). We observe that
on top- and bottom-right, respectively). We observe that 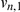 and
and 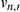 are indistinguishable in a linear scale when
are indistinguishable in a linear scale when 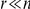 because, for each
because, for each 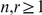 , it applies that (see Materials and Methods):
, it applies that (see Materials and Methods):
| (3) |
In terms of prediction intervals, if 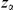 denotes the
denotes the  upper quantile of a standard Normal distribution, it follows from Esty's analysis [23] that if
upper quantile of a standard Normal distribution, it follows from Esty's analysis [23] that if 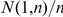 is not very near
is not very near 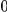 or
or  then
then
| (4) |
is approximately a 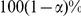 prediction interval for
prediction interval for 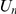 . In practice, and as seen in Fig. 2, when the center of the interval is of a similar or lesser order of magnitude than its radius, the ratio between the upper- and lower-bound of these intervals may oscillate erratically, sometimes over several orders of magnitude. This can be an issue in assessing the depth of sampling in rich environments. For instance, to be highly confident that
. In practice, and as seen in Fig. 2, when the center of the interval is of a similar or lesser order of magnitude than its radius, the ratio between the upper- and lower-bound of these intervals may oscillate erratically, sometimes over several orders of magnitude. This can be an issue in assessing the depth of sampling in rich environments. For instance, to be highly confident that 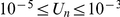 is not of practical use because one may need from
is not of practical use because one may need from 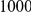 to
to 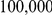 additional observations to discover a new species.
additional observations to discover a new species.
Figure 2. Prediction intervals in the human-gut and exponential urn.
95% prediction intervals for the conditional uncovered probability (black) of the human-gut and exponential urn as a function of the number of observations. Esty's prediction intervals in equation (4) (green), and predictions intervals based on the Embedding algorithm (blue, red), using the parameters 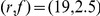 and
and 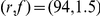 on the left and right, respectively. Blue and red curves correspond to the conservative-lower and -upper prediction intervals for the uncovered probability, respectively. The missing segments on the lower green-curves correspond to Esty's prediction intervals that contained
on the left and right, respectively. Blue and red curves correspond to the conservative-lower and -upper prediction intervals for the uncovered probability, respectively. The missing segments on the lower green-curves correspond to Esty's prediction intervals that contained  . Although the upper- and lower-bound of the Esty's intervals may be of different order of magnitude, our method produces intervals of a constant length in logarithmic scale. This length is controlled by the user-defined parameter
. Although the upper- and lower-bound of the Esty's intervals may be of different order of magnitude, our method produces intervals of a constant length in logarithmic scale. This length is controlled by the user-defined parameter 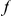 . In each urn, our method predicted accurately the uncovered probability of a random sub-sample of the
. In each urn, our method predicted accurately the uncovered probability of a random sub-sample of the 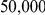 observations from the urn. See Fig. 4 for the associated rank curve in each urn.
observations from the urn. See Fig. 4 for the associated rank curve in each urn.
The issues of the aforementioned methods are somewhat expected. On one hand, the problem of predicting 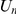 is very different from estimating
is very different from estimating 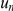 : the former requires predicting the exact proportion of balls in the urn with colors outside the random set
: the former requires predicting the exact proportion of balls in the urn with colors outside the random set  , rather than in average over all possible such sets. On the other hand, the point estimators of
, rather than in average over all possible such sets. On the other hand, the point estimators of 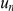 are unlikely to predict
are unlikely to predict 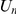 accurately in a logarithmic scale, unless the standard deviation of
accurately in a logarithmic scale, unless the standard deviation of 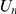 is small relative to
is small relative to 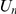 . Finally, the methods we have described from the literature were designed for static situations i.e. to predict
. Finally, the methods we have described from the literature were designed for static situations i.e. to predict 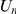 or estimate
or estimate 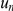 when
when  is fixed.
is fixed.
Results
Embedding Algorithm
Here we propose a new methodology to address the issues of the methods presented in the Introduction to predict 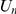 . Our methodology lends itself better for a sequential analysis and accurate predictions in a logarithmic scale; in particular, also in a linear scale–though it relies on randomized sample sizes. Due to this, in static situations i.e. for fixed sample sizes, our method only yields predictions for a random sub-sample of the original sample.
. Our methodology lends itself better for a sequential analysis and accurate predictions in a logarithmic scale; in particular, also in a linear scale–though it relies on randomized sample sizes. Due to this, in static situations i.e. for fixed sample sizes, our method only yields predictions for a random sub-sample of the original sample.
Randomized sample sizes are more than just an artifact of our procedure: due to Theorem 1 below, for any predetermined sample size, there is no deterministic algorithm to predict 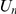 and
and 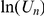 unbiasedly, unless the urn is composed by a known and flat distribution of colors. See the Materials and Methods section for the proofs of our theorems.
unbiasedly, unless the urn is composed by a known and flat distribution of colors. See the Materials and Methods section for the proofs of our theorems.
Theorem 1
If
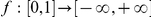 is a continuous and one-to-one function then the following two statements are equivalent: (i) there is a non-randomized algorithm based on
is a continuous and one-to-one function then the following two statements are equivalent: (i) there is a non-randomized algorithm based on
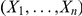 to predict
to predict
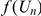 conditionally unbiased; (ii) the urn is composed by a known and equidistributed number of colors.
conditionally unbiased; (ii) the urn is composed by a known and equidistributed number of colors.
Our methodology is based on a so called Poissonization argument [24]. This technique is often used in allocation problems to remove correlations [25]. It was applied in [26] to show that the cardinality of the random set  is asymptotically Gaussian after the appropriate renormalization. Mao and Lindsay [27] used implicitly a Poissonization argument to argue that intervals such as in equation (4) have a
is asymptotically Gaussian after the appropriate renormalization. Mao and Lindsay [27] used implicitly a Poissonization argument to argue that intervals such as in equation (4) have a 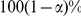 asymptotic confidence, under the hypothesis that the times at which each color in the urn is observed obey a homogeneous Poisson point process (HPP) with a random intensity. Here, asymptotic means that the
asymptotic confidence, under the hypothesis that the times at which each color in the urn is observed obey a homogeneous Poisson point process (HPP) with a random intensity. Here, asymptotic means that the  -diversity tends to infinity, which entails adding colors into the urn. Our approach, however, is not based on any assumption on the times the data was collected, nor on an asymptotic rescaling of the problem, but rather on the embedding of a sample from an urn into a HPP with intensity
-diversity tends to infinity, which entails adding colors into the urn. Our approach, however, is not based on any assumption on the times the data was collected, nor on an asymptotic rescaling of the problem, but rather on the embedding of a sample from an urn into a HPP with intensity  in the semi-infinite interval
in the semi-infinite interval 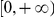 . We emphasize that the HPP is a mathematical artifice simulated independently from the urn.
. We emphasize that the HPP is a mathematical artifice simulated independently from the urn.
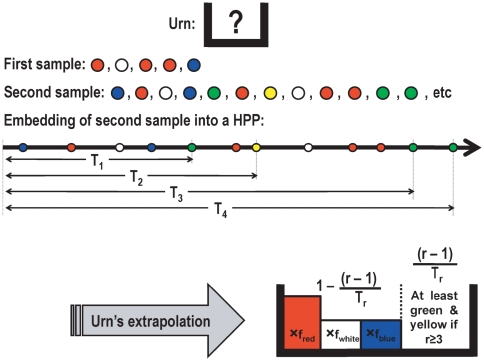
In what follows, 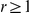 is a user-defined integer parameter. We have implemented the Poissonization argument in what we call the Embedding algorithm in Table 1. For a schematic description of the algorithm see Fig. 3 and, for its heuristic, consult the Materials and Methods section.
is a user-defined integer parameter. We have implemented the Poissonization argument in what we call the Embedding algorithm in Table 1. For a schematic description of the algorithm see Fig. 3 and, for its heuristic, consult the Materials and Methods section.
Table 1. Embedding algorithm.
| Input: |
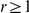 , a set , a set 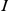 of colors known to be in the urn, and constants of colors known to be in the urn, and constants 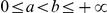 that satisfy condition (5). that satisfy condition (5). |
| Output: | Unbiased predictor of 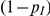 , , 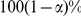 prediction interval for prediction interval for 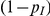 and an updated set and an updated set 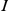 of colors known to belong to the urn. of colors known to belong to the urn. |
| Step 1. | Assign 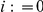 , , 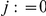 , and , and 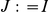 . . |
| Step 2. | While 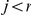 assign assign 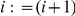 , and sample with replacement a ball from the urn. Let , and sample with replacement a ball from the urn. Let  be the color of the sampled ball. If be the color of the sampled ball. If 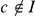 then assign then assign 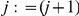 and and 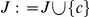 . . |
| Step 3. | Simulate 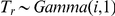 , and assign , and assign 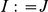 . . |
| Step 4. | Output 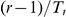 , , 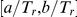 and and  . . |
Figure 3. Schematic description of the Embedding algorithm.
Suppose that in a first sample from an urn you only observe the colors red, white and blue; in particular, 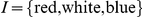 . Let
. Let  be the unknown proportion in the urn of balls colored with any of these colors i.e.
be the unknown proportion in the urn of balls colored with any of these colors i.e. 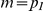 . To estimate
. To estimate 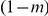 , sample additional balls from the urn until observing
, sample additional balls from the urn until observing  balls with colors outside
balls with colors outside 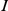 . Embed the colors of this second sample into a homogeneous Poisson point process with intensity one; in particular, the average separation of consecutive points with colors outside
. Embed the colors of this second sample into a homogeneous Poisson point process with intensity one; in particular, the average separation of consecutive points with colors outside 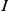 are independent exponential random variables with mean
are independent exponential random variables with mean 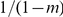 . The unknown quantity
. The unknown quantity 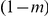 can be now estimated from the random variable
can be now estimated from the random variable 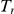 . As a byproduct of our methodology, conditional on
. As a byproduct of our methodology, conditional on 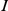 , if
, if 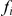 denotes the relative proportion of color
denotes the relative proportion of color  in the first sample then
in the first sample then 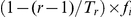 predicts the true proportion of color
predicts the true proportion of color  in the urn.
in the urn.
Suppose that a set 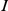 of colors is already known to belong to the urn and let
of colors is already known to belong to the urn and let 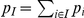 be the coverage probability of the colors in this set. We note that, in the context of the previous discussion,
be the coverage probability of the colors in this set. We note that, in the context of the previous discussion, 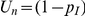 with
with 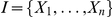 .
.
To predict 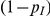 , draw balls from the urn until
, draw balls from the urn until  colors outside
colors outside 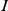 are observed. Visualize each observation as a colored point in the interval
are observed. Visualize each observation as a colored point in the interval 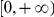 . The Poissonization consists in spacing these points out using independent exponential random variables with mean one. Due to the thinning property of Poisson point processes [28], the position
. The Poissonization consists in spacing these points out using independent exponential random variables with mean one. Due to the thinning property of Poisson point processes [28], the position 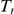 of the point farthest apart from
of the point farthest apart from 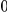 has a Gamma distribution with mean
has a Gamma distribution with mean 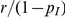 . We may exploit this to obtain conditionally unbiased predictors and exact prediction intervals for
. We may exploit this to obtain conditionally unbiased predictors and exact prediction intervals for 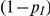 and
and 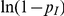 as follows. Regarding direct predictions of
as follows. Regarding direct predictions of 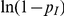 , note that measuring
, note that measuring 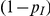 in a logarithmic rather than linear scale makes more sense when deep sampling is possible.
in a logarithmic rather than linear scale makes more sense when deep sampling is possible.
Theorem 2
Conditioned on
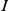 and the event
and the event
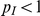 , the following applies:
, the following applies:
If
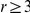 then
then
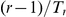 is unbiased for
is unbiased for
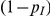 , with variance
, with variance
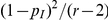 .
.If
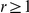 and
and
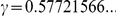 denotes Euler's constant then
denotes Euler's constant then
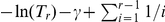 is unbiased for
is unbiased for
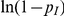 , with variance
, with variance
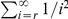 , which is bounded between
, which is bounded between
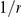 and
and
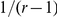 .
.- If
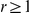 ,
, 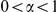 and
and
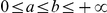 are such that
are such that
then the interval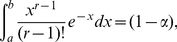
(5) 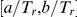 contains
contains
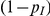 with exact probability
with exact probability
 ; in particular,
; in particular,
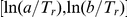 contains
contains
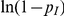 also with probability
also with probability
 .
.
We note that 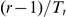 is the uniformly minimum variance unbiased estimator of
is the uniformly minimum variance unbiased estimator of 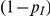 based on
based on  exponential random variables with unknown mean
exponential random variables with unknown mean 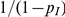 . Furthermore,
. Furthermore, 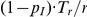 converges almost surely to
converges almost surely to  , as
, as  tends to infinity; in particular, the point predictors in part (i) and (ii) are strongly consistent.
tends to infinity; in particular, the point predictors in part (i) and (ii) are strongly consistent.
We also note that the logarithm of the statistic in part (i) under-estimates 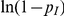 in average. In fact, the difference between the natural logarithm of the statistic in (i) and the statistic in (ii) is
in average. In fact, the difference between the natural logarithm of the statistic in (i) and the statistic in (ii) is 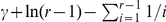 , which is negative for
, which is negative for 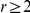 , and increases to zero as
, and increases to zero as  tends to infinity. From a computational stand point, however, the statistics
tends to infinity. From a computational stand point, however, the statistics 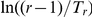 and
and 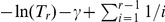 differ by at most
differ by at most 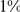 -units when
-units when 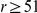 . The same precision may be reached for smaller values of
. The same precision may be reached for smaller values of  if larger bases are utilized. For instance, in base-10, the discrepancy will be at most
if larger bases are utilized. For instance, in base-10, the discrepancy will be at most 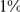 for
for 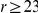 .
.
In regards to part (iii) of the theorem, we note that our prediction intervals for 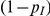 cannot contain zero unless
cannot contain zero unless 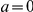 . On the other hand, since the density function used in equation (5) is unimodal, the shortest prediction interval for
. On the other hand, since the density function used in equation (5) is unimodal, the shortest prediction interval for 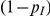 corresponds to a pair of non-negative constants
corresponds to a pair of non-negative constants  such that:
such that:
| (6) |
Similarly, optimal prediction intervals for 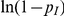 follow when
follow when
| (7) |
with 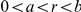 (see Materials and Methods for a numerical procedure to approximate these constants). In either case, because
(see Materials and Methods for a numerical procedure to approximate these constants). In either case, because 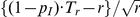 converges in distribution to a standard Normal as
converges in distribution to a standard Normal as  tends to infinity, one may select in (5) the approximate constants
tends to infinity, one may select in (5) the approximate constants 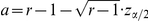 and
and 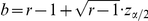 . With these approximate values, if
. With these approximate values, if 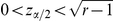 then the true confidence
then the true confidence  of the associated prediction intervals satisfies (see Materials and Methods):
of the associated prediction intervals satisfies (see Materials and Methods):
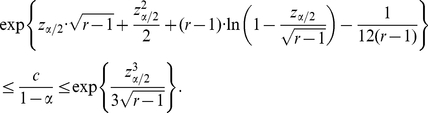 |
(8) |
(The term on the exponential on the left-hand side above is big-O of 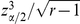 ; in particular, the lower-bound is of the same asymptotic order than the upper-bound.) We note that the constants produced by the Normal approximation may be crude for relatively large values of
; in particular, the lower-bound is of the same asymptotic order than the upper-bound.) We note that the constants produced by the Normal approximation may be crude for relatively large values of  , as seen in Table 2.
, as seen in Table 2.
Table 2. Optimal versus asymptotic 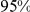 prediction intervals.
prediction intervals.

|
Predictioninterval for | Optimalconstants | Gaussianapproximation | Relativeerror 
|
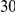
|
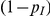
|
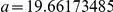
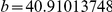
|
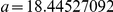
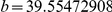
|
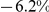
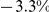
|
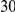
|
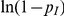
|
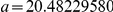
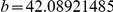
|
Same asabove |
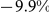
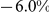
|
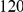
|
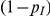
|
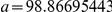
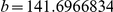
|
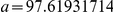
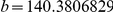
|
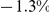
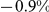
|
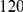
|
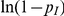
|
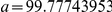
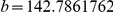
|
Same asabove |
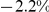
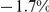
|
As high-throughput technologies allow deeper sampling of microbial communities, it will be increasingly important to have upper- and lower-bounds for 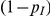 of a comparable order of magnitude. Since the prediction intervals for this quantity in Theorem 2 are of the form
of a comparable order of magnitude. Since the prediction intervals for this quantity in Theorem 2 are of the form 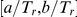 , and the ratio between the upper- and lower-bound of this interval is
, and the ratio between the upper- and lower-bound of this interval is 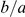 , one may wish to determine constants
, one may wish to determine constants  and
and 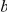 such that, not only (5) is satisfied, but also
such that, not only (5) is satisfied, but also
| (9) |
where 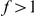 is a user-defined parameter. Not all values of
is a user-defined parameter. Not all values of 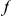 are attainable for a given
are attainable for a given  and confidence level. In fact, the smallest attainable value is given by the constants associated with the optimal prediction interval for
and confidence level. In fact, the smallest attainable value is given by the constants associated with the optimal prediction interval for 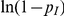 . Equivalently,
. Equivalently, 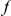 is attainable if and only if
is attainable if and only if
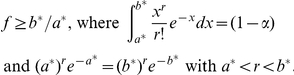 |
Conversely, and as stated in the following result, any value of 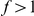 is attainable at a given confidence level, provided that the parameter
is attainable at a given confidence level, provided that the parameter  is selected sufficiently large.
is selected sufficiently large.
Theorem 3
Let
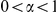 and
and
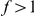 be fixed constants. For each
be fixed constants. For each
 sufficiently large, there are constants
sufficiently large, there are constants
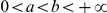 such that (5) and (9) are satisfied.
such that (5) and (9) are satisfied.
For a given parameter 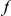 , there are at most two constants
, there are at most two constants 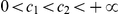 such that
such that 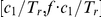 and
and 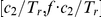 are prediction intervals for
are prediction intervals for 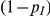 with exact confidence
with exact confidence  . We refer to these as conservative-lower and conservative-upper prediction intervals, respectively. We refer to intervals of the form
. We refer to these as conservative-lower and conservative-upper prediction intervals, respectively. We refer to intervals of the form 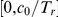 and
and 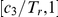 as upper- and lower-bound prediction intervals, respectively. See Table 3 for the determination of these constants for various values of
as upper- and lower-bound prediction intervals, respectively. See Table 3 for the determination of these constants for various values of  when
when 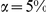 .
.
Table 3. Constants associated with 95% prediction intervals.

|
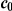
|
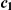
|
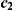
|
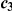
|
| 1 | 2.995732274 |

|

|
0.051293294 |
| 2 | 4.743864518 |

|

|
0.355361510 |
| 3 | 6.295793622 |

|

|
0.817691447 |
| 4 | 7.753656528 | 0.806026244 | 1.360288674 | 1.366318397 |
| 5 | 9.153519027 | 0.924031159 | 1.969902541 | 1.970149568 |
| 6 | 10.51303491 | 1.053998892 | 2.61300725 | 2.613014744 |
| 7 | 11.84239565 | 1.185086999 | 3.28531552 | 3.285315692 |
| 8 | 13.14811380 | 1.315076338 | 3.98082278 | 3.980822786 |
| 9 | 14.43464972 | 1.443547021 | 4.69522754 | 4.695227540 |
| 10 | 15.70521642 | 1.570546801 | 5.42540570 | 5.425405697 |
| 11 | 16.96221924 | 1.696229569 | 6.16900729 | 6.169007289 |
| 12 | 18.20751425 | 1.820753729 | 6.92421252 | 6.924212514 |
| 13 | 19.44256933 | 1.944257623 | 7.68957829 | 7.689578292 |
| 14 | 20.66856908 | 2.066857113 | 8.46393752 | 8.463937522 |
| 15 | 21.88648591 | 2.188648652 | 9.24633050 | 9.246330491 |
| 16 | 23.09712976 | 2.309712994 | 10.03595673 | 10.03595673 |
| 17 | 24.30118368 | 2.430118373 | 10.83214036 | 10.83214036 |
| 18 | 25.49923008 | 2.549923010 | 11.63430451 | 11.63430451 |
| 19 | 26.69177031 | 2.669177032 | 12.44195219 | 12.44195219 |
| 20 | 27.87923964 | 2.787923964 | 13.25465160 | 13.25465160 |
| 21 | 29.06201884 | 2.906201884 | 14.07202475 | 14.07202475 |
| 22 | 30.24044329 | 3.024044329 | 14.89373854 | 14.89373854 |
| 23 | 31.41481021 | 3.141481021 | 15.71949763 | 15.71949763 |
| 24 | 32.58538445 | 3.258538445 | 16.54903872 | 16.54903871 |
| 25 | 33.75240327 | 3.375240328 | 17.38212584 | 17.38212584 |
 upper-bound, conservative-lower, conservative-upper and lower-bound prediction intervals for
upper-bound, conservative-lower, conservative-upper and lower-bound prediction intervals for 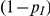 , when
, when 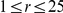 and
and 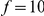 . By definition, this means that
. By definition, this means that 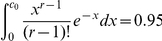 and
and 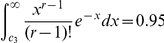 . Furthermore, the constants
. Furthermore, the constants 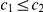 are solutions to the equation:
are solutions to the equation: ) denotes that the equation has no solution.
) denotes that the equation has no solution.Effect of non-randomized sample sizes
The Embedding algorithm provides conditionally unbiased predictors and intervals for 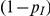 and
and 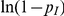 , provided that an arbitrary number of additional observations is possible until observing
, provided that an arbitrary number of additional observations is possible until observing  balls with colors outside
balls with colors outside 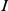 . When dealing with fixed sample sizes, there is a positive probability of not meeting this condition, in which case the Embedding Algorithm is inconclusive. In large samples however, such as those collected in microbial datasets, the algorithm may be applied sequentially until it yields an inconclusive prediction. In such case, the true confidence of the prediction intervals produced by the algorithm satisfy the following.
. When dealing with fixed sample sizes, there is a positive probability of not meeting this condition, in which case the Embedding Algorithm is inconclusive. In large samples however, such as those collected in microbial datasets, the algorithm may be applied sequentially until it yields an inconclusive prediction. In such case, the true confidence of the prediction intervals produced by the algorithm satisfy the following.
Theorem 4
Suppose that condition (5) is satisfied. Conditioned on
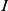 , if
, if
 balls with colors outside
balls with colors outside
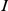 are observed in the next
are observed in the next
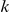 draws from the urn, then the true confidence
draws from the urn, then the true confidence
 of the prediction interval for
of the prediction interval for
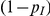 produced by the Embedding algorithm satisfies:
produced by the Embedding algorithm satisfies:
if
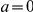 then
then
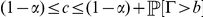 ;
;if
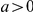 then
then
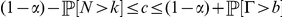 , where
, where
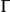 is a Gamma random variable with parameters
is a Gamma random variable with parameters
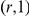 , and
, and
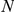 is a Negative Binomial random variable with parameters
is a Negative Binomial random variable with parameters
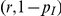 .
.
Thus, if the Embedding algorithm produces an output in what remains of a finite sample size, the upper-bound prediction interval for 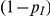 has at least the user-defined confidence. This is perhaps the case of most interest in applications: it allows the user to estimate the least number of additional samples to observe a color not seen in any sample. For the other three interval types, the true confidence is approximately at least the targeted one if the probability that the algorithm produces an output in what remains of the sample is large.
has at least the user-defined confidence. This is perhaps the case of most interest in applications: it allows the user to estimate the least number of additional samples to observe a color not seen in any sample. For the other three interval types, the true confidence is approximately at least the targeted one if the probability that the algorithm produces an output in what remains of the sample is large.
Discussion
Comparisons with Robbins-Starr estimators
Note that, like Robbins' and Starr's estimators, our method requires extracting additional balls from the urn to make a prediction. However, unlike the methods of the Introduction, our method uses only the additionally collected data–instead of all the data ever collected from the urn–to make a prediction. In terms of sequential analysis, this is advantageous to recover from earlier erroneous predictions (we expand on this point in the next section, see Fig. 1).
In what remains of this section, 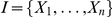 hence
hence 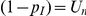 , the conditional uncovered probability of a sample of size
, the conditional uncovered probability of a sample of size  . Furthermore, to rule out trivial cases, we assume that
. Furthermore, to rule out trivial cases, we assume that 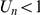 with positive probability i.e. the urn is composed by more than just balls of a single color.
with positive probability i.e. the urn is composed by more than just balls of a single color.
Part (i) of Theorem 1 provides a conditionally unbiased predictor for 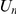 . We can show, however, that Robbins' and Starr's estimators are not conditionally unbiased for
. We can show, however, that Robbins' and Starr's estimators are not conditionally unbiased for 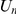 in the non-parametric case when
in the non-parametric case when 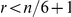 . To see this argument, first notice that
. To see this argument, first notice that 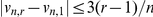 due to the inequality (3). On the other hand, if
due to the inequality (3). On the other hand, if  is a color in the urn such that
is a color in the urn such that 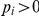 then
then
As a result:
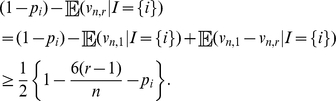 |
Hence, if there exists a color  in the urn that makes the above quantity strictly positive (there are infinitely many such urns, including all urns composed by infinitely many colors, because
in the urn that makes the above quantity strictly positive (there are infinitely many such urns, including all urns composed by infinitely many colors, because 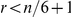 ) then
) then 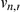 cannot be conditionally unbiased for
cannot be conditionally unbiased for 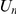 .
.
On the other hand, due to parts (i) and (ii) in Theorem 1, we obtain (see Materials and Methods):
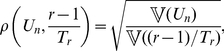 |
(10) |
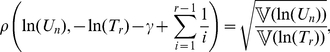 |
(11) |
where 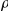 denotes correlation and
denotes correlation and 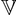 variance. Consequently, the point predictors in Theorem 1 are positively correlated with the quantities they were designed to predict. This contrasts with Robbins' estimator, which may be strongly negatively correlated with
variance. Consequently, the point predictors in Theorem 1 are positively correlated with the quantities they were designed to predict. This contrasts with Robbins' estimator, which may be strongly negatively correlated with 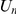 . For instance, if
. For instance, if 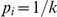 for
for 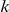 different colors in the urn, it is shown in [21] that the asymptotic correlation between
different colors in the urn, it is shown in [21] that the asymptotic correlation between 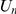 and Robbins' estimator
and Robbins' estimator 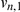 is asymptotically negative when
is asymptotically negative when 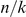 converges to a strictly positive but finite constant
converges to a strictly positive but finite constant 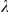 . In this same regime but provided that
. In this same regime but provided that 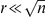 , we can show that (see Materials and Methods):
, we can show that (see Materials and Methods):
| (12) |
Since the right-hand side above is negative for all 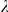 sufficiently small, Starr's estimator
sufficiently small, Starr's estimator 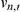 may also have a strong negative correlation with
may also have a strong negative correlation with 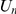 when
when  is much smaller than
is much smaller than 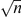 .
.
A further calculation based on parts (i) and (ii) in Theorem 1 shows that
In particular, for fixed  , the correlations in equations (10) and (11) approach to one as
, the correlations in equations (10) and (11) approach to one as  tends to infinity.
tends to infinity.
Finally, for non-trivial urns with finite  -diversity, i.e. urns composed by balls with at least two but a finite number of different colors, one can show for fixed
-diversity, i.e. urns composed by balls with at least two but a finite number of different colors, one can show for fixed  that the correlation in equation (10) approaches
that the correlation in equation (10) approaches 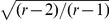 as
as  tends to infinity. Furthermore, if we again assume that
tends to infinity. Furthermore, if we again assume that 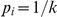 for
for 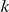 different colors in the urn and
different colors in the urn and 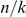 converges to a strictly positive but finite constant, then the correlation in equation (10) approaches zero from above. As we pointed out before, in this regime, Robbins' estimator is asymptotically negatively correlated with
converges to a strictly positive but finite constant, then the correlation in equation (10) approaches zero from above. As we pointed out before, in this regime, Robbins' estimator is asymptotically negatively correlated with 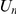 .
.
Selection of parameters
There are two main criteria to select the parameter  of the Embedding algorithm in a concrete application.
of the Embedding algorithm in a concrete application.
One criteria applies for point predictors. In this case, conditioned on 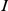 , the standard deviation of the relative error of our prediction of
, the standard deviation of the relative error of our prediction of 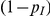 is
is 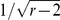 (Theorem 2, part (i)). To predict
(Theorem 2, part (i)). To predict 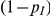 ,
,  should be therefore selected as small as possible so as to meet the user's tolerance on the average relative error of our predictions. The same criteria applies for point predictors of
should be therefore selected as small as possible so as to meet the user's tolerance on the average relative error of our predictions. The same criteria applies for point predictors of 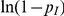 , for which the standard deviation of the absolute error is of order
, for which the standard deviation of the absolute error is of order 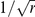 , uniformly for all
, uniformly for all 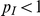 (Theorem 2, part (ii)).
(Theorem 2, part (ii)).
A different criteria applies for prediction intervals. In this case, conditioned on 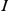 , the user should first specify the confidence level, and how much larger he wants the upper-prediction-bound to be in relation to the lower-prediction bound of
, the user should first specify the confidence level, and how much larger he wants the upper-prediction-bound to be in relation to the lower-prediction bound of 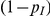 . Since the ratio between these last two quantities is given by the parameter
. Since the ratio between these last two quantities is given by the parameter 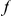 in (9),
in (9),  should be selected as small as possible to meet the user's pre-specified factor
should be selected as small as possible to meet the user's pre-specified factor 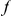 for the given confidence level of the prediction interval (Theorem 3). See Table 4 for the optimal choice of
for the given confidence level of the prediction interval (Theorem 3). See Table 4 for the optimal choice of  for various values of
for various values of 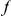 when
when 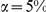 . Note that for the selected parameter
. Note that for the selected parameter  , the constants associated with the optimal prediction intervals are given in equations (6) and (7), see Materials and Methods.
, the constants associated with the optimal prediction intervals are given in equations (6) and (7), see Materials and Methods.
Table 4. Optimal selection of parameter  in terms of parameter
in terms of parameter 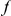 .
.
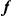
|

|
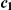
|
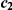
|
| 80 | 2 | 0.0598276655 | 0.355361510 |
| 48 | 2 | 0.1013728884 | 0.355358676 |
| 40 | 2 | 0.1231379857 | 0.355320458 |
| 24 | 2 | 0.226833483 | 0.346045204 |
| 20 | 3 | 0.320984257 | 0.817610455 |
| 12 | 3 | 0.590243030 | 0.787721610 |
| 10 | 4 | 0.806026244 | 1.360288674 |
| 6 | 6 | 1.822307383 | 2.58658608 |
| 5 | 7 | 2.48303930 | 3.22806682 |
| 3 | 14 | 7.17185045 | 8.27008349 |
| 2.5 | 19 | 11.26109001 | 11.96814857 |
| 1.5 | 94 | 75.9077267 | 76.5492088 |
| 1.25 | 309 | 275.661191 | 275.949782 |
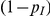 , when
, when 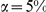 ; in particular, for each
; in particular, for each 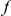 and
and  ,
, 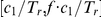 and
and 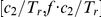 contain
contain 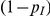 with a
with a 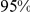 probability. For each
probability. For each 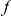 , the smallest value of
, the smallest value of  for which the equation:
for which the equation:Simulations on analytic and non-analytic urns
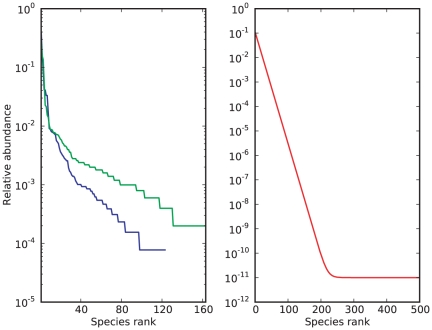
We tested our methods against an urn with an exponential relative abundance rank curve over 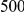 species, and an urn matching the observed distribution of microbes in a human-gut sample from [29]. We also analyzed a sample from a human-hand microbiota found in [30]. The gut and hand data are part of the largest microbial datasets collected thus far (see Fig. 4 for the relative abundance rank curve associated with each urn). The relative abundance rank curve, or for simplicity “rank curve”, associated with an urn is a graphical representation of its composition: the height of the graph above a non-negative integer
species, and an urn matching the observed distribution of microbes in a human-gut sample from [29]. We also analyzed a sample from a human-hand microbiota found in [30]. The gut and hand data are part of the largest microbial datasets collected thus far (see Fig. 4 for the relative abundance rank curve associated with each urn). The relative abundance rank curve, or for simplicity “rank curve”, associated with an urn is a graphical representation of its composition: the height of the graph above a non-negative integer  is the fraction of balls in the urn with the
is the fraction of balls in the urn with the  -th most dominant color.
-th most dominant color.
Figure 4. Rank curves associated with the human-gut, human-hand and exponential urn.
In a rank curve, the relative abundance of a species is plotted against its sorted rank amongst all species, allowing for a quick overview of the evenness of a community. On the left, rank curves associated with the human-gut (blue) and -hand data (green) show a relatively small number of species with an abundance greater than 1%, and a long tail of relatively rare species. The right rank curve of the exponential urn (red) simulates an extreme environment, where relatively excessive sampling is unlikely to exhaust the pool of rare species.
The blue dots and red curves on the plots on the left side in Fig. 1 show very accurate point predictions in log-scale of the conditional uncovered probability (as a function of the number of observations), when we apply the Embedding algorithm to a sample of size 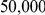 from the human-gut and exponential urn, respectively. In both instances, the parameter
from the human-gut and exponential urn, respectively. In both instances, the parameter  of the Embedding algorithm was set to
of the Embedding algorithm was set to 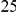 . The accuracy of our method is confirmed by the red clouds on the plots on the right side of Fig. 1, which are centered around
. The accuracy of our method is confirmed by the red clouds on the plots on the right side of Fig. 1, which are centered around 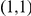 . The red clouds also indicate that our predictions recover more easily from offset predictions as compared to Robbins' and Starr's (correlation coefficient of red clouds,
. The red clouds also indicate that our predictions recover more easily from offset predictions as compared to Robbins' and Starr's (correlation coefficient of red clouds, 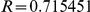 and
and 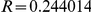 on top- and bottom-right, respectively). This is to be expected because the Embedding algorithm relies only on the additionally collected data to make a new prediction, whereas Robbins' and Starr's estimators use all the data ever collected from the urn. On the other hand, the red and blue curves in Fig. 2 show that the conservative-upper and -lower prediction intervals of the conditional uncovered probability (also as a function of the number of observations) contain this quantity with high probability and, unlike Esty's intervals, have a constant length in logarithmic scale. The intervals on the plots on the right side are tighter than those on the left because of the decrease of the parameter
on top- and bottom-right, respectively). This is to be expected because the Embedding algorithm relies only on the additionally collected data to make a new prediction, whereas Robbins' and Starr's estimators use all the data ever collected from the urn. On the other hand, the red and blue curves in Fig. 2 show that the conservative-upper and -lower prediction intervals of the conditional uncovered probability (also as a function of the number of observations) contain this quantity with high probability and, unlike Esty's intervals, have a constant length in logarithmic scale. The intervals on the plots on the right side are tighter than those on the left because of the decrease of the parameter 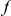 from
from 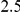 to
to 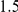 . In each case, the parameter
. In each case, the parameter  was selected according to the guidelines in Table 4. We note that sequential predictions based on the Embedding Algorithm in figures 1 and 2 were produced until the algorithm yielded inconclusive predictions. For this reason, our predictions ended before exhausting each sample.
was selected according to the guidelines in Table 4. We note that sequential predictions based on the Embedding Algorithm in figures 1 and 2 were produced until the algorithm yielded inconclusive predictions. For this reason, our predictions ended before exhausting each sample.
In the human-hand dataset, 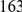 species were observed in a sample of size
species were observed in a sample of size 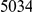 . To simulate draws with replacement from this environment, we produced a random permutation of the data (see Materials and Methods section). Using the Embedding algorithm with parameters
. To simulate draws with replacement from this environment, we produced a random permutation of the data (see Materials and Methods section). Using the Embedding algorithm with parameters 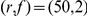 , and according to our point predictor,
, and according to our point predictor, 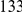 of the species observed in the sample represent
of the species observed in the sample represent 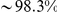 of that hand environment; in particular, the remaining
of that hand environment; in particular, the remaining 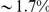 is composed by at least
is composed by at least 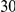 species. Furthermore, according to our upper-bound prediction interval, and with at least a
species. Furthermore, according to our upper-bound prediction interval, and with at least a 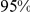 confidence, the species not represented in the sample account for less than
confidence, the species not represented in the sample account for less than 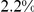 of that environment.
of that environment.
To test the above predictions, we simulated the rare biosphere as follows. We hypothesized that our point prediction of the conditional uncovered probability could be offset by up to one order of magnitude. We also hypothesized that the number of unseen species in the sample had an exponential relative abundance rank curve, composed either by 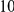 ,
, 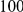 or
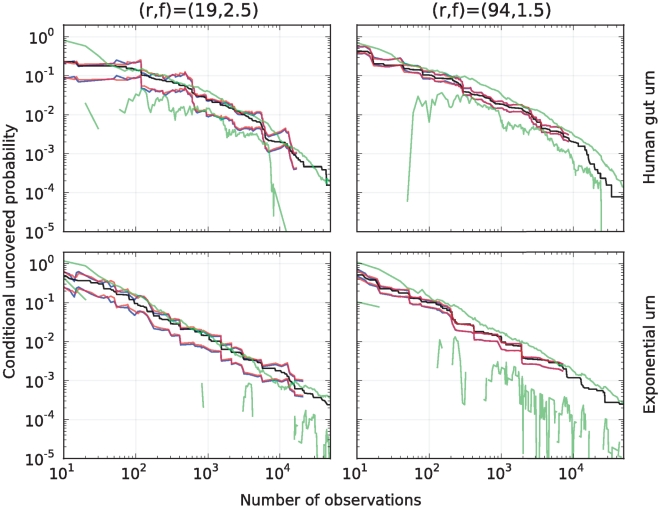
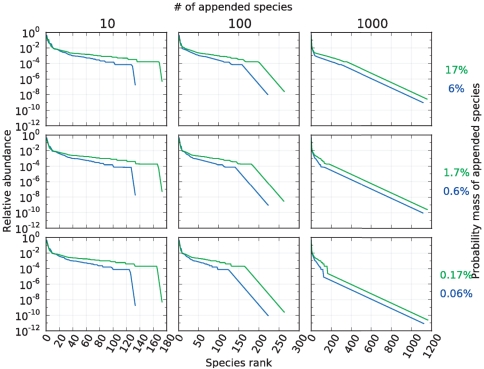
or 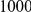 species. This leads to nine different urns in which to test our methods. These urns are devised such that they gradually change from the almost unchanged urn in the bottom left corner to the urn in the upper right, which is dominated by rare species (see Fig. 5 for the associated rank curves). As seen on the plots in Fig. 6, the Embedding algorithm yields very accurate predictions in each of these nine scenarios, for all the sample sizes considered.
species. This leads to nine different urns in which to test our methods. These urns are devised such that they gradually change from the almost unchanged urn in the bottom left corner to the urn in the upper right, which is dominated by rare species (see Fig. 5 for the associated rank curves). As seen on the plots in Fig. 6, the Embedding algorithm yields very accurate predictions in each of these nine scenarios, for all the sample sizes considered.
Figure 5. Rank curves associated with the rare biosphere simulation in the human-gut and -hand urn.
Rank curves associated with Fig. 6 (green) and Fig. 7 (blue).
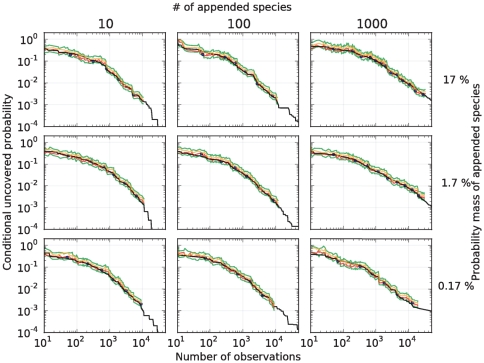
Figure 6. Predictions in the human-hand urn when simulating the rare biosphere.
Prediction of the conditional uncovered probability (black) in nine urns associated with a human-hand urn. Point predictions produced by the Embedding algorithm (blue), point predictions produced by the algorithm each time a new species was discovered (red), 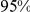 upper-bound interval (orange), and
upper-bound interval (orange), and 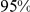 conservative-upper interval (green). The algorithm used the parameters
conservative-upper interval (green). The algorithm used the parameters 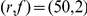 . The different urns were devised as follows. For each
. The different urns were devised as follows. For each 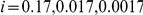 (indexing rows) and
(indexing rows) and 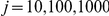 (indexing columns), a mixture of two urns was considered: an urn with the same distribution as the microbes found in a sample from a human-hand and weighted by the factor
(indexing columns), a mixture of two urns was considered: an urn with the same distribution as the microbes found in a sample from a human-hand and weighted by the factor  , and an urn consisting of
, and an urn consisting of 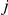 colors (disjoint from the hand urn), with an exponentially decaying rank curve and weighted by the factor
colors (disjoint from the hand urn), with an exponentially decaying rank curve and weighted by the factor  . See Fig. 5 for the rank curve associated with each urn.
. See Fig. 5 for the rank curve associated with each urn.
As seen in Fig. 7, our predictions are also in excellent agreement with the human-gut dataset when we simulate the rare biosphere. As expected, the conditional uncovered probability almost always lies between the predicted bounds. We also note that the predictions based on the Embedding algorithm are accurate even for a small number of observations. This suggests that our algorithm can be applied to deeply as well as shallowly sampled environments.
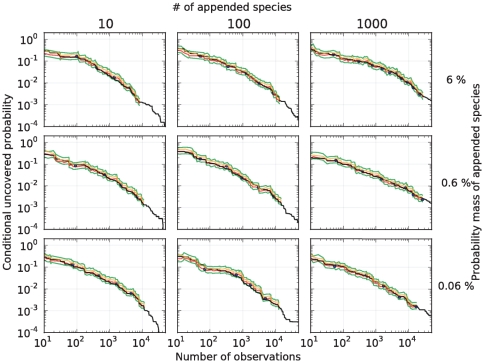
Figure 7. Predictions in the human-gut urn when simulating the rare biosphere.
In a sample of size 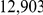 from a human-gut,
from a human-gut, 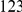 species were discovered. Based on our methods, we estimate that
species were discovered. Based on our methods, we estimate that 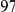 of these species represent
of these species represent 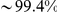 of that gut environment; hence, the remaining
of that gut environment; hence, the remaining 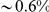 is composed by at least
is composed by at least 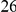 species. To test our predictions of the conditional uncovered probability (black), we simulated the rare biosphere by adding additional species and hypothesized that our point prediction could be offset by up to one order of magnitude: point predictions produced by the Embedding Algorithm (blue), point predictions produced by the algorithm each time a new species was discovered (red),
species. To test our predictions of the conditional uncovered probability (black), we simulated the rare biosphere by adding additional species and hypothesized that our point prediction could be offset by up to one order of magnitude: point predictions produced by the Embedding Algorithm (blue), point predictions produced by the algorithm each time a new species was discovered (red), 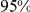 upper-bound (orange), and
upper-bound (orange), and 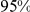 conservative-upper interval (green). The predictions used the parameters
conservative-upper interval (green). The predictions used the parameters 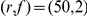 . The different urns were devised as follows. For each
. The different urns were devised as follows. For each 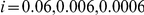 (indexing rows) and
(indexing rows) and 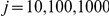 (indexing columns), a mixture of two urns was considered: an urn with the same distribution as the microbes found in the gut dataset, and weighted by the factor
(indexing columns), a mixture of two urns was considered: an urn with the same distribution as the microbes found in the gut dataset, and weighted by the factor  , and an urn consisting of
, and an urn consisting of 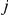 colors (disjoint from the gut urn), with an exponentially decaying rank curve and weighted by the factor
colors (disjoint from the gut urn), with an exponentially decaying rank curve and weighted by the factor  . See Fig. 5 for the rank curve associated with each urn.
. See Fig. 5 for the rank curve associated with each urn.
Materials and Methods
Heuristic behind the Embedding algorithm
The number of times a rare color occurs in a sample from an urn is approximately Poisson distributed. In the non-parametric setting, a direct use of this approximation is tricky because “rare” is relative to the sample size and the unknown urn composition. The embedding into a HPP is a way to accommodate for the Poisson approximation heuristic, without making additional assumptions on the urn's composition. To fix ideas, imagine that no ball in the urn is colored black. Make up a second urn with a single ball colored black. We refer to this as the “black-urn”. Now sample (with replacement) balls according to the following scheme: draw a ball from the original- versus black-urn with probability  and
and  , respectively, where
, respectively, where 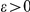 is a fixed but small parameter. Under this sampling scheme, even the most abundant colors in the original-urn are rare. In particular, the smaller
is a fixed but small parameter. Under this sampling scheme, even the most abundant colors in the original-urn are rare. In particular, the smaller  is, the closer is the distribution of the number of times a particular set of colors (excluding black) is observed to a Poisson distribution. This approach is not very practical, however, because the number of samples to observe a given number of balls from the original urn can be astronomically large when
is, the closer is the distribution of the number of times a particular set of colors (excluding black) is observed to a Poisson distribution. This approach is not very practical, however, because the number of samples to observe a given number of balls from the original urn can be astronomically large when  is very small. To overpass this issue imagine drawing a ball every
is very small. To overpass this issue imagine drawing a ball every  -seconds. Draws from the original urn will then be apart
-seconds. Draws from the original urn will then be apart 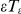 seconds, where
seconds, where 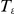 has a Geometric distribution with mean
has a Geometric distribution with mean 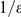 . As a result:
. As a result: 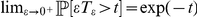 , for
, for 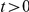 . Thus, as
. Thus, as  gets smaller, the time-separations between consecutive samples from the original urn resemble independent Exponential random variables with mean one. The black-urn can therefore be removed from the heuristic altogether by embedding samples from the original urn into a HPP with intensity one over the interval
gets smaller, the time-separations between consecutive samples from the original urn resemble independent Exponential random variables with mean one. The black-urn can therefore be removed from the heuristic altogether by embedding samples from the original urn into a HPP with intensity one over the interval 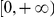 .
.
Simulating draws with replacement
To simulate draws with replacement using data already collected from an environment, produce a random permutation of the data. This can be accomplished with low-memory complexity using the discrete inverse transform method to simulate draws–without replacement–from a finite population [31].
Constants associated with optimal prediction intervals
To numerically approximate a pair of constants 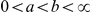 such that
such that 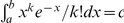 and
and 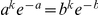 , where the integer
, where the integer 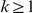 and the number
and the number 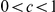 are given constants, introduce the auxiliary variable
are given constants, introduce the auxiliary variable 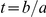 , and note that the later condition is fulfilled only when
, and note that the later condition is fulfilled only when 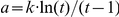 and
and 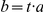 . Due to Newton's method, the sequence
. Due to Newton's method, the sequence 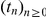 defined recursively as follows converges to the unique
defined recursively as follows converges to the unique  that satisfies the integrability condition, provided that
that satisfies the integrability condition, provided that 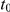 is chosen sufficiently close to
is chosen sufficiently close to  :
:
Proof of Inequality (3)
First notice that
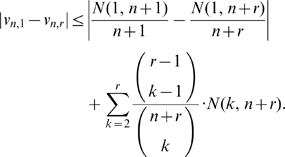 |
(13) |
To bound the first term on the right-hand side above, notice that 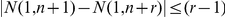 . As a result, since
. As a result, since 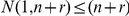 , we obtain that:
, we obtain that:
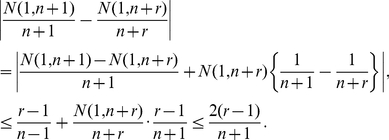 |
(14) |
On the other hand, to bound the second term on the right-hand side of equation (13), define the quantity 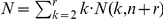 and notice that
and notice that 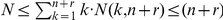 . Using that a weighted average is at most the largest of the terms averaged, we obtain that:
. Using that a weighted average is at most the largest of the terms averaged, we obtain that:
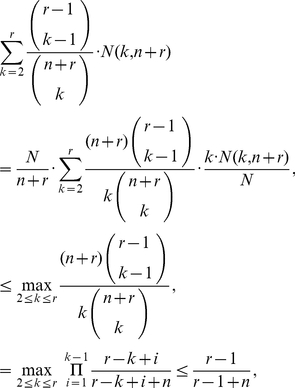 |
(15) |
where, for the last inequality, we have used that for each 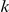 , the associated product is less or equal to the factor associated with the index
, the associated product is less or equal to the factor associated with the index 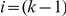 . Equation (3) is now a direct consequence of equations (13), (14) and (15).
. Equation (3) is now a direct consequence of equations (13), (14) and (15).
Proof of Theorem 1
In what follows, 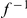 denotes the inverse function of
denotes the inverse function of 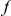 .
.
Define  to be the set of decreasing partitions of
to be the set of decreasing partitions of  i.e. vectors of the form
i.e. vectors of the form  , with
, with 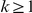 and
and 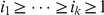 integers, such that
integers, such that  . To each possible sample
. To each possible sample 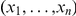 , let
, let 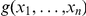 be the decreasing partition of
be the decreasing partition of  associated with the observed ranks in the sample.
associated with the observed ranks in the sample.
Define 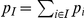 , for each set
, for each set  of colors. Part (i) in the theorem is equivalent to the existence of a function
of colors. Part (i) in the theorem is equivalent to the existence of a function 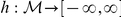 such that
such that
| (16) |
with probability one. This is because, in the non-parametric setting, the different colors in the urn carry no intrinsic meaning apart from being different. If there is a certain function  which satisfies condition (16) then
which satisfies condition (16) then 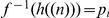 , for each color
, for each color  such that
such that 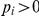 . In particular, the set
. In particular, the set 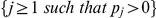 must be finite. Furthermore, if this set has cardinality
must be finite. Furthermore, if this set has cardinality 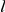 then
then 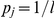 , for each color
, for each color 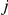 in the set; in particular,
in the set; in particular, 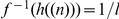 . Condition (ii) is therefore necessary for condition (i). Conversely, if condition (ii) is satisfied and the urn is composed by
. Condition (ii) is therefore necessary for condition (i). Conversely, if condition (ii) is satisfied and the urn is composed by 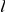 colors occurring in equal proportions then the function
colors occurring in equal proportions then the function 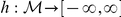 defined as
defined as 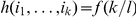 satisfies condition (16).
satisfies condition (16).
Proof of Theorem 2
Conditioned on the set 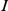 , and the random index
, and the random index  used in Step 3 of the Embedding algorithm,
used in Step 3 of the Embedding algorithm, 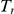 has a Gamma distribution with shape parameter
has a Gamma distribution with shape parameter  and scale parameter
and scale parameter  . However, because
. However, because  has a Negative Binomial distribution, conditioned on
has a Negative Binomial distribution, conditioned on 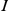 alone,
alone, 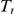 has Gamma distribution with shape parameter
has Gamma distribution with shape parameter  and scale parameter
and scale parameter 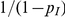 . In particular,
. In particular, 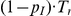 has probability density function
has probability density function 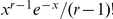 , for
, for 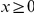 . From this, parts (i) and (iii) in the theorem are immediate. To show part (ii), notice first that
. From this, parts (i) and (iii) in the theorem are immediate. To show part (ii), notice first that 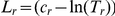 is conditionally unbiased for
is conditionally unbiased for 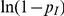 , where
, where
The second identity above is due to an integration by parts argument and only holds for 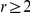 . However, since
. However, since 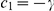 , we obtain that
, we obtain that 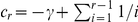 , for
, for 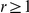 . This shows that
. This shows that 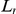 is conditionally unbiased for
is conditionally unbiased for 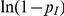 . To complete the proof of the theorem, notice that
. To complete the proof of the theorem, notice that 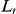 and
and 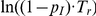 have the same variance. In particular,
have the same variance. In particular, 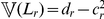 , where
, where
The last identity above holds only for 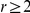 . Using that
. Using that 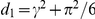 , we conclude that
, we conclude that 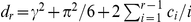 , for
, for 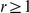 . As a result:
. As a result: 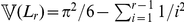 ; in particular, since
; in particular, since 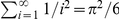 ,
, 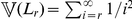 . The theorem is now a consequence of the following inequalities:
. The theorem is now a consequence of the following inequalities:
Proof of Equation (8)
Let 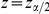 and assume that
and assume that 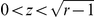 . Observe that:
. Observe that:
The factor multiplying the previous integral is an increasing function of  ; in particular, due to Stirling's formula, it is bounded by
; in particular, due to Stirling's formula, it is bounded by  from above. Furthermore, from section 6.1.42 in [32], it follows that
from above. Furthermore, from section 6.1.42 in [32], it follows that
On the other hand, if one rewrites the integrand of the previous integral in an exponential-logarithmic form and uses that 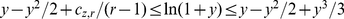 , for all
, for all 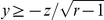 , where
, where
one sees that
All together, these inequalities imply that
from which the result follows.
Proof of Theorem 3
Due to the Central Limit Theorem, if 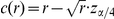 and
and 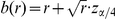 then
then
As a result, for all  sufficiently large,
sufficiently large, 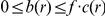 , and the integral on the left-hand side above is greater than or equal to
, and the integral on the left-hand side above is greater than or equal to  . Fix any such
. Fix any such  . Since the value of the associated integral may be decreased continuously by increasing the parameter
. Since the value of the associated integral may be decreased continuously by increasing the parameter 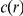 , there is
, there is 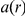 such that
such that 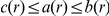 and
and
Define 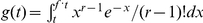 , for
, for  . Since
. Since 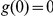 and, because
and, because 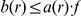 ,
, 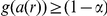 , the continuity of
, the continuity of 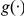 implies that there is
implies that there is 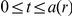 such that
such that 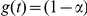 . Selecting
. Selecting  and
and 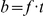 shows the theorem.
shows the theorem.
Proof of Theorem 4
The proof is based on a coupling argument. First observe that one can define on the same probability space random variables 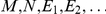 such that (1)
such that (1) 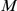 and
and 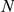 have Negative Binomial distributions with parameters
have Negative Binomial distributions with parameters 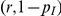 , but with
, but with 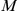 conditioned to be less than or equal to
conditioned to be less than or equal to 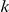 ; (2)
; (2) 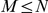 but
but 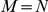 when
when 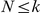 ; and (3)
; and (3) 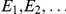 are independent Exponentials with mean
are independent Exponentials with mean  and independent of
and independent of 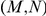 .
.
Let 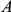 be the event “
be the event “ balls with colors outside
balls with colors outside 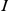 are observed in the next
are observed in the next 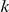 draws from the urn”. Conditioned on
draws from the urn”. Conditioned on 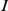 , we have that
, we have that 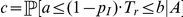 and
and 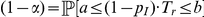 . As a result:
. As a result:
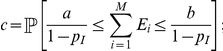 |
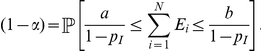 |
Since 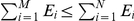 , and because
, and because 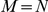 when
when 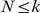 , we obtain that
, we obtain that
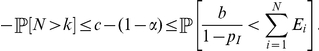 |
From this, the upper-bound in part (i) and both inequalities in part (ii) follow after noticing that 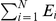 has a Gamma distribution with shape parameter
has a Gamma distribution with shape parameter  and scale parameter
and scale parameter 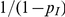 . To show the lower-bound in (i), we again notice that
. To show the lower-bound in (i), we again notice that 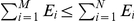 . In particular, if
. In particular, if 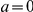 then
then
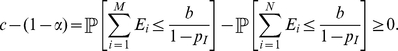 |
Proof of Equations (10) and (11)
Consider random variables  and
and 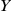 and a random vector
and a random vector 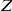 , defined on a same probability space. Assume that
, defined on a same probability space. Assume that 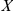 is square-integrable and conditionally unbiassed for
is square-integrable and conditionally unbiassed for 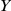 given
given 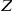 i.e.
i.e. 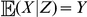 . Furthermore, assume that
. Furthermore, assume that 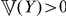 hence
hence 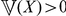 . Because
. Because 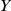 is also square-integrable and
is also square-integrable and 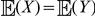 , we obtain that
, we obtain that
Hence 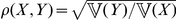 .
.
Equation (10) follows by considering 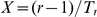 ,
, 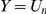 and
and 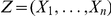 . Similarly, equation (11) follows by considering
. Similarly, equation (11) follows by considering 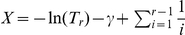 and
and 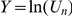 .
.
Proof of Inequality (12)
First note that
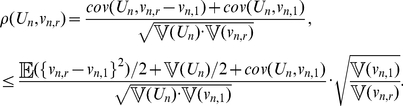 |
(17) |
Now observe that 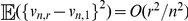 because of inequality (13), which implies that
because of inequality (13), which implies that 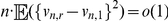 because
because 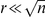 . On the other hand, because Robbins' and Starr's estimators are both unbiased for
. On the other hand, because Robbins' and Starr's estimators are both unbiased for 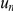 , we have
, we have 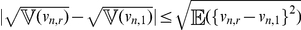 . Furthermore, according to the proof of Theorem 2 in [21],
. Furthermore, according to the proof of Theorem 2 in [21], 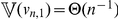 , therefore
, therefore
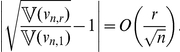 |
As a result, 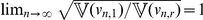 . Inequality (12) is now a direct consequence of inequality (17), and the next identities [21]:
. Inequality (12) is now a direct consequence of inequality (17), and the next identities [21]:
Acknowledgments
We would like to thank three anonymous referees for their careful reading of our manuscript and their numerous suggestions, which were incorporated in this final version. The authors are also thankful to R. Knight for contributing to an early version of the code, implementing some of the analyses, and commenting on the manuscript.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: M. Lladser was partially supported by NASA ROSES NNX08AP60G and NIH R01 HG004872. R. Gouet was supported by FONDAP, BASAL-CMM and Fondecyt 1090216. J. Reeder was supported by a post-doctoral scholarship from the German Academic Exchange Service (DAAD). M. Lladser and R. Gouet are thankful to the project Núcleo Milenio Información y Aleatoriedad, which facilitated a research visit to collaborate in person. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Sogin ML, Morrison HG, Huber JA, Welch DM, Huse SM, et al. Microbial diversity in the deep sea and the underexplored \rare biosphere”. Proc Natl Acad Sci USA. 2006;103:12115–12120. doi: 10.1073/pnas.0605127103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hughes JB, Hellmann JJ, Ricketts TH, Bohannan BJ. Counting the uncountable: statistical approaches to estimating microbial diversity. Appl Environ Microbiol. 2001;67:4399–4406. doi: 10.1128/AEM.67.10.4399-4406.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schloss PD, Handelsman J. Status of the microbial census. Microbiol Mol Biol Rev. 2004;68:686–691. doi: 10.1128/MMBR.68.4.686-691.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Curtis TP, Head IM, Lunn M, Woodcock S, Schloss PD, et al. What is the extent of prokaryotic diversity? Phil Trans R Soc Lond. 2006;361:2023–2037. doi: 10.1098/rstb.2006.1921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Roesch LF, Fulthorpe RR, Riva A, Casella G, Hadwin AK, et al. Pyrosequencing enumerates and contrasts soil microbial diversity. Isme J. 2007;1:283–290. doi: 10.1038/ismej.2007.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hong SH, Bunge J, Jeon SO, Epstein SS. Predicting microbial species richness. Proc Natl Acad Sci USA. 2006;103:117–122. doi: 10.1073/pnas.0507245102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Quince C, Curtis TP, Sloan WT. The rational exploration of microbial diversity. Isme J. 2008;2:997–1006. doi: 10.1038/ismej.2008.69. [DOI] [PubMed] [Google Scholar]
- 8.Turnbaugh PJ, Hamady M, Yatsunenko T, Cantarel BL, Duncan A, et al. A core gut microbiome in obese and lean twins. Nature. 2007;457:480–484. doi: 10.1038/nature07540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fierer N, Lauber CL, Zhou N, McDonald D, Costello EK, et al. Forensic identification using skin bacterial communities and/or references within. Proc Natl Acad Sci USA. 2010;107:6477–6481. doi: 10.1073/pnas.1000162107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Magurran AE. Measuring Biological Diversity. Oxford - Blackwell; 2004. [DOI] [PubMed] [Google Scholar]
- 11.Burnham KP, Overton WS. Estimation of the size of a closed population when capture probabilities vary among animals. Biometrika. 1978;65:625–633. [Google Scholar]
- 12.Chao A. Nonparametric estimation of the number of classes in a population. Scand J Stat. 1984;11:265–270. [Google Scholar]
- 13.Chao A. Estimating the population size for capture-recapture data with unequal catchability. Biometrics. 1897;43:783–791. [PubMed] [Google Scholar]
- 14.Mao CX, Lindsay BG. Estimating the number of classes. Ann Stat. 2007;35:917–930. [Google Scholar]
- 15.Bunge J, Fitzpatrick M. Estimating the number of species: A review. J Am Stat Assoc. 1993;88:364–373. [Google Scholar]
- 16.Hinsley F, Stripp A. Codebreakers: The Inside Story of Bletchley Park. Oxford Univ. Press; 1993. [Google Scholar]
- 17.Finch SJ, Mendell NR, Thode HC., Jr Probabilistic measures of adequacy of a numerical search for a global maximum. J Am Stat Assoc. 1989;84:1020–1023. [Google Scholar]
- 18.Mao CX. Predicting the conditional probability of discovering a new class. J Am Stat Assoc. 2004;99:1108–1118. [Google Scholar]
- 19.Good IJ. The population frequencies of species and the estimation of population parameters. Biometrika. 1953;40:237–264. [Google Scholar]
- 20.Robbins HE. On estimating the total probability of the unobserved outcomes of an experiment. Ann Math Stat. 1968;39:256–257. [Google Scholar]
- 21.Starr N. Linear estimation of the probability of discovering a new species. Ann Stat. 1979;7:644–652. [Google Scholar]
- 22.Clayton MK, Frees EW. Nonparametric estimation of the probability of discovering a new species. J Am Stat Assoc. 1987;82:305–311. [Google Scholar]
- 23.Esty WW. A Normal limit law for a nonparametric estimator of the coverage of a random sample. Ann Statist. 1983;11:905–912. [Google Scholar]
- 24.Aldous D. Probability Approximations via the Poisson Clumping Heuristic. Springer-Verlag; 1988. [Google Scholar]
- 25.Mahmoud HM. Sorting: A Distribution Theory. Wiley-Interscience; 2000. [Google Scholar]
- 26.Hwang HK, Janson S. Local limit theorems for finite and infinite urn models. Ann Probab. 2008;36:992–1022. [Google Scholar]
- 27.Mao CX, Lindsay BG. A poisson model for the coverage problem with a genomic application. Biometrika. 2002;89:669–681. [Google Scholar]
- 28.Durrett R. Essentials of stochastic processes. Springer Texts in Statistics; 1999. [Google Scholar]
- 29.Turnbaugh PJ, Ridaura VK, Faith JJ, Rey FE, Knight R, et al. The e_ect of diet on the human gut microbiome: A metagenomic analysis in humanized gnotobiotic mice. Sci Transl Med. 2009;1:6ra14. doi: 10.1126/scitranslmed.3000322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fierer N, Hamady M, Lauber CL, Knight R. The influence of sex, handedness, and washing on the diversity of hand surface bacteria. Proc Natl Acad Sci USA. 2008;105:17994–17999. doi: 10.1073/pnas.0807920105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ross SM. Simulation. Academic Press, third edition; 2002. [Google Scholar]
- 32.Abramowitz M, Stegun IA. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, ninth Dover printing, tenth GPO printing edition; 1964. [Google Scholar]