Influence of tissue metabolism and capillary oxygen supply on arteriolar oxygen transport: a computational model

Abstract

We present a theoretical model for steady-state radial and longitudinal oxygen transport in arterioles containing flowing blood (plasma and red blood cells) and surrounded by living tissue. This model combines a detailed description of convective and diffusive oxygen transport inside the arteriole with a novel boundary condition at the arteriolar lumen surface, and the results provide new mass transfer coefficients for computing arteriolar O₂ losses based on far-field tissue O₂ tension and in the presence of spatially distributed capillaries. A numerical procedure is introduced for calculating O₂ diffusion from an arteriole to a continuous capillary-tissue matrix immediately adjacent to the arteriole. The tissue O₂ consumption rate is assumed to be constant and capillaries act as either O₂ sources or sinks depending on the local O₂ environment. Using the model, O₂ saturation (SO₂) and tension (PO₂) are determined for the intraluminal region of the arteriole, as well as for the extraluminal region in the neighbouring tissue. Our model gives results that are consistent with available experimental data and previous intraluminal transport models, including appreciable radial decreases in intraluminal PO₂ for all vessel diameters considered (12–100µm) and slower longitudinal decreases in PO₂ for larger vessels than for smaller ones, and predicts substantially less diffusion of O₂ from arteriolar blood than do models with PO₂ specified at the edge of the lumen. The dependence of the new mass transfer coefficients on vessel diameter, SO₂ and far-field PO₂ is calculated allowing their application to a wide range of physiological situations. This novel arteriolar O₂ transport model will be a vital component of future integrated models of microvascular regulation of O₂ supply to capillary beds and the tissue regions they support.

1. INTRODUCTION

Longitudinal PO₂ gradients have been reported for arterioles by Duling and Berne [1], and it has been suggested that precapillary oxygen losses in the microcirculation might play an important role in the local regulation of blood flow by affecting the inlet capillary PO₂ thus altering capillary-tissue O₂ exchange. It has been observed that oxygen levels in the blood can diminish by up to two-thirds along the arteriolar tree before entering the capillary bed. Although it is not fully understood why this happens, Ellsworth and Pittman [2] have provided evidence that some of the O₂ leaving the arterioles diffuses to erythrocytes flowing through nearby capillaries resulting in an increase in their O₂ saturation. There have been very few experiments to measure PO₂ longitudinal changes along arterioles themselves and PO₂ radial changes in and around arterioles. New state-of-the-art PO₂ measurements have been made in the hamster cheek pouch microcirculation using an automated system based on phosphorescence quenching (Bertuglia et al. [3]). A 7% drop in hemoglobin O₂ saturation (SO₂) was measured along an arteriole of 500 microns as well as significant PO₂ drops across the vessel wall and into 100 µm of tissue. Such oxygen losses in arterioles have also been shown experimentally by Carvalho and Pittman [4]. Although it is clear that arterioles are losing substantial amounts of oxygen by diffusion, obtaining details of radial oxygen variations inside arterioles remains a challenge despite these recent experimental advances.

The present work is motivated by a desire to understand the role played by arterioles in both delivering O₂ and controlling the O₂ supply distribution. As noted above, arterioles can deliver O₂ to tissue by diffusion as well as deliver O₂ to smaller vessels by convection. Arterioles are also the site where the local blood flow (and hence O₂) distribution is regulated through dynamic changes in diameters and flow resistance [5]. One of the mechanisms for microvascular blood flow regulation that is under current investigation depends on the oxygen saturation-dependent release by red blood cells (RBCs) of the signaling molecule ATP [6]. Increased RBC ATP release due to decreased O₂ saturation results in a vasodilation signal that conducts upward through the microvascular tree. This signal can originate in arterioles, capillaries or venules. The regulation system has been modeled using a radially-averaged description of O₂ and ATP transport [7]; however, there are details of the system that remain to be investigated and require inclusion of both radial and longitudinal variations as well as time-dependent changes. Therefore, it is of interest to develop a realistic model of O₂ transport from an arteriole to the surrounding tissue that can be used to study diffusive delivery of O₂ and also oxygen-based flow regulation in microvascular networks which requires accurate and efficient estimates of O₂ loss from arterioles.

Popel and Gross [8] presented a mathematical model of oxygen transport in the precapillary microcirculation. This model, which included a continuum description of the role of capillaries as sinks/sources in the surrounding tissue, was used to simulate oxygen distributions in arterioles of the hamster cheek pouch. Theoretical predictions of transmural and longitudinal oxygen tension (PO₂) gradients were in qualitative agreement with experimental data. Subsequently, a mathematical model was developed by Weerappuli and Popel [9] to study the effect of capillary convection on oxygen transport around arterioles that are surrounded by capillaries. These capillaries carry unidirectional flow perpendicular to the arteriole. A convection equation describing the steady-state oxygen tension in the tissue was solved numerically in polar coordinates. From these numerical results a prediction of longitudinal gradients of hemoglobin-oxygen saturation along arterioles and venules was obtained. Although the previous two models did investigate the role of tissue properties on O₂ diffusion from arterioles, they did not include radial variations in intraluminal O₂.

In considering O₂ transport from arterioles, radial variations in intraluminal O₂ are important for two reasons. First, radial O₂ gradients inside an arteriole imply an inherent resistance to diffusive transport of O₂ from the vessel. Krogh’s original model of capillary-tissue O₂ transport [10], for example, does not consider intraluminal resistance. However, this resistance is now known to be important in determining O₂ losses from capillaries and has been calculated using a detailed intracapillary model [11]. Intraluminal resistance is similarly important in determining O₂ losses from arterioles [12]. The second reason that radial variations in intraluminal O₂ are important is that they determine the PO₂ environment in and around the vessel, which can affect the function of RBCs (as described above) and other cells (e.g., endothelial and smooth muscle).

To assess intraluminal resistance in arterioles, Hellums and co-workers [13,14,15] have developed a model for intraluminal oxygen transport in arteriole-size vessels (‘large capillaries’), where the vessel is considered to be embedded in a thin film of silicone rubber in order to match an in vitro experimental system [16, 17]. The model takes into account convection of plasma and RBCs in a cell-rich region together with a thin cell-free region of plasma. The model contains four coupled partial differential equations describing diffusion of free O₂ in the cell-free layer, in the plasma surrounding RBCs, and in RBCs, and diffusion of hemoglobin-bound O₂ in RBCs. Three of these equations are non-linear because of the slope of the oxyhemoglobin dissociation curve. These equations have a term defined as the reaction rate, which is the rate of oxygen dissociation from hemoglobin per unit volume of RBC. Since no hemoglobin escapes from the RBCs, the total heme concentration within the RBC remains constant. The convective terms have plasma and RBC velocity profiles together with a radial distribution of hematocrit. In simulating the experimental results of Boland et al. [16], transport in the silicone rubber phase is incorporated as a boundary condition at the capillary wall as described by Lemon et al. [17].

Using an intravascular O₂ transport model similar to that of Nair [13], Chen et al. [18] solved the coupled mass transport equations for O₂ and NO (nitric oxide) to determine their distribution inside the lumen of an arteriole and in the surrounding tissue. The purpose of this investigation was to study the effect of RBCs near the arteriole wall on NO and O₂ transport. Results were computed at the middle of a 250 micron long arteriole (15 micron luminal diameter) and showed a change in intravascular PO₂ of ~10 mmHg from the centerline to the plasma-RBC core interface. The effect of the presence or absence of RBCs near the endothelium was studied while varying the endothelial surface layer and plasma layer thicknesses. Chen et al. [19] investigated the co-transport of NO and O₂ in an arteriole–venule pair surrounded by capillary-perfused tissue. Their O₂ transport results suggested that the capillary bed around the paired arteriole and venule could significantly facilitate release of O₂ into the surrounding tissue. However, as in [18], their assumptions were such that tissue PO₂ rapidly fell to zero away from the arteriole-venule pair due to the absence of an independent capillary O₂ supply. Similarly, the model of arteriolar NO-O₂ transport described by Gundersen et al. [20] did not contain a realistic model of capillary-supplied tissue. Therefore, while these models provided new insights into intraluminal transport of NO and O₂, they did not adequately consider the effect of the surrounding tissue.

In this paper, we utilize the simplified model of Nair et al. [13] describing the intraluminal problem of oxygen transport in an arteriole containing a RBC-rich core with a plasma sleeve region joined to it. In this model, the four partial differential equations describing free and hemoglobin-bound O₂ transport [14] are reduced to one non-linear equation and one linear equation by: (1) assuming chemical equilibrium within the RBCs between oxygen and oxyhemoglobin, and (2) neglecting intracellular and extracellular boundary layer resistances. Here we consider the same nonlinear partial differential equation (PDE) used by Nair et al. [13] to describe O₂ transport in the RBC-rich core (see also Hellums et al. [12]) together with a steady-state convection-diffusion equation describing O₂ transport in the cell-free plasma region. A novel solution is presented for the oxygen transport from such an arteriole to a continuous capillary-tissue matrix immediately adjacent to the arteriole. The transport of oxygen in the capillary-tissue matrix is described in a similar fashion to [8] and [21]. As discussed by Goldman [21], oxygen transport in oxygen-consuming capillary-perfused tissue differs from transport by pure diffusion. Therefore, the use of a capillary-tissue matrix outside the arteriole provides a more realistic boundary condition than would alternative assumptions such as fixed PO₂ or O₂ flux on the boundary of the lumen, or the use of a purely diffusive medium surrounding the arteriole with specified far-field boundary conditions.

For the capillary-tissue matrix, a one-dimensional (1D) reaction-diffusion equation in cylindrical coordinates is presented that models oxygen delivery by capillaries and oxygen diffusion and consumption. The tissue O₂ consumption rate is assumed to be constant, and a PO₂-dependent description is given of the dual role of capillaries as sources and sinks. A steady-state analytical solution is presented which we incorporate via a boundary condition in the intraluminal problem involving the arteriole itself. The governing equation for oxygen transport in the arteriole is solved numerically in cylindrical coordinates using a Crank-Nicholson algorithm, and the solution includes parameters needed in the analytical solution describing oxygen transport in the tissue.

It is important to know to what extent such factors as blood flow rate, vascular diameter, and tissue PO₂ influence both longitudinal and radial PO₂ gradients in arterioles. The model presented here can be solved to determine saturation along the length of an arteriole with prescribed PO₂ values at the inlet of the vessel and in the tissue far from the vessel. In this paper, we first present the governing equations of oxygen transport in arterioles and then develop the boundary condition used for the capillary-tissue matrix. Next we describe a numerical procedure using the Crank-Nicholson method to solve the coupled arteriole-tissue problem and present verification of our intraluminal transport model. Finally, we present results for longitudinal and radial changes in arteriolar O₂ and arteriole-tissue mass transfer coefficients for O₂ obtained with our model, and discuss our results in the context of available experimental data and related models.

2. MATHEMATICAL MODEL

2.1 Intraluminal Oxygen Transport

The geometry of the present mathematical model is shown in Figure 1. The intravascular model considers a core region (r < R_r) containing a mixture of plasma and RBCs surrounded by a cell-free plasma layer (R_r < r < R_c) of thickness δ = R_c − R_r. The extravascular model considers a tissue layer (r> R_c) containing a continuous distribution of capillaries.

Figure 1.

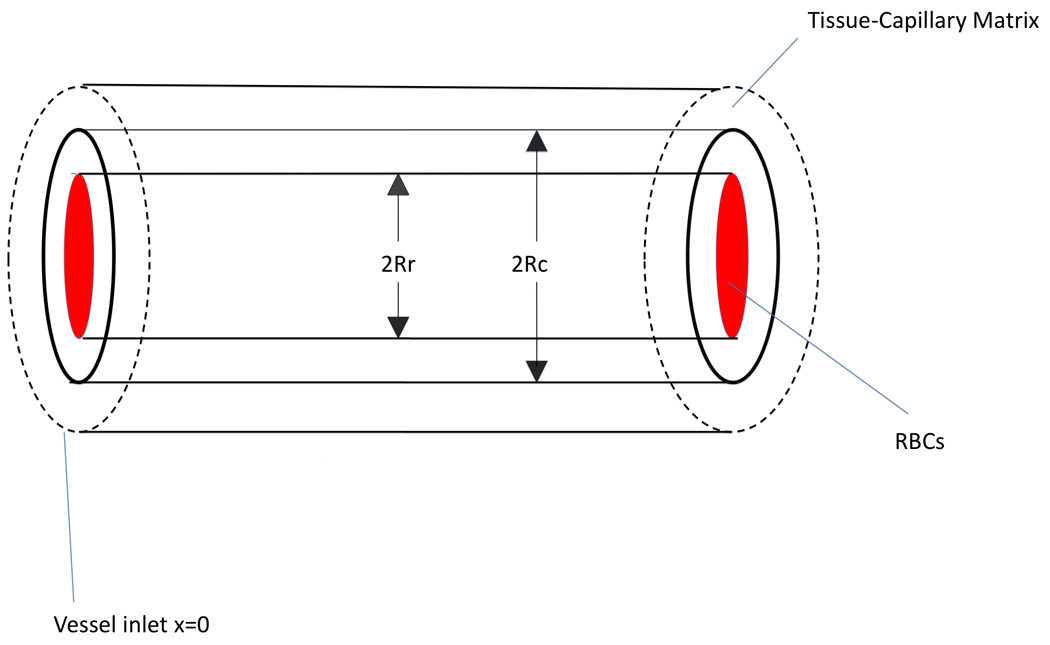
Geometry of mathematical model used.

The equations governing oxygen transport in the arteriole are [12]:

$$[(1-h(r))V_p(r)+\frac{{\alpha }_{\mathit{\text{rbc}}}}{{\alpha }_p}h(r)V_{\mathit{\text{rbc}}}(r)(1+\frac{{\mathit{\text{Hb}}}_T}{{\alpha }_{\mathit{\text{rbc}}}}\frac{\mathit{\text{dS}}}{\mathit{\text{dP}}})]\frac{\mathit{\partial }P}{\mathit{\partial }x}=D_p\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}[r\frac{\mathit{\partial }P}{\mathit{\partial }r}],0\le r\le R_r$$ (1a)

$$\begin{array}{cc}{V}_p^{\text{'}}\frac{\mathit{\partial }P}{\mathit{\partial }x}=D_p\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left[r\frac{\mathit{\partial }P}{\mathit{\partial }r}\right]\hfill & R_r\le r\le R_c\hfill \end{array}$$ (1b)

where the subscript ‘p’ denotes values in the plasma and the subscript ‘rbc’ denotes values in the RBCs. The term $\frac{\mathit{\text{dS}}}{\mathit{\text{dP}}}$ is the slope of the oxyhemoglobin dissociation curve and is a nonlinear function of P (see Nair et al. [13]). This dissociation curve can be approximated by the Hill equation:

$$S(P)=\frac{P^n}{P_{50}^n+P^n}$$ (2)

where n is an empirical constant and P₅₀ is the oxygen tension that yields S = 0.5. Hb_T is the total heme concentration which is equal to four times the hemoglobin concentration due to the fact that there are four heme groups on each hemoglobin molecule. D_p is the O₂ diffusion coefficient in plasma and has units of cm²/s, and α_rbc and α_p are the solubilities of O₂ in the RBCs and plasma, respectively, and have units of M/mmHg. Differentiating the Hill equation with respect to P gives the following equation

$$\frac{\mathit{\text{dS}}}{\mathit{\text{dP}}}=\frac{n{P}_{50}^n{P}^{n-1}}{{(P_{50}^n+P^n)}^2}$$ (3)

As a result of (3), the governing equation for PO₂ becomes a nonlinear parabolic partial differential equation.

The functions $h(r),V_p(r),V_p^{\text{'}}(r)$, and V_rbc(r) in Equation (1a) are now defined. It is assumed that there are many RBCs at any cross-section of the arteriole. The distribution of RBCs is such that hematocrit is higher at the center of the arteriole and lower near the wall. The RBC distribution given by Nair et al. [14] is

$$\begin{array}{cc}h(r)=h_m\left(1-\frac{r^m}{R_r^m}\right),\hfill & 0\le r\le R_r\hfill \\ h(r)=0,\hfill & R_r\le r\le R_c\hfill \end{array}$$ (4)

where we determine the constants h_m and m in the Appendix.

Convective transport in the cell-free (plasma) and cell-rich (RBCs) regions involves specific assumed velocity profiles. These are given as the following parabolic profiles [14]:

$$\begin{array}{cc}{V}_p^{\text{'}}=a\left(1-\frac{r^2}{R_c^2}\right),\hfill & R_r\le r\le R_c\hfill \\ V_p=b\left(1-\mathit{\text{Bl}}\frac{r^2}{R_c^2}\right),\hfill & 0\le r\le R_r\hfill \end{array}$$ (5)

where the velocity in the cell-rich region is a slight deviation from Poiseuille flow represented by the blunting factor Bl. Finally, the velocity of the RBCs is given as

$$\begin{array}{cc}{V}_{\mathit{\text{rbc}}}(r)=b(1-\mathit{\text{slp}})\left(1-\mathit{\text{Bl}}\frac{r^2}{R_c^2}\right),\hfill & 0\le r\le R_c\hfill \end{array}$$ (6)

where slp is called the slip velocity.

In reference [14] a method is described for determining the parameters a, b, h_m, and m but specific values for these parameters are not given. In the Results section we give values for a, b, h_m, and m which are obtained using Maple to solve four equations in four unknowns. The four equations (shown in Appendix) represent continuity of plasma velocities given by Equation (5) at r = R_r, overall RBC mass balance using the discharge hematocrit, overall plasma mass balance, and the tube hematocrit. In the present model, blood flow is scaled according the vessel cross-section $(\propto R_c^2)$ so that velocity is approximately constant for all vessel sizes (1.10–1.14 cm/s at the centreline).

Equations (1a)–(1b) require one boundary condition in x and two in r. For the boundary condition in x, we specify a constant inlet PO₂ at x =0: P(0, r)=P_in. The first boundary condition in r is zero flux at r =0: ∂P/∂r=0. For the second boundary condition in r, rather than specify PO₂ at the lumen surface (r = R_c), we require that intraluminal PO₂ match an analytical solution describing O₂ transport in the surrounding tissue.

2.2 Tissue Boundary Condition

We now consider a model of radial O₂ transport in tissue that can be solved analytically to obtain a boundary condition for the preceding intraluminal transport problem. This steady state 1D model of tissue PO₂ is given by the following [21]

$$D_t\left(\frac{{\mathit{\partial }}^{2}P}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }P}{\mathit{\partial }r}\right)-\frac{1}{\alpha }{M}_0+\kappa \left(1-\frac{P}{P^{*}}\right)=0$$ (7)

where D_t and α are the tissue O₂ diffusion coefficient and solubility respectively (units of cm²/s and M/mmHg), M₀ is the local O₂ consumption rate (units of M/s), P^* is the average capillary PO₂, and κ is a constant that depends on the capillary mass transfer coefficient and density and represents the average flux of O₂ for a given difference between tissue (P) and capillary (P^*) PO₂. Note that this model does not consider O₂ diffusion in the tissue in the direction parallel to the vessel (i.e., in x).

Equation (7) can be put in the form

$$D_t\left(\frac{{\mathit{\partial }}^{2}P}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }P}{\mathit{\partial }r}\right)+A-\mathit{\text{BP}}=0$$ (8a)

$$\text{where}A=\kappa -\frac{M_0}{\alpha }\text{ and }B=\frac{\kappa }{P^{*}}$$ (8b)

A is assumed positive [21] and represents the balance between capillary O₂ supply and tissue O₂ consumption when P = 0 (maximum O₂ flux into the tissue), while B determines how O₂ flux into the tissue decreases for P > 0.

Equation (8a) is solved subject to the boundary conditions at the surface of the arteriole (r = R_c when a separate vessel wall is not considered) and far from the arteriole. These conditions are: P(R_c) = P_w and $P(r\to \mathrm{\infty })=\frac{A}{B}$. Implementing the boundary conditions at the surface of the arteriole and at infinity we get the solution

$$\begin{array}{cc}P(r)=\frac{A}{B}+\frac{P_w-\frac{A}{B}}{K_0(\sqrt{B/D_t}{R}_c)}{K}_0(\sqrt{B/D_t}r)\hfill & R_c\le r<\mathrm{\infty }\hfill \end{array}$$ (9)

where K₀ is the zeroth order modified Bessel function of the second kind.

We now use this solution to obtain the boundary condition at r = R_c for the intraluminal problem. We first solve Equation (1b) to define a boundary condition for Equation (1a). In [13], for essentially the same intravascular transport model used here, Nair et al. showed that neglecting convection in the cell-free layer did not alter O₂ transport results in comparison to a similar model [14] that included convective transport in the cell-free layer. Therefore, we assume that convective transport of O₂ in the region R_r ≤ r ≤ R_c is small relative to transport by diffusion and set $V_p^{\text{'}}(r)\frac{\mathit{\partial }P}{\mathit{\partial }x}$ to zero in Equation (1b). We then have the following equation and general solution in the cell-free region:

$$\frac{D_p}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left(r\frac{\mathit{\partial }P}{\mathit{\partial }r}\right)=0$$ (10)

$$P=A_1\text{ln}(r)+A_2$$ (11)

where A₁ and A₂ are constants to be determined and the gradient in the cell-free region is

$$\frac{\mathit{\partial }P}{\mathit{\partial }r}=\frac{A_1}{r}$$ (12)

Continuity of PO₂ values and fluxes at R_c and R_r gives

$$R_r:P=P_r,D_r{\alpha }_r\frac{\mathit{\partial }{P}_r}{\mathit{\partial }r}{|}_{R_r}={D_p{\alpha }_p\frac{\mathit{\partial }P}{\mathit{\partial }r}|}_{R_r}=D_p{\alpha }_p\frac{A_1}{R_r}$$ (13)

$$R_c:P=P_w,D_p{\alpha }_p\frac{\mathit{\partial }P}{\mathit{\partial }r}{|}_{R_c}=D_p{\alpha }_p\frac{A_1}{R_c}=D_t{\alpha }_t\frac{\mathit{\partial }{P}_t}{\mathit{\partial }r}{|}_{R_c}$$ (14)

where 't' subscripts denote tissue values, 'r' subscripts denote values in the cell-rich region, and P_w = P_t(R_c). This gives four equations in 4 unknowns, P_w,A₁,A₂,P_r(R_r):

$$A_1\text{ ln }{R}_c+A_2=P_w$$ (15)

$$A_1\text{ ln }{R}_r+A_2=P_r(R_r)$$ (16)

$$D_t{\alpha }_t\frac{\mathit{\partial }{P}_t}{\mathit{\partial }r}{|}_{R_c}=D_p{\alpha }_p\frac{A_1}{R_c}$$ (17)

$$D_r{\alpha }_r\frac{A_1}{R_r}=D_r{\alpha }_r\frac{\mathit{\partial }{P}_r}{\mathit{\partial }r}{|}_{R_r}=D_r{\alpha }_r\left(P_r(R_r)-P_r(R_r-\mathrm{\Delta }r)\right)/\mathrm{\Delta }r$$ (18)

Solving for A₁, using the derivative flux in Eq. (13), and differentiating P_t w.r.t. r gives an equation which can be solved for P_w.

$$\frac{\mathit{\partial }{P}_t}{\mathit{\partial }r}{|}_{R_c}=\left(P_w-\frac{A}{B}\right)\frac{K_0^{\prime }(\sqrt{B1}{R}_c)\sqrt{B1}}{K_0(\sqrt{B1}{R}_c)}$$ (19)

$$B1=\frac{B}{D_t}$$

From Equation (17)

$$\frac{D_t{\alpha }_t\left(P_w-\frac{A}{B}\right)K_0^{\prime }(\sqrt{B1}{R}_c)\sqrt{B1}}{K_0(\sqrt{B1}{R}_c)}=\frac{D_p{\alpha }_p(P_w-P_r(R_r))}{R_c\text{ ln }\left(\frac{R_c}{R_r}\right)}$$ (20)

Solving for P_w:

$$P_w=\frac{-\frac{D_p{\alpha }_p}{R_c}\frac{P_r(R_r)}{\text{ln}\left(\frac{R_c}{R_r}\right)}+\frac{D_t{\alpha }_t\frac{A}{B}{K}_0^{\prime }(\sqrt{B1}{R}_c)\sqrt{B1}}{K_0(\sqrt{B1}{R}_c)}}{D_t{\alpha }_t\frac{K_0^{\prime }(\sqrt{B1}{R}_c)\sqrt{B1}}{K_0(\sqrt{B1}{R}_c)}-\frac{D_p{\alpha }_p}{R_c\text{ ln }\left(\frac{R_c}{R_r}\right)}}$$ (21)

$$\frac{\mathit{\partial }P}{\mathit{\partial }r}{|}_{r=R_r}=\frac{P_w-P_r(R_r)}{R_r\text{ ln }\left(\frac{R_c}{R_r}\right)}=\frac{P_w-\frac{A_1}{R_r}\mathrm{\Delta }r-P_r(R_r-\mathrm{\Delta }r)}{R_r\text{ ln }\left(\frac{R_c}{R_r}\right)}$$ (22)

Equations (21) and (22) together define our tissue model boundary condition. This boundary condition is used in the numerical solution of Equation (1a) by means of the Crank-Nicholson method.

2.3 Inclusion of an Avascular Vessel Wall

Popel and Gross [8] have solved the problem of oxygen transport through an avascular oxygen-consuming wall surrounded by an external region of tissue described by Equation (8a). However, in [8] radial oxygen gradients inside the vessel were not considered. Therefore, we add a vessel wall to our model to determine its effect on oxygen transport. We have confirmed the analytical solutions of [8] (p.H682, Equation 3) for the case where the penetration depth given is $l_t=\sqrt{D_t/B}$, with B given by Equation (8b). An arteriole is considered with inner radius R_c, outer radius R_e (including the wall), and constant oxygen consumption M_w. The Fick equation is solved in the wall of the arteriole together with Equation (8a) in the tissue region. The PO₂ in the wall region (R_c ≤ r ≤ R_e) is then given by:

$$P_w(r)=\frac{A}{B}+\frac{\psi }{\varphi }[P_w-\frac{A}{B}+\theta +\frac{R_e^2{M}_w}{2D_w{\alpha }_w}\text{ ln }(\frac{R_c}{R_e}\left)\right]+\frac{R_e^2{M}_w}{2D_w{\alpha }_w}\text{ ln }{R}_e-\frac{M_w{R}_e^2}{4D_w{\alpha }_w}-\frac{R_e^2{M}_w}{2D_w{\alpha }_w}\text{ ln }r+\frac{M_w{r}^2}{4D_w{\alpha }_w}$$

where

$$\begin{array}{c}\psi =K_0(\sqrt{B/D_t}{R}_e)-R_e\frac{D_t{\alpha }_t}{D_w{\alpha }_w}\sqrt{B/D_t}{K}_1(\sqrt{B/D_t}{R}_e)\text{ ln }\left(\frac{r}{R_e}\right)\hfill \\ \varphi =K_0(\sqrt{B/D_t}{R}_e)-\sqrt{B/D_t}{R}_e\frac{D_t{\alpha }_t}{D_w{\alpha }_w}{K}_1(\sqrt{B/D_t}{R}_e)\text{ ln }\left(\frac{R_c}{R_e}\right)\hfill \\ \theta =\frac{M_w(R_e^2-R_c^2)}{4D_w{\alpha }_w}\hfill \end{array}$$

With the solution for P_w(r) shown we calculate the saturation by means of a similar approach as in Equation (21). Differentiating P_w(r) and using

$$D_t{\alpha }_t\frac{{\mathit{\text{dP}}}_w}{\mathit{\text{dr}}}{|}_{r=R_c}=D_p{\alpha }_p\frac{P_w-P_r(R_r)}{R_c\text{ ln }\left(\frac{R_c}{R_r}\right)},$$

P_w is obtained and the boundary condition is determined. We used this boundary condition numerically as in the vessel-tissue model described above.

3. NUMERICAL METHODS

3.1 Solution of Coupled Vessel-Tissue Problem

Discretizing Equation (1a) using the Crank-Nicholson (C-N) method as a function of radius distance r and longitudinal distance x gives the following system of algebraic equations:

$$P_{i,j+1}-P_{i,j}=\frac{1}{2{\Lambda }_{i,j}}\frac{D_p\mathrm{\Delta }x}{\mathrm{\Delta }{r}^2}[(1+\frac{1}{2i})P_{i+1,j+1}-2P_{i,j+1}+(1-\frac{1}{2i})P_{i-1,j+1}+(1+\frac{1}{2i})P_{i+1,j}-2P_{i,j}+(1-\frac{1}{2i})P_{i-1,j}]$$ (23)

where i = 1,2,…,N_r and j = 1,2,…,N_x, and N_r and N_x are the number of subdivisions in the radial and axial directions of the vessel, respectively. Also

$${\Lambda }_{i,j}=(1-h(r))V_p{|}_{r=r_i}+\frac{{\alpha }_{\mathit{\text{rbc}}}}{{\alpha }_p}h(r)V_{\mathit{\text{rbc}}}(r){|}_{r=r_i}(1+[{\mathit{\text{Hb}}}_T]\frac{{\mathit{\text{nP}}}_{i,j}^{n-1}{P}_{50}^n}{{(P_{50}^n+P_{i,j}^n)}^2{\alpha }_{\mathit{\text{rbc}}}})$$ (24)

The accuracy of finite-difference formulas for partial differential equations is usually characterized by the approximation order of the local truncation error as determined by Taylor expansions. The local truncation error of the C-N formula is O(Δx² + Δr²) where Δx and Δr are the finite-difference grid spacings in the x and r directions, respectively.

The left side of Equation 22 is approximated by a first-order formula for the derivative of P w.r.t. r:

$$P_{N+1}-P_N=\frac{\mathrm{\Delta }r(P_w-\frac{A_1}{R_r}{\mathrm{\Delta }}_r-P_N)}{R_r\text{ln}(\frac{R_c}{R_r})}$$ (25)

where for clarity we let N = N_r and suppress the second subscript on P_ij. Note that P_N+1 = P_r(R_r).

Simplifying the above we set:

$$\mathrm{\Xi }=D_t{\alpha }_t\frac{K_0^{\prime }(\sqrt{B1}{R}_c)\sqrt{B1}}{K_0(\sqrt{B1}{R}_c)}-\frac{D_p{\alpha }_p}{R_c\text{ln}(\frac{R_c}{R_r})}$$ (26)

$$\mathrm{\Gamma }=\frac{A}{B}\frac{K_0^{\prime }(\sqrt{B1}{R}_c)}{K_0(\sqrt{B1}{R}_c)}\sqrt{B1}$$ (27)

After a few steps we arrive at:

$$P_{N+1}=\frac{P_N(1-\frac{\mathrm{\Delta }r}{R_r\text{ ln }(\frac{R_c}{R_r})})+\frac{\mathrm{\Delta }r{D}_t{\alpha }_t\mathrm{\Gamma }}{\mathrm{\Xi }{R}_r\text{ ln }(\frac{R_c}{R_r})}-\frac{\mathrm{\Delta }{r}^2{D}_t{\alpha }_t\mathrm{\Gamma }}{\mathrm{\Xi }{R}_r^2{(\text{ln}(\frac{R_c}{R_r}))}^2}}{1+\frac{\frac{\mathrm{\Delta }r{D}_p{\alpha }_p}{R_c\text{ ln }(\frac{R_c}{R_r})}}{R_r\text{ ln }(\frac{R_c}{R_r})\mathrm{\Xi }}-\frac{\mathrm{\Delta }{r}^2{D}_p{\alpha }_p}{R_c{R}_r^2\text{ ln }{(\frac{R_c}{R_r})}^3\mathrm{\Xi }}-\frac{\mathrm{\Delta }{r}^2}{R_r^2{(\text{ln}(\frac{R_c}{R_r}))}^2}}$$ (28)

Equation (28) is the desired relation for the PO₂ at the edge of the cell-rich region of the vessel (r = R_r) in the discretization of Equation (1a). As shown by Osterby [22], the accuracy of the C-N method (23–24) subject to (28) will actually be first order since we have used a first-order formula for the derivative (25). To solve the system of algebraic equations for each j given by (23)–(24), we use the Thompson algorithm [23], Appendix B pp491].

3.2 Verification of Intraluminal Transport Model

As mentioned in the Introduction, Nair et al. [13] have provided a relatively simple model for accurate simulation of O₂ transport from blood flowing in vessels larger than ~0.0020 cm and have presented results for the case where the capillary is embedded in a thin film of silicone rubber. In that model, Equation (1a) is solved subject to the following boundary condition:

$$-D_p\frac{\mathit{\partial }P}{\mathit{\partial }r}{|}_{r=R_r}=\frac{-D_p[P_{\mathit{\text{ext}}}-P{|}_{r=R_r}]}{R_r[\gamma +\text{ln}(\frac{R_c}{R_r})]}$$ (29)

where $\gamma =\frac{D_p{\alpha }_{\mathit{\text{rbc}}}}{K}\text{ln}\left(\frac{4d}{\pi R_c}\right)$ and P_ext is the PO₂ in the gas surrounding a silicone rubber film [13 pp210]. K is the O₂ permeability of silicone rubber and d is the half thickness of silicone rubber film. The following parameter values have been chosen in accordance with Nair et al. [14]: α_rbc = 1.47 × 10⁻⁶M/mmHg, α_p = 1.33 × 10⁻⁶ M/mmHg, D_p = 2.75 × 10⁻⁵ cm²/s, and γ=0.1752.

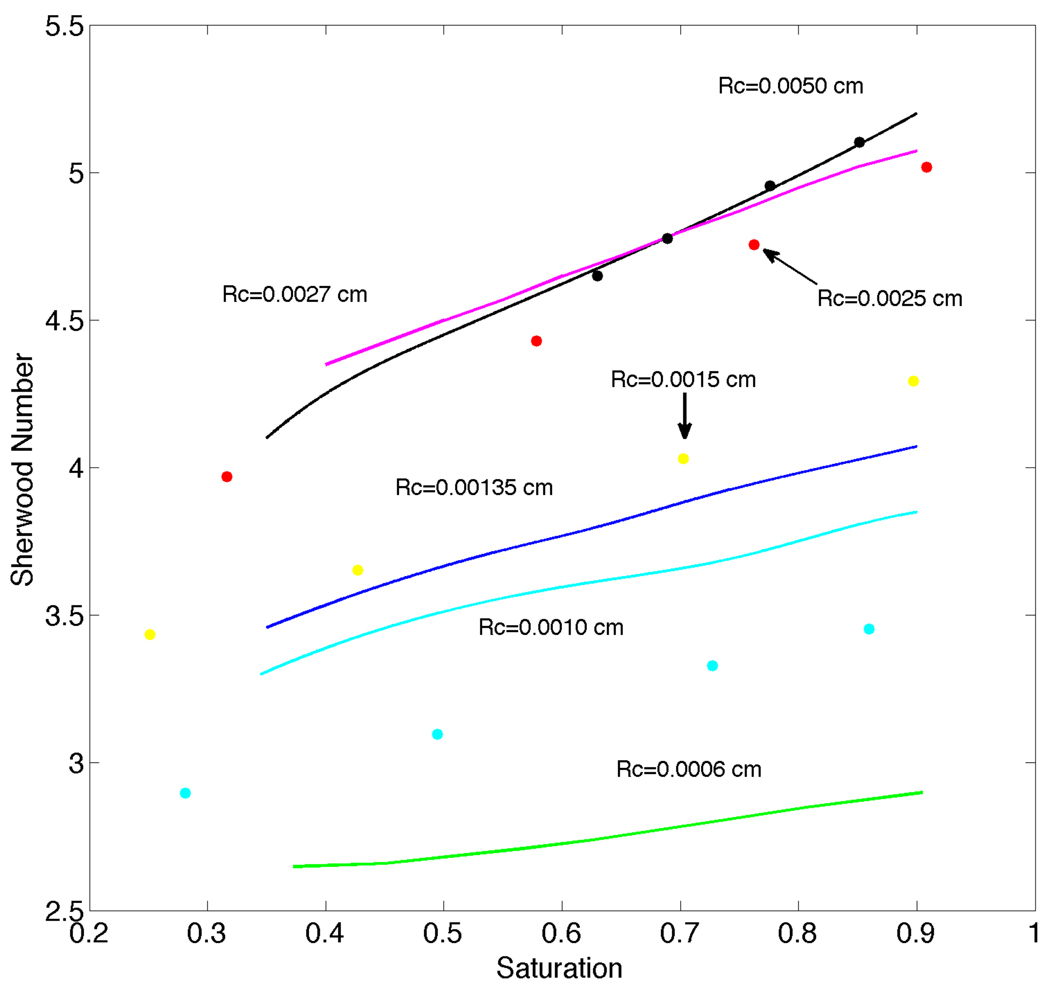
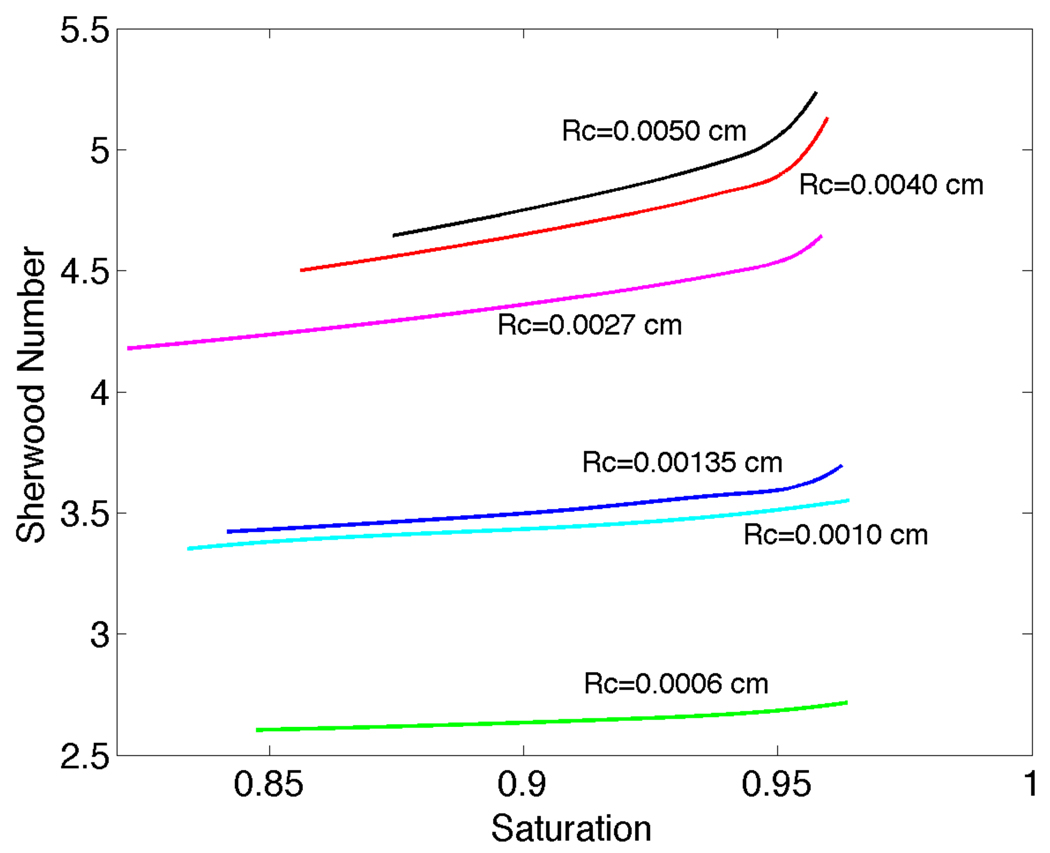
Our numerical results for the solution of Equation (1a) subject to the boundary condition (29) were obtained for both O₂ release (P_ext=0 mmHg, P_in=159.6 mmHg) and uptake (P_ext=159.6 mmHg, P_in=0). A volumetric flow rate of 3.33 × 10⁻⁶ml/s and a discharge hematocrit of 0.3 were used. Comparison of our results to those of Nair et al. [13: p.209 Figure 3] showed excellent agreement with calculated changes in intraluminal O₂ content (radially averaged SO₂) as a function of axial distance. We also found general agreement (especially for larger vessels, see Figure 2) with the Sherwood number (defined below and equivalent to the Nusselt number used in [12]) vs. O₂ saturation curves of Hellums et al. [12: p.14 Figure 13]. Figure 2 was obtained for near zero O₂ permeability of silicone rubber. The Sherwood number increases with increasing arteriole radius and for each radius the Sherwood number decreases with decreasing saturation. In addition, the plots of Sherwood number versus saturation have a greater slope as the radius of the arteriole increases. Based on these comparisons, we consider our intraluminal transport code validated and suitable for application to the main problem of interest in this paper, i.e., Equation (1a) subject to the boundary condition (28). Note that Nair et al. [13] verified their results by direct comparison to experimental measurements.

Figure 2.

Curves for Sherwood number versus saturation computed using the present intraluminal oxygen transport model with Dirichlet boundary conditions for R_c=0.0050, 0.0027, 0.00135, 0.0010 and 0.0006 cm. Filled circles show comparison results from Hellums et al. [12] for R_c=0.0050 (black), 0.0025 (red), 0.0015 (yellow) and 0.0010 cm (cyan). Differences in Sh for R_c≤0.0010 cm are believed to be due to the fixed plasma layer thickness (δ) in the present work vs. the variable layer thickness in [12].

4. RESULTS

4.1 Velocity and Hematocrit Profiles

We have solved the equations given in the Appendix to obtain m, h_m, a and b for the different vessel radii as shown in Table 1. For all of the radii we have used Bl = 0.9, in agreement with the in vitro values reported by Pittman and Ellsworth [24], and slp = 0.1 which was calculated for a single particle by Sinha [25]. The value δ =1.6µm is chosen to represent the upper end of the range used by Nair et al. [14]. As can be seen in Table 1, as the radius of the vessel increases from R_c = 0.0006cm to R_c = 0.0050cm the value of m increases, meaning that RBCs are more uniformly distributed across the vessel radius.

Table 1.

Hemodynamic parameters calculated from Appendix for H_D=0.3.

Rc (cm)	HT	m	hm	a	b
0.0006	0.2100	3.67	0.595	1.275	1.142
0.0010	0.2325	6.55	0.430	1.393	1.124
0.00135	0.2370	4.42	0.443	1.505	1.116
0.0027	0.2640	8.59	0.368	1.955	1.105
0.0040	0.2730	9.83	0.357	2.397	1.102
0.0050	0.2700	9.87	0.354	2.732	1.098

4.2 Other Parameters of the Model

To calculate the PO₂ distribution in the intravascular space, it is necessary to know all the parameters in the governing equation as well as those for the tissue model. The values of the intravascular parameters according to Nair et al. [14] are plasma O₂ diffusion coefficient D_p = 2.75 × 10⁻⁵ cm²/s, RBC O₂ solubility α_rbc = 1.47 × 10⁻⁶ M/mmHg, plasma O₂ solubility α_p = 1.33 × 10⁻⁶ M/mmHg, total heme concentration Hb_T = 5.35mM, P₅₀ = 27mmHg and n = 2.7 (values for human blood). At x = 0, P = P_in = 100mmHg.

The tissue parameters used are: α_t = 1.53 × 10⁻⁶ M/mmHg M₀ = 5.91 × 10⁻⁶ M/s, and D_t = 2.41 × 10⁻⁵ cm²/s in accordance with Vadappalli et al. [26]. In Equation (8b), A = 26.14 and B = 0.625 [21]. Therefore, in the tissue far from the vessel we have PO₂ = A / B = 41.8 mmHg. Note that $\sqrt{B/D_t}$ determines how quickly the far-field PO₂ value is reached. Taking luminal surface PO₂ (P_w) and far-field PO₂ (A/B) to be free parameters, we have found that the tissue PO₂ distributions measured in [27] near 10–20µm arterioles are generally well-matched by the tissue model with $\sqrt{B/D_t}$; 160. This is the same value given by our above choices for D_t and B, providing additional support for the parameters used in our tissue model.

4.3 Oxygen Transport Calculations

Using Equation (28) in Equations (23)–(24), we have verified first-order convergence in Δr for R_c = 0.0010cm and x=0.05cm using N_x = 8000 and N_r = 80, 160,…, 5120, 8000. We have also verified convergence in Δx using N_r =160 and N_x = 4000, 8000,…, 128000. Based on these convergence tests, we have used Δx=10⁻⁵cm (giving N_x = 40000 when x=0.4cm) and N_r = 160 to obtain the results below.

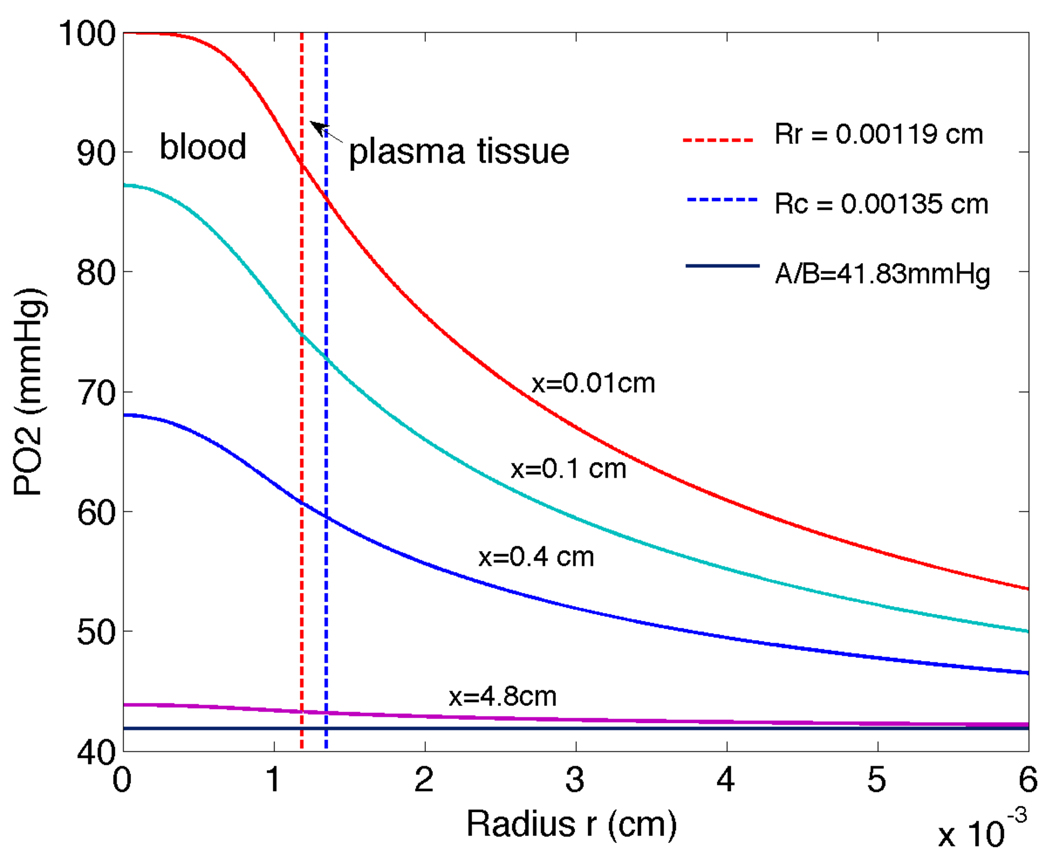
A plot of oxygen tension through the three layers considered (RBC core, plasma, tissue) is shown in Figure 3. Four distances downstream are shown: x=0.01cm, 0.1cm, 0.4cm and 4.8cm. In all cases it is clear that PO₂ decreases through the layers towards the far-field value A / B as r increases.

Figure 3.

Radial PO₂ (oxygen tension) changes through intravascular-plasma-tissue regions for vessel with R_c=0.00135cm at four axial distances downstream of entrance: x=0.01, 0.1, 0.4, 4.8cm. Results were computed using the tissue model boundary condition with P_∞=A/B=41.8mmHg.

PO₂ (P) in the cell-rich region was calculated as a function of r and x, and this was then converted to saturation (S) using the Hill equation (2). Radially-averaged S was obtained via the formula:

$$\overline{S}(x)=\frac{{\displaystyle \underset{r=0}{\overset{r=R_r}{\int }}}S(x,r)h(x,r)\mathit{\text{rdr}}}{{\displaystyle \underset{r=0}{\overset{r=R_r}{\int }}}h(x,r)\mathit{\text{rdr}}}$$ (30)

An average value for PO₂ at each x was then calculated by inverting the Hill equation:

$$\overline{P}(x)=P_{50}{\left(\frac{\overline{S}}{1-\overline{S}}\right)}^{1/n}$$ (31)

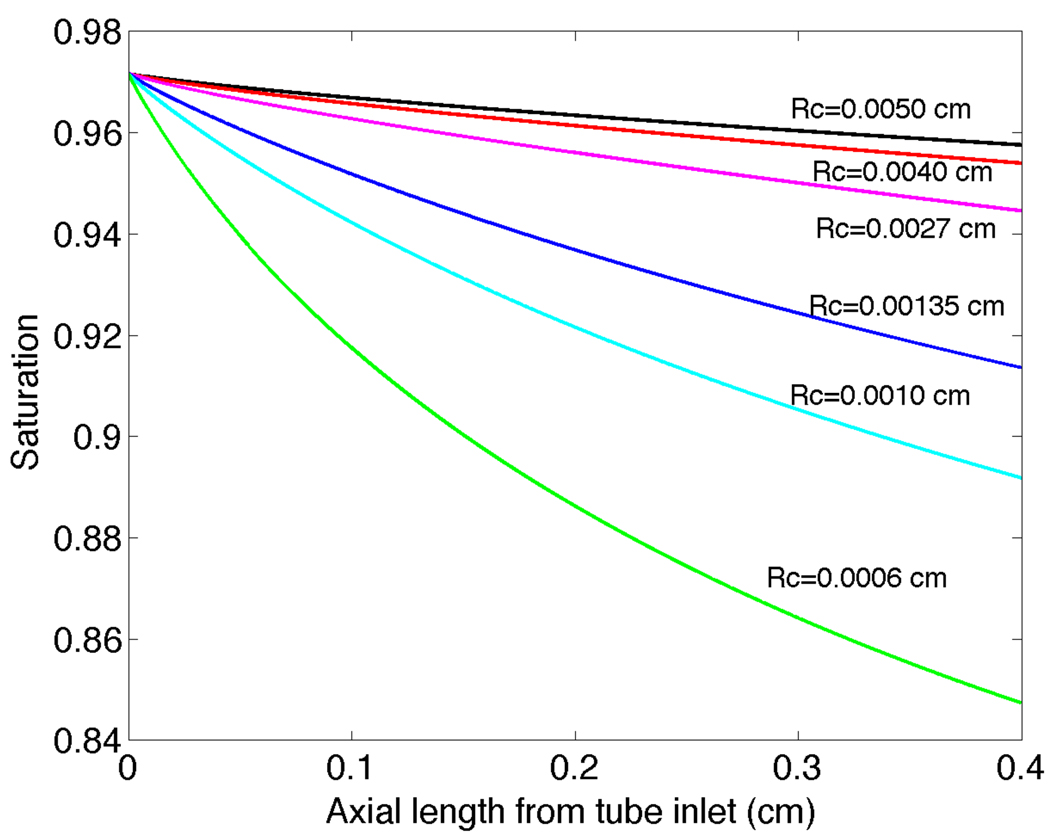
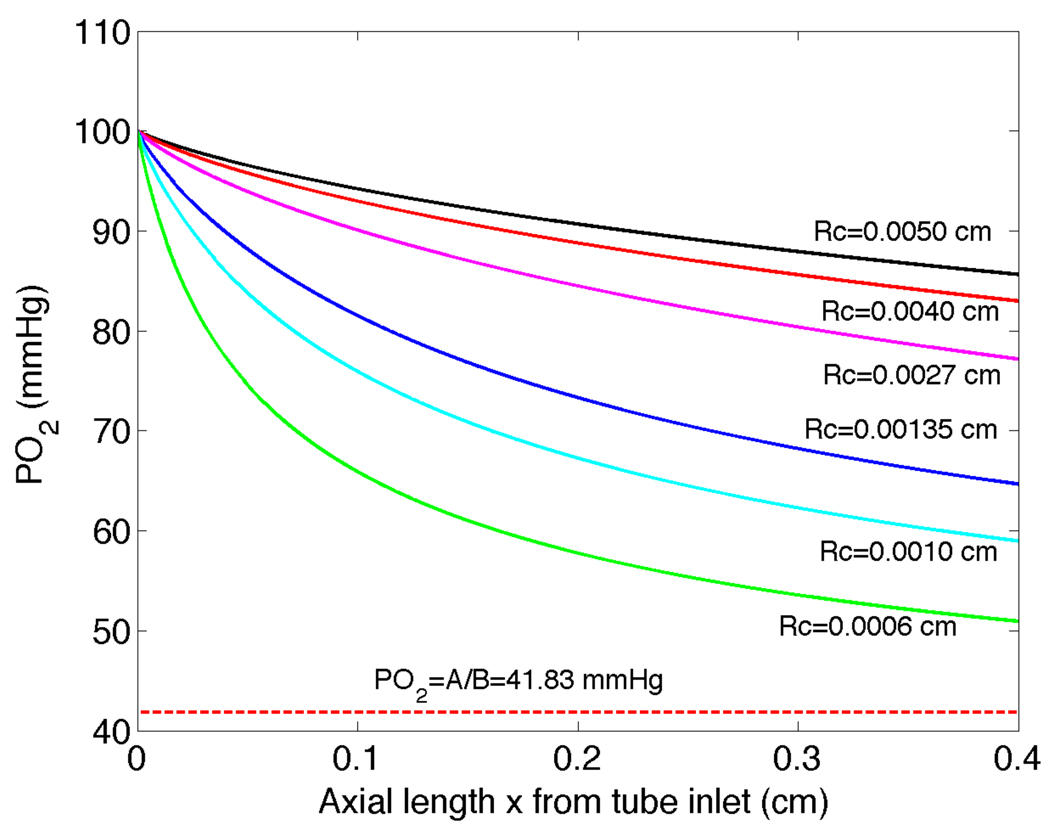
The saturation S̄ is plotted versus axial length in Figure 4 for a vessel of length 0.4 cm and a range of different vessel radii. The saturation decreases substantially for all radii, with a faster decrease for smaller vessels compared to larger vessels. In Figure 5 we plot P̄ versus x along with the reference value P_∞ = A / B. A trend is observed that the PO₂ decrease is greatest for the smallest vessel (R_c = 0.0006cm) and progressively decreases for increasing radii up to the largest vessel considered (R_c = 0.0050cm).

Figure 4.

Radially averaged oxygen saturation versus axial position x from the vessel entrance for six vessels with R_c = 0.0050, 0.0040, 0.0027, 0.00135, 0.0010 and 0.0006cm

Figure 5.

PO₂ versus axial position obtained from radially averaged oxygen saturation results shown in Figure 4.

The dimensionless Sherwood number is given by the following:

$$\mathit{\text{Sh}}=\frac{2R_c\frac{\mathit{\text{dP}}}{\mathit{\text{dr}}}{|}_{r=R_c}}{D_t{\alpha }_t(\overline{P}-P_w)}$$ (32)

where P̄ is given by (31). The dimensional radial gradient $\frac{\mathit{\text{dP}}}{\mathit{\text{dr}}}{|}_{r=R_c}$ is given by the right-hand side of Equation (20). Sh is plotted in Figure 6 versus S̄ for P_∞ = A / B = 41.8mmHg. Sh(S̄) is observed to be fairly flat for small radius (R_c = 0.0006cm) and become steeper as radius increases (up to R_c = 0.0050cm). This is similar to the findings for the verification model previously discussed. Note that, using the tissue model, Sh increases slightly as we decrease P_∞ from 41.83mmHg to 0mmHg, which could represent increased tissue O₂ consumption or decreased capillary O₂ supply. A far-field tissue PO₂ of P_∞ = 0 gives Sh versus saturation plots, as shown in Figure 2, that closely match those presented by Hellums [12:pp14 Figure 13] where a wall PO₂ of approximately zero was assumed. Although not discussed in [12], Sh results depend on the assumed wall PO₂ (or P_ext) for Dirichlet boundary conditions in a similar manner to their dependence on P_∞ for the tissue model.

Figure 6.

Sherwood number versus radially averaged oxygen saturation for vessels with R_c = 0.0050, 0040, 0.0027, 0.00135, 0.0010 and 0.0006cm.

To quantify the effect on arteriolar O₂ losses of varying far-field tissue PO₂, we have defined a modified, tissue PO₂-based Sherwood number:

$${\mathit{\text{Sh}}}_{\mathit{\text{tissue}}}=\frac{2R_c\frac{\mathit{\text{dP}}}{\mathit{\text{dr}}}{|}_{r=R_c}}{D_t{\alpha }_t(\overline{P}-A/B)}$$

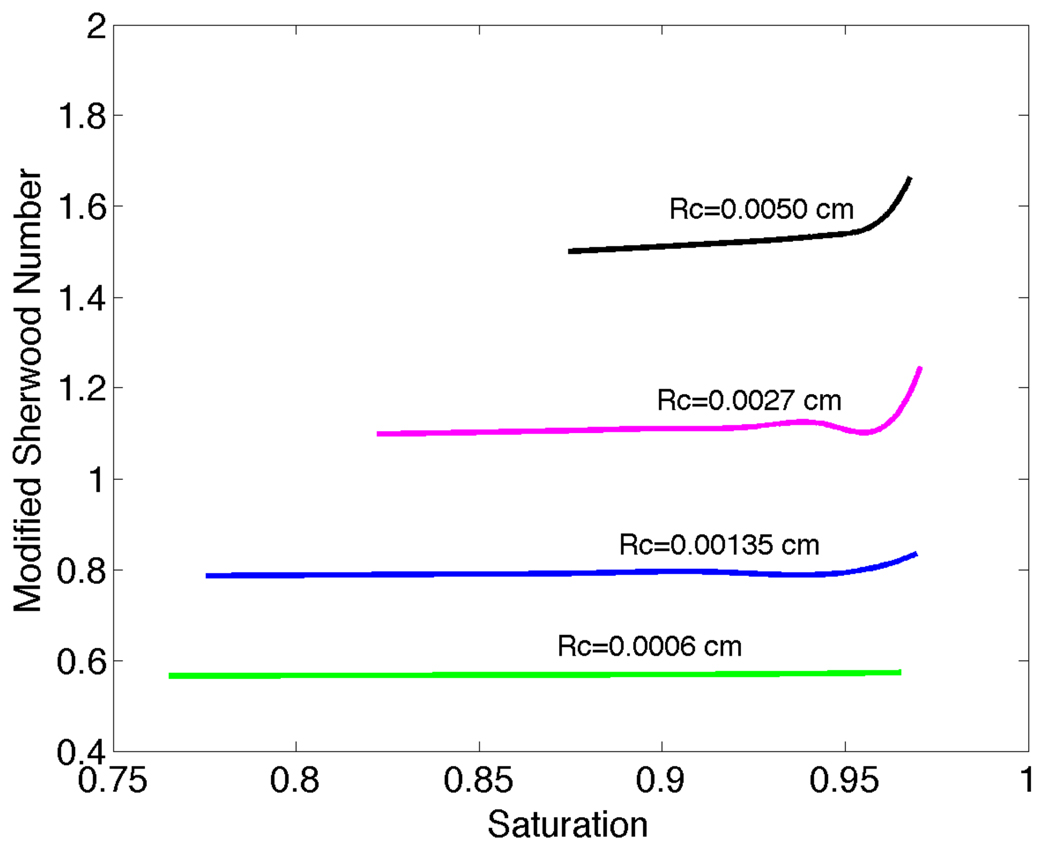
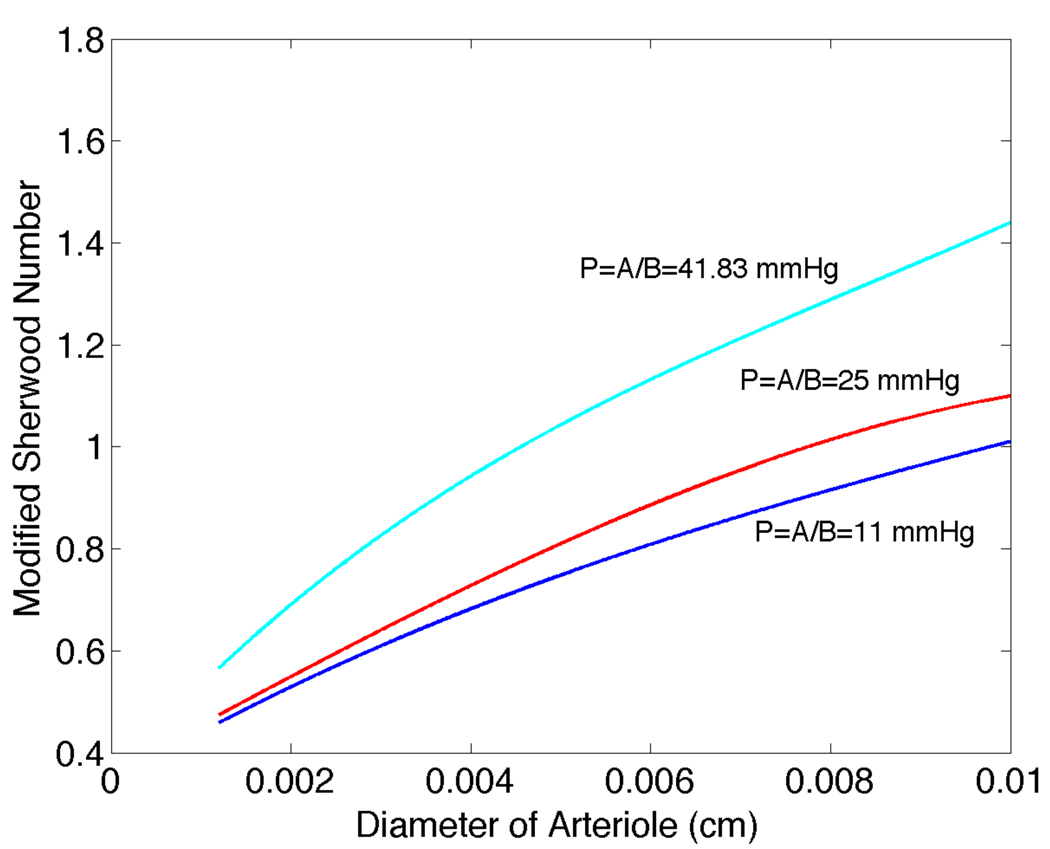
For P_∞ = 41.8mmHg, we have plotted Sh_tissue versus saturation and vessel radius in Figure 7. While Sh vs. S̄ curves change only slightly as tissue PO₂ varies from 41.8 to 10mmHg (see Figures 2 and 6), Sh_tissue changes substantially as seen in plots of Sh_tissue versus diameter for different values of P_∞ (Figure 8). These results provide mass transfer coefficients that can be used to calculate arteriolar O₂ losses in the absence of detailed information on the tissue PO₂ distribution.

Figure 7.

Modified Sherwood number Sh_tissue versus saturation and vessel radius for P_∞ = 41.83mmHg.

Figure 8.

Modified Sherwood number Sh_tissue versus arteriole diameter for S̄ = 0.8 and P_∞ = 41.83mmHg, 25mmHg, and 11mmHg.

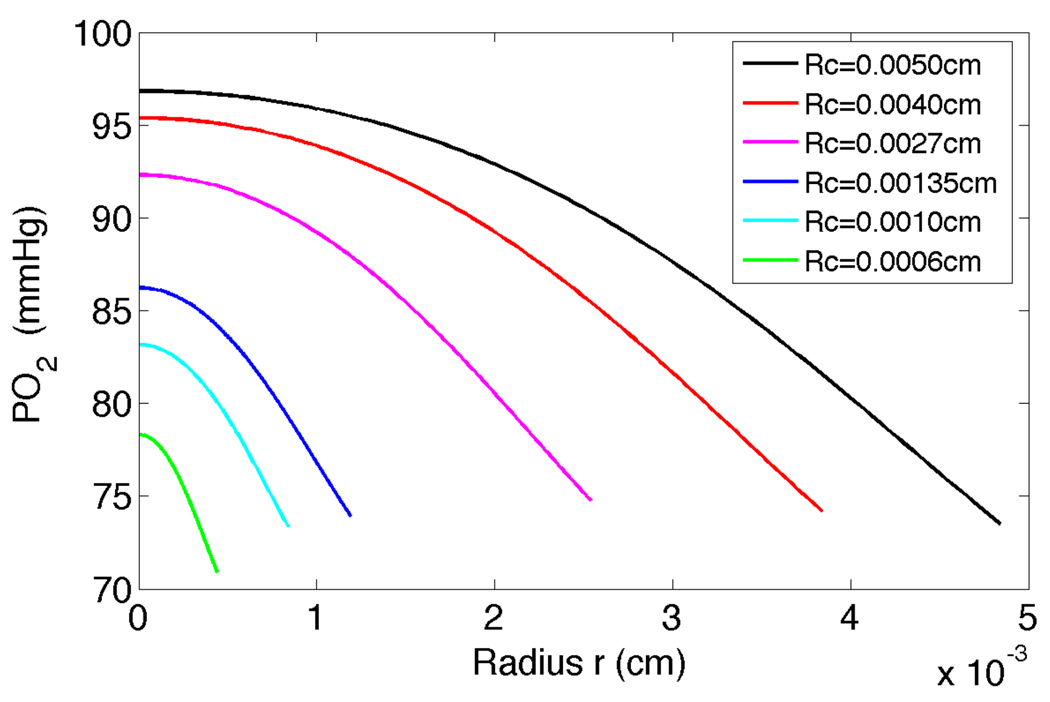
Radial PO₂ profiles in the RBC core at scaled distance β = x / R_c = 80 along the arteriole are shown in Figure 9 for 0 ≤ r ≤ R_r. There are significant radial gradients in PO₂ in arterioles between the centerline and plasma region particularly for larger diameter vessels. The PO₂ is flatter near the centre of the vessel for higher diameter vessels and remains flat for a significant distance from the centerline, whereas for small diameter vessels the PO₂ drops quickly from the centerline of the vessel. Radial PO₂ profiles at R_c = 0.00135cm and R_c=0.0050cm were obtained, respectively, for varying axial distance x. It is clearly seen that the decrease in PO₂ from inlet value is less for the larger diameter vessels, with the PO₂ increasing for a given x value as the radius of the vessel increases from R_c = 0.00135cm to R_c = 0.0050cm. Also, the drop in PO₂ across the radius of the vessel is greater for the larger diameter vessel compared to the smaller diameter vessel.

Figure 9.

PO₂ in the RBC core of the vessel versus radius r at scaled distance downstream of the entrance of β = x/R_c = 80 using the tissue model for six arterioles with R_c = 0.0050, 0040, 0.0027, 0.00135, 0.0010 and 0.0006cm.

To examine the effect of an avascular oxygen-consuming vessel wall, we used the same parameters as in our tissue model with the added wall consumption rate M_w = 1.18110236 × 10⁻⁵ M/s (twice the tissue O₂ consumption rate and in the range of estimates for smooth muscle given by Vadapalli et al. [28]) and wall O₂ diffusion coefficient and solubility, respectively, D_w = D_t and α_w = α_t. The vessel wall thickness was calculated according to [28] and Swain and Pittman [29] as w = 0.24d + 0.39µm, where d is the vessel diameter in µm.

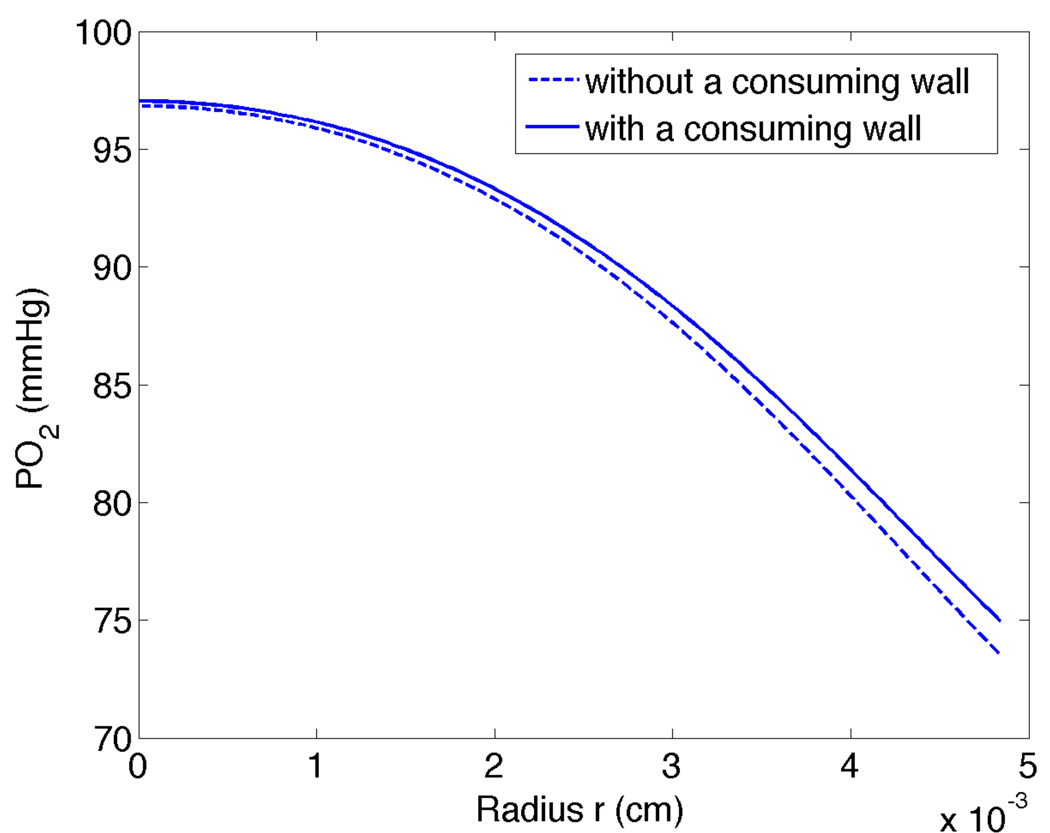
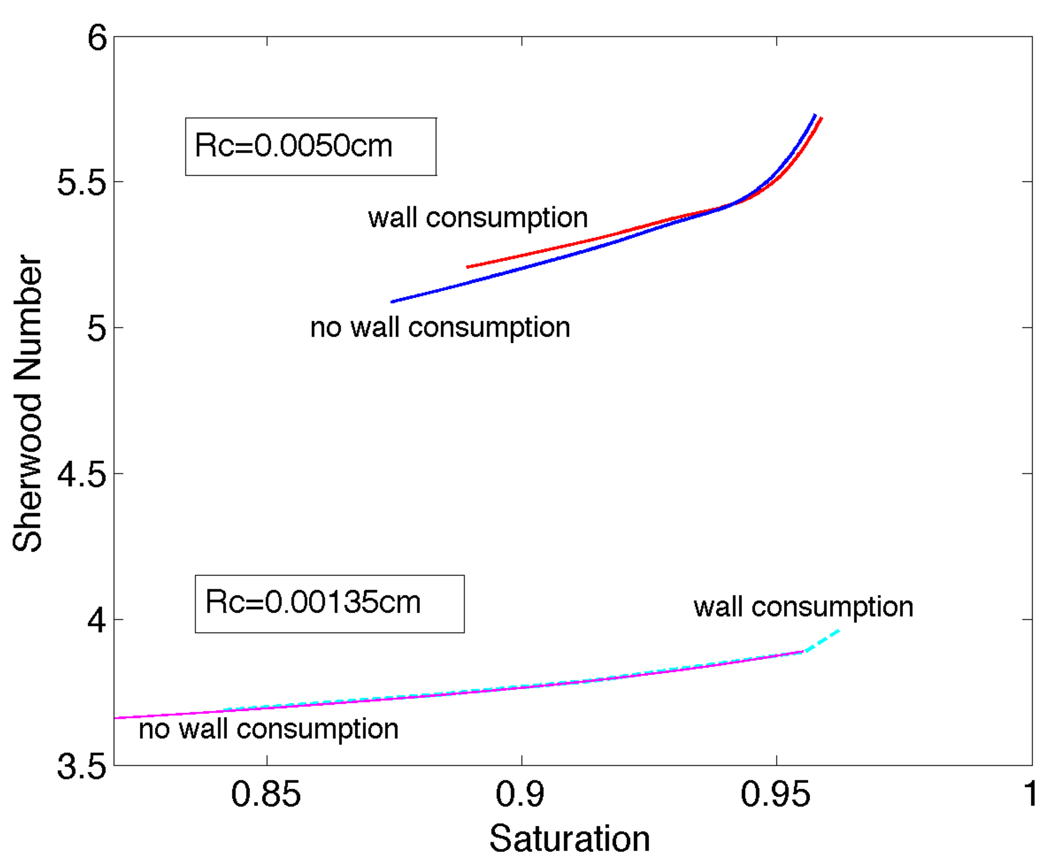
For smaller diameter arterioles, radial PO₂ profiles and saturation plots for the model with a vessel wall coincided almost exactly with the results for our model without a vessel wall (results not shown). For larger arterioles, as shown in Figure 10 for R_c = 0.0050cm, there was a slight difference in the radial PO₂ profiles computed with and without a consuming wall. Note that for the wall O₂ consumption rate used here there is actually a slight decrease in O₂ flux when a consuming wall is added, and hence the intraluminal PO₂ profile with a wall is higher and has a smaller gradient at the luminal surface compared to the profile without a wall. This effect, which is due to capillaries in the tissue model acting as sinks for wall PO₂ values much higher than the tissue equilibrium value (A/B), reverses for substantially higher wall O₂ consumption rates (results not shown). As shown in Figure 11, a consuming wall does not change Sh for smaller arterioles and causes only a slight change in Sh for larger arterioles. This is explained by P̄ − P_w being smaller for the model with a consuming wall, which tends to balance the decrease in flux out of the lumen and keep Sh approximately constant (see Eq. 32).

Figure 10.

PO₂ in the RBC core versus radius position r for tissue model with and without a consuming wall for x = 0.4cm downstream of the entrance and R_c = 0.005cm.

Figure 11.

Sherwood number versus saturation: comparison of models with and without O₂ consuming wall for R_c=0.00135cm and R_c=0.0050cm.

5. DISCUSSION

Our computational model of O₂ transport from an arteriole includes both a detailed model of intraluminal transport and a more physiological boundary condition than has been used previously. Using a simple model of capillary-perfused, O₂-consuming tissue, we are able to specify mean tissue PO₂ far from the vessel and obtain an appropriate vessel-tissue boundary condition. With this boundary condition, our vessel-tissue model allows us to calculate radial and axial variations in SO₂ and PO₂ inside individual arterioles containing flowing blood and surrounded by living tissue. For different size arterioles, we calculated how the radially-averaged oxygen saturation decreases with increasing distance x downstream from the vessel inlet (Figure 4) and how the corresponding average PO₂ decreases with increasing x (Figure 5). Radial decreases in PO₂ are also calculated inside the vessels (Figure 7), as well as in the tissue region for increasing distance from the vessel (Figure 3). Our calculations show appreciable radial drops in intraluminal PO₂ from the centerline to the edge of the RBC core (~10mmHg) for all vessel sizes considered, even at 80 diameters from the vessel inlet (Figure 7). These results are similar to the measurements in [4], where appreciable centerline-perivascular PO₂ decreases of 8.3mmHg and 4.0mmHg were found for large (0.00458 cm) and small (0.00199cm) arterioles, respectively.

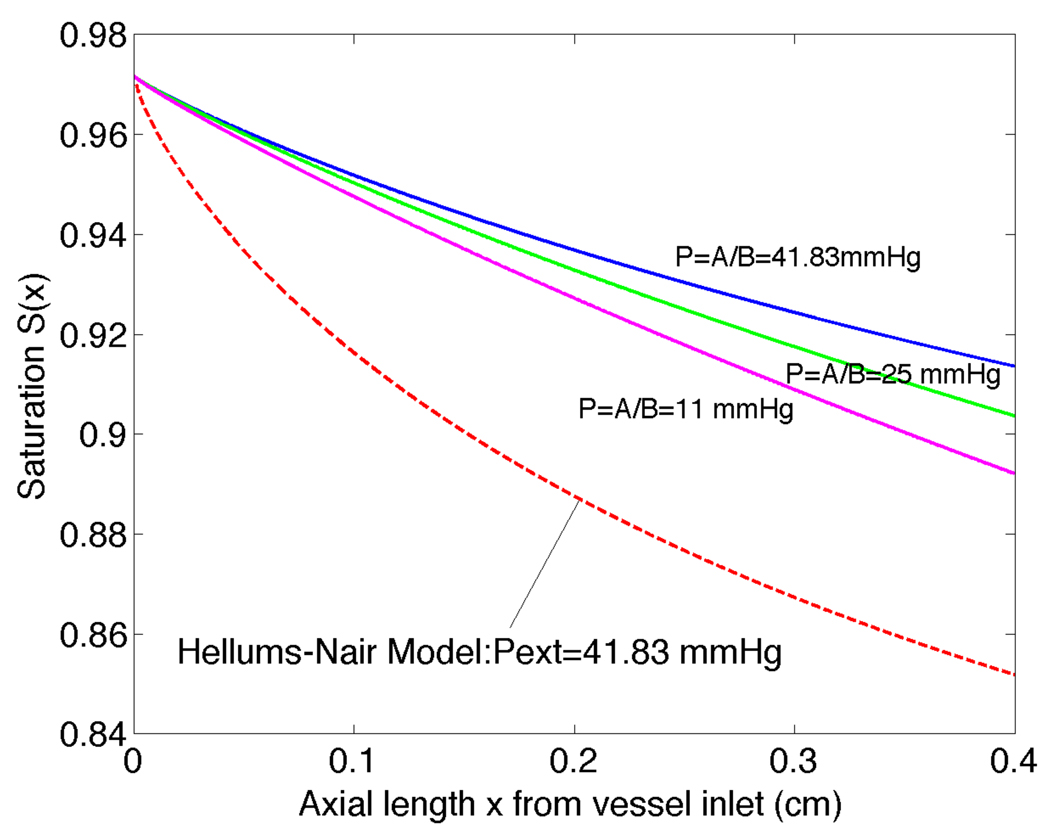
We can compare our vessel-tissue model to the case where PO₂ is specified at the edge of the lumen, which is a limiting case for our model when the length constant $\sqrt{D_t/B}$ is very small, i.e., when PO₂ decreases quickly near the arteriole. This comparison (Figure 12) shows for a range of different values of P_∞ (from 10mmHg to 41.83mmHg) that the oxygen loss is substantially less for our boundary condition derived from the tissue model than for the corresponding Dirichlet (fixed wall PO₂) boundary condition. Thus, our model demonstrates that it is important to consider the surrounding tissue’s intrinsic far-field PO₂ value (set by the balance between mitochondrial O₂ consumption and capillary O₂ supply) and transport properties when calculating O₂ losses from arterioles, and the appropriate mass transfer coefficients (Sh_tissue) must be used. This result is particularly significant because the O₂ content of arterioles is believed to be a key factor in the regulation of microvascular blood flow [6, 7].

Figure 12.

Radially averaged oxygen saturation versus axial length x for prescribed Dirichlet wall condition in the Nair model [13] compared to solution with the tissue model boundary condition for an arteriole with R_c=0.00135cm. The external fixed PO₂ for the Nair model was set to 41.8 mmHg, while the far-field PO₂ in the tissue model was 10–41.8 mmHg.

Another important finding of our numerical simulations is that most of the diffusional loss of oxygen in the arteriole is from RBCs near the wall of the vessel, at the edge of the cell-free plasma layer. This was found experimentally by Carvalho and Pittman [4] and is most apparent in our results for large diameter vessels as can be seen in the substantial drops in oxygen tension near the region r = R_r compared to the centerline of the vessel in Figure 7. These RBCs have a lower O₂ saturation than those nearer the centre of the vessel. This is supported by [30] where the largest part of the resistance to oxygen transport was intra-arteriolar. Chen et al. [18] also confirmed this finding with substantial changes in PO₂ from the centerline of a 0.0250 cm long arteriole to the plasma-core interface at a distance of 0.0125 cm from the inlet. The maximum intravascular change in oxygen tension was about 10mmHg for an arteriole of diameter 0.0019cm (including vascular wall), which is similar to our finding of a 13mmHg intravascular PO₂ drop for a vessel with R_c = 0.0010cm at a distance of 0.0125cm from the inlet. However, typical wall PO₂ found with the Chen et al. model (~30mmHg) was lower than our predictions (>70mmHg) due to the absence of a capillary supply of O₂. Chen et al. also showed that a blunter velocity profile can significantly enhance O₂ delivery to tissue. Their simulations demonstrated that the presence of RBCs in the plasma layer decreases NO availability, but enhances O₂ availability to tissue, and that the effect on NO transport is much more pronounced than that on O₂ transport.

Our numerical simulations showed that slower longitudinal decreases in PO₂ occurred for larger diameter vessels than for smaller diameter vessels, as seen in Figures 4–5. Although larger vessels had higher O₂ flux, their higher flow rates (since blood velocity was approximately constant) led to smaller longitudinal drops in PO₂. Our model likely overestimates actual flow rates in smaller vessels, implying their PO₂ decreases even faster than predicted. A supporting result was obtained experimentally by Vovenko [31] where the distribution of PO₂ was studied on the surface of arterioles, capillaries and venules of rat brain cortex, both longitudinally and radially (into the tissue). It was observed that the smallest arterioles show the largest decreases in SO₂, with 3^rd, 4^th and 5^th order arterioles having drops of 1%, 4% and 5%, respectively.

By including an avascular O₂-consuming wall in one version of our model, we showed that for modeling O₂ transport from arterioles in tissues with a moderate to high O₂ consumption rate, as considered here, inclusion of a separate vessel wall does not substantially change intraluminal O₂ distributions or Sherwood numbers. For less metabolically active tissues (such as mesentery) or situations where tissue metabolism is compromised (as in advanced sepsis [32]), the vessel wall would likely need be considered.

6. CONCLUSIONS

We have developed a novel computational model of O₂ transport from arterioles that combines a detailed description of intravascular transport and a realistic model of transport in tissue. This model has been verified by comparison to a previous intraluminal transport model and through convergence studies, and the results of our vessel-tissue model have been shown to be consistent with recent experimental measurements of O₂ transport from arterioles. This new model demonstrates the importance of considering the O₂ consumption rate and capillary O₂ supply of the surrounding tissue when calculating O₂ transport from arterioles and provides mass transfer coefficients that can be used to calculate arteriolar O₂ losses given mean tissue PO₂.

APPENDIX

Continuity of plasma velocities at the interface of the cell-free and cell-rich regions gives the first equation involving the parameters a and b

$$V_p^{\text{'}}(R_r)=V_p(R_r)$$ (A1)

The overall RBC mass balance defining the discharge hematocrit is

$${\mathit{\text{QH}}}_D={\displaystyle \underset{0}{\overset{R_c}{\int }}}2\pi r{V}_{\mathit{\text{rbc}}}(r)h(r)\mathit{\text{dr}}$$ (A2)

The overall plasma mass balance is

$$Q(1-H_D)={\displaystyle \underset{0}{\overset{R_r}{\int }}}2\pi r{V}_p(r)(1-h(r))\mathit{\text{dr}}+{\displaystyle \underset{R_r}{\overset{R_c}{\int }}}2\pi r{V}_p^{\text{'}}(r)\mathit{\text{dr}}$$ (A3)

The tube hematocrit is defined by

$$H_T=\frac{1}{\pi R_c^2}{\displaystyle \underset{0}{\overset{R_r}{\int }}}2\pi rh(r)\mathit{\text{dr}}$$ (A4)

Using equations [4], [5] and [6] and after some algebra we can rewrite (A1–A4) as

$$a(1-\frac{R_r^2}{R_c^2})=b(1-\mathit{\text{Bl}}\frac{R_r^2}{R_c^2})$$ (A5)

$${\mathit{\text{QH}}}_D=2\pi b(1-\mathit{\text{slp}})h_m[R_r^2(\frac{1}{2}-\frac{1}{m+2})-\mathit{\text{Bl}}\frac{R_r^4}{R_c^2}(\frac{1}{4}-\frac{1}{m+4})]$$ (A6)

$$Q(1-H_D)=2\pi b[R_r^2(\frac{1-h_m}{2}+\frac{h_m}{m+2})-\mathit{\text{Bl}}\frac{R_r^4}{R_c^2}(\frac{h_m}{m+4}+\frac{1-h_m}{4})]+2\pi a[\frac{1}{2}(R_c^2-R_r^2)-\frac{1}{4R_c^2}(R_c^4-R_r^4)]$$ (A7)

$$H_T=\frac{2h_m}{R_c^2}{R}_r^2(\frac{1}{2}-\frac{1}{m+2})$$ (A8)

For each vessel radius considered in this paper, we solve equations (A5–A8) for m, h_m, a, and b using specified blood flow Q and discharge hematocrit H_D, and a tube hematocrit H_T obtained from Gaehtgens [33].