Cardinal rules: Visual orientation perception reflects knowledge of environmental statistics

Abstract

Humans are remarkably good at performing visual tasks, but experimental measurements reveal substantial biases in the perception of basic visual attributes. An appealing hypothesis is that these biases arise through a process of statistical inference, in which information from noisy measurements is fused with a probabilistic model of the environment. But such inference is optimal only if the observer’s internal model matches the environment. Here, we provide evidence that this is the case. We measured performance in an orientation-estimation task, demonstrating the well-known fact that orientation judgements are more accurate at cardinal (horizontal and vertical) orientations, along with a new observation that judgements made under conditions of uncertainty are strongly biased toward cardinal orientations. We estimate observers’ internal models for orientation and find that they match the local orientation distribution measured in photographs. We also show how a neural population could embed probabilistic information responsible for such biases.

INTRODUCTION

Hermann von Helmholtz¹ (and to some extent, Al-Hazen²) described perception as a process of unconscious inference, generating a best guess about the world given the available sensory measurements and an internal model of the world. When sensory information is degraded, reliance on an internal model becomes advantageous. When reaching for the light switch in a dim room, for example, the knowledge that it is likely to be near the door is usually beneficial.

The Bayesian framework provides a quantitative formulation of the inference problem, and has been used to explain aspects of human perception^3–5, cognition⁶, and visuo-motor control^7,8. A Bayesian observer’s internal model of an environmental attribute is represented using a prior probability distribution. In order to achieve optimal inference, the observer’s prior should be matched to the actual distribution of the attribute in the environment, which we refer to as the environmental distribution. Here, we provide direct evidence that this requirement is satisfied for the perceptual task of estimating the orientation of local image structure.

To test the correspondence between the environmental distribution and observer’s prior, one must know or estimate these two distributions. Many previous studies have exposed observers to stimuli drawn from a known distribution^7,8, and compared their behavior to that of an optimal observer with full knowledge of that distribution. Such an approach is limited by the ability of humans to internalize the statistics within the time frame of the experiment, and leaves open the question of what prior knowledge humans use under natural conditions. Alternatively, one can attempt to derive an environmental distribution from known properties of the environment and the image-formation process. For example, sunlight comes from above, and humans appear to make use of this information⁹. However, a precise description of the illumination in an arbitrary scene is extraordinarily complex, and thus, development of a direct expression for the illumination distribution is likely to be intractable. As another alternative, one can attempt to estimate the quantity of interest directly from a large collection of photographic images, generating a distribution by binning values into histograms^4,10, or fitting a parametric form^9,11,12. This process can also be difficult: Measurement of the distribution of retinal image motion, for example, requires a head-mounted video camera and eye-tracker, and an accurate algorithm for estimating motion from video footage. Local image orientation, on the other hand, is relatively easy to estimate, and we use a histogram of such estimates to approximate the environmental distribution.

Determination of an observer’s internal prior distribution can also be difficult. One can assume a particular parametric form and use it to fit perceptual bias data^9,11, but this is only useful if the observer’s prior can be well approximated by the chosen form. Here, we use a recently developed methodology for estimating a non-parametric prior from measurements of perceptual bias and variability¹³. We show that the recovered observer’s prior and measured environmental distribution are well-matched, thus providing direct evidence that humans behave according to the rules of Bayesian inference in estimating the orientation of local image structure. In particular, we measured the distribution of local orientations in a collection of photographic images, and found it to be strongly non-uniform, exhibiting a preponderance of cardinal orientations. We also measured human observers’ bias and variability when comparing oriented stimuli under different uncertainty conditions, and found strong biases toward the cardinal axes when stimuli were more uncertain. The prior that best explains the observed pattern of bias and variability is well-matched to the environmental distribution. Lastly, the most distinctive and well-understood property of neurons in primary visual cortex is their selectivity for local orientation, and we show how a population of such neurons with inhomogeneities matching those reported in the physiological literature can give rise to both the observed perceptual biases and discriminability.

RESULTS

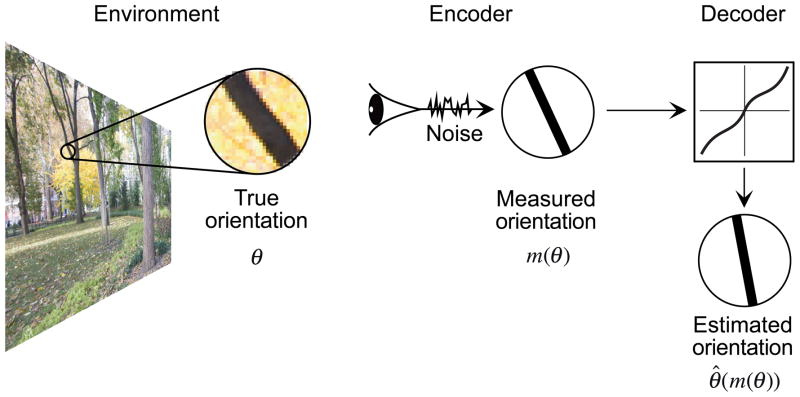
We assume that the observer’s sensory measurements, internal prior model, and estimates are related to each other through an encoder-decoder observer model¹³, as illustrated in Fig. 1 for the example of local orientation perception. Given a contour or edge with true orientation θ in the retinal image, the observer makes an internal measurement, m(θ), which is corrupted by sensory noise. Repeated presentations of the same stimulus result in slightly different measurements, and this collection of measurements can be described with a conditional probability function, p(m | θ). An estimator (decoder) is a function, typically nonlinear, that maps the noisy measurement to an estimate of the true orientation, θ̂(m(θ)). A Bayesian observer uses a particular estimator, optimized to minimize expected error for the given measurement noise and prior model (see Methods).

Figure 1.

Observer model for local 2D orientation estimation. Left panel: The environment. Each local edge has a true image orientation, θ. Central panel: The encoding stage, in which the observer obtains a visual measurement, m(θ), corrupted by sensory noise. Right panel: The decoding stage, in which a function (the estimator, black curve) is applied to the measurement to produce the estimated orientation, θ̂(m(θ)). Because of the sensory noise, the estimated orientation will exhibit variability across repeated presentation of the same stimulus, and may also exhibit a systematic bias relative to the true orientation.

The Bayesian encoder-decoder model provides a framework for understanding two fundamental types of perceptual error: bias and variability¹³. Perceptual variability arises from the sensory (encoder) noise, which is propagated through the estimator, and limits the precision with which the observer can discriminate stimuli. Perceptual bias is the average mismatch between the perceived and true orientations, and primarily arises because a Bayesian estimator prefers interpretations that have higher prior probability from amongst those consistent with the measurement. The origin of these two types of error makes it clear that one cannot predict one from the other. In particular, the direction and magnitude of bias are determined by the slope of the prior, which need not have any relationship to the variability.

Psychophysical measurements of bias and variability

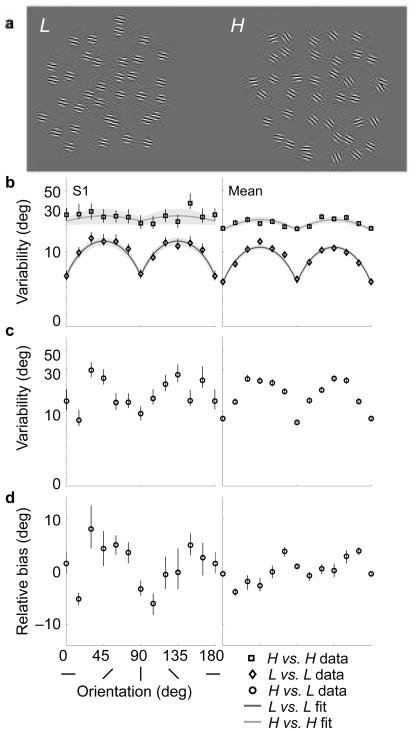
We conducted an experiment to estimate observers’ prior knowledge about orientation. We asked observers to compare the average orientations of two arrays of oriented Gabor patches (Gaussian-windowed sinusoidal gratings) (Fig. 2a). We assume that observers make local orientation estimates for each patch, and then average these to obtain an overall estimate of orientation for each array¹⁴. The low-noise stimuli (L, Fig. 2a left) had identical orientations whereas the high-noise stimuli (H, Fig. 2a right) were variable in orientation (individual Gabor orientations were drawn from a distribution with a standard deviation of about 22 deg; see Methods). Observers viewed the two stimuli simultaneously, symmetrically displaced to the right and left of fixation, and were asked to indicate whether the mean orientation of the right stimulus was clockwise or counter-clockwise relative to that of the left stimulus. Comparisons were made between three stimulus combinations: L vs. L, H vs. H, and H vs. L.

Figure 2.

Stimuli and experimental results. (a) Stimuli are arrays of oriented Gabor functions (contrast increased for illustrative purposes). Left: A low-noise stimulus (L). Right: A high-noise stimulus (H) with mean orientation slightly more clockwise. Observers indicated whether the right stimulus was oriented counter-clockwise or clockwise relative to the left stimulus. (b) Variability for the same-noise conditions for representative subject S1 (left column) and the mean subject (right column), expressed as the orientation discrimination threshold (i.e., the “just noticeable difference”, or JND). Mean subject values are computed by pooling raw choice data from all five subjects. Error bars indicate 95% confidence intervals. Dark gray and light gray curves are fitted rectified sinusoids, used to estimate the widths of the underlying measurement distributions. Pale gray regions indicate ± 1 s.d. of 1,000 bootstrapped fits. (c) Cross-noise (H vs. L) variability data (black circles). The horizontal axis is the orientation of the high-noise stimulus. (d) Relative bias, expressed as the angle by which the high-noise stimulus must be rotated counter-clockwise so as to be perceived as having the same mean orientation as the low-noise stimulus.

The discrimination thresholds are of interest because they can be related to the standard deviation of the internal measurement distributions (see Methods). The two “same-noise” conditions (L vs. L, H vs. H; Fig. 2b and Supplementary Fig. 1a) provide an estimate of measurement noise for each class of stimuli. For the low-noise stimuli, all subjects exhibited better discrimination at the cardinals, a well-studied behavior known as the “oblique effect”¹⁵. Since there is no noise in the stimuli, these inhomogeneities must arise from non-uniformity in the amplitude of the internal noise at different orientations. This effect is diminished with the high-noise stimuli, for which the inhomogeneous internal noise is presumably dominated by external stimulus noise. As expected, discrimination thresholds are significantly higher for the high-noise stimuli than the low-noise stimuli, for all subjects (98% of all JNDs across orientations and subjects, sign test p ≈ 0). The cross-noise variability data (Fig. 2d and Supplementary Fig. 1c) show a moderate oblique effect whose strength lies between that of the L vs. L and H vs. H conditions (98% of H vs. L JNDs are larger than L vs. L JNDs, sign test p ≈ 0; 73% of H vs. L JNDs are smaller than H vs. H JNDs, sign test p < 0.0005).

A non-uniform prior will cause a bias in estimation. Biases are not observable when comparing same-noise stimuli, since both stimuli presumably have the same bias. Cross-noise comparisons can be used to estimate relative bias¹³ (i.e., the difference between the low-and high-noise biases) by computing the difference between the mean orientation of the two stimuli when they are perceived to be equal. This represents the counter-clockwise rotation that must be applied to the high-noise stimulus to perceptually match the orientation of the low-noise stimulus. The relative bias is shown in Fig. 2c and Supplementary Fig. 1b. All subjects show a systematic bimodal relative bias indicating that a high-noise stimulus is perceived to be oriented closer to the nearest cardinal orientation (i.e., vertical or horizontal) than the low-noise stimulus of the same orientation. The relative bias is zero at the cardinal and oblique orientations, and as large as 12 deg in between. These relative biases suggest that perceived orientations are attracted toward the cardinal directions, and repelled from the obliques, and that these effects are stronger for the high-noise stimuli.

Estimation of observers’ likelihood and prior

If our human observers are performing Bayesian inference, what is the form of the prior probability distribution they are using? We assume our observers select the most probable stimulus according to the posterior density p(θ | m) (known as the maximum a posteriori (MAP) estimate). We note that the circular mean of the posterior produces similar estimates, because the posterior distributions are only slightly asymmetric (Supplementary Fig. 2). According to Bayes’ rule, the posterior is the product of the prior p(θ) and the likelihood function p(m | θ) normalized so that it integrates to one. We assume that the decoder is based on the correct likelihood function, which is simply the measurement noise distribution, interpreted not as a probability distribution over measurements, but as a function of the stimulus for a particular measurement. That is, we assume the observer knows and takes into account the uncertainty of each type of stimulus¹⁶ (see Methods).

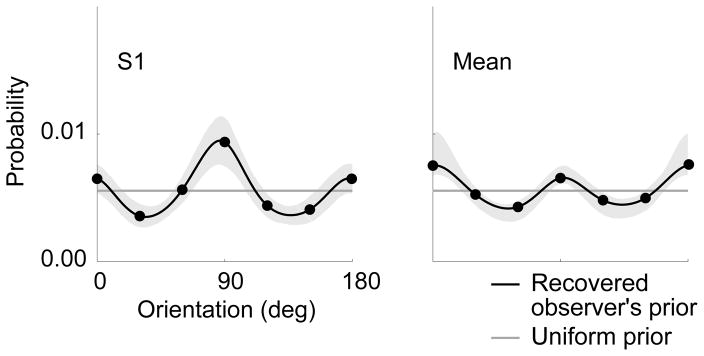
The observer model of Fig. 1 provides a link between the likelihood and prior and the two experimentally accessible aspects of perceptual behavior — bias and variability. Perceptual variability is caused by variability in the estimates, θ̂(m(θ)), which arises from variability in the measurements, m(θ). Relative bias corresponds to the difference in orientation between two stimuli of different uncertainty, θ_L − θ_H, whose estimates are (on average) equal, θ̂_H (m_H (θ_H)) = θ̂_L (m_L (θ_L)). Note that the two estimator functions, θ̂_H and θ̂_L, are noise-level dependent. These relationships allow us to estimate the likelihood width and prior (as functions of orientation), from the experimentally measured bias and variability¹³ (see Methods). Specifically, we obtain the likelihood functions directly from the same-noise variability data (Fig. 2b and Supplementary Fig. 1a). We represent the prior as a smooth curve and determine its shape for each observer by maximizing the likelihood of the raw cross-noise data. The recovered priors of all observers are bimodal, with peaks at the two cardinal orientations (Fig. 3 and Supplementary Fig. 3).

Figure 3.

Recovered priors for subject S1 and mean subject. The control points of the piecewise cubic spline (see Methods) are indicated by black dots. The gray error region shows ± 1 s.d. of 1,000 bootstrapped estimated priors.

Environmental orientation distribution

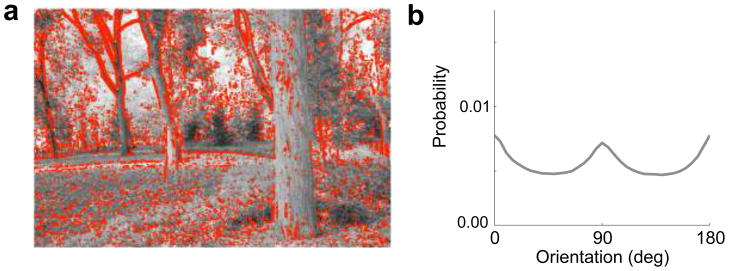
The prevalence of vertical and horizontal orientations in the environment has been previously suggested as the underlying cause of the anisotropy of orientation discriminability (i.e., the “oblique effect”)¹⁷. Here, we show that the environmental distribution of local orientation is quantitatively consistent with the orientation priors we have recovered from our human subjects, and thus explains the cardinal biases in their perception. Orientation content in images is often studied by averaging the Fourier amplitude spectrum over all spatial scales^18,19. For the purposes of our study, we defined the environmental distribution as the probability distribution over local orientation in an ensemble of visual images¹⁷, measured at a spatial scale roughly matched to peak human sensitivity (approximately the same as the scale of our experimental stimuli).

We obtained our measurements from a large database of photographs of scenes of natural content. We estimated the local image gradients by convolution with a pair of rotation-invariant filters²⁰, identified strongly oriented regions, computed their dominant orientations, and formed histograms of these values. The resulting estimated environmental distribution indicates a predominance of cardinal orientations (Fig. 4b). We chose the spatial scale that corresponds most closely to our 4 cycle/deg experimental stimuli and human peak spatial frequency sensitivity of 2–5 cycle/deg²¹. We found that this choice did not heavily impact the results: The dominance of cardinal orientations was similar across spatial scales (Supplementary Fig. 4).

Figure 4.

Natural image statistics. (a) Example natural scene from Fig. 1, with strongly oriented locations marked in red. (b) Orientation distribution for natural images (gray curve).

Observer’s priors vs. the environmental distribution

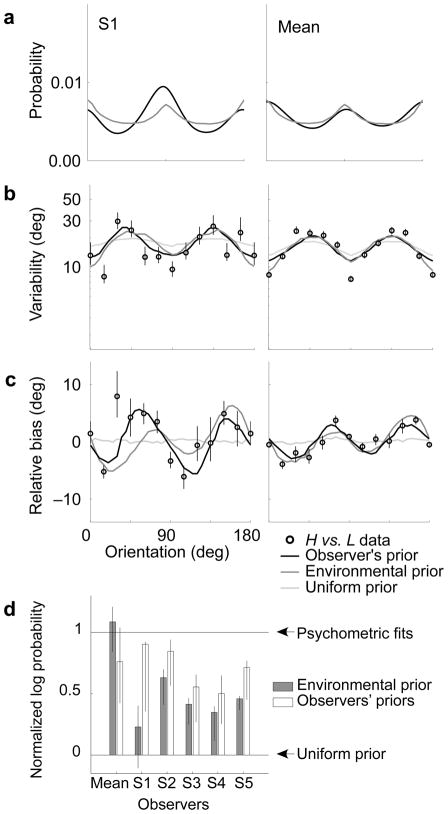
We compared the estimated human observers’ priors and environmental distribution, directly (as probability distributions), and also in terms of their predicted perceptual effects (bias and variability in cross-noise comparisons). The observers’ prior probability distributions and the environmental distribution all have local maxima at the cardinals and minima at the obliques, and the heights of the peaks and troughs are quite similar (Fig. 5a). We computed perceptual predictions of the trial-by-trial behavior of the Bayesian encoder-decoder model, by comparing simulated responses to each pair of stimuli shown to our observers. We find the relative variability (Fig. 5b and Supplementary Fig. 1b) and bias (Fig. 5c and Supplementary Fig. 1c) are similar for a model that uses either the environmental distribution or the human observer’s prior, and both closely resemble the human behavior.

Figure 5.

Comparison of human observers’ priors and environmental distribution for subject S1 (left column) and the mean subject (right column). (a) Human observers’ priors (black curves, from Fig. 3) and environmental distribution from natural images (medium gray curve, from Fig. 4b). (b) Cross-noise variability data (circles, from Fig. 2c) with predictions of the two Bayesian-observer models using each of the three priors shown in (a) and the uniform prior. The uniform prior predicts little or no effect of stimulus orientation on discrimination (light gray curves). In contrast, both the environmental prior (medium gray curves) and the recovered human observers’ priors (black curves) predict better discrimination at the cardinals, as seen in the human observers. (c) Relative bias data (circles, from Fig. 2d) with the predictions of Bayesian-observer models using three priors shown in (a). The uniform prior predicts no bias or a small bias in the opposite direction (e.g., Supplementary Fig. 1c, subject S2). In contrast, both non-uniform priors predict the bimodal bias exhibited by human observers. (d) Normalized log likelihood of the data for Bayesian-observer models using two different priors: environmental distribution (medium gray bars) and the recovered observer’s prior (dark gray bars). Error bars denote the 5th and 95th percentiles from 1,000 bootstrap estimates. Values greater than one indicate performance better than that of the raw psychometric fits, whereas values less than zero indicate performance worse than that obtained with a uniform prior.

To assess the strength of this result, we also considered a null hypothesis that observers use a uniform prior (equivalent to assuming that observers perform maximum-likelihood estimation). A Bayesian-observer model with a uniform prior does not produce the distinct bimodal relative bias (black line in Fig. 5c and Supplementary Fig. 1b). Instead, this model either produces no bias (e.g., mean subject and subjects S1, S3, S4 and S5) or sometimes produces a small relative bias away from the cardinal orientations (e.g., subject S2). This repulsive relative bias is due to the asymmetrical shape of the likelihoods near the cardinals, which pushes the low-noise estimates towards the cardinals more than the high-noise estimates. Further, the uniform-prior observer predicts little or no oblique effect for the cross-noise condition, unlike the human observers (black line in Fig. 5b and Supplementary Fig. 1c). This indicates that the human observers’ biases cannot arise purely from inhomogeneities in sensory noise, but require a non-uniform prior.

We also compared the ability of Bayesian encoder-decoder models with different priors to explain the raw experimental data. We computed the log likelihoods of the two non-uniform prior models and linearly rescaled them so that a value of zero corresponds to the uniform-prior model (degrees of freedom = 0) and a value of one corresponds to the raw psychometric fits (d.f. = 24; Fig. 5d). In general, a Bayesian observer with the recovered observer’s prior (d.f. = 6) performs quite well, often on a par with the raw psychometric fits to the data. For the mean observer, a Bayesian observer using the environmental distribution (d.f. = 0) as a prior predicts the data even better than using the observer’s recovered prior and better than the psychometric fits. It is important to note that these models are not nested: The recovered observer’s prior is constrained to a family of smooth shapes (see Methods) and cannot fully capture the peakedness of the environmental distribution. These results provide strong support of the hypothesis that human observers use prior knowledge of the non-uniform orientation statistics of the environment.

DISCUSSION

We have demonstrated that humans exploit inhomogeneities in the orientation statistics of the environment and use them when making judgements about visual orientation. Whereas previous work has largely focused on variability in orientation estimation (i.e., the oblique effect), we have emphasized the importance of bias, which is essential for studying the prior used by the observer¹³. We have directly demonstrated a systematic perceptual bias towards the cardinals, which had been hypothesized in previous work²². We used the measured bias and variability to estimate observers’ internal prior distributions, and showed that these were well-matched to estimates of the environmental distribution, exhibiting significant peaks at the cardinal orientations. In addition, when used as prior probabilities in a Bayesian-observer model, both distributions accurately predict our human observers’ perceptual biases.

Intuitively, one might have expected that a large bias would be a direct consequence of large variability, but our results indicate that this is not the case. Our observers’ orientation discriminability is worst at oblique angles, and best at the cardinals (Fig. 2b), but their biases are approximately zero at both the obliques and cardinals, and largest in-between (Fig. 2c). These results are consistent with a Bayesian observer that is aware of the environmental prior: The bias is approximately equal to the product of the variability and the slope of the (log) prior¹³. It is small at the cardinals because the variability is small (and the prior slope reverses sign), and it is small at the oblique orientations because the prior slope is small (and again, reverses sign). The well-known “tilt aftereffect”, in which adaptation to an oriented stimulus causes a subsequent reduction in variability and increase in bias, provides another example in which bias and variability do not covary²³.

Our observer model (Fig. 1) can be extended in a number of ways. For example, the decoding stage is deterministic, but could be made stochastic (i.e., incorporating additional noise). In the context of simulating our experimental task, this additional variability would act as a sort of “decision noise”, as has been used in may previous models of perceptual decision-making²⁴. This would, of course, entail an additional parameter that would need to be constrained by data. Our model (as well as our experiment) is also currently limited to estimation of retinal orientation. However, perception is presumably intended to facilitate one’s interactions with a 3D world of objects and surfaces. A full Bayesian model of orientation perception should incorporate priors on the 3D orientation of contours, observer orientation, and perspective image formaton, and would perhaps aim to recover aspects of the 3D scene²⁵. From this perspective, one can think of our model as effectively capturing a 2D marginal of a full 3D orientation prior.

A critical advantage of the Bayesian modeling framework is that the fundamental ingredients (likelihood, prior) have distinct meanings that extend beyond fitting the data in our experiments. As such, the model makes testable predictions. Our perceptual measurements were obtained under a specific set of viewing conditions including stimulus size, eccentricity, duration, contrast, and spatial frequency, which jointly determine the measurement noise. If we were to repeat these measurements having altered one of the viewing conditions that does not covary with orientation in the environment (e.g., contrast), we would expect subject responses to be consistent with the same orientation prior²⁶. For changes in viewing conditions that do covary with orientation in the environment (e.g., spatial frequency; Supplementary Fig. 4), we expect that a multi-dimensional prior (e.g., ref ¹⁰) would be required to explain the data.

The time scale over which priors are developed is an important open question in Bayesian modeling of perception. In some cases, priors appear to adapt over relatively short timescales^7,8. In contrast, our observers seem to use priors that are matched to the statistics of natural scenes, as opposed to human-made or blended scenes (Supplementary Fig. 4), perhaps suggesting that they are adapted over very long time scales. Nevertheless, the variation in the recovered priors of our observers might reflect differences in their previous perceptual experience.

The question of whether orientation priors are innate or learned may also be related to the development of the oblique effect. In support of the innate hypothesis is evidence of the oblique effect in 12-month old human infants²⁷, and a large variation in the strength of the oblique effect amongst observers raised in similar human-made environments²⁸. In support of the hypothesis that the prior is learned in our lifetimes is evidence that the strength of the oblique effect continues to grow from childhood through adulthood²⁹, and that early visual deprivation affects neural orientation sensitivity in kittens³⁰ and humans³¹. Both of these hypotheses could explain the slight individual differences we saw in the strength of the oblique effect and shape of the prior. Lastly, the oblique effect has been shown to be consistent with retinal, not gravitational, coordinates³², while our environmental prior is most naturally associated with gravitational coordinates (assuming all photographs in the database were taken with the camera held approximately level). The simplest interpretation is that the prior has emerged from retinal stimulation, but because humans tend to keep their heads vertical, retinal coordinates are generally matched to gravitational coordinates.

Finally, we consider the physiological instantiation of our encoder-decoder observer model (Fig. 1). The encoding stage of the model is most naturally associated with orientation-selective neurons in primary visual cortex (area V1). Non-uniformities in orientation discriminability (the oblique effect) have been posited to arise because of non-uniformities in the representation of orientation in the V1 population. Specifically, a variety of measurements (single-unit recording^33,34, optical imaging³⁵, and fMRI³⁶) have shown that cardinal orientations are represented by a disproportionately large fraction of V1 neurons, and that those neurons also tend to have narrower tuning curves³³. Additional non-uniformities have been reported in V1 and elsewhere (e.g., variations in gain, baseline firing rate, or correlations in responses), and these may also contribute to non-uniformities in perceptual discriminability.

Now consider the Bayesian decoding stage. For a uniform population of encoder neurons with Poisson spiking statistics, the log-likelihood may be expressed as the sum of the log tuning curves, weighted by the spike counts^37,38 (for a non-uniform population, this needs to be corrected by subtracting the sum of the tuning curves). A decoder population could compute the log-posterior at each orientation by computing this weighted sum, and adding the log prior. The desired estimate would be the orientation associated with the decoder neuron having maximum response (i.e., “winner-take-all”). Although this is an explicit computation of the Bayesian estimator, and would thus generate the same perceptual biases seen in our subjects, several aspects of this implementation seem implausible³⁹. In particular, the decoder utilizes an entire population of cells to “recode” the information in the encoder population, it must have complete knowledge of the encoder tuning curves as well as the prior, and the estimate is obtained with a winner-take-all mechanism that is highly sensitive to noise.

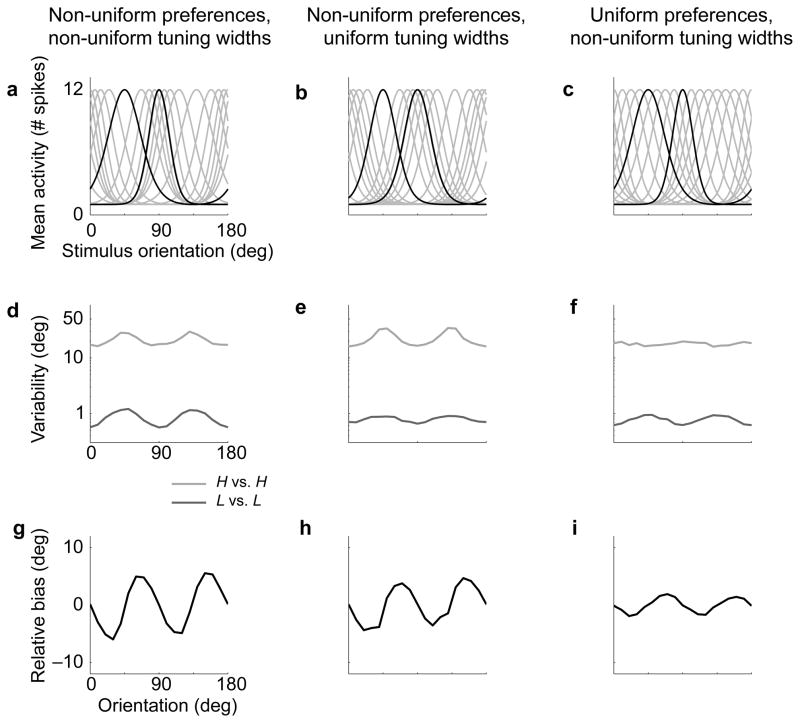
As an alternative, we wondered whether the optimal mapping from an encoder population to an estimate might be approximated by a simpler, more plausible computation (A.A. Stocker, N.J. Majaj, C. Tailby, J.A. Movshon, & E.P. Simoncelli, Front. Neurosci. Conference Abstract: Computational and Systems Neuroscience 2010. doi: 10.3389/conf.fnins.2010.03.00298; also see ref. 40). We simulated an encoder population whose spiking responses were generated as samples from independent Poisson distributions, with mean rates (in response to an oriented stimulus) determined by a set of orientation tuning curves with non-uniformities approximating those found in V1^33–35,41 (Fig. 6a). We used a standard “population vector” decoder⁴², which computes the sum of directional vectors associated with the preferred orientation of each encoder cell, weighted by the response of that cell. This decoder is robust to noise (compared to winner-take-all), does not require any knowledge of the prior, and requires only the preferred orientation of each cell in the encoding population (as opposed to the entire set of tuning curves). We used the full neural encoder-decoder model to simulate per-trial decisions on the same stimuli shown to our human subjects. From these we computed discriminability for the same-noise conditions, and bias for the cross-noise conditions. Remarkably, we find that this generic decoder, when combined with the non-uniform encoding population (Fig. 6a), produces bias and discriminability curves (Fig. 6d,g) that are quite similar to our human subjects (Fig. 5b,c). The narrower tuning near the cardinals leads to a substantial decrease in discrimination thresholds: Eliminating the non-uniform tuning widths (Fig. 6b) greatly reduces the oblique effect for the low-noise stimuli (Fig. 6e). The proportionally larger number of cells around the cardinals leads to a disproportionate influence on the weighted sum decoder, inducing biases toward the cardinals: Eliminating the non-uniform orientation preferences (Fig. 6c) substantially reduces the amplitude of the bias (Fig. 6i). And finally, eliminating both non-uniformities (i.e., an equal-spaced population of neurons with identical tuning, as is commonly assumed in the population coding literature^37,43,44) produces constant bias and discriminability curves, as expected (not shown).

Figure 6.

Simulations of neural models with non-uniform encoder, and “population vector” decoder. (a) Tuning curves of an encoder population with non-uniform orientation preferences and non-uniform tuning widths based on neurophysiology (only a subset of neurons shown). Neurons preferring 45 deg and 90 deg stimuli are highlighted in black. (b) Tuning curves of a population with non-uniform preferences and uniform widths. (c) Tuning curves of a population with uniform preferences and non-uniform widths. (d–f) Variability for the same-noise conditions for the populations in (a–c): L vs. L (dark gray) and H vs. H (light gray). (g–i) Relative bias for the cross-noise condition (H vs. L) for the populations in (a–c). The fully non-uniform population (a) produces variability and bias curves similar to those exhibited by humans (Fig. 2b,d and Supplementary Fig. 1a,c). Girshick, Landy, Simoncelli

The fact that this observer model is able to approximate the bias behavior of the optimal Bayesian decoder implies that the non-uniformities of the encoder are implicitly capturing the properties of the prior, in such a way that they can be properly utilized by a population-vector decoder⁴⁰. Recent theoretical work posits that the non-uniformities of neural populations reflect a strategy by which the brain allocates its resources (neurons and spikes) so as to optimally encode stimuli drawn from an environmental distribution⁴⁵. The current work suggests that encoder nonuniformities may also serve the role of enabling a decoder to perform Bayesian inference without explicit knowledge of the prior³⁹. If so, this solution could provide a universal mechanism by which sensory systems adapt themselves to environmental statistics, allowing for optimal representation and extraction of sensory attributes under limitations of neural resources.

METHODS

Psychophysical experiments

Five subjects participated. Subjects S2 and S3 were the first and second authors, respectively. Subjects S1, S4, and S5 were naïve to the aims of the experiment and were compensated $10/hour. All subjects had normal or corrected vision. Subjects stabilized their heads on a chin/forehead rest, and viewed the stimuli binocularly at a distance of 57 cm in a dark room.

Each stimulus consisted of an array of Gabor patches positioned on a randomly jittered grid. Each Gabor was composed of a high-contrast 4 cycle/deg sinusoidal grating windowed by a circular Gaussian whose full width at half height was 0.41 deg. The Gabors were on a gray background and the monitor was gamma linearized. The entire stimulus array subtended 10 deg and contained roughly 37 Gabors. Two new random stimuli were generated for each trial, and displayed simultaneously 2.5 deg to the left and right of the fixation point. Stimuli were visible for 0.75 sec (0.5 sec for subject S2). For each stimulus, Gabor orientations were either identical (L), or drawn from a Gaussian distribution (H) with standard deviation individually pre-determined for each subject (see below). The three comparison conditions were randomly interleaved: L vs. L, H vs. H, and H vs. L.

A central fixation point was presented between trials and we did not control for eye movements. Randomly interleaved staircases (2-up/1-down and 2-down/1-up) adjusted the mean orientation of the comparison stimulus, while the mean orientation of the standard stimulus remained fixed. On each trial, the standard was randomly positioned on the left or right, with the comparison on the other side. Subjects completed at least 7200 trials divided into 36 conditions (12 orientations of the standard for the 3 stimulus combinations), over at least six sessions. Subject S3 participated in an earlier version that was blocked by orientation. Before each session, subjects completed a few practice trials in the H vs. H condition with auditory feedback. These trials were not included in analysis, and there was no feedback during the main experiment.

For each condition, we fit a cumulative Gaussian psychometric function to the data using a maximum-likelihood criterion, resulting in an estimate of the mean (relative bias) and standard deviation σ_P (Just Noticeable Difference or JND). Because we used a two-interval task⁴⁶, the standard deviation of the underlying likelihood is $\sigma ={\sigma }_P/\sqrt{2}$.

In an initial experiment, we determined a level of orientation variability for the H condition such that each subject’s H vs. H JNDs were roughly three times larger than their L vs. L JNDs. Subjects first ran the L vs. L condition with the standard oriented at 105 deg. We then fit a cumulative Gaussian and calculated its standard deviation σ_L. Next, we fixed the two stimuli at 105 deg and 105 + 3σ_L deg and used two randomly interleaved 2-down 1-up staircases to adjust the amount of orientation noise (applied to both stimuli). We fit a reflected cumulative Gaussian to these data (which ranged from 100% to 50% correct), and estimated the noise level that yielded 76%-correct performance. This noise level was used for the H condition in the main experiment (24.3, 21.8, 26.7, 19.2, and 20.0 deg for the five subjects respectively).

We also ran a control experiment to ensure the relative bias was not induced by the rectangular frame of the monitor. Subject S2 viewed monocularly through a 16.8-degree circular aperture, 20 cm from the eyes, with a black hood that obscured everything except the stimuli. The stimuli were presented centrally in two temporal intervals of 0.4 sec each, with a 0.25 sec mask after each, consisting of non-oriented 4 cycle/deg noise. The relative bias was identical to the main experiment, ruling out the concern of an artifact.

Estimation of the likelihood functions

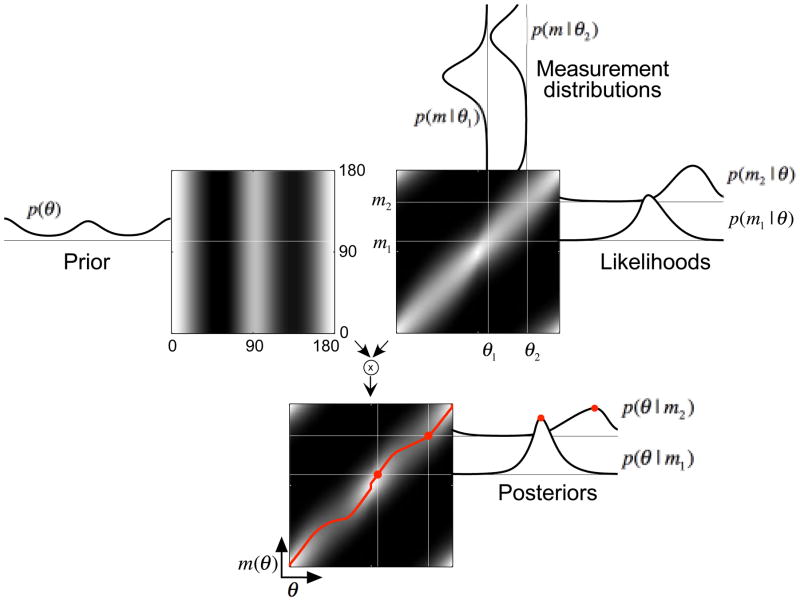
Fig. 7 (upper right) shows the formulation of the likelihood functions. The measurement distribution p(m | θ₁) describes the probability of a sensory measurement given a particular stimulus value, and is displayed as a two-dimensional grayscale image. We assume that sensory noise is drawn from a von Mises distribution (described below) whose variance can be related to the same-noise variability data. The measurement distributions are vertical slices through this two-dimensional function, whereas the likelihoods are horizontal slices. Note that the likelihood function p(m₁ | θ) is typically not normalized as a probability distribution. Although the measurement distributions are assumed symmetric, their width depends on orientation, and the resulting likelihood functions are generally asymmetric (see Fig. 7)⁴⁷. Supplementary Fig. 5 shows the corresponding likelihoods for the mean subject.

Figure 7.

Derivation of the estimator θ̂(m(θ)). In all three grayscale panels, the horizontal axis is stimulus orientation θ, the vertical axis is the measured orientation m(θ), and the intensity corresponds to probability. Upper-left panel: The mean observer’s prior, raised to the power of 2.25 and re-normalized for visibility, is independent of the measurements (i.e., all horizontal slices are identical). Upper-right panel: The conditional distribution, p(m | θ). Vertical slices indicate measurement distributions, p(m | θ₁) and p(m | θ₂), for two particular stimuli θ₁ and θ₂. The widths of the measurement distributions are the average of those for the low- and high-noise conditions for the mean observer (multiplied by a factor of 10 for visibility). Horizontal slices, p(m₁ | θ) and p(m₂ | θ), describe the likelihood of the stimulus orientation, θ, for the particular measurements, m₁ and m₂. Note that the likelihoods are not symmetric, because the measurement distribution width depends on the stimulus orientation. Bottom panel: The posterior distribution is computed using Bayes’ rule, as the normalized product of the prior and likelihood (top two panels). Horizontal slices correspond to posterior distributions p(θ | m₁) and p(θ | m₂), which describe the probability of a stimulus orientation given two particular measurements. Red dots indicate MAP estimates (the modes of the posterior) for these two likelihoods, θ̂(m₁) and θ̂(m₂). Circular mean estimates yield similar results (see Supplementary Fig. 2). The red curve shows the estimator θ̂(m) computed for all measurements. An unbiased estimator would correspond to a straight line along the diagonal.

To estimate the measurement noise, we fit functions to the same-noise JND data (Fig. 2b and Supplementary Fig. 1a, pale and dark gray curves). We used rectified two-cycle sinusoids peaking at the obliques for the L vs. L JNDs (j_L (θ)=α_L | sin(2θ) | +β_L) and H vs. H JNDs (j_H (θ)=α_H | sin(2θ) | +β_H). We used least-squares minimization to estimate the parameters α_L, β_L, α_H and β_H for each subject, and computed confidence intervals for these estimates using the standard deviation of estimates obtained on 1,000 bootstrap samples of the data.. The prior will have a similar effect on the two stimuli in the same-noise conditions, leading to a negligible same-noise bias, as seen in our data. Our model of the measurement distribution is a von Mises function that peaks every 180 deg:

$$P(m\mid \theta )\propto exp(\kappa cos(2(\theta -m)))$$

where κ is a concentration parameter, whose value was chosen so as to produce JND values matching the fitted j(θ).

Converting sensory measurements to Bayesian estimates

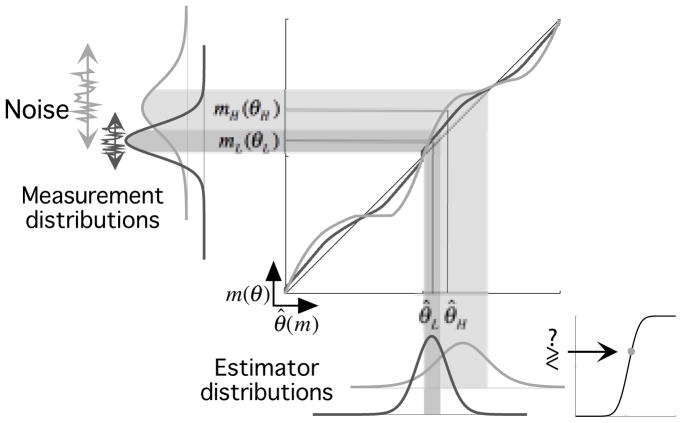
Fig. 7 shows how the Bayesian framework can be used to describe the decoding process. The estimator’s shape depends on both the measurement noise and prior; the bias is approximately the product of the likelihood width and the slope of the log of the prior¹³. The Bayesian decision-making process that produces simulated psychometric data is depicted in Fig. 8. The observer makes measurements m_L (θ_L) and m_H (θ_H), which are transformed by noise-appropriate estimators into values θ̂_L and θ̂_H. Repeated measurements fluctuate due to sensory noise, resulting in a measurement distribution. This distribution is propagated through the estimator, resulting in a distribution of estimates. These distributions are then compared using signal detection theory⁴⁶, resulting in a single point on a psychometric function.

Figure 8.

Example cross-noise comparison. The vertical axis is the measured orientation m(θ), and the horizontal axis is estimated stimulus orientation θ̂(m(θ)). Measurements corresponding to low-noise stimuli, m_L (θ_L) (dark gray), or high-noise stimuli, m_H (θ_H) (light gray), enter on the left. Each measurement is transformed by the appropriate nonlinear estimator (solid curves) into an estimate (bottom). The estimators correspond to those of the mean observer exaggerated for illustration as in Fig. 7. The high-noise estimator exhibits larger biases than the low-noise estimator. The sensory noise of the measurements propagates through the estimator, resulting in estimator distributions (note these should not be confused with the posteriors). Comparison of these distributions produces a single point on the psychometric function.

Estimation of the observers’ priors

The human observers’ priors (Fig. 3 and Supplementary Fig. 3) were estimated by fitting the behavior of a Bayesian observer to the human data in the cross-noise condition. To avoid any preconceptions of what the prior ought to look like, we used a globally non-parametric model. Our only constraints were that it integrate to one, that it be periodic with period 180 deg, and that the log prior be smooth and continuous. Stocker and Simoncelli¹³ also used a globally non-parametric model, in which the log prior was approximated as linear over the central span of the likelihood. This assumption could be wrong in our case, because the likelihoods are quite broad in a few cases (e.g., up to 30 deg standard deviation). Instead, we used cubic splines to smoothly interpolate between values of log(P(θ_i))) at neighboring control points θ_i and θ_{i +1}:

$$log(P(\theta )))=a_i{(\theta -{\theta }_i)}^3+b_i{(\theta -{\theta }_i)}^2+c_i(\theta -{\theta }_i)+d_i,$$

with the constraint that the neighboring splines’ first and second derivatives matched at the common boundary θ_i. The parameters of the model were the values of log(P(θ_i))) at six control points θ_i = {30, 60, 90, 120, 150, 180 deg}. Changing the number of control points resulted in similar recovered priors.

Given a candidate prior P(θ), for each stimulus pair used in the experiment we simulated 1,000 trials by drawing measurement samples from the appropriate measurement distributions. Each measurement leads to a likelihood function (the corresponding row of the pre-computed matrix, e.g., Fig. 7, upper right, and Supplementary Fig. 5), which is multiplied by the prior, and maximized to obtain the estimate. The 1,000 pairs of estimates were then compared to obtain the binary model response (“counter-clockwise” or “clockwise”), and the average of this set of binary decisions yielded a single point on the Bayesian-observer model-generated psychometric function (Fig. 8).

We estimated the best-fitting parameters of the log prior {log(P(θ_i))} for each human subject by maximizing the probability of their observed data, given the above model-generated psychometric functions. We performed bootstrapping by randomly sampling, with replacement, the raw crossnoise response data 1,000 times (this is separate from the 1,000 measurement samples described above). If the subject performed n trials for a particular pair of orientations, then n responses were sampled from the corresponding data. The variation of the estimated priors across bootstrap replications is shown as the gray regions in Fig. 3.

Estimating the environmental distribution

The distribution of orientations was computed from a publicly-available image database (Olmos, A. & Kingdom, F.A.A. McGill Calibrated Colour Image Database, http://tabby.vision.mcgill.ca, (2004)) containing 653 2560 × 1920 TIF photographs of natural scenes, with a pixel size of 0.0028 deg. We gamma-linearized the images using camera parameters provided with the database, and converted to XYZ-space. Each image was normalized by its mean luminance and only luminance information (Y channel) was used. We decomposed each image into six spatial resolutions using a Gaussian pyramid⁴⁸. At each scale, we used five-tap, rotation-invariant derivative filters²⁰ to compute gradients (x- and y-derivative pairs) centered on each pixel. We combined these into an orientation tensor⁴⁹, the local covariance matrix of the gradient vectors computed by averaging their outer products over square regions of 5×5 pixels. We calculated the tensor’s eigenvector decomposition (i.e., PCA) and from it computed three quantities for each pixel: the energy (the sum of eigenvalues), the orientedness (the eigenvalue difference divided by the sum), and the dominant orientation (the angle of the leading eigenvector). Tensors centered on the two pixels closest to the borders were discarded. We created a histogram of dominant orientations for tensors that exceeded two thresholds: Their orientedness was greater than 0.8, and their energy exceeded the 68th percentile of all the energy of the corresponding scale. We verified that our histograms were only weakly dependent on these two threshold values. Sub-threshold tensors were typically located in patches of sky, or in internal regions of non-textured objects. The histogram for each scale was converted to a probability density by dividing by the total number of supra-threshold tensors, thus providing an estimate of the probability distribution over orientation. We selected the scale whose derivative filters best matched the peak spatial frequency sensitivity of humans²¹ (2–5 cycle/deg) and the spatial frequency of the stimulus (4 cycle/deg). We also estimated the orientation distributions of scenes of primarily human-made content and blended scenes (e.g., an image of a tree and a house). These distributions also exhibit a preponderance of cardinal orientations, but the heights of the peaks differ (Supplementary Fig. 4).

Simulated neural model

We created simulated populations of 60 orientation-tuned V1 neurons for each Gabor. We randomly sampled 8 out of the 37 Gabors from the stimulus, consistent with human perceptual pooling¹⁴. The neural responses were characterized by independent Poisson noise, with expected number of spikes bounded between 1 and 12. The populations had either uniform or non-uniform tuning-curve widths, and either uniform or non-uniform preferred orientations, resulting in four different models. We used von Mises tuning curves, which have been shown to provide good fits to empirical tuning curves⁵⁰. For the models with uniform tuning-curve widths, the standard deviation of the tuning curves was 17 deg, which is typical of V1 orientation-tuned neurons^34,41. Non-uniform tuning widths were chosen according to a von Mises function (plus a constant) centered at the obliques with a concentration parameter of 42 deg. This produced standard deviations consistent with neurophysiology in both average tuning width (17 deg) and ratio of oblique to cardinal tuning widths (approximately 3:2)^34,41. Nonuniform preferred orientations were drawn from a von Mises distribution modified to peak at 0 and 90 deg with a standard deviation of 35 deg, producing a ratio of the density of oblique to cardinal neurons consistent with neurophysiology (approximately 9:5)^33,34. Simulations were run for the same conditions as shown to the human subjects: 12 orientations for each of three stimulus combinations. On every trial, we computed population vector estimates⁴² for the orientations of both stimuli, and a decision was made as to whether the comparison was counter-clockwise or clockwise of the standard.