Dynamics of Time-Lagged Gene-to-Metabolite Networks of Escherichia coli Elucidated by Integrative Omics Approach

Abstract

In the postgenomics era, integrative analysis of several “omics” data is absolutely required for understanding the cell as a system. Integrative analysis of transcriptomics and metabolomics can lead to elucidation of gene-to-metabolite networks. When integrating different time series “omics” data, it is necessary to take into consideration a time lag between those data. In the present study, we conducted an integrative analysis of time series transcriptomics and metabolomics data of Escherichia coli generated by cDNA microarray and Fourier transform ion cyclotron resonance mass spectrometry (FT-ICR/MS), respectively. We identified a 60-min time lag between transition points of transcriptomics and metabolomics data by using a Linear Dynamical System. Furthermore, we investigated gene-to-metabolite correlations in the context of time lag, obtained the maximum number of correlated pairs at transcripts leading 60-min time lag, and finally revealed gene-to-metabolite relations in the phospholipid biosynthesis pathway. Taking into consideration the time lag between transcriptomics and metabolomics data in time series analysis could unravel novel gene-to-metabolite relations. According to gene-to-metabolite correlations, phosphatidylglycerol plays a more critical role for membrane balance than phosphatidylethanolamine in E. coli.

Introduction

In the postgenomics era, a systematic and comprehensive understanding of the complex events in organisms is of great interest in biology. The majority of gene products function not in isolation, but by interacting with each other. Integration of “omics” approaches, thast is, genomics, transcriptomics, proteomics, and metabolomics, is required to understand organisms as a system. New advanced methods, strategies, and technologies for “omics” studies should be mainly directed at the elucidation of regulation and gene regulatory networks in integrative or systems biology perspectives at different levels, that is, genomics, transcriptomics, proteomics, and metabolomics (Castrillo and Oliver, 2004). Therefore, metabolomics offers insights into metabolism that complements information obtained from proteomics and transcriptomics (Fridman and Pichersky, 2005) and has the potential to elucidate gene functions and networks, especially when integrated with transcriptomics. A promising approach is pairwise gene-to-metabolite correlation analysis, which can unveil hidden correlations and shed light on candidate genes for regulating the metabolite content. The systematic integration of transcriptomics, proteomics, and metabolomics facilitates the unbiased, information-based reconstruction of underlying biochemical networks (Fiehn et al., 2001; Hirai et al., 2004, 2005; Urbanczyk-Wochniak et al., 2003; Walther et al., 2010). Pir et al. (2006) integrated metabolomics with transcriptomics by using PLS modeling, and metabolite data were modeled as a function of the transcriptome to determine their congruence.

In time series analysis, estimation of the transition point in several stages, that is, genomics, transcriptomics, and metabolomics, is important for understanding living cells as biochemical systems. Although clustering techniques have been applied to identify coexpressed genes in time series microarray analysis, several articles proposed methods to detect time-lagged relationships of gene expression profiles (Balasubramaniyan et al., 2005; Ji and Tan, 2005; Redestig et al., 2007). That is, expressions of gene products are regulated by each other not only directly but also indirectly after a certain time lag. Therefore, it is necessary to take into consideration a time lag between different “omics” data. Meanwhile, investigating the responses of cells to environmental changes often requires a system-level analysis. A key step in analyzing system responses to environmental changes is identifying large state changes or “transitions.” In the present study, we identified the time lag between transcriptomics and metabolomics data of Escherichia coli by using linear dynamical system (LDS) analysis (Morioka et al., 2007) and assessed time-lagged specific gene-to-metabolite correlation.

Materials and Methods

Strains and growth conditions

The strain used in this study was Escherichia coli K-12 W3110. An aliquot (8 mL) of an overnight liquid culture of W3110 in LB medium (Bacto Tryptone 1.0%, Bacto Yeast extract 0.5%, and NaCl 0.5%) at 37°C was inoculated into in 2 l LB (pH 7.4) medium in a 3-L jar fermenter. Cells were grown continuously at 37°C for ∼12 h, adjusting the agitation speed at 300 r.p.m. with fixed 2-L min⁻¹ air flow rate. Growth was monitored by measuring the optical density at 600 nm (OD₆₀₀).

cDNA Microarray analysis

Cells were collected by centrifugation at 135, 150, 170, 190, 250, 420, 480, and 720 min postinoculation (which correspond to T1, T2, T3, T4, T5, T6, T7, and T8) after adding RNA protect (Qiagen, Chatsworth, CA, USA) and stored at −80°C, while the control sample was collected at 130 min. RNA extraction, cDNA synthesis, and microarray analyses of E. coli were based on the method described in Kobayashi et al. (2007).

Normalization of microarray data

Gene expression levels are evaluated by scanning the fluorescence intensity for each spot, and there is usually some experimental variation that occurs in every microarray experiment. It is, therefore, important to minimize experimental variation, and although several methods of microarray normalization have been developed (Quackenbush, 2002; Yang et al., 2002). Normalization of the logarithmic ratio of expression intensity between target (R_i) (i.e., samples at T1, T2, T3, T4, T5, T6, T7, and T8) and control (G_i) (i.e., sample at 130 min) experiments was carried out based on MA plots (Dudoit et al., 2002), which can show the intensity-dependent ratio of raw microarray data using TREBAX (http://kanaya.naist.jp/Web/software/trebax/trebax2.html). The MA plot used 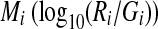as the y-axis and 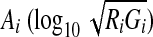as the x-axis. By plotting values of A_i on the abscissa and M_i on the ordinate of a coordinate system, it was possible to evaluate the bias error with respect to the average logarithmic intensities. The normalized log ratio 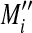was estimated as the difference between M_i and baseline 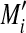. Here, using the relation between M_i and A_i (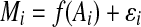, where ɛ_i is the difference between M_i and f(A_i) for the ith gene in the MA plot), the baseline for the ith gene was estimated by M′ = f(A_i). With this methodology, it is assumed that there is no large error due to expression intensity in the majority of the spots.

Transcriptomics and metabolomics data set

After normalization of 16 sets of microarray data (twice for each of eight time points, GEO data set GSE6033), the log ratio corresponding to each gene was averaged, and then genes with one or more missing values were removed. The remaining 3,945 genes were used for estimation of transition points in transcriptional levels. In order to extract differentially expressed genes compared with the control (at 130 min), 1,162 genes were selected for which at least one time point the expression value is more than or equal to the threshold mean ± 1.5 × SD determined in the context of all time point data of 3,945 genes, that is, judged by overall mean of log ratio values of 3,945 genes. These highly differentially expressed genes were used for gene-to-metabolite correlation analysis.

Metabolite accumulation profiles consisted of 220 peaks detected by Fourier transform ion cyclotron resonance mass spectrometry (FT-ICR/MS) (Takahashi et al., 2008), which were used for estimation of transition points in metabolite levels. Out of these, there were 174 metabolite derivative groups. To use in gene-to-metabolite correlation analysis, we prepared time-lagged data of metabolite accumulation profiles using linear interpolation as follows: in the case of the quantity of jth metabolite at time t, say m_j(t), is calculated using the following equations. In the case that t is in the interval between T_i and T_i+1 for s time series points,

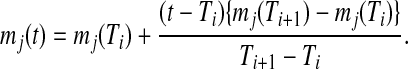(1)

In the case that t is outside of the largest sampling point T_s(t > T_s),

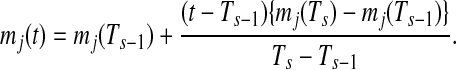(2)

Thus, nine sets of time-lagged data of metabolite accumulation profiles, that is, all 10-, 20-, 30-, 40-, 50-, 60-, 70-, 80-, and 90-min lagged data have eight time point profiles predicted by linear interpolation. Pearson correlation coefficient between kth gene expression 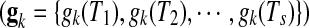, and jth metabolite accumulation profiles 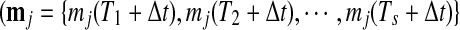, here, 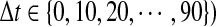was calculated for gene-to-metabolite correlation analysis.

Transition point estimation by LDS

LDS uses internal state variables in the generative model for cellular internal state changes. These internal states correspond to the compressed description of the observed biological system prior to adding noise factors. Details of the LDS were described in Morioka et al. (2007), so we briefly describe this method. First of all, the proposed model is defined by the following two equations:

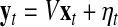(3)

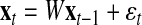(4)

Here, 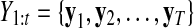and 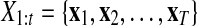correspond to observational “omics” data and internal state for each observational vector for time series 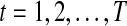, respectively. V is a D × N observational matrix in which D is the number of genes or metabolites, and N is the dimension of internal states, W is an N × N internal state transition matrix, D-dimensional vector η_t is an observational noise, and N-dimensional vector ɛ_t is a transition noise. The vectors x₁, ɛ_t and η_t are generated according to 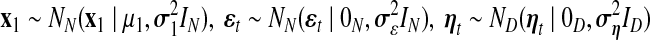. Here 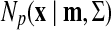is a probabilistic density function, that is,

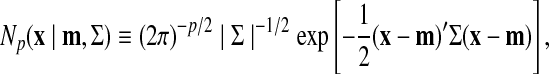(5)

where p dimensional probabilistic vector x obeys a normal distribution whose mean vector is m, and covariance matrix Σ.

We assume that the observational and internal transition noises are both Gaussian, and therefore the relationship is a first-order Markov process defined by Equation 6.

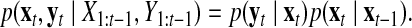(6)

The model parameters are defined as the set 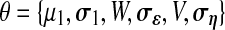. Note that the model corresponds to a Kalman Filter when θ is known (Kalman and Bucy, 1961). The initial state x₁ is defined as 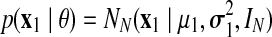and the following states are defined as 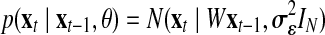. From Equations 3 and 6, the following function is obtained:

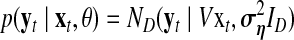(7)

Using these results, the following joint probability is obtained:

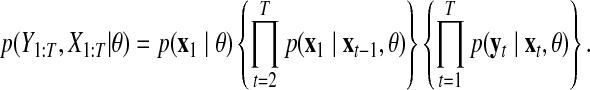(8)

The parameter optimization follows a standard EM algorithm. Using the resulting estimated parameters, the log-likelihood with respect to the present time point t when all time points are given, is defined by Equation 9:

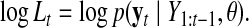(9)

“Likelihood values,” here means the generative probability of current data based on the condition of the past data. If this value is low, then the current data cannot be adequately explained by past data; in other words, a transition has occurred. log L_t is a quantitative index of transition of the current state t from the previous state t − 1 because log L_t is very small if the current state t cannot be predicted by the previous state t − 1.

Gene-to-metabolite correlation network functional analysis

All of the gene-to-metabolite networks were constructed based on Pearson correlation coefficient (PCC) r ≥ 0.9. Genes were functionally categorized using their Gene Ontology (GO) information with respect to “biological process” (Ashburner et al., 2000), and overrepresented GO terms were identified using Fisher's exact test. The one-tailed Fisher's exact p-value corresponding to overrepresentation of categories have been calculated based on counts in 2 × 2 contingency tables. Counts n₁₁, n₁₂, n₂₁, and n₂₂ in the contingency table refer to: n₁₁, number of observations of a particular category in the first gene set; n₁₂, number of other categories in the first gene set; n₂₁, number of observations of a category in second gene set; and n₂₂, number of observations of other categories in the second gene set. p-values were corrected by the FDR method (Benjamini and Hochberg, 1995), and the threshold was set to be 0.05.

Results and Discussion

Estimation of transition points of transcriptomics and metabolomics data using LDS

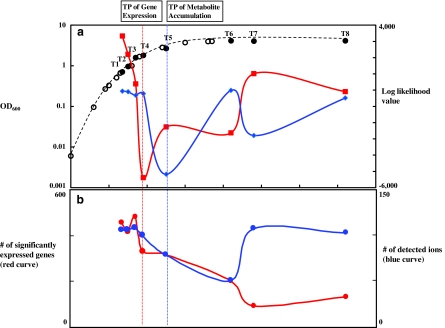
In the present study, we mainly focused on growth stage shift of E. coli, that is, from exponential into stationary phase, and performed time series experiments of E. coli to elucidate relationships between gene expression and time-lagged metabolite accumulation profiles from the nontargeted perspective under normal growth condition (LB medium). Samples were collected at 135, 150, 170, 190, 250, 420, 480, and 720 min postinoculation (which correspond to T1, T2, T3, T4, T5, T6, T7, and T8, as shown in Fig. 1a), where over night liquid culture cells were added into 2l LB medium. RNA was extracted at eight different growth stages of E. coli and cDNA microarray experiments were performed twice for each sample. Also, levels of metabolites were measured by using Fourier transform ion cyclotron resonance mass spectrometry (FT-ICR/MS) (Takahashi et al., 2008). After normalizing the time series data set, we got the expression profiles for 3,945 genes and accumulation profiles with 220 metabolites. In order to compare transition points at transcriptome and metabolome levels, we applied LDS to microarray and metabolomics data. LDS has been applied to identify transition points in transcriptome and metabolome in cells for several species such as Bacillus subtilis and Arabidopsis thaliana (Morioka et al., 2007). Transition changes for gene expression and metabolite accumulation profiles correspond to the log-likelihood values produced by LDS. Figure 1a shows the log-likelihood values calculated by using gene expression and metabolite accumulation profiles, which are indicated by red and blue curves, respectively. “Likelihood values,” here means the generative probability of current data based on the condition of the past data. If this value is low, then the current data cannot be adequately explained by past data; in other words, a transition has occurred. Transition points, here, correspond to lower conditional probability, which cannot be properly predicted by past data, indicating that drastic changes of cellular components, for example, gene expression and metabolite accumulation, occur and cellular condition moves to a different stage, which makes the cell possible to survive. Likelihood values were calculated twice for both directions, from 135 to 720 min and from 720 to 135 min, and then averaged values were used for detection of transition points. The lowest log-likelihood values were obtained at T4 corresponding to 190 min postinoculation in transcriptomics (−5.4 × 10⁻³), and at T5 corresponding to 250 min in metabolomics data (−5.2 × 10⁻³), suggesting that transition points corresponding to transcriptomics and metabolomics data are different (i.e., time lag), and transition occurs first at the transcriptional level, followed by the metabolite level. The number of genes with significantly abundant mRNA judged by mean (i.e., overall mean for 3,945 Cy5 intensity values) + 1.5 × SD for Cy5 intensity values, starts to decrease from time point T4 (red curve in Fig. 1b), indicating that this result coincides with the predicted transition point (T4) by LDS analysis of transcriptomics data. On the other hand, the number of detected ions transiently decreases at the time point T5 (blue curve in Fig. 1b), and this also coincides with the predicted transition point (T5) by LDS analysis of metabolite accumulation profiles. That is, 60-min time lag observed between transcriptomics and metabolomics data in E. coli corresponds to time lag of dynamical change of gene expression profiles and metabolite accumulation profiles within a cell.

FIG. 1.

Transition point (TP) analysis. (a) Growth curve of E. coli and log-likelihood values by LDS analysis. First and second axes correspond to OD₆₀₀ and log-likelihood values, respectively. Red and blue curves correspond to means of forward and backward time direction log-likelihood values calculated by LDS for gene expression and metabolite accumulation profiles, respectively. Eight sampling points are indicated by black circles with T1, T2, T3, T4, T5, T6, T7, and T8. Estimated transition points by using gene expression and metabolite accumulation profiles are indicated by vertical red and blue dot lines through (a) to (b), respectively. (b) The number of genes with significantly abundant mRNA and detected ions. First and second axes correspond to the number of genes and detected ions, respectively. For genes with significantly abundant mRNA, the threshold was set to be Mean + 1.5 × SD for Cy5 intensity values after normalization. Probe intensity values were used because mRNA abundances at each time point rather than profile changes through cell growth could affect transition points of the whole cell.

Gene-to-metabolite correlation analysis in the context of time lag between transcriptomics and metabolomics data

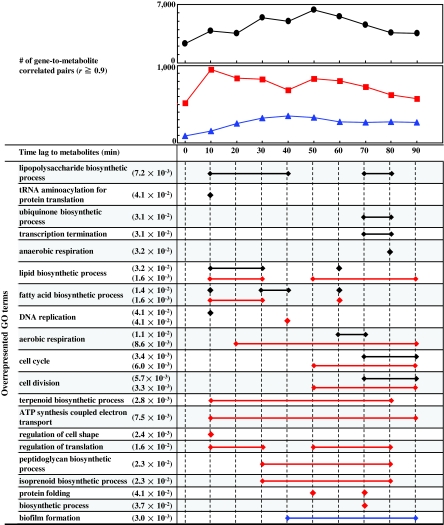
According to the analysis of transition points as described above, there is a 60-min time lag between transition points of transcriptomics and metabolomics data, which indicates that time-lagged gene-to-metabolite correlations could unravel novel gene-to-metabolite relations. First, to remove noise, we selected only significantly expressed genes and metabolites, and then calculated all gene-to-metabolite correlation pairs. A total of 1,162 genes and 174 metabolite profiles were used for gene-to-metabolite correlation analysis. We assumed that transition occurs first at the transcriptional level, followed by the metabolite level, because LDS results indicated that global transcriptional changes precede metabolite accumulation, although possibility of opposite relations, could not be excluded. We set the time lag of metabolite accumulation profiles to be between 0 and 90 min in 10-min steps, and decided to make time-lagged metabolite accumulation profiles by using linear interpolation because of its simplicity. Larger time lags (e.g., 100 min) were not considered in the present study as our main focus has been growth stage shift of E. coli, that is, from exponential into stationary phase around T3, T4, and T5. PCCs between gene expression profiles and time-lagged metabolite accumulation profiles were calculated. Figure 2 shows the number of highly correlated gene-to-metabolite pairs (r ≥ 0.9). The number of correlated pairs increases with time up to 50–60 min (indicated by the black line at the top of Fig. 2) and after that it decreases, suggesting that the time lag associated with the maximum number of gene-to-metabolite correlated pairs is consistent with that of transition points between transcriptome and metabolome as explained in Figure 1. Because LDS can predict conditional probability based on just one past data, time lags with higher resolution can be found by the finer intervals. The resolution of LDS can be considered to be in the range of 10 min because maximum number of correlation pairs was obtained at 50-min time lag. Thus, we concluded that a 60-min time lag was observed between transcriptomics and metabolomics data in E. coli.

FIG. 2.

Gene-to-metabolite correlation analysis considering time lag between transcriptomics and metabolomics data. The plot shows the number of gene-to-metabolite (top: black), gene-to-unsaturated phosphatidylglycerols (PGs) (middle: red), and gene-to-cycropropanated PGs (middle: blue) correlated pairs (PCC ≥0.9) using 1,162 genes and 174 metabolites, respectively. Time lag of abscissa shows considered time lag between transcriptomics and metabolomics data. GO terms with FDR corrected p-value ≤ 0.05 (minimum value is indicated, if any) are indicated at the left side. Diamond and bar correspond to overrepresented GO terms by Fisher's exact test. lipopolysaccharide biosynthetic process is, for example, overrepresented in correlated pairs between transcriptomics and 10-, 20-, 30-, 40-, 70-, and 80-min time-lagged metabolomics data.

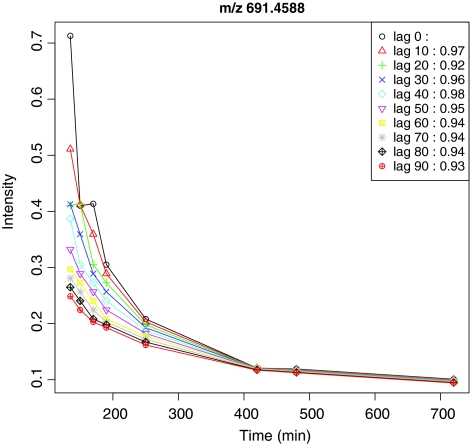
Many time-lagged-specific gene-to-metabolite correlated pairs can be detected by taking into consideration the time lag between transcriptomics and metabolomics data. In order to investigate what biological processes are associated with metabolites in a time-lagged-specific manner, we determined the overrepresentation of the GO annotations (Ashburner et al., 2000; Keseler et al., 2005) among the genes associated with highly correlated gene-to-metabolite pairs corresponding to different time-lagged data. Significant relations between the GO terms and metabolites were obtained by Fisher's exact test. Figure 2 shows the GO terms under the “biological process” annotation category that are significantly associated (FDR corrected p-value ≤0.05) with highly correlated gene-to-metabolite pairs determined by using gene expression profile and time-lagged metabolite accumulation profile data. For example, in 30-min time lag, GO terms, “lipopolysaccharide biosynthetic process,” “lipid biosynthetic process,” and “fatty acid biosynthetic process” are overrepresented, indicating that expression profiles of genes involved in those GO terms are significantly correlated with the levels of metabolites (indicated by black diamond or line in Fig. 2). Otherwise, those genes are not overrepresented if no time lag is considered. Genes involved in “cell division,” and “cell cycle” are overrepresented in 70-, 80-, and 90-min time-lagged data, whereas no significant GO terms can be associated with 50-min time-lagged data. Consequently, taking into consideration a time lag between transcriptomics and metabolomics data allows us to elucidate direct or time-lagged gene-to-metabolite relations, suggesting that taking into consideration a time lag between transcriptomics and metabolomics data could detect novel gene-to-metabolite relations. Daran-Lapujade et al. (2007) and Ralser et al. (2009) discussed about the regulation of metabolic pathways by transcription-independent process. Ralser et al. (2009) focused on pentose phosphate pathway, as a conclusion; an initial transcription-independent metabolic reconfiguration prevents a collapse of the cellular redox state. In our analysis, we considered only transcription-dependent process and detected particular cell processes, even if there are pathways controlled by transcription-independent mechanisms. Because known transcription-independent mechanisms are limited now, at the present study, our procedure could get global perspectives about dynamics of gene-to-metabolite correlation networks. Ideally, all time-lagged data set would be obtained by way of experiments. But because of unavailability of such data, in this study, we made nine time-lagged data predicted by linear interpolation, which might not predict particular metabolite accumulation profiles with nonlinear nature. Assuming that almost all metabolite accumulation profiles could be linearly expressed between two adjacent time points, we tentatively set 10 min to be as minimum time lag for correlation analyses. With this resolution, it has been possible to obtain maximum number of gene-to-metabolite correlation pairs at 50-min time lag (as shown in Fig. 2). Furthermore, as an example shown in Figure 3, time-lagged accumulation profiles for a metabolite generated using 10-min resolution are all different, and the highest correlation between original and time-lagged data was obtained in case of 40- min, but not 10-min time lag, indicating that generated profiles with 10-min resolution contain intrinsic information concerning time lag. Walther et al. (2010) addressed time-lagged correlation between transcripts and metabolites by the Granger causality approach, and presented relationships between transcripts and metabolites in yeast. We conclude that our observation of time-lagged correlations in E. coli could be valid for metabolites with linear behavior.

FIG. 3.

Illustration of time-lagged data for an ion with m/z = 691.4588. Original and nine time-lagged accumulation profiles for an ion with m/z = 691.4588. Each accumulation profile is indicated as follows: circle (black) for original; triangle (red) for 10 min; plus (green) for 20 min; times (blue) for 30 min; diamond (cyan) for 40 min; triangle point-down (magenta) for 50 min; square and times superimposed (yellow) for 60 min; plus and times superimposed (gray) for 70 min; diamond and plus superimposed (black) for 80 min; circle and plus superimposed (red) for 90-min time-lagged data. Pearson correlation coefficients between original and each time-lagged data are indicated at top right side of the figure, and x- and y-axes correspond to time (min) and relative intensity, respectively.

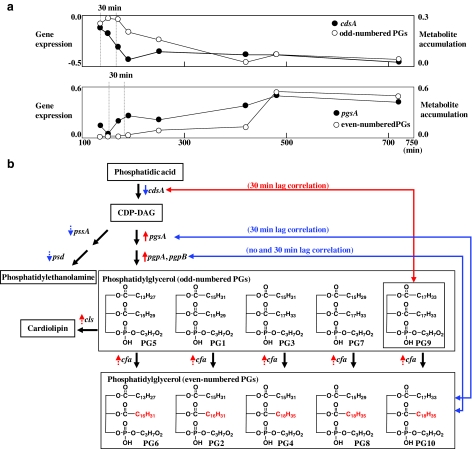
In metabolomics data, we previously detected ten phosphatidylglycerols (PG1-10 as shown Fig. 4b) as the most abundant metabolites in time series analysis (Takahashi et al., 2008). Five PGs (PG1, 3, 5, 7, and 9) and another five PGs (PG2, 4, 6, 8, and 10) are dominant in exponential and stationary phases, respectively. Cycropropanation of PGs is a key step of transition from exponential to stationary phase in E. coli (Grogan and Cronan 1997). Five pair of PGs (PG1 and PG2, PG3 and PG4, PG5 and PG6, and PG7 and PG8, PG9 and PG10) can be associated with cycropropanation process, that is, those PGs can be considered to be utilized as the marker molecules for assessing two phases. Thus, we analyzed gene-to-metabolite correlation with respect to two groups of PGs, unsaturated phospholipids, and cyclopropanated phospholipids, in order to elucidate gene-to-PG networks. Overrepresented GO terms with respect to gene-to-PG correlated pairs are shown in Figure 2. Genes associated with the “lipid biosynthetic process” and “fatty acid biosynthetic process” are correlated with unsaturated PGs in a time-lagged-specific manner (indicated by a red diamond or line in Fig. 2). These correlations, that is, lipid metabolism correlations between transcriptional and metabolite levels, coincide with biological meaning. Cycropropanated PGs are correlated with genes associated with “biofilm formation” in a time-lagged specific manner (indicated by a blue diamond or line in Fig. 2).

FIG. 4.

Phospholipid biosynthesis pathway. (a) Gene expression profiles (top: cdsA, bottom: pgsA) and metabolite accumulation profiles (top: unsaturated PGs, bottom: cycropropanated PGs). Metabolite accumulation profiles correspond to average values of each PG group. (b) The biosynthesis pathway from phosphatidic acid to phosphatidylethanolamine or cardiolipin. Metabolite and gene names are inside the squares and beside black solid arrows, respectively. Black solid arrows represent chemical reactions. Arrows beside gene names indicate up and down transcriptional activities through cell growth. Dashed arrows mean the weak expression changes. The red and blue lines between genes and metabolites indicate correlations between genes and unsaturated and cycropropanated PGs, respectively.

Finally, we focused on the gene-to-metabolite correlations with respect to the phospholipid biosynthesis pathway, in which PGs were synthesized. Figure 4b summarizes the relationships between genes and PGs in the phospholipid biosynthesis pathway. A key intermediate in phospholipid biosynthesis is cytosine diphosphate (CDP)-diacylglycerol (DAG), which is formed by CdsA from phosphatidic acid and cytosine triphosphate. In the biochemical regulation of phospholipid composition of membrane, the zwitterionic (phosphatidylethanolamine) and acidic (PG and cardiolipin) branches of phospholipid synthesis compete for a common pool of CDP-DAG. PGs are synthesized from CDP-DAG in two steps, by PgsA and PgpA/B (Zhang and Rock, 2008). In our correlated analysis with respect to PGs, the expression profiles of cdsA and pgsA were correlated with PG9 and all even-numbered PGs in 30-min time-lagged data, respectively, whereas no PGs correlated with those genes when no time lag was considered. Figure 4a shows expression profiles of cdsA and pgsA and average accumulation profiles of unsaturated and cycropropanated PGs, supporting the fact that there could be a time lag between gene expression and metabolite accumulation profiles, as predicted by LDS analysis. The expression profile of pgpA was correlated with some even-numbered PGs in both no and 30-min lagged data. Accumulation of PG9 and expression of cdsA were downregulated through cell growth, whereas those of even-numbered PGs, pgsA, and pgpA were upregulated. These results indicate that the content of CDP-DAG decreases according to decreasing of the transcriptional level of cdsA, and the pathway from CDP-DAG to PGs is active with the increase of the transcriptional level of pgsA and pgpA. There is another biochemical pathway from CDP-DAG, which leads to phosphatidylethanolamine. The expression values of two genes associated with this pathway decreased through cell growth, but the amount of change was not significant in our data, that is, below the threshold (indicated by blue dotted arrows beside gene names in Fig. 3b). These results indicate that the pool of CDP-DAG could be used to synthesize PGs, but not phosphatidylethanolamine, when E. coli enters into the stationary phase from the exponential phase. It has been reported previously that Bacillus subtilis PssA, a molecularly distinct integral membrane protein, was used to replace the transiently membrane-associated PssA in E. coli. Amplification of B. subtilis PssA increases the relative and absolute amounts of phosphatidylethanolamine and impairs growth (Saha et al., 1996a, 1996b). Therefore, the balance of zwitterionic (phosphatidylethanolamine) and acidic phospholipids (PGs) in E. coli is important. Thus, from this analysis, it can be concluded that PGs could be more responsible for membrane balance than phosphatidylethanolamine.

Conclusion

In the present study, we presented to our knowledge the first report taking into consideration the time lag between transcriptomics and metabolomics data, which revealed time-lagged-specific gene-to-metabolite relations.

Acknowledgments

This work was supported by a Grant-in-Aid for Scientific Research on Priority Areas, “Systems genomics”, from the Ministry of Education, Culture, Sports, Science and Technology of Japan.

Author Disclosure Statement

The authors declare that no conflicting financial interests exist.