Skip to main content
PMC home page
OMICS : a Journal of Integrative Biology logoLink to OMICS : a Journal of Integrative Biology
. 2011 Jun;15(6):393–398. doi: 10.1089/omi.2010.0090

Polygenic Modeling of Genome-Wide Association Studies: An Application to Prostate and Breast Cancer

John S Witte 1,✉, Thomas J Hoffmann 1
PMCID: PMC3125548  PMID: 21348634

Abstract

Genome-wide association studies (GWAS) have successfully detected and replicated associations with numerous diseases, including cancers of the prostate and breast. These findings are helping clarify the genomic basis of such diseases, but appear to explain little of disease heritability. This limitation might reflect the focus of conventional GWAS on a small set of the most statistically significant associations with disease. More information might be obtained by analyzing GWAS using a polygenic model, which allows for the possibility that thousands of genetic variants could impact disease. Furthermore, there may exist common polygenic effects between potentially related phenotypes (e.g., prostate and breast cancer). Here we present and apply a polygenic model to GWAS of prostate and breast cancer. Our results indicate that the polygenic model can explain an increasing—albeit low—amount of heritability for both of these cancers, even when excluding the most statistically significant associations. In addition, nonaggressive prostate cancer and breast cancer appear to share a common polygenic model, potentially reflecting a similar underlying biology. This supports the further development and application of polygenic models to genomic data.

Introduction

Genome-wide association studies (GWAS) of binary traits compare hundreds of thousands of single nucleotide polymorphisms (SNPs) in cases to those in controls to determine whether an association with disease exists (Lander, 1996; Risch and Merikangas, 1996). This approach leverages the successful sequencing of the human genome (Lander et al., 2001; Venter et al., 2001) and the identification of millions of SNPs—a subset of which can capture (“tag”) common variation via linkage disequilibrium (Daly et al., 2001; Frazer et al., 2007; Gabriel et al., 2002; HapMap, 2003, 2005). In conjunction with this, rapid technological advances have allowed for efficiently measuring over a million SNPs.

GWAS have detected highly statistically significant associations between hundreds of SNPs and a broad range of phenotypes, as listed in the National Human Genome Research Institute's “Catalog of Published Genome-Wide Association Studies” (http://www.genome.gov/gwastudies) (Hindorff et al., 2009). These results are especially exciting in light of the previous difficulties replicating genetic findings for many diseases, such as prostate cancer (Schaid and Chang, 2005). However, the associated SNPs highlighted by most of these studies explain a limited amount of disease heritability (Donnelly, 2008; Maher, 2008; Manolio et al., 2009; McCarthyet al., 2008). For example, although GWAS have detected over a dozen SNPs strongly associated with prostate cancer, these only account for approximately 15% of the familial risk of this disease (Witte, 2009). This in part reflects the small magnitude of effect for most SNPs reported by GWAS and their focus on common variants. Even if large SNP effects are found (e.g., for combinations of SNPs), these may not have high penetrance and so do not confer a high risk of disease.

The lack of heritability explained by GWAS could also reflect the focus on a handful of the most strongly associated SNPs—and the underlying assumption that the remaining SNPs have no impact on disease whatsoever. That is, only highly statistically significant findings are generally followed-up in GWAS due to the large multiple testing burden from considering so many SNPs (Witte et al., 2000). However, some diseases may follow a polygenic model whereby a large number of SNPs, including those with weaker associations, may explain the heritability of disease (Valdar et al., 2006). What has previously been termed “missing” heritability in GWAS may actually only be “hidden” and simply require a more comprehensive evaluation of genetic variation to detect (Yang et al., 2010). Moreover, such a model may explain some common polygenic effects between GWAS of different phenotypes (Purcell et al., 2009).

For example, when applying a polygenic model to GWAS of schizophrenia, as the number of SNPs considered was expanded to the tens of thousands, an increasing proportion of heritability was explained (Purcell et al., 2009). They also found that the polygenic model could be extended to different psychiatric conditions (e.g., bipolar disease) but not to nonpsychiatric traits (Purcell et al., 2009). As another example, findings from GWAS of height are said to explain only about 5% of genetic variability; however, a polygenic model that simultaneously evaluates the effects of all SNPs indicates that they may actually explain 45% of genetic variability (Yang et al., 2010). The remaining heritability in human height might be explained by variants that have been poorly assayed by current SNP chips due to low LD and/or their being rare (Yang et al., 2010).

In light of these intriguing results, here we consider the potential value of polygenic models in GWAS of prostate and breast cancer. These cancers are simultaneously investigated here because they may share factors in steroid biosynthesis pathways that impact the development of hormone dependent and independent tumors (Risbridger et al., 2010). We first describe the data and polygenic model and then present a detailed application. Our work suggests that a polygenic model may help further explain the genomic basis of prostate and breast cancers, and that this type of analysis may be generally beneficial for GWAS within and across phenotypes.

Materials and Methods

Prostate and breast cancer GWAS data

For this investigation we used data from the first-stage of the Cancer Genetic Markers of Susceptibility (CGEMS) GWAS of prostate and breast cancer (http://cgems.cancer.gov). The initial stage of the prostate cancer GWAS includes 1,172 cases and 1,157 controls of European-American ancestry who were selected from the Prostate, Lung, Colorectal, and Ovarian (PLCO) Cancer Screening Trial and genotyped using the Illumina 550K array (Thomas et al., 2008; Yeager et al., 2007). The cases were oversampled for men with more aggressive prostate cancer, allowing us to stratify our polygenic modeling by aggressive and nonaggressive disease. The first stage of the breast cancer GWAS includes 1,145 cases and 1,142 controls nested in the Nurses' Health Study (NHS) cohort; these women were also genotyped using the Illumina 550K chip (Hunter et al., 2007).

Both of these studies had additional stages and replication efforts that successfully detected genetic variants associated with prostate and/or breast cancer (Hunter et al., 2007; Thomas et al., 2008; Yeager et al., 2007). For example, the CGEMs GWAS of prostate cancer detected associated SNPs in distinct loci on chromosome 8q24—a region also associated with other cancers—and a risk SNP in the beta-microseminoprotein (MSMB) gene (Thomas et al., 2008; Yeager et al., 2007). Interestingly, due to limited power, the MSMB risk SNP (rs10993994) had only the 24,223rd smallest p-value in the initial CGEMs GWAS, but has been highly replicated (Thomas et al., 2008). This suggests that weakly associated SNPs may still play an important role in disease, that stringent significance thresholds could lead to false negative results (Witte et al., 1996), and supports a polygenic model for prostate carcinogenesis.

Polygenic model

The standard analysis of GWAS data individually evaluates the relationship between each SNP and disease. For example, one may a fit a logistic regression model to assess the association between the ith SNP and disease:

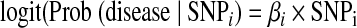graphic file with name M1.gif (1)

where SNPi is coded in a log additive manner to reflect the number of alleles an individual carries at this SNP (i.e., 0, 1, or 2), and βi is the parameter of interest: the log odds ratio reflecting the impact of one additional allele in SNP i on disease risk.

Most common complex diseases do not arise from a single genetic cause, but rather a combination of genetic and environmental factors (i.e., they are polygenic) (Witte, 2010). To assess such joint effects on disease, model (1) can be extended to include multiple SNPs, as well as nongenetic exposures. Conventional models can only evaluate a limited number of factors simultaneously, so these are often chosen for inclusion using some sort of model selection procedure (e.g., stepwise) (Cordell and Clayton, 2002). Such an approach, however, assumes with 100% certainty that all excluded factors have no effect whatsoever on disease; in a GWAS, this generally encompasses well over 99% of the SNPs initially considered.

A polygenic approach might first calculate log odds ratios for each individual SNP in one GWAS [Eq. (1)], and then apply these values to another GWAS in order to determine whether increasing numbers of SNPs explain an increasing amount of heritability (Purcell et al., 2009). Here, an overall score Sj is determined for the jth individual in the second GWAS as

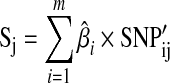graphic file with name M2.gif (2)

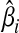where Inline graphic is the log odds ratio estimate for SNP i from the first GWAS, and 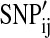Inline graphic is the number of ith SNP alleles individual j has in the second GWAS (Purcell et al., 2009). That is, a single global score for each individual in the second GWAS dataset is constructed from the sum of the number of alleles an individual possessed at each SNP, weighted by the log odds ratio estimate from the first GWAS. Then a logistic regression akin to model (1) but with the vector of weights S in place of SNPi is fit to compare the scores of cases to controls in the second GWAS.

We applied this polygenic model to the CGEMs data from prostate and breast cancer in two ways. First, we assessed whether an increasing number of SNPs explained more heritability within each cancer type alone. We used a resampling approach to randomly split the data into two equal sized subsets, a “training” set and a “test” set. In the training set, we estimated the univariate odds ratios [i.e., from Eq. (1)]. Then we used these odds ratios to calculate scores [Eq. (2)], and fit polygenic models within each cancer type, as well as prostate cancer subsets comprised of men with aggressive and nonaggressive disease. The second type of analysis assessed whether a common polygenic component was shared in breast cancer and prostate cancer. Here we used the breast cancer GWAS odds ratio estimates as weights for the prostate cancer GWAS and vice versa. Again, we stratified the prostate cancer cases into aggressive and nonaggressive disease. When looking within such subgroups comparisons were made to all prostate cancer controls.

For all of our analyses, to evaluate whether the heritability explained is driven by a small number of strongly associated SNPs, or more of a combined signal from many common SNPs, we constructed scores in the second GWAS dataset based only on SNPs from certain ranges of significance levels in the first GWAS dataset. If only a few highly significant SNPs were explaining most of the polygenic effect on disease, then we would expect only ranges including the most significant SNPs to be relevant. In contrast, if scores in the second GWAS excluding the most significant SNPs from the first GWAS remain significant, this supports a common polygenic inheritance model. SNPs were also filtered by pairwise linkage disequilibrium (LD) (r2 = 0.5) so that the score would represent the effect of independent SNPs. Without this filter it is possible that a number of linked SNPs all reflecting the same association with disease might drive much of an apparently polygenic model.

Results

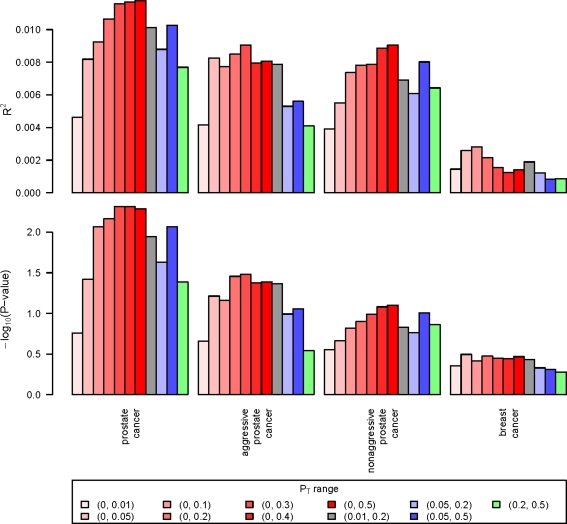
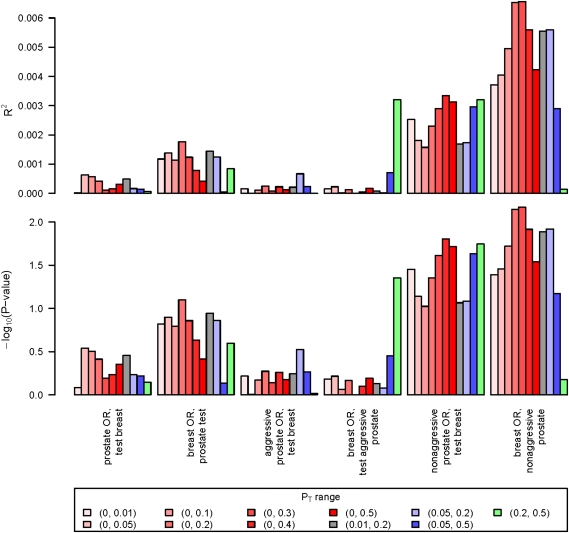
Figures 1 and 2 give the results from our application of the polygenic model to the CGEMs GWAS data for prostate and breast cancer. Figure 1 presents findings when evaluating the models within each cancer type using the resampling approach, whereas Figure 2 looks at whether there is a common polygenic model between these cancers. For both figures, the models considered are highlighted on the horizontal axis, and the colored bars reflect different p-value ranges for the log odds ratios included in the weight [Eq. (2)]. The red bars expand the upper p-value threshold—with deeper colors indicating a larger range—and the other colors are for p-value ranges that exclude the most statistically significant associations. The top panel gives the proportion of variance explained by the polygenic model, and the bottom panel the −log10(p-value) for association between the polygenic score [S in Eq. (2)] and disease.

FIG. 1.

FIG. 1.

Open in a new tab

Polygenic model results for prostate and breast cancer alone, using CGEMs genome-wide association study data. Within each grouping, data were split in half and one set was used to estimate SNP-specific odds ratios, which were applied to the other set (following Purcell et al., 2009). The top panel gives the proportion of variance explained by the polygenic model, and the bottom panel the −log10(p-value) for association between the polygenic score and disease. PT is the range of SNP association p-values included in the polygenic model. The colored bars reflect different p-value ranges for the log odds ratios included in the models. Red bars expand the upper p-value threshold with deeper colors indicating a larger range. The other colors are for p-value ranges that exclude the strongest associations.

FIG. 2.

FIG. 2.

Open in a new tab

Results from considering shared polygenic models between prostate and breast cancer. See Figure 1 legend for specific details on what is presented in the figure.

Focusing on Figure 1, the model grouping any type of prostate cancer to controls shows the most evidence of a polygenic model (p < 0.01). The p-values generally become smaller, and the heritability larger, as more SNPs are introduced into the model. This effect is maintained, although slightly less so, in the models not including the most statistically significant SNPs (i.e., from the training set). Aside: note that values plotted are the means from the 10 resampling iterations. These results suggest that in addition to the strongly associated SNPs, other SNPs that would be deemed “less significant” are also contributing to the polygenic model. That said, the variance explained by the model (Nagelkerke, 1991) is quite low (1%). When looking at the two prostate cancer subphenotypes, aggressive and nonaggressive, there is also the suggestion of a polygenic model (Fig. 1). These might be weaker than that observed for the overall prostate cancer group simply due to the smaller sample sizes. Breast cancer alone does not show much evidence for a polygenic model (Fig. 1).

Figure 2 gives results from our evaluation of a shared polygenic component in prostate and breast cancer. We see essentially no evidence of a shared polygenic component between prostate cancer and breast cancer, and even less support for a shared component between aggressive prostate cancer and breast cancer. There is suggestive evidence that there may exist a shared genetic component between nonaggressive prostate cancer and breast cancer (p < 0.01). We see a similar pattern here as above in Figure 1: smaller p-values and higher heritability when more SNPs are introduced into the model, and less so in the polygenic model that excludes the most significant SNPs (Fig. 2). As before, however, the heritability explained by this model is quite low.

Finally, the number of SNPs contributing to the weighted score in the polygenic models [Eq. (2)] increased linearly with the expansion of p-value ranges for inclusion in the model. Of the 550K SNPs originally measured by the GWAS, the number incorporated into the models when p < 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, and 0.5 was approximately 2.4K, 11.5K, 23K, 45K, 68K, 90K, and 112K, respectively. When restricting the p-value range to [0.05, 0.2] or [0.05, 0.5], the number of SNPs included in the polygenic models was about 34K or 100K, respectively.

Discussion

We found that applying a polygenic model to an increasing number of SNPs from one GWAS to another—within and across prostate and breast cancer—seemed to explain an increasing proportion of heritability, but this was quite low. Nevertheless, there is a growing appreciation that such common complex diseases may arise from a large number of genetic and environmental risk factors (Purcell et al., 2009; Yang et al., 2010). Applying polygenic models to genome-wide data can help explain a larger proportion of the heritability than simply focusing on the handful of most statistically significant results.

The strongest common polygenic model resulted from applying the breast cancer log odds ratios as weights to the non-aggressive prostate cancer genotypes. A slightly weaker shared model was observed when reversing this, and applying the nonaggressive prostate cancer log odds ratios to the breast cancer genotypes. The differences here may reflect the larger sample size in the breast cancer GWAS, which would allow for more accurate estimation of the log odds ratios. These cancers have biological similarities and common factors that may control hormone-dependent and -independent tumor development; in particular, there exist similarities in the key hormone signaling pathways (e.g., steroid biosynthesis) across these cancers (Risbridger et al., 2010). Why there is only a relationship between nonaggressive prostate cancer and breast cancer remains unclear. One possibility is that there exists a similar hormonal mechanism underlying the development of these cancers, but a distinct mechanism for disease progression. Another is that the CGEMs nonaggressive prostate and breast and cancer samples might be more similar because the latter were not selected based on phenotypic characteristics.

Our findings were only slightly weakened when we removed the most statistically significant associations from the model, restricting the p-value range to [0.01, 0.2] or [0.05, 0.2]. This suggests that the results are not entirely driven by the strongest associations, and that variants initially deemed “nonsignificant” in the GWAS of prostate and breast cancer may still help explain some of the heritability of these diseases. Moreover, the results were little changed when using different linkage disequilibrium filters to remove variants that are correlated and thus may reflect the same association with disease. In particular, when using a more conservative LD filter of r2 < 0.25, more SNPs were removed from consideration leading to slightly weaker results. And when there was no LD filter the findings were stronger than reported here. Note that SNPs that exhibit even lower LD (e.g., r2 < 0.1) with a limited number of causal variants could explain some of the findings observed here; further work will explore this possibility.

Although the proportion of heritability explained increased with larger numbers of variants in our polygenic model, the overall heritability remained quite low. This may reflect the reduced power due to limited sample sizes in the initial stages of the CGEMs GWAS considered here (Hunter et al., 2007; Yeager et al., 2007). Larger sample sizes may allow for more accurate estimation of the log odds ratio weights and for detecting more statistically significant results from the polygenic model. On a related topic, Nature Genetics is now requiring that power calculations be included in manuscripts presenting results from association studies (Anonymous, 2010). Calculating power post hoc is a bit nonsensical—because one has already completed the GWAS—and subject to much debate in the statistical literature (Hoenig and Heisey, 2001).

Although we have focused on common SNPs from GWAS, polygenic models can also incorporate less common variants and additional sources of genomic variation [e.g., copy number variants (CNVs)]. Continued scientific and technological advances will allow investigators to study less common and different sources of genetic variation. Results from the 1,000 Genomes project (www.1000genomes.org) can be leveraged to assay less common SNPs. Moreover, sequencing technologies are rapidly decreasing in costs, and eventually genome-wide sequence studies will become feasible and provide an unprecedented opportunity to investigate polygenic models for disease.

In contrast with the polygenic model considered here, the conventional approach to GWAS entails evaluating each genetic variant one at a time, and then attempting to replicate only those most strongly associated with disease. In light of the enormous number of tests undertaken with GWAS, a very small alpha-level is generally used to determine “statistical significance” (e.g., p < 5 × 10−8). Although adhering to such strict “significance” cut points helps address issues of multiple comparisons, they are somewhat arbitrary and do not reflect the potential clinical or biological importance of an association (Witte et al., 1996). Moreover, as shown here and elsewhere (Purcell et al., 2009; Yang et al., 2010), genetic variants that do not appear strongly associated may actually contribute to the underlying genomic basis of disease. By taking a broad “genome-wide” view, a polygenic model may provide a more complete understanding of the genetic architecture of complex phenotypes such as prostate and breast cancer (Witte, 2010).

Conclusion

We have described and applied a polygenic model that incorporates information from thousands of SNPs in the analysis of GWAS data. Prostate cancer may arise from large numbers of genetic variants with weak effects. Moreover, there is a potential common polygenic risk between breast cancer and nonaggressive prostate cancer. This suggests that there might be a shared biological basis for these cancers, such as both depending on hormone signaling pathways. If common complex traits are due to a plethora of genetic and environmental factors, the use of polygenic modeling may prove valuable for evaluating large-scale genomic studies.

Acknowledgments

This work was supported by grants CA88164, CA127298, CA127298, and CA112355 from the National Institutes of Health. We thank Eric Jorgenson for helpful comments on this article.

Author Disclosure Statement

Drs. Witte and Hoffmann have no commercial associations that might create a conflict of interest in connection with this manuscript.

References

  1. Anonymous. On beyond GWAS. Nat Genet. 2010;42:551. doi: 10.1038/ng0710-551. [DOI] [PubMed] [Google Scholar]
  2. Cordell H.J. Clayton D.G. A unified stepwise regression procedure for evaluating the relative effects of polymorphisms within a gene using case/control or family data: application to HLA in type 1 diabetes. Am J Hum Genet. 2002;70:124–141. doi: 10.1086/338007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Daly M.J. Rioux J.D. Schaffner S.F. Hudson T.J. Lander E.S. High-resolution haplotype structure in the human genome. Nat Genet. 2001;29:229–232. doi: 10.1038/ng1001-229. [DOI] [PubMed] [Google Scholar]
  4. Donnelly P. Progress and challenges in genome-wide association studies in humans. Nature. 2008;456:728–731. doi: 10.1038/nature07631. [DOI] [PubMed] [Google Scholar]
  5. Frazer K.A. Ballinger D.G. Cox D.R. Hinds D.A. Stuve L.L. Gibbs R.A., et al. A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Gabriel S.B. Schaffner S.F. Nguyen H. Moore J.M. Roy J. Blumenstiel B., et al. The structure of haplotype blocks in the human genome. Science. 2002;296:2225–2229. doi: 10.1126/science.1069424. [DOI] [PubMed] [Google Scholar]
  7. HapMap. The International HapMap Project. Nature. 2003;426:789–796. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
  8. HapMap. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hindorff L.A. Sethupathy P. Junkins H.A. Ramos E.M. Mehta J.P. Collins F.S., et al. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci USA. 2009;106:9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hoenig J.M. Heisey D.M. The abuse of power: the pervasive fallacy of power calculations for data analysis. Am Stat. 2001;55:19–24. [Google Scholar]
  11. Hunter D.J. Kraft P. Jacobs K.B. Cox D.G. Yeager M. Hankinson S.E., et al. A genome-wide association study identifies alleles in FGFR2 associated with risk of sporadic postmenopausal breast cancer. Nat Genet. 2007;39:870–874. doi: 10.1038/ng2075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lander E.S. The new genomics: global views of biology. Science. 1996;274:536–539. doi: 10.1126/science.274.5287.536. [DOI] [PubMed] [Google Scholar]
  13. Lander E.S. Linton L.M. Birren B. Nusbaum C. Zody M.C. Baldwin J., et al. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
  14. Maher B. Personal genomes: the case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. [DOI] [PubMed] [Google Scholar]
  15. Manolio T.A. Collins F.S. Cox N.J. Goldstein D.B. Hindorff L.A. Hunter D.J., et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. McCarthy M.I. Abecasis G.R. Cardon L.R. Goldstein D.B. Little J. Ioannidis J.P., et al. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet. 2008;9:356–369. doi: 10.1038/nrg2344. [DOI] [PubMed] [Google Scholar]
  17. Nagelkerke N. A note on a general definition of the coefficient of determination. Biometrika. 1991;78:691–692. [Google Scholar]
  18. Purcell S.M. Wray N.R. Stone J.L. Visscher P.M. O'Donovan M.C. Sullivan P.F., et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460:748–752. doi: 10.1038/nature08185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Risbridger G.P. Davis I.D. Birrell S.N. Tilley W.D. Breast and prostate cancer: more similar than different. Nat Rev Cancer. 2010;10:205–212. doi: 10.1038/nrc2795. [DOI] [PubMed] [Google Scholar]
  20. Risch N. Merikangas K. The future of genetic studies of complex human diseases. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
  21. Schaid D.J. Chang B.L. Description of the International Consortium For Prostate Cancer Genetics, and failure to replicate linkage of hereditary prostate cancer to 20q13. Prostate. 2005;63:276–290. doi: 10.1002/pros.20198. [DOI] [PubMed] [Google Scholar]
  22. Thomas G. Jacobs K.B. Yeager M. Kraft P. Wacholder S. Orr N., et al. Multiple loci identified in a genome-wide association study of prostate cancer. Nat Genet. 2008;40:310–315. doi: 10.1038/ng.91. [DOI] [PubMed] [Google Scholar]
  23. Valdar W. Solberg L.C. Gauguier D. Burnett S. Klenerman P. Cookson W.O., et al. Genome-wide genetic association of complex traits in heterogeneous stock mice. Nat Genet. 2006;38:879–887. doi: 10.1038/ng1840. [DOI] [PubMed] [Google Scholar]
  24. Venter J.C. Adams M.D. Myers E.W. Li P.W. Mural R.J. Sutton G.G., et al. The sequence of the human genome. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
  25. Witte J.S. Prostate cancer genomics: towards a new understanding. Nat Rev Genet. 2009;10:77–82. doi: 10.1038/nrg2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Witte J.S. Genome-wide association studies and beyond. Annu Rev Public Health. 2010;31:9–20. doi: 10.1146/annurev.publhealth.012809.103723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Witte J.S. Elston R.C. Schork N.J. Genetic dissection of complex traits. Nat Genet. 1996;12:355–356. doi: 10.1038/ng0496-355. [DOI] [PubMed] [Google Scholar]
  28. Witte J.S. Elston R.C. Cardon L.R. On the relative sample size required for multiple comparisons. Stat Med. 2000;19:369–372. doi: 10.1002/(sici)1097-0258(20000215)19:3<369::aid-sim335>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
  29. Yang J. Benyamin B. McEvoy B.P. Gordon S. Henders A.K. Nyholt D.R., et al. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Yeager M. Orr N. Hayes R.B. Jacobs K.B. Kraft P. Wacholder S., et al. Genome-wide association study of prostate cancer identifies a second risk locus at 8q24. Nat Genet. 2007;39:870–874. doi: 10.1038/ng2022. [DOI] [PubMed] [Google Scholar]

Articles from OMICS : a Journal of Integrative Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES