Inferring Genetic Causal Effects on Survival Data with Associated Endo-Phenotypes

Abstract

Age-at-onset phenotypes are important traits in genetic association analyses. Often, intermediate phenotypes that are related to the age-at-onset phenotype are also associated with the marker loci that are associated with the age-at-onset phenotype. In order to understand the genetic etiology of the observed associations, statistical methodology is needed to distinguish between a direct genetic effect on the age-at-onset phenotype and an indirect effect induced by the genetic association with the endo-phenotype that is correlated with the age-at-onset phenotype. In this communication, we introduce a new statistical approach to detect causal genetic effects on survival data in the presence of genetic associations with secondary phenotypes that might influence survival as well and thereby induce seemingly causal relationships. Derived using causal inference methodology, the proposed method is based on standard statistical methodology and can be implemented straight-forwardly, using standard software. Using simulation studies, the theoretical properties of the approach are verified and the power is assessed under realistic scenarios. The practical relevance of the approach is illustrated by an application to survival after cardiac surgery, where genetic components of myocardial infarctions are determined to not influence post-surgery hospital duration except through the MI-pathway.

1 Introduction

In order to understand the genetic mechanisms that influence complex traits such as the age-at-onset of a disease or survival after surgery, it is important to identify endo-phenotypes that are in the ”genetic path” between the marker locus and the phenotype of interest. Such endo-phenotypes can be standard phenotypes, e.g. blood measurements, symptom score, etc, or genomic or epi-genomic data such as expression profiles. The ability to distinguish between causal genetic associations and seemingly genetic associations that are induced by causal genetic associations with intermediate phenotypes can provide important clues into the underlying genetic architecture of the disease. For quantitative traits, VanSteenlandt et al [Vansteelandt et al. 2009] proposed a simple regression adjustment procedure that is applied to the quantitative phenotype of interest, adjusting for the potential presence of an association between the endo-phenotype and the test marker locus. The adjusted quantitative phenotype can then be used in standard genetic association tests for quantitative traits. Using causal inference methodology, VanSteenlandt et al [Vansteelandt et al. 2009] then show that the rejection of the null-hypothesis of no genetic association by a such modified genetic association test implies a direct causal effect of the marker locus on the quantitative phenotype of interest.

In this communication, we develop similar methodology for scenarios in which the phenotype of interest is a time-to-event trait. Using standard residual approaches for time-to-onset data, we propose an adjustment principle for causal genetic association testing for such phenotypes. We derive the methodology and analytically show its validity. Using simulation studies, we verify the theoretical properties of the approach and assess its power. An application to survival data after cardiac surgery illustrates the potential of the approach.

2 Materials and Methods

We work under the causal diagram, also known as a Directed Acyclic Graph (DAG) pictured below in Figure 1. Our main interest is to determine the direct effect of genetic marker X on survival phenotype T. This effect is complicated by the presence of a secondary phenotype K (not survival data), which is associated with both the genetic marker X and the target phenotype T, the latter due to non-genetic reasons, e.g. clinical links, environmental correlation, etc. In order to test for the direct effect between the marker locus X to the age-at-onset phenotype T, the standard analysis to simply have marker locus X, secondary phenotype K, and diagnostic criteria L as covariates in the regression model and test for the coefficient of marker locus X will lead to biased results. For an explanation of this phenomenon in terms of properties of the causal diagram, please see ”DAG Explanation” in the Appendix. However, a simple example can illuminate this point. First notice that diagnostic criteria L is effected by both marker locus X and unmeasured common cause U. Suppose the extreme case that the unmeasured common cause U and the genetic marker X are marginally independent and that diagnostic criteria L has the property that L = X − U (i.e. complete dependence on X and U). Notice that given L = l, U and X are perfectly dependent (U = X + l). Therefore, controlling for diagnostic criteria L induces a spurious association between unmeasured common cause U and genetic marker X. Since U cannot be controlled for (it is unmeasured), this spurious dependency induces bias in the estimated effect of X on primary survival outcome T when both marker locus X and diagnostic criteria L are used as explanatory variables to model primary survival outcome T. Yet if we do not control for diagnostic criteria L, then the coefficient of marker locus X will not represent the direct effect of X on primary survival outcome T, because it will also represent the indirect effects through diagnostic criteria L. The same story holds for secondary phenotype K, which, if controlled for, may induce a spurious relationship between marker locus X and diagnostic criteria L [Rothman et al. 2008].

Figure 1.

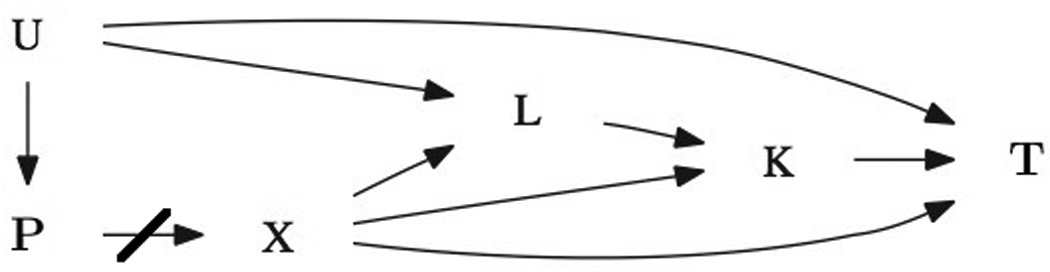
Causal DAG

To avoid this problem, we first look to quantify the direct effect of secondary phenotype K on survival outcome T. We then adjust the survival phenotype by subtracting out the direct effect of the secondary phenotype. In order to properly quantify the direct effect of the secondary phenotype on the primary survival outcome, one must model the effect of the secondary phenotype K on primary survival phenotype T while controlling for marker locus X and diagnostic criteria L to block all backdoor paths that could induce spurious associations. By subtracting out the effect of secondary phenotype K on survival outcome T, we are then under the altered causal diagram in Figure 2. We then test if the genetic locus X is associated with the adjusted phenotype T̃ by running a simple univariate regression. This is possible because there there are no open backdoor paths between genetic locus X and adjusted phenotype T̃ (and controlling for diagnostic criteria L and secondary phenotype K may induce spurious relationships as described above), thus testing for a direct causal effect, i.e. through pathways other than the secondary phenotype.

Figure 2.

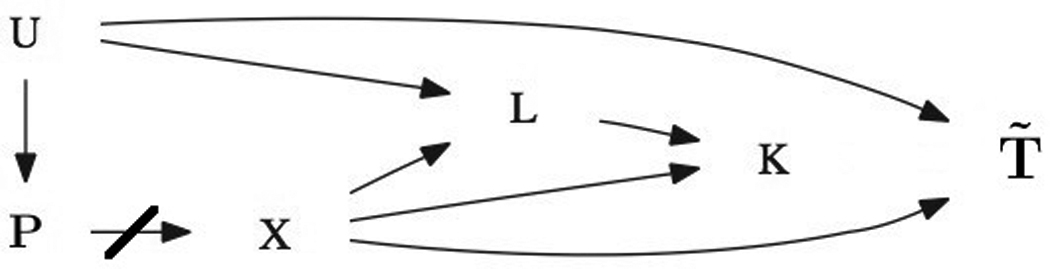
Causal DAG for Adjusted Primary Phenotype

U represents an unmeasured common cause, P represents factors leading to population stratification (that have been controlled for in the design stage), X is the marker coding, L represents the covariates/confounding variables for the secondary phenotype K, and T represents the target phenotype (survival data).

U represents an unmeasured common cause, P represents factors leading to population stratification (that have been controlled for in the design stage), X is the marker coding, L represents the covariates/confounding variables for the secondary phenotype K, and T̃ represents the target phenotype, adjusted for K’s direct effect.

2.1 Survival Models

Our data consists of the pairs (t_i, δ_i), where t_i is the time to the event T for person i and δ_i is an indicator for observing the event T for person i (i.e. δ_i = 1 if person i is not censured). Assuming independent and noninformative censuring, the likelihood function for survival analysis is:

$$L={\displaystyle \prod _i}{f}_i{(t_i)}^{{\delta }_i}{S}_i{(t_i)}^{1-{\delta }_i}$$ (1)

where f_i is the density function for person i′s time to primary phenotype and S_i is the survival function.

Modeling T: Proportional Hazards Model

Using the DAG introduced above, we model the hazard function of event T for person i under the proportional hazards framework, where we enter the appropriate covariates into the model to quantify the arrow from the secondary phenotype K to the primary outcome T. Thus, for person i, we control for diagnostic criteria L_i and marker coding X_i. The ${\beta }_j^{\prime }s$ then quantify the hazard ratio for a one unit increase in the j^th variable while holding other variables constant:

$$h_i(t)=h_0(t)\text{exp}\{{\beta }_1{K}_i+{\beta }_2{L}_i+{\beta }_3{X}_i\}$$ (2)

where h₀(t), the baseline hazard, is modeled using a standard survival distribution (e.g. Weibull). This hazard function then uniquely defines the density function and survival function in equation (1). Using equations (1) and (2), we can obtain estimates β̂₁, β̂₂, β̂₃ (and any parameters quantifying the baseline hazard) using maximum likelihood estimation. This notation will be used throughout the rest of the paper for estimates from this model.

Modeling T: Accelerated Failure Time Model

We may similarly model the hazard function of event T for person i under the accelerated failure time framework, where the ${\alpha }_j^{\prime }s$ quantify the multiplicative change in time to survival outcome T due to a one-unit increase in the j^th variable.:

$$h_i(t)=\text{exp}\{{\alpha }_1{K}_i+{\alpha }_2{L}_i+{\alpha }_3{X}_i\}{h}_0(\text{exp}\{{\alpha }_1{K}_i+{\alpha }_2{L}_i+{\alpha }_3{X}_i\}t)$$ (3)

Again, h₀(t), the baseline hazard, is modeled using a standard survival distribution. Using equations (1) and (3), we can obtain estimates α̂₁, α̂₂, α̂₃ (and any parameters quantifying the baseline hazard) using maximum likelihood estimation. This notation will be used throughout the rest of the paper for estimates from this model.

2.2 Using Family-Based Data

Under a family-based setting, the above methodology is slightly modified to account for the fact that we can control for population stratification by using the observable parental genotypes. Therefore, in Figure 1 and Figure 2, P (the factors that could possibly lead to population stratification) is replaced by E(X_i|P), the expected marker score given the parental genotypes and the arrow from E(X_i|P) for X_i is present (not crossed out). In Equation (2), we add β₄E(X_i|P) to the linear predictors in the models; In equation (3), we add α₄E(X_i|P) to the linear predictors in the models. This protects against population stratification. We also obtain β̂₄ and α̂₄ using maximum likelihood estimation.

2.3 Phenotype Adjustment

From models (2) and (3), we know that exp(β̂₁) estimates the hazard ratio of survival outcome T due to a one unit increase in secondary phenotype K, while exp(α̂₁) estimates the multiplicative change in time to survival outcome T due to a one unit increase in secondary phenotype K. Since we blocked on the marker genotype and the diagnostic criteria (and can control for population stratification in the family-based setting), these functions can be used to properly quantify the arrow from the secondary phenotype to the survival outcome of interest. We need to adjust the survival phenotype (t_i) by some function of exp(β̂₁K_i) or exp(α̂₁K_i) to subtract out the arrow. We then work with the adjusted phenotype to quantify the direct effect from the genetic marker to the survival phenotype. This is achieved using the residuals from the above models, as detailed below. Equations discussed relate to proportional hazards models: similar equations hold for accelerated failure time models, where β̂_i is replaced by α̂_i.

2.4 Residuals

In survival analysis, there are three common types of residuals: Cox-Snell residuals, Martingale residuals, and Deviance residuals. The Cox-Snell residuals estimate –logS(t), where S(t) is again the survival function. The Martingale residuals quantify the difference between the observed number of events for the i^th individual and the estimated number of events in (0, t_i). The Deviance residuals transform the Martingale residuals to be nearly symmetric about zero. In addition, they have the standard deviance interpretation in some situations [Collett, 1994].

2.5 Partial Residuals

In this application, we take the partial Cox-Snell residual r_cpi and modify it into a partial Deviance residual. This function then estimates the direct effect of the secondary phenotype K on the survival phenotype T. The partial Cox-Snell residual has the form $r_{c_{p_i}}=\text{exp}\{{\widehat{\beta }}_1(K_i-\overline{K})\}{\widehat{H}}_0(t)\text{where}{\widehat{H}}_0(t)={\displaystyle {\int }_0^t}{\widehat{h}}_0(u)\mathit{\text{du}}$, the estimated cumulative hazard function. We then modify it into a partial Martingale residual by r_mpi = δ_i − r_cpi. Finally, we have the partial Deviance residual as needed, defined as $r_{d_{p_i}}=\text{sgn}(r_{m_{p_i}})\sqrt{-2[r_{m_{p_i}}+{\delta }_i\text{log}({\delta }_i-r_{m_{p_i}})]}$

3 The Adjusted Phenotype

After identifying the proper form of the residual, we adjust the primary survival phenotype T using the following, where t̄ is defined as the mean of the survival phenotypes, effectively removing the secondary phenotype’s direct influence:

$${\tilde{t}}_i=t_i-\overline{t}-r_{d_{p_i}}$$ (4)

Using simple linear regression and equation (4), we can model the adjusted phenotype using the following:

$${\tilde{t}}_i={\alpha }_0+{\alpha }_1{X}_i$$ (5)

and α̂₁ estimates the direct effect of the marker genotype X on the primary phenotype T, meaning the effect other than through secondary phenotype K.

4 Variance Adjustment

Since there is variability in the parameter estimates that factor into the adjustment of t_i to t̃_i, the typical variance calculation of α̂₁ is not proper. Following [Vansteelandt et al. 2009], we have the selected association test τ (e.g. standard score test, Wald test, or likelihood ratio test) with expectation of zero under the null hypothesis of no association between the phenotype of interest and the marker genotype, that is of the general form

$$\tau ={\displaystyle \sum _{i=1}^n}{\tau }_i$$ (6)

where τ_i denotes the i^th subject’s contribution to the test statistic, defined as follows for population-based and family-based studies, respectively:

$${\tau }_i=X_i{\tilde{t}}_i$$ (7a)

$${\tau }_i=(X_i-\mathrm{E}[X_i|P_i]){\tilde{t}}_i$$ (7b)

then the statistic

$${\tau }^2/(n\sum )$$ (8)

follows a ${\chi }_1^2$ distribution under the null hypothesis of no direct effect, where

$$\begin{array}{c}\hfill \sum =\text{Var}({\dot{\tau }}_i)\hfill \\ \hfill {\dot{\tau }}_i={\tau }_i-\mathrm{E}[{\tau }_i^{\prime }{K}_i]\frac{K_i-{\mu }_K^{(i)}}{{\sigma }_K^2}{\epsilon }_i\hfill \end{array}$$

where ${\tau }_i^{\prime }$ is the first derivative of equations (7a) or (7b) with respect to t̃_i, i.e. for population-based tests, we have ${\tau }_i^{\prime }=X_i$ and, for family-based tests, ${\tau }_i^{\prime }=X_i-\mathrm{E}[X_i|P_i]$. The variable ε_i is the (full) Deviance residual from equation (2) or (3). In population based designs, μ_K and ${\sigma }_K^2$ are obtained by fitting a regression for secondary phenotype K_i with the covariates of diagnostic criteria L_i and marker genotype X_i. For family-based studies, the covariate E[X|P_i] is included in the regression as well to protect against population stratification. The predicted value for secondary phenotype K_i is then defined as ${\mu }_K^{(i)}=\mathrm{E}[K|L_i,X_i]\text{or by}{\mu }_K^{(i)}=\mathrm{E}[K|L_i,X_i,\mathrm{E}[X|P_i]]$ , the fitted values from the regression. The residual variance of the regression model is denoted by ${\sigma }_K^2$.

5 Simulation Studies

Using simulation studies, we examine the robustness of this approach under realistic scenarios. In all simulations, we focus on quantitative traits and assume no ascertainment condition (i.e. no population stratification) and work under a population-based setting. Results presented are based on 10,000 replicates. A sample size of 1000 probands is selected. The genotype data, coded additively, are generated with a binomial distribution, with allele frequency of 0.25. All phenotypic variables are drawn from a normal distribution, except the primary phenotype (T) is drawn from a weibull distribution with mean between 10 to 15 following [Jiang et al. 2006], and the shape parameter is set at 0.5, 1 (for exponential distribution), and then 1.5. Genotype to phenotype effect sizes (r²) are roughly 1%, while phenotype to phenotype effect sizes are between 5% and 10%.

5.1 Results - Type 1 Error Calculations

In the situation represented by Figure 1, the null hypothesis exists when the arrow marker genotype X → primary survival outcome T does not exist. Within this null hypothesis, there are eight possible scenarios, or models, depending on whether the subset of arrows marker genotype X → diagnostic factors L, marker genotype X → secondary phenotype K, and secondary phenotype K → primary survival outcome T are present. These eight null hypothesis models are outlined in Table 1. Empirical type-1 error rates for testing the association between marker genotype X and primary outcome T, using the method developed above, at α = 0.05, are reported below in Table 2. We see that the method has proper type 1 error rates.

Table 1.

null hypotheses models, Y=if arrow is present, N=arrow is not present, corresponding to Figure 1

null #:	X → L	X → K	K → T
1	N	N	Y
2	Y	N	Y
3	Y	Y	Y
4	N	Y	Y
5	N	N	N
6	Y	N	N
7	Y	Y	N
8	N	Y	N

Table 2.

type 1 error rates at α = 0.05 for 8 null hypothesis models by 3 shape parameters

null hypothesis:	1	2	3	4	5	6	7	8
shape = 0.5	0.049	0.048	0.046	0.051	0.048	0.048	0.047	0.052
shape = 1.0	0.045	0.050	0.059	0.058	0.053	0.049	0.053	0.051
shape = 1.5	0.038	0.034	0.054	0.053	0.043	0.044	0.042	0.041

5.2 Results - Power Calculations

Data was simulated under eight alternative hypotheses, under scenarios identical to those used in type 1 error rates, with genetic marper X also directly affecting primary survival phenotype T with an effect size (r²) of 1 %. Power calculations at α = 0.05 are listed in Table 3. We see that method maintains strong power under these realistic scenarios. It is important to note that the power of the method will depend upon the accuracy of the model specification, as in all regression techniques.

Table 3.

power for methods at α = 0.05 for 8 scenarios, 3 shape parameters

alternative hypotheses:	1	2	3	4	5	6	7	8
shape = 0.5	0.947	0.946	0.941	0.929	0.965	0.964	0.962	0.963
shape = 1.0	0.987	0.988	0.941	0.935	0.926	0.926	0.925	0.926
shape = 1.5	0.869	0.872	0.917	0.905	0.911	0.903	0.906	0.909

6 Application: Cardiac Data Results

The methods described above were applied to a cardiac dataset, consisting of 890 caucasian individuals genotyped at 28 SNPs in gene P2RY12. The patients underwent surgery due to severe coronary artery disease. During surgery, 10% of patients experienced a myocardial infarction (MI). In this application, the primary survival outcome of interest T is post-surgery hospital duration. MI plays the role of the intermediate phenotype K.

First, MI was modeled using a logistic regression with diagnostic criteria defined in the Appendix. Effect sizes reasonably matched previous literature (Table 4).

Table 4.

logistic regression modeling MI status results, diagnostic criteria defined in Appendix

variable	estimate	std. error	z value	p-value
Intercept	−2.7311	1.0717	−2.55	0.0108
TNI.pre 1	1.0825	0.3140	3.45	0.0006
Institution 1	0.1221	0.3561	0.34	0.7317
Age	0.0117	0.0116	1.01	0.3121
Gender 1	−0.4783	0.2680	−1.78	0.0743
Last MI 1	0.1161	0.3192	0.36	0.7162
CPB 1	−1.1830	0.5090	−2.32	0.0201
CPB time	0.0142	0.0026	5.56	0.0000
Creatinine	0.1436	0.0393	3.66	0.0003
Statin 1	−0.1670	0.2648	−0.63	0.5283
Stenosis 1	−0.5545	0.4610	−1.20	0.2291
Stenosis 2	−0.5288	0.4300	−1.23	0.2187

Previous research suggested that gene P2RY12 is associated with MI. When each SNP was entered into the logistic regression, along with diagnostic criteria to explain MI status, this previously found association was strongly suggested at SNP 3 (Bonferroni-corrected p-value = 0.10), seen in Table 5.

Table 5.

Testing association between SNP and MI status

SNP name	number	p-value
rs1491980	1	0.2544
rs1466684	2	0.2245
rs3732757	3	0.0037
rs4146770	4	0.6952
rs9877389	5	0.1814
rs7644001	6	0.5211
rs10513393	7	0.8676
rs2307020	8	0.4688
rs13090236	9	0.8551
rs6772253	10	0.0191
rs1565574	11	0.8082
rs13095610	12	0.4672
rs10935839	13	0.3752
rs1352887	14	0.1517
rs6790748	15	0.1868
rs6782212	16	0.3697
rs4679802	17	0.1509
rs12487835	18	0.3149
rs3975404	19	0.1648
rs9849395	20	0.0240
rs6770918	21	0.8801
rs13322120	22	0.8309
rs12497065	23	0.2338
rs17283010	24	0.2926
rs6787801	25	0.6551
rs7429509	26	0.5443
rs1491974	27	0.5835
rs9653953	28	0.3431

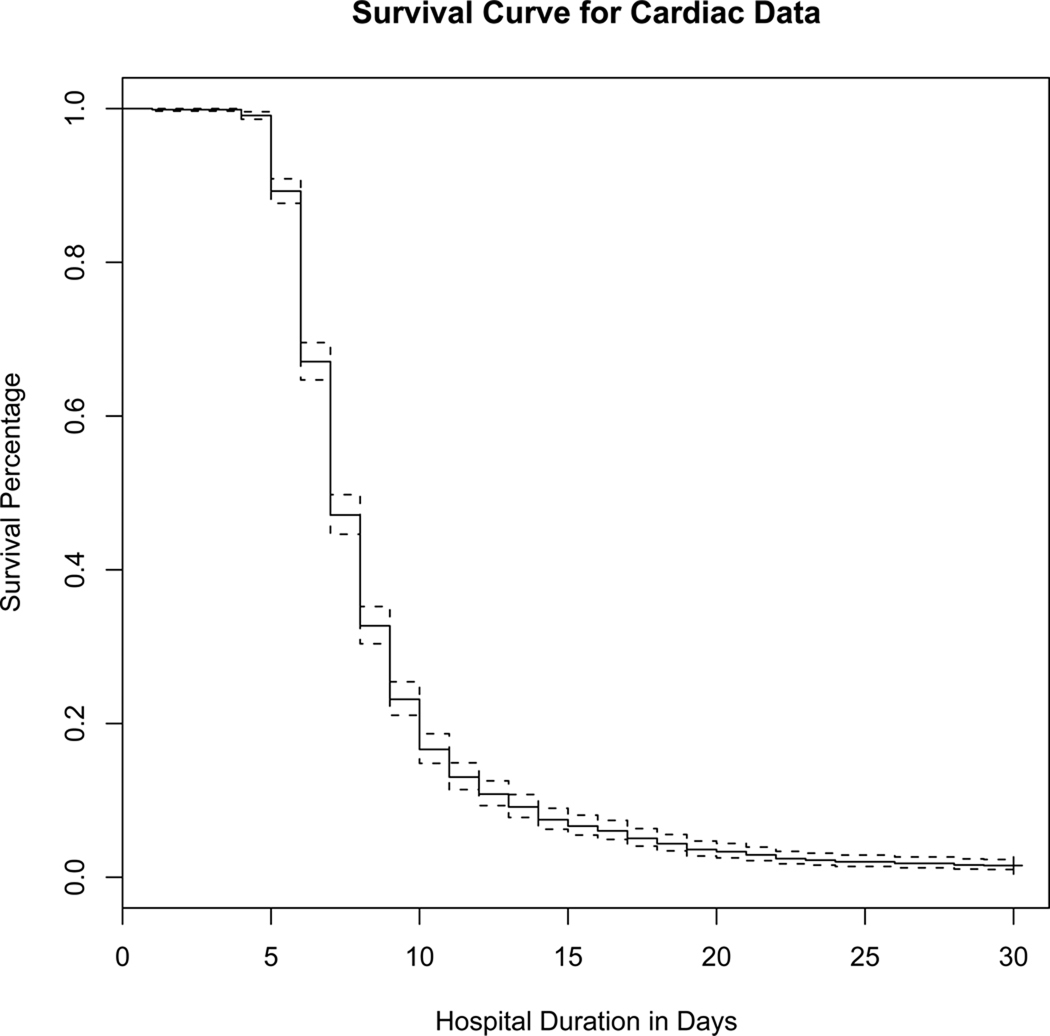
In addition, MI status is typically associated with increased stay in hospital post-surgery (censored at 30 days for 22 subjects), which is a marker for intensity of cardiac disease. This association is confirmed in table 6, with hospital duration modeled using the Weibull distribution under the accelerated failure time framework as a function of MI status and diagnostic criteria. MI status is strongly associated with hospital duration with effect size e^0:2441 = 1:28 and p-value = 2.7e-06. Note that if we entered the SNP’s into this AFT model, SNP 3 is associated (p=0.009) with hospital duration. However, this association may only be due to the MI-pathway, hence we need to perform the methods developed in this paper.

Table 6.

Modeling Hospital Duration, accelerated failure time framework

variable	coeff	sd	z	p
Intercept	1.7106	0.1468	11.6553	2.155e-31
MI	0.2441	0.0520	4.6906	2.724e-06
TNI pre 1	−0.0192	0.0490	−0.3916	0.6953
Institution1	0.2165	0.0420	5.1582	2.493e-07
Age	0.0118	0.0015	8.0599	7.633e-16
Gender	−0.0282	0.0385	−0.7318	0.4643
Last MI 1	0.1544	0.0455	3.3971	0.000681
CPB 1	−0.4921	0.0900	−5.4676	4.561e-08
CPB time	0.0024	0.0004	5.9603	2.518e-09
Creatinine	0.0396	0.0098	4.0446	5.24e-05
Statin 1	−0.0204	0.0356	−0.5722	0.5672
Stenosis 1	−0.1166	0.0630	−1.8491	0.06445
Stenosis 2	−0.0747	0.0607	−1.2322	0.2179
Log(scale)	−0.8304	0.0225	−36.8463	3.347e-297

The Kaplan-Meier estimate of the hospital duration curve is seen in Figure 3.

Figure 3.

Kaplan-Meier Survival Curve

In order to test if the SNPs were directly associated (i.e. not through secondary phenotype of MI status) with hospital duration, the methods of this paper were employed. Results are in Table 7, which provide no evidence to reject the null hypothesis of no direct effect on hospital duration.

Table 7.

P-values for test of direct effect, 28 SNPS to Hospital Duration

SNP	p-value
1	0.59
2	0.66
3	0.22
4	0.34
5	0.57
6	0.71
7	0.65
8	0.64
9	0.34
10	0.67
11	0.86
12	0.81
13	0.75
14	0.72
15	0.75
16	0.71
17	0.60
18	0.36
19	0.57
20	0.89
21	0.24
22	0.71
23	0.89
24	0.92
25	0.99
26	0.98
27	0.95
28	0.39

7 Discussion

Here, we presented a new statistical approach to detect causal genetic effects on survival data in the presence of a secondary phenotype that might confound the results. The proposed method is based on standard statistical methodology and can be implemented straight-forwardly. Using simulation studies, the theoretical properties of the approach were verified and the power was assessed under realistic scenarios. The practical relevance of the approach was illustrated by an application to survival after cardiac surgery. There was no evidence to suggest that the SNPs genotyped within gene P2RY12 directly effect post-surgery hospital duration (i.e. through pathways other than MI status.)

10 Appendix

10.1 DAG Explanation

In order to test for the direct effect between the marker locus X to the age-at-onset phenotype T in Figure 1, it is not proper to simply have marker locus X, secondary phenotype K, and diagnostic criteria L as covariates in the regression model. This is because both secondary phenotype K and diagnostic criteria L are colliders in Figure 1. It is well known in causal methodology that having colliders as covariates in a regression model does not ”block” the path of interest, but, in fact, may induce a spurious relationship. Therefore, if we add secondary phenotype K and diagnostic criteria L into the model, the coefficient for the marker locus X variable will not only quantify the direct effect from the marker locus X to the primary phenotype T, but will also quantify the ”opened” paths from marker locus X (to secondary phenotype K) to diagnostic criteria L to unmeasured common cause U to primary survival type T. Because of the existence of these colliders, standard regression techniques fail to quantify the effect of interest from marker locus X to primary phenotype T.

10.2 Variable Definitions: MI & Diagnostic Criteria

• MI: 1/0, indicator of having a myocardial infarction, 1: yes, in top 10% for cardiac Troponin I level on day 1 after surgery

• TNI.pre: 1/0 - 1: cardiac Troponin I level before surgery > 0.1

• Institution: 1/0 - 1: Patient was at Texas Heart Institute, 0:Patient was at Brigham and Women’s Hospital

• Age: quantitative, age of patient

• Gender: 1/0 - 1: male patient, 0: female patient

• Last.mi: 1/0 - 1: yes, patient’s last MI was within 2 weeks of the surgery

• Hospital.duration: quantitative, length of hospital stay after surgery

• Cpb: 1/0 - 1:yes, a cardiopulmonary bypass was used

• Cpb.time: quantitative, the amount of time, in minutes, the cardiopulmonary bypass was used

• Creatinine: quantitative, the amount of creatinine present in the patient

• Statin use: 1/0 - 1: yes, the patient used statins

• Stenosis: 2/1/0 - 2: 3 vessels with > 50% stenosis, 1: 2 vessels with > 50% stenosis, 0: 0 or 1 vessels with > 50% stenosis