Computational and Mathematical Modeling of Angiogenesis

Abstract

Over the past two decades, a number of mathematical and computational models have been developed to study different aspects of angiogenesis that span the spatial and temporal scales encompassed by this complex process. For example, models have been built to investigate how growth factors and receptors signal endothelial cell proliferation, how groups of endothelial cells assemble into individual vessels, and how tumors recruit the ingrowth of whole microvascular networks. A prudent question to pose is: “what have we learned from these models?” This review aims to answer this question as it pertains to angiogenesis in the context of normal physiological growth, tumorigenesis, wound healing, tissue engineering, and the design of therapeutic strategies. We also provide a framework for parsing angiogenesis models into categories, according to the type of modeling approach used, the spatial and temporal scales simulated, and the overarching question being posed to the model. Finally, this review introduces some of the simplification strategies and assumptions used in model building, discusses model validation, and makes recommendations for application of modeling approaches to unresolved questions in the field.

Introduction

Angiogenesis is a complex process, whereby existing microvessels give rise to new capillaries (via sprouting) that are capable of delivering additional oxygen and nutrients to a growing, injured, or inflamed tissue. This process occurs during normal growth and development and in pathological adaptations, such as embryogenesis, tumorigenesis, peripheral arterial disease, diabetic retinopathy, and wound healing. Angiogenesis is complex in that it relies on the precise coordination of different cell types, a number of different cellular behaviors (i.e. proliferation and migration), and biomechanical and biochemical signals that operate locally (i.e. at cell-cell contact interfaces) and across distances spanning hundreds of microns in the tissue (i.e. diffusion of VEGF). The outcome is a remodeled microvascular network that contains a new cohort of capillary-sized vessels. At the tissue-level, the new vessels are able to augment blood flow and oxygenation to the extent required by the metabolic demand of the tissue or induced by the pathology (e.g. tumor). Since the mid 1900’s, a number of experimental models have been developed to study both physiological and pathological angiogenesis [9;26]. Within the past two decades, the application of mathematical and computational models have supplemented experimental approaches and enhanced our understanding of this complex process.

This review will summarize the types of questions that mathematical and computational models of angiogenesis have been designed to address, overview commonalities and differences in different modeling approaches, and highlight the key advances in understanding that mathematical and computational models have contributed to the field. We will also describe simplification strategies and common assumptions of published models, discuss the importance of and techniques for model validation, and bring to light some unanswered questions in angiogenesis that could be addressed by mathematical and computational models in the future.

Modeling the different biological scales of angiogenesis

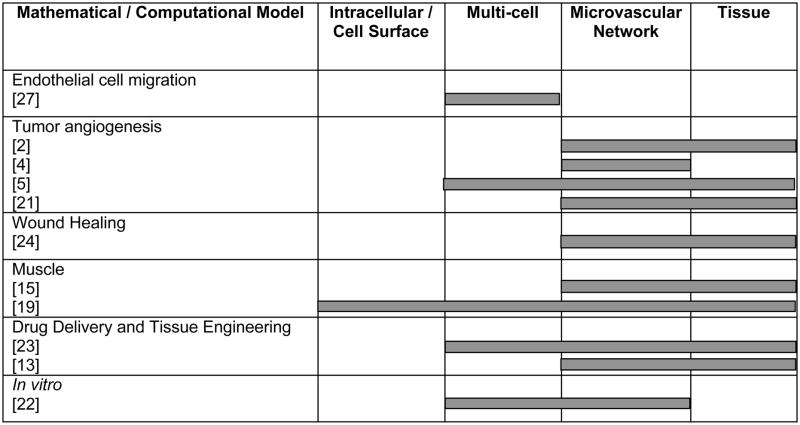
One way to parse the existing set of published models is to categorize them according to the spatial scale(s) that they were developed to encompass (Table 1). While some models have focused on signaling phenomena at the level of a cell’s membrane-bound receptors [20], others have studied microvascular network remodeling at the whole tissue level [23]. Another way to parse the existing set of published models is according to the temporal scales that they were designed to simulate. Some models, for example, have simulated biological events on the order of minutes [8], while others have considered processes that occur over weeks [11]. The distinguishing factor for any model, however, is the central question that the model was developed to investigate, and ultimately, it is this motivating question that serves to define the scope of the spatial and temporal scales included in the model.

Table 1.

The biological scales encompassed by published mathematical and computational models.

Recently, “multi-scale” models have incorporated both biomechanical and biochemical phenomena and accounted for their interactions across spatial and temporal scales [8;18;23]. These models are proving to be powerful tools for the study of angiogenesis, which is inherently a multi-scale process, because their integration of single-cell, multi-cell, and tissue-level/microvascular network-level phenomena expands the number and types of questions that they can be used to answer. We emphasize multi-scale models in this review, as we view this type of modeling approach as offering tremendous additional benefit in helping to address important unanswered questions in the field of angiogenesis and microvascular remodeling.

Although this review focuses on mathematical and computational models of angiogenesis (i.e. capillary sprouting from existing vessels), there are also references to models of other types of microvascular growth and adaptation, including intussusception, microvascular stabilization, arteriogenesis, and vasculogenesis. Computational models of in vitro vasculogenesis have also been developed to study the interactions of endothelial cells and how they give rise to new vascular structures in culture. This process is particularly relevant to recent tissue engineering efforts to fabricate microvascular networks ex vivo, and we review some models of in vitro vasculogenic processes, as well.

Types of modeling approaches

Before we overview the different physiological and pathological settings where angiogenesis modeling has been employed, we briefly describe different types of modeling approaches from a mathematical and computational standpoint. These types of modeling approaches are not mutually-exclusive; a model can include one or more of the following approaches, and in subsequent sections we review a number of models that combine two or more of the following approaches.

One type of modeling approach is continuum-based modeling, where the system being modeled is approximated as a continuous series of entities or events. In continuum modeling, the individual parts are very similar to their nearest neighbor, and variation across the system is accounted for by gradual transitions lacking discontinuities. In the context of angiogenesis modeling, continuum models ignore details of the constituents (e.g. cell-level details) and new capillary growth, for example, is often modeled as changes in vascular density at the network level [12]. Continuum models are usually implemented by solving systems of differential equations that describe physical phenomena as being a continuous spread in space and/or time.

Other types of models utilize a discrete approach, where the entities being modeled (e.g. endothelial cells) and their unique behaviors (e.g. proliferation) are explicitly represented. Discrete models consider increments of time and space as distinct entities and the objects within the environment as individual, unique units. Discrete models of angiogenesis, for example, account for the behaviors of individual endothelial cells [7;28]. Discrete models are often implemented by solving systems of differential equations at discrete locations (i.e. points on a 2-D grid) or by using computational algorithms where individual behaviors are explicitly modeled according to logic algorithms using discrete event simulators (e.g. agent-based modeling).

Stochastic modeling approaches use probabilities to define biological phenomena. These models explicitly accommodate the randomness associated with biological processes by using probability distributions to dictate the probable outcomes of simulated events [27]. Stochastic modeling assumes that random variation and fluctuation in the system dominates the overall behavior of the system.

Deterministic models, unlike stochastic modeling approaches, presume that later states of the system are determined by previous states of the system. In this way, deterministic models predict actual outcomes, and not just probable outcomes. In a deterministic model, if all inputs are specified and the changes in the states of the system are prescribed accordingly, the outcome will always be the same, unlike in a stochastic model where random variability will give rise to alternative outcomes.

The type of modeling approach (or combination thereof) that is used to simulate a particular aspect(s) of angiogenesis, much like the spatial and temporal scale of the simulation, is usually selected based on the question that the model seeks to address and the types of available data with which to construct the model. In this way, the type of modeling approach(s) utilized in a particular model is important, but certainly secondary to the biological facets of the overarching study.

Insights offered by mathematical and computational models of angiogenesis

The majority of this review is focused on summarizing specific examples of previous insights provided by angiogenesis models and abstracting these examples into more generic types of insights that can be expected from performing such analyses (Box 1). Mathematical and computational models of angiogenesis have generated basic science understanding about the processes of capillary assembly and morphogenesis during development, growth, and pathological insults. Models have also been developed with the intention of supporting applied biomedical research and development--for the purpose of identifying new therapeutic targets and clinically relevant approaches for either inhibiting or stimulating angiogenesis. The impetus for such models has included the identification of putative drug candidates or drug combination strategies and the engineering of vascularized tissue constructs ex vivo. The following sub-sections are organized according to the central physiological or pathological settings in which the process of angiogenesis was studied and the overarching questions that motivated the development of the models.

Box 1. Abstracted key questions that prior models of angiogenesis have been developed to answer.

• If there are alternate, competing, or conflicting hypotheses, which one should be pursued and/or how should the hypothesis be refined?

• What experiments should be conducted next?

• What are the key variables/parameters in the system and which ones are necessary, sufficient, or unnecessary for the system to function properly? What parameters are targets for therapeutic manipulation?

• To variations in which parameters is the system robust? To variations in which parameters is the system sensitive?

• What is the predicted set-point of variables that are difficult to quantify empirically, such as the in vivo concentration of growth factors?

Endothelial cell migration

One of the most frequently cited angiogenesis models has been developed by Stokes and Lauffenburger [27]. Their discrete mathematical model simulated individual cell movements by considering cell motility and chemotaxis as partially stochastic events. They used the model to assess microvascular endothelial migration in the presence or absence of aFGF. They validated the model by conducting experiments and comparing the mean square displacements of each cell. In the simulation, adding aFGF increased cell migration speed by decreasing persistence time, suggesting that the intracellular mechanisms that control the rate of movement may be decoupled from those that govern the direction of movements. Importantly, this work demonstrated that it is possible to estimate chemotactic sensitivity by measuring the dynamics of population-level migration. More recent models of cell migration have used force-based dynamics approaches to simulate internally generated forces and external traction forces, as well as matrix compliance and ECM stiffness [31].

In vitro vasculogenesis

A recently developed 2-dimensional discrete model by Merks et al., 2006 simulates the process of in vitro vasculogenesis, or the assembly of human umbilical vein endothelial cells (HUVECs) into networks of connected cells in a Matrigel environment [22]. This Cellular Potts model represents each endothelial cell discretely, and an effective energy function describes the state of the cells as they behave according to a small set of phenomenological rules: 1) endothelial cells secrete a morphogen (angiogenic factor, such as Vascular Endothelial Growth Factor, VEGF₁₆₅), which diffuses over the simulation space and decays producing local gradients, 2) endothelial cells extend filopodia up morphogen gradients, and 3) endothelial cells rapidly elongate after contact with the extracellular matrix. The authors use the model to study how cell-level behaviors impact tissue-level shape changes, and they validate their model by qualitative comparison to in vitro Matrigel experiments. The simulation suggests that the elongated shape of the endothelial cells is essential for correct spatio-temporal vasculogenesis in vitro. This prediction is consistent with a published study, in which it was reported that VEGF induces and elongated cell shapes [10]. The authors infer from their model that ECM-binding form of VEGF (VEGF₁₈₉ or VEGF₂₀₆) may be the predominant signaling molecule for vasculogenesis, since the generation of stable vascular-like in vitro patterns of simulated endothelial cells required a morphogen that diffused quickly and was quickly inactivated (i.e. a “short-range” signal). Thus, this model was useful in linking observed patterning phenomena at the tissue-level to underpinning cell-level behaviors and suggesting how the differential presentation of a growth factor (matrix-bound or diffusible) may functionally impact this particular vascular assembly process.

Tumor angiogenesis

The vascularized phase of tumor growth has dominated as the most common context in which to develop mathematical and computational models of angiogenesis. Many of these models have built upon one another or evolved over time in a series of publications. While early models were focused on accurately replicating key observed behaviors during this process, more recent models have been able to test specific hypotheses and suggest useful strategies for drug development.

One of the most highly cited early models of tumor angiogenesis is a dynamic model of endothelial cell migration that predicted, for the first time, that chemotaxis is needed to orient vascular growth toward the tumor [28]. Since then, a number of models have built on the chemotaxis model by simulating a diffusible tumor angiogenesis factor (TAF), which is likened to the biologically relevant growth factor, VEGF, that acts as a potent chemokine for endothelial cells [6;25].

Of particular interest in the field of tumor angiogenesis is the temporal transition between the avascular growth phase and the vascular growth phase of the tumor. Hogea et al., 2006 developed a 2-dimensional computational framework based on a Cartesian mesh/narrow band level-set method, of the avascular and vascular phases of tumor growth, and the simulation is capable of simulating when the transition occurs [12]. The interactions of the tumor, which can be simulated as having spherical symmetry or arbitrary geometries, with the surrounding vascular tissue are explicitly incorporated, and their model considers the effect of TAF, which diffuses into the healthy surrounding tissue and simulates the capillary network surrounding the tumor to grow into it. The model predicts that the spatial arrangements of pre-existing capillaries in the surrounding tissue dictate a more complex tumor boundary orientation in the moderate vascularization regime, but during the high vascularization regime, the tumor boundaries are less complex.

In addition to probing the spatio-temporal events that lead to the transition, or switch, between avascular and vascular tumor growth, models have been developed to elucidate the tissue-level impact of different types of microvascular adaptations on tumor growth. For example, Komarova and Mironov, 2005 developed a model of tumor angiogenesis using a system of ODEs, where the key dependent variables were tumor mass and the number of bone marrow-derived endothelial progenitor cells (EPCs) [16]. They use their model to test the hypothesis that angiogenesis-driven tumorgenesis is different than vasculogenesis-driven tumor growth. Their model assumes that both processes, angio- and vasculogenesis, can occur within the same simulated tumor, and this allows the authors to predict what happens if either type of vessel growth dominates over the other. Their model predicts that if angiogenesis dominates, tumor mass will grow as a cubic power of time and bone marrow-derived EPCs remain at a constant level in the tumor. However, if vasculogenesis dominates, tumor mass is characterized by linear growth when the bone marrow has been depleted of EPCs. The authors validate their model by citing papers that have experimentally measured the growth kinetics of tumors. There is evidence for both linear growth rates and cubic growth rates, suggesting that more refined experiments with multiple measurement time points may be fruitful in helping to determine whether angiogenesis or vasculogenesis drives tumor vessel growth.

Other models have simulated the effects of more specific, physiologically relevant growth factors on tumor angiogenesis, as opposed to the effect of TAF, which is a generic endothelial cell chemokine. For example, an ODE-based model by Arakelyan et al., 2002 considers tumor cell proliferation, angiogenesis, and vessel stabilization and maturation in order to predict the effects of targeting these different processes, alone and together, with a cocktail of drugs [2]. They investigate the role of four growth factors, including Ang-1, Ang-2, VEGF, and PDGF, and model the influence of anti-angiogenesis (VEGF production inhibitor) and anti-maturation (Ang-1 production inhibitor) treatments targeted at these molecules. Administered alone, these simulated therapies only partially attenuated tumor growth. Tumor size continued to increase nonlinearly, even when the drug doses were increased and the treatment period was extended. Dual treatment with anti-VEGF and anti-Ang-1 resulted in prolonged suppression of tumor growth and a significant linear decrease in the average size of the tumor. These results were not dependent on initial conditions, but interestingly, the efficacy of anti-VEGF therapy depended on the extent of initial vessel maturation at the onset of treatment, whereas, the efficacy of anti-Ang-1 treatment and combination treatment was independent of the degree of initial vessel maturation.

Gevertz and Torquato, 2006 developed a 2-dimensional discrete cellular automata model of early brain tumor growth that also couples angiogenesis with simulated changes in tumor mass, allowing the interdependence between tumor growth and vascular network expansion to be investigated quantitatively [11]. Each agent in the simulation represented 50 biological cells, and a system of reaction-diffusion equations was used to calculate regional concentrations of VEGF, Ang-1, and Ang-2. The model predicted that the presence of VEGF and the angiopoietins are both sufficient for allowing unbounded tumor growth, but blocking VEGF effectively inhibits angiogenesis and limits tumor size to 1–2 mm. Interestingly, the model also suggested that tumor expansion can occur in a well-vascularized environment, even when angiogenesis is inhibited, which may have profound implications when it comes to the timing of anti-angiogenic drug administration.

Bauer et al., 2007 developed a cell-based model that also describes diffusion, uptake, and decay of pro-angiogenic factors secreted by tumor cells and used it to understand the roles of cell-cell and cell-matrix dynamics in regulating tumor angiogenesis [5]. The model incorporates both discrete and continuous modeling approaches. A PDE describes diffusion, uptake, and half-life decay of tumor-secreted VEGF, while a discrete lattice Monte Carlo model (cellular Potts model), based on system energy reduction was used to describe endothelial cell migration, growth, division, and adhesion, as well as ECM degredation. The model simulates a number of cell-level phenomena, including (1) VEGF binding to VEGF receptors on the endothelial cell surface, (as well as internalization and recycling of VEGF receptors, although these events are not modeled explicitly), (2) VEGF-mediated cellular activation, migration, and proliferation, and (3) proteolytic ECM degredation. However, notably, the intracellular events are not modeled explicitly. Their rules for cell behavior do not prescribe vessel branching or anastomosis explicitly, but these properties emerge from the independent behaviors of the individual simulated endothelial cells. The authors use their model to determine if the differential presence of matrix-bound vs. soluble VEGF results in different vascular morphologies. The model suggests that differences in the ECM-binding affinity of VEGF could affect the VEGF concentration profile and the presence of steep or shallow VEGF gradients result in different capillary morphologies (narrow vessels vs. wider vessels). They also use the model to determine if the location of the proliferating region of cells within a capillary sprout (i.e. tip cells vs. stalk cells) has an impact on capillary morphology and the rate of capillary sprout elongation. Their model shows that as the proliferating region on the sprout stalk moves further from the sprout tip (toward the parent vessel), sprout extension is more rapid due. Another important question that the authors address with their model is to what extent the composition of the stroma (ECM density and anisotropy) and the presence of other cells (i.e. tumor cells) influences angiogenesis. The model predicts that local anisotropies in the stroma, such as variable matrix fiber density and the presence of other tissue cells, influences sprout migration and morphology. Model validation was accomplished by comparing simulated capillary sprout diameters (length and cell width) to VEGF-induced sprout diameters measured experimentally, and the comparison suggested a good match between model and experiment.

In addition to considering the role of the ECM as an important modulator of tumor angiogenesis, Levine et al., 2000 built a model to study the initiation of capillary formation (i.e. the onset of angiogenesis) in tumor growth with respect to the role of pericytes, macrophages, and two hypothesized mechanisms of angiostatin protease inhibition [17]. The model uses reinforced random walks to govern cell movements and Michaelis-Menten kinetics to describe the catalysis of angiogenic factors into proteolytic enzymes by endothelial cells. The degredation of the basal lamina by the active proteases is modeled using a simple catalytic reaction. Angiostatin prevents the degradation of fibronectin in the basal lamina, and its putative actions in modulating tumor angiogenesis were modeled in two ways: as a direct inhibitor of protease and as a stimulator of endothelial cells to produce a protease inhibitor. The model suggests that when angiostatin operates via inducing endothelial cell production of protease inhibitor, it is more effective in redistributing endothelial and pericyte cells and returns fibronectin to a uniform profile than when it acts as a direct protease inhibitor. A secondary prediction is that angiostatin must be supplied continuously in order to combat the stimulation of endothelial cells by chemotactic agents.

A recent model by McDougall et al., 2006, termed DATIA, or “dynamic adaptive tumor-induced angiogenesis” model, simulates multi-scale phenomena impacting tumor angiogenesis [21]. This model was inspired by an earlier continuous model of tumor-induced angiogenesis [1], and integrates vessel growth with blood flow, such that blood flow directly impacts capillary growth. Key assumptions of the model are that endothelial cells migrate via random walk, tumor angiogenesis factor (TAF)-mediated chemotaxis, and fibronectin-induced haptotaxis. The model operates in two stages, which are coupled together via a single parameter, wall shear stress. A discrete simulation of individual endothelial cell migration is paired with a continuum method to calculate blood flow according to Poieusille’s law and vessel adaptations in response to shear stress, pressure, and a metabolic mechanism. Vessel branching is dependent on a probability function that considers the combined effects of local wall shear stress and TAF concentrations, such that high values of wall shear stress in the presence of high local TAF concentrations lead to a higher branching probability, whereas low values of one or both give rise to a lower branching probability. To account for the two different timescales that impact blood flow (seconds) and angiogenic sprouting (days), respectively, the authors devised a clever way of running the two parts of the simulation separately and juxtaposing them together. During the early time points of the simulation when the overall microvascular network is still relatively small, capillary growth is simulated on a longer time scale, the simulation is paused when new anastomoses form, and blood flow in the network is modeled on a shorter timescale until a new steady state has been reached. This process is repeated for consecutive time windows. However, as the simulated network of vessels (i.e. the number of individual vessels) grows over time, flow simulation is performed at periodic intervals during the growth process so as to keep the model computationally tractable.

The model predicts that shear stress-induced branching leads to the earlier formation of dilated vessels close to the parent vessel. A sensitivity analysis was performed by changing a few key physical parameters, such as cell-matrix interactions and endothelial cell haptotaxis, and the results suggested an interesting therapeutically-relevant phenomenon: that reducing the influence of haptotaxis leads to networks with less anastamoses and a delayed onset of flow. The authors also used the simulation to quantify the abilities of different patterns of vascular networks to transport blood, nutrients, and chemotherapeutic drugs into the tumor. This analysis led to the identification of a therapeutic target—the manipulation of the haptotactic response of the migrating endothelial cells. This was predicted to lead to a capillary network characterized by reduced lateral migration and shear-induced branching. Although tumors with this pattern of vascular network would have abundant access to nutrients and therefore increased growth potential, they would also be susceptible to chemotherapeutic treatments. This simulation prediction is also consistent with a current hypothesis regarding the therapeutic manipulation of tumor vasculature: by remodeling the tumor vasculature such that leaky tumor vessels become stabilized and abnormal vessel network patterns become “normalized”, tumor growth and metastasis will be curbed [14].

To study how vascular network structures in normal tissues vs. tumors differ in terms of their transport behaviors, Baish et al., 1996 developed an invasion percolation-based network model [4]. Their model describes 2-D tumor vessel architecture in a murine dorsal skinfold model using fractal dimensions, and assumes that vascular growth in tumors is random and governed by local cues as opposed to global cues that are optimized at the tissue level. The authors abstract general physical properties of tumor networks that are indicated by a large sample of images and tumor types, and their stochastic method for generating model networks allows them to reproduce the large variability in tumor vascular network architectures that is observed experimentally. The authors conclude that their model generates more realistic representations of tumor vasculature architecture, with fewer large avascular spaces relative to the number of smaller avascular spaces and higher geometrical resistance due to increased vessel tortuosity.

Wound healing

Wound healing is a complex process that relies, in part, on angiogenesis. To better understand the interactions of endothelial cell behaviors and macrophage-derived chemotactic agents on dermal wound healing, Pettet et al., 1995 developed a continuum model, a system of PDEs, that models the growth of new blood vessels in an experimental rabbit ear wound model, which is approximated by the model as a 2-dimensional wound [24]. The numerical simulations generate a normal wound healing response (successful closure of the wound), as well as a dysfunctional wound healing response, as occurs in chronic wounds. The model explores how the balance between chemotaxis, cell proliferation, and cell apoptosis impacts the speed of healing. A negative feedback loop in their model limits angiogenesis by regulating the rate at which new endothelial cells migrate into the wound and the production of the pro-angiogenic factor, which is correlated with the density of the vascular bed. If the vessel density increases beyond a certain threshold, the macrophages cease to produce the pro-angiogenic-factor, which, in turn, reduces the extent of new endothelial cells migrating into the wound bed. The simulations reproduce some experimentally-observed features of the wound healing environment, including the formation of a well-developed vascular network at the wound border, known clinically as the “brush border”. The simulation identifies a maximum wave speed for the edge of the healing wound, as well as limits on the vascular density of healed wounds. The model was validated by comparing predictions to qualitative observations of wound healing in the rabbit ear wound model.

Designing tissue engineered constructs

The development of tissue engineered constructs greater than approximately 1 mm³ is limited by the necessity to overcome oxygen diffusion limitations. Thus, the development of novel approaches for engineering microvascular networks ex vivo or inducing their ingrowth upon implantation of the construct is imperative if ex vivo tissue engineering approaches are to be realized in the clinical setting. In an effort to provide a quantitative, predictive analysis tool for achieving this tissue engineering design goal, Jabbarzadeh and Abrams, 2007 recently developed a discrete model of VEGF-mediated endothelial cell chemotaxis through a porous membrane in response to three different time and position-dependent VEGF presentation strategies: (1) line source, (2) line source plus point sources distributed along boundaries of the construct, and (3) line source plus release throughout the construct boundary [13]. VEGF diffusion over 2, 6, and 10 days was simulated using standard reaction-diffusion equations, and the model was used to address the central question: How does VEGF transport inside the porous membrane regulate EC migration? Based on their model predictions, the authors conclude that Strategy #3 leads to a microvascular network that has a more uniform distribution over the area of the construct. The model also suggests that longer release durations of VEGF lead to more extensive vascular coverage of the construct. Likewise, a continuous release, even if it is at a lower release rate, sustains the concentration of VEGF so that new vascular branches can form and vessel elongation can continue into the construct. The model permits the quantitative evaluation of how key parameters, including porosity and pore size of the membrane, and VEGF release rate, location, and duration impact angiogenesis in a simulated tissue engineered construct.

Corneal angiogenesis

A popular model for studying angiogenesis is the corneal pocket model, in which exogenous growth factors can be supplied in a controlled manner to induce reproducible angiogenic sprouting from the limbic vessels. This experimental model has also been the subject of a mathematical model developed by Tong and Yuan, 2001 [30]. They developed a 2-dimensional model of angiogenesis in the rat cornea, considering the diffusion of an exogenously delivered pro-angiogenic factor, bFGF, and its activation of and uptake by endothelial cells. The model accounted for the following processes: 1) release of exogenously delivered bFGF from an implanted pellet, 2) diffusion of bFGF into the interstitial space and uptake of bFGF by endothelial cells, 3) formation and growth of angiogenic sprouts in response to bFGF, and 4) anatamoses between vessels. The model excluded the effects of subsequent vessel remodeling via recruitment of perivascular cells (smooth muscle cells and pericytes). The model used a system of 6 coupled PDEs that was solved numerically using a finite difference method carried out on 2-D discrete meshes. Since the formation of sprouts and direction of vessel growth were governed by stochastic rules (i.e. probabilities), each simulation was repeated 10 times. The simulated time window encompassed 12 hours. Although the simulation predicted rather intuitive relationships (e.g. that a decrease in endothelial cell uptake of bFGF resulted in increases in vessel density, number of vessel loops, and the speed of the advancing vascular front), the authors validated their model by performing an extensive quantitative comparison of geometric parameters (e.g. vessel lengths and numbers) to in vivo assays of corneal angiogenesis [3]. They also performed a sensitivity analysis to the parameter, S_max, the rate constant of sprout formation. By varying this parameter a factor of five above and below the baseline value, they were able to establish that this parameter is a key modulator of the “brush border” that has been observed experimentally in the cornea assay.

Impact of hemodynamics on angiogenesis and remodeling

Godde and Kurz, 2001 developed a vessel network-level model to probe the effects of hemodynamics on angiogenesis and vascular remodeling. Their 2-D model was implemented on an isometric grid in which simulated bifurcating vessels could proliferate or regress based on random deterministic processes. Pressure, flow, and velocity distributions in the network were considered, and the Fahraeus-Lindqvist effect was included. When a shear-stress-dependent growth probability was incorporated, their model recapitulated experimentally-observed interdigitation between the terminal branches of arterioles and venules. Inclusion of pressure-dependent remodeling lead to a reduction in the number of venules. The authors noted qualitative similarities to the remodeling patterns observed in the network to chick chorioallantoic membrane.

Peirce et al., 2004, developed an agent-based model to study biomechanical and biochemical phenomena impacting microvascular growth and remodeling at the tissue-level [23]. The effects of altering circumferential wall stress on arterialization and the impact of focal exogenous VEGF delivery on angiogenesis were modeled. The initial simulated vessel network architectures were obtained directly from in vivo tissues in a small animal model (rat), and the predictions of the agent-based model were validated against the actual remodeling responses measured empirically. The independent validation suggested that the module of rules governing cell behaviors was sufficient for quantitatively capturing key network-level features of the multi-cell system.

The impact of flow on intussusceptive angiogenesis was modeled by Szczerba and Szekeley [29]. Although their model ignores biochemical factors and oxygenation, it recapitulated translumenal pillar formation and splitting of vessels in response to steady-state flow-driven remodeling, and suggested that shear stress is the primary driving force of the intussusceptive remodeling under these conditions. Ji and Popel, 2006 developed a computational model of muscle at a moderate and high oxygen consumption rates (i.e. exercise) to assess how different modes of capillary growth, capillary sprouting vs. intussusceptive splitting, impact oxygen transport [15]. The model predicts that under moderate oxygen consumption rates, these two modes of angiogenesis give rise to similar volume fractions of hypoxic tissue. However, at high oxygen consumption rates where the pressure drop from the arteriole to venule is equal, the splitting regime generated the smallest volume fraction of hypoxic tissue. Interestingly, the sprouting network delivered oxygen more homogeneously and more extensively throughout the muscle when total blood flow was normalized. This model is particularly interesting because it gives quantitative predictions of phenomena that are currently impossible to approximate in vivo.

Angiogenic growth factors

A series of molecularly-detailed models have been developed to study the role of the VEGF receptors in physiological and pathological angiogenesis in response to various stimuli, such as exercise [19], pathological levels of ischemia [18], and breast tumorigenesis [20]. Mac Gabhann and Popel, 2006 developed a computational model that included, in addition to VEGF and the VEGF receptors, Neuropilin-1, a non-signaling co-receptor for VEGF [20]. In this paper they extend a previous model to simulate in vivo VEGF transport and binding in breast cancer and use the model to compare three different putative therapeutic approaches (i.e. “drug interventions”) for inhibiting VEGF signaling via Neuropilin manipulation: 1) blockade of Neuropilin-1 expression, 2) inhibition of VEGF-Neuropilin-1 binding, and 3) inhibition of VEGF-R/Neuropilin-1 coupling. The model describes the system by a set of coupled nonlinear ODEs, which are solved to find the steady state-concentrations of all the molecular species. The model simulates the 48 hours following each of the three “drug” interventions, and all parameters were either obtained or estimated from the literature. Importantly, their model predicts that targeting the same molecule (i.e. VEGF) using different molecular-level strategies may result in different angiogenesis-related outcomes with different levels of therapeutic efficacy. Specifically, the model predicts that blocking VEGF-R/Neuropilin coupling may be the most effective strategy because it effectively transforms Neuropilin into an endogenous anti-angiogenic co-receptor that sequesters VEGF and prevents its signaling through the VEGF-R. An experimental study has since confirmed the ability of a Neuropilin antibody to inhibit pathological angiogenesis in the eye. This work also generated testable predictions, including the increase in interstitital VEGF concentration in response to all three therapeutic manipulations. Thus, the model was useful for assisting in the design of experimental studies in addition to aiding in the design of therapeutic strategies.

In 2007, Mac Gabhann et al. developed a 3-D model of exercise-induced hypoxia in the rat extensor digitorum longus (skeletal) muscle in order to approximate in vivo spatio-temporal concentrations and concentration gradients of VEGF at the single cell level—information that is impossible to obtain using currently available experimental techniques, and information that is critical for understanding how cells sense and respond to growth factor gradients in tissues [19]. Their model is multi-scale in that it integrates molecular details of VEGF distributions with tissue-level details, including oxygen transport and blood flow. Specifically, blood flow levels are calculated based on the microvascular network architecture. The simulated hemodynamics also account for the Faraheus-Lindqvist effect and variable hematocrit that occurs due to phase separation at microvascular bifurcations. Tissue oxygenation levels, resulting from the hemodynamic calculations (blood flow) and the oxygen consumption rate by myofibers, are determined by using a previously developed model of the same tissue [15]. VEGF secretion rates, in turn, are calculated according to a function that depends on local myocyte oxygen tension. VEGF transport within the ECM is described by mass balance equations, while the kinetics of VEGF binding to its receptor on endothelial cells is calculated based on data obtained in in vitro studies with receptor concentrations based on in vivo measurements. The majority of parameters were estimated or obtained directly from the literature. Their model predicts that hypoxic muscle contains large gradients of VEGF (spanning distances of single endothelial cells) and spatially heterogeneous VEGF receptor activation levels. While longitudinal VEGF gradients along the length of muscle fibers are considerable, the transverse gradients perpendicular to the muscle fibers are ten times steeper. The authors suggest that this steep VEGF gradient, predicted for the first time by their multi-scale model, may explain an important observed behavior of capillary sprouting in muscle tissue: why sprouts bud off parent vessels at angles perpendicular to muscle fibers.

More recently, this model has been used to investigate the effects of therapeutically manipulating VEGF concentrations and gradients in the face of ischemic insult using three different strategies: 1) VEGF gene therapy, 2) VEGF cell-based therapy, and 3) chronic exercise, or upregulation of VEGF-receptor expression [18]. The model predicted that exercise training causes increased VEGF secretion from hypoxic muscle fibers, as well as increased VEGF receptor expression levels, and this combination of downstream events is suggested to both elevate local VEGF concentrations and generate steeper VEGF gradients. Thus, their model suggests that exercise is the most effective of the three stimuli for treating peripheral arterial disease (PAD).

Challenges of modeling angiogenesis

As with any analysis technique, be it experimentally or theoretically-based, there are certain challenges, caveats, and pitfalls that must be acknowledged and dealt with in a scientifically rigorous manner if the data/predictions produced by the analysis are to be trusted. The next section will overview some of the conceptual hurdles that arise when building computational and/or mathematical models of complex biological processes. Although these are challenges are not limited to angiogenesis models, we will use published models of angiogenesis to showcase how modelers have attempted to overcome issues relating to systems-level complexity, parameter identification, and model validation.

Model complexity, assumptions, and simplification strategies

Angiogenesis and related processes (e.g. microvascular remodeling, regression, and intusussception) can be considered complex biological phenomena in that their systems-level behaviors are dynamic, spatially heterogeneous, frequently non-linear, and they span many orders of magnitude, both spatially and temporally. In order to construct models of a complex process that generate meaningful and useful results (and are solvable and/or computable), it is necessary to make assumptions about the system and to employ simplification strategies. For angiogenesis modeling, these simplification strategies can be broadly parsed into geometric simplifications, process simplifications, and temporal simplifications. One type of geometric simplification is assuming a 2-dimensional geometry for a 3-dimensional tissue structure by defining the boundaries of the model to simulate a cross-sectional slice through the tissue. Another geometric simplification strategy is abstracting the complex branching pattern of a microvascular network into a more regular pattern that has attributes of the complex network (e.g. vessel length density) but does not simulate the exact structure of the network on a vessel-by-vessel basis. An example of a process simplification strategy is consolidating the number of growth factors in a model that impact a certain process by focusing on a few key factors or by attributing key behaviors to one “hypothetical” growth factor (e.g. TAF). A frequently employed temporal simplification in angiogenesis modeling is the modeling of discrete timeframes during which key phenomena are thought to occur. Specific examples of these types of simplification strategies that have been used in published models of angiogenesis are provided in Table 2.

Table 2.

Types of simplification strategies and examples of each from published models of angiogenesis.

Geometric	Process	Temporal
Initial parent vessel configuration is a single straight line vessel [13;21;27]	Treat cell as a black box; ignore specific intracellular signaling events [5;23]	Model blood flow through the network at steady state [8]
Model considers a two-dimensional cross-section through a spherical tumor [11] or a two-dimensional (flattened) cornea [30]	Simplify/reduce the number of angiogenic growth factors [13;24]	Cell behaviors (e.g. migration, proliferation) are modeled on a coarse (e.g. 6-hour) time scale [23;31]
Tree-like architecture of network is sacrificed at the expense of fractal analysis [4]	Simplify the number of cell types (e.g. consider endothelial cells exclusively) [13;24]	Total time required for certain biological processes to occur is compressed [23;30]

Parameter identification

Another challenge in modeling any complex biological phenomena, including angiogenesis, is the identification of suitable parameters—fixed or adjustable variables that quantitatively dictate how the model will behave. Depending on the type of model (e.g. discrete, continuous, stochastic, deterministic), there can be anywhere from one to hundreds of parameters, and often these are derived from (or estimated from) published experimental data. Some parameters, are difficult, if not impossible to measure in vivo using currently available experimental techniques, but they may be attainable in in vitro assays. It is, therefore, quite common for an angiogenesis model builder to cull parameter values from a combination of experimental assays and techniques. On occasion, model parameters will be determined by making incremental adjustments in their values until the model output “fits” a realistic or observed experimental output. The abundance of published angiogenesis models use a combination of fit and literature-derived parameters [11;17], although there are some models that rely exclusively on published parameter values [23]. It can be quite informative to perform a sensitivity analysis, whereby the levels of certain parameters are adjusted systematically in order to quantitatively appreciate the impact that different parameters will have on generalized outcomes of the model [5]. Quite often, sensitivity analyses are capable of providing insights into how the system functions as a whole, identifying targets for therapeutic manipulation, and serving as reality-checks for the biological accuracy of the model.

Model validation and verification

To assess the predictive power of a model (i.e. how realistically it recapitulates the biological process), it is necessary to validate the model. Model validation is accomplished by comparing model outputs to experimentally observed phenomena. This comparison can be accomplished using qualitative and/or quantitative metrics, although the latter is arguably more rigorous [5;23]. A noteworthy distinction is the difference between model validation and model verification. Model verification is the process of confirming that the model is “working” as the model builder expects it to—that the equations are accurately implemented, that model outputs match what is expected based on the model inputs, that the model was built “correctly”. When verifying a model it is perfectly suitable to compare model outputs to the data set that was used to construct the model (i.e. model inputs), with the expectation that they will match one another if the model has been constructed properly. In contrast, the process of validating a model requires that independent data sets be used for model construction (i.e. model inputs) and validation. Thus, validating a model answers a fundamentally different question: “Does the model generate outputs that are realistic or observed in nature.” It is immediately apparent that the reliance of models on experimental data is critical for each stage in a model’s development—from construction, to verification, to validation. Without intimate pairing of theoretical and experimental approaches throughout a models inception and implementation, the model’s utility and applicability is undermined.

Conclusions

We have overviewed different types of mathematical and computational modeling approaches that have been employed in the study of angiogenesis and summarized an array of published models aimed at answering different questions relevant to angiogenesis-related processes. A main focus of this review has been to showcase how these models have contributed to either basic understanding of angiogenesis or improved design of angiogenesis-targeted therapies. We have also discussed some of the challenges associated with constructing and utilizing mathematical and computational angiogenesis models.

Arguably, theoretical models of angiogenesis are as diverse as their experimental counterparts, and the type and value of information they provide are equally as varied. We submit, however, that the value of modeling a complex biological process, such as angiogenesis, is not simply in the end result—a validated model that (perhaps to some extent) recapitulates, or predicts, relevant or observed phenomena. Rather, the model building process itself adds value to the discovery process by pinpointing voids in understanding, suggesting new experiments, providing an additional framework for hypothesis testing, and by generating new hypotheses that have quantitative basis and may not be immediately apparent from experimental pursuits alone. With the ability to track the individual behaviors of thousands of cells, perform in silico “knockout” experiments that are technically infeasible genetic manipulations experimentally, and perform high-throughput/low-cost sensitivity analyses to identify key parameters in complex systems, mathematical and computational modeling serve as additional quantitative “assays” that complement the available experimental models.

With the explosion of research in this area over the last twenty years, the field is rich in experimental data and yet critical, long-standing questions remain: How does the multitude of identified pro- and anti-angiogenic growth factors and their receptors orchestrate angiogenesis? How do vascular support cells and circulating cells interact with endothelial cells during angiogenesis and remodeling, and what biochemical signals modulate their interactions? What role do mechanical signals play in modulating capillary sprouting? Answering each of these questions relies on obtaining information—regarding spatio-temporal gradients of growth factors, single cell trafficking patterns, and high-resolution appreciation of the hemodynamic and interstitial flow environments--that cannot completely be assessed using existing experimental approaches alone. Mathematical and computational models, and particularly multi-scale models that are emerging with capabilities to integrate biological processes that span spatial and temporal scales across orders of magnitude, can be constructed in such a way complement experimental studies and address some of these important, unanswered questions in our field.