A Unifying Framework for Assessing Changes in Life Expectancy Associated with Changes in Mortality: The Case of Violent Deaths

Abstract

For over forty years, demographers have worked intensely to develop methods that assess the gain in life expectancy from a reduction in mortality, either hypothetical or observed. This considerable body of research was motivated by assessing the gains in life expectancy when mortality declined in a particular manner and determining the contribution of a cause of death in observed changes in life expectancy over time. As yet, there has been no framework unifying this important demographic work. In this paper, we provide a unifying framework for assessing the change in life expectancy given a change in age and cause-specific mortality. We consider both conceptualizations of mortality change–counterfactual assessment of a hypothetical change and a retrospective assessment of an observed change. We apply our methodology to violent deaths, the leading cause of death among young adults, and show that realistic targeted reductions could have important impacts on life expectancy.

1 Introduction

For over forty years, demographers have worked intensely to develop methods that assess the gain in life expectancy from a reduction in mortality, either hypothetical or observed. This considerable body of research was motivated by assessing the gains in life expectancy when mortality declined in a particular manner and determining the contribution of a cause of death in observed changes in life expectancy over time. The first attempt came in the form of single decrement life tables, which estimated the gain in life expectancy at birth under the assumption that one cause of death was completely eliminated (United States Department of Health, Education, and Welfare, 1968). Recognizing the tenuousness of this assumption, Keyfitz (1977) derived the proportional change in life expectancy at birth when either all-cause or cause-specific mortality was reduced by a constant percentage across age. Later developments focused on decomposition approaches. For example, Pollard (1982); Andreev (1982); Arriaga (1982); United Nations (1982); Arriaga (1984); Pressat (1985); Pollard (1988); Andreev et al. (2002) examined absolute gains in life expectancy resulting from absolute reductions in cause and age specific mortality between two discrete times. Subsequently, Vaupel (1986) and Vaupel and Canudas-Romo (2003) further developed decomposition approaches from a continuous-time perspective focusing on continuous progress against mortality. Recently, Beltrán-Sánchez et al. (2008) connected cause-elimination techniques with decomposition methods.l

All of these approaches addressed substantively important research questions. Yet their development was motivated by the very specific type of mortality decline envisioned. Consequently, their development was largely accomplished independently of one another; little opportunity arose to deduce connections. For example, the framework of mortality decline, either hypothetical or retrospective, leads to two seemingly different approaches. Only recently has their equivalence been demonstrated (Beltrán-Sánchez et al., 2008).

In this paper, we provide a systematic review of the literature within the unified functional calculus framework. We use functional calculus to demonstrate that previous approaches for assessing changes in life expectancy may be derived from a common formulation. With this framework, we are now able to concisely study how a change in age and cause-specific mortality contributes to changes in life expectancy. We apply our method to violent deaths, the leading cause of death among young adults. Other methods have been developed to decompose other demographic quantities of interest: the mean, median, mode, and standard deviation of the age of death distribution; healthy life expectancy; and total fertility rate (Das Gupta, 1991, 1999; Andreev et al., 2002; Horiuchi et al., 2008). In contrast, we focus on life expectancy and provide greater mathematical rigor reconciling previous developments related to decomposing changes in life expectancy over time.

2 Theoretical Derivations

2.1 Functionals

We use functional differential calculus to link changes in age and cause-specific mortality with changes in life expectancy. Functional differential calculus was first applied to demography by Arthur (1981, 1984) and by Preston (1982). A function f : 𝒜 → ℬ is a mapping that consists of two sets 𝒜 and ℬ with a rule that assigns to each element a ∈ 𝒜 a specific element of ℬ, which is denoted as f (a). Similarly, a functional F is a mapping from a vector space, ℱ, to the field underlying the vector space (usually the real numbers ℝ), which is denoted as ℱ [f]. Whereas a function is an element-by-element mapping, a functional maps an entire function to an element. For example, the probability of surviving from birth to age a at time t, p(a, t), is equal to exp $(-{\displaystyle \underset{0}{\overset{a}{\int }}}\mu (s,t)\mathit{\text{ds}})$, where μ(s, t) corresponds to the hazard rate at age s time t. Using a functional approach, p(a, t) is equal to exp (F[μ]), where F[μ] is defined as:

$$F[\mu ]=-{\displaystyle \underset{0}{\overset{a}{\int }}}\mu (s,t)\mathit{\text{ds}}.$$ (1)

F[μ] assigns to every function μ a real number corresponding to the negative of the definite integral of that function μ from 0 to a. Notice that μ could be any function of hazard rates, for example, a Gompertz function. Using the functional F, life expectancy at birth at time t, e(0, t), can be written as ${\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\text{exp}[F[\mu ]]\mathit{\text{da}}$.

2.2 Functional Differentials

The functional differential of F[f], denoted by δF[f; h], approximates the change in F when f changes by a function h (Luenberger, 1968). This functional differential is defined as:

$$\delta F\left[f;h\right]=\underset{\alpha \to 0}{\text{lim}}\frac{F(f+\alpha h)-F(f)}{\alpha }.$$

In general, when a model explicitly expresses a variable of interest, say r, in terms of functions f_i and parameters x_j for i = 1, …, n and j = 1, …, m such that r = F(f₁, f₂, …, f_n, x₁, x₂, …, x_m), we can write the differential change in r as

$$\delta r={\displaystyle \sum _{i\in I}}\delta r[\delta f_i]+{\displaystyle \sum _{j\in J}}\delta r[\delta x_j].$$ (2)

where I and J represent the set of functions and parameters indices, respectively, which may change (Arthur, 1984). In other words, the differential change in the variable r corresponds to the sum of differential changes in functions and parameters. When the variable of interest r is implicitly expressed in the model, we have an implicit functional model of the form: 0 ≡ F(r, f₁, f₂, …, f_n, x₁, x₂, …, x_m). Thus, we have the following functional differential:

$$0=\delta F[\delta r]+{\displaystyle \sum _{i\in I}}\delta F[\delta f_i]+{\displaystyle \sum _{j\in J}}\delta F[\delta x_j].$$ (3)

For example, suppose our variable of interest is the probability of survival from birth to age a at time t, p(a, t). In this case we have an explicit model linking p(a, t) with μ(a, t). Our functional F takes a single argument, a function μ(a, t), as shown in equation 1. Further, suppose we want to find the change on this survivorship when there is a change in μ(a, t). Using equation 2 and the chain rule, the functional change in p(a, t) is defined as¹:

$$\delta p(a,t)=\delta \text{ exp }[F[\mu ]]=\frac{\partial (\text{exp}[F])}{\partial F}\delta F[\delta \mu ]=\text{exp}[F]\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]=-p(a,t){\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}.$$ (4)

The quantity δμ(a, t) expresses a change in the force of mortality that may occur along both the age and time dimensions. Thus, from equation 2, we can define δμ(a, t) as

$$\delta \mu (a,t)=\{\begin{array}{c}\underset{\alpha \to 0}{\text{lim}}\frac{\mu (a+\alpha h,t)-\mu (a,t)}{\alpha }\text{ for changes over the age dimension},\hfill \\ \underset{\alpha \to 0}{\text{lim}}\frac{\mu (a,t+\alpha h)-\mu (a,t)}{\alpha }\text{ for changes over the time dimension}.\hfill \end{array}$$

2.3 First Derivations

Let G be a functional defined as:

$$G[\mu ,t]={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\text{exp}[F[\mu ]]\mathit{\text{da}}-e\left(0,t\right)\equiv 0.$$

where F[μ] is defined in equation 1. Using equation 3, the functional differential of G is given by (see A.1):

$$0=\delta G[\delta \mu ]+\delta G[\delta t].$$ (5)

Evaluating each term of the above equation leads to:

$$\frac{\partial e(0,t)}{\partial t}=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\delta \mu (s,t)}{\delta t}p(s,t)e(s,t)\mathit{\text{ds}}.$$ (6)

The relative change in life expectancy at birth, defined as é(0, t), is obtained by diving equation 6 by e(0, t)

$$\mathit{é}(0,t)=\frac{-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\delta \mu (s,t)}{\delta t}p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}.$$ (7)

2.4 Multiple Causes of Death

Let μ₁, …, μ_N be a set of mutually exclusive and exhaustive causes of death. Replacing μ with its sum μ₁ + ⋯ + μ_N in equation 6, the continuous change in life expectancy at birth due to changes in cause-specific mortality equals:

$$\frac{\partial e(0,t)}{\partial t}=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{{\displaystyle \sum _{i=1}^N}\delta {\mu }_i(s,t)}{\delta t}p(s,t)e(s,t)\mathit{\text{ds}}.$$ (8)

Similarly, replacing μ with its sum in equation 7, the relative change in life expectancy at birth due to changes in cause-specific mortality equals:

$$\mathit{é}(0,t)=\frac{-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{{\displaystyle \sum _{i=1}^N}\delta {\mu }_i(s,t)}{\delta t}p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}.$$ (9)

2.5 Particular Cases

The expression δμ(s, t)/δt and in equations 6 and 7 and δμ_i(s, t)/δt in equations 8 and 9 represent the changes in all cause and cause-specific force of mortality, respectively, for every unit of time. It is precisely these quantities and their evaluation under different contexts that provide a unifying framework linking changes in life expectancy with changes in forces of mortality. For example, we may be interested in estimating how much of the observed change in life expectancy between two time periods is attributed to changes in a particular cause of death (Arriaga, 1982; Pollard, 1982). Similarly, we may also be interested in evaluating the change in life expectancy under two different mortality scenarios (Keyfitz, 1977). In these cases, the functional differential of μ(s, t) and μ_i(s, t) would be evaluated in the context of a discrete change over time or its equivalent–a discrete change between two different scenarios. Additionally, we may be interested in both of the above questions from a continuous time perspective (Vaupel, 1986; Vaupel and Canudas-Romo, 2003; Beltrán-Sánchez et al., 2008). Then, the functional differential of μ(s, t) and μ_i(s, t) would be evaluated in the context of a continuous time framework. Equations 6, 7, 8, and 9 precisely represent these approaches in a concise and unifying framework. We fully explore these ideas and their relationship with previous work in the next section.

2.5.1 Discrete Case

There are two general approaches when thinking of discrete changes in mortality. The first case relates to proportional changes in mortality rates, while the second approach is concerned with absolute changes. The first scenario was originally proposed by Keyfitz (1977) and the second approach was derived by several researchers (Pollard, 1982; Andreev, 1982; Arriaga, 1982; United Nations, 1982; Arriaga, 1984; Pressat, 1985; Pollard, 1988; Andreev et al., 2002), but two of the most commonly used formulas are those of Arriaga (1982) and Pollard (1982).

First, we consider a proportional change in mortality. Suppose there is a new scenario in which the force of mortality is proportionally reduced at all ages, i.e. μ*(a, t) = (1 + k) μ (a, t) where k is a small negative number (see Keyfitz, 1977). The functional differential of μ(a, t) is equal to its change between the two scenarios,

$$\delta \mu (a,t)=k\mu (a,t).$$

Then, substituting the above functional differential into equation 7 leads to a well known result of proportional change in life expectancy by Keyfitz (1977, p.413) (see A.1.1):

$$\begin{array}{cc}\frac{e^{*}(0,t)}{e(0,t)}\hfill & =1-k\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\mu (s,t)p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}\hfill \\ \hfill & =1-k\left[-\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}p(s,t)\text{ ln }[p(s,t)]\mathit{\text{ds}}}{e(0,t)}\right]\hfill \\ \hfill & =1-kH.\hfill \end{array}$$

The equivalence of the first and second lines in the above equation were shown by Vaupel (1986) and Goldman and Lord (1986).

Now suppose there is a new scenario in which the cause-specific force of mortality is proportionally reduced at all ages, i.e. ${\mu }_i^{*}(a,t)=(1+k){\mu }_i(a,t)$ for cause i, where k is a small negative number (see Keyfitz, 1977). In this case, the functional differential of μ_i(a, t) is equal to k μ_i(a, t). Following the same approach as in all-cause mortality, one can show that equation 9 reduces to another well known result of proportional change in life expectancy by Keyfitz (1977, p.414):

$$\begin{array}{cc}\frac{e^{*}(0,t)}{e(0,t)}\hfill & =1-k\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}{\displaystyle \sum _{i=1}^N}{\mu }_i(s,t)p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}\hfill \\ \hfill & =1-k{\displaystyle \sum _{i=1}^N}\left(-\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}p(s,t)\text{ ln }[p_i(s,t)]\mathit{\text{ds}}}{e(0,t)}\right)\hfill \\ \hfill & =1-{\displaystyle \sum _{i=1}^N}{\mathit{\text{kH}}}_i.\hfill \end{array}$$

Second, we consider an absolute change in mortality. Suppose there is an absolute improvement ϕ in the force of mortality μ(a, t) for some a ∈ [x, x + Δx], i.e. μ*(a, t) = μ(a, t) + ϕ, where ϕ is a small negative number (see Pollard, 1982). Substituting this result into equation 6 reduces to the well known result for attributing absolute changes in mortality and the corresponding absolute changes in life expectancy by Pollard (1982) (see A.1.2):

$$e^{*}(0,t)-e(0,t)={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}[\mu (s,t)-{\mu }^{*}(s,t)]p(s,t)e(s,t)\mathit{\text{ds}}.$$

Now suppose there is an absolute improvement $\frac{\varphi }{N}$ for each cause-specific force of mortality such that $\delta {\mu }_i=\frac{\varphi }{N}$. Following the same approach as in all-cause mortality, equation 9 reduces to the cause-specific mortality result of Pollard (1982) (see A.1.2):

$$e^{*}(0,t)-e(0,t)={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}{\displaystyle \sum _{i=1}^N}[{\mu }_i(s,t)-{\mu }_i^{*}(s,t)]p(s,t)e(s,t)\mathit{\text{ds}}.$$

Pollard (1988) showed the equivalence between his previously developed approach (Pollard, 1982) and that of Arriaga (1982). Similarly, Andreev et al. (2002) showed Pollard (1982) is a special case of the stepwise replacement algorithm.

In addition, we can use our framework to derive a simple formula for the cause-eliminated life table model. This model considers the change in life expectancy when cause-specific mortality rates are set to zero and mortality for all other causes is held constant. Let i represent the cause eliminated. Set k = −1 for cause i; the functional differential of μ_i(a, t) is equal to −1 μ_i(a, t). Set k = 1 for all other causes j ≠ i; the functional differential of μ_j(a, t) is equal to 1 μ_j(a, t). Substituting these functional differentials into equation 8 leads to the cause-eliminated life table model.

2.5.2 Continuous Case

First, suppose there is continuous progress against all-cause mortality with respect to time such that the rate of progress in μ(a, t) is given by $\rho (a,t)=\frac{\partial \mu (a,t)/\partial t}{\mu (a,t)}$ (see Vaupel, 1986). Then, the ratio of the functional differential of μ to that of time, $\frac{\delta \mu (a,t)}{\delta t}$, is equivalent to $\frac{-\partial \mu (a,t)}{\partial t}$. Thus, equation 7 reduces to the well known result of Vaupel (1986).

$$\pi (t)=\frac{\partial e(0,t)/\partial t}{e(0,t)}=-\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{-\partial \mu (s,t)}{\partial t}p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\rho (s,t)\eta (s,t)\mathit{\text{ds}},$$

where η(s, t) = μ(s, t) p(s, t) e(s, t)/e(0, t).

Similarly, when there is continuous progress against cause-specific mortality with respect to time, ${\displaystyle \sum _{i=1}^N}\frac{\delta {\mu }_i(a,t)}{\delta t}$ is equivalent to ${\displaystyle \sum _{i=1}^N}\frac{-\partial {\mu }_i(a,t)}{\partial t}$. Thus, equation 9 reduces to:

$$\frac{\partial e(0,t)}{\partial t}={\displaystyle \sum _{i=1}^N}{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial {\mu }_i(s,t)}{\partial t}p(s,t)e(s,t)\mathit{\text{ds}},$$

which is the Vaupel and Canudas-Romo (2003) result for decomposing changes in life expectancy by causes of death.

Second, suppose we are interested in the change with respect to time in the gain in life expectancy at birth when one cause of death is eliminated. This question was recently addressed by Beltrán-Sánchez et al. (2008). The years of life gained at birth at time t if cause of death i is eliminated is computed as D_i(0, t) = e_−i(0, t)−e(0, t), where e_−i(0, t) represents life expectancy at birth at time t when cause of death i is eliminated. Then, the change in D_i(0, t) with respect to time is given by

$$\frac{\partial D_{-i}(0,t)}{\partial t}=\frac{\partial e_{-i}(0,t)}{\partial t}-\frac{\partial e(0,t)}{\partial t}.$$ (10)

Both terms on the right hand side of the above equation are particular cases of equation 6. Thus, evaluating the functional differential of these terms leads to the main result of Beltrán-Sánchez et al. (2008) for linking decomposition approaches and cause-deleted life tables (see A.1.3):

$$\frac{\partial D_i(0,t)}{\partial t}={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial p_{-i}(s,t)}{\partial t}[1-p_i(s,t)]\mathit{\text{ds}}-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial p_i(s,t)}{\partial t}{p}_{-i}(s,t)\mathit{\text{ds}}.$$

2.6 Varying Proportional Declines By Age and Cause of Death

Revisiting our main substantive research question, suppose we are interested in the change in life expectancy if there had been declines in particular age-specific motor vehicle, homicide, and suicide mortality rates over time. Our quantity of interest is life expectancy at birth. Under this scenario, we suppose there are targeted proportional reductions in the force of mortality for specific ages and causes. Let 𝒜₁, …, 𝒜_m be the set of targeted age groups for j = 1, …, m. Let cause one be motor vehicle accident mortality, cause two be homicide, cause three be suicide, and cause four be all other causes of death, so that $\mu (a,t)={\displaystyle {\sum }_{i=1}^4}{\mu }_i(a,t)$ for any given age a at time t. Let k_i,𝒜j ≤ 0 be the proportional reduction in mortality for cause i and age group 𝒜_j, j = 1, …, m. As discussed in Section 2.5.1, the functional differential of μ_i(a, t) is equal to:

$$\delta {\mu }_i(a,t)=\{\begin{array}{cc}{k}_{i,{𝒜}_j}{\mu }_i(a,t)\hfill & \text{for}j=1,\dots ,m,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (11)

In other words, the change in cause-specific mortality after the targeted reduction is proportional to the original cause-specific mortality for ages within the targeted age range and is zero otherwise. Substituting equation 11 into equation 8, the change in life expectancy at birth between the two scenarios is equal to:

$$\begin{array}{cc}{e}^{*}(0,t)-e(0,t)\hfill & =-\left[{\displaystyle \underset{{𝒜}_1}{\int }}{\displaystyle \sum _{i=1}^4}{k}_{i,{𝒜}_1}{\mu }_i(s,t)p(s,t)e(s,t)\mathit{\text{ds}}+\cdots +{\displaystyle \underset{{𝒜}_m}{\int }}{\displaystyle \sum _{i=1}^4}{k}_{i,{𝒜}_m}{\mu }_i(s,t)p(s,t)e(s,t)\mathit{\text{ds}}\right]\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^m}\left[{\displaystyle \sum _{i=1}^4}(-k_{i,{𝒜}_j}){\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p(s,t)e(s,t)\mathit{\text{ds}}\right].\hfill \end{array}$$ (12)

The integral in the above equation represents the potential years of life lost (YLL) at time t due to cause i in age group 𝒜_j. A similar quantity, aggregated over cause, was previously noted by Vaupel (1986) and further developed by Vaupel and Canudas-Romo (2003); Zhang and Vaupel (2008, 2009). The scalar −k_i,𝒜j represents the recovery of potential years of life lost for cause i age group 𝒜_j. For example, if −k_i,𝒜j = 0.80, we recover 80% of the potential years of life lost at time t due to cause i in age group 𝒜_j. Finally, the product represents the realized years of life gained at time t due to cause i in age group 𝒜_j.

Although the theoretical derivation of the change in life expectancy at birth is given within the continuous-time framework, data are typically recorded in a discrete form. In this case, equation 12 contains an additional interaction term (see A.1.4):

$$e^{*}(0,t)-e(0,t)=\{\begin{array}{cc}\text{Main effect}:\hfill & {\displaystyle \sum _{j=1}^m}\left[{\displaystyle \sum _{i=1}^4}-k_{i,{𝒜}_j}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p(s,t)e(s,t)\mathit{\text{ds}}\right]\hfill \\ \text{Interaction}:\hfill & {\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}{\displaystyle \sum _{z=1}^{\mathrm{\infty }}}\frac{{\left(-k_{i,{𝒜}_j}\right)}^{z+1}}{z!}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p(s,t)e(s,t){(-\text{ln}[p_i(s,t)])}^z\mathit{\text{ds}}\hfill \end{array}$$ (13)

Using life table notation, the above terms can be estimated as:

$$\begin{array}{cc}\text{Main Effect}\hfill & \approx {\displaystyle \sum _{j=1}^m}\left[{\displaystyle \sum _{i=1}^4}-k_{i,{𝒜}_j}\frac{{}_{n_j}{d}_{a_{j_{\mathit{\text{start}}}},i}}{l_0}\frac{{}_{n_j}{L}_{a_{j_{\mathit{\text{start}}}},-i}}{n}\frac{e_{a_{j_{\mathit{\text{start}}}}}+e_{a_{j_{\mathit{\text{end}}}}}}{2}\right]\hfill \\ \hfill \text{Interaction}& \approx {\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}{\displaystyle \sum _{z=1}^{\mathrm{\infty }}}\frac{{(-k_{i,{𝒜}_j})}^{z+1}}{z!}\frac{{}_{n_j}{d}_{a_{j_{\mathit{\text{start}}}},i}}{l_0}\frac{{}_{n_j}{L}_{a_{j_{\mathit{\text{start}}}},-i}}{n}\frac{e_{a_{j_{\mathit{\text{start}}}}}+e_{a_{j_{\mathit{\text{end}}}}}}{2}\frac{{(-\text{ln}[p_i(a_{j_{\mathit{\text{start}}}})])}^z+{(-\text{ln}[p_i(a_{j_{\mathit{\text{end}}}})])}^z}{2}\hfill \end{array}$$ (14)

where a_j,start and a_j,end represent the starting and ending ages of the age group 𝒜_j; l₀ represents the life table radix, and e_ajstart and e_ajstart represent life expectancy at age a_jstart and age a_jend, respectively, in the life table for all-cause mortality. Terms with subindex i and −i refer to life table quantities where cause of death i and −i, respectively, is the only cause operating in the population. Thus, _njd_{ajstart, i} represents the number of life table deaths in age group 𝒜_j and p_i(a) represents the probability of surviving from birth to age a when there is only cause i. The term _njL_{ajstart, −i} represents the person-years lived in age group 𝒜_j when all causes of death except cause i are operating in the population.

3 Applications

3.1 Data

We calculated 1970 and 2005 death counts for the total United States (U.S.) population from the Mortality Detail Files (U.S. Department of Health and Human Services, 2010, 2008), which contain information on all deaths registered on individual U.S. death certificates transmitted to the National Center for Health Statistics. Deaths were disaggregated by age and sex, as well as the following causes: motor vehicle accidents, homicides, suicides, and all other causes. Hereafter, we refer to motor vehicle accident mortality, homicides, and suicides as violent deaths. Comparable codes for these causes of death were derived from the Centers for Disease Control and Prevention (CDC, 2001). We use exposure-to-risk calculated by the Human Mortality Database University of California, Berkeley (USA) and Max Planck Institute for Demographic Research (Germany) (2006). Finally, we combine death counts and exposure-to-risk to calculate mortality rates by age, sex, and cause for 1970 and 2005. The terminal age category begins at age 100.

Considerable progress had been made against violent deaths for most of the ages between 1970 and 2005, as shown in Table 1. For example, improvements in vehicle safety and the introduction of car seats, especially rear-facing car seats, in part led to a more than 60% decline in motor vehicle accident mortality for children under age 10 in this period. Notable exceptions are male and female infanticide and male late adolescent homicide and suicide. For example, infanticides increased by 78% and 59% for males and females between 1970 and 2005, respectively.

Table 1.

Proportion of Total, Motor Vehicle Accidents, Homicide, and Suicide Deaths & Change in Motor Vehicle Accidents, Homicide, and Suicide Mortality Rates: 1970 and 2005, Males and Females.

	Total Deaths		Motor Vehicle Accidents			Homicide			Suicide
Age Group	Prop. of Deaths		Prop. of Deaths		Δ Mort. Rate	Prop. of Deaths		Δ Mort. Rate	Prop. of Deaths		Δ Mort. Rate
	1970	2005	1970	2005		1970	2005		1970	2005
Male
0–1	3.9	0.9	0.4	0.6	−63.1	0.2	1.4	78.7	0	0	–
1–4	0.6	0.2	13.8	13.7	−68.7	2	8.7	35.2	0	0	–
5–9	0.5	0.1	27.3	22.9	−75.4	1.2	4.5	11.3	0	0.1	1.1
10–14	0.5	0.2	24.4	21.5	−63.5	2.8	5.8	−15.1	1.8	8.3	85.7
15–19	1.4	0.9	40.6	27.4	−52.9	8.1	15.3	32	5.6	10.7	33.9
20–24	1.6	1.4	37.3	23.7	−49.7	11.8	15.5	4	8.5	11.1	3.5
25–29	1.2	1.3	27.3	17.7	−47.6	13.9	14.1	−18	9.7	11.3	−5.6
30–34	1.2	1.3	18.4	14.4	−43.3	11.8	10.2	−37	8.6	12	1.6
35–39	1.6	1.5	12.1	11.3	−44	7.7	6.1	−51.8	6.7	11.1	−0.4
40–44	2.6	2.2	7.7	8.5	−40.3	4.3	3.9	−51.2	4.8	9.3	4.4
45–49	4.1	3	4.9	6.2	−41.6	2.4	2.4	−53.4	3.6	7.1	−7.2
50–54	5.9	3.5	3.1	4.6	−40.3	1.3	1.4	−57.6	2.5	5.2	−15.1
55–59	8.2	4.1	2.2	3.2	−48.8	0.7	0.7	−64.7	1.8	3.4	−32.7
60–64	10.4	4.8	1.5	2	−50.8	0.4	0.4	−62.9	1.2	2.1	−32.8
65–69	11.9	5.7	1.1	1.3	−51.1	0.2	0.2	−66.5	0.8	1.3	−41.1
70–74	12.7	7.8	0.9	0.9	−52.1	0.1	0.1	−54.5	0.6	0.9	−32.7
75–79	12.6	11.3	0.7	0.6	−54	0.1	0.1	−46.2	0.5	0.7	−18.5
80–84	10.1	15.3	0.6	0.4	−52	0.1	0	−66.7	0.4	0.4	−15.6
85–89	6.1	15.9	0.4	0.2	−36.1	0	0	−68.2	0.3	0.2	−14.6
90–94	2.3	12.3	0.3	0.1	−47.1	0	0	−71.2	0.1	0.1	30.4
95–99	0.5	5.3	0.1	0	−20.5	0	0	–	0.1	0	24.9
Female
100+	0.1	1.2	0.3	0	−67.7	0	0	–	0	0	–
0–1	3.7	1.4	0.6	0.4	−67.2	0.2	0.8	58.8	0	0	–
1–4	0.6	0.2	13.3	11.5	−66.6	2.5	6.7	1.3	0	0	–
5–9	0.4	0.1	23	19.9	−64.4	1.6	3.4	−13.3	0	0	–
10–14	0.4	0.2	22.2	17.2	−53.3	3	4.5	−8.7	1	3.5	110.9
15–19	0.7	0.4	36.8	32.2	−30	5.2	5	−22.6	4.7	5.5	−5.2
20–24	0.7	0.6	27	19.5	−35.7	8.3	6.3	−32.3	7.4	5.7	−31.7
25–29	0.7	0.6	15	11.8	−33.7	7.2	5.3	−37.8	9.5	5.2	−53.6
30–34	0.8	0.8	10.6	8.7	−32.9	4.7	3.6	−37.3	7.7	5.4	−42.4
35–39	1.2	1.3	7.1	5.7	−36.7	3.3	2.7	−36.4	6.1	4.1	−47.6
40–44	2	2.4	4.6	3.5	−33.1	2	1.4	−39.1	4.6	3	−42.8
45–49	3.1	3.8	3.2	2.2	−38.9	1	0.7	−36.1	3	2.1	−35.4
50–54	4.2	5.2	2.5	1.3	−51.1	0.5	0.3	−44	2	1.3	−39.8
55–59	5.6	6.5	1.7	1	−47.3	0.3	0.2	−45.5	1.3	0.8	−46.2
60–64	7.2	7.4	1.3	0.7	−46.8	0.2	0.1	−43.2	0.8	0.4	−49.7
65–69	9.4	8.4	1	0.6	−46	0.1	0.1	−34	0.4	0.2	−54.5
70–74	12.1	10.7	0.7	0.4	−52.6	0.1	0.1	−24.7	0.3	0.1	−60.5
75–79	14.6	13.7	0.5	0.4	−44.9	0	0	−23.2	0.1	0.1	−50.3
80–84	14.7	15.3	0.3	0.3	−35.1	0	0	−37	0.1	0.1	−33.7
85–89	10.9	12.2	0.1	0.3	−8.7	0	0	−14.7	0	0.1	−28.5
90–94	5.3	6.6	0.1	0.2	−1.1	0	0	−52	0	0	−59
95–99	1.5	1.9	0.1	0.1	−75.1	0	0	–	0	0	−40.2
100+	0.2	0.3	0	0.2	–	0.1	0	−100	0	0	–

Note: Prop. is proportion, Mort. is mortality, and Δ represents change For age groups and causes in which no deaths occurred in 1970 and 2005, the change is not applicable (–). Source: Mortality Detail Files, 1970 and 2005, and Human Mortality Database.

3.2 Case 1

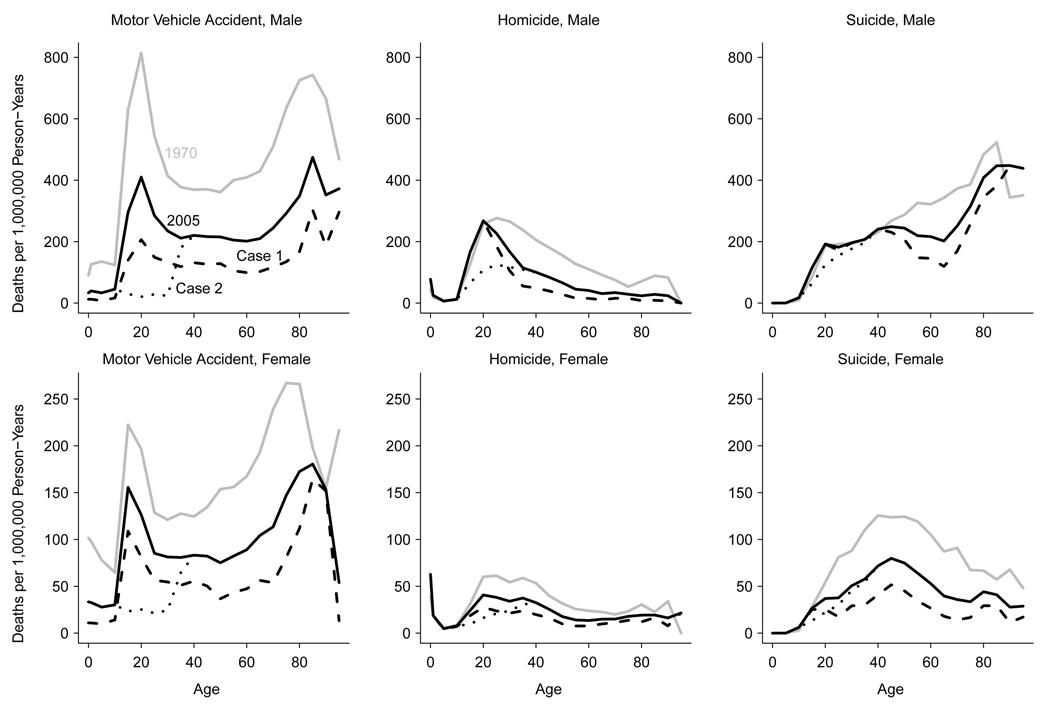
Suppose we are interested in the change in life expectancy at birth if the same proportional reductions as historically observed in Table 1 are again applied to 2005 mortality rates. For example, there was a 75.4% decline in male age 5–9 motor vehicle accident mortality between 1970 and 2005; in this new scenario, the 2005 male motor vehicle accident mortality rate for this age group is reduced by another 75.4%. If the mortality rate increased between 1970 and 2005, it remains at the 2005 level in the new scenario. The matrix of k_i,𝒜j values for this scenario is identical to columns 6, 9, and 12 of Table 1 (“Δ Mort. Rate”) except that positive values are replaced with 0. We present the mortality rates of this new scenario in Figure 1, along with historically observed 1970 and 2005 rates. We also calculate period life expectancy in 2005, as well as under this new mortality scenario in Table 2.

Figure 1.

Age Profiles of U.S. Male and Female Motor Vehicle Accident, Homicide, and Suicide Mortality Rates: 1970, 2005, Case 1, and Case 2.

Note: The age profile is shown as a grey line for 1970, black line for 2005, dashed line for Case 1, and dotted line for Case 2. Source: Mortality Detail Files, 1968–2005 and Human Mortality Database.

Table 2.

Change in Male and Female Life Expectancy at Birth: Case 1 and Case 2 Compared Year 2005.

		Case 1		Case 2
	e0	New Scenario e0	Difference	New Scenario e0	Difference
Male	74.91	75.28	0.37	75.36	0.45
Female	80.49	80.66	0.17	80.63	0.14

Note: Change in Male and Female Life Expectancy at Birth: Case 1 and Case 2 Compared to Year 2005. Source: Authors’ calculations based on data from Mortality Detail Files and Human Mortality Database.

We estimate the gain in life expectancy at birth under this scenario using equation 14 and present results in Table 3. The estimated potential years of life lost $(\widehat{\mathit{\text{YLL}}})$ by age and cause are shown in columns (2), (5), and (8). The age and cause-specific reductions, which form the −k_i,𝒜j matrix, are shown in columns (1), (4), and (7). The pairwise product that represents the estimated years of life gained under this scenario is shown in columns (3), (6), and (9). Finally, column (10) represents the contribution of each age group to the total gain in life expectancy.

Table 3.

Estimated Gain in Life Expectancy at Birth by Sex Assuming a Proportional Change in Age and Cause-Specific Mortality Rates for Year 2005.

Age Group	Motor Vehicle Accidents			Homicide			Suicide			Total
	−k𝒜j (1)	$\widehat{\mathit{\text{YLL}}}$ (2)	(3)= (1)×(2)	− k𝒜j (4)	$\widehat{\mathit{\text{YLL}}}$ (5)	(6)= (4)×(5)	− k𝒜j (7)	$\widehat{\mathit{\text{YLL}}}$ (8)	(9)= (7)×(8)	(10)= (3)+(6)+(9)
Male
0–1	0.631	0.002	0.002	0.000	0.006	0.000	0.000	0.000	0.000	0.002
1–4	0.687	0.011	0.008	0.000	0.007	0.000	0.000	0.000	0.000	0.008
5–9	0.754	0.011	0.008	0.000	0.002	0.000	0.000	0.000	0.000	0.008
10–14	0.635	0.014	0.009	0.151	0.004	0.001	0.000	0.005	0.000	0.010
15–19	0.529	0.085	0.045	0.000	0.048	0.000	0.000	0.033	0.000	0.045
20–24	0.497	0.108	0.054	0.000	0.071	0.000	0.000	0.051	0.000	0.054
25–29	0.476	0.068	0.032	0.180	0.054	0.010	0.056	0.043	0.002	0.045
30–34	0.433	0.051	0.022	0.370	0.036	0.013	0.000	0.042	0.000	0.035
35–39	0.440	0.041	0.018	0.518	0.022	0.011	0.004	0.040	0.000	0.029
40–44	0.403	0.037	0.015	0.512	0.017	0.009	0.000	0.040	0.000	0.023
45–49	0.416	0.031	0.013	0.534	0.012	0.006	0.072	0.036	0.003	0.022
50–54	0.403	0.026	0.011	0.576	0.008	0.005	0.151	0.030	0.004	0.020
55–59	0.488	0.021	0.010	0.647	0.004	0.003	0.327	0.022	0.007	0.020
60–64	0.508	0.016	0.008	0.629	0.003	0.002	0.328	0.017	0.006	0.016
65–69	0.511	0.012	0.006	0.665	0.002	0.001	0.411	0.012	0.005	0.012
70–74	0.521	0.010	0.005	0.545	0.001	0.001	0.327	0.010	0.003	0.009
75–79	0.540	0.008	0.004	0.462	0.001	0.000	0.185	0.008	0.002	0.006
80–84	0.520	0.005	0.003	0.667	0.000	0.000	0.156	0.006	0.001	0.004
85–89	0.361	0.003	0.001	0.682	0.000	0.000	0.146	0.003	0.000	0.002
90–94	0.471	0.001	0.000	0.712	0.000	0.000	0.000	0.001	0.000	0.000
95–99	0.205	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
Total		0.569	0.277		0.304	0.062		0.407	0.033	0.373
Female
0–1	0.672	0.003	0.002	0.000	0.005	0.000	0.000	0.000	0.000	0.002
1–4	0.666	0.010	0.007	0.000	0.006	0.000	0.000	0.000	0.000	0.007
5–9	0.644	0.010	0.007	0.133	0.002	0.000	0.000	0.000	0.000	0.007
10–14	0.533	0.010	0.005	0.087	0.003	0.000	0.000	0.002	0.000	0.006
15–19	0.300	0.049	0.015	0.226	0.008	0.002	0.052	0.008	0.000	0.017
20–24	0.357	0.037	0.013	0.323	0.012	0.004	0.317	0.011	0.003	0.020
25–29	0.337	0.023	0.008	0.378	0.010	0.004	0.536	0.010	0.005	0.017
30–34	0.329	0.020	0.006	0.373	0.008	0.003	0.424	0.012	0.005	0.015
35–39	0.367	0.018	0.006	0.364	0.008	0.003	0.476	0.013	0.006	0.015
40–44	0.331	0.016	0.005	0.391	0.006	0.002	0.428	0.014	0.006	0.014
45–49	0.389	0.014	0.005	0.361	0.004	0.002	0.354	0.013	0.005	0.012
50–54	0.511	0.011	0.006	0.440	0.003	0.001	0.398	0.011	0.004	0.011
55–59	0.473	0.010	0.005	0.455	0.002	0.001	0.462	0.008	0.004	0.009
60–64	0.468	0.009	0.004	0.432	0.001	0.001	0.497	0.005	0.003	0.007
65–69	0.460	0.008	0.004	0.340	0.001	0.000	0.545	0.003	0.002	0.006
70–74	0.526	0.006	0.003	0.247	0.001	0.000	0.605	0.002	0.001	0.005
75–79	0.449	0.006	0.003	0.232	0.001	0.000	0.503	0.001	0.001	0.003
80–84	0.351	0.004	0.001	0.370	0.000	0.000	0.337	0.001	0.000	0.002
85–89	0.087	0.002	0.000	0.147	0.000	0.000	0.285	0.000	0.000	0.000
90–94	0.011	0.001	0.000	0.520	0.000	0.000	0.590	0.000	0.000	0.000
95–99	0.751	0.000	0.000	0.000	0.000	0.000	0.402	0.000	0.000	0.000
Total		0.277	0.105		0.081	0.023		0.126	0.046	0.174

Note: Columns 1, 4, and 7 correspond to proportionate reductions in age and cause-specific mortality. Columns 2, 5, and 8 correspond to the estimated maximum potential years of life gained for complete reduction, $\widehat{\mathit{\text{YLL}}}$, and includes contributions from the main effects and interaction shown in equation 14. Columns 3, 6, and 9 correspond to the estimated realized years of life gained under Case 1 reductions by sex, age, and cause. Column 10 corresponds to the total estimated realized years of life by age and sex. Source: authors’ calculations.

Columns (2), (5), and (8) show that, among men in 2005, violent deaths were responsible for 1.28 years of life lost: 0.57 years from motor vehicle accidents, 0.30 years from homicides, and 0.41 years from suicides. Applying the mortality reductions shown in columns (1), (4), and (7) leads to a gain in life expectancy at birth for men of about 0.28 years from motor vehicle accidents, 0.06 years from homicides, and about 0.03 years from suicides, for a total of about 0.37 years of life gained (column 10). Even when we apply these large declines in age and cause-specific mortality rates, we are only able to recover about half, one-fifth and one-tenth of the potential years of life lost from motor vehicle accidents, homicides and suicides, respectively.

Of course, if the outcome of interest is simply the total gain in life expectancy at birth when violent death mortality is reduced by a targeted amount, then the calculation of a life table under this new scenario would suffice. Yet from a policy perspective, it is equally important to know for which ages and for which specific causes a change in mortality rates would produce the greatest gain in life expectancy at birth, as shown in Table 3.

3.3 Case 2

A closer look at Table 3 shows that the greatest loss of potential life years occurs between ages 15 and 34 for most of the violent deaths. Thus, we can imagine a new scenario in which we focus on reducing mortality rates at these particular ages. We show this case as a dashed line in Figure 1. Such declines might reflect the result of an aggressive and targeted public health and safety campaign. For example, we assume a decline of 95% in motor vehicle accidents, 60% in homicide, and 35% in suicide among 20–24 year old men (Table 4). We then estimate the highest gain in life expectancy at birth that would occur for the 20–24 year old age group.

Table 4.

Estimated Gain in Male Life Expectancy at Birth by Sex Assuming a Targeted Proportional Change in Age and Cause-Specific Mortality Rates for Year 2005.

Age Group	Motor Vehicle Accidents			Homicide			Suicide			Total
	−k𝒜j (1)	$\widehat{\mathit{\text{YLL}}}$ (2)	(3)= (1)×(2)	−k𝒜j (4)	$\widehat{\mathit{\text{YLL}}}$ (5)	(6)= (4)×(5)	−k𝒜j (7)	$\widehat{\mathit{\text{YLL}}}$ (8)	(9)= (7)×(8)	(10)= (3)+(6)+(9)
Male
15–19	0.900	0.085	0.077	0.600	0.048	0.029	0.450	0.033	0.015	0.120
20–24	0.950	0.108	0.103	0.600	0.071	0.042	0.350	0.051	0.018	0.163
25–29	0.900	0.068	0.061	0.450	0.054	0.024	0.150	0.043	0.007	0.092
30–34	0.900	0.051	0.045	0.300	0.036	0.011	0.100	0.042	0.004	0.060
35–39	0.150	0.041	0.006	0.050	0.022	0.001	0.050	0.040	0.002	0.009
Total		0.569	0.292		0.304	0.107		0.407	0.045	0.444
Female
15–19	0.850	0.049	0.042	0.600	0.008	0.005	0.500	0.008	0.004	0.051
20–24	0.800	0.037	0.029	0.600	0.012	0.007	0.400	0.011	0.004	0.041
25–29	0.750	0.023	0.017	0.450	0.010	0.005	0.200	0.010	0.002	0.024
30–34	0.700	0.020	0.014	0.300	0.008	0.002	0.100	0.012	0.001	0.017
35–39	0.200	0.018	0.004	0.180	0.008	0.001	0.050	0.013	0.001	0.006
Total		0.277	0.105		0.081	0.020		0.126	0.012	0.138

Note: Columns 1, 4, and 7 correspond to proportionate reductions in age and cause-specific mortality. Columns 2, 5, and 8 correspond to the estimated maximum potential years of life gained for complete reduction, $\widehat{\mathit{\text{YLL}}}$, and includes contributions from the main effects and interaction shown in equation 14. Columns 3, 6, and 9 correspond to the estimated realized years of life gained under Case 1 reductions by sex, age, and cause. Column 10 corresponds to the total estimated realized years of life by age and sex. Source: authors’ calculations.

Case 2 yields a similar gain in life expectancy through these targeted age and cause-specific reductions as in Case 1. Moreover, in Case 2, reductions are targeted at ages in which the assumption of independence among causes of death is far more plausible. For males, targeted motor vehicle accident, homicide, and suicide reductions contribute about 0.29, 0.11, and 0.05 years of life expectancy, respectively (Table 4). Similarly for females, the corresponding gains are 0.11, 0.02, and 0.01 years of life expectancy. This leads to a total gain in life expectancy at birth of 0.44 years for males and 0.14 years for females.

In both cases, we utilize our common formulation to link changes in life expectancy with changes in the forces of mortality. For each case, we simply evaluate its particular change in cause-specific forces of mortality for every unit of time, δμ_i(s, t)/δt. One could certainly envision other cases of hypothesized mortality reduction, as well. Once δμ_i(s, t)/δt is evaluated in this new context, the same methodology developed in Section 2 applies.

4 Concluding Remarks

In this paper, we develop two important results. First, we provide a unifying framework for assessing the change in life expectancy given a change in age and cause-specific mortality. Two conceptualizations of mortality change are possible: a counterfactual assessment of a hypothetical change or a retrospective assessment of an observed change. Our framework, developed in Sections 2.3 and 2.4, shows how these conceptualizations can be easily implemented to assess changes in life expectancy with respect to time, both for all-cause and multiple cause of death. In doing so, we thus connect previous demographic research into a sound and parsimonious formulation.

Second, when we apply our methodology to a particular case of targeted age and cause-specific mortality reductions, we obtain an especially useful byproduct: the maximum potential years of life lost, specific to each age and cause, given current mortality. This quantity provides an estimate of the theoretical maximum years of life that could be potentially recovered if all deaths in this age and cause could be averted. In a particular case, only a proportion of deaths would be averted; then only this proportion of years of life would be recovered. For example, the estimated maximum years of life lost due to male 20–24 year old motor vehicle accidents is 0.11 years in 2005. If we could decline mortality in this cause and age group by 65%, we would recover 0.07 years of life expectancy at birth.

An important limitation in this area of demographic research is the assumption of independence among causes of death. Whereas the assumption may hold for violent deaths among young adults, it is far more tenuous for other causes of death among older adults. For age groups 15 to 34, which we study in Section 3.3, violent deaths are the leading cause of death. The risk of death from other causes, notably leading causes among the elderly (cardiovascular disease, cancer, and stroke) is considerably smaller. For example, if a young adult’s motor vehicle accident death could have been averted, the decedent’s risk of death from other causes would likely changed very little. On the other hand, if an older adult’s diabetes death could have been averted, this decedent’s risk of death from other causes will likely change because of diabetes-related comorbidities.

Tsiatis (1975) showed in the absence of specified joint distribution of potential survival times, the model of potential survival times is not identifiable. Tsiatis (1975) further identified the problem and challenges of directly verifying a particular specification. The multiple-decrement life table model follows a competing risks framework (see Preston et al., 2001, Ch. 4) and the identification problem is a core concern. Thusfar, three approaches have been developed to solve the identification problem in competing risks models, but all of them require additional assumptions regarding the duration until death from different causes of death and a functional form for the mortality process (Honoré and Lleras-Muney, 2006). For example, Yashin et al. (1986) developed a multivariate stochastic process in which the different cause specific hazards were jointly dependent to formulate a solution for the dependent competing risk model of longitudinal data. Yashin et al. (2009) assumed a multivariate log-normal frailty model in their approach of a dependent competing risks model capturing negative correlations between causes of death. Llorca and Delgado-Rodríguez (2001) developed a Markov chain model to study the association between cardiovascular disease, coronary heart disease and cancer in Spain. Honoré and Lleras-Muney (2006) developed a solution for the competing risk model in a semi-parametric accelerated failure time model with grouped durations. All these approaches, however, require additional information that is unavailable from cross-sectional data at the population level. However, the unifying framework we present addresses the contribution of a cause of death to a change in life expectancy, and as noted by Yashin et al. (1986): “adjustment for cause dependency is more important … when estimating the resulting population life expectancy after elimination than when producing an estimate of the effect of a given disease (p.135).”

Our methodological and substantive results have immediate implications for health demography. Health demographers often require an assessment of possible gains in life expectancy that could result from a public health campaign aimed at reducing mortality for specific ages and causes of death. We provide a theoretical framework and simple tools² that inform these important health policy decisions.

A Appendix

A.1 First Derivations

After applying the chain rule, the first term of equation 5 is equivalent to:

$$\begin{array}{cc}\delta G[\delta \mu ]\hfill & ={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\delta \text{exp}[F[\mu ]]\mathit{\text{da}}={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial \text{exp}[F[\mu ]]}{\partial F}\delta F[\delta \mu ]\mathit{\text{da}}\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\text{exp}[F]{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds da}}\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}{\displaystyle \underset{0}{\overset{a}{\int }}}p(a,t)\delta \mu (s,t)\mathit{\text{ds da}}\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\delta \mu (s,t){\displaystyle \underset{s}{\overset{\mathrm{\infty }}{\int }}}p(a,t)\mathit{\text{da ds}}\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\delta \mu (s,t)p(s,t)e(s,t)\mathit{\text{ds}}.\hfill \end{array}$$ (A-1)

The second term of equation 5 is equivalent to:

$$\delta G[\delta t]=-\frac{\partial e(0,t)}{\partial t}\delta t.$$ (A-2)

Substituting equations A-1 and A-2 into equation 5 we obtain:

$$0=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\delta \mu (s,t)p(s,t)e(s,t)\mathit{\text{ds}}-\frac{\partial e(0,t)}{\partial t}\delta t.$$

Thus,

$$\frac{\partial e(0,t)}{\partial t}=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\delta \mu (s,t)}{\delta t}p(s,t)e(s,t)\mathit{\text{ds}}.$$ (A-3)

The relative change in life expectancy at birth, defined as é(0, t), is obtained by diving equation 6 by e(0, t):

$$\mathit{é}(0,t)=\frac{-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\delta \mu (s,t)}{\delta t}p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}.$$ (A-4)

A.1.1 Discrete Case: Proportional Changes in Mortality

In the discrete case, the time unit change is equal to 1, δt = 1. Then, substituting the functional differential of μ(a, t), k μ(a, t), into equation A-4, the relative change in life expectancy at birth reduces to:

$$\mathit{é}(0,t)=\frac{e^{*}(0,t)-e(0,t)}{e(0,t)}=-\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}k\mu (s,t)p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}.$$ (A-5)

Thus, from equation A-5 we derive the well known result of proportional change in life expectancy by Keyfitz (1977, p.413):

$$\begin{array}{cc}\frac{e^{*}(0,t)}{e(0,t)}\hfill & =1-k\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\mu (s,t)p(s,t)e(s,t)\mathit{\text{ds}}}{e(0,t)}\hfill \\ \hfill & =1-k\left[-\frac{{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}p(s,t)\text{ ln }p(s,t)\mathit{\text{ds}}}{e(0,t)}\right]\hfill \\ \hfill & =1-\mathit{\text{kH}}.\hfill \end{array}$$ (A-6)

A.1.2 Discrete Case: Absolute Change in Mortality

Let μ(a, t) and μ*(a, t) denote the force of mortality before and after some change in mortality. Under this two-time period scenario, the change in μ, δμ(a, t), is equal to μ*(a, t) − μ(a, t). Similarly, let p(a, t) and p*(a, t) be the probability of surviving from birth to age a before and after the change in the force of mortality, respectively. Recall that $p(a,t)=\text{exp}[-{\displaystyle \underset{0}{\overset{a}{\int }}}\mu (s,t)\mathit{\text{ds}}]$ and $p^{*}(a,t)=\text{exp}[-{\displaystyle \underset{0}{\overset{a}{\int }}}{\mu }^{*}(s,t)\mathit{\text{ds}}]$. The change in p(a, t), δp(a, t) is equal to δp(a, t) = p*(a, t)−p(a, t).

Rearranging terms leads to the following:

$$\begin{array}{cc}\delta p(a,t)\hfill & =p^{*}(a,t)-p(a,t)=p(a,t)\frac{p^{*}(a,t)}{p(a,t)}-p(a,t)\hfill \\ \hfill & =p(a,t)\text{ exp }\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}[{\mu }^{*}(s,t)-\mu (s,t)]\mathit{\text{ds}}\right]-p(a,t)\hfill \\ \hfill & =p(a,t)\text{ exp }\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]-p(a,t)\hfill \\ \hfill & =p(a,t)\left(\text{exp}\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]-1\right)\hfill \\ \hfill & =p^{*}(a,t)\left(1-\text{ exp }\left[{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]\right)\hfill \end{array}$$ (A-7)

The then change in life expectancy at birth, δe(0, t) is equal to:

$$\begin{array}{cc}\delta e(0,t)\hfill & ={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\delta p(a,t)\mathit{\text{da}}={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}p(a,t)\left(\text{exp}\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]-1\right)\mathit{\text{da}}\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\left(\text{exp}\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]-1\right)d[e(a,t)p(a,t)]\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}e(a,t)p(a,t)d\left(\text{exp}\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]-1\right)\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}e(a,t)p(a,t)\delta \mu (a,t)\text{ exp }\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}\right]\mathit{\text{da}}\hfill \end{array}$$

For changes in cause-specific mortality, the change in life expectancy at birth is:

$$\delta e(0,t)=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}e(a,t)p(a,t){\displaystyle \sum _{i=1}^N}\left(\delta {\mu }_i(a,t)\text{ exp }\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}\delta {\mu }_i(s,t)\mathit{\text{ds}}\right]\right)\mathit{\text{da}}.$$ (A-8)

Dividing by e(0, t) yields the relative change in life expectancy at birth, é(0, t).

When the force of mortality changes continuously over time, equation A-7 converges to equation 4, which is the basis for developing equations 6, 7, 8, and 9. We want to show:

$$\delta p(a,t)\equiv \underset{h\to 0}{\text{lim}}\frac{p(a,t+h)-p(a,t)}{h}=-p(a,t){\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}.$$

Recall that $e^x=1+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}}\frac{x^k}{k!}$ for x ∈ ℝ. Let $z={\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}}$. Using equation A-7, the limit as h approaches zero corresponds to:

$$\begin{array}{cc}\underset{h\to 0}{\text{lim}}\frac{p(a,t+h)-p(a,t)}{h}\hfill & =\underset{h\to 0}{\text{lim}}\frac{p(a,t)\left(\text{exp}\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}}\right]-1\right)}{h}\hfill \\ \hfill & =p(a,t)\underset{h\to 0}{\text{lim}}\frac{\text{exp}\left[-{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}}\right]-1}{h}\hfill \\ \hfill & =p(a,t)\underset{h\to 0}{\text{lim}}\frac{1+(-{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}})+{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{{(-{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}})}^k}{k!}-1}{h}\hfill \\ \hfill & =p(a,t)\underset{h\to 0}{\text{lim}}\frac{-{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}}+{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{{(-{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}})}^k}{k!}}{h}\hfill \\ \hfill & =p(a,t)\left[\underset{h\to 0}{\text{lim}}-{\displaystyle \underset{0}{\overset{a}{\int }}}\frac{\mu (s,t+h)-\mu (s,t)}{h}\mathit{\text{ds}}-\underset{h\to 0}{\text{lim}}{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{{({\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}})}^k}{hk!}\right]\hfill \\ \hfill & =-p(a,t){\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}-p(a,t)\underset{h\to 0}{\text{lim}}{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{({\displaystyle \underset{0}{\overset{a}{\int }}}{[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}})}^k}{hk!}\hfill \end{array}$$ (A-9)

The series converges to e^z and the second term of equation A-9, $p(a,t){\text{lim}}_{h\to 0}{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{{({\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}})}^k}{hk!}$, approaches zero as h becomes smaller, so

$$\begin{array}{cc}p(a,t)\underset{h\to 0}{\text{lim}}{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{z^k}{hk!}\hfill & =p(a,t)\underset{h\to 0}{\text{lim}}\frac{1}{h}{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{z^k}{k!}\frac{z^{-2}}{z^{-2}}=p(a,t)\underset{h\to 0}{\text{lim}}\frac{z^2}{h}{\displaystyle \sum _{k=2}^{\mathrm{\infty }}}\frac{z^{k-2}}{k!}\hfill \\ \hfill & =p(a,t)\underset{h\to 0}{\text{lim}}\frac{z^2}{h}{e}^z=p(a,t)\underset{h\to 0}{\text{lim}}\frac{{({\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}})}^2\text{ exp }[{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}}]}{h}\hfill \\ \hfill & =p(a,t)\underset{h\to 0}{\text{lim}}{\left({\displaystyle \underset{0}{\overset{a}{\int }}}\frac{[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}}}{h^{1/2}}\right)}^2\text{ exp }[{\displaystyle \underset{0}{\overset{a}{\int }}}[\mu (s,t+h)-\mu (s,t)]\mathit{\text{ds}}]\hfill \end{array}$$

Recall μ is a continuous function. The first term of the limit in the above equation approaches zero as h approaches zero, while the exponential function approaches to one. Thus, the second term of equation A-9 approaches zero. From equation A-9, we conclude that when looking at continuous changes in mortality with respect to time, $\delta p(a,t)=-p(a,t){\displaystyle \underset{0}{\overset{a}{\int }}}\delta \mu (s,t)\mathit{\text{ds}}$.

A.1.3 Continuous Case: Change in the gain in life expectancy

Both terms on the right hand side of equation 10 are particular cases of equation 6. Thus,

$$\frac{\partial e_{-i}(0,t)}{\partial t}=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\delta {\mu }_{-i}(s,t)}{\delta t}{p}_{-i}(s,t)e_{-i}(s,t)\mathit{\text{ds}}=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial {\mu }_{-i}(s,t)}{\partial t}{p}_{-i}(s,t)e_{-i}(s,t)\mathit{\text{ds}}$$ (A-10)

because the ratio of functional differentials, $\frac{\delta {\mu }_{-i}(s,t)}{\delta t}$, is equal to $\frac{\partial {\mu }_{-i}(s,t)}{\partial t}$. Similarly,

$$\begin{array}{cc}\frac{\partial e(0,t)}{\partial t}\hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\delta \mu (s,t)}{\delta t}p(s,t)e(s,t)\mathit{\text{ds}}=-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial \mu (s,t)}{\partial t}p(s,t)e(s,t)\mathit{\text{ds}}\hfill \\ \hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial {\mu }_i(s,t)}{\partial t}p(s,t)e(s,t)\mathit{\text{ds}}-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial {\mu }_{-i}(s,t)}{\partial t}p(s,t)e(s,t)\mathit{\text{ds}}.\hfill \end{array}$$ (A-11)

Substituting equations A-10 and A-11 into equation 10 leads to the main result of Beltrán-Sánchez et al. (2008) for linking decomposition approaches and cause-deleted life tables:

$$\begin{array}{cc}\frac{\partial D_i(0,t)}{\partial t}\hfill & =-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial {\mu }_{-i}(s,t)}{\partial t}{p}_{-i}(s,t)e_{-i}(s,t)\mathit{\text{ds}}+{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial {\mu }_i(s,t)}{\partial t}p(s,t)e(s,t)\mathit{\text{ds}}+{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial {\mu }_{-i}(s,t)}{\partial t}p(s,t)e(s,t)\mathit{\text{ds}}\hfill \\ \hfill & ={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial p_{-i}(s,t)}{\partial t}\mathit{\text{ds}}-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial p_i(s,t)}{\partial t}{p}_{-i}(s,t)\mathit{\text{ds}}-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial p_{-i}(s,t)}{\partial t}{p}_i(s,t)\mathit{\text{ds}}\hfill \\ \hfill & ={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial p_{-i}(s,t)}{\partial t}[1-p_i(s,t)]\mathit{\text{ds}}-{\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}}\frac{\partial p_i(s,t)}{\partial t}{p}_{-i}(s,t)\mathit{\text{ds}}.\hfill \end{array}$$

A.1.4 Varying Proportional Declines by Age and Cause of Death

Recall that $e^x=1+{\displaystyle \sum _{k=1}^{\mathrm{\infty }}}\frac{x^k}{k!}$. Applying equation A-8 to equation 12 leads to

$$\begin{array}{cc}{e}^{*}(0,t)-e(0,t)\hfill & ={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}-k_{i,{𝒜}_j}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p(s,t)e(s,t)\text{ exp }[-k_{i,{𝒜}_j}{\displaystyle \underset{0}{\overset{s}{\int }}}{\mu }_i(x,t)\mathit{\text{dx}}]\mathit{\text{ds}}.\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}-k_{i,{𝒜}_j}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p(s,t)e(s,t)[1+{\displaystyle \sum _{z=1}^{\mathrm{\infty }}}\frac{{(-k_{i,{𝒜}_j}{\displaystyle \underset{0}{\overset{s}{\int }}}{\mu }_i(x,t)\mathit{\text{dx}})}^z}{z!}]\mathit{\text{ds}}\hfill \end{array}$$

Thus, we can split the change in life expectancy, e*(0, t)−e(0, t), into the sum of two parts: a main effect and interaction.

$$\begin{array}{cc}\text{Main effect}\hfill & ={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}-k_{i,{𝒜}_j}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p(s,t)e(s,t)\mathit{\text{ds}}.\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}-k_{i,{𝒜}_j}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p_i(s,t)p_{-i}(s,t)e(s,t)\mathit{\text{ds}}.\hfill \\ \hfill \text{Interaction}& ={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}{\displaystyle \sum _{z=1}^{\mathrm{\infty }}}\frac{{(-k_{i,{𝒜}_j})}^{z+1}}{z!}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p(s,t)e(s,t){(-\text{ln}[p_i(s,t)])}^z\mathit{\text{ds}}\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}{\displaystyle \sum _{z=1}^{\mathrm{\infty }}}\frac{{(-k_{i,{𝒜}_j})}^{z+1}}{z!}{\displaystyle \underset{{𝒜}_j}{\int }}{\mu }_i(s,t)p_i(s,t)p_{-i}(s,t)e(s,t){(-\text{ln}[p_i(s,t)])}^z\mathit{\text{ds}}\hfill \end{array}$$

Using life table notation, the above terms can be estimated as

$$\begin{array}{cc}\text{Main effect}\hfill & \approx {\displaystyle \sum _{j=1}^m}[{\displaystyle \sum _{i=1}^4}-k_{i,{𝒜}_j}\frac{{}_{n_j}{d}_{a_{j_{\mathit{\text{start}}}},i}}{l_0}\frac{{}_{n_j}{L}_{a_{j_{\mathit{\text{start}}}},-i}}{n}\frac{e_{a_{j_{\mathit{\text{start}}}}}+e_{a_{j_{\mathit{\text{end}}}}}}{2}]\hfill \\ \hfill \text{Interaction}& \approx {\displaystyle \sum _{j=1}^m}{\displaystyle \sum _{i=1}^4}{\displaystyle \sum _{z=1}^{\mathrm{\infty }}}\frac{{(-k_{i,{𝒜}_j})}^{z+1}}{z!}\frac{{}_{n_j}{d}_{a_{j_{\mathit{\text{start}}}},i}}{l_0}\frac{{}_{n_j}{L}_{a_{j_{\mathit{\text{start}}}},-i}}{n}\frac{e_{a_{j_{\mathit{\text{start}}}}}+e_{a_{j_{\mathit{\text{end}}}}}}{2}\frac{{(-\text{ln}[p_i(a_{j_{\mathit{\text{start}}}})])}^z+{(-\text{ln}[p_i(a_{j_{\mathit{\text{end}}}})])}^z}{2}\hfill \end{array}$$