Abstract
Current understanding of the lymphatics draining the breast is controversial, despite its known importance in the spread of breast cancer. Similarly, knowledge regarding the spatial distribution of primary tumours in the breast is limited. This study sought to test commonly held assumptions in this field, including: (i) that breast lymphatic drainage and tumour prevalence are symmetric between the left and right sides of the body, (ii) that males and females have the same drainage patterns and tumour prevalences, and (iii) that lymphatic drainage in the breast occurs independently to different node fields. This study has used lymphoscintigraphy data from 2304 breast cancer patients treated at the RPAH Medical Centre, Sydney, Australia. Symmetry of lymphatic drainage and tumour distribution as well as gender differences were tested using Fisher's exact test. Drainage independence was assessed using Fisher's exact test, and a multivariate probit model was used to test for drainage correlations. Results showed that the breasts are likely to have symmetric lymphatic drainage and tumour prevalence, and that there is no significant difference between males and females. Furthermore, results showed that direct lymphatic drainage of the breasts is likely to be independent between node fields. Collectively, these results serve to further our understanding of lymphatic anatomy and the distribution of tumours in the breast.
Keywords: breast, gender, lymphatic anatomy, lymphatic drainage, symmetry
Introduction
Over the years, there have been relatively few detailed studies to characterise the lymphatics of the breast (Suami et al., 2009). Current knowledge of the breast lymphatics is based mainly on the work of Sappey (1874), who performed the first gross anatomical mappings of the lymphatic system by injecting mercury into the lymphatic vessels of human cadavers. His technique was derived from the early work of Cruikshank (1786), who investigated the lymphatics by injecting mercury through the nipple. Other important early work includes that of Delamere et al. (1903) who, based on these prior results, created composite diagrams describing the lymphatics of the breast. More recently, cadaveric studies have been performed which have effectively delineated the lymphatics of the breast using more reliable methods (Suami et al., 2008).
Techniques used to aid the treatment of breast cancer have also shed light on our knowledge of breast lymphatics. Sentinel lymph node biopsy (SLNB), which utilises lymphoscintigraphy (LS) imaging, was initially developed to map the lymphatics of the skin for patients with melanoma (Morton et al., 1992). It is now also used to map the lymphatics of the breast in patients with breast cancer (Uren et al., 1999). During LS, the breast is injected with a radiocolloid, which is then tracked through the lymphatic vessels to draining lymph nodes in surrounding node fields. Nodes receiving direct lymphatic drainage from the primary tumour site are termed ‘sentinel nodes’ (SNs). Each SN is then surgically excised to check for metastatic cancer. Examples of LS images are shown in Fig. 1 which clearly delineate the lymphatics of the breast.
Fig. 1.
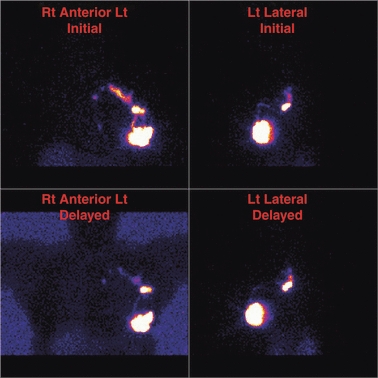
Anterior and lateral lymphoscintigraphy images of a patient with left breast cancer. Initial and delayed imaging shows two collectors draining to two SNs in the left axilla and a single faint collector draining to a single faint SN in the left internal mammary chain.
Collectively, these studies have shown a number of node fields directly drain the breasts, with the most prominent being the axillary node field. The axillary lymphatic pathway was first located by Cruikshank (1786), and Sappey (1874) later concluded that the axillary node field received lymphatic drainage from the entire breast via the subareolar plexus. It has now become common knowledge that the axillary node field almost always drains the breast, with clinicians commonly performing axillary dissection during breast cancer treatment (Benson et al., 2007). In addition to the axilla, there are other node fields that directly drain the breasts, including the interpectoral, infraclavicular, supraclavicular, intercostal and internal mammary node fields. Occasionally, patients can show drainage to lymph nodes in the breast tissue between the injection site and a predefined node field, which are termed interval nodes (Uren et al., 1999).
Accumulated LS studies for breast cancer have provided important information regarding patterns of breast lymphatic drainage. A number of clinical studies have presented tabulated results and graphical displays to summarise their findings (Borgstein et al., 1998; Byrd et al., 2001; Uren et al., 2001; Estourgie et al., 2004). To the authors’ knowledge, there has never been a thorough statistical analysis of breast LS data. For example, consideration has never been given to whether breast lymphatic drainage patterns are independent between node fields. That is, whether drainage to one node field influences the likelihood of drainage to another. It has also never been quantified whether lymphatic drainage or tumour prevalence is symmetric between the right and left sides of the body, or whether there is a difference between males and females. We sought to address these issues, building upon previous work that statistically analysed lymphatic drainage of the skin (Reynolds et al., 2010).
This study used LS data collected between October 1992 and November 2009 from breast cancer patients treated at the RPAH Medical Centre in Sydney, Australia. During LS, four peritumoural injections of Technetium-99m-antimony sulphide colloid (99mTcSb2S3) were administered around the primary tumour. Injections were given under ultrasound guidance, at the depth of the centre of the tumour at the 12, 3, 6, and 9 o'clock positions, and the draining SNs were located (Uren et al., 1995). The region of each primary tumour and the node field locations of each SN were then recorded in a database.
Each patient's primary tumour location was recorded according to its quadrant location in the breast (see Fig. 2). These regions were defined as the upper inner (UI), lower inner (LI), lower outer (LO) and upper outer (UO) quadrants, with an additional region defined behind the nipple (BN). To provide a more accurate primary tumour location, when the tumour overlapped two quadrants, it was recorded as located in the upper inner outer (UIO), upper lower inner (ULI), lower outer inner (LOI) or upper lower outer (ULO) regions. For example, a primary tumour was classified in the UIO region if it was located in both the UO and UI quadrants. Thus, each patient's primary tumour was recorded in one of nine possible regions.
Fig. 2.
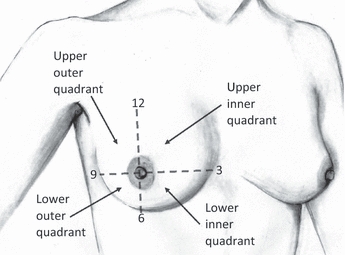
Partition of the right breast into quadrants. Original sketch created by Shea Shochat.
Figure 3 illustrates the approximate location of each node field that directly drained the breast, which included the axillary, interpectoral, internal mammary, infraclavicular and supraclavicular node fields. Intercostal nodes also directly drained the breasts; however, they have been recorded as interval nodes as it was difficult to determine their exact anatomical position during LS. In total there were 2363 patients in the LS database, 57 of whom (2.4%) did not display drainage to a SN, and two patients only displayed drainage to interval nodes. Note that drainage to interval nodes, and thus also intercostal nodes, was not included during testing as these nodes do not have a consistent anatomical location. This study has analysed the remaining 2304 patients, 2284 of whom were female and 20 of whom were male.
Fig. 3.
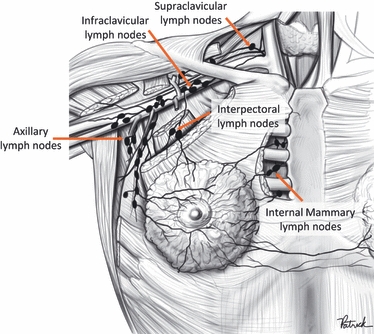
Node fields that directly drain the breast. Adapted from Macea & Fregnani (2006) with permission, original sketch created by Patrick Braga.
Table 1 details the number of cases with drainage to each combination of node fields on each side of the body. It can be seen that drainage to the axillary [n = 2263 (98.2%)] and internal mammary [n = 813 (35.3%)] node fields were markedly more frequent compared with drainage to the interpectoral [n = 15 (0.7%)], infraclavicular [n = 25 (1.1%)] and supraclavicular [n = 70 (3.0%)] node fields. Patients usually had drainage to one node field (63.6%); however, it was possible for drainage to occur to multiple node fields (36.4%) from a primary tumour site. There were no cases of contralateral drainage to any node field (i.e. drainage to the other side of the body); however, drainage was observed to occur across the nipple centre line of the breast. On average, patients displayed drainage to 1.4 node fields.
Table 1.
Number of patients with lymphatic drainage to different node fields, on either side of the body. Note that drainage to interval nodes has been excluded from testing, as they do not have a defined anatomical position
| Draining node fields | No. patients | |
|---|---|---|
| Left | Right | |
| Axilla only | 708 | 725 |
| Axilla & internal mammary | 371 | 351 |
| Axilla & supraclavicular | 12 | 9 |
| Axilla & infraclavicular | 11 | 9 |
| Axilla & interpectoral | 4 | 7 |
| Axilla, internal mammary & supraclavicular | 25 | 17 |
| Axilla, infraclavicular & internal mammary | 8 | 5 |
| Axilla, infraclavicular, internal mammary & supraclavicular | 0 | 1 |
| Internal mammary only | 11 | 18 |
| Internal mammary & supraclavicular | 2 | 0 |
| Internal mammary & infraclavicular | 1 | 2 |
| Internal mammary & interpectoral | 1 | 0 |
| Internal mammary, supraclavicular & interpectoral | 0 | 1 |
| Supraclavicular only | 2 | 0 |
| Supraclavicular & interpectoral | 1 | 0 |
| Infraclavicular only | 0 | 1 |
| Interpectoral only | 0 | 1 |
| Total | 1157 (50.2%) | 1147 (49.8%) |
Materials and methods
Standard statistical tests were applied to assess for drainage and tumour prevalence symmetry, gender difference and drainage independence. Statistical analyses were carried out using the r statistical software package (R Development Core Team, 2009). All P-values were two-sided; hypothesis testing was conducted adjusting for multiple comparisons using the procedure described by Benjamini and Hochberg (1995), with a false discovery rate (FDR) upper bound of 5%.
Symmetry and gender analysis
For a given patient, the observance of lymphatic drainage to any node field can be thought of as a binary variable, that is, either there is drainage to that node field or there is no drainage to that node field. To test for symmetry and gender difference in patterns of lymphatic drainage, the LS data were organised into a series of 2 × 2 contingency tables with counts conditioned on the primary tumour region. For symmetry testing, the variables compared were ‘node field drainage’ and ‘side’. For gender testing, the variables compared were ‘node field drainage’ and ‘gender’.
Using these tabulations, a series of Fisher's exact tests (Fisher, 1922) were carried out, using the r function fisher.test. The association between node field drainage and side, and node field drainage and gender were tested conditioned on primary tumour region. In turn, the null hypotheses that node field drainage is symmetric between sides of the body, and that node field drainage is invariant of gender were tested for each primary region. These two tests, one for symmetry and one for gender invariance, being conducted for five different node fields for nine separate primary regions, gave a total of 90 hypothesis tests.
This methodology was similarly carried out testing ‘tumour prevalence’ against ‘side’ and ‘gender’. The null hypotheses were that tumour prevalence is symmetric between sides of the body, and that tumour prevalence is invariant of gender. With nine primary regions and two separate tests, one for symmetry and one for gender invariance, there were a total of 18 hypo-thesis tests.
Independence testing
Fisher's exact test was used to test the null hypothesis that lymphatic drainage of the breast is independent between node fields. Pair-wise relations of the five defined node fields were tested conditioned on each primary region. Hence, for each combination of any two node fields say A and B, the number of times drainage occurred to both, to just A, to just B, and to neither A nor B were tallied. This allowed for a 2 × 2 contingency table to be constructed with variables ‘drainage to A’ and ‘drainage to B’.
In addition to testing drainage independence with Fisher's exact test, an alternative approach was also implemented. The benefits of using two different paradigms of analysis are two-fold; first it offers additional insight into drainage independence, and secondly it provides a means of validating findings. This alternative method used a Bayesian multivariate probit (MVP) model. An implementation of this was adapted from a model previously applied to marketing survey data (Rossi et al., 2005), which had the same structure as the LS data. Implementing the MVP model utilised the r library bayesm, and the rmvpGibbs function (Rossi & McCulloch, 2008) which uses Gibbs sampling (Geman & Geman, 1984) for posterior simulation. The MVP model takes the form of a p-dimensional multivariate regression model:
| (1) |
where w is a latent variable, Xi = (zi’⊗ Ip), β contains model coefficients, εi is an error term, p is the number of node fields, yij is the drainage outcome of the jth node field for the ith patient, zi is a vector of observations on covariates, Ip is a p × p identity matrix, and Σ is the covariance matrix. In the analysis, priors of the following form were used:
| (2) |
Markov chain Monte Carlo simulations were used to find the covariance matrix and thus the correlations between each of the node fields, which provided a measure of deviation from independence. Correlations were summarised for each region of the breast using 95% Bayesian confidence intervals. To test the hypothesis that node fields were uncorrelated, one must evaluate whether zero is bracketed within each confidence interval. For any two node fields, if their correlation confidence interval brackets zero, then drainages from the node fields are deemed independent.
Results
Table 2 gives the number and proportion of cases with drainage to each node field from each region of the left and right breasts. Table 3 gives the number and proportion of cases with drainage to each node field from each region for females and males. It is apparent that the UO region had the most cases, with 35.6% of all patients having tumours in this region; the UIO (13.7%), UI (13.7%) and ULO (10.8%) also had relatively high counts. In contrast, the lower regions and behind the nipple had a small number of cases, ranging between 1.8 and 5.5% of all patients.
Table 2.
Number and proportion of patients with drainage to each node field, from each breast region, on either side of the body
| Node Field | |||||||
|---|---|---|---|---|---|---|---|
| Breast Region | Side | No. Patients (%) | Axilla | Infraclavicular | Internal mammary | Interpectoral | Supraclavicular |
| UIO | L | 170 (7.4) | 168 (98.8) | 3 (1.8) | 65 (38.2) | 3 (1.8) | 8 (4.7) |
| R | 146 (6.3) | 144 (98.6) | 3 (2.1) | 51 (34.9) | 1 (0.7) | 2 (1.4) | |
| UI | L | 166 (7.2) | 159 (95.8) | 5 (3.0) | 91 (54.8) | 1 (0.6) | 7 (4.2) |
| R | 149 (6.5) | 135 (90.6) | 6 (4.0) | 82 (55.0) | 1 (0.7) | 5 (3.4) | |
| ULI | L | 46 (2.0) | 43 (93.5) | 0 (0) | 27 (58.7) | 0 (0) | 3 (6.5) |
| R | 42 (1.8) | 41 (97.6) | 1 (2.4) | 27 (64.3) | 0 (0) | 4 (9.5) | |
| LI | L | 52 (2.3) | 49 (94.2) | 1 (1.9) | 26 (50.0) | 1 (1.9) | 2 (3.8) |
| R | 69 (3.0) | 68 (98.6) | 0 (0) | 36 (52.2) | 0 (0) | 0 (0) | |
| LOI | L | 52 (2.3) | 51 (98.1) | 0 (0) | 26 (50.0) | 0 (0) | 2 (3.8) |
| R | 63 (2.7) | 63 (100) | 0 (0) | 30 (47.6) | 0 (0) | 0 (0) | |
| LO | L | 92 (4.0) | 92 (100) | 0 (0) | 45 (48.9) | 0 (0) | 1 (1.1) |
| R | 100 (4.3) | 100 (100) | 0 (0) | 39 (39.0) | 0 (0) | 1 (1.0) | |
| ULO | L | 121 (5.3) | 121 (100) | 1 (0.8) | 40 (33.1) | 0 (0) | 4 (3.3) |
| R | 127 (5.5) | 126 (99.2) | 3 (2.4) | 37 (29.1) | 1 (0.8) | 2 (1.6) | |
| UO | L | 409 (17.8) | 407 (99.5) | 9 (2.2) | 77 (18.8) | 1 (0.2) | 15 (3.7) |
| R | 409 (17.8) | 405 (99.0) | 5 (1.2) | 79 (19.3) | 6 (1.5) | 13 (3.2) | |
| BN | L | 49 (2.1) | 49 (100) | 1 (2.0) | 22 (44.9) | 0 (0) | 0 (0) |
| R | 42 (1.8) | 42 (100) | 0 (0) | 14 (33.3) | 0 (0) | 1 (2.4) | |
| TOTAL | L | 1157 (50.2) | 1139 (98.4) | 20 (1.7) | 419 (36.2) | 6 (0.5) | 42 (3.6) |
| R | 1147 (49.8) | 1124 (98.0) | 18 (1.6) | 395 (34.4) | 9 (0.8) | 28 (2.4) | |
L, left; R, right; U, upper; L, lower; I, inner; O, outer quadrants; BN, behind the nipple.
Table 3.
Number and proportion of patients with drainage to each node field, from each breast region, for females and males
| Node field | |||||||
|---|---|---|---|---|---|---|---|
| Breast Region | Gender | No. Patients (%) | Axilla | Infraclavicular | Internal mammary | Interpectoral | Supraclavicular |
| UIO | F | 313 (13.7) | 309 (98.7) | 6 (1.9) | 116 (37.1) | 4 (1.3) | 10 (3.2) |
| M | 3 (15.0) | 3 (100) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | |
| UI | F | 314 (13.7) | 293 (93.3) | 11 (3.5) | 173 (55.1) | 2 (0.6) | 12 (3.8) |
| M | 1 (5.0) | 1 (100) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | |
| ULI | F | 86 (3.8) | 83 (96.5) | 1 (1.2) | 52 (60.5) | 0 (0) | 6 (7.0) |
| M | 2 (10.0) | 1 (50.0) | 0 (0) | 2 (100) | 0 (0) | 1 (50.0) | |
| LI | F | 121 (5.3) | 117 (96.7) | 1 (0.8) | 62 (51.2) | 1 (0.8) | 2 (1.7) |
| M | 0 (0) | – | – | – | – | – | |
| LOI | F | 113 (4.9) | 112 (99.1) | 0 (0) | 54 (47.8) | 0 (0) | 2 (1.8) |
| M | 2 (10.0) | 2 (100) | 0 (0) | 2 (100) | 0 (0) | 0 (0) | |
| LO | F | 192 (8.4) | 192 (100) | 0 (0) | 84 (43.8) | 0 (0) | 2 (1.0) |
| M | 0 (0) | – | – | – | – | – | |
| ULO | F | 248 (10.9) | 247 (99.6) | 4 (1.6) | 77 (31.0) | 1 (0.4) | 6 (2.4) |
| M | 0 (0) | – | – | – | – | – | |
| UO | F | 816 (35.7) | 810 (99.3) | 14 (1.7) | 156 (19.1) | 7 (0.9) | 28 (3.4) |
| M | 2 (10.0) | 2 (100) | 0 (0) | 0 (0) | 0 (0) | 0 (0) | |
| BN | F | 81 (3.5) | 81 (100) | 1 (1.2) | 34 (42.0) | 0 (0) | 1 (1.2) |
| M | 10 (50.0) | 10 (100) | 0 (0) | 2 (20.0) | 0 (0) | 0 (0) | |
| TOTAL | F | 2284 (99.1) | 2244 (98.2) | 38 (1.7) | 808 (35.4) | 15 (0.7) | 69 (3.0) |
| M | 20 (0.9) | 19 (95.0) | 0 (0) | 6 (30.0) | 0 (0) | 1 (5.0) | |
F, female; M, male; U, upper; L, lower; I, inner; O, outer quadrants; BN, behind the nipple.
Symmetry and gender analysis
The associations between nodal drainage, and gender and side were tested using Fisher's exact test. Fisher's exact test was also used to test the associations between tumour prevalence, and gender and side. For all symmetry tests, the null hypotheses were not rejected. Thus both lymphatic drainage and tumour distribution can be considered symmetric between each side of the body.
Gender invariance testing concluded in not rejecting the null hypotheses for all draining node fields, as well as for all breast regions except the BN (p = 7.52 × 10−10) region. Thus there was no statistical difference between males and females in terms of lymphatic drainage. Tumour prevalence was statistically similar between genders except for the BN region, where there was a significantly greater proportion of male than female cases.
Independence testing
As nodal drainage and tumour prevalence were found to be symmetric, the LS data were reflected to one side of the body for independence testing. In addition, both female and male cases were combined for this analysis.
Drainage occurrences were analysed for each possible pair of node fields using Fisher's exact test. Table 4 summarises the P-values found between each node field pair, for each region. Adjusting for multiple comparisons, it was found that regions with a statistically significant association between node fields were the UI and UO regions. For the UI region, drainage was interdependent between the axilla and internal mammary node fields. The UO region experienced interdependent drainage between the axilla and internal mammary, and the internal mammary and supraclavicular node fields.
Table 4.
P-values of interactions between draining node fields, from each breast region
| Node field crosses | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Breast region | A-IC | A-IM | A-IP | A-SC | IC-IM | IC-IP | IC-SC | IM-IP | IM-SC | IP-SC |
| UIO | 1.000 | 0.018 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.301 | 0.006 | 1.000 |
| UI | 0.538 | 0.000 | 0.004 | 0.187 | 0.760 | 1.000 | 1.000 | 0.503 | 0.072 | 0.075 |
| ULI | 1.000 | 0.156 | 1.000 | 0.030 | 0.386 | 1.000 | 1.000 | 1.000 | 0.241 | 1.000 |
| LI | 1.000 | 0.619 | 0.033 | 0.065 | 0.488 | 1.000 | 1.000 | 0.488 | 1.000 | 0.017 |
| LOI | 1.000 | 1.000 | 1.000 | 0.017 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| LO | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.190 | 1.000 |
| ULO | 0.016 | 1.000 | 1.000 | 1.000 | 0.314 | 1.000 | 1.000 | 1.000 | 0.077 | 1.000 |
| UO | 0.004 | 0.001 | 0.050 | 1.000 | 0.008 | 1.000 | 0.388 | 0.358 | 0.000 | 1.000 |
| BN | 1.000 | 1.000 | 1.000 | 1.000 | 0.396 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
U, upper; L, lower; I, inner; O, outer quadrants; BN, behind the nipple; A, axilla; IM, internal mammary; IP, interpectoral; IC, infraclavicular; SC, supraclavicular.
A Bayesian MVP model was applied to the LS dataset whereby a series of correlations between node fields were found for each breast region. Bayesian confidence intervals were quantified for each of the correlations between all node fields. Table 5 shows the correlation confidence intervals between each pair of node fields, for each region. Most intervals contained zero within their confidence intervals, and hence showed independence. There were a few node field combinations that had non-zero correlations; regions with correlated node fields were the UIO, UI, ULI, LI, LOI, ULO and UO regions, with similar associated node field combinations as found using Fisher's exact test at the 5% significance level if adjustments for multiple comparisons had not been applied.
Table 5.
Bayesian confidence intervals of correlations between draining node fields, from each breast region
| Node field crosses | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Breast region | A-IC | A-IM | A-IP | A-SC | IC-IM | IC-IP | IC-SC | IM-IP | IM-SC | IP-SC |
| UIO | (−0.55, 0.65) | (−0.94, −0.14) | (−0.34, 0.93) | (−0.64, 0.38) | (−0.42, 0.34) | (−0.69, 0.57) | (−0.75, 0.46) | (−0.94, −0.01) | (0.12, 0.69) | (−0.82, 0.35) |
| UI | (−0.43, 0.36) | (−0.82, −0.38) | (−0.93, −0.33) | (−0.65, −0.01) | (−0.22, 0.39) | (−0.61, 0.47) | (−0.80, 0.32) | (0.18, 0.94) | (0.03, 0.59) | (0.03, 0.80) |
| ULI | (−0.43, 0.96) | (−0.95, −0.03) | (−0.90, 0.86) | (−0.87, −0.08) | (−0.94, 0.22) | (−0.91, 0.84) | (−0.90, 0.44) | (−0.83, 0.87) | (−0.05, 0.75) | (−0.82, 0.85) |
| LI | (−0.65, 0.92) | (−0.68, 0.21) | (−0.93, 0.00) | (−0.90, −0.02) | (−0.83, 0.32) | (−0.93, 0.75) | (−0.95, 0.70) | (−0.62, 0.57) | (−0.41, 0.63) | (0.11, 0.94) |
| LOI | (−0.81, 0.82) | (−0.44, 0.79) | (−0.82, 0.85) | (−0.93, −0.03) | (−0.73, 0.71) | (−0.77, 0.77) | (−0.80, 0.83) | (−0.72, 0.74) | (−0.56, 0.55) | (−0.84, 0.81) |
| LO | (−0.75, 0.78) | (−0.80, 0.81) | (−0.77, 0.74) | (−0.78, 0.80) | (−0.82, 0.83) | (−0.73, 0.77) | (−0.81, 0.79) | (−0.82, 0.80) | (−0.11, 0.90) | (−0.80, 0.79) |
| ULO | (−0.91, −0.14) | (−0.30, 0.89) | (−0.83, 0.76) | (−0.52, 0.87) | (−0.89, 0.07) | (−0.75, 0.78) | (−0.89, 0.43) | (−0.86, 0.45) | (−0.01, 0.67) | (−0.81, 0.69) |
| UO | (−0.76, −0.14) | (−0.73, −0.15) | (−0.71, 0.15) | (−0.41, 0.56) | (0.12, 0.57) | (−0.57, 0.51) | (−0.30, 0.48) | (−0.65, 0.15) | (0.19, 0.55) | (−0.93, 0.16) |
| BN | (−0.79, 0.84) | (−0.85, 0.85) | (−0.78, 0.81) | (−0.80, 0.86) | (−0.29, 0.91) | (−0.80, 0.82) | (−0.87, 0.63) | (−0.84, 0.85) | (−0.91, 0.37) | (−0.85, 0.81) |
U, upper; L, lower; I, inner; O, outer quadrants; BN, behind the nipple; A, axilla; IM, internal mammary; IP, interpectoral; IC, infraclavicular; SC, supraclavicular.
Discussion
This study has quantitatively assessed previous assumptions regarding breast lymphatic drainage and tumour prevalence. First, a sequence of contingency tables was used to test whether lymphatic drainage and tumour distribution were symmetric and/or gender invariant. Secondly, the assumption that lymphatic drainage is independent between node fields was tested using both Fisher's exact test and a Bayesian MVP model.
It is not surprising that the lymphatic drainage of the breasts was found to be symmetric, as the underlying anatomy is also largely symmetric. The ribs (12 on each side) and musculature (pectoralis minor and pectoralis major, serratus anterior, external oblique muscles and the intercostal muscles) are the same on each side, as is the arterial vascular supply and the venous drainage (Macea & Fregnani, 2006). Furthermore, the overall structure of the lymphatic vessels tends to follow the structure of the major veins, which are themselves largely symmetric (Uren et al., 1999). This anatomical symmetry is consistent with the symmetric patterns of lymphatic drainage quantified in this study.
It is significant to consider these results in light of a recent cadaveric study by Pan et al. (2009) which analysed the breasts and anterior upper torso lymphatics of a female human cadaver. Interestingly, their study showed the cadaver had asymmetric lymphatic vessels draining the breast. Whilst our results indicate there is symmetry in lymphatic drainage of the breasts across a population, there clearly are asymmetries in lymphatic drainage of the breast in individual patients. Hence, symmetry cannot be assumed in single patients and an individualised approach must still be employed during breast cancer treatment.
Whilst previous studies have shed light on lymphatic drainage symmetry, to the authors’ knowledge, symmetry in the spatial distribution of breast tumours has never been assessed. It has been observed, however, that breast mass and size asymmetry are predictors of breast cancer development (Manning et al., 1992; Scutt et al., 1997, 2006) and that the left breast is more likely to develop tumours than the right breast (Dane et al., 2008). It has also been found that tumour location is an important prognostic factor in determining survival outcomes, with medial tumour patients experiencing diminished survival rates compared to lateral tumour patients (Gaffney et al., 2003). It is significant then, in light of these studies, that we found symmetric tumour prevalence in the breast.
From an anatomical perspective, the structure of the breast is the same between males and females, although women usually have more glandular tissue and fat. Hence, it is also not surprising that our study concluded that lymphatic drainage, and for the most part tumour prevalence, of the breasts is the same between sexes. A recent study by Suami et al. (2008) also investigated the lymphatic drainage patterns of the breast between the sexes by assessing five male and nine female cadavers. They injected the breast lymphatic vessels of each cadaver with a tracer and followed the drainage patterns to draining lymph nodes. It was shown that the breast lymphatic vessels had no significant structural differences between males and females (Suami et al., 2008); this further supports our finding that drainage patterns are invariant of gender.
The result which showed males were more likely to experience tumours behind the nipple was interesting. This could be due to the fact that male breasts typically have very little mammary tissue, and what tissue is present is mostly behind the nipple. Note that with only 20 male cases in our sample (0.87%), any conclusions with regard to gender are tentative due to low counts. To be more certain in future, a larger sample size would be required.
Previous studies have not assessed the possibility of breast lymphatic drainage independence between node fields, that is, that the appearance of drainage to one node field does not affect the likelihood of drainage to any other node field. We have addressed this assumption by testing against the null hypothesis of independence between node fields, both using an exact test and by quantifying the drainage correlations between node fields. By using two different paradigms of analysis we have provided additional insights and validation of findings. Most node field combinations were found to be insignificant for interdependence, whilst those that were significant were conditioned upon upper regions and involved the internal mammary node field. However, it is difficult to draw any definite conclusions regarding possible deviations from drainage independence due to limitations in the LS dataset.
As the analysis was systematically conducted on subsets of the data, there were several breast regions which displayed very few counts. This was typically observed for the infraclavicular, supraclavicular and interpectoral node fields. In addition, the LS injection technique utilised four separate injections around the primary tumour, which can cause a large region of breast tissue to contain radioactive tracer, thus making observations less precise. In future, to conclude whether there is indeed interdependence between node fields, more data would be required which had ideally been collected in a more controlled manner. Overall, however, it appears likely that breast lymphatic drainage is independent between node fields.
The analyses carried out here have allowed testing to be conducted by considering nine separate breast regions. This has the advantage of providing a highly spatially refined analysis; however, it has also meant that some regions contained a sparse amount of data. As more data is collected over time, this limitation will be minimised. In addition, the quantified symmetry between both sides of the body and, to a somewhat limited extent, gender invariance provides justification for reflecting the data to one side of the body and grouping the genders for future studies. This would effectively double the sample size, thus allowing more precise inferences to be made. The finding that node field drainage likelihoods are predominantly independent of each other has implications whereby the probability of drainage to a given node field can be considered in isolation from all other node fields.
In summary, this study has provided the first quantitative assessment of symmetry and gender difference of lymphatic drainage and tumour prevalence in the breast. Using a large LS dataset, we have quantified that although individual patients can exhibit asymmetric drainage, drainage patterns are likely the same in both left and right breasts across the population. In addition, we have quantified that tumour prevalence is symmetric and that males and females show the same patterns of drainage and for the most part similar tumour distributions. Furthermore, we have found that direct lymphatic drainage is largely independent between node fields. As more data is collected in the future, we may be able to determine whether drainage between node fields exhibits a marked deviation from independence. These results serve to further our understanding of breast lymphatics by quantifying characteristics of this vitally important system.
Acknowledgments
Thanks to Cameron G. Walker and Alan J. Lee for providing statistical consultation. We gratefully acknowledge the Foundation for Research, Science & Technology for providing funding for this study. Martyn P. Nash and Poul M. F. Nielsen are supported by James Cook Fellowships administrated by the Royal Society of New Zealand on behalf of the New Zealand Government.
Author contributions
R. Uren provided access to the RPAH Medical Centre's LS database, which he had collected and recorded. H. Reynolds, M. Nash, and P. Nielsen supervised this research, and M. Nash and P. Nielsen obtained funding. E. Blumgart conceived the approach and implemented the statistical methods, carried out the statistical analysis, and drafted the manuscript. All authors provided critical revision of the manuscript and approved the article.
References
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc. Series B (Methodol) 1995;57:289–300. [Google Scholar]
- Benson JR, Della Rovere GQ, Axilla Management Consensus Group Management of the axilla in women with breast cancer. Lancet Oncol. 2007;8:331–348. doi: 10.1016/S1470-2045(07)70103-1. [DOI] [PubMed] [Google Scholar]
- Bickley LS. Guide to Physical Examination and History Taking. Philadelphia: Lippincott Williams & Wilkins; 2003. [Google Scholar]
- Borgstein PJ, Pijpers R, Comans EF, et al. Sentinel lymph node biopsy in breast cancer: guidelines and pitfalls of lymphoscintigraphy and gamma probe detection. J Am Coll Surg. 1998;186:275–283. doi: 10.1016/s1072-7515(98)00011-8. [DOI] [PubMed] [Google Scholar]
- Byrd DR, Dunnwald LK, Mankoff DA, et al. Internal mammary lymph node drainage patterns in patients with breast cancer documented by breast lymphoscintigraphy. Ann Surg Oncol. 2001;8:234–240. doi: 10.1007/s10434-001-0234-y. [DOI] [PubMed] [Google Scholar]
- Cruikshank WC. Anatomy of the Absorbing Vessels of the Human Body. London: G. Nicol; 1786. [Google Scholar]
- Dane S, Yildirim S, Koc M, et al. Asymmetries in breast cancer lateralization and both axillary lymph node number and metastatic involvment. Lymphology. 2008;41:75–79. [PubMed] [Google Scholar]
- Delamere G, Poirier P, Cuneo B. The lymphatics. In: Leaf CH, editor. General Anatomy of the Lymphatics. Westminster: Archibald Constable and Co. Ltd; 1903. p. 216. [Google Scholar]
- Estourgie SH, Nieweg OE, Valdés Olmos RA, et al. Lymphatic drainage patterns from the breast. Ann Surg. 2004;239:232–237. doi: 10.1097/01.sla.0000109156.26378.90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. On the interpretation of χ2 from contingency tables, and the calculation of P. J Roy Stat Soc. 1922;85:87–94. [Google Scholar]
- Gaffney DK, Tsodikov A, Wiggins CL. Diminished survival in patients with inner versus outer quadrant breast cancers. J Clin Oncol. 2003;21:467–472. doi: 10.1200/JCO.2003.12.047. [DOI] [PubMed] [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Macea JR, Fregnani JHTG. Anatomy of the thoracic wall, axilla and breast. Int J Morphol. 2006;24:691–704. [Google Scholar]
- Manning JT, Scutt D, Whitehouse GH, et al. Breast asymmetry and phenotypic quality in women. Evol Hum Behav. 1992;18:223–236. [Google Scholar]
- Morton DL, Wen DR, Wong JH, et al. Technical details of intraoperative lymphatic mapping for early stage melanoma. Arch Surg. 1992;127:392–399. doi: 10.1001/archsurg.1992.01420040034005. [DOI] [PubMed] [Google Scholar]
- Pan WR, Rozen WM, Stella DL, et al. A three-dimensional analysis of the lymphatics of a bilateral breast specimen: a human cadaveric study. Clin Breast Cancer. 2009;9:86–91. doi: 10.3816/CBC.2009.n.016. [DOI] [PubMed] [Google Scholar]
- R Development Core Team . R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing; 2009. [Google Scholar]
- Reynolds HM, Walker CG, Dunbar PR, et al. Functional anatomy of the lymphatics draining the skin: a detailed statistical analysis. J Anat. 2010;216:344–355. doi: 10.1111/j.1469-7580.2009.01183.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossi PE, McCulloch RE. Bayesm: Bayesian Inference for Marketing/Micro-Econometrics. 2008 2.2-2 ed. R package. [Google Scholar]
- Rossi PE, Allenby GM, McCulloch RE. Bayesian Statistics and Marketing. Hoboken: John Wiley & Sons Ltd; 2005. [Google Scholar]
- Sappey MPC. Anatomie, Physiologie, Pathologie des Vaisseaux Lymphatiques consideres chez L'Homme et les Vertebres. Paris: A. Delahaye & E. Lacrosnier; 1874. [Google Scholar]
- Scutt D, Manning JT, Whitehouse GH, et al. The relationship between breast asymmetry, breast size and the occurrence of breast cancer. Br J Radiol. 1997;70:1017–1021. doi: 10.1259/bjr.70.838.9404205. [DOI] [PubMed] [Google Scholar]
- Scutt D, Lancaster GA, Manning JT. Breast asymmetry and predisposition to breast cancer. Breast Cancer Res. 2006;8 doi: 10.1186/bcr1388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suami H, Pan WR, Mann B, et al. The lymphatic anatomy of the breast and its implications for sentinel lymph node biopsy: a human cadaver study. Ann Surg Oncol. 2008;15:863–871. doi: 10.1245/s10434-007-9709-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suami H, Pan WR, Taylor GI. Historical review of breast lymphatic studies. Clin Anat. 2009;22:531–536. doi: 10.1002/ca.20812. [DOI] [PubMed] [Google Scholar]
- Uren RF, Howman-Giles RB, Thompson JF, et al. Mammary lymphoscintigraphy in breast cancer. J Nucl Med. 1995;36:1775–1780. [PubMed] [Google Scholar]
- Uren RF, Thompson JF, Howman-Giles RB. Lymphatic Drainage of the Skin and Breast: Locating the Sentinel Nodes. Amsterdam: Harwood Academic; 1999. [Google Scholar]
- Uren RF, Howman-Giles RB, Renwick SB, et al. Lymphatic mapping of the breast: locating the sentinel lymph nodes. World J Surg. 2001;25:789–793. doi: 10.1007/s00268-001-0006-7. [DOI] [PubMed] [Google Scholar]


