Intrinsic Detection of Motion in Segmented Sequences

Abstract

While many motion correction techniques for MRI have been proposed, their use is often limited by increased patient preparation, decreased patient comfort, additional scan time or the use of specialized sequences not available on many commercial scanners. For this reason we propose a simple self-navigating technique designed to detect motion in segmented sequences. We demonstrate that comparing two segments containing adjacent sets of k-space lines results in an aliased error function. A global shift of the aliased error function indicates the presence of in-plane rigid-body translation while other types of motion are evident in the dispersion or breadth of the error function. Since segmented sequences commonly acquire data in sets of adjacent k-space lines, this method provides these sequences with an inherent method of detecting object motion. Motion corrupted data can then be reacquired proactively or in some cases corrected or removed retrospectively.

INTRODUCTION

Patient motion is one of the dominant sources of artifact in MRI. Techniques developed to detect and correct motion include those that utilize specialized hardware to detect patient motion, those that utilize special k-space trajectories with some inherent motion correction ability, those that acquire additional navigator data for the purpose of motion correction and those considered to be self-navigating.

Motion detection techniques that rely on specialized hardware include reflecting laser beams off specialized markers (1), optical tracking with one or more cameras (2–5), tracking using small receiver coils (6–8), infrared tracking systems (9, 10) and using spatial-frequency tuned markers(11).

Techniques that use specialized trajectories for motion correction include acquiring rotated sets of overlapping parallel lines (12), interleaving spiral trajectories (13, 14), acquiring data in some sort of hybrid Radial-Cartesian fashion (15–17) or using alternating frequency/phase encode directions (18–20).

Other techniques acquire additional navigator data as a Cartesian projection in the absence of either phase or frequency encoding (21) or with a floating navigator (22, 23). Orbital navigators utilize a circular k-space trajectory to detect object motion (24) while spherical navigators sample spherical k-space shells (25, 26). When multiple receive coils are used the complimentary data can be used to detect and replace motion corrupted data (27). In particular, spatial harmonics in SMASH reconstruction (28) can be utilized to compare newly measured data with predictions calculated from previously sampled data (29). Alternatively, a SENSE based reconstruction (30) can be used to replace motion detected from low resolution images (31). While all these techniques have shown success in their respective applications, their use is often limited by one or more of the following: increased complexity in patient preparation, decreased patient comfort, additional scan time or the required use of specialized sequences not available on many commercial scanners. For this reason there has always been marked interest in the category of motion detection with self-navigation.

Several proposed self-navigating techniques address a specific type of motion (typically in-plane and rigid-body) but none seem to address both rigid and non-rigid body motion that can occur both in and out of plane. For example, motion in the readout direction has been detected by taking the Fourier Transform of a line of acquired data and trying to determine the edges of the object's profile (32, 33). The edges become increasingly difficult to determine from lines encoded near the edges of k-space and high contrast markers are often added to the patient to overcome this problem. Motion in the phase encode direction can be detected using a symmetric density constraint along the phase encoding axis (33). However, the algorithm is restrictive on the object type and may not perform well for large motion in the phase encode direction (34). Another approach is to apply a spatial constraint to the object and then use an iterative phase retrieval algorithm to calculate the desired phase of the object (35). The calculated phase is compared to the measured phase to simultaneously find motion in the readout and phase encode directions. The algorithm performs well for sub-pixel motions but is unable to correct an artifact caused by large translations (34). Combinations of these self navigating methods have also been proposed to overcome some of their pitfalls (34, 36). Motion may also be determined by iteratively minimizing the entropy of motion induced ghosts and blurring in an otherwise dark region of an image (37, 38). Alternatively, data correlations between adjacent data lines can provide information about in-plane rigid body translation(39, 40). Radial sequences can provide a self-navigating method for rigid-body motion correction using moments of spatial projections (41) or the phase properties of radial trajectories (42). Motion correction in the slice direction has also been explored by monitoring amplitude modulations of the acquired data (43, 44). A combination of some of these proposed techniques can be utilized to fully correct in-plane rigid-body motion but doesn't include the ability to address other types of motion. While it may not be possible to correct out-of-plane motion or motion that is not rigid-body, it is necessary and may be sufficient to at least be able to detect which data lines are corrupt.

The focus of this work is the detection of data that is corrupted by out-of-plane or non-rigid body motion. The proposed technique was designed and implemented in a carotid imaging application; however, the principles are easily adapted to other imaging applications.

THEORY

Two adjacent (closely spaced) points in k-space will typically show some degree of correlation. This correlation will occur when the object being imaged does not fill the entire FOV or when the object's signal intensity is modified by the receive coil's sensitivity profile. In the latter case, the k-space data is convolved with the Fourier transform of the receive coil's sensitivity profile which introduces correlations between data points.

These data correlations can be exploited with a proposed self-navigating technique to detect various types of object motion. Consider an image acquisition that is divided into N_Seg segments that each sample a set of equally spaced k-space lines with a sampling function:

$$S_L\left(k_x,k_y\right)=\sum _{j=0}^{N_{Line}-1}\delta \left(k_y-\left(L+j{N}_{Seg}\right)\Delta k_y\right)$$ [1]

where L is the current segment, N_Line is the number of lines sampled per segment and Δk_y is the distance between adjacent phase encode lines in the fully sampled k-space. The number of lines per segment is kept small enough that the object can be assumed to be approximately stationary during the acquisition of a single segment. Now consider the correlation of two adjacent data segments. Since each segment samples a different set of k-space lines, to compare the L^th and the (L+1)^th segments, the k-space data of the (L+1)^th segment is shifted by Δk_y. A weighted cross correlation is then taken as:

$$C_L\left(k_x,k_y,t\right)=\frac{F_L\left(k_x,k_y,t\right)F_{L+1}^{\ast }\left(k_x,k_y+\Delta k_y,t+\Delta t\right)}{\mid F_L\left(k_x,k_y,t\right)\mid \cdot \mid F_{L+1}\left(k_x,k_y+\Delta k_y,t+\Delta t\right)\mid }$$ [2]

where F_L(k_x,k_y,t) is the Fourier transform of the object's image weighted by the sampling function S_L(k_x,k_y) given in Eqn. [1]. The phase of the weighted cross correlation function is separated into a linear term, representing rigid-body translation (40), and a non-linear term for motion not classified as rigid-body translation. The cross correlation function with the new phase separation is:

$$C_L\left(k_x,k_y,t\right)=e^{i[k_{x}dx\left(t\right)+k_{y}dy\left(t\right)]}{e}^{i\phi (k_x,k_y,t)}{S}_L\left(k_x,k_y\right)$$ [3]

where φ(k_x,k_y,t) is the non-linear portion of the phase and dx(t) and dy(t) quantify the rigid-body translation between the acquisition at time t and the acquisition at t+Δt. If an error function is defined as:

$$\epsilon \left(x,y,t\right)=\Im \left[e^{i\phi (k_x,k_y,t)}\right]$$ [4]

then the weighted cross correlation in image space is similar to the previously published result (40), except it is modified by the error function as:

$$c_L(x,y,t)=N_{Line}\sum _{j=0}^{N_{Seg-1}}{e}^{i\pi \left(\frac{2L}{N_{Seg}}+N_{Line}-1\right)j}\epsilon [x-dx\left(t\right),y-dy\left(t\right)-j{N}_{Line}\Delta y,t]$$ [5]

where Δy is the image space voxel size in the phase encoding direction. The basic result is an aliased set of error functions defined by Eqn. [4] that are collectively shifted proportionally to the object's rigid-body translation. The error function ε(x,y,t) is a measure of data correlation between the L^th and L+1^th data segments. If there are enough echoes in the echo train, the aliased copies of ε(x,y,t) will be spaced far enough apart for one to characterize the general shape of the error function (40). Our main postulate is that object motion can be correlated with the error function dispersion (a measure of how peaked or spread out the error function is).

METHOD

All data sets were obtained on a Siemens Trio 3T MRI scanner. All human studies were approved by the institutional review board and informed consent was obtained from the volunteers.

TSE 2D axial neck images were obtained from two volunteers using a 2 element surface coil (one anterior and one posterior coil) and a third volunteer using a 4 element surface coil (45). Data from the first volunteer (Fig. 2a) was acquired with 252×256 pixels, a resolution of 0.8mm × 0.8mm × 5mm, TR=1.5s, TE=6.8ms and 7 echoes per echo train. Data from the second volunteer (Fig. 1, 2b and 3) was acquired with 512×512 pixels, a resolution of 0.35mm × 0.35mm × 5mm, TR=1.5s, TE=8.6ms and 16 echoes per echo train.

Figure 2.

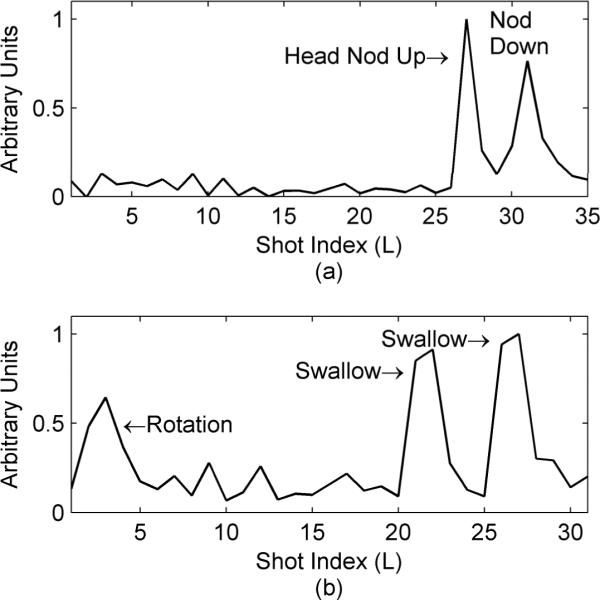
Detection of volunteer motion using the error function dispersion. Both plots are the error function dispersion for two different volunteers. The first volunteer (a) nodded their head down, held it for a few seconds and then returned to the original position near the end of the scan (TR/TE=1.5s/6.8ms, 7 echoes per echo train with 36 echo trains required to fill k-space). The second volunteer (b) slightly rotated their head and quickly returned to the original position near the start of the scan and then swallowed during later acquisitions (TR/TE=1.5s/8.6ms, 16 echoes per echo train with 32 echo trains required to fill k-space).

Figure 1.

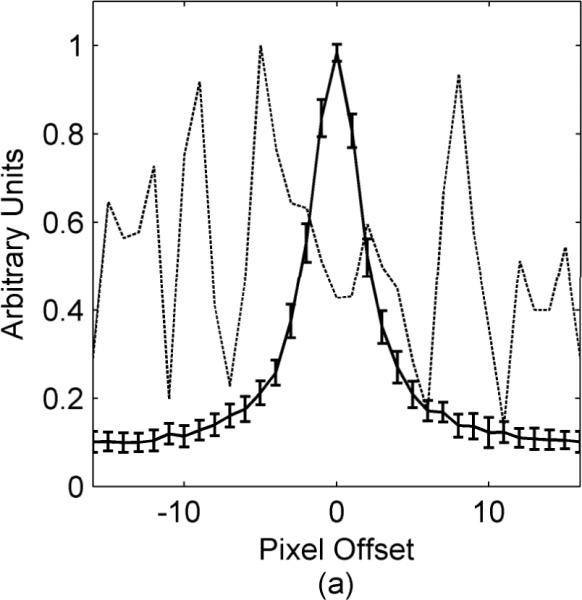
Error function dispersion for a volunteer who swallowed during an axial 2D TSE neck scan. The solid line shows a plot through the average error function obtained from comparing all sets of adjacent data segments excluding the segment where swallowing occurred. The error bars on the solid line indicate the standard deviation of all these error functions. The dashed line is a plot through the error function when the volunteer swallowed.

Figure 3.

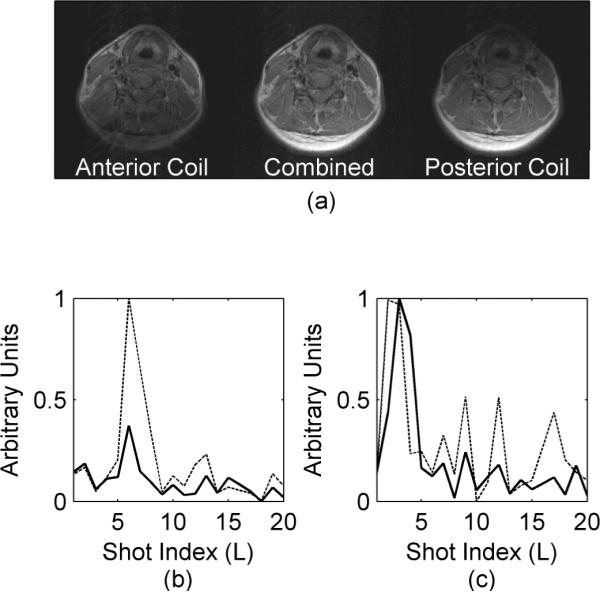
Receive coil dependence of error function dispersion. The images in (a) are the anterior coil only (left), both coils combined with a sum of squares (center) and the posterior coil only (right). The solid lines in the graphs are from the posterior receive coil while the dashed lines are from the anterior receive coil. The volunteer swallowed during the acquisition in (b) while the head was rotated during the acquisition in (c).

For the third volunteer (Fig. 4), reacquiring data prospectively was simulated by acquiring two complete data averages; the first data average is acquired with volunteer motion while the second data average is acquired with no motion. Once the corrupt data segments are identified in the first average, they are replaced with data from the second average. This replaced data is similar to what we would have achieved if the data was reacquired. The data from the third volunteer was acquired with 264×256 pixels, a resolution of 0.6mm × 0.6mm × 2mm, 12 echoes per segment, 2 averages and a TR/TE of 2.5s/61ms.

Figure 4.

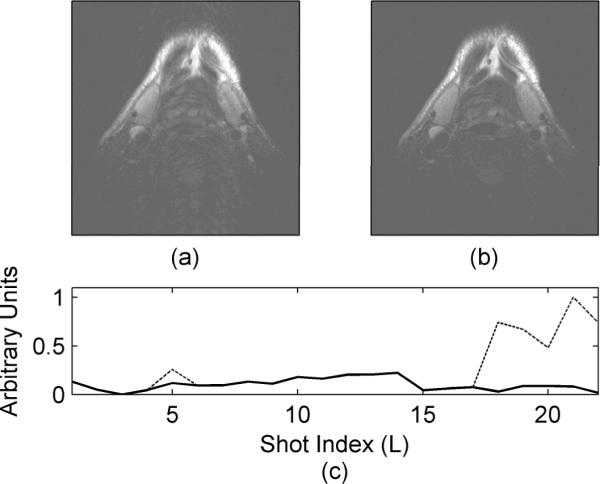
Motion artifact reduction using the proposed intrinsic detection technique. The motion corrupted image is shown in (a) with the corrected image shown in (b). The dashed line in (c) is the original error function dispersion. After corrupted data segments were identified and replaced, the resulting error function dispersion is shown in (c) by the solid line. Data was acquired with a 4 element receive coil, a resolution of 0.6mm × 0.6mm × 2mm, 12 echoes per segment, 22 segments to fill k-space and a TR/TE of 2.5s/61ms.

To measure the dispersion of the error function, we first determine any rigid-body translation (dx(t) and dy(t) in Eqn. [5]) by measuring the offset of the correlation function from the origin (40). The dispersion of the error function is then measured with a weighted summation such that pixels far from the error function's origin (expected to increase with error function broadening) contribute more significantly to the total summation. While several weighting schemes were tested, a simple linear weighting was found to give the most robust results. Additionally, since the maximum value of c_L(x,y,t) varies depending on which two data segments are compared, c_L(x,y,t) is normalized to unity prior to measuring dispersion. The error function is estimated as:

$$D_L\left(t\right)=\frac{\sum _{x=-n}^n\sum _{y=-n}^n\mid c_L\left(x-dx\left(t\right),y-dy\left(t\right),t\right)\mid \cdot x\cdot y}{\underset{x,y}{\max }\mid c_L\left(x,y,t\right)\mid }$$ [6]

where n=ceil(0.5*N_Line*Δy) selects the central copy of the aliased error function which repeats every N_LineΔy pixels. When data is analyzed from multiple receive channels, dispersion is calculated for each channel independently and the results are averaged. If there are just a few corrupt data segments then the standard deviation of the dispersion will be low and any segments with a dispersion more than one or two standard deviations from the mean are identified as corrupt.

RESULTS

Since the error function in Eqn. [5] is aliased and two dimensional, we only display the central portion of a profile through the origin of the error function (in the phase encode direction). While showing just a profile of a two dimensional error function does not yield a complete picture, it is sufficient for display purposes to show a trend or general concept. The actual motion detection is based on the dispersion of the error function (Eqn. [6]) and considers the two dimensional error function rather than the profiles shown in the figures.

The average error function profile for a volunteer who swallowed during an axial 2D TSE neck scan is shown in Fig. 1. The data set contains 32 segments with one segment corrupted when the volunteer swallowed. The solid line shows the average error function profile found from comparing all adjacent data segments except the ones including the corrupt data segment. The deviation of the error function profiles are shown by the error bars on the solid line. For comparison, the dashed line in Fig. 1 shows how much the error function changes when motion corruption, swallowing in this case, is present.

The results of two volunteer studies are summarized in Fig. 2. First a volunteer was asked to lie still during the first part of the scan and then to nod their head down, hold it for a few seconds and then return their head to the original position as best they could. The dispersion of the error function, as measured with Eqn. [6], is shown in Fig. 2a. In the second study the volunteer was asked to slightly rotate their head for a second (about one degree), return to the original position and then swallow several times near the end of the scan (Fig. 2b). All instances of the motion are clearly discernable when considering the dispersion of the error function.

The ability to detect object motion is also dependent on the sensitivity profile of the coil element being considered. The sensitivities of a two element coil are shown in Fig. 3. While both elements were almost equally sensitive to the volunteer rotating their neck (Fig. 3c), the anterior element (dashed line in Fig. 3b) was more sensitive to volunteer swallowing than the posterior element (solid line in Fig. 3b).

Finally, the proposed self-navigating correction technique is applied to a volunteer neck study as shown in Fig. 4. The motion corrupted image is shown in Fig. 4a with the corrected image shown in Fig. 4b. Several corrupt data segments appear in the original error function dispersion (dashed line in Fig. 4c). Once these corrupt data segments are replaced with reacquired data, the error function dispersion no longer shows the presence of the corrupted data segments (solid line in Fig. 4c).

DISCUSSION

In our prior work we demonstrated that rigid-body translation can be detected and compensated using the correlation of adjacent data segments (40). This work deals primarily with the detection of data measurements corrupted by other types of motion. It does not solve the problem of correcting the corrupt data, but instead requires motion corrupted measurements to be reacquired or eliminated during reconstruction. This error function-based motion detection method is based on two enabling observations: First, in the absence of motion, the error function obtained from the correlation of any two adjacent data segments remains strongly peaked near the origin. Second, when motion not classified as non-rigid-body translation occurs, the error function becomes spread or dispersed with a greatly diminished or missing peak.

We note that a combination of rigid-body translation with other types of object motion (such as out-of-plane motion or swallowing) may distort the error function appreciably so that it is not possible to quantify the rigid-body translation. However, even if the rigid-body translation could be quantified in this case, the data would still be corrupted with the other types of motion and a correction of just rigid-body translation would result in limited improvements.

Another limitation comes when the data is analyzed in a retrospective manner. In this case, even when the object's motion occurs over a single segment of data, two segment comparisons with correspondingly high measures of dispersion are observed. For example, in the second study in Fig. 2, where the volunteer swallowed during the acquisition of the 22^nd data segment (Fig. 2b), both the error functions at L=21 (comparing the 21^st and 22^nd data segments) and at L=22 (comparing the 22^nd and 23^rd data segments) show a large dispersion. Hence object motion will typically result in two or more closely spaced peaks in the measure of error function dispersion. In this case, the motion corrupted segmented is detected as the only segment with high dispersion on both adjacent comparisons. Segments that have a high dispersion in only one adjacent comparison are likely not corrupted by motion. Motions over longer periods of time can involve more segments and require a more complicated analysis to determine which lines are corrupted.

The proposed technique detects in which segments motion is likely to have occurred, but does not quantify the motion or discern the type. Additional information about the motion type can be discerned by analyzing individual coils. With the two channel coil utilized in this study, the posterior receive coil is less sensitive to swallowing than the anterior receive coil (Fig. 3b) because motion in the neck due to swallowing is mostly limited to the anterior portion of the neck. Conversely, both receive coils appear to be equally sensitive to the rotation (Fig. 3c) since the entire image is affected by that type of motion. One point of interest is that the anterior element appears to detect the rotation one segment earlier than the posterior element (Fig. 3c). We note that while lying on a table, a rotation of the neck tends not to be rigid-body and the rotation is about a point in the posterior of the neck rather than the middle. As a result, the anterior part of the neck moves more than the posterior during the rotation and may therefore be detected as moving first.

In most cases, the number of corrupted data segments is small and the corrupted lines can be reacquired, or can be recreated using parallel imaging techniques (46), a constrained reconstruction (47), or a variety of other methods being studied by our group and others to deal with motion corrupted data.

CONCLUSION

When segmented data is acquired in sets of adjacent lines in k-space (as it is often done in TSE and segmented GRE techniques), this work has demonstrated that correlations between data sets can be exploited to detect various types of motion. While in most cases the motion can not be fully quantified, the method provides a valuable and simple way to detect corrupted data so that it can be reacquired prospectively or removed from the data set retrospectively.