Abstract
Viral genomic RNA adopts many conformations during its life cycle as the genome is replicated, translated, and encapsidated. The high-resolution crystallographic structure of the satellite tobacco mosaic virus (STMV) particle reveals 30 helices of well-ordered RNA. The crystallographic data provide global constraints on the possible secondary structures for the encapsidated RNA. Traditional free energy minimization methods of RNA secondary structure prediction do not generate structures consistent with the crystallographic data, and to date no complete STMV RNA basepaired secondary structure has been generated. RNA-protein interactions and tertiary interactions may contribute a significant degree of stability, and the kinetics of viral assembly may dominate the folding process. The computational tools, Helix Find & Combine, Crumple, and Sliding Windows and Assembly, evaluate and explore the possible secondary structures for encapsidated STMV RNA. All possible hairpins consistent with the experimental data and a cotranscriptional folding and assembly hypothesis were generated, and the combination of hairpins that was most consistent with experimental data is presented as the best representative structure of the ensemble. Multiple solutions to the genome packaging problem could be an evolutionary advantage for viruses. In such cases, an ensemble of structures that share favorable global features best represents the RNA fold.
Introduction
Viral genomes are the dark matter of structural virology—the existence and importance of the viral genome have been acknowledged, but structural biologists have not yet been able to fully visualize the RNA genomes inside virus particles. Single virion imaging of HIV particles revealed significant heterogeneity in the structures of the capsid and internal RNA genome structures (1). Cryo-electron microscopy (cryo-EM) and x-ray crystallography revealed ordered helical RNA in several icosahedral viruses (2,3). In addition to possible heterogeneity in the RNA structures, the icosahedral averaging used to solve these structures obscures the identity of the nucleotide basepairs in the helices observed on icosahedral symmetry axes. When the attachment of the MS2 bacteriophage to the Escherichia coli pili at the fivefold vertex is used to orient the virus particles, then density for 90% of the ordered RNA genome is observed in cryo-EM at 9 Ǻ (4). Thus, crystallography and cryo-EM both provide tantalizing clues that the RNA genomes in icosahedral viruses are ordered and well structured.
The crystal structure of satellite tobacco mosaic virus (STMV) particles at 1.8 Ǻ resolution reveals 30 RNA helices of at least nine basepairs on the icosahedral two-fold axes (Fig. 1) (3,5–7). The low b-factors for the central pairs in the RNA helix provide the best evidence that all 30 sites are occupied by an RNA helix (5). The b-factors for the central RNA pairs are on par with regions of the capsid protein, which is present at full occupancy. The terminal pairs of the RNA helices have higher b-factors, indicating greater heterogeneity at the ends of the helices. The minimum number and lengths of helices provide a global experimental constraint for the ensemble of RNA conformations in the STMV particle. The minimum distance between two RNA helices in the STMV crystal structure is 9 Ǻ (Protein Data Bank No. 1A34), which provides a constraint for a minimum of at least two single strand nucleotides between RNA helices. A model for the secondary structure of STMV RNA proposes a series of hairpins that would be consistent with cotranscriptional folding and assembly of the virus particle, although this model does not suggest any specific or probable basepairs in helices (7). Simulations of the STMV particle confirm that the RNA helices are essential for the structural integrity of the virus particle (8). Previous secondary structure predictions for regions of STMV RNA (9,10) are not consistent with the crystallographic data or the new chemical probing data presented here for encapsidated STMV RNA.
Figure 1.
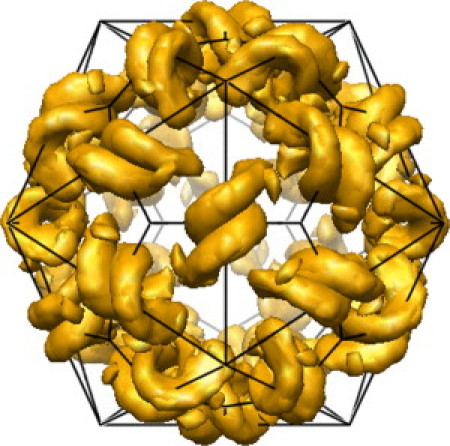
Model of electron density for RNA helices in the 1.8 Ǻ crystal structure of STMV virus particles from the VIPER database (Protein Data Bank 1A34) (3,5). The length of the RNA helix shown in yellow is 36.5 Ǻ.
Although the crystallography and cryo-EM data challenge the traditional views of RNA genomes in icosahedral viruses as completely disordered, recent studies of the secondary structures of RNA genomes are based on the assumption of a single structure for each functional state of the RNA genome. Secondary structures for three RNA viral genomes have been proposed on the basis of chemical probing and sequence analysis: cucumber mosaic virus (CMV) (11), rhinovirus (12), and human immunodeficiency virus (HIV) (13). Chemical probing of CMV with dimethyl sulfate (DMS) demonstrated that the structure of the RNA genome is different in plantae, inside virion particles, and for in vitro transcribed RNA (11). SHAPE chemical probing of Moloney murine leukemia virus identified both regions of similarity and regions with significant differences between in virio and ex virio genomic RNA (14,15). The 5′untranslated region (UTR) of HIV also shows changes in nucleotide chemical accessibility between in vitro and in vivo experiments (16,17). The HIV-1 5′UTR undergoes several secondary structural conformational changes as proteins bind (18) and dimerization occurs (19). The ability to change conformations is essential for the viral genome during the many stages of the virus life cycle.
This work presents an ensemble view of encapsidated viral RNA genomes that lies between the traditional views of completely disordered genomes and a single structure for the encapsidated genome. When encapsidated in the virion, the ensemble of RNA structures likely shares common global features that facilitate and stabilize the formation of the virus particle. Thus, the crystallographic density observed for helices in icosahedral viruses is the result of a combination of the averaging methods used to solve the structure, rotations of the virus particle in the crystal lattice, and heterogeneity in the ensemble of RNA secondary structures (2).
Ensemble approaches to RNA secondary structure prediction have improved predictions for other types of RNA. For example, the computation of a centroid structure with programs such as SFOLD improves predictions of miRNA-mRNA interactions (20). The consideration of suboptimal RNA folds and the probabilities of basepairs improve the accuracy of RNA secondary structure predictions (21–24). Chemical probing provides additional constraints for secondary structure determination and helps identify more accurate structures from a group of low energy structures (21). The information content of chemical probing, however, may not always be sufficient to identify a single correct structure, and RNA may actually exist in an ensemble of conformations (25). The predicted minimum free energy (MFE) secondary structure for an RNA sequence may not always represent the functional RNA conformation because these predictions do not consider tertiary interactions, protein interactions, or kinetics of RNA folding. Free energy minimization is not sufficient to accurately identify a unique RNA conformation for long RNA sequences (23,24,26,27). This is especially true in the case of STMV RNA, which shows a wide diversity of predicted structures within a small range of free energies (28).
The Wuchty algorithm computes completely all possible folds for an RNA sequence within a specified energetic range above the MFE structure (27). The new Crumple algorithm described here computes all possible folds for an RNA sequence using a simpler computational structure and no consideration of energetics. The new algorithm uses less memory and thus more efficiently computes the entire RNA folding funnel. Output from the Crumple algorithm can be filtered with experimental constraints. The Crumple algorithm can be used with a Sliding Windows and Assembly approach to compute all possible folds for STMV RNA within a defined region of conformational space and to find the best representative structure of the ensemble. The chemical probing data provide nucleotide specific constraints, and the minimum number and length of helices provide constraints on the global features of the secondary structures. To our knowledge, this technique of computing all possible folds and then filtering with experimental constraints is a new approach for predicting RNA secondary structures for an ensemble of RNA conformations.
Fig. 2 shows how diverse experimental constraints can define a subset of possible conformations within an RNA folding funnel. The largest gray funnel represents all possible conformations for an RNA sequence. The next largest funnel represents the set of possible structures after lonely pairs are excluded. The long, narrow funnel represents the set of structures that are consistent with the local pairing in a series of hairpins as predicted by the cotranscriptional folding and assembly hypothesis. The smaller funnel to the right represents the set of structures that are consistent with the chemical probing data. The smaller funnel to the left represents the structures that are consistent with the crystallographic data. Selecting a group of structures with a minimum number and length of helices excludes many structures near the top of the funnel that have few basepairs. The intersection of all these sets is shown in red. All possible structures in the intersection of these experimentally defined regions of the folding funnel are combinations of the hairpins computed by the Sliding Windows analysis. This ensemble view of encapsidated viral RNA includes common favorable global features but also allows for variation and heterogeneity, and thus may best represent the folding of the viral RNA. The ensemble of secondary structures presented here is consistent with chemical probing data, crystallographic data, and the hypothesis of cotranscriptional folding and virus assembly.
Figure 2.
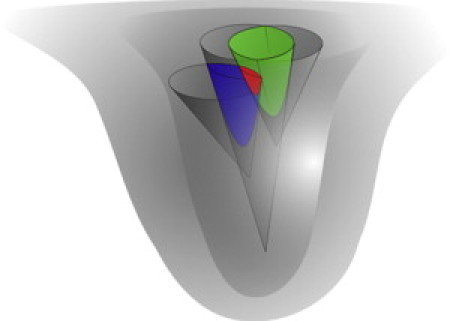
Experimental constraints define a region of the RNA folding funnel. Each smaller gray cone represents a filter based on experimental data such as chemical modification, the minimum number and lengths of helices, local pairing, or no lonely pairs. The intersection of all the filters is represented in red.
Materials and Methods
Virus particle purification and chemical probing
Details regarding the methods and protocols used in this study are provided in the Supporting Material.
Helix Find & Combine
Helix Find identifies and lists all possible places where a helix might occur within a given RNA sequence. Helix Combine considers all possible combinations of the listed helices, including pseudoknotted helices. A helix is defined as consecutive basepairs allowing up to three consecutive mismatches or bulged nucleotides. Helix Find & Combine builds on previous combinatorial approaches to RNA structure prediction (29) and allows noncanonical pairs to occur in helices.
Crumple algorithm
The Crumple algorithm enumerates all possible Watson-Crick and GU pairings for an RNA sequence without consideration of thermodynamics. The algorithm performs a depth-first search and consumes very little memory. The Crumple algorithm is so named because, just as with paper, crumpling is a faster, less discriminate way to fold. The Crumple algorithm computes more efficiently all possible structures for an RNA sequence over the full free energy range of a folding funnel than other existing RNA prediction algorithms. The Crumple algorithm considers only two possibilities for each nucleotide: paired or unpaired. For each interval, or section of a sequence, the algorithm first evaluates each of the possible pairs for the final nucleotide in that interval and then evaluates the structures where that nucleotide does not pair at all. The pseudocode in the Supporting Material describes the two recursions in the Crumple algorithm that are used for helices and all types of loops, including hairpin loops, internal loops, and multibranch loops. Lonely pairs that do not stack with another pair can be actively filtered out while a list of structures is produced.
Sliding Windows and Assembly
The Sliding Windows and Assembly approach consists of six steps: 1), create windows containing short pieces of the RNA sequence; 2), generate all possible single helix structures in each window; 3), filter the structures with experimental constraints; 4), sort the helices by end position and length; 5), score the helices (vide infra); and 6), assemble the helices using a dynamic programming algorithm. Analyzing the structures in a series of windows on the sequence is one approach to approximating the local pairing that occurs during cotranscriptional folding and assembly.
The STMV sequence is divided into each possible subsequence of 30 nucleotides to generate 1028 windows. All possible hairpin structures that are consistent with the chemical modification and crystallographic data are generated for each window with the use of the Crumple algorithm. To eliminate redundancy with the structures in adjacent windows, the final 3′ nucleotide is required to pair in the Crumple computation. All possible combinations of these hairpins describe the ensemble of structures for encapsidated STMV RNA within the defined conformational space.
The structures within each window are filtered for compliance with chemical modification and crystallographic data. If a nucleotide shows a strong chemical modification, then that nucleotide is not allowed to form a Watson-Crick pair between two other Watson-Crick pairs. Chemically modified nucleotides are allowed at the end of a helix, adjacent to an internal loop or bulge, or adjacent to a GU pair. Helices of nine pairs that include up to three consecutive mismatches are consistent with the observed crystallographic data. The definition of a helix in the helix filters allows up to three consecutive terminal noncanonical pairs, which is consistent with free energy measurements on dangling end motifs and measurements of the persistence length of RNA (30,31). However, helices with the fewest noncanonical pairs and the least asymmetry in internal loops are more likely to appear as crystallographically averaged A-form helices.
The set of all possible helices that are consistent with chemical modification and crystallographic data is then assembled into a secondary structure containing 30 helices using a dynamic programming algorithm that is linear with respect to the number of helices. The “best” helix is selected from within overlapping windows according to how well each helix satisfies the experimental chemical modification and crystallographic data. The first four criteria select helices that are most likely to appear as A-form in the averaged electron density from crystallography. The first criterion counts and ranks the types of pairs in the helix; the priority in the ranking is Watson-Crick pairs first, then GU pairs, then terminal mismatches, and finally mismatches in internal loops. The second criterion selects the least asymmetry in internal loops. The third criterion selects the helix with the smallest internal loop. The fourth criterion selects the helix with the fewest terminal mismatches. The fifth criterion considers the different possible ways to meet the chemical modification constraint. A chemical modification satisfaction score places priority on chemical modification in nucleotides that are single stranded or in hairpin loops first, nucleotides in terminal mismatches or internal loops second, Watson-Crick pairs at the end of a helix third, Watson-Crick pairs adjacent to an internal loop fourth, and lastly Watson-Crick pairs adjacent to internal GU pairs. The helix scoring function summarizes these criteria as follows:
Helix score = 1 × number of Watson-Crick pairs
+ 2 × number of GU pairs
+ 3 × number of terminal mismatches
+ 4 × number of internal mismatches
+ 5 × number of asymmetry of internal loops
+ 2 × number of chemically modified nucleotides pairing adjacent to helix ends or GU. (1)
Favorable thermodynamic stability is not directly considered, although the first four criteria favor thermodynamically stable helices. Thermodynamic stability can be included as another score for evaluating helices in the Sliding Windows and Assembly program.
Results
The helices in encapsidated STMV RNA contain mismatches
Helix Find identifies 83 places in the STMV RNA sequence where a perfect helix of nine Watson-Crick or GU pairs may form (Table S1), but there is no possible simultaneous combination of 30 of these helices. Chemical probing eliminates 24 of these possible helices. Thus, the encapsidated STMV RNA structure must contain imperfect helices. The Helix Find & Combine program allows long-range pairing and pseudoknot pairing. There is also no possible simultaneous combination of 30 helices of at least six perfect pairs. Thus some of the mismatched pairs are likely to be in internal, hairpin, or bulged loops. Many internal loops and single mismatches in a helix are energetically favorable (21,32–34). Consecutive mismatches at the ends of helices can also be thermodynamically favorable (30). The icosahedral averaging used to solve the crystal structure could obscure any non-A-form deviations caused by noncanonical pairs.
Crumple correctly computes all possible basepairings for a given sequence
The Crumple algorithm correctly computes all possible pairings for a given sequence. This was tested manually with a 14-mer oligonucleotide (Table S3). Additionally, all 30-nucleotide windows in the STMV sequence were computed with both Crumple and the Vienna RNA Websuite (22) implementation of the Wuchty algorithm allowing lonely pairs (isolated pairs that do not stack on another pair) and using a 1000 kcal/mol energy window. Both computations gave identical results for every 30-nucleotide window. However, Crumple is faster, uses less memory, and correctly implements the no-lonely-pair constraint for a full folding funnel. The results from the Crumple calculations for every 30-nucleotide window are included in Supporting Material.
Sliding Windows generates many possible hairpins consistent with experimental data
The output from Crumple for each 30-nucleotide window is scored using Eq. 1 and sorted by length. Fig. 3 shows the hairpin with the best score for each length in all windows. There is a normal distribution of scores for the hairpins. There are a few hairpins with very high scores or very low scores, but many hairpins have medium scores. There are some regions of the STMV sequence that have many very different possible helices, and some regions with few or no hairpins. Many possible combinations of 30 of these hairpins are possible. Thus, there are many possible secondary structures for STMV RNA that satisfy the chemical modification data, crystallography observations, and local pairing predicted by the cotranscriptional folding and assembly model. This array of possible hairpins and the many combinations of these hairpins lead to the ensemble view of a set of secondary structures with common global characteristics as the best description of encapsidated STMV RNA structure.
Figure 3.
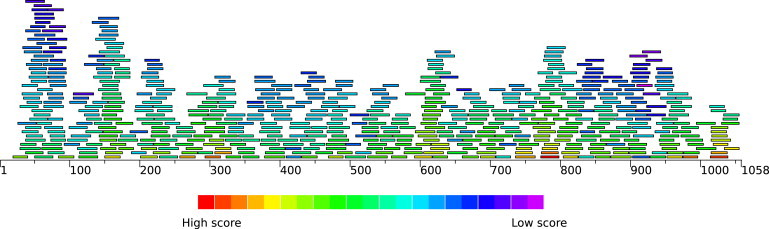
Hairpins with the best score for each length in every 30-nucleotide window are shown as bars with a length corresponding to the number of nucleotides used to form the hairpin. The color of the bar represents the score for the hairpin calculated using Eq. 1. All of these hairpins are the input for the Assembly algorithm.
The Assembly algorithm correctly predicts hairpins in HIV-1 5′UTR
Assembly is a dynamic algorithm that finds the best combination of a specific number of hairpins based on the scoring function in Eq. 1. The set of hairpins from Crumple and Sliding Windows analysis (shown in Fig. 3) is the input for the Assembly algorithm. The output is a single secondary structure with the best combination of hairpins for a given scoring function. The result depends on the scoring function, a truism for all RNA folding algorithms. The advantage of the Assembly algorithm is the capability to directly control the weighting for different types of experimental data. For example, to explore metastable structures in which kinetics rather than free energy minimization is the driving force, the impact of thermodynamic parameters can be minimized or removed.
The 5′UTR of HIV-1 is a good test case for the Assembly algorithm and poses many of the same challenges for RNA folding and secondary structure prediction as STMV RNA. In the current model for the secondary structure of the HIV-1 5′UTR, a series of hairpins form and then long-range basepairing occurs as nucleocapsid proteins bind (18). Further secondary structure conformational changes occur in the 5′UTR when the HIV-1 RNA dimerizes (35). The secondary structure model based on in vitro and in vivo chemical probing, mutagenesis, phylogenic alignment and nucleotide covariation, and NMR spectroscopic studies does not match predictions based on free energy minimization (16–19,36). Predictions from a genetic algorithm RNA folding analysis of the HIV-1 5′UTR sequence also reveal many possible hairpins and secondary structure conformations (37). The series of hairpins that include the psi packaging signal (PSI), the splice donor site (SD), and the dimerization initiation signal (DIS) maintain the same conformation in vitro and in vivo, and as proteins bind (16–19). The extensive biochemical studies on HIV-1 5′UTR provide a good test case for the Assembly algorithm.
The strongest sites of chemical modification from chemical probing in vivo (16) and in vitro (17) were used as constraints for folding the 96 nucleotides of the region of the 5′UTR of HIV-1 sequence that includes the PSI, SD, and DIS hairpins. The RNA was folded with Crumple, Sliding Windows and Assembly, RNAStructure 4.6 (21), Sfold (38), and Vienna RNAfold (22). When folding with Assembly, the folding constraint was three hairpins of at least four pairs. The Assembly algorithm was run both with and without the penalty for asymmetric helices in Eq. 1 because in the case of the HIV-1 5′UTR, there is no crystallography data constraint for unbent A-form helices. Sfold and RNAfold were used both with and without chemical modification constraints because these programs use only hard single strand constraints for chemically modified nucleotides rather than the subtleties of allowing chemically modified nucleotides to occur in basepairs adjacent to helix ends, internal loops, bulges, or GU pairs. RNAfold uses an earlier set of thermodynamic parameters (32) than the other programs. The results of all the different computational folding methods are shown in Fig. S3.
The Sliding Windows and Assembly approach performs as well as other standard folding programs. Sliding Windows and Assembly correctly predicts the three hairpins (Fig. S3 B), although the basepairs slide over near the bulge loop in the stem of the DIS hairpin and additional basepairs are added to the PSI hairpin. With the penalty for asymmetry, Sliding Windows and Assembly cannot correctly predict the SD hairpin, but predicts the hairpin nucleotides correctly for the DIS and PSI loops with a slight variation in the stem helices. RNAStructure 4.6 predicts the same structure with and without chemical modification, although the possible suboptimal structures change with chemical modification constraints. RNAStructure 4.6 also adds additional basepairs to the PSI hairpin. The basepairs around the bulge loop in the DIS hairpin have <50% pairing probabilities, which lend credence to the alternative pairings predicted by Sliding Windows and Assembly. Sfold and RNAfold perform much better without chemical modification constraints, and correctly predict only the DIS hairpin with chemical modification constraints. Without chemical modification constraints, Sfold predicts the SD and PSI hairpins in the centroid structure and the SD, PSI, and DIS hairpins with additional basepairs in the MFE structure. The centroid structure predicted by RNAfold without chemical modification constraints produces the correct structure exactly with no extra pairs and no sliding around the bulge. It is somewhat surprising and ironic that no chemical modification constraints and less accurate thermodynamic parameters produce the best prediction.
The predictions of all the RNA folding programs depend on exactly how constraints are applied and the definition of the scoring function. Slight changes in the scoring function in either the thermodynamic parameters or other experimental constraints can cause large changes in the predicted secondary structures. Slippery sequences, such as the helix around the bulge in the DIS hairpin, are especially sensitive to slight variations in scoring and probably exist in multiple conformations. Thus, an ensemble view of RNA secondary structure may best represent this stochastic diversity in RNA structures.
STMV RNA secondary structures consistent with chemical probing and crystallographic data
The minimum number and lengths of helices provide constraints on the global fold of the RNA, and the chemical modification data provide nucleotide-specific constraints on possible pairing. Only the strongest hits (164 constraints in total) from DMS, CMCT, and kethoxal probing were used as constraints because in an ensemble of RNA structures, a weak hit could be due to either a strong reactivity in only a few structures or a weak hit in many structures. The strongest hits are most likely to be common to the majority of structures in the ensemble. The local pairing that results from the Sliding Windows approach demonstrates the feasibility of the cotranscriptional folding and assembly hypothesis. The secondary structure that best satisfies the cotranscriptional folding and assembly hypothesis and experimental constraints, including crystallography and chemical modification data, is shown in Fig. 4. This secondary structure highlights the best combination of the highest scoring hairpins that are consistent with experimental constraints. Although additional local and long-range basepairing interactions are possible in Fig. 4, no predictions beyond the best 30 helices are attempted at this point because such interactions are likely convoluted with the tertiary and quaternary structure of the STMV RNA and capsid proteins.
Figure 4.
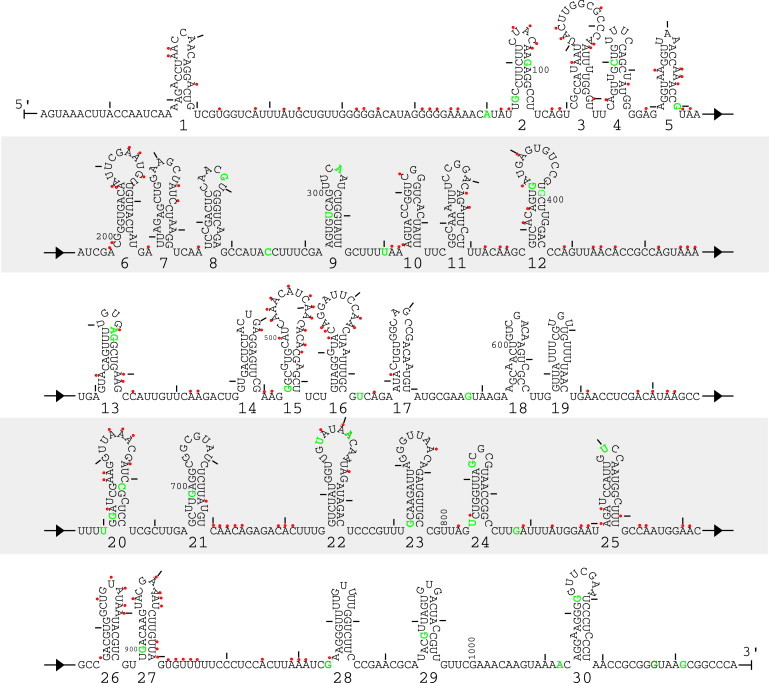
Best representative 30 hairpins from the ensemble of STMV RNA secondary structures generated by the Crumple and Sliding Windows and Assembly algorithms. Red dots indicate nucleotides chemically modified by DMS, kethoxal, or CMCT. No constraints or interpretation is applied to nucleotides protected from chemical modification because there are many sources of protection from chemical modification, including basepairing, RNA tertiary interaction, protein-RNA interactions, and slower diffusion into the center of the virus capsid. The figure emphasizes the 30 hairpins that are consistent with the crystallographic observations, chemical modification, and the model of cotranscriptional folding and assembly. Other long-range basepairing interactions are possible between nucleotides outside of the 30 hairpins shown, but no attempt is made to predict further secondary structure elements. Primer extension reactions begin reporting chemical modification at nucleotide 970. Green nucleotides are sites of natural variation in STMV RNA (39–41). Tick marks indicate every 10 nucleotides.
To test whether the window size affects the structure predictions, the ensemble centroids and hairpin probabilities in the STMV RNA sequence were calculated with Sfold (26). The 134 nucleotides hit by DMS were constrained as single stranded. The maximum basepairing distance was set to 25, 30, 35, 40, or 50, and then the probability of hairpin formation in the centroid ensembles was evaluated. The probability of hairpin formation did not vary as a function of the maximum pairing distance constraint for the 3′ end of the STMV RNA (nucleotides 650–1058), although more variation occurred in the 5′ region of the sequence (nucleotides 1–400) (Fig. S4). When parameters for the helix assembly were varied, most of the variation in secondary structure also occurred in the 5′ end of the STMV. This suggests more confidence in the helices in the 3′ end.
The secondary structural model presented in Fig. 4 is largely consistent with known sequence variations in STMV RNA (39–41). Of 35 sites of known sequence heterogeneity, 19 are unpaired nucleotides; seven would change a Watson-Crick pair to a GU or AC pair; nine would disrupt a Watson-Crick or GU pair and create a mismatch; and one would change a mismatch to another mismatch. The number of helices containing GU and AU pairs is consistent with the bias toward G-to-A substitutions in natural variants of STMV (39). The helices observed crystallographically for STMV RNA must allow some mismatches to occur, so single point mutations may not always disrupt a helix.
Different methods yield similar predictions for the 3′ region of STMV RNA
Although current RNA prediction programs, including mfold, Sfold, RNASTAR, Vienna RNAfold, and RNAStructure4.6 (21,22,38,42–44), do not generate secondary structures that are fully consistent with the crystallographic data, several different approaches predict similar hairpins in the 3′ end of STMV RNA, which increases confidence in the predictions for this region (Fig. 4 and Fig. S5). Folding the STMV RNA sequence with chemical modification constraints using RNAStructure 4.6 did not predict secondary structures with 30 helices of at least nine pairs. Constraining the basepairing within 30–50 nucleotides improved the consistency with the crystallographic data and generated structures with 20–25 helices. Selection of suboptimal structures and manual adjustments to the predicted structure generated structures that satisfied the crystallographic data (Fig. S5). The Zuker method of sampling suboptimal structures (24) does not combine two suboptimal substructures (45). This demonstrates the value of alternative methods, such as the Wuchty algorithm and Sliding Windows and Assembly, to combine suboptimal structures more thoroughly in ways that are not generated by other programs.
The basepairing probabilities calculated in RNAStructure 4.6 with the McCaskill algorithm show high probabilities of >90% mainly in the hairpins in the 3′ end of the STMV sequence. The predicted hairpins in the 3′ end of the STMV sequence do not vary with the size of the basepairing window in Sfold predictions (Fig. S4). Thus there is higher confidence in the hairpins in the 3′ end of the STMV secondary structure in Fig. 4.
Folding the STMV sequence with DMS constraints and constraining the pairing distance within 30 nucleotides using the Sfold program generated a centroid structure that did not contain 30 helices of at least nine pairs, although two of 10 randomly selected structures did contain 30 helices of nine pairs (Fig. S5). The additional CMCT and kethoxal constraints are consistent with these structures. However, these structures contain some highly asymmetric internal loops that would be less likely to show A-form-like electron density for the RNA helices at the twofold axes in the crystal structure. The secondary structure in Fig. 4 contains nine helices in common with the centroid structure, with the most common and highly probable helices occurring in the 3′ end of the sequence.
Previous folding experiments with RNASTAR to predict the 3′ end of STMV RNA showed some structural similarities with predicted structures for other tobamoviruses (9). However, this predicted structure is not compatible with the STMV crystallographic data or the new chemical modification data, and thus differs from the structures presented here (Fig. 4). For example, chemical modification at nucleotides 936 and 922 preclude the formation of proposed pseudoknotted helix E in a proposed tRNA-like model (10). Similarly, chemical modification at nucleotides 663, 668, 678, 716, 918, and 935 precludes several predicted pseudoknotted helices (9). Previous predictions for the 3′ end of STMV RNA contain many short, highly pseudoknotted structures. The previous prediction for the last 400 nucleotides contains only five helices that are long enough to satisfy the crystallography data well, which is very unlikely to leave enough remaining nucleotides for 30 helices of at least nine pairs (9). Gultyaev et al. (9) also noted the need for more experimental data to distinguish between multiple predicted structures. The structures predicted with RNASTAR may be more representative of STMV at another stage of the viral life cycle.
Discussion
The Crumple and Sliding Windows and Assembly approaches and the use of filters from experimental data provide new tools to generate an ensemble of RNA structures in a defined region of conformational space. The helix filters (i.e., the minimum number and length of helices) are a global experimental constraint that can be applied to other encapsidated viral RNA predictions and RNAs studied by low-resolution crystallography or cryo-EM (46). These new tools are necessary to explore viral RNA structures when the assumptions of traditional free energy minimization may not hold true.
The main advantage of the Sliding Windows and Assembly approach is the capability to maximize consistency with experimental data and modulate the dependency on free energy minimization. In the case of STMV, the secondary structures were generated to maximize consistency with the crystallographic data. When the chemical modification satisfaction score was not used, another alternative secondary structure was generated (Fig. S5) that has only 14 helices in common with the STMV secondary structure shown in Fig. 4. The STMV secondary structure in Fig. 4 has only 14 places where chemically modified nucleotides form Watson-Crick pairs at the ends of helices or adjacent to internal loops or GU pairs, whereas these types of chemically modified Watson-Crick pairs occur in 40 pairs in the alternative STMV secondary structure. However, the predicted free energies of the structure shown in Fig. 4 and the alternative structure shown in the Supporting Material are −73.4 kcal/mol and −101.1 kcal/mol, respectively. Thus, although both structures are consistent with the crystallographic data, the structure in Fig. 4 is more consistent with chemical modification data, and the alternative structure has a more favorable predicted free energy. Note also that the free energy of helix formation is not the same as the stability of an RNA helix bound to a capsid protein. On the other hand, Sfold generates structures that minimize free energy and maximize chemical modification satisfaction (chemical modification is only allowed as a single strand constraint in Sfold) but are less consistent with the crystallographic data. These examples reveal the wide range of free energies for structures that satisfy all of the experimental data. Thus, an emphasis on different types of experimental data generates very different structures. In this work, the structure that was most consistent with the crystallography and chemical modification data was identified as the best representative of the ensemble, rather than the lowest free energy structure, because there are many unaccountable contributions to the overall folding from RNA-protein interactions and a kinetically controlled process of cotranscriptional folding and virus assembly.
The helix assembly process does not consider other possible secondary structures in the nucleotides between the helices. Additional hairpins, pseudoknots, and helices forming multibranch loops are all possible interactions of the unpaired nucleotides and could make the free energy of the structure more favorable. These nucleotides may also interact with the C-termini of the capsid proteins that extend toward the adjacent capsid protein and then into the interior of the virus particle and may help stabilize the close packing of the negatively charged RNA backbones in a manner similar to the long extended tails of ribosomal proteins (47). Thus, the regions of unpaired nucleotides between helices in Fig. 4 may have significant functional and energetically stabilizing structures. The identification of these potential tertiary and quaternary structures will require future modeling experiments beyond the scope of secondary structure prediction. However, the ensemble of secondary structures presented here is an important first step in modeling the complete three-dimensional structure of the STMV virus particle.
An ensemble of structures with common favorable global characteristics for the encapsidated viral RNA genome could be an evolutionary advantage for the virus. Statistical mechanics predicts an ensemble of structures, and a virus would have to do work to select one structure for encapsidation from this ensemble. A single RNA conformation would be a brittle solution to the RNA folding problem. Stochastic diversity in encapsidated viral RNA conformations presents a more robust solution to packaging a viral genome. Stochastic diversity in functional conformations of group I introns has been demonstrated by single molecule techniques (48) and may be common for RNA structures. More than one solution to the RNA folding problem may also help the virus avoid kinetic traps during assembly. Because a virus repeatedly folds and unfolds during its life cycle, a single low energy structure would be less advantageous than a broad, shallow folding funnel. If a virus can encapsidate many different structures, then less cost would be associated with a single point mutation, and greater variation could occur more rapidly. The computational techniques described here present a new (to our knowledge) approach to the challenging problem of predicting dynamic ensembles of RNA structures.
Acknowledgments
We thank Montana Rowe for generating Fig. 2, and Sean Lavelle, Montana Rowe, and Adam Heck for programming advice and assistance. We also thank Cal Lemke at the University of Oklahoma greenhouses for providing Nicotiana tabacum plants for some of the STMV samples.
This work was supported by grants from the Oklahoma Center for the Advancement of Science and Technology, the Pharmaceutical Research and Manufacturers of America Foundation, and the National Science Foundation (CAREER award No. 0844913).
Footnotes
Theodore Gibbons's present address is the Graduate Program in Biological Sciences, University of Maryland, College Park, Maryland.
Deborah M. Mathews present address is Department of Plant Pathology and Microbiology, University of California, Riverside, California.
Supporting Material
References
- 1.Benjamin J., Ganser-Pornillos B.K., Jensen G.J. Three-dimensional structure of HIV-1 virus-like particles by electron cryotomography. J. Mol. Biol. 2005;346:577–588. doi: 10.1016/j.jmb.2004.11.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schneemann A. The structural and functional role of RNA in icosahedral virus assembly. Annu. Rev. Microbiol. 2006;60:51–67. doi: 10.1146/annurev.micro.60.080805.142304. [DOI] [PubMed] [Google Scholar]
- 3.Shepherd C.M., Borelli I.A., Reddy V.S. VIPERdb: a relational database for structural virology. Nucleic Acids Res. 2006;34(Database issue):D386–D389. doi: 10.1093/nar/gkj032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Toropova K., Basnak G., Ranson N.A. The three-dimensional structure of genomic RNA in bacteriophage MS2: implications for assembly. J. Mol. Biol. 2008;375:824–836. doi: 10.1016/j.jmb.2007.08.067. [DOI] [PubMed] [Google Scholar]
- 5.Larson S.B., Day J., McPherson A. Refined structure of satellite tobacco mosaic virus at 1.8 A resolution. J. Mol. Biol. 1998;277:37–59. doi: 10.1006/jmbi.1997.1570. [DOI] [PubMed] [Google Scholar]
- 6.Larson S.B., Koszelak S., McPherson A. Double-helical RNA in satellite tobacco mosaic virus. Nature. 1993;361:179–182. doi: 10.1038/361179a0. [DOI] [PubMed] [Google Scholar]
- 7.Larson S.B., McPherson A. Satellite tobacco mosaic virus RNA: structure and implications for assembly. Curr. Opin. Struct. Biol. 2001;11:59–65. doi: 10.1016/s0959-440x(00)00166-4. [DOI] [PubMed] [Google Scholar]
- 8.Freddolino P.L., Arkhipov A.S., Schulten K. Molecular dynamics simulations of the complete satellite tobacco mosaic virus. Structure. 2006;14:437–449. doi: 10.1016/j.str.2005.11.014. [DOI] [PubMed] [Google Scholar]
- 9.Gultyaev A.P., van Batenburg E., Pleij C.W.A. Similarities between the secondary structure of satellite tobacco mosaic virus and tobamovirus RNAs. J. Gen. Virol. 1994;75:2851–2856. doi: 10.1099/0022-1317-75-10-2851. [DOI] [PubMed] [Google Scholar]
- 10.Felden B., Florentz C., Giegé R. A histidine accepting tRNA-like fold at the 3′-end of satellite tobacco mosaic virus RNA. Nucleic Acids Res. 1994;22:2882–2886. doi: 10.1093/nar/22.15.2882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rodriguez-Alvarado G., Roossinck M.J. Structural analysis of a necrogenic strain of cucumber mosaic cucumovirus satellite RNA in planta. Virology. 1997;236:155–166. doi: 10.1006/viro.1997.8731. [DOI] [PubMed] [Google Scholar]
- 12.Palmenberg A.C., Spiro D., Liggett S.B. Sequencing and analyses of all known human rhinovirus genomes reveal structure and evolution. Science. 2009;324:55–59. doi: 10.1126/science.1165557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Watts J.M., Dang K.K., Weeks K.M. Architecture and secondary structure of an entire HIV-1 RNA genome. Nature. 2009;460:711–716. doi: 10.1038/nature08237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gherghe C., Leonard C.W., Weeks K.M. Secondary structure of the mature ex virio Moloney murine leukemia virus genomic RNA dimerization domain. J. Virol. 2010;84:898–906. doi: 10.1128/JVI.01602-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gherghe C., Lombo T., Weeks K.M. Definition of a high-affinity Gag recognition structure mediating packaging of a retroviral RNA genome. Proc. Natl. Acad. Sci. USA. 2010;107:19248–19253. doi: 10.1073/pnas.1006897107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Paillart J.-C., Dettenhofer M., Marquet R. First snapshots of the HIV-1 RNA structure in infected cells and in virions. J. Biol. Chem. 2004;279:48397–48403. doi: 10.1074/jbc.M408294200. [DOI] [PubMed] [Google Scholar]
- 17.Abbink T.E., Berkhout B. A novel long distance base-pairing interaction in human immunodeficiency virus type 1 RNA occludes the Gag start codon. J. Biol. Chem. 2003;278:11601–11611. doi: 10.1074/jbc.M210291200. [DOI] [PubMed] [Google Scholar]
- 18.Spriggs S., Garyu L., Summers M.F. Potential intra- and intermolecular interactions involving the unique-5′ region of the HIV-1 5′-UTR. Biochemistry. 2008;47:13064–13073. doi: 10.1021/bi8014373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huthoff H., Berkhout B. Multiple secondary structure rearrangements during HIV-1 RNA dimerization. Biochemistry. 2002;41:10439–10445. doi: 10.1021/bi025993n. [DOI] [PubMed] [Google Scholar]
- 20.Shao Y., Chan C.Y., Ding Y. Effect of target secondary structure on RNAi efficiency. RNA. 2007;13:1631–1640. doi: 10.1261/rna.546207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mathews D.H., Disney M.D., Turner D.H. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl. Acad. Sci. USA. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gruber A.R., Lorenz R., Hofacker I.L. The Vienna RNA website. Nucleic Acids Res. 2008;36(Web Server issue):W70–W74. doi: 10.1093/nar/gkn188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McCaskill J.S. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1119. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]
- 24.Zuker M. On finding all suboptimal foldings of an RNA molecule. Science. 1989;244:48–52. doi: 10.1126/science.2468181. [DOI] [PubMed] [Google Scholar]
- 25.Quarrier S., Martin J.S., Laederach A. Evaluation of the information content of RNA structure mapping data for secondary structure prediction. RNA. 2010;16:1108–1117. doi: 10.1261/rna.1988510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ding Y., Lawrence C.E. A statistical sampling algorithm for RNA secondary structure prediction. Nucleic Acids Res. 2003;31:7280–7301. doi: 10.1093/nar/gkg938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wuchty S., Fontana W., Schuster P. Complete suboptimal folding of RNA and the stability of secondary structures. Biopolymers. 1999;49:145–165. doi: 10.1002/(SICI)1097-0282(199902)49:2<145::AID-BIP4>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 28.Schroeder S.J. Advances in RNA structure prediction from sequence: new tools for generating hypotheses about viral RNA structure-function relationships. J. Virol. 2009;83:6326–6334. doi: 10.1128/JVI.00251-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pipas J.M., McMahon J.E. Method for predicting RNA secondary structure. Proc. Natl. Acad. Sci. USA. 1975;72:2017–2021. doi: 10.1073/pnas.72.6.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Clanton-Arrowood K., McGurk J., Schroeder S.J. 3′ terminal nucleotides determine thermodynamic stabilities of mismatches at the ends of RNA helices. Biochemistry. 2008;47:13418–13427. doi: 10.1021/bi801594k. [DOI] [PubMed] [Google Scholar]
- 31.Seol Y., Skinner G.M., Halperin A. Stretching of homopolymeric RNA reveals single stranded helices and base-stacking. Phys. Rev. Lett. 2007;98:158103–158107. doi: 10.1103/PhysRevLett.98.158103. [DOI] [PubMed] [Google Scholar]
- 32.Mathews D.H., Sabina J., Turner D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- 33.Schroeder S.J., Turner D.H. Factors affecting the thermodynamic stability of small asymmetric internal loops in RNA. Biochemistry. 2000;39:9257–9274. doi: 10.1021/bi000229r. [DOI] [PubMed] [Google Scholar]
- 34.Schroeder S.J., Burkard M.E., Turner D.H. The energetics of small internal loops in RNA. Biopolymers. 1999-2000;52:157–167. doi: 10.1002/1097-0282(1999)52:4<157::AID-BIP1001>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 35.Jossinet F., Paillart J.C., Marquet R. Dimerization of HIV-1 genomic RNA of subtypes A and B: RNA loop structure and magnesium binding. RNA. 1999;5:1222–1234. doi: 10.1017/s1355838299990982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Huthoff H., Berkhout B. Two alternating structures of the HIV-1 leader RNA. RNA. 2001;7:143–157. doi: 10.1017/s1355838201001881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kasprzak W., Bindewald E., Shapiro B.A. Structural polymorphism of the HIV-1 leader region explored by computational methods. Nucleic Acids Res. 2005;33:7151–7163. doi: 10.1093/nar/gki1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ding Y., Chan C.Y., Lawrence C.E. Sfold web server for statistical folding and rational design of nucleic acids. Nucleic Acids Res. 2004;32(Web Server issue):W135–W141. doi: 10.1093/nar/gkh449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kurath G., Rey M.E., Dodds J.A. Analysis of genetic heterogeneity within the type strain of satellite tobacco mosaic virus reveals variants and a strong bias for G to A substitution mutations. Virology. 1992;189:233–244. doi: 10.1016/0042-6822(92)90699-p. [DOI] [PubMed] [Google Scholar]
- 40.Kurath G., Heick J.A., Dodds J.A. RNase protection analyses show high genetic diversity among field isolates of satellite tobacco mosaic virus. Virology. 1993;194:414–418. doi: 10.1006/viro.1993.1278. [DOI] [PubMed] [Google Scholar]
- 41.Kurath G., Dodds J.A. Mutation analyses of molecularly cloned satellite tobacco mosaic virus during serial passage in plants: evidence for hotspots of genetic change. RNA. 1995;1:491–500. [PMC free article] [PubMed] [Google Scholar]
- 42.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gultyaev A.P., van Batenburg F.H., Pleij C.W. The computer simulation of RNA folding pathways using a genetic algorithm. J. Mol. Biol. 1995;250:37–51. doi: 10.1006/jmbi.1995.0356. [DOI] [PubMed] [Google Scholar]
- 44.Hofacker I.L. Vienna RNA secondary structure server. Nucleic Acids Res. 2003;31:3429–3431. doi: 10.1093/nar/gkg599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mathews D.H. Revolutions in RNA secondary structure prediction. J. Mol. Biol. 2006;359:526–532. doi: 10.1016/j.jmb.2006.01.067. [DOI] [PubMed] [Google Scholar]
- 46.Baird N.J., Ludtke S.J., Sosnick T.R. Discrete structure of an RNA folding intermediate revealed by cryo-electron microscopy. J. Am. Chem. Soc. 2010;132:16352–16353. doi: 10.1021/ja107492b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ban N., Nissen P., Steitz T.A. The complete atomic structure of the large ribosomal subunit at 2.4 A resolution. Science. 2000;289:905–920. doi: 10.1126/science.289.5481.905. [DOI] [PubMed] [Google Scholar]
- 48.Solomatin S.V., Greenfeld M., Herschlag D. Multiple native states reveal persistent ruggedness of an RNA folding landscape. Nature. 2010;463:681–684. doi: 10.1038/nature08717. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


