A Direct Coupling between Global and Internal Motions in a Single Domain Protein? MD Investigation of Extreme Scenarios

Abstract

Proteins are not rigid molecules, but exhibit internal motions on timescales ranging from femto- to milliseconds and beyond. In solution, proteins also experience global translational and rotational motions, sometimes on timescales comparable to those of the internal fluctuations. The possibility that internal and global motions may be directly coupled has intriguing implications, given that enzymes and cell signaling proteins typically associate with binding partners and cellular scaffolds. Such processes alter their global motion and may affect protein function. Here, we present molecular dynamics simulations of extreme case scenarios to examine whether a possible relationship exists. In our model protein, a ubiquitin-like RhoGTPase binding domain of plexin-B1, we removed either internal or global motions. Comparisons with unrestrained simulations show that internal and global motions are not appreciably coupled in this single-domain protein. This lack of coupling is consistent with the observation that the dynamics of water around the protein, which is thought to permit, if not stimulate, internal dynamics, is also largely independent of global motion. We discuss implications of these results for the structure and function of proteins.

Introduction

Over several decades it has become clear that protein motions play critical roles in aspects of protein structure and function including folding and stability, catalysis, protein-ligand binding, and protein-protein association (1). In addition to motions that involve certain substructures (and are said to be protein internal), there are also fluctuations that affect the protein as a whole. Specifically, these are translational and rotational diffusive motions of the entire molecule in the solvent. It is known that such global stochastic events are broadly related to the size and shape of the protein (2). For small globular proteins (∼8–20 kDa), the rotational correlation times are ∼4–12 ns and occur on the same timescale as some of the protein internal motions. It is therefore possible that the global motion of a protein can affect its internal dynamics, and vice versa.

The concept of a coupling between global and internal motions in molecules has been discussed for some time. Experimental investigations suggest that a direct influence of one type of motion on the other is negligible in most proteins (3–5). There has been some controversy, for example, as to whether the analysis of NMR relaxation data is accurate if the two motions are coupled or even on the same timescale (3,6). Computational studies of global motions have been carried out mostly with simplified models and it has recently become apparent that a more detailed treatment is needed, especially for the hydrophobic surfaces of proteins (see, e.g., Walser and van Gunsteren (7) and de la Torre (8)). Both internal and global motions are governed by solvent motions, providing a common correlate for the two types of dynamics (9,10). Loops that protrude into the solvent are thought to provide a frictional drag on translational and rotational motions. One question is whether the flexibility of such loops would have an effect on the global motion. Another is whether there is an effect of global motions on internal dynamics, e.g., whether global stochastic motions may enhance conformational transitions in loops. To our knowledge, no all-atom protein simulation study has been carried out to specifically address these issues, i.e., of a coupling between global and internal motions at a fundamental level. A direct coupling would suggest that protein size and loop flexibility have significant effects on protein function, especially if loop fluctuations can be communicated to other regions of the protein, including its core. In that case, communication of dynamic events could occur not only through protein structural elements, but also by signal propagation through a change in global motion. This would be an attractive mechanism for the regulation of enzyme activity and cell signaling events, which often involve changes in global motion by protein association or localization to cellular (sub)compartments (11–13).

In experiments, it is difficult to quantitatively investigate protein internal and global motions for such conditions or to separate them from other effects, e.g., from those involving conformational changes upon protein association or changes in solvent viscosity. Thus, in this report, we used molecular dynamics (MD) simulations to investigate the possibility of a coupling between global and internal protein motion. We do so by studying a number of extreme scenarios that are possible in silico. Using an ubiquitin-fold model protein, which has extensive internal motions due to its long, flexible loops and termini (Fig. 1), we carried out simulations that allow global but no internal motions or internal but no global motions. Statistical analyses of the trajectories show that a time-averaged coupling between these two types of motions is negligible for this single-domain globular protein. Both the internal protein motions and the solvent dynamics—which are thought to allow, if not to stimulate, the protein fluctuations—are independent of global motions. The results suggest that internal protein dynamics and the underlying structural determinants have evolved to avoid a direct connection to global fluctuations.

Figure 1.

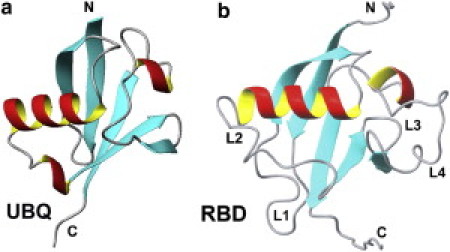
Main-chain fold of ubiquitin (a) compared with that of the Rho- GTPase binding domain (RBD) of plexin-B1 (b). The longer loops in the plexin domain are labeled (L1–L4).

Methods

Simulation details

In each simulation, the protein human ubiquitin (Protein Data Bank code 1UBQ) or the Rho-GTPase binding domain (RBD) of plexin-B1 (Protein Data Bank code 2JPH) (14) was first immersed in a cubic box of explicitly represented water, and periodic boundary conditions were applied. The system was then energy-minimized, heated up, and equilibrated. To enhance sampling, all simulations were carried out in quadruplicate using different random starting seeds for the initial velocity assignment. The standard particle-mesh-Ewald method was used to calculate the long-range electrostatic interactions, and counterions were added to neutralize the system. The CHARMM27 all-atom potential function was used with CMAP correction throughout this study. For nonbonded calculations, a cut-off of 12 Å was used, and the time step was chosen to be 2 fs. All bonds involving hydrogens were kept rigid using the SHAKE algorithm. The Berendsen thermostat and the Langevin piston method were employed to run simulations at constant temperature (T = 300 K) and pressure (P = 1 atm). The unrestrained (UNR) simulations were carried out using the NAMD (15) program, which is well parallelized. High-frequency removal of the global or internal motions is not currently possible in NAMD, so the program CHARMM (16) was used for simulations involving these restraints. It is important to note that conformational space is similarly sampled by both simulators since the same potential function is used (data not shown). In all rigid (RIG) simulations internal degrees of freedom were removed using the SHAPE facility. The internal-motions-only (INT) simulations were run using a slightly modified version of the program, which allowed using its NTRF command (every 20 steps) to remove the rotational and translational motions of the protein, as well as those of the whole system. Global motions are known to be slower than protein internal motions, and thus, using a lesser frequency for the removal of these dynamics was deemed adequate and much less computationally expensive than removal of global motions at every simulation step. (As a test, it was shown that the latter gave the same result, even for the fast motions of the water molecules).

To remove global motion, the following approach was employed: The velocity of the ith atom due to internal motions is given by v_int = v_i − v_CM − r_i x ω, where v_CM is the velocity vector of the center of mass, ω is the angular velocity vector of the protein, v_i is the uncorrected (total) velocity, and x denotes the cross product. We confirmed that the overall translational and rotational motion of the protein was essentially removed by this procedure (diffusion coefficients are reduced by a factor of >100 compared to those in the UNR simulations). Each of the four ubiquitin simulations were run for 110 ns, whereas the three kinds of RBD simulations were run for 55 ns due to the fact that CHARMM requires much more computational time. Since internal motions in ubiquitin are very modest on the picosecond–nanosecond timescale, the project focused on the plexin domain and the INT and RIG simulations were only run for this protein.

Rotational and translational diffusion

To analyze the trajectories, we calculated a number of parameters, including rotational correlation functions defined as $C_2=\langle P_2\left(\cos \theta \right)\rangle$, where P₂(x) is the second rank Legendre polynomial and θ is the angular displacement of a unit vector attached to the protein. One can consider three unit vectors along the three principal axes of the protein. For simplicity, the three correlation functions were averaged for this analysis. The second-rank rotational correlation functions of the RBD and ubiquitin were averaged over 1100 time origins. The correlation times were then found by an exponential fit. These calculations were carried out using the 5–55 ns time interval of the RBD and 10–110 ns of the ubiquitin trajectories. The mean-squared displacement (MSD) plots were calculated by averaging over 2200 time origins for the ubiquitin and RBD simulations. The last 0.5 ns of these plots were then used to determine the diffusion coefficients (D = slope/6). The MSD and correlation function plots in this study (see Fig. 3) are for the average of the four simulations. The standard deviation (given in Table 1) reflects the difference between the fits of the four simulations and is greater than the uncertainty in the fit of the four-simulation average. It is worth noting that the TIP3 water model results in faster diffusion (17,18), and that the size of the simulation box has a significant effect on the calculated translational diffusion coefficients from simulations (19). Thus, we have not compared our simulation-derived diffusion rates with experimental results. The goal of this article is to compare the results of UNR and INT simulations. Although the timescale of the global, and possibly also of the internal motion may not be entirely accurate, the scenarios explored by the simulations are the most extreme and should, therefore, in their comparison reveal a correlation between internal and global motion, if one exists.

Figure 3.

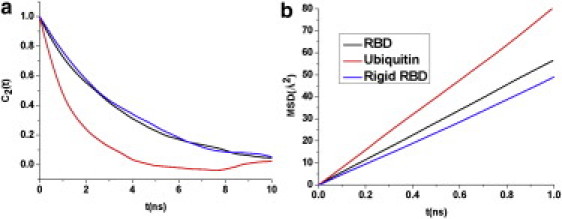
Second-rank rotational correlation functions (a) and MSD (b) of the centers of mass of ubiquitin, plexin RBD, and rigid plexin RBD (no internal motion).

Table 1.

Global protein translational and rotational diffusion data

Protein	Ubiquitin	RBD (UNR)	RBD (RIG)
D (× 10−5 cm2/s)	13.6 ± 2.0	9.5 ± 0.4	8.4 ± 0.7
τm (ns)	1.4 ± 0.4	3.4 ± 0.3	3.7 ± 0.8

D, translational diffusion; τ_m, decay time of the global rotational correlation function.

Change in protein shape and distinction between internal and global motion

The principal moments of the proteins' inertia tensors were calculated as a function of simulation time using the standard procedure in CHARMM, which diagonalizes the moments of inertia tensor to yield eigenvalues (the principal moments). The program of Prompers and Brüschweiler was used to carry out isotropic reorientational eigenmode dynamics (iRED) of rank 2 and calculate g2, a parameter that indicates the separability between global and internal motions (20). Briefly, an isotropically averaged covariance matrix (M) is constructed with the dot products of normalized bond vectors (e.g., of all amide groups of the protein). Since only inner products between vectors are involved, the matrix is rotationally invariant and no overall rotation needs to be removed, whereas an isotropic overall directional sampling is added by transforming the matrix. A principal-component analysis is performed on the covariance matrix, yielding eigenvectors and eigenvalues, λ_m (mode amplitudes). The five eigenvectors with the largest eigenvalues represent the global motion if they are separated sufficiently from the next-largest eigenvectors. The extent of this separation is indicated by g2, the separability index of rank 2 (for details, see Prompers and Brüschweiler (20)).

Order parameters and associated correlation times

The Lipari-Szabo order parameters and also correlation times for main-chain N-H bonds of the RBD were calculated (using CHARMM) over the time interval 5–55 ns of the trajectories according to previously established protocols (21), We used a cut-off for the correlation function of 5 ns, close to the TIP3P scaled global correlation times determined experimentally (the results are independent over a 4–10 ns range of cut-off values). We also employed a recently proposed procedure (22) that does not remove the global motion from the trajectories and incorporates an estimated correlation time from the MD simulations (in our case, the rotational correlation function, given in Table 1) in a fitting of the C₂ residue correlation functions. This procedure did not, however, produce better comparisons with the experimentally derived S². In fact, as expected, the fitting becomes problematic when the timescale of the global and internal motions are close for several of the residues. In any case, the procedure could not be used to analyze the INT trajectories (23).

Z-scores for individual residues were used to establish whether differences in the derived order parameters between the UNR and INT simulations are statistically significant (24). The Z-score for a residue i is calculated as Z_i = P_ia − P_ib/((σP_ia + σP_ib)/2) where P_i is a four-simulation average dynamic parameter (S² or τ_e) for that residue (comparing data sets a and b) and σP_i a,b is the standard deviation of motions seen in the four simulations, datasets a and b, respectively. The difference in dynamics is statistically significant if |Z-scores| > 1.96, corresponding to the 5% probability cut-off. The underlying distribution (as well as the uncertainties) is assumed to be normal. The Wilcoxon signed rank test, which avoids this assumption, is also used to compare UNR and INT simulations for several regions of the protein. Four regions of the protein were examined: the N-terminus (residues 2–6), loop1 (residues 16–26), loop2 (residues 85–92), and the C-terminus (residues 113–122). For each region, the order parameters from the four simulations were combined in a single column. In the case of the five-residue N-terminal region, for example, the order parameters from the four simulations were used to form two 20-row columns, comparing the same residues of simulation UNR1 with those of INT1, UNR2 with INT2, etc. The simulation pairs were then cycled so that UNR1 is compared with INT2, UNR2 with INT3, etc., extending the column to 80 pairs of the same residues, but different simulation pairs. The Wilcoxon tests were then carried out by inserting the two columns into a web-based calculator (25). The calculated p-values are reported in Table 2. A value of <0.05 is normally regarded as statistically significant. One of the UNR trajectories (simulation 3) can be regarded as an outlier as far as the behavior of the C-terminus is concerned. To compare the four INT and the remaining three UNR simulations, the above protocol was used, but simulations INT1–INT4 were omitted in turn, yielding the average p-value of the comparison.

Table 2.

P-value data

Comparison protein segment	UNR and INT p value
N-terminus (2–6)	0.330
L1 (16–26)	0.946
L4 (85–92)	0.031
C-terminus (113–122)	< 0.001

Numbers in parentheses indicate the residues involved in the protein segment. The Wilcoxon signed rank test was used to calculate p values for comparison of S² in different regions of the plexin RBD between UNR and INT simulations.

Side-chain dynamics as indicated by quasiharmonic entropy analysis

The behavior of side chains in proteins is more complex than that of the main chain, making detailed comparisons difficult. To determine whether side-chain motions are on average affected by global motions, we estimated their entropy using the method of Andricioaei and Karplus (26), as implemented in wordom (27). The results are shown in Table 3.

Table 3.

Side-chain entropy

Simulations/entropy S (J/mol K)	All side-chain atoms (residues 5–112)	>40% surface-accessible	RBD/GTPase interface
UNR	7090 ± 84	6497 ± 57	1179 ± 42
INT motion only	6743 ± 268	6296 ± 112	1148 ± 81

Entropy average and spread over the four INT and UNR simulations for side-chain nonhydrogen atoms (Cβ and further out from the main chain) of the entire protein, the solvent-exposed residues only (>40% surface-accessible surface area), and residues at the Rho-GTPase binding site (residues 67–82 and 96–101).

Analysis of water dynamics around the protein

We calculated the orientational and translational diffusion of water molecules using established procedures (28). Briefly, as water motions are rapid, trajectories were extended at 55 ns for 100 ps, saving coordinates at the increased sampling interval of 20 fs. Waters were classified as first-shell (<4 Å distance from oxygen to the nearest protein heavy atom) or second-shell (between 4 and 7 Å) if they have residence times of >20 ps and >5 ps, respectively. (See Fig. 5 for diffusion coefficients and second-order orientational correlation functions.)

Figure 5.

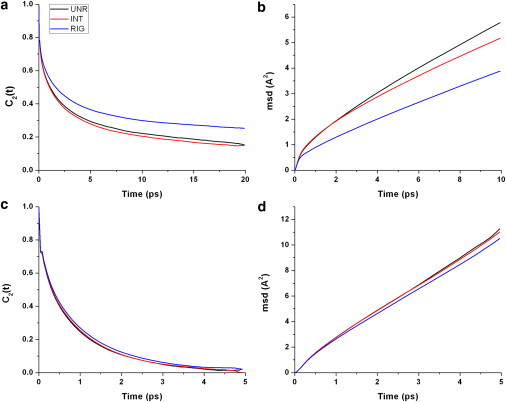
Second-order autocorrelation functions of rotational (left column) and translational diffusion (right column) of water molecules in the first (a and b) and second (c and d) shells, for the UNR (black line), INT (red line), and RIG (blue line) simulations.

Results/Discussion

Molecular dynamics simulations have become powerful tools in the study of proteins. The calculations make predictions that can be tested experimentally, but—as is the case here—in silico experiments can also examine conditions that are difficult, if not impossible, to create experimentally. To investigate a coupling between overall and internal motion, a number of extreme scenarios that can be produced in silico are likely to delimit the extent of a direct relationship between two parameters (for example, by setting one of them to zero). Specifically, we carried out restrained simulations in which either global motions or internal fluctuations are removed, examining the effect of this manipulation on the remaining fluctuations. In this study, the RBD of plexin-B1 was used as a model system, with ubiquitin as a reference for some of the calculations. Ubiquitin has short, relatively rigid turns rather than loops. By contrast, the 120-residue RBD protein, which also has a ubiquitin fold (Fig. 1), has several long flexible loops inserted into the structure (14). It has been shown experimentally that some of these loops and the termini undergo picosecond–nanosecond motions on a timescale that approaches that of the global rotational correlation time of the protein (23). It is anticipated that a coupling is strongest between fluctuations that occur on a similar timescale, and thus, the system is well suited to test this possible relationship between internal and global motions. Furthermore, many methods for the analysis of NMR relaxation data require a separability between internal and global motions (as both contribute to the measurements) (see, e.g., Shapiro and Meirovitch (3) and Wong et al. (6)). Generally, a timescale separation is seen in most proteins examined thus far. However, our system provides an interesting test case in this regard, as noted above. A proximity in timescale is also evident from the simulations, as calculated by a separability index, g2, using the iRED program of Prompers and Brüschweiler (20). For our four ubiquitin trajectories this parameter ranges from 5.66 to 6.47, with an average close to that previously reported for trajectories of the native protein (g2 = 6.3) (20). For the four unrestrained plexin trajectories, the g2 range is 2.79–3.17 and is close to the value of 2.51 obtained for a partially folded state of ubiquitin (20). Fig. 2, a and b, shows representative examples of both. Although the gap in the plot is not as obvious as in partially folded ubiquitin (g2 does not measure the gap per se), the lowest 5–10 eigenmodes do not show the usual downward trend, seen for other globular proteins. Thus, the separability between global and internal motion is in doubt for the fluctuations of the plexin RBD.

Figure 2.

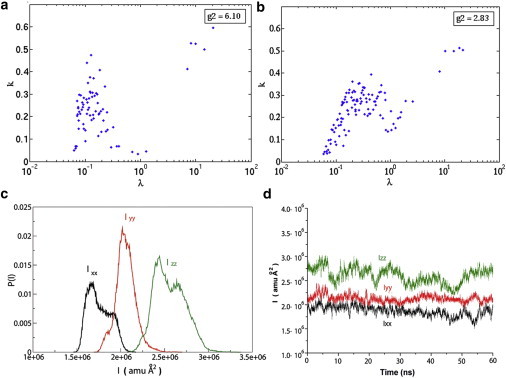
iRED analysis between global and internal motion. (a and b) The mode collectivities (k) are plotted versus eigenvalues (λ) from an iRED analysis with rank 2. The separability index (g2) factor, broadly corresponding to the gap between the largest five eigenvectors and the next-largest eigenvalue, is indicated for a representative simulation of ubiquitin (a) and the RBD (b). (c and d) Principal moments of the inertia tensors for the four RBD UNR simulations plotted as a histogram (c) and as a function of time for a representative simulation (d).

As in other studies (21–23,28–30), however, a good correspondence exists between the Lipari-Szabo order parameters for internal motion derived from NMR relaxation data (which assume separability of internal and global motions) and those derived from simulations (where global motions are removed before order-parameter derivation (Fig. S1 in the Supporting Material)). This suggests that neither the timescale proximity nor a direct coupling between global and internal motions is a significant issue. Given these two contrasting indicators, our in silico work sought to examine further a possible relationship between the two types of motion by studying several extreme scenarios. Specifically, in addition to lengthy UNR simulations, two types of restrained simulations were carried out for the plexin RBD. The details of all MD simulations are described in Methods. Briefly, in one type of restrained calculation (INT), global motions were removed every 20 steps (40 fs). For the RIG simulations, internal degrees of freedom were removed, also using CHARMM.

Change in protein shape, nature of global motion, and effect of internal motions

Rotational and translational motions of the protein are likely to be affected by changes in the shape of the protein. As an indication of this, the fluctuations in the moments of the protein's inertia tensor (principal components after matrix diagonalization) are calculated as a function of simulation time, and their distribution is examined for the unrestrained RBD simulations. The eigenvalues of the moments of the inertia tensor are similar among the simulations, ranging over the duration of the trajectory from 1.69 to 1.86 for Ixx, 2.00 to 2.11 for Iyy, and 2.47 to 2.63 for Izz (all units in amu Ų × 10⁶). A histogram of these values, collected over all four UNR simulations is plotted in Fig. 2 c. Apart from the slight variation in Ixx and Izz, these differences are not appreciably different, given the standard deviation within each calculation. It is interesting that Izz varies between two populations within the trajectory (Fig. 2 d). It is clear that the dimensions of the proteins fluctuate by approximately ±7% around each axis. Thus, the fluctuations in shape are very limited. Furthermore, the shape can be approximated as a spherical top in each case, and a small anisotropy of 1.3 (Dpara/Dperp), close to the value derived from NMR relaxation measurements (23), is maintained throughout the simulations.

Examining the time-averaged global motional properties, it was found, as expected, that the lengthy termini and loops provide a hydrodynamic drag and slow down the global fluctuations. This is evident in the comparison of the timescale of RBD motions with those of the more compact ubiquitin (Fig. 3). The correlation time for the global rotational motion can be estimated from an exponential fit of the second-order correlation function, C₂, that is relevant to NMR relaxation (31) and is reported in Table 1. Comparing the different RBD simulations, we find that the averaged rotational motion of the rigid RBD approximates that of the unrestrained molecule (Fig. 3 a). This is in agreement with many hydrodynamics calculations, using either ensembles of rigid structures or snapshots from dynamics trajectories (2), and it emphasizes the nature of diffusion rates as a population- and time-averaged property. To estimate the global translational motion, the MSD of the center of mass of the two proteins was calculated from the simulations (Fig. 3 b). The results, shown in Table 1, suggest that the translational diffusion for the RBD, a protein with flexible loops, is marginally, but not significantly, faster compared to the same protein with rigid loops. However, loop flexibility has no discernable effect on the rate of rotational motion. Similar to another recent simulation study (18), we can show that the global motions are of a diffusive nature by considering the ratio of orientational autocorrelation functions of different rank and by analysis of the angular momentum autocorrelation functions (M. Zerbetto, M. Buck, and A. Polimeno, unpublished).

Effect of global motion on internal dynamics

Order parameters, S², are among the most popular measures for characterizing local protein dynamics and comparing simulations with experiments (21,22,29,30). Main-chain N-H S² values and their associated correlation times, τ_e, were calculated for the RBD to investigate possible effects of removing the global tumbling during the simulation on these parameters (INT trajectories). Fig. 4, a and b, shows that derived parameters are very similar to those obtained from the UNR simulations. The linear correlation coefficients are 0.74 for τ_e and 0.93 for S². By contrast to the agreement for S², comparisons between experimental and simulation-derived correlation times are generally poor (see Buck et al. (21) for possible reasons), but the general trend as a function of sequence/structure is reproduced. The point we want to make, however, is that the correlation times for the internal motions are similar in the presence and absence of global motion. For S², a few differences are apparent between the simulations at the C-terminus (residues 113–122) and in loop 4 (residues 85–92), but the uncertainties in the derived parameters—here shown as the average of four trajectories—are large. Beyond the overall correspondence, we also examined individual residues and protein regions using statistical analyses. A significant difference in dynamics (|Z-score| > 1.96) between the 5–55 ns segments of the UNR and INT trajectories is seen in only a few residues: 108, 115, 116, 120, and 121. Although the results are also significant given that the order parameters for some of the residues are well converged, they may be misleading. First, residue 108 is in a very rigid part of the protein, and the Z-score appears to benefit from very low deviations between the four simulations in the two sets of trajectories. For the other residues, all belonging to the unstructured C-terminus, the situation is different. Here, the averages and wide deviations are due to one of the four trajectories from the UNR simulation, which shows less motion in these regions (see Fig. S1 in the Supporting Material). The UNR trajectory of simulation 3 is regarded as an outlier, as observed in Fig. S2. When the C-terminal region of simulation 3 is not considered in the statistical analysis, the difference between the internal dynamics at the C-terminus in simulations with and without global motion is reduced but remains significant as far as the Z-scores are concerned (in part because the standard deviations between the three remaining UNR simulations are reduced). Nevertheless, the results are in overall good agreement among the different kinds of simulations and indicate only small differences between the UNR and INT simulations at the RBD C-terminus. These likely arise due to variations in the sampling of the conformational space between some of the trajectories. Such lack of complete convergence is not unusual, even when lengthy trajectories are run.

Figure 4.

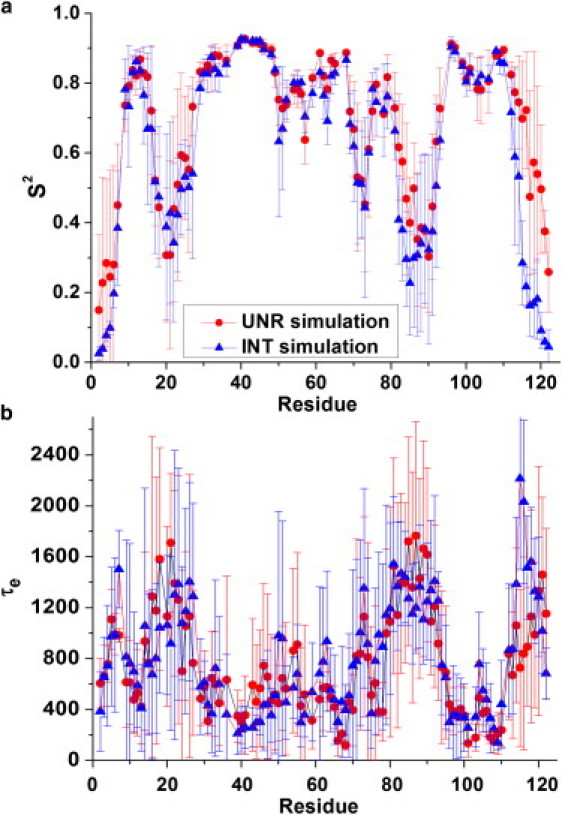
The main-chain N-H Lipari-Szabo order parameter (S²) and internal correlation time (τ_e) derived from the unrestrained (UNR) and internal-dynamics-only (INT) simulations and plotted as a function of sequence for the RBD. The averages of four simulations are shown, with error bars indicating the deviation between them.

Although the Z-score compares individual residues, the Wilcoxon signed rank test was used to examine whether the differences between order parameters derived from the UNR and INT simulations are significant for entire regions of the plexin RBD. The results (p values) are given in Table 2, where a p value of <0.05 suggests that the differences are statistically significant for the C-terminus and for loop 4. As noted above, UNR simulation 3 is considerably different from the three others for the C-terminus, but rerunning this test with this simulation excluded does not eliminate the significance. For the region of loop 4, there is no clear outlier but a wide spread of order parameters among the INT simulations (thus, the Z-score statistics are not significant). The loop 4 region is of particular interest since it is adjacent to the Rho-GTPase binding site in the plexin domain. However, out of four UNR and four INT simulations, only one simulation (INT3) is able to accurately reproduce experimentally derived S² for this loop. Given the strong tendency of the MD to oversample in this case, the difference between INT3 and the others cannot be attributed to the presence or absence in global motion. There appears to be a general offset in average order parameters, for the C-terminus INT simulations give order parameters 0.07 lower than UNR, whereas for loop 4, the situation is reversed (on average, INT simulations have S² values higher by 0.07 than those derived from UNR). This difference is small and not systematic in the way one might anticipate if there were a strong coupling between global and internal motion. We need to eliminate the variations in sampling and the deficiencies in the current potential function (e.g., 32,33) to assess with absolute confidence the differences among the trajectories for certain regions of the protein. However, this is at present beyond the resources and computation time available. Overall, the data strongly suggest, nevertheless, that the global motion has a negligible, if not merely small, effect on the order parameters.

The extent of correlation among the internal motions that affect individual residues can also be measured by calculating the normalized covariance matrix (defined in the Methods section in the Supporting Material) for the C_α atoms of all residues. Fig. S3 shows that these correlations differ slightly among a few protein regions, but these small differences are not statistically significant in the context of the extent of sampling seen in the trajectories. Overall, then, the patterns of correlations reflecting the extent and direction of the internal motions are highly similar with and without global motions.

Comparison of side-chain dynamics estimated by quasiharmonic entropy analysis

In addition to certain loops, side chains provide the main interface in protein-protein or protein-ligand interactions and are typically the key contributors to enzyme catalysis (1). Changes in the dynamics and the associated entropy of side chains therefore play a critical role in biological mechanisms. At the same time, side-chain dynamics can be highly complex, and given the confines of this study, we simply examine whether global motion has a direct effect on the dynamics of a group of side chains. The entropies, listed in Table 3, show that there is no significant difference between side-chain dynamics in the UNR and INT trajectories, even when subsets of side chains are considered that are surface-accessible or located at the GTPase binding region of the RBD.

Effect of global motions on first- and second-shell water motions

Global stochastic translational and rotational motions are thought to originate from temporary imbalances in the dynamics of solvent around the protein according to the theory of Brownian motion and Debye (10). Water dynamics around the protein is facilitating internal protein fluctuations. We therefore wanted to see whether the removal of global or internal protein motions has an effect on the dynamics of the solvent around the protein. Translational and orientational motions of waters in the first and second shell were compared between the simulations with and those without global motions and were also calculated for the simulation with no protein internal motion (Fig. 5). The results show that the lack of global motion has no significant effect on solvent dynamics. An explanation for this behavior is likely to be related to the timescales of the motions involved. The dynamics of TIP3P waters are fast in the simulation: except for bound waters, waters move on average a linear distance of 0.3 Å/ps and 1 Å/ps in the first and second shells, respectively, and orientational correlation times are on the order of 5–0.5 ps. This compares with protein internal fluctuations of the main chain on the timescale of 40–2000 ps and with the protein global correlation time in TIP3P solvent of ∼3500 ps. Although some of the local and global fluctuations can be much faster (data not shown), these events are rare, and on average, the solvent moves several orders of magnitude more quickly than the protein, consistent with the view that local and global protein motions are not in response to the motions of a few water molecules. The motions of the waters, in turn, are not directly affected by global protein motions. However, internal motions have a significant effect on the first-shell water dynamics (Fig. 5, a and b). In the RIG simulations, water dynamics are slowed, especially for the protein-bound waters in the first shell, as the interactions with the protein can persist longer in the absence of protein internal motion. Both types of protein motions, global and internal, are dampened by the solvent, which on average experiences an interaction with the protein surface. For well folded proteins, such behavior (also known as slaving) arises from the polar/nonpolar and geometric properties of the protein surface, but also from the faster protein motions that frequently break the contacts to the solvent.

Conclusions/Implications

The molecular dynamics simulations (totaling 660 ns) run here for a small but flexible protein demonstrate that a direct coupling between internal and global motions is essentially absent. This does not mean that there is no relationship between the two, however, as changes in solvent motion are known to affect both global and internal motions (4,6,34,35). It should be noted, for example, that the solvent-slaving model of protein dynamics (36,37) has two components: First, global and larger-scale diffusive motions of the protein are connected to the bulk solvent and are viscosity-dependent, whereas internal dynamics the second component are coupled to motions in the hydration shell. Consistent with our simulation results, experimental studies have shown that the two types of protein motions can be largely independent of one another. Thus, a recent solid-state NMR study suggests that internal motions in a crystalline protein that is not able to move globally are comparable to those observed in solution (38). A similar conclusion was reached by fluorescence measurements of a gel-embedded protein (39). Related to this behavior, a comparison between our simulations with and without global motions shows that the dynamics of water molecules in the first and second solvation shells of the protein remain essentially unchanged. Recent work has provided evidence that internal and global motions are more likely to be coupled to one another when proteins undergo substantial conformational changes or domain motions that result in changes in protein shape and in the character of the exposed surface area (see, e.g., Lavalette et al. (4).). It is expected, for example, that some of the internal fluctuations will correlate with the direction of the domain motions via protein hinges. This hierarchical picture of protein dynamics has been supported by recent work of Kern and co-workers on the ADK system (40), also pointing to the fact that the timescale of motions can be considerably separated in such a coupling involving a conformational change. Further study is needed for such systems and for partially folded proteins to determine whether individually correlated events are sufficient in number to indicate a direct coupling that involves transitions, or whether the local and global dynamics are separate and can simply be represented by a population average of the different states involved (see, e.g., Wong et al. (6)).

The potential advantages of a direct coupling between global and internal motions for protein function are apparent given that proteins can be localized to environments in the cell that allow little global motion. Moreover, many enzymes and cell-signaling proteins also transition between different states of oligomerization. It is intriguing to consider, then, why nature has not utilized global motions in the same way that internal motions play a role in protein function. One answer may lie in the stochastic nature of the global motions themselves. Although individual reorientational events can be coupled to specific loop motions, the probability that such events occur at considerable frequency compared to other motions is likely to be low given the random and often nearly isotropic nature of the global motion. Coupled events would thus be swamped out by the many other global and internal fluctuations. In some systems, however, it is clear that even stochastic motions can be converted into directional dynamics (e.g., in the case of the ATPase pump (41)). This then raises the second possible answer: perhaps a direct coupling to stochastic global motions has been deliberately avoided by structural features of the polypeptide chain and of the loops (35,42). Investigations in this direction are in progress in our laboratory.