Transfer of Arginine into Lipid Bilayers Is Nonadditive

Abstract

Computer simulations suggest that the translocation of arginine through the hydrocarbon core of a lipid membrane proceeds by the formation of a water-filled defect that keeps the arginine molecule hydrated even at the center of the bilayer. We show here that adding additional arginine molecules into one of these water defects causes only a small change in free energy. The barrier for transferring multiple arginines through the membrane is approximately the same as for a single arginine and may even be lower depending on the exact geometry of the system. We discuss these results in the context of arginine-rich peptides such as antimicrobial and cell-penetrating peptides.

Introduction

Arginine residues are important in a number of biological processes involving cell membranes. They are the main voltage-sensing residues in voltage-gated ion channels (1,2). They are common in antimicrobial peptides, which often contain a large number of cationic residues combined with hydrophobic residues across a wide variety of structures (3). Arginine residues are also a major component of other membrane-active compounds with less certain mechanisms of actions, including cell-penetrating peptides from a variety of sources (4–7).

The transport of arginine-rich peptides—such as the cell penetrating peptides human immunodeficiency virus-trans-acting activator of transcription (Tat) and nona-arginine—has received considerable attention (5,6). These peptides contain many basic residues, yet they are able to rapidly cross the membrane—in apparent contradiction with the conventional view of ion-membrane interactions. The exact mechanism of transport is not clear and may involve the endocytotic pathway (4). Two recent studies, however, observed rapid transport of nona-arginine across a lipid bilayer in the absence of endocytosis (6,7).

At first sight, it is puzzling that arginines play an important role in membrane systems. If the interactions between arginine and membranes are governed by a Born-type free energy—partitioning a charge between aqueous (dielectric constant, ɛ ≈ 80) and hydrocarbon (ɛ ≈ 2) environments—then the cost of placing an arginine in the membrane should be as high as ∼170 kJ/mol (8). Such a high free energy would prevent significant interactions with the membrane core. The experimentally derived translocon scale (9), however, suggests that the free energy cost to transfer an arginine to the center of the membrane is modest—although considerable controversy surrounds the interpretation of these experiments (10,11).

Membranes are flexible, dynamic structures and should not be thought of as rigid slabs of hydrocarbon. Several computational studies show that lipid-ion interactions cannot be described by a simple continuum model (8,12–22). Simulations from several groups, using different models and techniques, show that the free energy of transfer for moving an arginine from water to the membrane center is ∼60–80 kJ/mol (8,13,15,19). In most calculations, the pKa of arginine is high enough that the arginine remains charged at the center of the membrane (13,15,20–23). The cost of transferring an arginine side chain into the bilayer core is similar to the cost of forming a transmembrane pore (24) and the resulting water defects resemble the defects caused by a variety of other membrane perturbing agents (25). The transfer of an arginine side chain analog into phosphatidylcholine bilayers reveals a complex perturbation of the membrane dipole potential (16).

In many membrane systems arginines occur in spatially localized groups. There are usually four arginines clustered together in the voltage sensor domains of voltage-gated channels (1,2). Antimicrobial peptides are rich in basic residues and often contain clusters of multiple arginines (3). Cell penetrating peptides, such as TAT peptide from HIV, usually contain around eight arginines within a short sequence (4,26). For TAT and nona-arginine, it has been demonstrated that multiple arginines are required for these peptides to efficiently cross the membrane (27,28). Hexapeptides enter cells less efficiently when arginines are replaced by lysines (27). Given the standard view that membrane partitioning of arginine is prohibitively expensive, it is curious why these systems would contain multiple arginines closely clustered together.

The prevalence of clusters of arginine residues raises a simple question: What is the free energy to place multiple arginine residues in the core of membrane? We hypothesize that the first arginine pays a large free energy cost to enter the membrane interior and form a water defect, whereas the cost of adding a second or third arginine inside the membrane will be significantly reduced—provided they can make use of the same water defect. In the remainder of this work, we show the results of computer simulations that confirm this hypothesis. We find that the transfer of arginine into lipid bilayers is highly nonadditive. The free energy for adding additional arginines is significantly less than the first and—depending on the geometry of the system—may be favorable. These results have implications for understanding the behavior of arginine residues in many important membrane systems.

Methods

Simulation protocol

All molecular dynamics computer simulations were performed using the GROMACS 3.3.1 software package (29). The arginine side chains were modeled using the OPLS-AA force field (30).The backbone was removed by replacing the α-carbon with a hydrogen atom and adjusting the charge on the β-carbon. Simulations were carried out at constant temperature (298 K) using the weak coupling algorithm (31). The weak coupling algorithm (31) was used to maintain a pressure of 1 bar. A semi-isotropic scheme was used where the pressure in the plane of the bilayer was coupled separately (32) from the pressure normal to the bilayer. The SETTLE algorithm (33) was used to constrain water bond lengths and angles, whereas the LINCS algorithm (34) was used to constrain all other bond lengths. A 2 fs time step was used. The smooth particle mesh Ewald method (35) was used for electrostatic interactions with a real space cutoff of 1.0 nm, 0.12 nm grid spacing, and fourth-order spline interpolation. Lennard-Jones interactions were evaluated with a 1.0 nm cutoff.

The lipid system was composed of 64 dioleoylphosphatidylcholine (DOPC) lipids modeled with the Berger et al. (36) force field and 2800 Simple Point Charge water molecules (37). The simulation box contained seven sodium and seven chloride ions, for a salt concentration of ∼140 mM. One additional chloride ion was added for every arginine to yield a system with zero total charge. The negatively charged chloride ions do not bind to the arginine side chains in any of the simulations. We measured the average minimum distance between an arginine and any chloride ion and found that it is always >0.8 nm. When the arginine is at the center of the bilayer the average distance increases to 2.5 nm, which indicates that chloride ions are not binding to arginine at the membrane core.

The water-cyclohexane biphasic system consisted of 324 cyclohexane molecules and 749 water molecules. The molecules were placed into a rectangular box of dimensions 3.0 × 3.0 × ∼9.2 nm, which yielded an ∼7 nm thick slab of cyclohexane surrounded by bulk water. The x and y box dimensions were held fixed and the pressure was maintained at 1 bar by changing the length of the box in the z direction using the weak-coupling algorithm (31).

Free energy calculations

For the single arginine and di-arg potentials of mean force (PMF), we grew the arginines into the system by starting with all of the interactions between arginine and the rest of the system turned off and the arginine restrained to lie at the desired depth. We then slowly ramped the interactions up to normal strength over the course of a 1 ns simulation using the thermodynamic integration facilities in GROMACS. To generate the two-arginine systems, we took the final structure from the umbrella window with a single arginine at the center of the bilayer as the starting structure. We then grew the second arginine into the desired position using the same protocol, while restraining the first arginine at the center of the membrane. We produced the three-arginine system in a similar fashion. We did not sequentially pull the arginine into the bilayer. In cases where water or lipid headgroups are located at the center of the membrane, it is because they spontaneously moved there and not because we pulled them in along with the arginine.

The potentials of mean force in the DOPC bilayer were calculated using a combination of umbrella sampling (38) and the weighted histogram analysis method (39). The umbrella sampling protocol used a harmonic restraint with a force constant of 3000 kJ mol⁻¹ nm⁻². A spacing of 0.1 nm was used in the direction normal to the bilayer, resulting in a total of 38 simulations to sample the entire reaction coordinate. Each umbrella sampling simulation was 60 ns long. The effects of the harmonic biasing potential were removed using the weighted histogram analysis method after discarding the first 10 ns as equilibration. The standard error was calculated from the difference of the PMFs for the two leaflets of the bilayer. We performed umbrella sampling on the second arginine with the same protocol, except that the first arginine was restrained to the center of the bilayer with a force constant of 3000 kJ mol⁻¹ nm⁻². For the three arginine system, we ran umbrella sampling on the third arginine, while restraining the first arginine at the center and the second arginine at 0.35 nm. At no time were lateral restraints applied to any arginines.

The PMF in the cyclohexane system was calculated by slowly pulling the arginine parallel to the z axis. A spring was attached to the center of mass of the arginine molecule with a force constant of 3000 kJ mol⁻¹ nm⁻². The other end of the spring was pulled in the z direction at a rate of 6.2 × 10⁻⁵ nm/ps. No force was applied to the molecule in the x and y directions. The PMF was obtained by integrating the force parallel to the z axis as the spring is pulled through the system. A total of four runs were performed and the average of all four runs, as well as the pulling into and out of the cyclohexane was used to calculate the PMF. The standard error was calculated from the variation across the four simulations and the two halves of the cyclohexane. We also averaged the different trajectories using the Jarzynski equality (40), but the results did not differ significantly from simple averaging—indicating that our results are near equilibrium already.

Di-arg molecule

We constructed an artificial di-arg molecule by tethering two arginine molecules together with two harmonic springs. We attached the CB atoms together with an equilibrium distance of 0.60 nm; we attached the CZ atoms together with an equilibrium distance of 0.86 nm. We used a force constant of 3000 kJ mol⁻¹ nm⁻² for both springs. This arrangement approximates the geometry of two arginines in a 1–4 arrangement on an α-helix.

Analyses

The number of hydrogen bonds to the arginine molecule was calculated using the g_hbond tool in the GROMACS software suite (29). A hydrogen bond was defined as when the donor-acceptor distance was <0.35 nm and the acceptor-donor-hydrogen angle was <60 degrees.

The hydration number was calculated using the program g_rdf from the GROMACS software suite. We calculated the radial distribution function between guanidine (defined as the center of mass of the NE, CZ, NH1, and NH2 atoms) and the oxygen atoms of water and DOPC. The radial distribution function was then integrated (over volume) to the end of the first hydration shell (0.46 nm) to obtain the average number of water molecules in the first shell.

The density calculations were performed using the g_density program from the GROMACS software suite with 100 slices along the direction normal to the bilayer.

Results and Discussion

Single arginine

The free energy for transferring a single arginine from water into the center of the bilayer is ∼60 kJ/mol (Fig. 1 A). The arginine at the center of the bilayer provokes a large water defect that hydrates the arginine and lowers the free energy change compared to transfer into bulk hydrocarbon (8,13,15).

Figure 1.

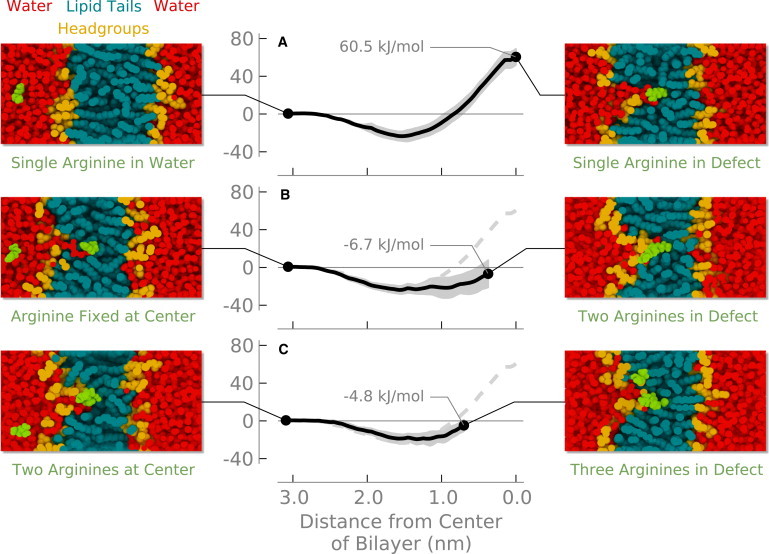
Free energy to transfer an arginine from water into a DOPC lipid bilayer: (top) a single arginine; (middle) a second arginine with the first arginine fixed at the center of the bilayer; (bottom) a third arginine with the first arginine fixed at the center of the bilayer and the second arginine at 0.35 nm from the center. Shading indicates the standard error.

The water defect maintains hydration of the arginine even at the center of the bilayer. Although the number of first-shell oxygen atoms around the arginine decreases slightly (Fig. 2), the arginine maintains a nearly constant number of hydrogen bonds—even at the center of the bilayer (Fig. 3). This result is consistent with previous simulations where one lipid headgroup and four or five water molecules coordinate with the arginine. The interaction energies between arginine and both water and the lipid headgroups are strong and favorable, but when entropic and indirect effects are included there is significant strain energy—it costs energy to form the water defect (8). By incorporating a simple model of bilayer elastic deformations into a continuum electrostatics model, one can obtain good agreement with experimental and simulation results (14). Treating the bilayer as a rigid, low dielectric slab, however, produces transfer free energies that are too high.

Figure 2.

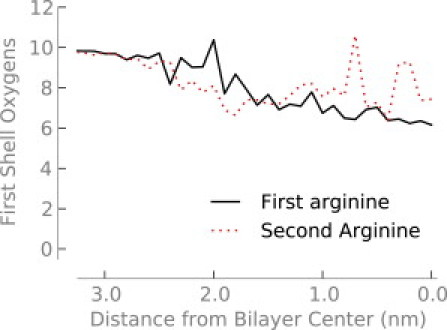
Number of oxygen atoms in the first hydration shell (out to 0.46 nm) of the first and second arginine molecules as a function of depth in the bilayer.

Figure 3.

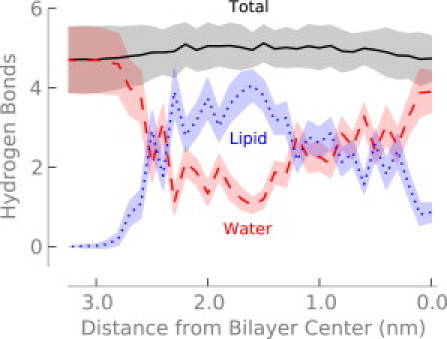
Number of hydrogen bonds to arginine as a function of depth in the bilayer. Shading indicates the standard error.

Cyclohexane

Previous simulations of an arginine containing helix moving through a membrane do not have a prominent interfacial minimum (8). One explanation for the discrepancy is simply because one system is a helix and the other is an isolated side chain. Another possibility is that the interfacial minimum in our results is due to differences in lipid force fields, for example in the charges on the phosphate or carbonyl groups. To test this, we calculated the PMF in cyclohexane (Fig. 4), where the charges are all near zero. We also performed a similar simulation using the CHARMM27 force field (41) and obtained similar results (Fig. S1 in the Supporting Material). The profile still displays a minimum at the interface in cyclohexane, although it is not as deep as in the bilayer. The transfer of methylguanidinium through 1,2-dipalmitoyl-sn-glycero-3-phosphocholine bilayers (42) shows a similar interfacial minimum. A variety of other molecules at water-air (43–45) and water-hydrocarbon (46) interfaces also display interfacial minima. These interfacial minima occur due to a balance of opposing contributions from electrostatic and hydrophobic effects, which are trending in opposite directions as the molecule moves across the water-hydrocarbon interface. We believe that the interfacial minimum arises in the bilayer because of this effect, in addition to favorable interactions with the polar lipid headgroups.

Figure 4.

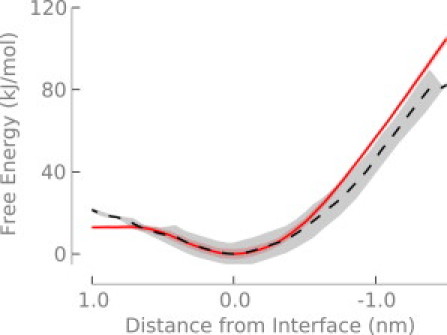
Free energy of transferring arginine from the interfacial minimum into cyclohexane (solid; red) or a DOPC bilayer (dashed; black). The cyclohexane-water system is described in the text. Both free energy profiles are aligned at the interfacial minimum. Shading indicates the standard error.

When moving both polar and charged side chain analogs across the bilayer, a water defect forms near the interface (13,15). For polar residues, the defect dissipates before reaching the center of the membrane. Charged residues, however, cause a defect even at the center of the membrane. We hypothesize that two energetic terms govern the free energy of transfer 1), the cost of dehydrating a polar or charged molecule and 2), the cost of creating a water defect to maintain hydration. The side chain will remain hydrated by a water defect until the cost of forming the defect becomes greater than the dehydration energy. At this point the defect will break and the free energy will plateau.

To test this hypothesis, we constructed a thick slab of cyclohexane—as a crude mimic of the hydrocarbon core of a bilayer—embedded in water. If the formation of the water defect balances the cost of dehydration, the defect will then break when the cost of lengthening it is greater than the dehydration energy. Fig. 5 shows that this hypothesis is correct. When the free energy reaches ∼140 kJ/mol, the defect breaks, leaving a hydrated arginine ion in bulk hydrocarbon. This result suggests that the thickness of the lipid bilayer is an important determinant of the free energy barrier for translocation of ions. When the membrane is thick, the barrier should be roughly constant and comparable to the Born energy. Partial hydration will lower the energy somewhat and the dipole potential will be increasingly unfavorable as the hydrated complex moves away from the interface, although both of these effects are small compared to the Born energy. As the membrane becomes sufficiently thin, however, the barrier should decrease substantially. We have also observed this pattern for lipid flip-flop, which involves a similar defect mediated mechanism (47) and similar trends have been observed for the transfer of amino acid analogs across different membranes (48).

Figure 5.

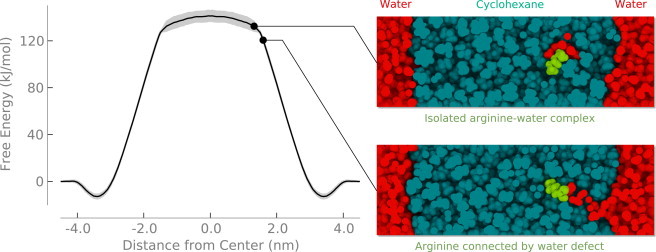
Free energy to transfer an arginine from water into cyclohexane. Shading indicates standard error.

Multiple arginines

When we place additional arginine molecules in the system, they share the water defect created by the first arginine (Fig. 1, B and C). Placing a single arginine at the center of the bilayer shifts both the phosphate and water densities toward the center of the bilayer—a water defect is formed (Fig. 6, black and red lines). The addition of a second or third arginine causes little change in the distribution of water or headgroups (Fig. 6, green and blue lines).

Figure 6.

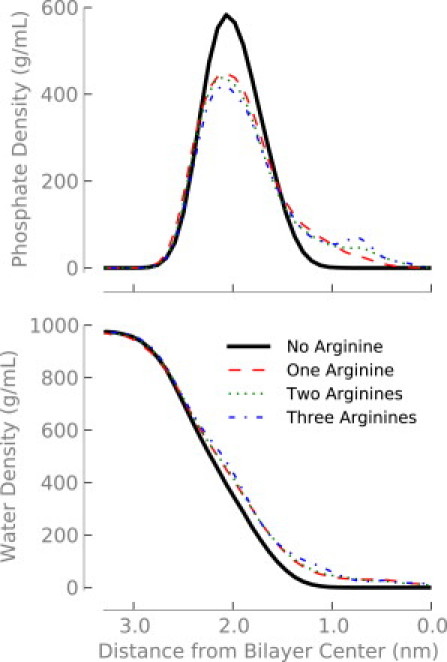
Density of phosphorous (top) or water (bottom) depending on how many arginine molecules are located near the center of the bilayer.

Because the defect is relatively unperturbed after the addition of more arginines, adding a second or third arginine into the bilayer should cause only a small free energy change. The stabilizing interactions with water and lipid headgroups are still present, although the cost of forming the water defect has already been paid by the first arginine. Previous studies found that a single arginine at the center of the membrane left a wake in the electrostatic potential, leaving the potential in the remainder of the water defect the same as bulk (16). This result implies that no energy would be required to transfer additional charges into the defect. Indeed, we find that the free energy for transferring a second (Fig. 1 B) and third (Fig. 1 C) arginine is near zero when there is already an arginine at the center of the bilayer.

Tethered di-arg molecule

To verify our scheme of sequentially pulling first one arginine, then a second (or third) into the bilayer, we calculated the free energy for transferring a synthetic di-arg molecule (see Methods) into the center of the bilayer. Moving this di-arg molecule into the center of the bilayer (Fig. 7) has a free energy of ∼80 kJ/mol—about 30% more than for a single arginine.

Figure 7.

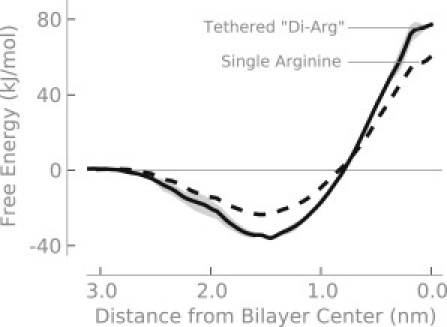
Free energy to transfer a di-arginine from water into the center of a DOPC bilayer. The geometry of the di-arginine construct is described in the text.

The geometry of the di-arg molecule at the center of the bilayer differs from when we pulled the two molecules serially. We used the center of mass of the di-arg molecule as a reference. When the di-arg molecule is restrained to the center of the bilayer, both guanidium groups are located at the center of the bilayer. For the serial experiments, we pulled one arginine to the center of the bilayer, whereas the second arginine was pulled to 0.35 nm from the center. If we continue the experiment shown in Fig. 1 B until both arginines are at the center of the bilayer, we calculate a free energy of ∼20 kJ/mol (plus ∼60 kJ/mol for the first arginine), which agrees well with the di-arg results (∼80 kJ/mol).

Free energy for transferring arginine into membranes

We calculate that the cost of transferring arginine into the center of a membrane is ∼60 kJ/mol. This energy is significantly lower than would be predicted based on continuum electrostatics calculations or bulk hydrocarbon solvation (8). Arguments against the passive diffusion of arginine and cell penetrating peptides across lipid bilayers based on the Born energy barrier (49) are not relevant because of the defect mediated mechanism. This energy, however, is significantly higher than measured in the experiment (9), although the experimental results are difficult to interpret due to the unknown environment of the side chain and possible nonequilibrium nature of the measurement (10).

Computer simulations show that the addition of helical proteins into the membrane reduces the free energy for transferring polar amino acids into the membrane (50). The mechanism remains similar—it still involves a water defect, but the presence of the slightly polar protein surface makes the water defects easier to form. We observed similar effects for lipid flip-flop in the presence of membrane proteins (32). A simulation using a coarse-grained model shows that including the structure of the translocon into the calculation gives better agreement with the experiment and concludes that the apparent free energy measured in the experiment is not as simple as the free energy difference between the side chain in water and the side chain in the membrane (51). All together, these results suggest that the inclusion of protein components in the membrane will lower the free energy barrier compared to a pure lipid bilayer.

Biological membranes are complex mixtures containing many different components—including negatively charged lipids. Fluorescence experiments demonstrated that including 40 mol% negatively charged lipid in giant unilamellar vesicles caused rapid translocation of TAT and transient pore formation (7). Polyarginine and polylysine were shown to bind tightly to the interface of bilayers containing phosphatidic acid and increase their charge (52). Calculations show that in mixed phosphatidylcholine and phosphatidylglycerol bilayers, the interfacial binding is moderately more favorable and the barrier for translocation is reduced by the presence of negatively charged phosphatidylglycerol lipids (53). Experimental results show that the correct folding and function of voltage-gated potassium channels depends on the presence of anionic lipids (54,55). These results suggest that negatively charged lipids may decrease the barrier for arginine translocation compared to neutral lipids, although other computer simulations have shown that the inclusion of negatively charged lipids did not significantly change the PMF for arginine insertion (48).

We have previously suggested that the transfer of nonpolar amino acids to the center of the bilayer—at the same time as the arginine—would further lower the free energy (13). The experimental design of Hessa et al. is based on this idea (9)— nonpolar amino acids can stabilize the presence of polar amino acids in the membrane. Their results suggest that considerably less energy is required to place an arginine at the center of a lipid bilayer than might be expected.

Taken together, we believe that the current experimental and theoretical evidence suggests that our results are an overestimate of the free energy to transfer an arginine to the center of a biological—rather than model—membrane.

Our calculations show that there is essentially no additional energetic cost to transfer additional arginines into a preexisting water defect. This result is consistent with the presence of water defects that hydrate the charges—only the first residue has to pay the free energy penalty to form the water defect. The additional residues can simply use the existing defect for free.

Biological implications of nonadditivity

The nonadditivity of arginine transfer has important implications for the interactions of arginine-rich peptides—such as HIV-Tat, nona-arginine, and antimicrobial peptides—with membranes. Our results show that the free energy will not continue to go up as charges are added to the membrane. In fact, our calculations suggest the opposite: when there are three arginines in the membrane at depths of 0.00, 0.35, and 0.70 nm from the center of the bilayer, the free energy is 11.5 kJ/mol lower than when there is a single arginine at the center of the bilayer. The additional charges reduce, rather than increase, the cost of maintaining the defect. On the basis of our previous calculations, this free energy could be overcome by the simultaneous transfer of three or four leucine residues (13,15). We do not suggest that the peptide LLLRRR would necessarily actively cross the membrane—more likely it would bind to the interface. Instead, we hypothesize that a peptide with similar composition could cross the membrane with little barrier if it was part of a larger structure that prevented binding to the membrane surface.

Computer simulations show that TAT can spontaneously translocate a lipid bilayer on the nanosecond time scale (26). A subsequent work disputed this result by determining the free energy barrier for penetration translocation, estimated at 75 kJ/mol (56). However, it is challenging to completely sample this system to accurately calculate the free energy.

There are now many simulations available for models of voltage-gated potassium channels (11,57–61). In all cases, the simulations show the formation of a water defect, although the defect is partially shielded by protein in some cases. It seems clear that the voltage sensor of these channels contains a water defect or pore, although some debate remains about how much the defect is lipid-exposed versus shielded by protein.

Biological membranes are composed of many different types of lipid, carbohydrate, and protein—along with an asymmetric distribution of lipids between membrane leaflets (62). Our simulations show that the free energy for transferring arginine to the bilayer core is largely due to the formation of a water defect. This suggests that the free energy would change depending on the composition and physical properties of the membrane. We have shown previously that the free energy for lipid flip-flop and pore formation depends on the length of the acyl chains and the number of double bonds (47). Increasing the concentration of cholesterol also increases the free energy for 1,2-dipalmitoyl-sn-glycero-3- phosphocholine flip-flop and prevents pore formation (63). The addition of proteins to the membrane caused the free energy barrier to decrease (32,50). Therefore, although the cost of ∼60 kJ/mol for arginine to cross a DOPC bilayer is too high to support the passive diffusion of cell penetrating or antimicrobial peptides, in different bilayers the energy barrier could differ substantially depending on the exact composition of the membrane. Our calculations show that partitioning multiple arginines into a DOPC bilayer is nonadditive, and we expect this phenomenon to extend to cell membranes in general.

Conclusion

Our simulations show that transfer of multiple arginine residues into the bilayer core is nonadditive. The cost of forming a water defect for the first arginine is the dominant energetic factor. Once this defect is formed, the cost of transferring additional arginines is minimal and can even be negative. This suggests a mechanism for pore formation and translocation of arginine-rich peptides. It further complicates the discussion of the energetics of transmembrane proteins that contain charged residues that may be exposed to the hydrocarbon core of the bilayer. Such residues are likely to create significant defects rather than face hydrocarbon.