How Do Thermophilic Proteins and Proteomes Withstand High Temperature?

Abstract

We attempt to understand the origin of enhanced stability in thermophilic proteins by analyzing thermodynamic data for 116 proteins, the largest data set achieved to date. We compute changes in entropy and enthalpy at the convergence temperature where different driving forces are maximally decoupled, in contrast to the majority of previous studies that were performed at the melting temperature. We find, on average, that the gain in enthalpy upon folding is lower in thermophiles than in mesophiles, whereas the loss in entropy upon folding is higher in mesophiles than in thermophiles. This implies that entropic stabilization may be responsible for the high melting temperature, and hints at residual structure or compactness of the denatured state in thermophiles. We find a similar trend by analyzing a homologous set of proteins classified based only on the optimum growth temperature of the organisms from which they were extracted. We find that the folding free energy at the temperature of maximal stability is significantly more favorable in thermophiles than in mesophiles, whereas the maximal stability temperature itself is similar between these two classes. Furthermore, we extend the thermodynamic analysis to model the entire proteome. The results explain the high optimal growth temperature in thermophilic organisms and are in excellent quantitative agreement with full thermal growth rate data obtained in a dozen thermophilic and mesophilic organisms.

Introduction

Thermophilic proteins denature at a much higher temperature than regular mesophilic proteins. Understanding the origin of this enhanced thermostability in such proteins has become a fundamental goal in the field of protein biochemistry. Studying different mechanisms by which proteins increase or decrease stability can teach us the fundamentals of protein thermodynamics and help us design new enzymes with desired stability. The vast majority of biophysical studies have been directed toward understanding the origin of enhanced stability in proteins under conditions of high temperature (1–6), and only a few studies have investigated acidophilic and halophilic (7) enzymes as well. The unusual tolerance to high temperature raises several interesting questions: What is responsible for the stability of thermophilic proteins? Is it the significant alteration of the average enthalpy, entropy, or specific heat, or a combination of all these? Is there any systematic principle that proteins may utilize to withstand such high temperatures? Does a high melting temperature, T_m, also imply a high maximal stability free energy?

Various researchers have tried to address these questions by directly comparing different homologs of proteins extracted from mesophilic and thermophilic organisms (1,2,8–14). However, it is not clear which of these mechanisms proteins adopt, or whether proteins adopt different mechanisms simultaneously to a different extent. It has been widely demonstrated that reduced $\Delta C_p$ leads to increased stability (11,13–15) by broadening the melting curve while keeping the location and magnitude of the maximum of the stability curve unchanged. A direct comparison between several thiermophilic and mesophilic homologs supports this observation (11). However, a significant number of studies suggested otherwise by demonstrating little dependence between T_m and the $\Delta C_p$ of unfolding (9,16). Furthermore, mounting evidence indicates a possible connection between the denatured state and enhanced stability (13,15,17–20). Several careful analyses have shown that denatured states are more compact in thermophiles than in mesophiles and may retain residual structure (13,18), indicating the role of entropy in determining stability. Anther possibility is that specific amino acid substitutions lead to reduced entropy in the unfolded state due to different degrees of flexibility associated with them (17,21). The effect of entropy on increased stability may also arise from different degrees of compactness in the native structure as a result of different mutations (22). The role of electrostatics has also been attributed to enhanced stability (23–30). Genome- and proteome-wide analyses have been carried out to elucidate the origin of stability (5,25,31–36).

These different and often contradictory studies make it very hard to identify the principle behind increased stability. Conclusions are very specific to proteins, and to date no systematic study (8) has employed a large data set of different protein families to explain increased stability. Sometimes the conclusions conflict depending on the list of proteins studied. We believe this is mainly due to the lack of 1), a systematic analysis of a large data set (as previous studies were mostly restricted to smaller sets of proteins); and 2), proper decoupling of different driving forces. The latter point is related to the fact that enthalpy and entropy changes are significantly temperature-dependent. Due to nonzero $\Delta C_p$ arising from the hydrophobic effect, both enthalpic and entropic changes are temperature-dependent in the following manner (37,38):

$$\Delta S\left(T\right)=\Delta S\left(T_s\right)+\Delta C_p\text{log}\left(\frac{T}{T_s}\right);\Delta H\left(T\right)=\Delta H\left(T_h\right)+\Delta C_p\left(T-T_h\right).$$ (1)

where T_h and T_s are two reference temperatures. This also raises the natural question: At what temperature should one compute these quantities for comparison? From Eq. 1 it is evident that both enthalpy and entropy changes have different hydrophobic contributions (due to nonzero $\Delta C_p$) at different temperatures. For example, the total change in entropy has a contribution due to the configurational entropy of the protein chain as well as the mixing entropy of amino acids. This makes it difficult to isolate and study the role of different driving forces separately.

To significantly decouple the hydrophobic effect from conformational entropy and purely enthalpic contribution (polar and van der Waals forces), one should compute $\Delta H\left(T\right)$ and $\Delta S\left(T\right)$ at temperatures where these effects are minimal. Extensive studies (37,39–42) showed the existence of a temperature at which enthalpy and entropy (per residue) for many different proteins converge. This temperature, known as the convergence temperature, is now believed to be the temperature at which hydrophobic effects are zero and the contribution to enthalpy is purely due to van der Waals or polar (hydrogen bond) interactions. Similarly, at the convergence temperature, entropy is primarily conformational in origin, because the hydrophobic contribution is minimal. Hydrocarbon-transfer experiments by Baldwin demonstrated the existence of a similar convergence temperature at which the transfer entropy is zero and very close to the protein convergence temperature (41). This finding strongly suggests that at this temperature, the protein chain conformational entropy is significantly decoupled from the solvent entropy. Extensive work by Robertson and Murphy (37) provided the most recent and reliable estimate of these convergence temperatures based on the largest set of proteins: $T_s=385K$ for entropy, and $T_h=373.5$ K for enthalpy. Along with the original work by Robertson and Murphy (37), in a previous study (38) we showed that $\Delta H\left(N\right)$, $\Delta S\left(N\right)$ can be very well approximated as a linear function of chain length N when computed at 373.5 K and 385 K, respectively. In fact, the correlation coefficient between the changes in enthalpy and entropy versus chain length is highest at these two temperatures (37). Based on all of these findings, and several other studies (43,44), it is clear that at these temperatures, sequence effects are minimal and the major contribution to enthalpy and entropy is due to the polymeric nature of the protein alone (37,45). Thus, the slope and intercept of the linear dependence of these properties on protein chain length give us an average estimate of changes in enthalpy, conformational entropy, and specific heat of a protein upon folding purely based on the chain length N. This defines an ideal thermal protein and can serve as a first estimate for the folding free energy when we do not have any information about the protein other than its chain length (38).

In this work, we compute and compare changes in entropy and enthalpy of thermophilic and mesophilic proteins at $T_s=385K$ and $T_h=373.5K$, respectively, for two reasons: 1), at these convergence temperatures, the hydrophobic effect can be separated from enthalpy and conformation entropy, and thus different driving forces are maximally decoupled; and 2), it provides a common reference temperature to compare different proteins. This has not been explored before and is in striking contrast to common practice of computing thermodynamic properties at the T_m for comparison. However, it is not guaranteed that at T_m the hydrophobic effect is separate from the conformational entropy.

Below, we outline how we carry out the analysis to derive ideal-thermal-protein parameter values from the largest protein set achieved to date, almost doubling the previous largest set (37). We then proceed to further divide this set into two classes: one based on T_m-values, and a smaller set of homologous proteins based on the optimal growth temperature of the organism from which proteins were selected. From our classification scheme, we find new ideal-thermal-protein parameter values for thermophilic (high T_m) and mesophilic (low T_m) proteins. We carry out a statistical analysis on the distribution of entropy, enthalpy, and specific heat changes (per amino acid) between these two classes of proteins. The results reveal a new, to our knowledge, thermodynamic principle that proteins on average may adopt to withstand high temperature. In general, we find that lower entropic loss upon folding may be responsible for enhanced stability in thermophilic proteins. Finally, we show how, based on these new parameters, we can model the entire proteome of different organisms and compare the results with thermal growth rate data.

Materials and Methods

Model

We carried out a thermodynamic analysis of proteins based on a significantly large data set (116 proteins), almost doubling the number of proteins (n = 63) from the earlier work of Robertson and Murphy (37). In this analysis we compute the differences in entropy $\Delta S$, enthalpy $\Delta H$, and specific-heat $\Delta C_p$ between two states (denatured and native). Thus, $\Delta S$ is defined as $S_u-S_f$ where S_u is the entropy of the unfolded state and S_f is the entropy of the folded state. This definition is used throughout for enthalpy, specific heat, and free-energy change as well.

As outlined above, it is most instructive to compute $\Delta H$ at 373.5 K and $\Delta S$ at 385 K to maximally decouple the effects of sequence and other driving forces. Furthermore, at these two special temperatures, $T_h=373.5$K and $T_s=385$ K, the changes in enthalpy and entropy show a strong linear chain length dependence (37). One can compute these quantities from enthalpy and entropy values reported at T_m using the following equation:

$$\Delta H\left(373.5\right)=\Delta H\left(T_m\right)+\Delta C_p\left(373.5-T_m\right);\Delta S\left(385\right)=\Delta S\left(T_m\right)+\Delta C_p\text{log}\left(385/T_m\right).$$ (2)

We assume that specific heat is independent of temperature (37,39). We removed all of the proteins that were either multimeric or non-two-state folders from the original list of the Robertson and Murphy (37) analysis. We added several new two-state folders for which we could find changes in enthalpy, entropy, and specific heat. Furthermore, our search was limited to only monomeric proteins under conditions where reversible transition was observed and closer to the isoelectric point to further decouple the electrostatic contributions. This resulted in a total of 116 strictly monomeric proteins, which are listed in Table S1 of the Supporting Material along with their sources. Our analysis also extends the range of applicability by including proteins with a longer chain length and a wider range of T_m-values than originally considered in the Robertson and Murphy (37) analysis.

However, because this set does not distinguish moderate-T_m (mesophilic) and high-T_m (thermophilic) proteins, which may have different thermodynamic properties, we further divided the set of 116 proteins into two sets. We achieve this by defining a cutoff T_m (T_c). For this classification, we revisited the analysis described above. We determined the optimal cutoff temperature T_c by minimizing the least-square error of fitting the chain-length-dependent linear equation for all three thermodynamic quantities $(\Delta H,\Delta S,$ and $\Delta C_p)$ separately when proteins were subdivided into two classes: 1), proteins with T_m > T_c; and 2), proteins with T_m < T_c. This method yielded a choice of $T_c=341K$ when the least-square error was minimized for enthalpy, entropy, and specific heat change independently. Thus, we determine $T_c=341K$ as the T_m below which we identify proteins as mesophilic, and above which they are termed thermophilic for this analysis. We also note the least-square fitting error of these quantities with chain length was significantly reduced when proteins were subdivided into two families compared with the undivided set.

Results

We found that the linear correlation of the overall set was slightly lower than that reported by Robertson and Murphy (37), but the average thermodynamic parameters changed slightly. Fig. S1 shows the results of this analysis. The slopes and intercepts of these different thermodynamic quantities against chain length determine the properties of an ideal thermal protein (38).

Ideal mesophilic and thermophilic proteins have different thermodynamic properties

It is likely that proteins with higher T_m evolved with a different set of thermodynamic rules than their mesophilic counterparts. Thus, it is natural to think that thermophiles and mesophiles would have significantly different ideal-thermal-protein parameter values. Several indirect experimental results support this. For example, by comparing thermodynamic properties between thermophilic and mesophilic homologs based on a native-state hydrogen exchange, Hollien and Marqusee (46) demonstrated that the increased stability is not a result of localized effect, but is distributed throughout. A proportional increase in stability for all residues results in an overall enhanced stability, indicating the possible role played by simple properties (e.g., chain length) in stability determination, and highlighting the importance of studying average parameters. Prompted by this, we subdivided our master set into two classes as described in Materials and Methods. Based on the analysis outlined above, we find a good correlation between thermodynamic parameters and chain length for mesophilic proteins (see Fig. S2). These 59 proteins, out of a total of 116, have T_m-values below $341K$. Thus, based on this analysis of a modified data set of proteins, we find the new parameters for ideal mesophilic protein to be

$$\begin{array}{l}\Delta H\left(373.5\right)=\left(4.0N+143\right)kJ/\text{mol}\hfill \\ \Delta S\left(385\right)=\left(13.27N+448\right)J/K-\text{mol}\hfill \\ \Delta C_p=\left(0.049N+0.85\right)kJ/K-\text{mol}.\hfill \end{array}$$ (3)

We classified the remaining 57 proteins with T_m ≥$341K$ as thermophilic proteins and carried out a similar analysis on this set (see Fig. S3). Once again, we find a good correlation between the thermodynamic parameters and the protein chain lengths for this thermophilic protein set. The new thermodynamic parameters thus obtained define an ideal thermophilic protein as

$$\begin{array}{l}\Delta H\left(373.5\right)=\left(3.30N+112\right)kJ/\text{mol}\hfill \\ \Delta S\left(385\right)=\left(10.90N+291\right)J/K-\text{mol}\hfill \\ \Delta C_p=\left(0.051N-0.26\right)kJ/K-\text{mol}.\hfill \end{array}$$ (4)

In the absence of any information other than the chain length, one can estimate the thermophilic and mesophilic protein thermodynamic parameters based on Eqs. 3 and 4.

Specific enthalpy and entropy changes at the convergence temperature are lower in thermophiles than in mesophiles on average

Based on the slopes and intercepts reported above, it is clear that changes in entropy and enthalpy upon folding are lower in thermophiles than in mesophiles. Here, we use a slightly different and more rigorous approach to verify this finding. We compute changes in thermodynamic parameters per amino acid for mesophilic and thermophilic sets, and construct the distribution of $\Delta H\left(373.5\right)/N$, $\Delta S\left(385\right)/N$ and $\Delta C_p/N$. We compare the mean of these quantities between mesophiles and thermophiles. Our results are summarized in Table 1. From the numbers reported in the table, it is clear that thermophilic proteins on average have a lower value of enthalpic, entropic, and specific heat change per residue. We performed a two-sample t-test on these distributions, and the results indicate that thermophiles have a lower change in entropy per amino acid than mesophiles, with a p-value of 0.00002. We also find that changes in enthalpy per amino acid are lower for thermophiles than for mesophiles, with a p-value of 0.001, whereas for specific heat the p-value is 0.008.

Table 1.

Mean values of thermodynamic parameters normalized by chain length

Mean values of parameters
	Mesophile	Thermophile	p-Value
$\frac{\Delta H\left(373.5K\right)}{N}\left(\frac{kJ}{mol\cdot res}\right)$	5.18	4.52	0.001
$\frac{\Delta S\left(385K\right)}{N}\left(\frac{J}{K\cdot mol\cdot res}\right)$	16.97	14.12	0.00002
$\frac{\Delta C_p}{N}\left(\frac{kJ}{K\cdot mol\cdot res}\right)$	0.055	0.049	0.008
$\frac{\Delta H\left(T_m\right)}{N}\left(\frac{kJ}{mol\cdot res}\right)$	2.72	3.65	5.3 $\times {10}^{-8}$
$\frac{\Delta S\left(T_m\right)}{N}\left(\frac{J}{K\cdot mol\cdot res}\right)$	8.26	10.22	0.00003
$T_S\left(K\right)$	281.6	284.2	0.3
$\frac{\Delta G\left(T_S\right)}{N}\left(\frac{kJ}{mol\cdot res}\right)$	0.21	0.40	3.3 $\times {10}^{-6}$

Comparison at convergence temperatures reveals that the changes in enthalpy and entropy are smaller in thermophiles than in mesophiles. When we compare enthalpy and entropy changes at T_m-values, the thermophilic changes are greater. T_S is the temperature of maximal stability that appears to be similar between thermophiles and mesophiles on average. However, free energy ($\Delta G\left(T_S\right)$) at the temperature of maximal stability (per amino acid) is significantly more favorable in thermophiles than in mesophiles. The p-value is a measure of confidence from testing the difference of two means.

However, when enthalpy and entropy changes are computed at their respective T_m-values, we find the reverse effect. Based on the numbers reported in Table 1, we find that thermophiles have a higher change in specific entropy and enthalpy than mesophiles when computed at the T_m, in agreement with an earlier study (9).

Maximal stability free energy is more favorable in thermophiles than in mesophiles

Based on our two sets, we calculate the average of the temperature of maximal stability (T_s) and the free-energy change at this temperature ($\Delta G\left(T_s\right)$). We find that the temperature of maximal stability is similar between thermophiles and mesophiles. However, the free-energy change at this temperature is almost twice as favorable in thermophiles compared with mesophiles (see Table 1), in accordance with previous studies (9,47). This is also evident from a comparison of the stability curves of the ideal mesophilic (blue) and ideal thermophilic (red) proteins in Fig. 1.

Figure 1.

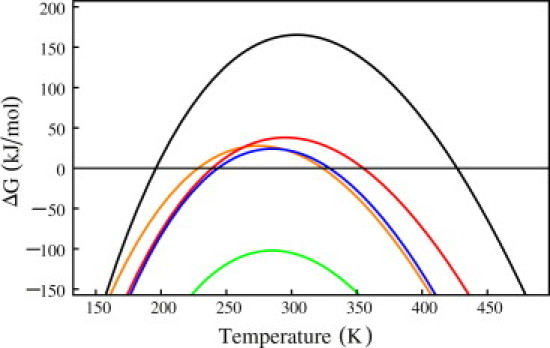
(Color online) Plot of the folding free energy of ideal thermophilic protein (red), showing a taller, broader, and right-shifted curve compared with ideal mesophilic protein (blue). Insertion of thermophilic specific heat change into the ideal mesophilic free energy slightly reduces T_m (orange), whereas insertion of thermophilic enthalpy change dramatically reduces stability (green). The substitution of thermophilic entropy into the mesophilic free-energy change (black) is the only parameter that shows increased stability and T_m.

Reduction in folding entropy (per amino acid) is responsible for high T_m

Using the thermodynamic parameters reported in Eqs. 3 and 4, we can compute the temperature-dependent free energy $\Delta G\left(T\right)$ (in kJ/mol) of an ideal thermophilic and ideal mesophilic protein as

$$\Delta G{\left(N,T\right)}_{meso}=\left(4.0N+143\right)+\left(0.049N+0.85\right)\left(T-373.5\right)-T\frac{\left(13.27N+448\right)}{1000}-T\left(0.049N+0.85\right)\text{log}\left(\frac{T}{385}\right),$$ (5)

$$\Delta G{\left(N,T\right)}_{thermo}=\left(3.30N+112\right)+\left(0.051N-0.26\right)\left(T-373.5\right)-T\frac{\left(10.90N+291\right)}{1000}-T\left(0.051N-0.26\right)\text{log}\left(\frac{T}{385}\right).$$ (6)

Using the average chain length ($N=136$) of our 116 protein data set in the equations above, and plotting $\Delta G$ as a function of temperature in Fig. 1, we can make the following points: 1) We see that the thermophilic curve (red) is broader and shifted upward and slightly to the right compared with the mesophilic curve (blue). 2) The thermophilic T_m is 25 K higher than the mesophilic T_m ($355K$ versus $330K$), and these temperature ranges are approximately in the same range as reported earlier (47). 3) The cold denaturing temperature of thermophiles (239 K) is slightly colder than that of mesophiles (244K), as previously suggested (48). 4) When the mesophilic specific heat change is replaced by the corresponding thermophilic parameter, keeping others intact, we find almost negligible change in free energy with a slight destabilizing effect (orange curve). 5) If we substitute the mesophilic enthalpy change by the thermophilic value, keeping other parameters for mesophilic proteins intact, we find a strong destabilizing effect (green curve). 6) On the contrary, substituting only the mesophilic entropy by the thermophilic parameter, we find a significant stabilizing effect that shifts the T_m at a much higher value (black curve). Thus, varying all three parameters individually, we clearly demonstrate that an ideal thermophilic protein gains a high T_m by lowering the entropic loss upon folding.

Next, we directly compare all possible pairings of thermophilic with mesophilic parameters against the pairings' respective T_m-values. After decomposition, the above analysis yields 59 mesophiles and 57 thermophiles, leading to a total of 3363 comparable pairs. Also, from the above analysis, all thermophilic T_m-values are greater than the mesophilic values, so when we consider the difference in T_m-values of the i^th thermophile to the j^th mesophile, we get $\Delta T_m={\left[T_m\right]}_i-{\left[T_m\right]}_j>0$. Computing the difference in specific entropy for the same i^th thermophile to j^th mesophile pair gives

$$\Delta \left(\frac{\Delta S\left(385\right)}{N}\right)={\left(\frac{\Delta S\left(385\right)}{N}\right)}_i-{\left(\frac{\Delta S\left(385\right)}{N}\right)}_j.$$ (7)

Plotting $\Delta T_m$ versus $\Delta \left(\Delta S\left(385\right)/N\right)$ for all 3363 possible i,j pairs, we see that $70\%$ of the pairs have a higher T_m associated with differences in entropic changes (per amino acid) that are less than zero. This implies that thermophilic $\Delta S/N$ is less than mesophilic $\Delta S/N$ for $70\%$ of possible pairings (see Fig. 2). We performed similar calculations for specific changes in enthalpy and specific heat. The difference in specific enthalpy change plot shows that $65\%$ of the pairings have a lower thermophilic enthalpic gain (per amino acid) than their mesophilic counterpart, and $61\%$ of the thermophilic $\Delta C_p/N$ is less than its mesophilic counterpart.

Figure 2.

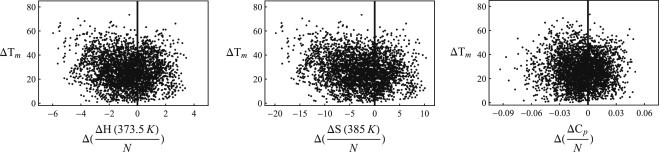
Direct comparison of thermophiles and mesophiles, shown as the difference in change of the thermodynamic parameter (Eq. 7) versus the difference in T_m per pairing. Points left of the Y axis signify thermophilic proteins with a smaller change in the respective thermodynamic quantity. For enthalpy, 65% of cases thermophiles have lower enthalpy than mesophiles. Similarly, the numbers are 70% for entropy and 61% for specific heat.

This analysis based on each protein pair shows a significant correlation between increased T_m and reduced entropy change upon folding, further justifying our claim based on the ideal-protein parameter comparison.

Homologous protein pairs reveal a similar trend

Thus far, our analysis has been based on a mean-field approach for a data set in which we classified proteins into thermophile and mesophile groups based on their respective T_m-values. Here we consider an alternate approach by constraining the data set to consist of only pairs, or groupings, of mesophile and thermophile homologs in which the classification is based on the organism from which the proteins have been extracted. Several proteins derived from thermophilic organisms have been studied (1,2,10,11) and compared with their homologs extracted from mesophilic organisms. The protein pairs considered here show either a low root mean-square deviation (RMSD) or a high sequence identity, and have been published as a relevant grouping based on their homology. Our 10 groupings of homologs include six thermophilic-mesophilic pairs and four groupings of at least four proteins, giving a total of 16 thermophiles and 17 mesophiles. The majority of the data shared at least $40\%$ sequence identity with the homologs and a backbone RMSD of <2 Å within each pairing or group. The following groups were published as being homologous, but were either below this criterion or unavailable to calculate: The pairing of MGMT-AdaC showed only $20\%$ sequence identity, but had a calculated backbone RMSD of 1.9 Å (49). The S16 pair had $33\%$ identity, but calculation of RMSD was unavailable (19). Calculation of sequence identity and RMSD was unavailable for Phycocyanin (50). Within the SH3 domain-containing group of eight proteins, certain pairs (e.g., Sac7d and Fyn) had an RMSD as high as 9.9 Å (9,16).

As described in the previous section, we compared each thermophilic protein with all other mesophilic proteins within the same group to compute differences in changes in specific entropy: $\left(\Delta \left(\Delta S\left(385\right)/N\right)\right)$, enthalpy $\left(\Delta \left(\Delta H\left(373\right)/N\right)\right)$, specific heat $\left(\Delta \left(\left(\Delta C_p\right)/N\right)\right)$ , and change in T_m ($\Delta T_m$). When we directly compare these quantities only within groupings of homologs, we find that a high percentage $\left(79\%\right)$ of thermophilic entropy changes (per amino acid) are smaller than the mesophilic entropy changes (per amino acid) in the same group. Also, $68\%$ of changes in enthalpy (per amino acid), and $75\%$ of changes in specific heat (per amino acid) are smaller in thermophiles compared with their mesophilic counterparts (see Fig. 3). Thus, a direct comparison of normalized thermodynamic data shows that thermophiles have a high propensity to experience reduced entropic, enthalpic, and specific heat changes compared with their mesophilic counterparts. This gives additional support to our previous analysis based on T_m alone. Due to the small amount of data points, linear regression was not informative.

Figure 3.

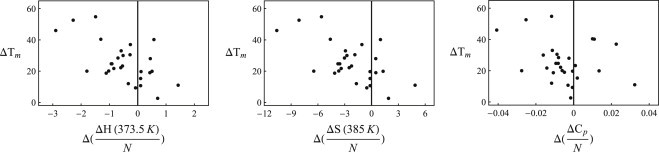
Direct comparison of homologous thermophiles and mesophiles, shown as the difference in change of the thermodynamic parameter (Eq. 7) versus the difference in T_m per pairing. Points to the left of the Y axis signify thermophilic proteins with a smaller change in the respective thermodynamic quantity. For enthalpy, 68% of cases thermophiles have lower enthalpy than mesophiles. Similarly, the numbers are 79% for entropy and 75% for specific heat.

Growth-rate calculation of organisms and comparison with experiments

Based on our analysis above, we can model protein stability as a function of chain length using parameters of the ideal thermal protein (38,51). We can extend this to calculate the stability distribution of the entire proteome by using the chain length distribution $P\left(N\right)$ of the proteome. For many organisms, the chain length distribution can be modeled as a Gamma distribution (52):

$$P\left(N\right)=\frac{N^{\alpha -1}\text{exp}\left(-N/\theta \right)}{\Gamma \left(\alpha \right){\theta }^{\alpha }},$$ (8)

where α and θ are two parameters. We previously used this approach to model proteome stability distribution for different organisms (e.g., Escherichia coli, yeast, and Caenorhabditis elegans) and growth rates (51). However, in this work, using the proteome chain length distribution and free-energy equations (Eqs. 5 and 6), we compute the free-energy distribution $P\left(\Delta G\right)$ of the entire proteome to calculate the growth rate $r\left(T\right)$ of several mesophilic and thermophilic organisms. As before, for a given proteome, we take

$$r\left(T\right)=r_0\text{exp}\left(-\Delta H^{†}/RT\right)\prod _{i=1}^{\Gamma }\frac{1}{1+\text{exp}\left(-\Delta G_i/RT\right)},$$ (9)

where r₀ is an intrinsic rate, and $\Delta H^{†}$ represents an Arrhenius activation barrier for a metabolic reaction rate (51,53,54). The product term describes the stabilities of proteins $i=1,2,3,\dots ,\Gamma$, where Γ is the number of essential proteins that are important for the growth rate. The expression above assumes that fitness depends on all of the essential proteins and their propensity to be in the folded state. This is motivated by the fact that compromising the stability of any of these essential proteins is lethal to the organism. This explains the product in Eq. 9. Furthermore, it assumes that growth rate is related to fitness. Equation 9 has already been successfully used to model growth rates in different organisms (51,53,54). Taking the logarithm of the rate gives Eq. 9 as

$$\text{log}r\left(T\right)=\text{log}{r}_0-\frac{\Delta H^{†}}{RT}-\sum _{i=1}^{\Gamma }\text{log}\left(1+\text{exp}\left(-\Delta G_i/RT\right)\right).$$ (10)

We approximate the sum as the integral over the entire proteome free-energy distribution, $P\left(\Delta G\right)$, and express the average rate (53) as

$$\text{log}r\left(T\right)=\text{log}{r}_0-\frac{\Delta H^{†}}{RT}-\Gamma \int \text{log}\left(1+\text{exp}\left(-\Delta G/RT\right)\right)P\left(\Delta G\right)d\Delta G.$$ (11)

The expression above requires the stability distribution $P\left(\Delta G\right)$. We estimate this distribution by using the proteome length distribution (Eqs. 8) and free energy (Eq. 5 for mesophiles and Eq. 6 for thermophiles). Equation 11 predicts that cellular growth rates increase with temperature at low temperature due to the assumed activated process. However, growth rates decrease at high temperatures due to proteome denaturation (see Fig. 4). It predicts maximum growth at an optimal growth temperature. These curves are highly asymmetrical near their temperature of maximum growth, and our model predicts this well. For this calculation, our model requires two free parameters, $\Delta H^{†}$ and Γ, which we determine by fitting the experimental data on several mesophilic and thermophilic organisms (see Fig. 4). The values of the fitted parameters are reported in Table S2 using corresponding expressions of $\Delta G$ for the respective organism.

Figure 4.

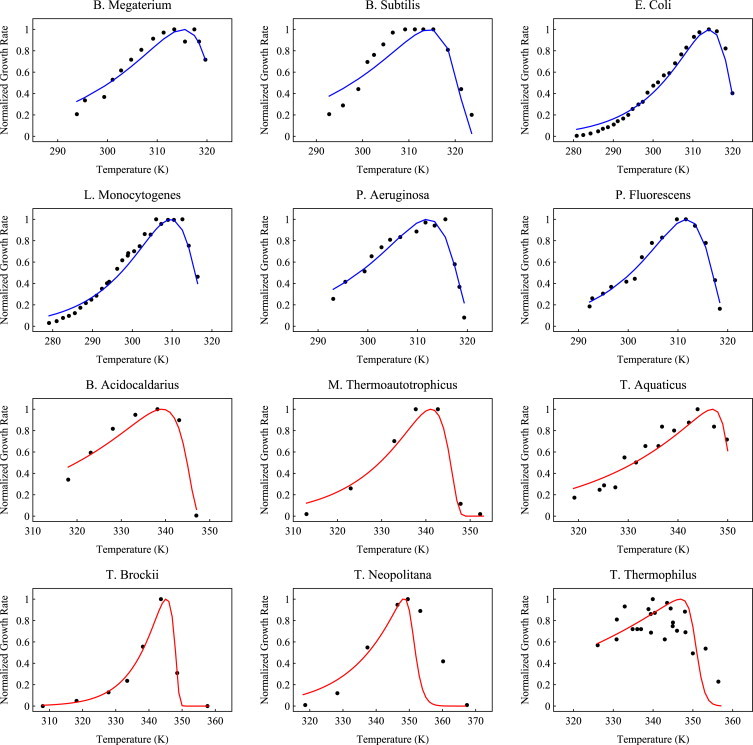
(Color online) Black circles denote the growth rate as a function of temperature for the species listed. In the Y axis we plot the growth rate normalized with respect to maximum growth rate, and in the X axis we plot the temperature. Solid lines are fit to data from Eq. 11. The names of the species are given in the graph. Red curves denote thermophilic species, and blue curves indicate mesophiles. The sources of the growth-rate data for different organisms are given in Table S2 next to the species' names. Proteome chain length information about each organism was obtained from GenBank (72).

Discussion

In this work, we analyzed the largest data set obtained to date to compare thermodynamic properties between thermophiles and mesophiles. In contrast to previous studies, we computed enthalpy (per amino acid) and entropy (per amino acid) changes at the convergence temperature to compare thermophiles and mesophiles. Our rationale was to separate hydrophobic effects from other driving forces, e.g., to decouple conformational entropy and solvation entropy. With this definition, we find, in general and with high statistical confidence, a smaller gain in enthalpy (per amino acid) upon folding in thermophiles than in mesophiles. This is a destabilizing effect. However, when we consider conformational entropy, we find that, on average, thermophiles sacrifice less entropy upon folding than mesophiles, thus overcompensating for the destabilizing effect due to enthalpy. This is responsible for the extra stability in thermophiles. It may appear that our finding is in conflict with studies that predicted higher specific entropy and enthalpy in thermophiles than in mesophiles (9). This apparent contradiction is due to the temperatures at which the thermodynamic quantities were calculated. When we compute entropy and enthalpy at the T_m, we are able to reproduce the results of Kumar et al. (9). However, as noted above, the entropy computed at the T_m is not purely conformational due to the presence of solvation entropy. We find the temperatures for maximal stability to be similar among thermophiles and mesophiles, whereas the folding free energy (per amino acid) at these temperatures is significantly more favorable in thermophiles than in mesophiles, in agreement with previous studies (9,47).

To our knowledge, the analysis presented here is novel because it computes thermodynamic properties at the convergence temperature to depict the lower folding entropy (conformational) and enthalpy associated with thermophiles. Furthermore, the combined findings of reduced entropy loss and lowered enthalpy gain raise the possibility that thermophiles may retain partial contacts in their denatured state. The presence of strong hydrophobic interactions, disulfide bonds (31,55), or electrostatic interactions (24,25,56) may be responsible for such residual structure in the denatured state. This would explain the lowered gain in enthalpy upon folding, as there are already existing favorable interactions in the denatured state. However, due to the presence of these native/nonnative contacts, the conformational entropy in the denatured state will also be lowered. This could explain the reduced loss in folding entropy (conformational) observed in thermophiles. This is consistent with experimental studies indicating that a reduction of the unfolded state entropy is responsible for enhanced stability (17,18,20). The existence of residual structure in the unfolded state (13,15), and the compact denatured state (19) in thermophiles provide strong evidence that a reduced entropy change upon folding is responsible for the high T_m. Wallgren et al. (19) showed that thermophilic ribosomal protein S16 has a more compact denatured state than the mesophilic homolog. Similar observations based on radius measurements were made by Liu et al. (18) in connection to their studies on Taq DNA polymerase. A comparative investigation of two thermophilic α-amylases showed a more compact unfolded state when they were denatured thermally than when they were denatured chemically. Also, the amylase with the higher thermal stability showed a more compact state than the amylase with lower T_m (20). Residual structure has been seen in thermophilic RNases H, but not in the mesophilic homolog (13). The existence of residual structure and native/nonnative contacts, and local compactness of the denatured ensemble have been addressed in several other contexts as well (24,57–64). The presence of residual structure in the denatured state would be responsible for a lowered solvent-accessible surface area compared with a fully unfolded extended state. This would consequently explain a lower $\Delta C_p$ in thermophiles, and is consistent with other works in the literature (11,13–15) as well. Thus, our finding of a reduction in folding entropy is not in contradiction to studies hinting at reduced $\Delta C_p$, but in accordance. It appears that our calculation based on the convergence temperature reconciles previous observations by properly extracting the conformational entropy. However, it should be remembered that lowering $\Delta C_p$ alone, and keeping $\Delta H\left(373.5\right)$ and $\Delta S\left(385\right)$ intact, will lead to destabilization rather than stabilization of the protein (see Fig. 1).

Another possible explanation for the reduced change in folding entropy is that specific amino acid substitutions lead to reduced entropy in the unfolded state due to the different degrees of flexibility associated with them (17,21). This is also consistent with the technique of enhancing stability by reducing conformational entropy of the denatured state by adding proline residues in β turns and at other locations in proteins (65,66). Nemethy et al. (67) quantified possible changes in unfolded chain entropy from amino-acid substitution. The effect of entropy on increased stability may also arise from different degrees of compactness in the native structure as a result of different mutations (22). Substitution of amino acids could change the entropy of the folded state. Factors such as rigidity, compactness, and rotameric states in the native state also play an important role in stabilizing thermophiles, and would be related to the entropy change as well. In computational studies, rubredoxin was found to be more globally rigid with respect to temperature than its mesophilic counterpart (68), and thermophilic RNase H was shown to have less backbone flexibility at the same temperatures, and less conformational entropy over a large temperature range than its mesophilic homolog (69).

However, a more microscopic model will be needed to further investigate the quantitative contribution that arises from the unfolded and native-state entropy difference. Based on our finding at the convergence temperature, the lowered change in entropy and enthalpy is in accordance with several experimental studies that point to residual structure and reduced specific heat change (11,13–15,18–20). Our finding does not contradict previous studies; rather, it reconciles all of them. However, reduced enthalpy and specific heat upon folding have a destabilizing effect that is overcompensated for by the reduced loss in entropy imparting higher stability in thermophiles. Thus, we conclude that the key factor behind increased thermal tolerance is the reduction of folding entropy.

In addition, our study, which is based on a homologous series, emphasizes the role of entropy in thermal stabilization of proteins. As expected, as a result of our stringent comparison of homolog families, the general trend is clearer (see Fig. 3). Moreover, the quantitative agreement between experimental thermal growth data and our proteome modeling based on ideal-mesophilic-protein and ideal-thermophilic-protein parameters provides additional support for our approach and findings. Growth rates computed using Eq. 11, along with protein thermodynamic data, capture the optimum growth temperature as well as the asymmetric temperature-dependent growth curve across many thermophilic and mesophilic organisms. Furthermore, it should be noted that we can only use mesophilic (thermophilic) ideal protein parameters to fit mesophilic (thermophilic) organisms. We obtain unphysical parameter values and a poor fit when we use mesophilic protein parameters to fit thermophilic-organism growth data, and vice versa. Thus, the extreme sensitivity of the thermodynamic parameters to model growth data, and successful modeling only upon proper selection of protein thermodynamic parameters, suggest that engineering protein stability is one of the key factors used by organisms to adopt to these temperatures. It should also be noted that application of the growth rate (Eq. 9) to model fitness may not always be accurate and depends on the nutrient condition (70,71).

Summary

In the thermodynamic analysis presented here, we attempted to elucidate the origin of enhanced stability in thermophilic proteins and proteomes. We make six key points: First, we construct and analyze thermodynamic properties of the largest set of proteins (n = 116) achieved to date for which full thermal data are available. Second, we calculate entropy and enthalpy changes at the convergence temperature to maximally decouple the effect of different driving forces, in contrast to previous attempts. Third, based on these results, we find that, on average, thermophilic proteins have less change in specific enthalpy and entropy upon folding. However, lower enthalpic gain ($\Delta H\left(373.5\right)$) or reduced $\Delta C_p$ has a destabilizing effect that is compensated for by reduced entropic loss, which is ultimately responsible for the high T_m. We also find the temperature of maximal stability (T_s) to be similar among the two classes, although the gain in folding free energy (per amino acid) at the maximal stability temperature is significantly higher in thermophiles than in mesophiles, in agreement with previous studies (9,47). Fourth, our analysis allows us to directly extract conformational entropy, in contrast to previous studies, and hints at a possible role of residual/compact structure in the denatured state. Furthermore, based on the average parameters, we give equations for ideal mesophilic and ideal thermophilic protein free energy as a function of temperature that can be used in the absence of any information other than the chain length of the protein. Fifth, our analysis based on homologous protein sets reveals a similar trend. It supports the role of entropy in increased denaturation temperatures. Finally, we extend our ideal protein calculation to model the proteome free-energy distribution and predict the growth rates of several mesophilic and thermophilic organisms. We find that our model captures high optimal temperatures in thermophiles and is in excellent quantitative agreement with thermal growth data. This also hints at the possibility that altering protein thermodynamics to gain high T_m is a strategy that thermophilic organisms may have adopted to deal with high temperature.