Abstract
Transport of molecules in cells is a central part of cell biology. Frequently such trafficking is not just for material transport, but also for information propagation, and serves to couple signaling circuits across cellular compartments. Here, I show that trafficking transforms simple local signaling pathways into self-organizing systems that span compartments and confer distinct states and identities to these compartments. I find that three motifs encapsulate the responses of most single-compartment signaling pathways in the context of trafficking. These motifs combine with different trafficking reactions to generate a diverse set of cellular functions. For example, trafficked bistable switches can oscillate or become quad- or tristable, depending on trafficking mechanisms and rates. Furthermore, the analysis shows how compartments participating in traffic can settle to distinct molecular compositions characteristic of distinct organelle identities. This general framework shows how the interplay between molecular movement and local reactions can generate many system functions, and give distinct identities to different parts of the cell.
Introduction
The movement of molecules in cells is a highly regulated and extremely diverse process. It underlies many key cellular phenomena, ranging from formation of molecularly distinct cellular compartments to maintenance of distinct connection properties in thousands of synapses on a neuron. Several studies have analyzed the implications of trafficking for molecular segregation and compartmentalization (1–5). Steep molecular gradients and local domains may also emerge from localized phosphorylation and second messenger production (6–8). The process of trafficking control may be separated into two components: the mechanisms of molecular movement, and the chemical modification of molecules that confer directionality to this movement. For example, the insertion and removal of glutamate receptors into the synaptic membrane is regulated by their phosphorylation state (9), and the direction of vesicle cycling is specified by the GTP-bound status of Rab molecules (1,2). Many trafficking events occur in cycles, and directionality arises because one chemical form of a molecule M is trafficked to a cellular compartment A, where it is converted through signaling chemistry into a different form M∗. M∗ is then shipped back to compartment B through a separate trafficking step.
The signaling mechanisms that govern function and traffic can be extremely complex, and several attempts have been made to organize signaling networks in terms of their functional or topological motifs. These include oscillators, timers, differentiators, various logical and analog operations, and memory switches (10,11). Trafficking motifs appear to further complicate this diversity into an unpromising landscape of special cases. In this study, I develop a general theory to encompass and abstract out this diversity. This framework predicts a diverse set of cellular and functional properties.
Results
I first analyze mass action models of signaling networks from a database to show that many single-compartment cellular trafficking and signaling processes fall into just three categories. I then develop a framework to analyze stable states in systems exchanging molecules between two compartments. I illustrate this framework for a wide range of trafficking situations, and then carry out mass action simulations and steady-state analysis for example situations. Finally, I compare the outcomes of this analysis with several previously studied and quantitatively modeled cellular trafficking phenomena and show that it offers a concise and predictive framework.
Nomenclature
M: Amount of trafficked molecules in first state.
M∗: Amount of trafficked molecules in second state.
Mtot: Total amount of trafficked molecules, in M, M∗, and all intermediate states, in a specified compartment.
Tot: Total amount of M in all states in all compartments in reaction system.
M-versus-Mtot curve: steady-state dependence of M on Mtot.
P: Amount of anchor protein in unbound state. Unless stated otherwise, P is assumed to bind to all states of molecule M, in compartment A only.
Ptot: Total amount of anchor protein in all states in entire system.
The terms M, M∗, and Mtot are general. When referring specifically to compartment A and B the following terms are used:
MA: Amount of M in compartment A.
MA∗: Amount of M∗ in compartment A.
Atot: Total amount of MA, MA∗, and any intermediate states of M in compartment A.
Similarly, MB, MB∗, and Btot apply to compartment B.
If there is any ambiguity, I refer to the molecule species as molecule M, molecule M∗, and so on, otherwise I use these terms both as molecule identifiers and as amounts of the specified molecules.
Many signaling systems fall into one of three categories
Trafficked molecules are controlled through a wide variety of signaling processes that may be very complex. I scanned through signaling models from the Database of Quantitative Chemical Signaling (12) and research publications to find common features that might be important in the context of trafficking. Specifically, I looked for systems where a molecule M was converted to a second chemical state M∗ by the signaling network, and where M and M∗ might undergo trafficking. I selected 32 published models that met these criteria, and computed the dependence of steady-state levels of M on Mtot, the total amount of M in the compartment. I did so by solving the systems of ordinary differential equations (ODEs) in the models and running out to steady state, using the simulator MOOSE (13).
Despite the diversity of models, I found that they fell into only three major categories: bistable (or breaking wave) (16%), negative slope (28%), and positive slope (56%) systems (Fig. 1, Table S1 in the Supporting Material). Bistable systems have a region in which the system exhibits hysteresis, and thus persists in either of two stable states (Fig. 1 C). Negative slope systems have a region in which the concentration of M decreases with increasing Mtot (Fig. 1 D). Positive slope systems have monotonically increasing levels of M with increasing Mtot (Fig. 1 E). One of the complex signaling cases (mitogen-activated protein kinase (MAPK) feedback) model with 81 molecules, Fig. 1 C vi (14), combined two of these forms. Two characteristic bistable motifs in the dataset were positive feedback loops and multisite phosphorylation (Table S1 (15–18)), . The negative slope models also frequently had feedback and multiple phosphorylation motifs. These cases included several kinase activation models (Table S1), and one of the Rab models (2). The remaining signaling motifs were positive slope systems. These curves included zero-order ultrasensitivity (19) and high Hill-coefficient activation systems. Five of the small-GTPase family models in this selection, including Ras, Ran, and Rheb, had positive slopes (Table S1).
Figure 1.
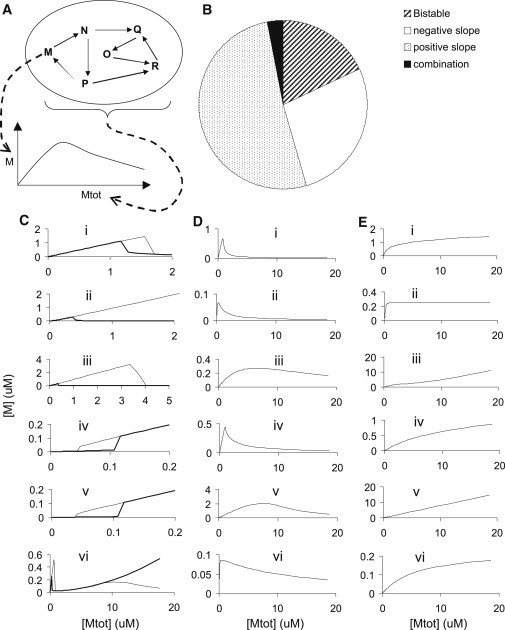
Signaling responses fall into three categories. Steady-state M versus Mtot curves for 18 example cases out of 32 cases studied. (A) Schematic of generation of M-versus-Mtot curve. In a compartment, the molecule M can be converted into several chemical forms. The total amount of M in all these forms is Mtot. In the subsequent plots, M is plotted against Mtot. (B) Summary of frequencies of occurrence of each category. (C) Bistable cases. These are (i) bistable feedback model. (ii) Multisite phosphorylation bistability model (16), which has irreversible enzyme reactions, giving an infinitely large hysteresis range. (iii) Same model with added reversibility, giving a finite hysteresis. (iv, v), Oscillatory MAPK models from (10) for the kinase and phosphatase, respectively, and have a form consistent with M∗ versus Mtot. (vi) Large MAPK feedback model with 81 molecular species, from (14). It has an initial bistable domain similar to (C i) in the physiological range of Mtot, but at high Mtot it seems to adopt a negative slope behavior similar to those in D. (D) Negative slope cases. (E) Positive slope cases. Details of models and calculations are in Table S1.
Although this selection of models was biased by database availability, it was notable that these classifications covered all the models tested. What biochemical features lead to these classifications? I explored this using simple example models that replicated the observed categories of curves (Fig. 2 A: bistable models (15–18); Fig. 2 B: singly stable models, rates in Dataset S1 in the Supporting Material). The bistable models in the database, by definition, had a hysteretic region in their M-versus-Mtot curves, where the system could take two stable values. Outside this region, there were two behaviors. In some cases M approached zero at large Mtot (Fig. 1 C i and iii). This is the characteristic breaking wave shape that identifies this motif. In the other cases the large-Mtot limit of M was nearly linear with Mtot (Fig. 1 C iv and v). I constructed dose-response curves for M-versus-Mtot for the example bistable models including the unstable fixed points (Fig. 2, C and D). These examples showed that the two forms of the M-versus-Mtot curve were complementary. In these models, the molecule M exists in two primary forms M and M∗. In the bistable examples in Fig. 2, C and D, M approached zero at large Mtot, and M∗ converged toward Mtot itself. Thus, the two forms of the responses of the models from the database could be ascribed to which of two major forms of M was being monitored.
Figure 2.
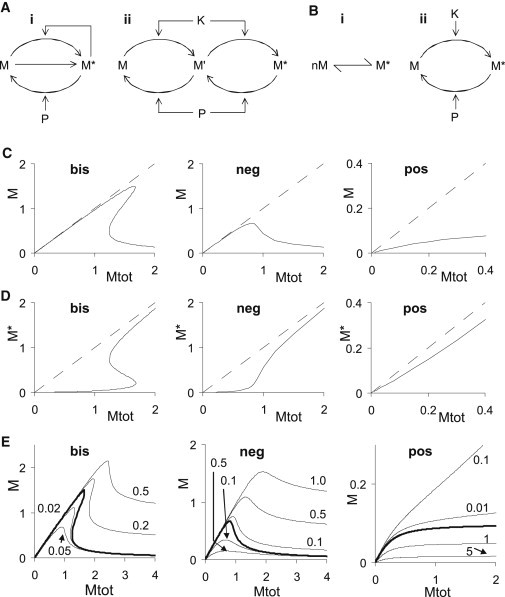
Reference models for three signaling categories. (A i) Feedback model with bistability. (A ii) Multisite phosphorylation model that can be bistable or negative slope depending on parameters. (B i) Simple reaction scheme with positive slope. (ii) Zero-order ultrasensitive reaction (19) also has positive slope. For the bistable, negative slope, and positive slope categories, I used models A i, A ii, and B i, respectively. (C) Typical responses of intracompartmental reactions for bistable, negative slope, and positive slope systems. (D) Same responses as in C, showing dependence of M∗ on Mtot. M∗ is the modified form of the trafficked molecule. (E) Effects of flux on M versus Mtot curves for bistable, negative slope, and positive slope systems, respectively. Solid curve is reference, curves above it have reverse flux terms added, and curves below it have forward flux terms added. The categorization of the model does not change with flux except for the bistable model in Ei, which converts into a negative slope system for forward flux > 0.02 or backward flux > 0.5.
By changing the model parameters for the cases in Fig. 2 A, the bistable models became singly stable but with a negative slope region. A similar set of curves were constructed using these models (A ii), and models with positive slope (B i and ii). As with the bistables, the example models generated reference curves that matched all the forms from the database models, either in terms of M versus Mtot, or M∗ versus Mtot.
Categories are largely robust to additional flux terms
These canonical M-versus-Mtot curves express steady-state relationships. How do these curves change in the presence of flux of molecules due to traffic? To address this I introduced an additional flux term that transferred molecules between M and M∗, so that Mtot was not altered. I then recomputed the M-versus-Mtot curves. Forward flux was defined as flux from M to M∗, and vice versa. These rates were normalized by the fastest internal rates of the reaction system to estimate flux rates as a fraction of internal compartment rates. From Fig. 2 E (bis) we see that this bistable system retained bistability in a range of 2% forward fluxes to 20% reverse flux, and outside this range it behaved like a negative slope system. The negative slope and positive slope systems did not change their classification for any value of flux tested (up to 100% of internal rates), but there were quantitative changes in responses.
A similar conclusion may be obtained by the following argument. Let M be the nominal concentration in the steady-state M-versus-Mtot curve. If the fastest rate in this system is k, then an additional flux term with the same rate k will approximately halve (or double) the value of M depending on whether it removes or adds M. If the state classification is sensitive to ∼20% changes, such as in some bistable systems (16,20,21), then allowable values for flux rates are also in this range. If the state classification is insensitive to changes up to 100% (true for the negative and positive slope cases), then the trafficking rates can be as large as the fastest rates in the compartmental reaction system.
System states can be predicted from flux balance between compartments
The next stage of the analysis investigated how the steady states of the system as a whole could be determined from the motifs obtained above. The MA-versus-Atot curve forms a steady-state curve or nullcline, where MA does not change if Atot is steady. However, if Atot is steady, then so is Btot, and we can obtain another curve for MB. The key step was to evaluate the flux balance requirement so as to convert the equation for MB into another relationship between MA and Atot. This gave a second nullcline of MA as a function of Atot. The intersection points of these two nullclines specify the fixed points of the combined signaling/trafficking system.
At steady state, the number of molecules M entering each compartment should be identical to the number leaving it. I made two further assumptions: that intracompartment reactions settle faster than the trafficking timescales, and that almost all trafficked molecules in each compartment are either in state M or M∗. Note that this assumption does not restrict levels of any other molecular species in the compartment.
From the trafficking motif analysis above, we know how the level of M depends on the total contents of the compartment. This can be expressed as
| (1a) |
| (1b) |
for molecule M in compartments A and B, respectively.
Here,
| (2a) |
| (2b) |
It is useful to express Btot as
| (3) |
where Tot is the total amount of all states of M in the entire system. Tot is conserved.
Applying the flux-balance requirement, we get
| (4a) |
| (4b) |
Expressing as rate equations using rate terms from Fig. 3 A:
| (4c) |
Substituting for MA∗ and MB∗ from Eqs. 2a and 2b:
| (5) |
Rearranging:
| (5a) |
Substituting in Eqs. 1b and 3 we get MA in terms of Atot:
| (6) |
This is the second nullcline of the system. Parameter variations on this equation are explored in Fig. 3. The analysis from this point forward consists of finding intersection points of the nullclines for different system parameters.
Figure 3.
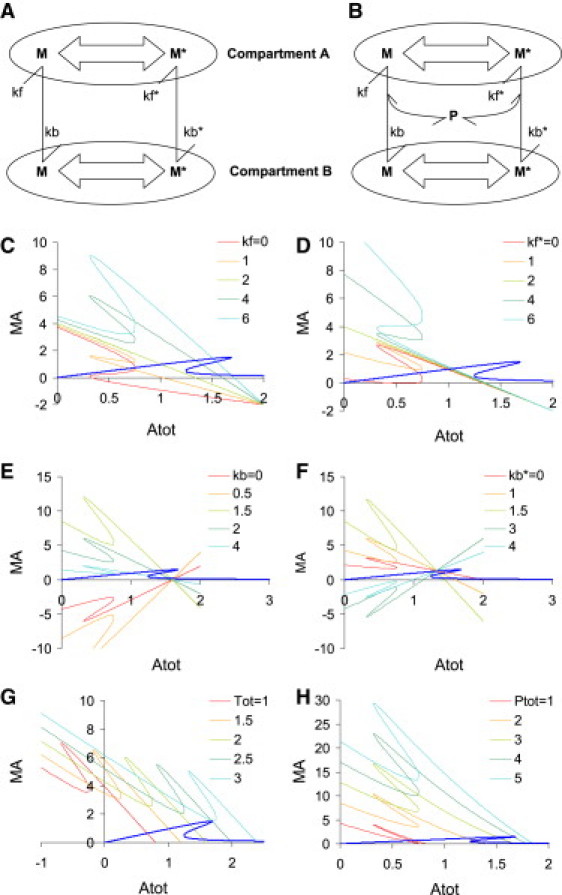
Reaction control parameters. (A) Reaction scheme for trafficking. (B) Reaction scheme for trafficking with an anchor protein molecule P required for molecules to go into compartment A. (C–H): Transformations of nullcline curve as a function of different trafficking control parameters. In all these curves a reference M-versus-Mtot curve is shown in blue to help visualize intersection points. (C) Varying kf. (D) Varying kf∗. (E) Varying kb. (F) Varying kb∗. (G) Varying Tot. (H) Varying Ptot in reaction scheme shown in panel B. For visualization purposes, the bistable model from Fig. 2A i has been taken. The reference trafficking parameters for C–G are: kf = kf∗ = kb = 2/s; kb∗ = 1/s; Tot = 2 μM. For panel H, the trafficking parameters are kf = 4/s, kf∗ = kb = 2/s, kb∗ = 1/s, Tot = 2 μM.
This procedure is easy to extend to other trafficking situations. For example, we obtain a similar equation if there is a requirement for an anchor protein P for molecule MB to move into compartment A (Fig. 3 B). In such situations an additional conservation equation applies
| (7) |
where the constant Ptot is the total amount of molecule P in the entire system. The equation with the addition of the term for P is
| (8) |
It is useful to note that Eqs. 6 and 8 also apply to systems with different volumes. If we use the volume of compartment A (VA) as reference, the volume scaling factor.
folds into the rate terms kf and kf∗ as a constant scaling factor, and the argument in fB 23 must also be scaled by Vr.
Equations 6 and 8 define how trafficking parameters affect stable states of the system
In Fig. 3, I consider the nullclines in compartment A arising from a bistable reaction in compartment B. In Fig. 3, C and D, flux into compartment A is varied. Both curves have an underlying negative slope line arising from the negative dependence on Atot in Eqs. 6 and 8. Thus, the system is likely to have at least two stable states (intersections with the MA-versus-Atot curve) when the reaction in compartment A is bistable or negative slope, for a wide range of the kf and kf∗ parameters. The flip in vertical orientation in Fig. 3, C and D, comes when the kf (or kf∗) term exceeds the flux due to the reverse kb (or kb∗) term.
In Fig. 3, E and F, flux out of compartment A is varied. Here, the kb and kb∗ terms determine the underlying slope of the nullcline, and the shape of the MB versus Btot curve is overlaid on this. When kb is greater than kf, the line slope is negative, so again bistability is likely. However, for smaller values of kb, the underlying slope is positive and furthermore the y intercept is below zero. Thus, systems with a small kb are likely to have only a single stable state. The converse is the case in Fig. 3 F, for kb∗, therefore systems with a large kb∗ will usually have only a single stable state.
The dependence on total concentration of trafficked molecule in the entire system (Tot) is straightforward: large values of Tot shift the nullcline to the right (Fig. 3 G). Thus, multiple intersections (multistable states) are likely only for intermediate values of Tot. Specifically, multistability is likely when Tot is in the same range as the start of the negative slope portion of the MA-versus-Atot curve.
Large amounts of anchor molecule P encourage movement into compartment A. Thus, high values of Ptot increase the amount of MA, while retaining the overall shape of the negative slope nullcline (Fig. 3 H). This means that multistability is likely only in an intermediate range of values for Ptot. This range is determined by the product of kb and kb∗ with Tot.
Together with the original M-versus-Mtot curves, these nullclines provide a graphical basis to understand the kinds of stable states that might emerge from various combinations of signaling and trafficking between two compartments. I next investigate specific examples of trafficking and signaling, and use numerical simulations of the resulting cases to show that the nullcline analysis does predict stable states of the system.
Diffusive and transport processes can be described in this framework
A wide range of trafficking processes are special cases of Eqs.6 and 8: diffusive, unidirectional mass action, and unidirectional zero-order reactions. Diffusive traffic is bidirectional and concentration driven, and is effective at small length scales. Signal flow in bacteria is frequently diffusive (22). To obtain diffusive equations from Eq. 6, we simply set
| (9a) |
and
| (9b) |
and assign a ratio of these rates
| (9c) |
Substituting these terms into Eq. 6, we get
| (10) |
Mass action traffic is typically directed, and occurs when the rate of traffic is proportional to the amount of trafficked molecules. For example, Rab-mediated traffic is substantially determined by the amount of GTP-bound Rab (1). To analyze this, we set
| (11a) |
for counterclockwise traffic around the reaction loop in Fig. 3, and
| (11b) |
for clockwise traffic. Putting these terms into Eq. 6 we get
| (12a) |
| (12b) |
SNARE trafficking can be approximated in this framework
N-ethylmaleimide sensitive factor attachment protein receptor (SNARE)-dependent trafficking is a special case of unidirectional mass action traffic, where the rate is proportional to molecular levels both in the originating vesicle and target compartments (4). I treat compartment A as the composite of organelle A and the vesicles budding off it and the reaction within the compartment represents the fast processes involved in this budding and insertion of the SNARE M into the vesicle. Thus, MA represents SNAREs in the organelle, and MA∗ the SNARES in the vesicles budded from organelle A. I assume traffic goes directionally with the vesicles MA∗ fusing to compartment B, and the vesicles MB∗ fusing to compartment A. These biological assumptions are discussed more fully below. The flux balance equation in this case is
| (13) |
Let
| (14a) |
and then using Eqs. 2 and 3, we get
| (14b) |
which rearranges to
| (15) |
Motor transport and protein synthesis can be represented as zero-order variants of the framework
Finally, zero-order kinetics occurs when a directed molecular transport mechanism is itself limiting. For example, motor-mediated traffic may be saturating, therefore it depends only on the amount of the motor, and not on cargo. The same equations also apply to protein turnover, which can be approximated as a combination of a zero-order process of protein synthesis, and a mass action process of degradation (10) To obtain this relationship, we put in the zero-order term Z into Eq. 4c, and set the reverse reaction to zero. This can be done for various permutations of two directions (cw and ccw) and the zero-order term on the left or right, but given the symmetry of the reaction system it reduces to just two unique cases:
| (16a) |
| (16b) |
Here, kcw and kccw are rates in the clockwise and anticlockwise directions, respectively.
Multiple systems properties emerge from trafficked signaling systems
Put together, the functional motifs and the flux-balance permutations provide a rich substrate for diverse system properties. I considered a representative list of 32 permutations of trafficking in both directions from compartments A and B (Fig. 4). For analytical simplicity I considered cases where either the reaction in compartments A or B was identical, or where the reaction in compartment B was a simple conversion reaction: M <==> M∗. Although this offered analytic convenience, it did not limit the generality of the findings, as the number and relative slopes of intersection points from the graphical analysis depend on the forms of fA() and fB() and the trafficking parameters (Fig. 3), rather than the exact equations underlying fA() and fB().
Figure 4.
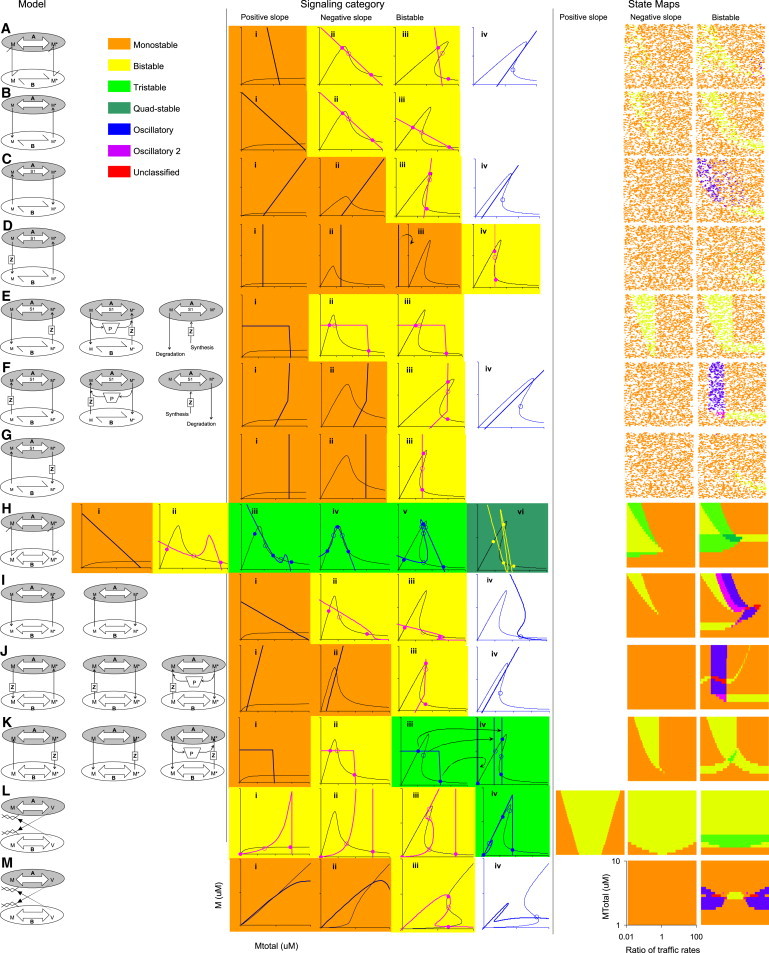
Many system properties emerge from combinations of signaling and trafficking. Left column shows the model schematic, with one to three cases that obey the same equations. Middle columns show different signaling categories as M versus Mtot curves, along with example solutions. Tick marks on graph axes are at 1 μM intervals. Solutions are also shown from numerical computation of steady states, using dots for stable solutions and open circles for saddles and unstable solutions. Graphs are color-coded to indicate the solution class. Oscillatory solutions (blue) are indicated by blue lines on a white background; the rest have the indicated color as background. All graphs are for compartment A, except for panel J(i–iv)), which is for compartment B, and panel (K iv), which shows how solutions from compartment A in K iii map to compartment B. State maps are shown in the rightmost three columns for positive slope, negative slope, and bistable systems, respectively. These maps indicate by color code the system states that occur for various levels of Mtot (y axis) and ratio of trafficking rates (x axis). The positive slope cases were all singly stable, except for panel L, and were therefore left blank. State map generation is explained in the Methods in the Supporting Material.
I carried out a graphical analysis and then generated over 50 example ODE models to confirm the properties of the interesting cases predicted graphically (Dataset S1 in the Supporting Material). I then systematically varied trafficking rates and molecular concentrations to generate a state map of resultant systems properties for selected trafficking permutations (Fig. 4).
This exploration of signaling and trafficking gave two broad findings: First, complex systems properties emerged when simpler signaling systems underwent trafficking, and second, trafficking parameters regulated the kinds of properties that could be generated. The first point is emphasized in the graphs in the middle columns in Fig. 4, which are color-coded for system properties. At least six distinct system properties were observed: 1 to 4 stable states, simple relaxation oscillators, and a combination state with a relaxation oscillator but also a stable point (labeled as Oscillatory 2). Oscillatory systems are familiar in biology (10,11,23), but the oscillations described here were distinctive as they spanned multiple compartments. The greatest diversity of states arose when bistable systems underwent trafficking. Negative slope systems gave rise to 1 to 3 stable states, but not oscillations. Finally, positive slope systems were singly stable, except in the case of SNARE-type trafficking (Fig. 4 L).
Trafficking parameters regulate emergent system properties
The second broad result was that trafficking mechanisms and parameters strongly influenced emergent system properties. Thus, similar trafficking configurations led to similar system outcomes, as seen in their state maps. For example, in Fig. 4, E, H, I, and K, the bistable (yellow) regions of the negative slope state maps were similar to the corresponding regions of the bistable state maps. This similarity was also seen between cases when the trafficking was identical except for the reaction in compartment B (e.g., Fig. 4, E and K, F and J). Among the trafficking categories studied, multistability was least likely in the cases in Fig. 4, D and G, and most likely by far for SNARE trafficking (Fig. 4 L). Oscillations were found in 6 of the 13 cases in Fig. 4.
Beyond these overarching effects where trafficking mode determined what states were accessible, there were also important quantitative regulatory effects. One observation was that there were large and distinct domains in the state maps for different functional properties. The size of the functional domains is a measure of robustness of system behavior with respect to parameter variation. With the exception of oscillations in Fig. 4 A, and bistability in Fig. 4 D, these domains were large, typically spanning at least one log unit.
The graphical analysis produces good estimates of stable states despite assumptions about steady state and intermediates
The graphical analysis predicts system stable states based on two key assumptions: the flux terms have a negligible effect on the shape of the M-versus-Mtot curves, and Mtot ∼ M + M∗ are in each compartment (Eq. 2). As discussed above, moderate flux terms are expected to give quantitative but not qualitative shifts in the stable states. The impact of the second assumption can be examined because the biochemical models in Fig. 4 have intermediate states, in the form of enzyme-substrate complexes for each enzymatic step. Thus, there are two intermediates between M and M∗ in each compartment in which there is a bistable or negative slope model.
To quantitatively test the effect of the two assumptions, I compared the graphical solutions with numerically accurate solutions obtained for the complete ODE systems in Fig. 4. The numerical solutions were obtained by solving the ODE equations for zeros, as described in the Methods in the Supporting Material. These solutions are plotted in the middle column of Fig. 4 as dots for stable states, and circles for unstable fixed points. In almost all cases the overlap with the graphical intersection points is excellent. Notable discrepancies occurs for some of the oscillatory models (blue on white background) and for panels A(iii), I(ii), J(iii), and L(iv). The average error of the graphical estimate was only 5.4% over the 100 stable and unstable states estimated in Fig. 4 (Methods in the Supporting Material).
The analysis predicts properties of known biological and model systems
I finally applied this analysis to selected published experimental and modeling studies that involve molecular traffic. These included diverse cellular phenomena such as compartmental identity, long-term state switches, and protein turnover.
A major mechanism for the formation of distinct cellular compartments involves SNARE trafficking. I considered just one pair of complementary SNARE molecules, t and v, that can dock with each other to enable vesicle fusion (Fig. 5). Following (4), I assigned them the symbols X and U, and assumed they would remain at equal concentrations. This enables the mixture of X and U to be mathematically represented simply as molecule M. I do not make any assumptions about the mechanisms involved in generating vesicles from the parent compartment, except that the process falls into one of the three cases for M-versus-Mtot curves. M represents the compartment-bound SNARE molecule and M∗ the vesicle-bound SNARE (Fig. 5, A and B). The rate to dock onto compartment B is proportional both to MA∗ (vesicular SNARE from compartment A) and MB (SNARE on compartment B). The converse applies for docking from MB∗ to compartment A.
Figure 5.
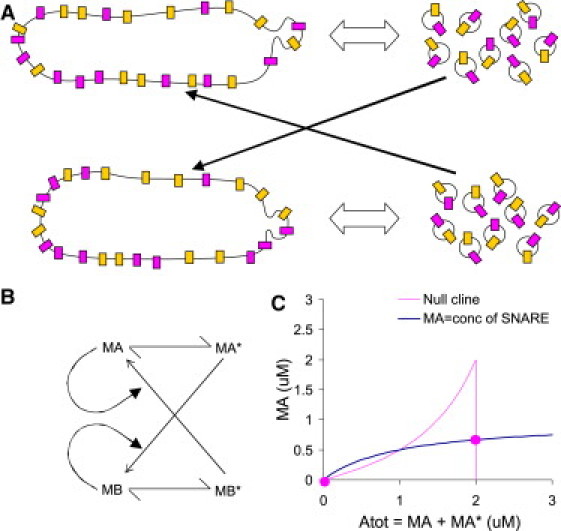
Analysis of SNARE trafficking. (A) Schematic of SNARE trafficking, between two compartments each of which bud out vesicles. The SNARE molecules X and U are represented as differently shaded membrane proteins in the compartments and in the vesicles. Trafficking is indicated by the thick black arrows. (B) Reduced reaction scheme for current analysis. The two SNARE species X and U are represented by MA in compartment A, MA∗ in vesicles originating from compartment A, MB in compartment B, and MB∗ in vesicles budding from compartment B. The formation of vesicles is a reversible conversion reaction in compartments A and B. For docking to occur the complementary SNAREs must be present on the target, thus the reaction depends both on vesicle and target compartment levels of SNARE. (C) Nullcline analysis of stable points of SNARE system. Here, total molecule concentration = Tot = 2.When all the molecules are in compartment A, MA can then take any value below Atot, hence the vertical line at Atot = Tot = 2.
Using Eq. 15, I found that the SNARE-mediated trafficking equations generated bistability over a wide parameter range regardless of whether the vesicle formation process was positive slope, negative slope, or bistable. If we stipulate that M (which represents specific SNAREs) confers compartment identity, the property of bistability results in the formation of complementary compartments identified by high and low levels of M, respectively. This has the interesting prediction that the generation of distinct compartment identities by SNARE traffic should be substantially independent of the specifics of the reaction systems for budding off and docking vesicles.
I next investigated long-term cellular switches. Some of the most detailed models of long-term switches are in synaptic plasticity. At least four such switches have been described (20,21,24,25). I considered two that involve trafficking: CaMKII and glutamate receptor (AMPAR) switches. CaMKII is a dodecamer that is activated by Ca4.CaM as well as by autophosphorylation. CaMKII translocates rapidly to the postsynaptic density (PSD) when it binds to Ca4.CaM. We treat CaMKII as molecule M, and Ca4.CaM.CaMKII as M∗, and regard the PSD as compartment A (Fig. 6 A). CaMKII has been proposed to be bistable on its own (24). However, in the model used as the basis for this study (20), neither the cytoplasmic nor the PSD-bound forms were individually bistable. Instead, the autophosphorylation resulted in a negative slope curve for CaMKII in the PSD. I took into account the role of the N-methyl-D-aspartate receptor as an anchor protein, and therefore used Eq. 8. I considered directional mass action traffic to set kb∗ = 0, kf = 0, and as in Eq. 11a. Although the actual reactions were complex, preliminary simulations showed that the dependence of MB∗ on MB was nearly linear. I therefore approximated MB∗ as
| (17a) |
Applying Eq. 2b: , we get
| (17b) |
Combining Eqs. 8, 11a, and 17b, we get
| (17c) |
The graphical analysis predicts bistability with steady states close to the original study (Fig. 6 B). This is an interesting outcome as it shows that CaMKII-mediated synaptic bistability need not depend on bistability of the autophosphorylation reactions.
Figure 6.
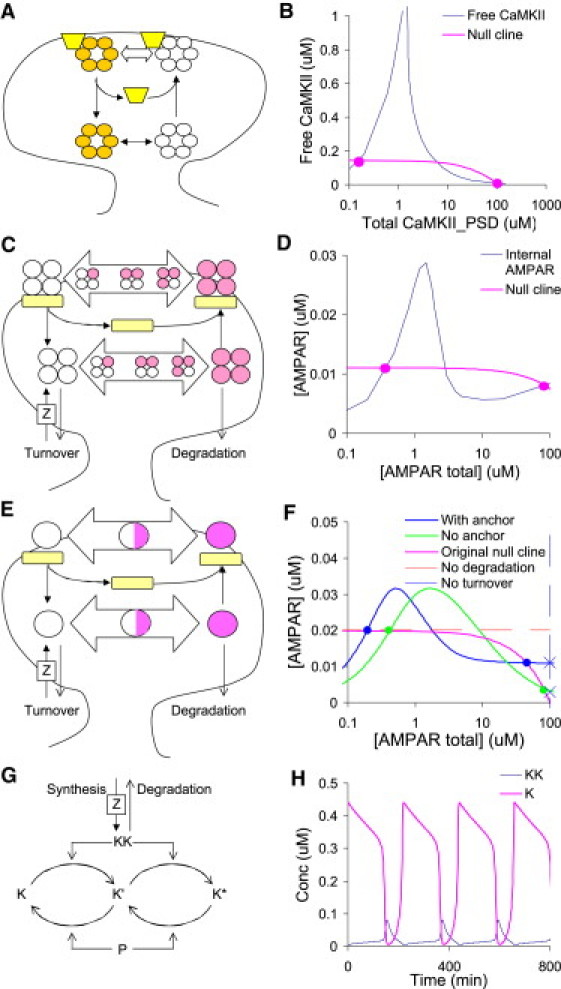
Analysis of synaptic plasticity and oscillator models. (A) CaMKII model schematic, based on model from (20). CaMKII is represented by a hexagon of six circles, which are shaded when phosphorylated. When calcium enters the synapse it binds to CaM, which in turn binds to CaMKII and promotes its translocation to the postsynaptic density near the membrane. This binding occurs on an anchor protein, which is the N-methyl-D-aspartate receptor. The terminal autophosphorylated state releases the CaM, and CaMKII returns to the cytosol. (B) Nullcline calculations for the CaMKII trafficking cycle. This system has two stable states. (C) Reaction schematic for AMPAR trafficking cycle (20). AMPAR undergoes turnover in the basal state and also degradation from the phosphorylated state. Several of the higher-phosphorylation states can associate with PSD-95 and thus translocate to the PSD. (D) Nullcline diagram for the major low-phosphorylation state in the bulk. This predicts bistability. (E) Reduced model of AMPAR trafficking, with fewer intermediates and single rather than tetrameric receptors. (F) Nullcline intersection diagrams for stable states of the reduced model, with or without anchor molecule. Bistability is retained for the original nullcline, but not if turnover or degradation are removed. (G) Model for MAPK cascade oscillations, in which the kinase KK is synthesized at a constant rate and is degraded at a rate proportional to the amount of KK (10). (H) Oscillations as predicted from an implementation of this turnover model.
I then considered trafficking and turnover of the alpha-amino-3-hydroxy-5-methyl-4-isoxazoleproprionic (AMPA) receptor at the synapse using the original model in accession 60 from DOQCS, from the same study (20). I constructed the MA-versus-Atot curve for the spine compartment, and replaced the AMPAR turnover and degradation reactions with the corresponding trafficking terms. The nullcline equation is very similar to Eq. 16b, with an additional term for the degradation step of the system:
| (18) |
Here, MA represents the unphosphorylated, internalized form of AMPAR. (open circles in Fig. 6 C). Once the stable points were estimated from the null-clines (Fig. 6 D), the levels of PSD-expressed AMPAR were computed by setting the system to these levels and running the model to steady state. The results were close to the original stable-state estimates: ∼16 AMPARs in the PSD for the low state and ∼148 for the high state. Original values were ∼20 and 135, respectively. In addition to its predictive value, this analysis simplifies understanding of the properties of a particularly complex model that has over 200 molecular species.
To further dissect out the role of trafficking conditions and reaction intermediates in the formation of bistability, I constructed a simplified version of the AMPAR trafficking model that eliminated many of the intermediates (Fig. 6 E). Here, the trafficked receptor had only one subunit and only one intermediate phosphorylation state (represented by a half-shaded circle). This had a similar M-versus-Mtot curve as the original system and similar predicted bistable states (Fig. 6 F, blue trace, blue dots to represent stable states). As a first variant, I eliminated the anchor protein (green trace, green dots). This too was bistable, but at somewhat different state values. As a second variant, I eliminated the degradation step. This resulted in a different nullcline, (indicated by the dashed red line). This system was now only singly stable. As a third variant, I eliminated the turnover step specified by reaction rate kb in Eq. 18. This resulted in the nullcline indicated by the dashed blue line. This again was only singly stable (blue crosses for the with-anchor and no-anchor cases). This series of tests established that, in this case at least, a), the presence or absence of intermediates did not remove bistability, b), the presence or absence of an anchor protein also did not eliminate bistability, but c), removing either of the key trafficking terms did eliminate bistability.
A final comparison based on models from the literature considered an example of protein turnover of MAPK regulators of multisite phosphorylation, leading to oscillations (10). Unlike other models considered here, this system involves synthesis and degradation of the regulatory kinase KK and phosphatase P (Figs. 4 F and 6 G), rather than trafficking. This turns out to have the same mathematical form as zero-order trafficking considered in Eq. 16a:
I considered the turnover of the kinase KK. As seen in Fig. 6 H, this system can indeed oscillate, as predicted in the original study (10). The current results uncover an interesting mathematical equivalence between protein turnover and trafficking.
Discussion
The current study integrates signaling and trafficking in a predictive mathematical framework that works for a large number of systems. The analysis is based on a survey of models of signaling systems that are based on experimental data. The survey reveals a new kind of signaling motif, to my knowledge, that constrains how a system will behave in the context of intercompartmental traffic. The current mathematical analysis builds on these motifs to predict system behavior for a wide range of trafficking mechanisms. The special strength of the analysis is that it is agnostic to the actual molecular mechanisms of reactions occurring within compartments. The domain of applicability of the current analysis is for systems where the compartmental reactions are substantially (at least 5 times) faster than the trafficking steps. Thus, it includes numerous trafficking configurations, including SNAREs. It also applies to many cases of molecular turnover. The analysis does not extend to several interesting nuclear and transcriptional switches and oscillators (Table S2).
Signaling motifs for trafficking
Signaling motifs provide important unifying concepts in studying complex biochemical networks, and are especially valuable in predicting likely functions (11,26,27). The current study identifies a new kind of signaling motif, to my knowledge, that applies when biochemical systems undergo molecular traffic. Here, I describe three such motifs: the breaking wave form, typical of bistable systems, the negative slope form, and the positive slope form (Fig. 2). Previously defined motifs have considered chemical connectivity features such as feedback and feedforward loops, and typically apply to small numbers of chemical reactions. Unlike such motifs, the present trafficking motifs are defined in terms of system properties, and are applicable to quite complex reaction networks. However, the trafficking motifs serve a similar role in identifying key components of a larger system, and predicting the kinds of behavior that may emerge when they are combined.
Trafficking and compartmental identity
The fundamental prediction of this analysis is that a variety of multistable and relaxation oscillator systems emerge from molecular trafficking between two compartments. This prediction has two main implications. First, for cell biology, it suggests molecular mechanisms for generating distinct compartmental identities, as determined by molecular composition. The multistable systems predicted in the current study result in a differential distribution of key signaling molecules between compartments. Here, the relevant feature of multistability is not that the system as a whole can flip states, but that the symmetry between compartments is broken when the system settles into any one state. In biological terms, as soon as the trafficking mechanisms bring the system into the bistable regime, the two compartments begin to settle into distinct molecular states predicted by the current analysis (e.g., Fig. S1). This kind of self-organization has already been analyzed for SNARE trafficking using specific assumptions about reaction mechanisms (4). This study generalizes this analysis, and shows that SNARE trafficking can generate distinct compartmental identities for a wide range of mechanisms for vesicle formation and trafficking parameters.
Trafficking and synaptic states
The second major implication of the study applies to synaptic plasticity. Bistable systems, such as the CaMKII autophosphorylation switch, are candidate mechanisms for long-term changes in synaptic properties (24). However, bistability typically appears for a rather narrow range of chemical parameters, and candidate bistable chemical mechanisms are rather few in number. For example, in the CaMKII autophosphorylation switch, the level of phosphatase activity is a rather tight constraint on the emergence of bistability (28). The current study incorporates the observation that many molecules translocate to or from the postsynaptic density following trigger stimuli such as Ca2+ influx. These include CaMKII itself, and the AMPA receptor. I have shown that even in the absence of biochemical bistability, this translocation may result in an overall bistable system (Fig. 6). Thus trafficking, which is essential for changing synaptic composition during plasticity, may simultaneously play an integral role in defining distinct stable states of the synapse.
Generalization
Given that two compartments and a single trafficked molecular species yield such a wide range of functional states, it is interesting to consider how such mechanisms might scale to more compartments and more trafficked molecules. At a trivial level, if each compartment holds N independent trafficking reactions, each of which gives rise to bistability, then there are potentially 2N possible compartmental states or identities. It is more biologically plausible that the trafficked molecules interact, thus reducing the number of states but resulting in coordinated functioning of the resulting compartments. It is known that cells can rapidly lose and then rebuild an array of compartmental subtypes following metabolic insults. The proposed mechanism may provide insights into this kind of self-organization of distinct compartment types.
Overall, this study shows that the combination of trafficking and signaling is a potent mechanism for creating and maintaining multiple distinct molecular signatures and states of cellular compartments.
Acknowledgments
I thank M. Thattai, R. Ramdass, E. Lebow, M. Rao, and members of the Bhalla lab for insightful comments.
This work was supported by the Department of Atomic Energy-Science Research Council (DAE-SRC) Outstanding Research Fellowship to U.S.B., the Department of Biotechnology, India, and the National Center for Biological Science (NCBS).
Supporting Material
References
- 1.Stenmark H. Rab GTPases as coordinators of vesicle traffic. Nat. Rev. Mol. Cell Biol. 2009;10:513–525. doi: 10.1038/nrm2728. [DOI] [PubMed] [Google Scholar]
- 2.Del Conte-Zerial P., Brusch L., Deutsch A. Membrane identity and GTPase cascades regulated by toggle and cut-out switches. Mol. Syst. Biol. 2008;4:1–9. doi: 10.1038/msb.2008.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gong H., Sengupta D., Schwartz R. Simulated de novo assembly of golgi compartments by selective cargo capture during vesicle budding and targeted vesicle fusion. Biophys. J. 2008;95:1674–1688. doi: 10.1529/biophysj.107.127498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Heinrich R., Rapoport T.A. Generation of nonidentical compartments in vesicular transport systems. J. Cell Biol. 2005;168:271–280. doi: 10.1083/jcb.200409087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Resat H., Ewald J.A., Wiley H.S. An integrated model of epidermal growth factor receptor trafficking and signal transduction. Biophys. J. 2003;85:730–743. doi: 10.1016/s0006-3495(03)74516-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brown G.C., Kholodenko B.N. Spatial gradients of cellular phospho-proteins. FEBS Lett. 1999;457:452–454. doi: 10.1016/s0014-5793(99)01058-3. [DOI] [PubMed] [Google Scholar]
- 7.Kholodenko B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 2006;7:165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Neves S.R., Tsokas P., Iyengar R. Cell shape and negative links in regulatory motifs together control spatial information flow in signaling networks. Cell. 2008;133:666–680. doi: 10.1016/j.cell.2008.04.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Malinow R., Malenka R.C. AMPA receptor trafficking and synaptic plasticity. Annu. Rev. Neurosci. 2002;25:103–126. doi: 10.1146/annurev.neuro.25.112701.142758. [DOI] [PubMed] [Google Scholar]
- 10.Wang X., Hao N., Elston T.C. Bistability, stochasticity, and oscillations in the mitogen-activated protein kinase cascade. Biophys. J. 2006;90:1961–1978. doi: 10.1529/biophysj.105.073874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tyson J.J., Chen K.C., Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003;15:221–231. doi: 10.1016/s0955-0674(03)00017-6. [DOI] [PubMed] [Google Scholar]
- 12.Sivakumaran S., Hariharaputran S., Bhalla U.S. The Database of Quantitative Cellular Signaling: management and analysis of chemical kinetic models of signaling networks. Bioinformatics. 2003;19:408–415. doi: 10.1093/bioinformatics/btf860. [DOI] [PubMed] [Google Scholar]
- 13.Ray S., Bhalla U.S. PyMOOSE: Interoperable Scripting in Python for MOOSE. Front Neuroinformatics. 2008;2:1–16. doi: 10.3389/neuro.11.006.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bhalla U.S., Ram P.T., Iyengar R. MAP kinase phosphatase as a locus of flexibility in a mitogen-activated protein kinase signaling network. Science. 2002;297:1018–1023. doi: 10.1126/science.1068873. [DOI] [PubMed] [Google Scholar]
- 15.Ferrell J.E., Xiong W. Bistability in cell signaling: how to make continuous processes discontinuous, and reversible processes irreversible. Chaos. 2001;11:227–236. doi: 10.1063/1.1349894. [DOI] [PubMed] [Google Scholar]
- 16.Markevich N.I., Hoek J.B., Kholodenko B.N. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 2004;164:353–359. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thomson M., Gunawardena J. Unlimited multistability in multisite phosphorylation systems. Nature. 2009;460:274–277. doi: 10.1038/nature08102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ramakrishnan N., Bhalla U.S. Memory switches in chemical reaction space. PLOS Comput. Biol. 2008;4:e1000122. doi: 10.1371/journal.pcbi.1000122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Goldbeter A., Koshland D.E., Jr. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA. 1981;78:6840–6844. doi: 10.1073/pnas.78.11.6840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hayer A., Bhalla U.S. Molecular switches at the synapse emerge from receptor and kinase traffic. PLOS Comput. Biol. 2005;1:137–154. doi: 10.1371/journal.pcbi.0010020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bhalla U.S., Iyengar R. Emergent properties of networks of biological signaling pathways. Science. 1999;283:381–387. doi: 10.1126/science.283.5400.381. [DOI] [PubMed] [Google Scholar]
- 22.Lipkow K., Andrews S.S., Bray D. Simulated diffusion of phosphorylated CheY through the cytoplasm of Escherichia coli. J. Bacteriol. 2005;187:45–53. doi: 10.1128/JB.187.1.45-53.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tsai T.Y.-C., Choi Y.S., Ferrell J.E., Jr. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science. 2008;321:126–129. doi: 10.1126/science.1156951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lisman J.E. A mechanism for memory storage insensitive to molecular turnover: a bistable autophosphorylating kinase. Proc. Natl. Acad. Sci. USA. 1985;82:3055–3057. doi: 10.1073/pnas.82.9.3055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Aslam N., Kubota Y., Shouval H.Z. Translational switch for long-term maintenance of synaptic plasticity. Mol. Syst. Biol. 2009;5:1–13. doi: 10.1038/msb.2009.38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Alon U. Network motifs: theory and experimental approaches. Nat. Rev. Genet. 2007;8:450–461. doi: 10.1038/nrg2102. [DOI] [PubMed] [Google Scholar]
- 27.Ma'ayan A., Lipshtat A., Sontag E.D. Proximity of intracellular regulatory networks to monotone systems. IET Syst. Biol. 2008;2:103–112. doi: 10.1049/iet-syb:20070036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Miller P., Zhabotinsky A.M., Wang X.J. The stability of a stochastic CaMKII switch: dependence on the number of enzyme molecules and protein turnover. PLoS Biol. 2005;3:e107. doi: 10.1371/journal.pbio.0030107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


