Origins and Consequences of Velocity Fluctuations during DNA Passage through a Nanopore

Abstract

We describe experiments and modeling results that reveal and explain the distribution of times that identical double-stranded DNA (dsDNA) molecules take to pass through a voltage-biased solid-state nanopore. We show that the observed spread in this distribution is caused by viscous-drag-induced velocity fluctuations that are correlated with the initial conformation of nanopore-captured molecules. This contribution exceeds that due to diffusional Brownian motion during the passage. Nevertheless, and somewhat counterintuitively, the diffusional Brownian motion determines the fundamental limitations of rapid DNA strand sequencing with a nanopore. We model both diffusional and conformational fluctuations in a Langevin description. It accounts well for passage time variations for DNA molecules of different lengths, and predicts conditions required for low-error-rate nanopore-strand DNA sequencing with nanopores.

Introduction

Solid-state nanopores are capable of detecting and characterizing individual charged polymers in solution. Recent work in solid-state (1–4) and protein-based nanopores (5–7) has focused on detecting DNA (8–11) with the aim of developing a rapid, inexpensive single-molecule DNA strand sequencing capability. The potential advantages of a nanopore approach to sequencing are many, as are fundamental challenges to its realization. In particular, a sequencing nanopore should have subnanometer spatial, and sufficient temporal, resolution for detecting and identifying individual bases along a DNA molecule as it passes through the nanopore (8). The recent development of single-layer graphene nanopores (12), multilayer graphene nanopores (13), and coated graphene nanopores (14) is an important step in achieving the required spatial resolution. But in connection with the time resolution, little attention has been paid to the impact of motional fluctuations of the DNA molecule in the nanopore. Thus the accuracy of a “read”, or sequence, will depend on the uniformity of DNA motion through the pore. In particular, backward motion of the DNA in the nanopore, caused by large velocity fluctuations, will give rise to sequencing errors and pose a potential limitation to the accuracy of nanopore strand sequencing.

Virtually all of the literature on the dynamics of DNA passage, or “translocation”, through biological and solid-state pores, focuses on understanding the relationship between DNA length and total translocation time. Experimental results show a superlinear power-law relationship (2,3,5,15,16), consistent with scaling-law predictions (16–19) and simulations (20,21). Escape time experiments in biological ion channels indicate interaction of the DNA molecule with the biological channel (6,7,22); loss rates in single-molecule trapping experiments suggest that similar interactions may occur in solid-state nanopores (23).

Given its importance for DNA sequencing, it is surprising that there has been little discussion of the variation in observed translocation times of identical DNA molecules. This variation has been reported in some cases (3,24), but quantitatively characterizing, modeling, and identifying the origins of the variations have not been achieved.

Here we present a study of the electrophoretic motions of double-stranded (dsDNA) molecules during nanopore translocation. We present experimental results for translocation time distributions of DNA molecules of two different DNA lengths that are selected to have an unfolded, single-file passage through the same nanopore. A simple model that relates the variation in translocation time to the unraveling of different (equally probable) initial conformational geometries of otherwise identical molecules is shown to agree well with experiments. The model predicts large velocity fluctuations during nanopore translocation that are produced by fluctuations in the drag force on a time-varying part of captured DNA molecules that have yet to pass through the pore. These fluctuations are correlated with the unraveling kinetics of DNA molecules from their random conformations during translocation through the nanopore. They are responsible for the spreads in translocation time distributions. Conformation-induced velocity fluctuations are to be distinguished from the diffusional Brownian motion fluctuations during the translocation event. We evaluate the consequences of Brownian motion fluctuations for strand sequencing and show that controlling their contribution is critical for strand sequencing, and derive conditions necessary for strand sequencing with a nanopore.

DNA Translocation Experiments

Experimental methods

Nanopore translocation experiments were designed to allow us to simultaneously study a mixture of two different length (5.3- and 10-kilobase) dsDNA molecules that pass through the same nanopore. These two lengths of molecules exhibit well-separated translocation time distributions. A nanopore of diameter 8–10 nm was fabricated with a 200 keV model No. 2010F transmission electron microscope (JEOL USA, Peabody, MA) in a 60-nm-thick freestanding membrane of low stress silicon nitride, as previously described (25). To reduce capacitance and associated electronic noise, the nitride layer was framed by a 2-μm-thick support layer of thermal silicon dioxide grown on the underlying silicon substrate. Nanopores fashioned in this way have an hourglass shape with a central cylindrical region whose effective channel length is ∼20 nm (26).

Fig. 1 shows a schematic of the experiment as a captured DNA molecule, from a random conformation, passes through a nanopore. Also shown in Fig. 1 is a freely jointed chain model of the DNA molecule that is used in the model. The free standing membrane with the nanopore separates two reservoirs filled with 1.6 M KCl maintained at pH 8 by a 10 mM Tris, 1 mM EDTA buffer. The trans reservoir was biased at V_bias = +100 mV relative to the cis reservoir by an Axopatch 200B patch-clamp amplifier (Molecular Devices, Sunnyvale, CA) coupled to the two reservoirs by Ag/AgCl electrodes. Under these conditions, a stable ionic current of 9 nA flowed through the nanopore, consistent with the nanopore geometry described above.

Figure 1.

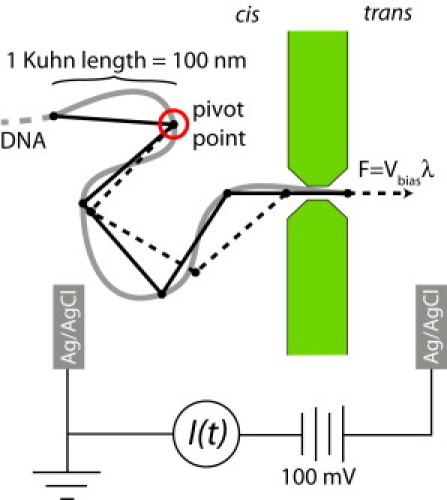
Geometry of DNA nanopore translocation experiment (schematic) and model. The DNA is rendered as a molecule with smooth conformational changes (shaded) and as a freely jointed chain used in the model (solid and dashed lines). In the model, a “pivot-point” is defined as the (changing) point on the molecule nearest to the nanopore and beyond which its conformation is unchanged as each Kuhn length is driven through the nanopore.

Double-stranded DNA (dsDNA) of length 5.3 kilobases (kb) was prepared from a ϕ×174RF1 plasmid (obtained from New England Biolabs, Ipswich, MA) by cutting the plasmid with SspI restriction enzyme and purifying by gel electrophoresis. A quantity of 10 kb dsDNA was purchased from New England Biolabs and purified by gel electrophoresis to yield no detectable contaminants. A 1:1 mixture of the purified 5.3-kb and 10-kb fragments was prepared at ∼1 nM each and injected into the cis reservoir. Single-molecule DNA-nanopore translocation events were observed as transient ionic current blockades. The ionic current data for each event was filtered by an eight-pole 40 kHz low-pass Bessel filter and digitized at 250 kilosamples/s. Approximately 4700 single-molecule current blockade events were observed. Previous work (2) has confirmed that these events are the result of single dsDNA molecules translocating through the solid-state nanopore and that the structure of each event is related to the folding of captured molecules in the nanopore (Fig. 2 a, inset). Nanopores may “clog”, either showing persistent current blockages and/or extended translocation times. This clogging is likely due to the sticking of DNA molecules or other impurities on the nanopore wall. No events after such a “clogging” incident have been included in the data presented here.

Figure 2.

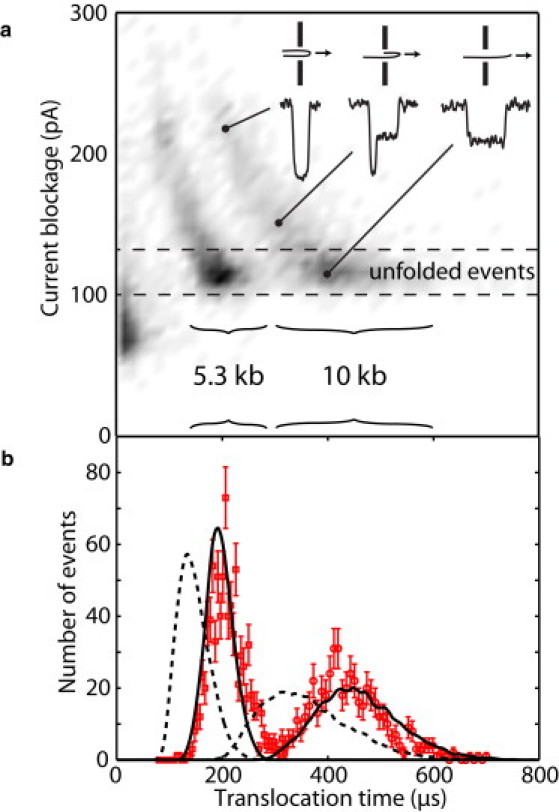
Translocation time distributions. (a) Density histogram of translocation events for 5.3 kb and 10 kb DNA. (Inset) Typical time traces for folded and unfolded events. (b) Translocation time histogram of 1350 unfolded events. (Error bars) Counting error in each histogram bin. The bin size is 4.9 μs for the 5.3 kb data and 7.8 μs for the 10 kb data. (Solid and dashed curves) Predictions of the two-dimensional models with and without a 300-nm center-of-mass offset, respectively.

All dsDNA translocation current trace events were processed using MATLAB code (MATLAB software; The MathWorks, Natick, MA) that fits each event to a series of sharp current steps modified by the transfer function of the experimental low-pass filter. The results comprise a data set represented by a two-dimensional histogram of average ionic current blockage versus event duration (Fig. 2 a). Approximately 1350 events corresponding to only unfolded DNA translocations (single-level events, in which only one double-helix occupies the pore at all times during the translocation process) were selected. The distribution of these translocation times was then compared to simulated DNA translocation events (Fig. 2 b) using a model described in Modeling Velocity Fluctuations, in Appendix A, and Appendix S1 in the Supporting Material.

Experimental results and discussion

The populations of all 5.3-kb and 10-kb events are readily distinguishable as two crescent-shaped structures in the two-dimensional current blockage-translocation time histogram shown in Fig. 2 a. Only the events between the dotted lines correspond to molecules that have passed through the pore unfolded, and it is these events that allow velocity fluctuations to be modeled and applied to the analysis of translocation time distributions in a straightforward way.

Translocation time distributions of 1350 unfolded events from the experiment are plotted in Fig. 2 b. These distributions are slightly asymmetric with the average translocation time larger than the most probable value. The most probable translocation time for 10 kb DNA (417 ± 5 μs) is slightly more than twice that of the 5.3-kb DNA (202 ± 1 μs), in agreement with previous findings (2,16). The average translocation times for 5 kb and 10 kb DNA are 211 ± 1 μs and 443 ± 5 μs, respectively. Error bars were calculated from numerical analysis of the translocation time distributions.

The experimental distribution widths (full width at half-maximum) are seen to be ∼33% of the mean unfolded event translocation times. These widths are significantly larger than would be expected from the diffusive motion of the molecule during the translocation. This can be seen by considering the velocity ν of the molecule in the nanopore to be described by a one-dimensional Langevin equation:

$$m\frac{dv}{dt}+\gamma v-F=A\left(t\right).$$ (1)

A DNA molecule of mass m and linear charge density λ translocating through the nanopore experiences a driving force, F = V_biasλ, due to the electric field in the nanopore. With λ ≈ 0.2 e⁻/bp (see Appendix S3) and a bias voltage of 100 mV, this driving force is F ≈ 9.4 pN. The DNA also experiences a stochastic thermal (Brownian) force A(t) from random molecular collisions. The driving force is opposed by a drag force −γν on the part of the molecule being moved through the solution. Experimentally, the mean translocation velocity $\langle \overline{v}\rangle$ for the 10 kb DNA is 7.4 mm/s. Assuming that the velocity of the DNA in the nanopore is roughly constant during the translocation, the fluctuation-dissipation theorem predicts an average diffusion constant given by $\langle D\rangle =k_{\text{B}}T/\gamma =\langle \overline{v}\rangle k_{\text{B}}T/F\approx 3.3\times {10}^{-12}{\text{m}}^2/\text{s}$. The ratio between the translocation time full width at half-maximum, $2\sqrt{2\ln 2}{\sigma }_t$, and the mean translocation time, t₀, is

$$2\sqrt{2\ln 2}\frac{{\sigma }_t}{t_0}\approx 2.35{\left(\frac{2\langle D\rangle t_0}{t_0^2{\langle \overline{v}\rangle }^2}\right)}^{0.5}\sim 0.038,$$ (2)

resulting in a translocation time width of ≈4% of the mean translocation time, whereas the experimentally observed widths in Fig. 2 b, are ≈33% of the mean. Thus, Brownian motion during the translocation is not the dominant factor responsible for the observed translocation time widths.

Modeling Velocity Fluctuations

Basic theory

We posit that the main contribution to spread in translocation times is from fluctuations in the drag force that can be modeled as a time-dependent drag coefficient γ in Eq. 1. Thus, as each molecule unraveled from its own geometrical conformation in the solution when it passes through the nanopore, only part of the molecule chain is being dragged through the solution (the “dragged part”) toward the nanopore at any given time. The rest of the chain (the “undragged part”) remains unaffected. The time-varying position along the molecule that separates the dragged and undragged regions along the molecule will be called the “pivot-point” (Fig. 1). Details of how the “pivot-point” is identified in our modeling simulations are discussed below and in Appendix S1.

What happens to the undragged region of the molecule during the translocation event depends on the details of the relaxation kinetics. The relaxation time for the entire molecule to attain an equilibrium conformation in solution is estimated by Zimm dynamics to be

$${\tau }_{Zimm}=\frac{\eta {\left(\sqrt{N}{l}_0\right)}^3}{\sqrt{3\pi }{k}_{\text{B}}T},$$ (3)

where N is the number of Kuhn segments of length l₀ and η is the viscosity of the solution (27). For a 10-kb dsDNA molecule in water, the Zimm time is τ_Zimm ≈ 20 ms, two orders-of-magnitude longer than the experimentally observed translocation times. Thus, for our experimental conditions, one is justified in assuming that the molecule conformation past the pivot-point is frozen during the translocation process. We note that this assumption is not valid for short single-stranded DNA (ssDNA) molecules passing through a protein nanopore because the Zimm time is much shorter than the ssDNA translocation time (28). Also, the freely-jointed chain model is reasonable only for dsDNA molecules longer than a few Kuhn lengths and applies to our experimental situation.

Consider a generalized Langevin equation of motion for the time-dependent “dragged” part of the translocating DNA molecule. As it unravels, the drag coefficient γ(t) and mass m(t) change with time. Thus

$$m\left(t\right)\frac{dv}{dt}-\gamma \left(t\right)v\left(t\right)-F=A\left(t;\gamma \left(t\right)\right).$$ (4)

Averaging Eq. 4 over times shorter than the translocation time of a Kuhn length, but much longer than the inertial relaxation time ${\tau }_R=m\left(t\right)/\gamma \left(t\right)\sim {10}^{-12}\text{s}$ (29), A and $dv/dt$ average to zero. One obtains a conformation-dependent time-varying average velocity

$$\overline{v}\left(t\right)=F/\gamma \left(t\right).$$ (5)

The fluctuations from Brownian motion are implicitly contained in Eq. 5 through an application of the fluctuation-dissipation theorem which relates the microscopic high frequency fluctuations in A(t) to the damping constant γ(t). The role of Brownian motion for nanopore sequencing will be discussed later in this article.

The calculational details used to study the time-variation of the drag force in Eq. 5 are provided in Appendix A, and Appendix S1. Briefly, the DNA is modeled by a freely jointed chain where each rigid segment is one Kuhn length long (100 nm or ∼294 basepairs). The 5.3-kb and 10-kb DNA molecules used in the experiment are 18 and 34 Kuhn lengths, respectively. The motion of the freely jointed chain passing through the nanopore is calculated as the molecule unravels from each member of an ensemble of appropriately selected random initial conformations. For each translocating segment at the nanopore, the calculation determines the minimum unraveling motion required from the rest of the molecule that enables the segment to pass through the pore. The changing pivot-point is therefore uniquely determined as each segment passes through the nanopore. The drag force, summed over each of the dragged Kuhn segments before the pivot-point, determines the molecular velocity of the translocating segment and, hence, the segment translocation time. This calculation is carried out for successive segments to yield the translocation time of the whole chain. The configuration of the molecule is restricted to a two-dimensional hexagonal lattice for computational accessibility. The plane of the lattice passes through the nanopore and lies perpendicular to the membrane. We find that the reduced dimensionality and the coarse lattice structure do not have a significant influence on the results (see Appendix S2).

Modeling the translocation dynamics of chains of the same length but different initial conformations provides predictions of translocation time distributions. The obtained translocation time for each conformation is sensitive to two free parameters in the model. The first is the linear charge density λ of the DNA molecule and the second is a center-of-mass offset, defined as the number of segments which are assumed unraveled and straight when the DNA translocation begins. This parameter accounts for an electric field gradient unraveling effect on the molecule before it actually begins to translocate through the nanopore, as well as any short-range drag force from the portion of the molecule on the trans side of the nanopore. The special role of the center-of-mass position of a particular conformation is discussed later in the article. Because all the equations are linear in the charge density, this parameter linearly scales the distribution with respect to the time axis. As described in Appendix A, the center-of-mass offset changes the initial conformation distribution. Comparison of the dashed and solid lines in Fig. 2 b illustrates that distributions with larger center-of-mass offsets are narrower and shifted to longer translocation times.

Modeling results

Calculated translocation time distributions for 10⁴ DNA molecules of 18 and 34 Kuhn lengths are shown as the smooth curves in Fig. 2 b. The dashed curves come from the model translocation dynamics of random-walk-generated conformations with no electric field gradient molecule straightening (zero center-of-mass offset) before capture into the nanopore. The experimental data are, however, best described by a center-of-mass offset of three Kuhn lengths and an effective charge density of 0.22 e⁻/bp plotted as the solid line in Fig. 2 b. The distribution shapes, widths, and positions are in very good agreement with the experimental data, and the effective charge density is consistent with previous measurements of DNA mobility (see Appendix S3). An additional data set (not shown) of a slightly smaller pore in 1 M KCl (conductance ≈30 nS, compared to ≈90 nS in 1.6 M KCl for the data shown) was best fit with a center-of-mass offset of three Kuhn lengths and an effective charge density of 0.30 e⁻/bp. The larger effective charge density in a smaller nanopore is in agreement with the literature (30).

With the help of the generalized Langevin model, we have also studied the correlation between the initial center-of-mass distance from the nanopore of each conformation and the translocation time for that conformation. Fig. 3, a histogram of the results for all modeled conformations of both 5.3 kb (18 Kuhn lengths) and 10 kb (34 Kuhn lengths), shows that shorter translocation times belong to molecules whose initial conformations on capture into the pore are centered near the pore, while molecules whose initial conformations are centered far from the pore take longer to translocate. The correlation is very strong and linear for both 5.3 and 10 kb DNA. For sufficiently long molecules, this means that the spread in translocation times arises primarily from the spread in this distance for different molecule conformations. This correlation likely lies behind the success of the scaling arguments used to relate most probable translocation time to molecular length (15,16).

Figure 3.

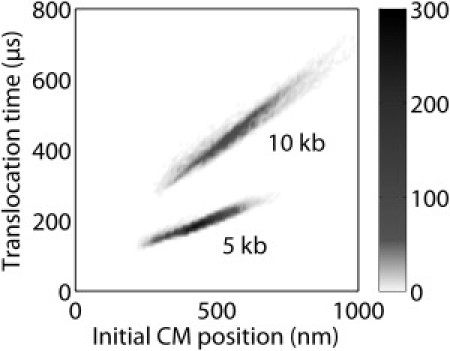
Distribution of translocation times as a function of initial center-of-mass position from the nanopore. Parameters are those used in the solid curves in Fig. 2.

The fluctuation of the translocation velocity for a single molecule due to its unraveling was also explored with the model. (Unfortunately, no one has figured out how to measure this experimentally yet.) Fig. 4 shows the predicted velocity $\overline{v}\left(t\right)$ for three molecule conformations. The average velocities, and hence translocation times, of these three conformations are very different, and in all cases the instantaneous velocity differs significantly from the average velocity during the translocation event. The first few molecular segments that enter the pore traverse quickly because only a few segments from the molecule's initial conformation contribute to the drag. As more segments are pulled through the pore, additional segments on the cis side of the nanopore become correlated to the motion of the segment in the pore, increasing the drag and reducing the translocation speed; that is, as the molecule translocates, the pivot-point, on average, moves away from the nanopore. Toward the end of the process, the molecule on the cis side is completely stretched. As it is pulled through the pore, it now becomes shorter, the drag force becomes less, and the translocation speed increases. These effects are particularly pronounced for molecules whose center-of-mass starts out far from the nanopore (molecule 3 in Fig. 4); for molecules whose center-of-mass is close to the nanopore (molecule 1), these trends are less pronounced than the velocity fluctuations due to the unraveling of a complicated initial conformation.

Figure 4.

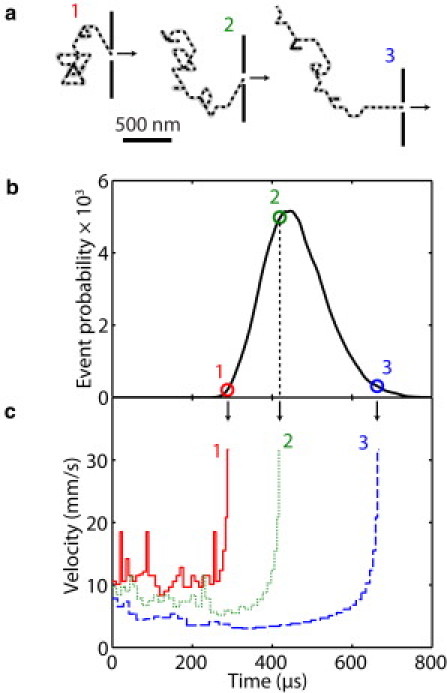
Examples of velocity and translocation time fluctuations from modeling results of 10-kb DNA molecules. (a) Initial conformations of three otherwise identical molecules with short, average, and long translocation times. (b) Modeled distribution of 10 kb molecules showing the translocation times of the conformations in panel a. (c) Velocity profiles of these three molecules during the translocation event.

Implications for DNA Strand Sequencing

Velocity fluctuations of the translocating molecule present a challenge to nanopore sequencing strategies by complicating the relationship between the elapsed translocation time and the “read position” along a DNA strand. The conformational velocity fluctuations discussed in the previous sections are important only on timescales corresponding to the translocation of a single Kuhn length. For DNA sequencing applications, these velocity fluctuations will be important to take into account, especially if the detector has limited time resolution or sensitivity. For an arbitrarily fast and sensitive detector operating at the much shorter timescales corresponding to successive translocations of individual bases, velocity fluctuations from Brownian motion will dominate the fluctuations over unraveling the initial conformations.

This effect is illustrated by the velocity power spectra plotted in Fig. 5. The power spectra are calculated from the model time-dependent velocity profile of a 10-kb molecule with a translocation time near the most probable translocation time (molecule 2 in Fig. 4). The solid curve is the power spectrum of conformational velocity fluctuations only, while the shaded curve includes Brownian motion (see Appendix S4 for details). The power spectral density of the velocity profile that includes Brownian motion is frequency-independent above the typical inverse translocation time of a single Kuhn length segment and dominates conformational velocity fluctuations at high frequencies. Note that under the experimental conditions in this article, the single-base translocation rate is ∼30 MHz (by comparison, the maximum bandwidth of the Axopatch 200B amplifier used for these measurements is 60 kHz). The contribution from the Brownian diffusional motion, $S_{thermal}=4k_{\text{B}}T\overline{v}\left(t\right)/F$, also fluctuates on slow timescales where the conformational velocity fluctuations dominate. The model velocity noise spectrum extending to high frequencies is shown in Fig. 5, which is calculated for the entire duration of the translocation event. It is directly related to the average spatial diffusion constant: $S_{thermal}=4k_{\text{B}}T\langle \overline{v}\rangle /F=4\langle D\rangle$ up to the damping relaxation frequency of the correlated segments, γ(t)/2πm(t) ≈ 10¹² Hz (29).

Figure 5.

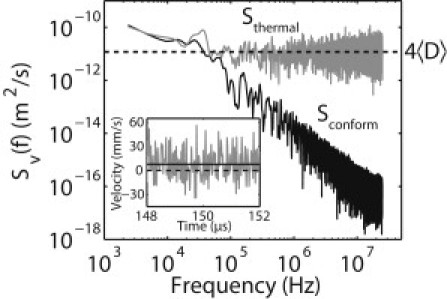
Power spectral density S_v(f) of the modeled translocation velocity profile of a 10-kb DNA molecule. (Shaded) Velocity power spectrum including Brownian motion. (Solid curve) Velocity power spectrum from unraveling the initial conformation only. Power spectra were calculated with a Blackman window function and slightly smoothed for clarity. The upper limit of frequency, 25 MHz, is similar to the single base translocation rate in our experiments. (Inset) Four microseconds of a simulated translocation sampled at 50 MHz. (Solid line) Average velocity in this time window. (Dashed line) Zero velocity.

The inset to Fig. 5 demonstrates how Brownian velocity fluctuations result in sequencing errors. In the small time window presented here, the conformational velocity fluctuations are minimal (solid curve), and Brownian motion dominates (shaded curve). When the instantaneous velocity drops below zero, the molecule is moving backward. (Large forward velocities fluctuations can result in skipped bases if the sampling interval is comparable to the rate of successive base passage.) Note that the conformational velocity fluctuations modeled earlier in the article do not result in backward molecular motions.

Consider a dsDNA molecule with basepair spacing a = 0.34 nm traversing a nanopore with our experimental mean velocity $\overline{v}\approx \langle \overline{v}\rangle =7.4\text{mm}/\text{s}$. The minimum bandwidth required for sequencing is $f_s=\overline{v}/a\approx 22\text{MHz}$. To avoid re-reading the same basepair from a backward fluctuation in the motion (Fig. 5, inset) the contributions to the root-mean-square thermal velocity fluctuation up to f_s, ${\overline{v}}_s$, must be smaller than $\overline{v}$. That is,

$${\overline{v}}^2\gg {\overline{v}}_s^2=S_{thermal}{f}_s=\left(4k_{\text{B}}T\overline{v}/F\right)\cdot \left(\overline{v}/a\right),$$

or

$$\frac{4k_{\text{B}}T}{Fa}\ll 1.$$ (6)

For our experimental conditions, a value of ∼5 is obtained for the left-hand side of Eq. 6. Therefore, Brownian diffusion would not make accurate sequencing of two adjacent basepairs possible under these conditions.

A more precise calculation of the error rate of strand sequencing from Brownian motion can be obtained by using a moving spatial Gaussian diffusion kernel, which describes the probability distribution of the position of a particle undergoing Brownian motion. If x₀ is the known position of the object in question at time t = 0, then

$$P\left(x,t\right)=\frac{1}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-x_0-\overline{v}t\right)}^2}{4Dt}\right).$$ (7)

Assume a high spatial resolution base identification mechanism (such as with a 0.6-nm-long graphene nanopore (12)) located at x = 0 that reads a base at t = 0. The probability that the next base is in the detection region between [−a/2, a/2] after a time t is

$$P_2\left(t\right)=\underset{-a/2}{\overset{a/2}{\int }}\frac{1}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x+a-\overline{v}t\right)}^2}{4Dt}\right)dx.$$ (8)

The probability this next base is at the detector after a characteristic time $\tau =a/\overline{v}$ is

$$P_2\left(\tau \right)=\underset{-a/2}{\overset{a/2}{\int }}\frac{1}{\sqrt{4\pi D\tau }}\exp \left(-\frac{x^2}{4D\tau }\right)dx=\text{erf}\left(\frac{1}{2}\sqrt{\frac{a^2}{4D\tau }}\right)=\text{erf}\left(\frac{1}{4}\sqrt{\frac{Fa}{k_{\text{B}}T}}\right).$$ (9)

The misread or error probability is

$$E_2=1-P_2\left(\tau \right)=\text{erfc}\sqrt{\frac{Fa}{16k_{\text{B}}T}}.$$ (10)

Equation 10 predicts a 75% read-error under the conditions in our experiments. These expressions are easily generalized to the n^th base:

$$E_n=1-P_n\left(\tau \right)=\text{erfc}\sqrt{\frac{Fa}{16\left(n-1\right)k_{\text{B}}T}}.$$ (11)

The effective error-free “read-length” for a single read of a nanopore-based strand-sequencing device is the base number n for which E_n falls below a critical accuracy level, say 95%. These results are plotted in Fig. 6 for n = 2, 4, 6. For n = 2, a driving force ∼50 times larger than that used in these experiments is necessary to achieve the 95% accuracy level. These results should also be applicable to ssDNA with the appropriate base spacing and driving force.

Figure 6.

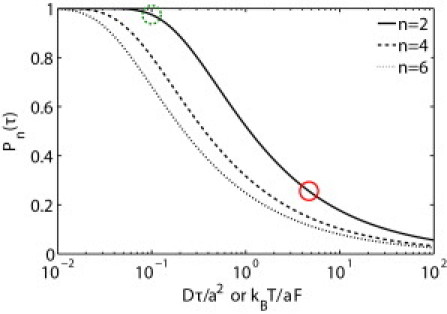
The sequencing probability success rate depends on the ratio of thermal motion to the work done by the driving force to drive a single base through the nanopore. (Solid circle) Current experimental conditions. (Dashed circle) Force necessary to achieve a 95% single-read success rate for two bases.

As shown in Eqs. 6 and 9, the relevant parameter for predicting strand sequencing error rates is the ratio of thermal energy to the work done to translocate the DNA from one base to the next, k_BT/Fa. One way to experimentally reduce the errors introduced by Brownian motion is to increase the driving force F. The resulting shorter times available for experimentally identifying bases can then, in principle, be offset by increasing the viscosity of the solution. It must be noted that simply changing the viscosity to slow down the molecule's motion does not reduce the diffusional contribution. Any reduction in the diffusion constant by increasing the viscosity of the solution is offset by the longer time each base has to diffuse as it passes through the nanopore, which is why there is no viscosity dependence in the sequencing parameter k_BT/Fa.

The importance of considering the Brownian motion of the strand in the nanopore is illustrated in Fig. 7, which demonstrates the limitations Brownian motion imposes on the ability to discriminate among 10 basepairs with an ideal instrument. We do not consider other important practical issues, such as electronic readout signal/noise or the spatial resolution of the nanopore. Under ideal conditions (k_BT/Fa → 0), the molecule translocates at a constant speed, and the signals from each base will be readily distinguished (Fig. 7 a). Fig. 7 b shows the effect of Brownian motion under our present experimental conditions, denoted by the solid circle in Fig. 6. With a 75% read-error, the Brownian fluctuations are dominant within these timescales; we obtain periodic discrimination between basepairs but not enough to generate an accurate sequence in a single read. Increasing the driving force by at least an order of magnitude is sufficient to achieve base discrimination, as shown in Fig. 7 c. Under these conditions, the accuracy is ∼95%, and although variations in the velocity of the molecule still exist, these have been sufficiently suppressed to yield distinguishable signals from each of the 10 bases in our simulated molecule.

Figure 7.

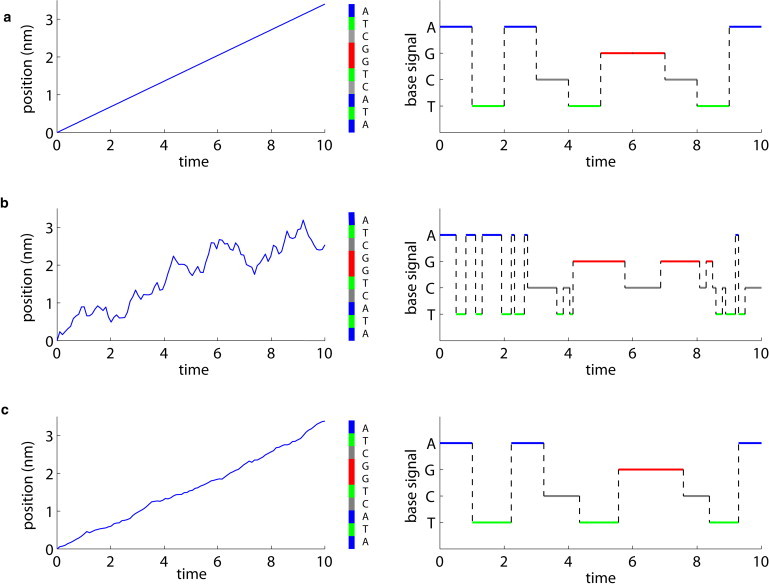
A 10-base DNA strand passes through a detector with single base resolution under various experimental conditions. Time units are normalized to the average base translocation time $\tau =a/\overline{v}$. (a) If the molecule traverses the detector with a constant speed, the signal recorded will be clear. (b) With Brownian motion at our experimental driving force, the recorded signal is full of errors. (c) By applying a driving force 50 times larger to suppress the relative motion fluctuations (and increasing the solution viscosity by a factor of 50 to maintain the same velocity), the read is much improved.

The foregoing treatment of Brownian motion in the nanopore may require some modification to very accurately account for the relaxation dynamics of the diffusing DNA strand. During translocation of ssDNA, for example, the translocation time of a single base is similar to molecular relaxation times, and the relaxation dynamics may contribute to the random motion of the strand in the nanopore on these timescales. For dsDNA, the translocation time of a single base is much faster than the molecular relaxation times of the molecule, and we do not expect the relaxation dynamics to affect the calculated error rate. A kind of effective diffusion, which is influenced by the conformation of the entire molecule, has been described by “fractional Brownian motion” (31–33). It will be interesting to see whether further refinement of our model is necessary to account for experimental sequencing results.

Finally, we note that forces other than the driving force F may be used to overcome the Brownian diffusion. For example, additional large clamping or ratcheting forces acting on the DNA during the read can reduce the errors, as appears to have been achieved in Lieberman et al. (34) by biochemical means. Control of a single molecule's motion through a nanopore has also been achieved by optical tweezers (35,36), and could potentially be achievable by AFM/nanotube sensors (37), though the practicality of these methods for rapid sequencing is unclear. Also, errors can be reduced by performing multiple reads on identical molecules or on nanopore-recaptured molecules as has been reported in Gershow and Golovchenko (23).

Conclusion

We demonstrate the existence of different mechanisms that give rise to mechanical fluctuation effects for single molecules passing through solid state nanopores. Conformational differences between molecules of the same length determine the spread in their translocation time distribution. These differences in translocation time impact measurements whose goal is to determine molecular lengths. During each translocation event, a simple Langevin model shows that the translocation velocity undergoes large fluctuations as the initial molecular conformation is unraveled. Brownian fluctuations dominate at the short timescales required to achieve rapid single-molecule strand sequencing and may be overcome with sufficiently high driving voltage and other applied control forces to the translocating DNA molecule. Realizing base-scale subnanometer molecular control that overcomes Brownian motion for strand sequencing is a major challenge that may be solved by introducing large forces based on biochemical or physics-based nanotechnology methods. Improvements by error correction based on resequencing may also be anticipated.

Appendix A: Simple Translocation Model

Each initial conformation is generated on a two-dimensional hexagonal lattice as a random walk from a node corresponding to the nanopore. As shown in Fig. 8, the first m steps of the random walk are directly away from the nanopore, and the random walk is also excluded from a distance of m Kuhn lengths from the membrane. The parameter m is called the “center-of-mass offset” and is a free parameter in our model. The center-of-mass offset accounts for the fact that the electric field gradient just outside the nanopore will stretch the “equilibrium” conformations as a molecule approaches the nanopore; it also can account for the added drag associated with pushing a short length of the molecule into the fluid on the trans side of the membrane, which, although not modeled explicitly, should correspond to the drag from only one or two Kuhn lengths.

Figure 8.

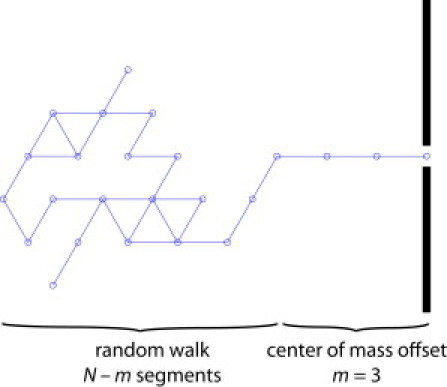
Illustration of the center-of-mass offset m used to generate the initial molecule conformations. The first m segments are straight; the remaining N – m segments undergo a random walk but are excluded from a distance m from the membrane.

The center-of-mass offset m = 3 cited in the main text was chosen to provide the best agreement between the simulated and experimental translocation times. Note that, in general, the center-of-mass offset may depend weakly on both the applied potential and the length of the molecule. As high field gradients distort the “equilibrium” molecular conformation, the center-of-mass offset will become larger. Long molecules may also contribute additional drag as the molecule is pushed away from the nanopore on the trans side of the membrane. Because our model is intended for qualitative understanding of the effects of molecular rearrangement on the translocation velocity, we do not consider these effects further.

Because we experimentally study unfolded events, we are interested in only those initial conformations in which an end of the molecule is presented to the nanopore. To generate our initial conformations, we discard all conformations for which the molecule crosses into the excluded membrane region. This procedure is in contrast with the usual method of generating random conformations in equilibrium, which involves a reflection principle for random walks that cross the membrane (38).

For the translocation process of a molecule chain, each simulation step describes the motion of one Kuhn length, or segment, of dsDNA through the nanopore. The index of the segment passing through the nanopore is i. The value of the drag coefficient γ_i depends on the details of the molecular conformation resulting from the previous step and is calculated for use in evaluating the average segment velocity ${\overline{v}}_i=F/{\gamma }_i$ and the segment translocation time ${\tau }_i=l_0/{\overline{v}}_i$. The total translocation time for each molecule is $\tau ={\sum }_i{\tau }_i$. The detailed algorithm is described in Appendix S1.