Spectroscopic and Computational Characterization of the Base-off Forms of Cob(II)alamin

Abstract

The one-electron reduced form of vitamin B₁₂, cob(II)alamin (Co2+Cbl), is found in several essential human enzymes, including the cobalamin-dependent methionine synthase (MetH). In this work, experimentally validated electronic structure descriptions for two “base-off” Co²⁺Cbl species have been generated by using a combined spectroscopic and computational approach, so as to obtain definitive clues as to how these and related enzymes catalyze the thermodynamically challenging reduction of Co²⁺Cbl to cob(I)alamin (Co¹⁺Cbl). Specifically, electron paramagnetic resonance (EPR), electronic absorption (Abs), and magnetic circular dichroism (MCD) spectroscopic techniques have been employed as complementary tools to characterize the two distinct forms of base-off Co²⁺Cbl that can be trapped in the H759G variant of MetH, one possessing a five-coordinate and the other a four-coordinate, square-planar Co²⁺ center. Accurate spin Hamiltonian parameters for these low-spin Co²⁺ centers have been determined by collecting EPR data using both X- and Q-Band microwave frequencies, while Abs and MCD spectroscopic techniques have been employed to probe the corrin-centered π → π* and Co-based d → d excitations, respectively. By using these spectroscopic data for evaluating electronic structure calculations, it was found that density functional theory provides a reasonable electronic structure description for the five-coordinate form of base-off Co²⁺Cbl. However, it was necessary to resort to a multireference ab initio treatment to generate a more realistic description of the electronic structure of the four-coordinate form. Consistent with this finding, our computational data indicate that in the five-coordinate Co²⁺Cbl species, the unpaired spin density is primarily localized in the Co 3d_z²-based molecular orbital, as expected, whereas in the four-coordinate form, extensive Co 3d orbital mixing, configuration-interaction, and spin-orbit coupling cause the unpaired electron to delocalize over several Co 3d orbitals. These results provide important clues with regards to the mechanism of enzymatic Co²⁺Cbl → Co¹⁺Cbl reduction.

1. Introduction

The enzymatic reduction of base-off cob(II)alamin (Co²⁺Cbl) to cob(I)alamin (Co¹⁺Cbl) represents a thermodynamic challenge due to a mismatch between the reduction potentials of the electron acceptor, base-off Co²⁺Cbl (Eº ≈ −500 mV vs. SHE),¹ and the ultimate source of reducing equivalents under physiological conditions, nicotinamide adenine dinucleotide phosphate (NADPH, Eº = −320 mV vs. SHE).² Base-off Co²⁺Cbl contains a central Co²⁺ ion coordinated equatorially by four nitrogens derived from a tetrapyrrole macrocycle, termed the corrin ring, and axially ligated by a solvent-derived water ligand (Figure 1).³ Upon Co²⁺ → Co¹⁺ reduction, the axial Co–OH₂ bond is broken to produce a four-coordinate Co¹⁺Cbl species,^4,5 which is an extremely potent nucleophile.^6,7 This supernucleophillic Co¹⁺Cbl species is utilized by methyltransferases, such as the cobalamin-dependent methionine synthase (MetH),⁸ and by adenosine-5′-triphoshpate:corrinoid adenosyltransferases (ATRs),⁹ to generate the biologically-active forms of the B₁₂ cofactor, methylcobalamin (MeCbl) and adenosylcobalamin (AdoCbl), respectively. To elucidate the mechanisms by which these enzymatic systems access Co¹⁺Cbl, it is critical to develop a detailed understanding of the electronic properties of its precursor, base-off Co²⁺Cbl. Although in principle this goal can be accomplished solely by computational methods, the complexity of this species requires that the results obtained in theoretical studies be carefully validated on the basis of spectroscopic data.

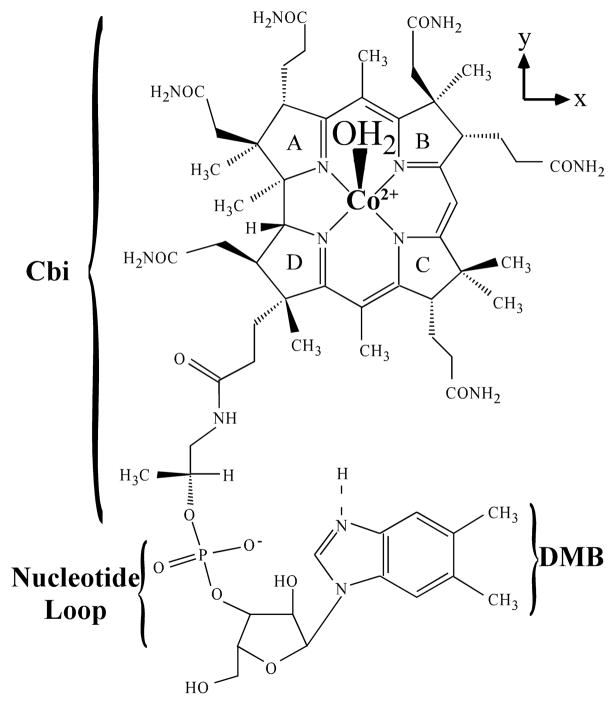
Figure 1.

Chemical structure of base-off Co²⁺Cbl. The Co²⁺ ion is bound equatorially by a corrin ring and axially by a solvent-derived water ligand. The dimethylbenzimidazole (DMB) base can be displaced from the Co²⁺ center by protonation at low pH, as indicated by the dashed line, or interaction with enzyme active-site residues. The Co²⁺Cbi⁺ derivative lacks the nucleotide loop and the DMB base; therefore, this species possesses an axially bound solvent molecule regardless of pH.

The electronic structure of five-coordinate base-off Co²⁺Cbl, a low-spin (S = 1/2) 3d⁷ species, has been well characterized by electron paramagnetic resonance (EPR) spectroscopy, which is particularly sensitive to the compositions and relative energies of the Co 3d-based molecular orbitals (MOs). The EPR spectrum of cob(II)inamide (Co²⁺Cbi⁺, also a low-spin 3d⁷ species), a truncated derivative of the B₁₂ cofactor that serves as a model for base-off Co²⁺Cbl at neutral pH (Figure 1), is nearly axial, with g_⊥ = 2.3 and g_|| = 2.0, and exhibits hyperfine structure due to strong coupling between the unpaired electron and the ⁵⁹Co (I = 7/2) nucleus, A_⊥ (⁵⁹Co) = 215 MHz and A_||(⁵⁹Co) = 395 MHz.^10–13 The large isotropic contribution to the hyperfine tensor, A_iso(⁵⁹Co) = 275 MHz, indicates that the majority of the unpaired spin density is localized on the Co²⁺ center, which implies that the singly-occupied MO (SOMO) is a Co 3d-based orbital. Indeed, the pattern of g values observed for Co²⁺Cbi⁺ is consistent with a Co (3d_x²-y²)²(3d_xz)²(3d_yz)²(3d_z²)¹ electronic configuration, where the 3d_xz and 3d_yz orbitals are nearly degenerate.¹⁴ In agreement with this deduction of a Co 3d_z²-based SOMO, the results obtained using hyperfine sublevel correlation (HYSCORE) spectroscopy, a pulsed EPR technique, have revealed that weak hyperfine couplings exist between the unpaired electron and the corrin ring nitrogens, which are oriented properly to interact with the torus of the Co 3d_z² orbital.¹³ However, a quantitative interpretation of low-spin Co²⁺ EPR parameters requires that one considers spin-orbit and configuration-interaction (CI) mixing of the Co 3d → 3d ligand field (LF) excited states with the ground state.¹⁵

The second form of base-off Co²⁺Cbl contains a four-coordinate Co²⁺ center that lacks any significant axial bonding interactions; this form has been identified only in several enzyme active sites.^16–21 Qualitatively, the Co²⁺ coordination number change from five to four should preferentially stabilize the Co 3d_z²-based SOMO by eliminating the μ-antibonding interaction along the Co–OH₂ bond coordinate.²² As a result, the Co 3d_xz → 3d_z² and Co 3d_yz → 3d_z² LF excited states will be stabilized in energy and engage in more extensive spin-orbit mixing with the ground state, thus causing a greater deviation of the g_⊥ value from the free electron value, g_e = 2.0023.¹⁴ Additionally, the A(⁵⁹Co) parameters are anticipated to be larger for the four-coordinate form of base-off Co²⁺Cbl than for the five-coordinate form, because dissociation of the axial ligand will decrease the ligand orbital character and increase the Co 3d_z²-orbital character in the SOMO. Therefore, the large g_⊥ and A(⁵⁹Co) values observed for certain enzyme-bound Co²⁺Cbl species have been interpreted as spectroscopic signatures of four-coordinate Co²⁺Cbl. In strong support of this proposal, similarly large g_⊥ and A(⁵⁹Co) EPR parameters have consistently been reported for square-planar, low-spin Co²⁺-phthalocyanine^23–27 and Co²⁺-porphine^27–38 complexes, which can be viewed as axially symmetric models for four-coordinate Co²⁺Cbl.

The electronic absorption (Abs) and magnetic circular dichroism (MCD) spectra of the putative four-coordinate Co²⁺Cbl species also exhibit several distinct differences from those of five-coordinate base-off Co²⁺Cbl and Co²⁺Cbi⁺. These spectral perturbations have been rationalized in terms of a stabilization of the Co 3d_z²-based SOMO based upon a spectro/structural correlation that was established by carrying out density functional theory (DFT) calculations on Co²⁺Cbi⁺ models in which the axial Co–OH₂ bond length was systematically increased from its equilibrium value of 2.20 Å.¹⁸ However, as detailed later in this paper, several features of the EPR and MCD spectra of four-coordinate Co²⁺Cbl suggest that LF excited states exist that are sufficiently low in energy to markedly perturb the ground-state properties of this species. Consequently, it may be necessary to treat the electronic structures of the four- and five-coordinate base-off Co²⁺Cbl forms as being fundamentally different.

The primary goal of this study was to develop experimentally validated electronic structure descriptions for both forms of base-off Co²⁺Cbl by using a combined spectroscopic and computational approach. To accomplish this goal, two major challenges needed to be overcome. First, the Co²⁺ coordination number change from five to four preferentially stabilizes the Co 3d_z²-based MO, shifting this orbital close in energy to the Co 3d_xz- and 3d_yz-based MOs. In the Co²⁺-phthalocyanine and Co²⁺-porphine complexes of approximately D_4h symmetry, this causes the ²A_1g and ²E_g states to shift close in energy; thus, the ground state electron configuration becomes somewhat ambiguous.¹⁵ Second, four-coordinate Co²⁺Cbl has only idealized C_2v symmetry due to the low symmetry of the corrin ring (Figure 1). This symmetry reduction lifts the degeneracy of the Co 3d_xz- and 3d_yz-based MOs and leaves three distinct candidates for the electronic ground state of four-coordinate Co²⁺Cbl; namely, ²A₁, 2B₁, and 2B₂ (in the C_2v parent point group). Knowing which of these serves as the ground state is essential for fully understanding the mechanism of electron transfer to base-off Co²⁺Cbl in the process of Co²⁺ → Co¹⁺ reduction. For example, in the ²A₁ ground state the “redox-active” MO will have predominantly Co 3d_z²-character and electron transfer will be fastest from an electron donor positioned directly above or below the plane defined by the corrin ring.³⁹ Alternatively, ²B₁ and ²B₂ ground states will favor electron transfer from diagonally above or below the corrin ring, along the x- and y-axes of the cofactor, respectively (see Figure 1).

In this work, we have used EPR spectroscopy to characterize Co²⁺Cbl bound to the H759G variant of MetH, a species that can be stabilized in two distinct conformations, one favoring the five-coordinate form and the other the four-coordinate form of base-off Co²⁺Cbl.¹⁹ Combined fits of the EPR spectra collected at two different microwave frequencies were used to extract precise spin Hamiltonian parameters for each species. To obtain complementary information about the electronic structures of these species, we probed the relative energies of the Co 3d-based and corrin π-based MOs by utilizing MCD and Abs spectroscopies, respectively. The insights gained in these experimental studies have been used to evaluate electronic structure descriptions generated by using DFT and spectroscopy oriented configuration interaction (SORCI)⁴⁰ calculations for both forms of base-off Co²⁺Cbl. Collectively, the results obtained in this work provide significant new insight into the electronic structure of four-coordinate Co²⁺Cbl and, thus, the mechanism of Co²⁺ → Co¹⁺ reduction employed by MetH and related enzymes.

2. Experimental Methods

2.1. Sample Preparation

Glycerol was purchased from Sigma-Aldrich, degassed on a vacuum line at 55 °C, and backfilled with nitrogen gas. Argon gas was purchased from Linde and used without purification. The expression and purification of the two fractions of Co²⁺Cbl-bound H759G MetH has been described previously.^19,41 After purification, these two fractions were stored at −80 °C in 10 mM potassium phosphate buffer (pH 7.2).

For low-temperature X-Band EPR, Abs, and MCD spectroscopic measurements, the two fractions were thawed on ice and mixed with degassed glycerol (60% v/v) to ensure glass formation at cryogenic temperatures. The glycerol solutions were purged with a stream of argon gas prior to loading the MCD cells and X-Band EPR tubes under an inert atmosphere to prevent oxidation of the Co²⁺Cbl cofactor. The MCD cells were immediately frozen in liquid nitrogen, whereas the EPR tubes were placed in an ice bath for 10–15 minutes prior to freezing to draw the solutions to the bottom of the tubes. The final concentration of Co²⁺Cbl in each sample was ~280 μM.

For 35 GHz (commonly called Q-Band) EPR spectroscopic measurements, the two fractions of H759G MetH-bound Co²⁺Cbl were thawed on ice, mixed with degassed glycerol (10% v/v), and loaded into 2 mm i.d. 35 GHz EPR tubes under an atmosphere of nitrogen gas. The final concentration of Co²⁺Cbl in each sample was ~600 μM.

2.2. Spectroscopy

X-Band (~9 GHz) EPR spectra were collected with a Bruker ESP 300E spectrometer equipped with a Varian EIP model 625A CW frequency counter. The sample temperature was maintained at 20 K by an Oxford Instruments ESR 900 continuous flow liquid helium cryostat regulated by an Oxford ITC4 temperature controller. All X-Band EPR spectra presented in this work were collected with 1 mW of microwave power, a 100 kHz field modulation of 10.5 G, and a time constant of 82 ms. Q-Band (~35 GHz) EPR spectra were collected using a modified Varian E-109 spectrometer equipped with a liquid helium immersion dewar for measurements at 2 K. Q-Band EPR spectra were acquired with an attenuation of 40 and 50 dB (~10 and 1 μW of microwave power, respectively), a field modulation of 1.5 G, and a time constant of 64 ms. The Q-Band EPR spectra were collected under “rapid passage” conditions, which facilitate the observation of broad spectral features.⁴²

Abs, MCD, and variable-temperature variable-field (VTVH) MCD data were obtained using a Jasco J-715 spectropolarimeter in conjunction with an Oxford Instruments SM4000-8T magnetocryostat. All MCD spectra presented in this paper were obtained by taking the difference between data obtained with the magnetic field applied parallel and anti-parallel to the light propagation axis to remove contributions from the natural circular dichroism and glass strain.

2.3. Spectral Analysis

The relative contributions from the five- and four-coordinate forms of base-off Co²⁺Cbl to the X-Band EPR spectra of the two fractions of H759G MetH-bound Co²⁺Cbl were determined from the g_|| region of each spectrum. Because the two base-off Co²⁺Cbl forms exhibit distinct saturation behaviors, the contributions from each form to the Q-Band EPR spectra of the two fractions could be separated by using two different microwave powers. The SIMPOW6 program, which was developed by Dr. Mark Nilges at the University of Illinois based on the QPOW program,⁴³ was used to simulate the EPR spectra and extract the spin Hamiltonian parameters. For each species, the X- and Q-Band EPR spectra were fit with identical g and A(⁵⁹Co) tensors, which were assumed to be collinear to limit the number of adjustable parameters. The complete parameter sets obtained from these EPR spectral fits are available in the Supporting Information (Tables S1–S4).

The MCD spectra of the two H759G MetH fractions were deconvoluted by assuming that the ~16500 and ~13500 cm⁻¹ features can be solely attributed to the five- and four-coordinate forms of base-off Co²⁺Cbl, respectively. The resulting MCD spectra were then decomposed into the minimal acceptable number of Gaussian bands of fixed width to resolve the individual electronic transitions that contribute to the overall traces. Complete parameter sets obtained from these MCD spectral fits are available in the Supporting Information (Figures S1–S2 and Tables S5–S6). To determine the polarization of the electronic transition associated with the prominent low-energy MCD feature of four-coordinate base-off Co²⁺Cbl, VTVH MCD saturation curves were collected at 742 nm and fit with the MCD saturation magnetization fitting program written by Professor Frank Neese by using the principal g values determined from the simulation of the corresponding EPR spectrum (Figure S3 and Table S7).⁴⁴

2.4. DFT Computations

All electronic structure calculations presented in this work were carried out on a cluster of 22 Intel Xeon processors (ACE computers) running the Fedora 8 (Red Hat) operating system. The initial geometric models for base-off Co²⁺Cbl were derived from the X-ray crystal structure of Co²⁺Cbl (CSD file KECWUK),⁴⁵ where all side-chains and methyl groups attached to the periphery of the corrin macrocycle were removed and replaced by hydrogen atoms. For the five-coordinate form, a water molecule was added to the “lower” face of the cofactor at a distance of 2.3 Å from the Co center. For the initial geometric model of N-rac-[Co²⁺-5,7,7,12,14,14-hexamethyl-1,4,8,11-tetraazacyclotetradeca-4,11-diene(H₂O)] (abbreviated [Co²⁺(Me₆[14]dieneN₄)(H₂O)], Scheme 1), atomic positions were taken from the corresponding X-ray crystal structure (CSD file JASKUJ)⁴⁶ and the methyl groups attached to the periphery of the tetraaza macrocycle were replaced by hydrogen atoms. These initial models were refined by complete geometry optimizations using the Amsterdam Density Functional 2007.01 software package.^47–49 The unrestricted Kohn-Sham calculations utilized a density functional composed of the Vosko-Wilk-Nusair-5 local density and the Perdew-Burke-Ernzerhof (PBE) generalized gradient functionals,^50,51 the TZP basis set with a small frozen core, and an integration parameter of 5.0. The geometry optimizations used the following convergence criteria: 0.0001 Hartree change in total energy, 0.001 Hartree/Å in the Cartesian gradients, and 0.001 Å change in the Cartesian coordinates between subsequent cycles.

Scheme 1.

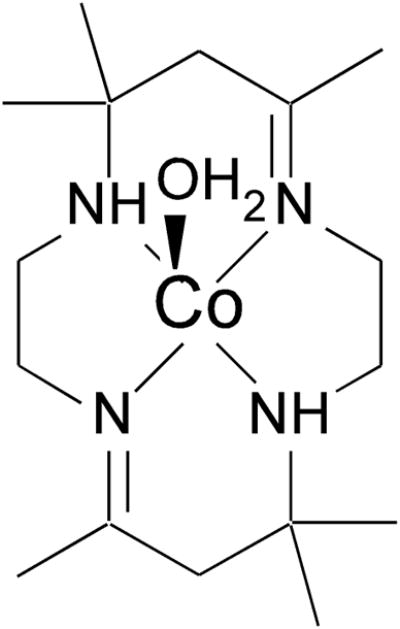
Chemical Structure of [Co²⁺(Me₆[14]dieneN₄)(H₂O)]

Unrestricted single-point DFT and EPR parameter calculations for both forms of base-off Co²⁺Cbl as well as [Co²⁺(Me₆[14]dieneN₄)(H₂O)] were performed with the ORCA 2.6–35 software package using the Perdew-Wang 91 local density and the PBE generalized gradient functionals.^49,51,52 The TZVP basis set was used for Co and all ligating atoms, while the SVP basis set was used for all other atoms.⁵³ The resolution of the identity (RI) approximation was used to speed up the calculation of the Coulomb term by approximating the molecule’s charge distribution with the SV/J auxiliary basis set.^54,55 The EPR g and A(⁵⁹Co) tensors were computed using coupled-perturbed self consistent field (CP-SCF) theory,⁵⁶ with a complete mean-field treatment of spin-orbit coupling and the IGLO gauge origin.⁵⁷

The energies and Abs intensities of the electronic transitions of base-off Co²⁺Cbl and [Co²⁺(Me₆[14]dieneN₄)(H₂O)] were predicted with time-dependent DFT (TDDFT) as implemented in ORCA 2.6–35, using the same functionals and basis sets as described above for the EPR parameter calculations.^{49,51–54,58} A total of 60 excited states were computed by including all single excitations between MOs with orbital energies between −5 and +5 Hartrees using the RI and Tamm-Dancoff approximations.⁵⁹

To facilitate the interpretation of the DFT computational results, isosurface plots of the quasi-restricted MOs were generated with the gOpenMol program using an isodensity value of 0.03 au.^60–63 Additionally, the TDDFT results were used to simulate Abs spectra by assuming that each predicted transition gives rise to a Gaussian band of constant width (ν_1/2 = 1250 cm⁻¹) to allow for a visual comparison with our experimental Abs data.⁴⁹

2.5. SORCI Computations

Multireference descriptions of the doublet ground state and four low-lying doublet LF excited states for both forms of base-off Co²⁺Cbl as well as for [Co²⁺(Me₆[14]dieneN₄)(H₂O)] were obtained using the SORCI method with a CAS(7,5) reference space, as implemented in ORCA 2.6–35.⁴⁰ The Abs intensities for the electronic excitations from the ground state to these four LF excited states were also predicted by SORCI. The initial orbitals included in these calculations were the five Co 3d-based quasi-restricted MOs derived from the DFT calculations described above (section 2.4).⁶³ The thresholds T_sel, T_pre, and T_nat were set to 10⁻⁶ Hartrees, 10⁻⁴, and 10⁻⁵, respectively, and the MO integrals were evaluated “on the fly” by using the RI approximation with the SV/J auxiliary basis set to speed up the calculations.^54,55 Isosurface plots of the approximate average natural orbitals (AANOs) were created with the gOpenMol program using an isodensity value of 0.03 au.^60–62

3. Results

3.1. EPR spectroscopy

The primary goal of this study was to characterize the ground state electronic structures of the five-coordinate and four-coordinate base-off Co²⁺Cbl species associated with the two different conformations of the H759G variant of MetH. The three potential electronic ground states outlined in the Introduction differ with respect to their Co 3d orbital occupations. EPR spectroscopy is particularly well suited to differentiate among these three possibilities, as this technique offers a uniquely sensitive probe of the ground-state wavefunction and the relative energies of the metal d-based MOs in paramagnetic transition-metal complexes.¹⁴ In particular, for an S = 1/2 system with an orbitally non-degenerate ground state, such as the Co²⁺Cbl species investigated here, g shifts from the free-electron value of g_e = 2.0023 arise from spin-orbit coupling between the ground state and LF excited states. Thus, an analysis of the g values can reveal the identity of the electronic ground state and provide an estimate of the relative Co 3d orbital energies. Complementary insight into the nature and composition of the SOMO can be obtained from the A(⁵⁹Co) values, which are particularly sensitive reporters of the unpaired spin-density distribution.

The EPR spectrum of base-off Co²⁺Cbl is quite complex as a result of the magnetic dipole interaction between the unpaired electron and the ⁵⁹Co (I = 7/2, 100%) nucleus and the low symmetry of the Co²⁺Cbl cofactor (Figure 1). However, the principal values of the g and A(⁵⁹Co) tensors can be determined quite conveniently by collecting EPR data at two different microwave frequencies. This multi-frequency EPR approach has been extensively employed with Cu²⁺ complexes,⁶⁴ but less so for low-spin Co²⁺ species. The resonance position associated with each g value depends on the choice of microwave frequency, whereas the hyperfine splitting is independent of this choice. Consequently, the g values can be determined with greater accuracy at a higher frequency (Q-Band, ~35 GHz), while the A(⁵⁹Co) values are more readily obtained at a lower frequency (X-Band, ~9 GHz). In this study we have taken advantage of this characteristic of multi-frequency EPR spectroscopy by alternatively fitting the g values to the Q-Band spectra and the A(⁵⁹Co) values to the X-Band spectra.

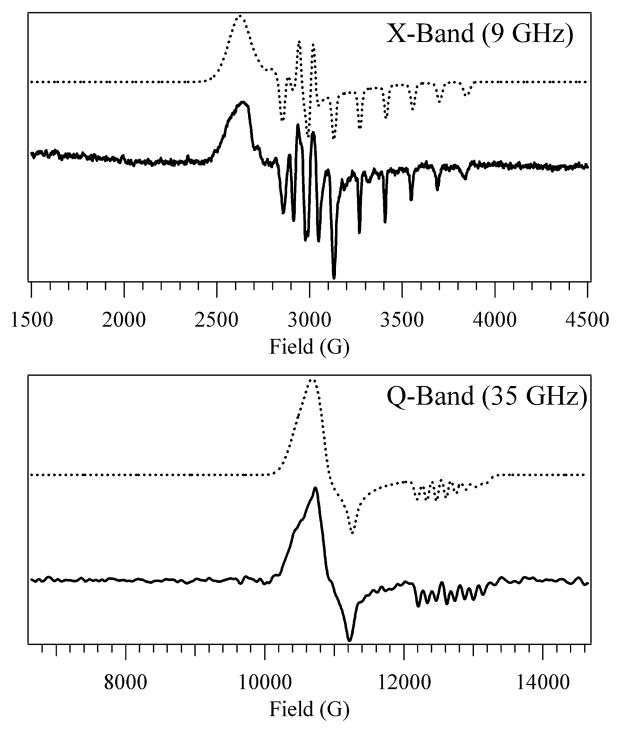
The contributions from the five-coordinate form of base-off Co²⁺Cbl to the X- and Q-Band EPR spectra of H759G MetH-bound Co²⁺Cbl are shown in Figure 2. The spin Hamiltonian parameters extracted from a simulation of these spectra are in excellent agreement with those reported recently for base-off Co²⁺Cbl in aqueous solution (Table 1).¹³ The pattern of g values (g₁ ≥ g₂ > g₃ ≈ g_|| ≈ g_e) observed for this species is consistent with a Co 3d_z²-based SOMO. The large g shifts of the g₁ and g₂ values reflect relatively strong spin-orbit mixing of Co 3d_xz → 3d_z² and Co 3d_yz → 3d_z² LF excited-state character into the electronic ground state. The A(⁵⁹Co) values are also consistent with a Co 3d_z²-based SOMO, based on the anisotropy in the A(⁵⁹Co) tensor that is largely determined by the magnetic dipole-dipole interaction between the unpaired electron and the ⁵⁹Co nucleus.

Figure 2.

Top: X-Band EPR spectrum at 20 K of five-coordinate base-off Co²⁺Cbl. Bottom: Q-Band EPR spectrum at 2 K of five-coordinate base-off Co²⁺Cbl. Solid lines: experiment. Dotted lines: simulation.

Table 1.

Experimental EPR parameters

				A(59Co, MHz)
	g1	g2	g3	A1	A2	A3
5-coordinatea	2.382	2.302	1.992	206	229	392
4-coordinateb	2.814	2.534	1.935	695	556	495
Diene modelc	2.43	2.43	2.016

^aThis work, Figure 2;

^bThis work, Figure 3;

^c[Co²⁺(Me₆[14]dieneN₄)(H₂O)], from ref. 69.

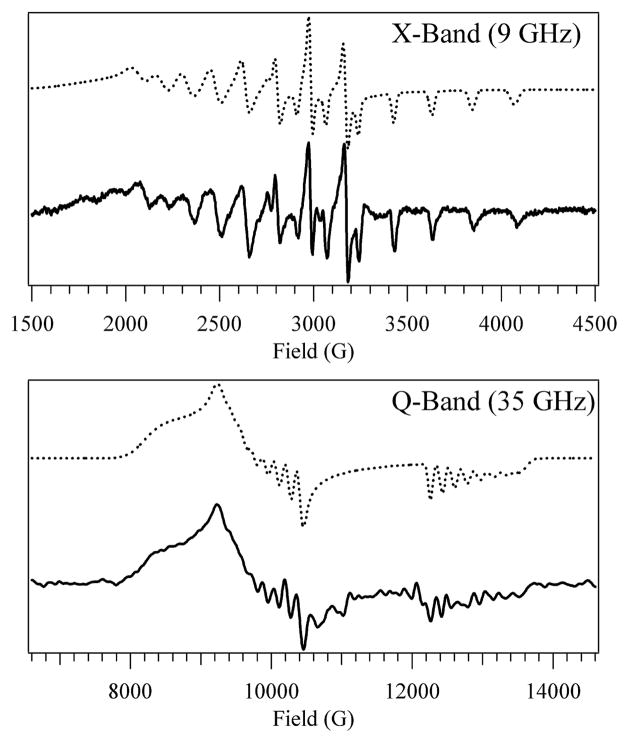
The contributions from the four-coordinate form of base-off Co²⁺Cbl to the X- and Q-Band EPR spectra of Co²⁺Cbl bound to H759G MetH are shown in Figure 3. The g shifts and A(⁵⁹Co) values for this species are uniformly larger than those associated with the five-coordinate form (Table 1), as expected on the basis of the qualitative arguments presented above. In particular, the removal of the axial ligand stabilizes the Co 3d_z²-based SOMO, thereby enhancing spin-orbit mixing between the ground state and LF excited states and thus causing an increase in the g shifts. Concomitantly, the SOMO becomes more localized on the Co center, thereby giving rise to a larger Fermi contact (isotropic) contribution to the A(⁵⁹Co) tensor. However, the g values of the four-coordinate base-off Co²⁺Cbl species are not entirely consistent with a Co 3d_z²-based SOMO, and thus with a pure 2A₂ ground state. Specifically, the g₃ ≈ g_|| value should be very close to g_e = 2.0023 for a Co 3d_z²-based SOMO, yet our EPR spectral simulations indicate that g₃ = 1.935. A likely explanation for this discrepancy is that the four-coordinate Co²⁺Cbl species does not have rigorous C_2v symmetry due to the side-chains and methyl groups attached to the periphery of the corrin ring (Figure 1). Thus, the SOMO may actually also have sizeable contributions from Co 3d orbitals other than 3d_z², thereby causing g₃ to deviate from g_e.

Figure 3.

Top: X-Band EPR spectrum at 20 K of four-coordinate base-off Co²⁺Cbl. Bottom: Q-Band EPR spectrum at 2 K of four-coordinate base-off Co²⁺Cbl. Solid lines: experiment. Dotted lines: simulation.

3.2. Abs and MCD spectroscopy

To complement the multi-frequency EPR experiments described above, we also carried out Abs and MCD spectroscopic studies of the H759G MetH-bound five- and four-coordinate forms of base-off Co²⁺Cbl. Previous studies have revealed that when these techniques are used collectively, they offer extremely sensitive probes of the electronic structures of Co²⁺Cbl species.^{16–19,22,65} The Abs spectra of these species are dominated by electric-dipole allowed transitions, such as corrin centered π → π* excitations. Accordingly, this technique reports on the relative energies of the corrin π- and π*-based MOs, which primarily depend on the geometric and electronic structures of the corrin macrocycle. Alternatively, the formally electric-dipole forbidden Co 3d-based LF transitions, which are too weak to be discerned in the Abs spectrum, can be detected by MCD spectroscopy. Consequently, MCD spectroscopy provides a means by which to determine the energies of the Co²⁺ LF excited states, which can be correlated with the g shifts observed by EPR spectroscopy. In addition, a careful analysis of the VTVH MCD saturation data collected for a particular band can reveal the polarization of the corresponding electronic transition relative to the molecular coordinate system (as defined by the g tensor), thereby aiding the identification of the donor and acceptor MOs involved in this transition.⁴⁴

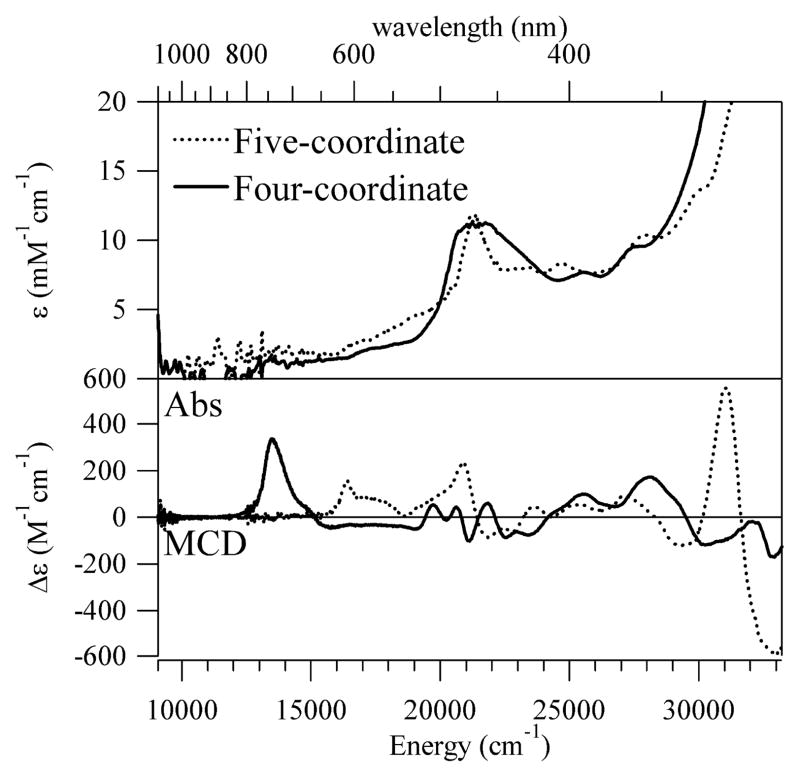
The Abs spectra of Co²⁺Cbl bound to H759G MetH in the two different enzyme conformations were used to determine the “pure” spectra of the five- and four-coordinate base-off Co²⁺Cbl species via spectral deconvolution (Figure 4, top). Because the dominant feature in the visible region of the Abs spectrum arises from corrin-centered π → π* transitions, its peak position is nearly identical for the five- and four-coordinate base-off Co²⁺Cbl species. Thus, Abs spectroscopy is rather poorly suited to monitor changes in the axial coordination environment of base-off Co²⁺Cbl.

Figure 4.

Abs spectra at 2 K (top) and MCD spectra at 2 K and 7 T (bottom) of five- and four-coordinate base-off Co²⁺Cbl.

Compared to Abs spectroscopy, MCD spectroscopy offers a superior probe of the electronic structure of base-off Co²⁺Cbl, as it permits individual electronic transitions, including those involving the Co²⁺ 3d-based MOs, to be resolved (Figure 4, bottom). The MCD spectrum of the five-coordinate species is very similar to that of Co²⁺Cbi⁺,²² consistent with our EPR data presented above. The Co²⁺Cbi⁺ MCD spectrum has recently been analyzed within the framework of DFT calculations,¹⁸ and the results obtained in this analysis provide an excellent basis for interpreting our MCD spectra presented in Figure 4. The positively-signed band at 16500 cm⁻¹ has been assigned to the Co 3d_x²-y² → 3d_z² LF transition, while the Co 3d_xz → 3dz² and Co 3d_yz → 3d_z² LF transitions have been shown to occur outside the spectral range accessible to our MCD instrument (< 9000 cm⁻¹). The other feature of interest is the negatively-signed band at 21700 cm⁻¹, which corresponds to a corrin π → π* transition involving a donor MO that contains a small amount of Co 3d_z² orbital character.¹⁸

As expected, major differences are evident between the MCD spectra of the five-coordinate and four-coordinate forms of base-off Co²⁺Cbl (Figure 4, bottom). The positively signed band centered at 16500 cm⁻¹ in the five-coordinate base-off Co²⁺Cbl MCD spectrum red-shifts by 2900 cm⁻¹, to 13600 cm⁻¹, upon removal of the axial water ligand. VTVH MCD data collected for four-coordinate Co²⁺Cbl indicate that the corresponding transition (formally Co 3d_x²-y² → 3d_z²)¹⁸ is 62% z-polarized relative to the g tensor coordinate system (Figure S3 and Table S7), a result that will be used below to assess the accuracy of computed electronic structure descriptions for this species. In contrast to the red-shift observed for the lowest-energy MCD band, the corrin π → π* transition associated with the negatively-signed feature at 21700 cm⁻¹ in the five-coordinate Co²⁺Cbl MCD spectrum blue-shifts by 600 cm⁻¹, to 22300 cm⁻¹, in the spectrum of the four-coordinate species. As discussed above (section 3.1), removal of the axial water ligand from base-off Co²⁺Cbl should preferentially stabilize the Co 3d_z²-based SOMO. This prediction is consistent with the observed red-shift of the 3d_x²-y² → 3d_z² LF transition as well as the blue-shift of the corrin π → π* transition, given the small admixture of Co 3d_z² orbital character to the corresponding corrin π-based donor MO.²² However, our deconvolutions of the MCD spectra in Figure 4 into sums of individual Gaussian bands indicate that it is not possible to establish a one-to-one correlation between the electronic transitions of five- and four-coordinate base-off Co²⁺Cbl (Figures S1–S2 and Tables S5–S6). This finding suggests that it may be an oversimplification to describe the electronic structure of the four-coordinate Co²⁺Cbl species in terms of a slight deviation from that of the five-coordinate form, in agreement with our EPR spectroscopic results presented above.

3.3. DFT Computations

To complement our spectroscopic data and generate quantitative electronic structure descriptions for both forms of base-off Co²⁺Cbl, we have performed DFT computations on suitably truncated cofactor models. DFT has proven to be an extremely useful method for the study of free and enzyme-bound Co²⁺Cbl species, because it features a reasonably accurate and efficient means to approximate electron correlation,⁶⁶ which is quite significant for transition metal complexes.⁶⁷ However, DFT has several limitations that must be taken into consideration when interpreting computational results; namely, the approximate treatment of electron exchange and correlation and the use of a single determinantal wavefunction.⁶⁸ To assess whether these approximations compromise the accuracy of the computed electron and spin distributions for the five- and four-coordinate base-off Co²⁺Cbl species, we have also used DFT to predict the corresponding Abs and EPR spectroscopic parameters and compared these to the experimental results presented above.

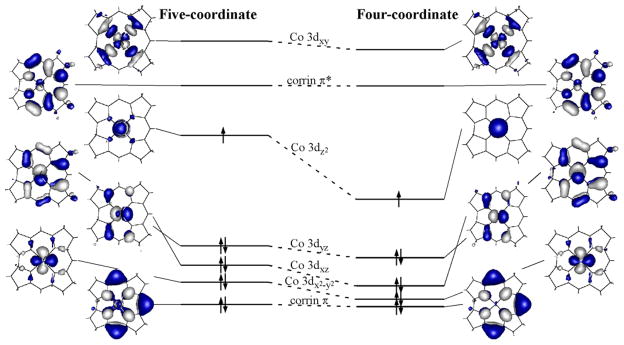
The relevant portions of the DFT-computed energy-level diagram of the quasi-restricted MOs for five- and four-coordinate base-off Co²⁺Cbl are shown in Figure 5.⁶³ The energies of the corrin π- andπ*-based MOs that correspond to the highest occupied and lowest unoccupied MOs of the 14 electronπ-system of this macrocycle, respectively, are virtually identical for the two forms of base-off Co²⁺Cbl. In contrast, the Co 3d_z²-based MO is considerably stabilized in four-coordinate Co²⁺Cbl due to the elimination of the μ-antibonding interaction with the axial water ligand that exists in the five-coordinate form. This DFT-predicted large stabilization of the Co 3d_z²-derived MO in response to a Co2+ coordination number change from five to four, but with a relative insensitivity of the corrin π- and π*-based orbitals, are both consistent with our spectroscopic data.

Figure 5.

Isosurface plots and relative orbital energies of the DFT-computed quasi-restricted MOs for base-off Co²⁺Cbl.

The g and A(⁵⁹Co) tensors for each form of base-off Co²⁺Cbl and the five-coordinate model complex [Co²⁺(Me₆[14]dieneN₄)(H₂O)] were calculated using the DFT/CP-SCF computational scheme to assess the feasibility of the DFT-predicted electronic structures on the basis of the experimental EPR data.⁵⁶ Importantly, these DFT/CP-SCF calculations properly reproduce the experimental trends in g shifts and A(⁵⁹Co) parameters from five- to four-coordinate Co²⁺Cbl (cf. Tables 1 and 2). Additionally, they successfully predict that the g₁ and g₂ values of [Co²⁺(Me₆[14]dieneN₄)(H₂O)] are intermediate between those of five- and four-coordinate Co²⁺Cbl and that the g₃ value is larger for the model complex than for either form of base-off Co²⁺Cbl.⁶⁹ Yet, while the DFT/CP-SCF calculations qualitatively reproduce the experimental trend in g shifts, the magnitudes of these shifts are considerably underestimated. The lack of quantitative agreement between the experimental and computed g shifts could be attributed to a systematic shortcoming of the DFT/CP-SCF computational scheme when applied to low-spin Co²⁺ complexes. However, the failure of the DFT/CP-SCF calculation to yield the correct symmetry of the g and A(⁵⁹Co) tensors for four-coordinate Co²⁺Cbl indicates that there may be a more fundamental problem with the DFT-computation. Specifically, the description of the SOMO of four-coordinate base-off Co²⁺Cbl as possessing almost exclusively Co 3d_z² orbital character is overly simplistic, which has the consequence of yielding axial, rather than the observed rhombic, g and A(⁵⁹Co) tensors.

Table 2.

DFT/CP-SCF-computed EPR parameters

				A(59Co, MHz)
	gx	gy	gz	Ax	Ay	Az
5-coordinate	2.175	2.161	2.003	356	384	894
4-coordinate	2.322	2.261	2.004	506	541	1034
Diene modela	2.221	2.177	2.008

^a[Co²⁺(Me₆[14]dieneN₄)(H₂O)]

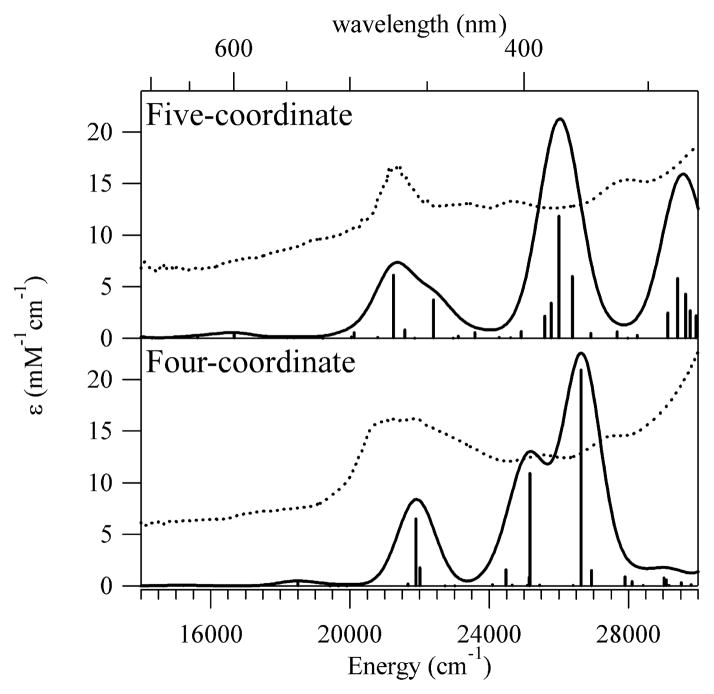
While the DFT/CP-SCF predicted EPR parameters are well suited to assess the accuracy of the DFT-computed relative energies and compositions of the Co 3d-based MOs, they do not permit a meaningful evaluation of the theoretical description of the corrin π system. Therefore, TDDFT calculations were performed for both forms of base-off Co²⁺Cbl to test the accuracy of the DFT-computed corrin π- and π*-based MOs on the basis of the experimental Abs spectra, which are dominated by corrin π → π* transitions. As shown in Figure 6, TDDFT correctly reproduces the energy and intensity of the dominant feature in the visible region of the Abs spectrum, as well as the slight blue-shift of this feature from five- to four-coordinate base-off Co²⁺Cbl. The overall good agreement between the experimental and TDDFT-computed Abs spectra indicates that DFT provides a reasonable description of the corrin π system for both forms of base-off Co²⁺Cbl. Thus, the shortcomings of the DFT-computed electronic structure descriptions for these species are largely limited to the energies and compositions of the Co 3d-based MOs.

Figure 6.

Top: TDDFT-computed (solid line) and experimental 2 K (dotted line) Abs spectra of five-coordinate base-off Co²⁺Cbl. Bottom: TDDFT-computed (solid line) and experimental 2 K (dotted line) Abs spectra of four-coordinate base-off Co²⁺Cbl.

MCD spectroscopy offers another sensitive probe of the Co 3d-based MOs, yielding information about the two forms of base-off Co²⁺Cbl that nicely complements the insights gained from EPR spectroscopy. Consequently, a comparison of the TDDFT-predicted transition energies and polarizations to those derived from our MCD data provides an independent test of the computational results. While TDDFT correctly predicts the dramatic blue-shift of the Co 3d_x²-y² → 3d_z² transition accompanying a change in Co²⁺ coordination number from five to four, it largely underestimates the energy of this transition for both forms of base-off Co²⁺Cbl, and to a lesser extent also for [Co²⁺(Me₆[14]dieneN₄)(H₂O)] (Table 3).⁶⁹ In addition, TDDFT severely overestimates the Co 3d_yz → 3d_z² and Co 3d_xz → 3d_z² transition energies for [Co²⁺(Me₆[14]dieneN₄)(H₂O)], suggesting that the energies of these transitions are also overestimated for base-off Co²⁺Cbl. Also, neither the Co 3d_x²-y² → 3d_z² transition, nor any other low-energy electronic transition in the TDDFT-computed Abs spectrum, is predicted to have the experimentally determined polarization of the 13600 cm⁻¹ band of four-coordinate base-off Co²⁺Cbl (section 3.2). Collectively, these results provide further evidence that the DFT-computed electronic structure descriptions for base-off Co²⁺Cbl are somewhat inaccurate and suggest that a more realistic ground-state wavefunction may be obtained by using a multireference ab initio approach, especially in case of the four-coordinate species.

Table 3.

Experimental, TDDFT-computed, and SORCI-computed Co 3d → 3d_z² electronic transition energies

			Donor MO
		3dyz	3dxz	3dx2-y<2
5-coordinate	Exp.	< 9000 cm−1	< 9000 cm−1	16500 cm−1
base-off	TDDFT	7886 cm−1	9346 cm−1	13376 cm−1
Co2+Cbl	SORCI	4340 cm−1	4102 cm−1	13387 cm−1
4-coordinate	Exp.	< 9000 cm−1	< 9000 cm−1	13600 cm−1
base-off	TDDFT	3322 cm−1	5207 cm−1	9214 cm−1
Co2+Cbl	SORCI	256 cm−1	2154 cm−1	9389 cm−1
Diene Modela	Exp.b	5900 cm−1	5900 cm−1	13500 cm−1
	TDDFT	7693 cm−1	9131 cm−1	13137 cm−1
	SORCI	3833 cm−1	4594 cm−1	11789 cm−1

^a[Co²⁺(Me₆[14]dieneN₄)(H₂O)];

^bRef. 69

3.4. SORCI Computations

The SORCI method was used to generate multireference descriptions of the ground states and low-lying LF excited states for both forms of base-off Co²⁺Cbl, because this method has been shown to yield better agreement with the experimental Abs spectra of bare divalent transition metal ions and free-base porphin than the more commonly utilized complete active space self consistent field (CASSCF)-based approaches.^40,70,71 Presumably, this improved agreement between the SORCI-computed and experimental data derives from the use of approximate average natural orbitals (AANOs), which leads to a balanced description of electron correlation in each state, and the application of difference dedicated CI,⁷² a strategy devised for the accurate calculation of energy differences. Additionally, SORCI is a computationally efficient multireference ab initio method that can be applied to relatively large transition-metal complexes, such as base-off Co²⁺Cbl. This efficiency stems from the use of the RI approximation and, especially, an initial reference space derived from restricted or quasi-restricted Kohn-Sham orbitals. Importantly, a recent SORCI study of [FeO(NH₃)₅]²⁺ demonstrated that an initial reference space of Kohn-Sham orbitals yielded very similar results to those obtained using a more cumbersome CASSCF reference wavefunction.⁷³

The SORCI-computed multireference descriptions for the two base-off Co²⁺Cbl species were validated on the basis of a comparison between the computed and experimental LF transition energies (Table 3). Although the TDDFT and SORCI-computed energies for the Co 3d_x²-y² → 3d_z² transition are quite similar, those predicted for the Co 3d_yz → 3d_z² and Co 3d_xz → 3d_z² transitions are significantly different. These LF transitions occur below the spectral range accessible to our MCD instrument, but in the Abs spectrum of the [Co²⁺(Me₆[14]dieneN₄)(H₂O)] model complex, these transitions are responsible for a broad band centered at 5900 cm⁻¹.69 Thus, compared to TDDFT, SORCI yields a better description of the two lowest-energy LF excited states for [Co²⁺(Me₆[14]dieneN₄)(H₂O)] in terms of their relative energies and their separation from the ground state. By analogy, it is expected that SORCI offers more accurate descriptions of the three lowest-energy electronic states of base-off Co²⁺Cbl.

The SORCI-computed ground-state wavefunction for five-coordinate base-off Co²⁺Cbl is very similar to that obtained by DFT (Section 3.3). The AANOs utilized in the final steps of the SORCI calculation closely resemble the quasi-restricted orbitals derived from DFT (Figures 5 and 7). Additionally, the DFT-predicted ground state electronic configuration, Co (3dx_²-y²)²(3d_xz)²(3d_yz)²(3d_z²)¹, represents 91% of the SORCI multireference ground-state wavefunction (Table 4). Yet, the SORCI-based description of the first two LF excited states deviates quite substantially from that obtained by DFT/TDDFT. Specifically, the SORCI calculation indicates that extensive CI mixing occurs between the Co (3d_x²-y²)²(3d_xz)²(3d_yz)¹(3d_z²)² and Co (3d_x²-y²)²(3d_xz)¹(3d_yz)²(3d_z²)² electronic configurations, which are associated with the two lowest-energy excited states in the TDDFT calculations. Presumably, this mixing, along with dynamic electron correlation, is the primary reason for the large differences between the SORCI- and TDDFT-computed energies for these two transitions.

Figure 7.

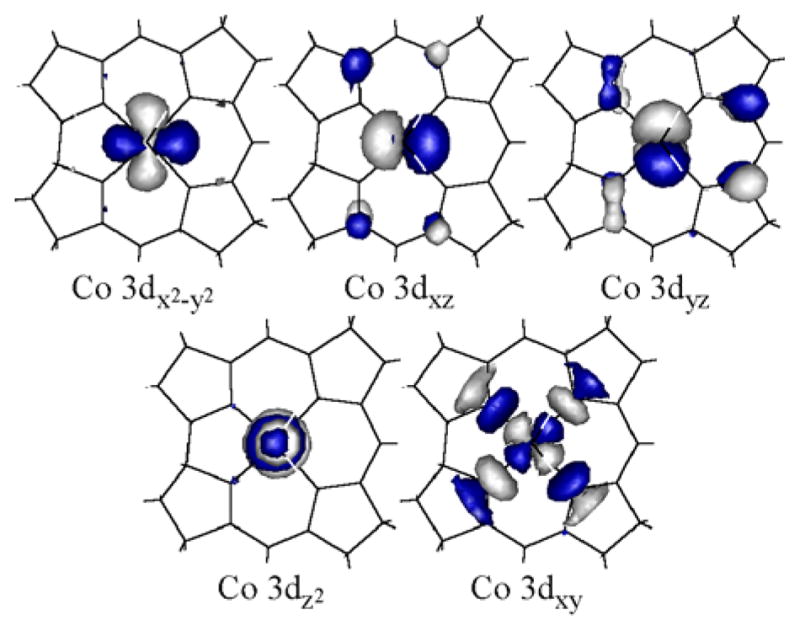
Isosurface plots of the SORCI-computed approximate average natural orbitals (AANOs) for five-coordinate base-off Co²⁺Cbl.

Table 4.

SORCI-computed relative energies and dominant (>10%) Co 3d electronic configurations for the four lowest-energy states of five-coordinate base-off Co²⁺Cbl

		Co 3d orbital occupations
E (cm−1)	%	x2-y2	xz	yz	z2	xy
0	91	2	2	2	1	0
4102	52	2	1	2	2	0
	36	2	2	1	2	0
4340	50	2	2	1	2	0
	37	2	1	2	2	0
13387	80	1	2	2	2	0

As expected, for four-coordinate Co²⁺Cbl the SORCI-computed ground-state wavefunction differs more significantly from that obtained by DFT than in the case of the five-coordinate form. First, due to the extensive mixing between the Co 3d_x²-y²- and 3d_z²-based MOs utilized in the SORCI calculation, the resulting AANOs possess almost equal contributions from these two orbitals; therefore, they are hereafter referred to as 1a₁ and 2a₁ based on their transformation behavior in the C_2v parent point group (Figure 8). Additionally, considerable CI mixing occurs between the Co (1a₁)²(3d_xz)²(3d_yz)²(2a₁)¹ and Co (1a₁)¹(3d_xz)²(3d_yz)²(2a₁)² electronic configurations in both the ²A₁ ground state and the ²A₁ LF excited state at 9389 cm⁻¹ (Table 5). Finally, a ²B₂ state deriving from the Co (1a₁)²(3d_xz)²(3d_yz)¹(2a₁)² configuration is predicted to lie only 256 cm⁻¹ above the ²A₁ ground state. According to Boltzmann statistics, ~25% of a four-coordinate base-off Co²⁺Cbl population should be found in this ²B₂ state at 298 K. Consequently, our SORCI computational results suggest that the unpaired spin density in the four-coordinate form of Co²⁺Cbl is distributed over the Co 3d_z² and 3d_x²-y² orbitals, and possibly also the 3d_yz orbital, at physiologically-relevant temperatures.

Figure 8.

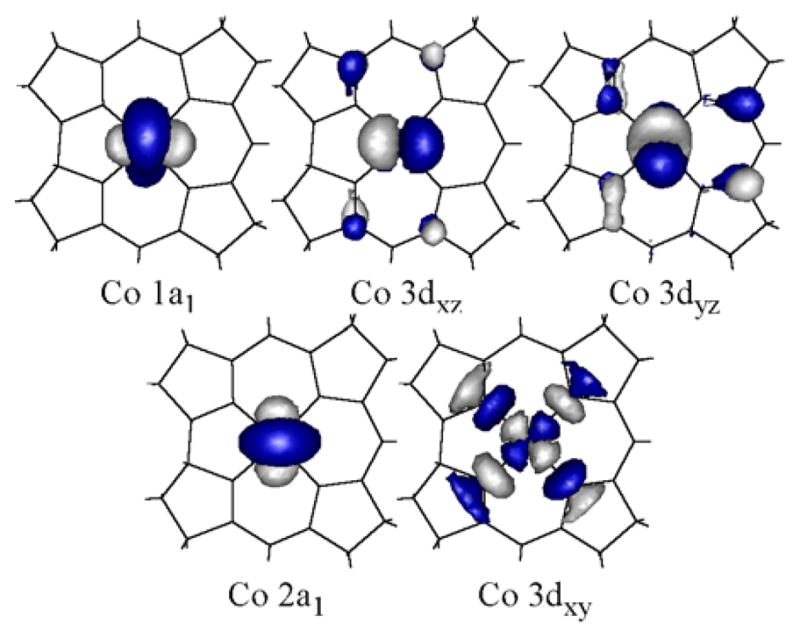
Isosurface plots of the SORCI-computed approximate average natural orbitals (AANOs) for four-coordinate base-off Co²⁺Cbl.

Table 5.

SORCI-computed relative energies and dominant (>10%) Co 3d electronic configurations for the four lowest-energy states of four-coordinate base-off Co²⁺Cbl

			Co 3d orbital occupations
E (cm−1)	%	1a1	xz	yz	2a1	xy
0	51	2	2	2	1	0
	38	1	2	2	2	0
256	81	2	2	1	2	0
2154	89	2	1	2	2	0
9389	43	1	2	2	2	0
	36	2	2	2	1	0

4. Discussion

4.1. Electronic ground state of four-coordinate base-off Co²⁺Cbl

The experimental results obtained in this study strongly suggest that the Co 3d_z² orbital is not the only Co 3d orbital contributing to the SOMO of four-coordinate base-off Co²⁺Cbl. This conclusion is supported by SORCI computations, which indicate that substantial mixing occurs between the Co 3d_z² and 3d_x²-y² orbitals and that extensive CI mixing takes place between these two ²A₁ electronic configurations (Figure 8 and Table 5). In addition, the SORCI calculation predicts the presence of two low-lying LF excited states, ²B₂ and ²B₁, in which the single unpaired electron occupies the Co 3d_yz and 3d_xz orbitals, respectively. Although not accounted for by SORCI,⁴⁰ the ²A₁ ground state may thus be perturbed further through spin-orbit mixing with these two energetically proximate LF excited states. Accordingly, the proposed ground-state wavefunction of four-coordinate Co²⁺Cbl is multi-configurational in nature. The SORCI-computed energy differences among all of these four states are quite small, which suggests that slight geometric perturbations of four-coordinate base-off Co²⁺Cbl (e.g., as imposed via enzyme active site interactions) can drastically alter the distribution of the seven electrons over the Co 3d orbitals in the electronic ground state.

The spectroscopic parameters derived experimentally clearly favor the multi-configurational ground-state wavefunction for the four-coordinate base-off Co²⁺Cbl species suggested by SORCI calculations over that obtained by DFT. Generally, large g shifts from the free electron value, such as those observed for base-off Co²⁺Cbl, reflect extensive spin-orbit mixing between the ground state and LF excited states.¹⁴ Unfortunately, perturbation theory-based approaches to EPR g value calculations (e.g., the DFT/CP-SCF strategy employed here) fail when LF excited states lie within a few thousand wavenumbers of the ground state, which is almost certainly the case here, based on the SORCI results (Table 5). Although the same problem arises when attempts are made to compute the changes in the A(⁵⁹Co) tensor upon the Co²⁺ coordination number change, useful insights can already be obtained from a qualitative analysis of the DFT-predicted and SORCI-based multi-configurational ground-state wavefunctions. The A(⁵⁹Co) hyperfine coupling tensor is more anisotropic in five-coordinate than in four-coordinate base-off Co²⁺Cbl (Table 1), which indicates that the unpaired spin density distribution is more spherically symmetric in the latter species. This result is consistent with a relatively pure Co 3d_z²-based SOMO in the five-coordinate form, while the composition of the SOMO in the four-coordinate form is more complex.

Both the SORCI-based multi-configurational and the DFT-computed descriptions of the ground-state wavefunction are equally consistent with the experimental Abs spectrum of four-coordinate base-off Co²⁺Cbl (Figure 4), as the dominant features arise from electronic transitions within the corrin π system. However, the MCD spectrum of this species is noticeably more consistent with our SORCI-based description, especially when spin-orbit mixing of LF excited-state character into the ground state is invoked. First, this spin-orbit mixing should lead to an additional stabilization of the ground state, which could account for the underestimation of the Co 3d_x²-y² → 3d_z² transition energy by both the TDDFT and SORCI calculations (Tables 3 and 5). Second, this mixing would provide a rationale for the peculiar off-axis polarization of the prominent MCD feature of four-coordinate Co²⁺Cbl at 13600 cm⁻¹ (vide supra), since in the C_2v parent point group electronic transitions are strictly x-, y-, or z-polarized.

4.2. Implications for enzymatic Co²⁺Cbl → Co¹⁺Cbl reduction

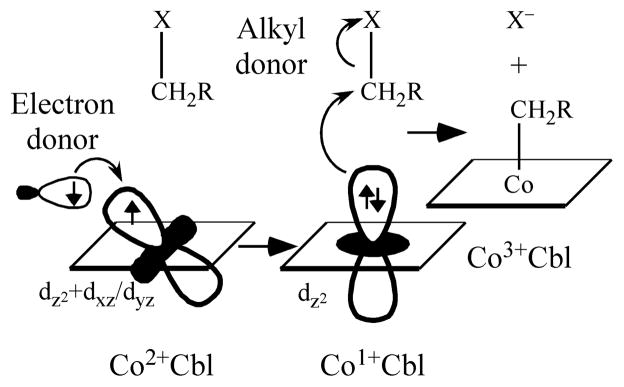
The ground state electronic structure description deduced for the four-coordinate form of base-off Co²⁺Cbl implies that the single unpaired electron, and thus the electron hole, is not entirely confined to the Co 3d_z² orbital; rather, it is partially delocalized over several Co 3d orbitals. This is an important finding because four-coordinate base-off Co²⁺Cbl species have been proposed to serve as intermediates in the reductive alkylation reactions catalyzed by MetH and the ATR enzymes.^{16–18,20,21} This description of the electron hole as being delocalized over several Co 3d orbitals leads to the conclusion that the corresponding reducing agents do not necessarily have to approach these four-coordinate Co²⁺Cbl intermediates perpendicular to the plane defined by the corrin ring; rather, a tangential approach can occur without compromising the rate of electron transfer.³⁹ Indeed, in this scenario, the subsequent Co¹⁺Cbl alkylation step may proceed rapidly, since the alkyl donor and the electron donor can approach the Co center from different directions (Figure 9). Note that this model assumes that the highest occupied MO of Co¹⁺Cbl is primarily Co 3d_z2 in character, consistent with the results obtained in a recent spectroscopic/computational investigation of free Co¹⁺Cbl.⁷⁴ Such a tightly-coupled mechanism would minimize the lifetime of the Co¹⁺Cbl “supernucleophile”,^6,7 thereby significantly suppressing the likelihood of deleterious side reactions between Co¹⁺Cbl and amino-acid residues in the enzyme active site. Intriguingly, this mechanism would also allow for a close coupling between the Co²⁺Cbl reduction and alkyl-transfer steps.

Figure 9.

Proposed mechanism for the reductive alkylation of the four-coordinate Co²⁺Cbl intermediates in the MetH and ATR enzyme active sites.

The X-ray crystal structures of MetH in the cofactor activation conformation (PDB codes 1K7Y and 3BUL)^75,76 are consistent with the proposed tangential approach of the flavodoxin reducing agent (note, however, that the actual Co²⁺Cbl intermediate that is formed in the cofactor activation process must not necessarily possess the same geometric and electronic structures as the four-coordinate Co²⁺Cbl species investigated in this work). In particular, the MetH residues that have been implicated in flavodoxin docking are positioned such that a tangential approach of flavodoxin on enzyme-bound base-off Co²⁺Cbl appears most likely.⁷⁷ Moreover, a solvent access channel extends diagonally from the “upper” (or β-) face of the cofactor along the x-axis (Figure 1) to the exterior of the protein. In contrast, based on the X-ray crystal structure of the CobA-type ATR from Salmonella typhimurium (PDB code 1G64),⁷⁸ external reductants are likely to approach the four-coordinate Co²⁺Cbl intermediate diagonally along the y-axis. To this end, it is interesting to note that the Co 3d_x²-y² → 3d_z² transition of the four-coordinate Co²⁺Cbl species bound to ATR and MetH occur at slightly different energies,^17,18,21 indicating that the electronic structure of the cofactor is differentially perturbed in these two enzymes. It is tempting to speculate that the MetH active-site induces distortions of the cofactor (e.g., via folding of the corrin macrocycle) so as to promote spin-orbit mixing of the ground state with the Co 3d_xz → 3d_z² excited state, whereas the ATR active site causes a distortion that leads to preferential mixing with the Co 3d_yz → 3d_z² excited state.