ParAlign: a parallel sequence alignment algorithm for rapid and sensitive database searches

Abstract

There is a need for faster and more sensitive algorithms for sequence similarity searching in view of the rapidly increasing amounts of genomic sequence data available. Parallel processing capabilities in the form of the single instruction, multiple data (SIMD) technology are now available in common microprocessors and enable a single microprocessor to perform many operations in parallel. The ParAlign algorithm has been specifically designed to take advantage of this technology. The new algorithm initially exploits parallelism to perform a very rapid computation of the exact optimal ungapped alignment score for all diagonals in the alignment matrix. Then, a novel heuristic is employed to compute an approximate score of a gapped alignment by combining the scores of several diagonals. This approximate score is used to select the most interesting database sequences for a subsequent Smith–Waterman alignment, which is also parallelised. The resulting method represents a substantial improvement compared to existing heuristics. The sensitivity and specificity of ParAlign was found to be as good as Smith–Waterman implementations when the same method for computing the statistical significance of the matches was used. In terms of speed, only the significantly less sensitive NCBI BLAST 2 program was found to outperform the new approach. Online searches are available at http://dna.uio.no/search/

INTRODUCTION

The total size of the public sequence databases is rapidly increasing and has doubled in the last 6 months. Searching databases for sequences similar to a given sequence is one of the most fundamental and important tools for predicting structural and functional properties of uncharacterised proteins. The availability of good tools to perform these searches is hence important. There exist a number of tools with varying speed and sensitivity. The Smith–Waterman algorithm (1) is generally considered to be the most sensitive, but long computation times limit the use of this algorithm. To increase speed, several heuristic alternatives have been developed, such as FASTA (2), BLAST (3,4) and WU-BLAST (W.Gish, http://blast.wustl.edu). These programs sacrifice sensitivity for speed and therefore more distant sequence relationships may escape detection. Special purpose hardware with parallel processing capabilities has also been constructed to perform Smith–Waterman searches at high speed, but these machines are quite expensive (5).

A form of parallel processing capability termed the single instruction multiple data (SIMD) technology enables microprocessors to perform the same operation (logical, arithmetic or other) in parallel on several independent data sources. It is possible to exploit this by dividing wide registers into smaller units in the form of microparallelism or SIMD within a register. However, modern microprocessors have added special registers and instructions to make the SIMD technology easier to use. The technology is included in some of the most widely used modern microprocessors, including the Intel Pentium MMX, II and III. A form of SIMD technology called MMX (multimedia extensions) is included in the former two, while an enhanced version called SSE (streaming SIMD extensions) is included in the latter (6). Processing of sound, images and video are the main application areas, but the technology is also useful for other signals and can be applied to processing of genetic sequences.

Several investigators (7–11) have used SIMD technology to speed up the Smith–Waterman algorithm, but there seem to be no heuristic sequence alignment algorithms designed specifically to take advantage of the SIMD technology.

Here a semi-heuristic method specifically designed to exploit the advantages of the SIMD technology to perform both rapid and sensitive sequence database searches is presented. It has been implemented using the Intel MMX/SSE technology, but can be adapted to other microprocessor architectures.

MATERIALS AND METHODS

The software was written in C++ with inline assembler code and compiled with the GNU egcs compiler. Due to the limited support for MMX instructions in high level languages and in order to be able to optimise the code as much as possible, the code for the core of the algorithm was written in assembly language. The computer used had a single Intel Pentium III 500 MHz microprocessor and 128 MB RAM and employed the Red Hat Linux 6.1 operating system.

Algorithm and implementation

Background. For each sequence in the database, similarity search programs compute an alignment score that represents the degree of similarity between the query and the database sequence. This score is based on a substitution score matrix representing the similarity between two symbols and an affine gap penalty function based on a gap open and a gap extension penalty. The optimal local alignment score can be computed by the dynamic programming algorithms of Smith and Waterman (1) and Gotoh (12). An optimal local alignment can be represented by a path through an m × n alignment matrix spanned by the query sequence and the database sequence. The path consists of patches parallel to the major diagonal, representing matching symbols, and vertical or horizontal patches, representing gaps in the query or database sequence. The score of an alignment is the sum of the substitution scores in the included cells minus the penalty for the gaps. The optimal alignment is the alignment giving the highest score. Usually the path of an optimal alignment consists of a few long diagonal patches connected by short gaps.

Ungapped alignment can be considered as a special case of alignment with infinitely large gap penalties. The interdependence between the diagonals then disappears, and an alignment score can be computed separately for each diagonal and the highest of these is the optimal ungapped alignment score. The alignment score for each diagonal is equal to the maximum partial sum of substitution scores along a continuous part of the diagonal. Many heuristic search algorithms, including FASTA and BLAST, are based on first identifying high scoring ungapped alignments. In the BioSCAN system (13) computation of diagonal scores as described above was performed by special purpose hardware as the basis of a database search method.

Problems with current heuristic methods. The sequence alignment performed by most heuristic database search algorithms can be divided into two phases. In the first phase regions of similarity between the two sequences are identified without considering gaps. In the second phase gapped alignments are constructed on the basis of the most interesting regions initially identified. The way the initial screening of the database sequences is performed by the traditional heuristic algorithms like FASTA and BLAST leads to increased speed, but also to reduced sensitivity compared to the Smith–Waterman algorithm. In order for the sequence similarities to be detected by these programs it is required that the similarity between the sequences is in some way concentrated. Enough similarity must be present within a small group of identical or highly conserved consecutive amino acids on a single diagonal in the alignment matrix. If the similarity between the two sequences is more spread along one diagonal in the alignment matrix or divided on several diagonals it may not be detected. ParAlign has been designed to avoid these problems, without the extensive computation time required by the Smith–Waterman algorithm.

Efficient parallel computation of the optimal ungapped alignment score for all diagonals. In the first phase both FASTA and BLAST scan for short regions of 1–3 consecutive amino acids that are identical or very similar between the two sequences. More precisely, FASTA requires 1 or 2 amino acids (specified by the ktup parameter) to be identical. By default, BLAST requires 3 amino acids to be very similar, i.e. the sum of the three score matrix elements corresponding to the three pairs of amino acids must exceed a certain limit. NCBI BLAST v.2 additionally requires that there are two such groups on the same diagonal within a distance of ∼40 amino acids. Hence, if the similarity is more distributed along one diagonal it may not be detected by the present heuristic methods. This weakness is overcome in ParAlign by calculating the exact ungapped alignment score for each diagonal. Consider a query sequence A of length m, a database sequence B of length n and a score matrix Z. The optimal ungapped alignment score S_d for diagonal d, which is a maximum partial sum of substitution scores along the diagonal, can be computed iteratively using equations 1–3 below with row i going from g to h, where g = max(1,1 – d) and h = min(m,n – d):

e_i = max(e_{i – 1} + Z[A_i, B_{i + d}],0) e_{g – 1} = 0 1

f_i = max(f_{i – 1},e_i) f_{g – 1} = 0 2

S_d = f_h 3

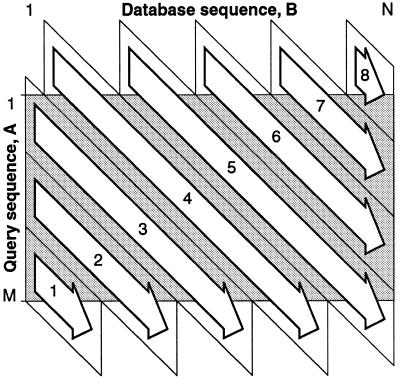
An exceptionally fast way to perform this operation using the SIMD technology has been found. In the present implementation, an eight-way parallel processing approach is used. The calculation of e_i and f_i is performed in diagonal bands, 32 cells wide, parallel to the major diagonal in the matrix. The computation is started in the lower left corner of the matrix and continued in the order indicated in Figure 1. This arrangement enables very efficient computation. The 64 bit MMX registers were divided into eight 8 bit units in order to obtain the largest number of parallel computations. Four of the MMX registers are used for the e_i values, while the remaining four registers are used for the f_i values. The resulting maximum partial sum of scores on each diagonal is saved and used in the subsequent calculations.

Figure 1.

Computation of the diagonal scores using SIMD technology. Computation of the diagonal scores is performed efficiently in the order indicated using bands that are 32 diagonals wide.

When computing e_i by adding the substitution scores from Z to e_{i – 1} the signed and saturated addition instruction PADDSB (packed add with saturation byte) is used. When f_i is computed as the maximum of f_{i – 1} and e_i the unsigned maximum instruction PMAXUB (packed maximum unsigned integer byte) is used. Using only a byte for e_i and f_i limits the precision of the calculations to 8 bits. However, in order to enable the use of the PADDSB and PMAXUB instructions the range had to be further limited to 0–127 and represented by values in the range –128 to –1 by biasing e_i and f_i by –128. Limiting the precision to 7 bits poses no real problems because a score close to 127 will always be considered significant and the correct score will be computed in the subsequent computations of a more accurate alignment score with a wider score range as described below.

Initially, a query sequence profile is created for the query sequence in order to speed up computations. This profile contains the substitution score for matching each of the possible amino acid symbols with each symbol in the query sequence. The scores for matching symbol A with each symbol in the query sequence is followed by the scores for matching symbol B with each symbol in the query sequence, and so on. The scores for matching one database symbol with a group of 32 consecutive symbols from the query sequence could then be retrieved by loading four MMX registers from consecutive addresses. The entire query profile will usually be kept in the first level cache of the central processing unit (CPU), resulting in very fast access.

Computation of an approximate gapped alignment score. The second phase of sequence alignment also has its problems. Sequence similarities may pass undetected if the similarity is evenly distributed on several diagonals, in which case the optimal alignment contains many gaps. Many heuristic algorithms select a small fraction (e.g. 2%) of the database sequences for a more rigorous examination using an optimal alignment algorithm within a band (FASTA) or region (NCBI BLAST v.2) surrounding the most interesting initially identified regions. BLAST uses only the score of the highest scoring initial region to determine whether a more accurate gapped alignment should be constructed. It is hence unable to recognise an otherwise significant alignment if none of the high scoring segment pairs found has a score above about 40 with a typical length query. FASTA is more advanced and makes this decision based on an approximate gapped alignment score, initn, computed by joining several compatible regions and subtracting joining penalties from their scores.

ParAlign employs a new heuristic for computing an estimated gapped alignment score, which is used to select the most interesting fraction of database sequences for further examination. When the ungapped alignment scores for all diagonals have been found, as described previously, the scores for each diagonal are combined in a new inter-diagonal scoring function, which is also a kind of maximum partial sum of scores function. Using this function, high scoring regions on neighbouring diagonals will receive a high score. The chosen inter-diagonal scoring function has been found to be very effective in filtering the sequence database.

Some simplifications are present in this calculation of an approximate gapped alignment score. First, only the single highest scoring region on each diagonal is considered. In addition, only diagonals scoring above average are considered interesting. This is achieved by deducting the expected score for a diagonal, c, from the score of each diagonal. This expected score is dependent on the length of the query sequence. Equation 4 below is used to estimate the expected diagonal score:

c = lnKm′/λ 4

Here, K and λ are the parameters for calculating the statistical significance of an ungapped alignment as described by Karlin and Altschul (14). The values estimated by Altschul and Gish (15) for the given substitution score matrix were used. The edge-corrected length of the query sequence is represented by m′. The relative position of regions on different diagonals is not considered, only the distance between the diagonals, which is used for computing gap penalties. The resulting scores are summed for neighbouring diagonals and the optimal combination of these is found. The approximate gapped alignment score T for an alignment is computed by equations 5–7 below, with diagonal d going from 1 – m to n – 1:

u_d = max(u_{d – 1} + max[S_d – c – q,0] – r,0) u_–m = 0 5

v_d = max(v_{d – 1},u_d) v_–m = 0 6

T = c + q + r + v_{n – 1} 7

Here, q and r are the gap open and extension penalties, respectively. An example calculation is shown in Figure 2. The use of this approximate gapped alignment scoring function allows the identification of sequence similarities that are distributed so evenly on several diagonals that an alignment with gaps is necessary to detect the similarity.

Figure 2.

Computation of the estimated gapped alignment score. The numbers within the matrix are the temporary scores (e_i) along the diagonals from the initial computation of the diagonal scores. The numbers directly outside the matrix are the optimal ungapped alignment scores (S_d) for each diagonal. The second numbers outside the matrix are the temporary scores (u_d) used in the calculation of the estimated gapped alignment score (T), which in this example is 3 + 11 + 1 + 22 = 37. The BLOSUM62 matrix was used in combination with the parameters q = 11, r = 1 and c = 3 in this example. The calculations were performed in order of increasing diagonal numbers.

The fraction containing ∼1% of the highest scoring database sequences is finally subjected to a rigorous Smith–Waterman alignment that is also implemented using SIMD technology (11). The cut-off value (w) for selecting the ∼1% (assuming random sequences) of the highest scoring sequences is calculated by equation 8 below:

w = (ln[Km′n′] + ln[100])/λ 8

Here, K and λ are the parameters for calculating the statistical significance of a gapped alignment as described and estimated by Altschul and Gish (15). The edge effect-corrected lengths of the query and database sequences are represented by m′ and n′. This formula for the cut-off value assumes a score distribution that is equal to an optimal gapped alignment score. This approximation has been shown in practice to give a useful cut-off value.

RESULTS

The ability of ParAlign to detect homologous proteins was evaluated and compared to other methods for pairwise sequence alignment. The programs evaluated are listed in Table 1.

Table 1. Database search programs tested.

Program	Version	Description	Reference
SSEARCH	3.3t08	Full dynamic programming	(16)
FASTA	3.3t08	Heuristic, tested with both ktup 1 and 2	(2)
NCBI BLAST	2.0.14	Heuristic	(4)
NCBI BLAST	1.4.9	Heuristic, ungapped alignments	(3)
WU-BLAST	2.0a19	Heuristic	W.Gish (http://blast.wustl.edu/)
ParAlign	1.9.7	Heuristic, SIMD implementation	This paper
SWMMX	1.9.7	Full dynamic programming, SIMD implementation	(11)
SALSA	1.8.4	Heuristic	(17)

The performance assessment was carried out as described by Brenner et al. (18). The evaluation is based on the PDB40D-B database [provided by Brenner et al. (18)], which consists of domains of proteins from the SCOP database (19) classified according to their tertiary structure. The ability of the different database search methods to correctly identify the ‘true’ homologous proteins in this database can be tested using the SCOP superfamily classification as a reference. The PDB40D-B database contains 1323 protein domains that are <40% identical to each other. There are 9044 ordered pairs of domains belonging to the same superfamily out of a total of 1 749 006 ordered pairs. Both the coverage (true positives), defined as the fraction of homologous pairs correctly identified, and the number of errors per query (EPQ) (false positives), defined as the number of incorrectly reported sequences per query sequence, were examined. Thus, both the ability of a program to detect homologous protein pairs (sensitivity) and its ability to discriminate between homologous and non-homologous pairs (selectivity) is assessed. An all-versus-all comparison of the sequences in the database was performed. All hits were recorded and sorted on the statistical significance ranking parameter reported by the programs, e.g. the P value (match probability) for NCBI BLAST v.1 and WU-BLAST and the E value (expected matches) for the other programs. The number of correctly and incorrectly identified homologous pairs was counted and recorded for each reported significance level.

The database scanning approach, the choice of score matrix, the choice of gap penalty scheme and the method of statistical evaluation of the scores are four different aspects of a database search that may be assessed individually. Regarding the first aspect, the SSEARCH and SWMMX programs both take a full dynamic programming approach to database scanning, while the other programs use different heuristics.

By default the SSEARCH and FASTA programs use the BLOSUM50 amino acid substitution score matrix (20) in combination with a gap penalty of 10 + 2k. On the other hand, NCBI BLAST v.2, SALSA, ParAlign and SWMMX use the BLOSUM62 matrix with a gap penalty of 11 + k by default. To make a fair comparison both scoring schemes were tested. However, the former set of matrix and gap penalty parameters were not tested with SALSA and NCBI BLAST v.2 because these programs would not run with these parameters due to the lack of corresponding precomputed Karlin–Altschul constants.

There are different ways of calculating the statistical significance of a match based on its raw alignment score. The SSEARCH and FASTA programs by default calculate the statistical significance of the matches by regression against the length of the library sequence. However, by specifying the –z 3 option, these programs will use Karlin–Altschul statistics (14,15) with precomputed λ, K and H constants. NCBI BLAST v.1 by default uses sum statistics (21), while the other programs use Karlin–Altschul statistics (14). There are some differences between the implementations of the Karlin–Altschul statistics, related to the method of length correction, and in the K, λ and H constants. For the FASTA and SSEARCH programs both the default and the Karlin–Altschul method of statistical significance calculation were examined.

All programs were run with options set to show up to 500 scores with an expect value below 10 and no alignments. WU-BLAST and SALSA were run using the recommended postsw and –o options, respectively, in order to compute the optimal alignment score for all reported hits.

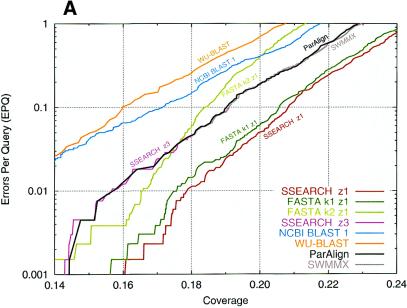
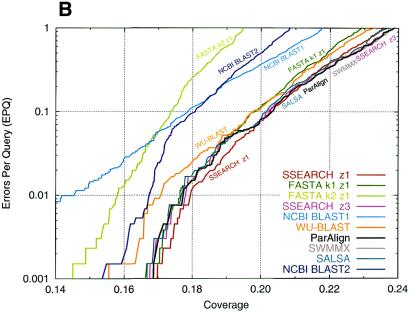
Plots of the performances are shown in Figure 3. The SSEARCH program using default (length regression) statistics achieved the best overall performance. When Karlin–Altschul statistics were employed the best results were obtained with the BLOSUM62 matrix and 11 + k gap penalties. In that case the best performance was obtained with ParAlign, SSEARCH, SWMMX and SALSA, which all performed essentially equally. FASTA with ktup 1 and WU-BLAST performed nearly as well, but FASTA with ktup 2 and both versions of NCBI BLAST performed significantly worse.

Figure 3.

Comparison of database search sensitivity and selectivity. The sensitivity (coverage) versus the selectivity (EPQ) is plotted for a range of database search programs using either (A) the BLOSUM50 matrix and a 10 + 2k gap penalty or (B) the BLOSUM62 matrix and a 11 + k gap penalty.

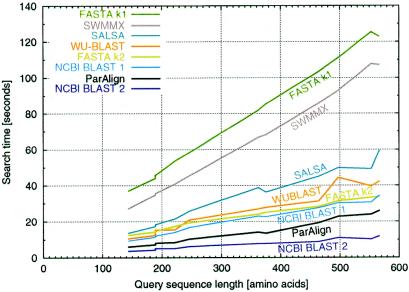
Because of the rather small size of the PDB40D-B database compared to the sizes of databases usually searched, the speed of the various algorithms was assessed by searching the SWISS-PROT release 39 database (22). A set of 11 test query sequences (SWISS-PROT accession nos P00762, P01008, P01111, P02232, P03435, P05013, P07327, P10318, P10635, P14942 and P25705) with lengths in the range 143–567 was used. These test sequences have previously been used in the evaluation of NCBI BLAST v.2 (4). The BLOSUM62 matrix was used in combination with a gap penalty of 11 + k; other program options were set as described earlier. A plot of the search time versus the query sequence length for each query sequence and program is shown in Figure 4. Overall, ParAlign was found to be 4.4 times faster than the Smith–Waterman algorithm as implemented in SWMMX and 28 times faster than the implementation in SSEARCH. ParAlign was also found to be faster than any of the heuristic algorithms except for NCBI BLAST v.2, which was twice as fast as ParAlign. ParAlign was 1.8 times faster than WU-BLAST, 2.3 times faster than SALSA, 5.4 times faster than FASTA with ktup 1 and 1.6 times faster than FASTA with ktup 2. There was no noticeable speed difference between the two different statistical methods for FASTA and SSEARCH.

Figure 4.

Comparison of database search speed. Search time versus query sequence length is plotted for the different search programs and the 11 query sequences (see Results). The search time used is the total CPU time of the fastest of three consecutive runs on a minimally loaded computer. With a database of only 29 and 128 MB of RAM, all of the database was cached in the computer’s RAM; disk reading time should then be negligible.

DISCUSSION

A fast and sensitive new sequence alignment and database search algorithm has been designed specifically to exploit the advantages of the SIMD technology. High sensitivity was achieved by a combination of two main factors. First, computation of the exact optimal ungapped alignment score of each diagonal in the alignment was performed. Secondly, a novel heuristic for estimating a gapped alignment score taking into account the amount of sequence similarity on several diagonals in the alignment matrix was employed. This estimate is used to identify a 1% fraction of the most interesting database sequences that are subsequently aligned with the query sequence by the Smith–Waterman method. The rapidity of the method was achieved using a very efficient SIMD computation of the ungapped alignment scores of all diagonals and the SIMD Smith–Waterman implementation. The heuristic for computing the estimated gapped alignment score is also fast.

When the sensitivity and selectivity were assessed, ParAlign was among the top performers, together with the programs employing a full dynamic programming Smith–Waterman alignment method, when Karlin–Altschul statistics were employed. However, even better performance was obtained with SSEARCH using length regression statistics. It is likely that the performance of ParAlign would have been equal to SSEARCH if length regression statistics had been implemented in ParAlign.

As shown by the evaluation, the choice of statistical significance evaluation method is important to obtain optimal performance. In addition to the score matrix and gap penalty scheme used, the actual length and composition of the sequences aligned must be taken into account. An improved statistical evaluation method should be implemented and evaluated in future versions of this software in order to improve performance further. The method described by Mott (23) seems especially interesting.

The speed of ParAlign was only surpassed by NCBI BLAST v.2, which proved significantly less sensitive in this test. Considerably improved speed will probably be obtained with ParAlign when 128 bit SIMD technology becomes available. Most other heuristic alignment algorithms cannot take advantage of improvements in SIMD technology.

Modern methods that take advantage of the information gained from multiple related protein matches in the database are often able to detect many more homologues than the simple pairwise alignment methods. Such programs include PSI-BLAST (4), Sam-T98 (24) and MISS (25). However, all these methods initially depend on a pairwise alignment method. Increased speed and/or sensitivity of the overall iterative method can probably be obtained using an improved pairwise alignment method, of which ParAlign might be a good choice.

Many search algorithms include initial filtering of the database before a more accurate comparison is performed. It is important that this initial filtering has a high sensitivity so that all significant similarities are revealed, but it must also be selective so that time-consuming post-processing does not involve too many sequences. The initial filtering method used in ParAlign seems to be very sensitive (few false negatives), but may give too many unwanted false positives in some cases. This happens occasionally with certain query sequences and seems to be caused by repetitions in the sequences. However, it does not seem to be a major problem and may be reduced by low complexity masking of the query sequence using, for example, the SEG program (26).

There are several issues that will be considered for further development in the algorithm. Taking proper care of frameshifts when searching translated DNA databases is important. There should also be possibilities of speed improvements. Currently a full SIMD Smith–Waterman alignment is performed for ∼1% of the database sequences that achieve the best initial scores. These alignments currently account for nearly 10% of the total time used by ParAlign. By restricting the Smith–Waterman alignment to a band of diagonals the alignment may be speeded up with, hopefully, only a moderate reduction in sensitivity.

It may also be possible to create other homology search algorithms using the SIMD technology with a sensitivity at the level of NCBI BLAST v.2 but at a significantly higher speed.

It is likely that the algorithm can also be implemented efficiently on most other microprocessors with the SIMD technology. Future generations of computers will probably include a more advanced SIMD technology, e.g. microprocessors with 16-way parallel processing, that might allow even faster performance.

Online searches with ParAlign in a number of databases are available on the Web site at http://dna.uio.no/search/, and executable binaries will be made available subject to a license.