Estimating changes in free-living energy intake and its confidence interval

Abstract

Background: Free-living energy intake in humans is notoriously difficult to measure but is required to properly assess outpatient weight-control interventions.

Objective: Our objective was to develop a simple methodology that uses longitudinal body weight measurements to estimate changes in energy intake and its 95% CI in individual subjects.

Design: We showed how an energy balance equation with 2 parameters can be derived from any mathematical model of human metabolism. We solved the energy balance equation for changes in free-living energy intake as a function of body weight and its rate of change. We tested the predicted changes in energy intake by using weight-loss data from controlled inpatient feeding studies as well as simulated free-living data from a group of “virtual study subjects” that included realistic fluctuations in body water and day-to-day variations in energy intake.

Results: Our method accurately predicted individual energy intake changes with the use of weight-loss data from controlled inpatient feeding experiments. By applying the method to our simulated free-living virtual study subjects, we showed that daily weight measurements over periods >28 d were required to obtain accurate estimates of energy intake change with a 95% CI of <300 kcal/d. These estimates were relatively insensitive to initial body composition or physical activity level.

Conclusions: Frequent measurements of body weight over extended time periods are required to precisely estimate changes in energy intake in free-living individuals. Such measurements are feasible, relatively inexpensive, and can be used to estimate diet adherence during clinical weight-management programs.

See corresponding article on page 3.

INTRODUCTION

Evaluation of weight-management strategies in humans is complicated by the well-known difficulties in measuring free-living energy intake (EI) (1). This has been called “the fundamental flaw of obesity research” (2), and addressing this flaw is of paramount importance. The gold standard doubly labeled water (DLW) method is an expensive and specialized technique that provides an accurate measurement of average CO₂ production over time intervals of 1–2 wk. Translating the measured CO₂ production rate to an estimate of EI requires several assumptions about the composition of the diet, and any changes in body weight (BW) or body composition further complicate the calculation.

Recently, several publications have suggested that mathematical models of human energy metabolism and BW change might provide an inexpensive and convenient way to estimate free-living EI (3–5). Whereas some investigators have emphasized the use of such methods to estimate the average free-living EI in groups (3, 4), it has also been proposed that such models can determine EI in individuals (5). Individual EI estimates would be extremely valuable for assessing diet adherence and patient compliance during a weight-loss program. However, such an application would require an estimate of the EI CI to identify dietary compliance.

Here, we propose a simple methodology for using longitudinal BW measurements to estimate changes in EI (ΔEI) from its energy-balanced value. Importantly, our method provides an explicit calculation of the ΔEI CI and does not require solving a differential equation. The method can also be used with arbitrary weight change models to define the parameter values. We evaluated the method by using individual weight-loss data from inpatient feeding studies in which energy intake was controlled. To investigate the accuracy and precision of the method in a free-living situation with significant variations in day-to-day EI and realistic body water fluctuations, we simulated data from groups of “virtual study subjects” with the use of a validated computational model of human metabolism (3). We show that frequent BW measurements over extended time periods are required to obtain a reasonably precise estimate of ΔEI in free-living individuals.

METHODS

Estimating changes in EI and its 95% CI

As we have shown previously (6), any mathematical model of human energy metabolism and BW change can be linearized around an initial BW value, BW₀, to yield the following differential equation:

where ρ is the effective energy density associated with the BW change and ϵ is a parameter that defines how energy expenditure depends on BW. This linearized energy balance equation can be solved for the change of energy intake as follows (4):

where a is an estimate of the rate of change of BW over the corresponding time interval t. Because ρ/ϵ >365 d, we can safely assume that the time course of BW can be fit with a linear model over times shorter than ≈60 d, such that BW_i = at_i + b. We show in Appendix A that the ΔEI estimate has a variance (var) of:

where n is the number of data points and T is the time interval between data points over a time interval t = nT. The precision of ΔEI is optimized by maximizing the number of points n (and as a consequence minimizing the interval between measurements T). Thus, daily BW measurements (ie, T = 1 d) provide the most precise estimate of ΔEI. Using n = 28 along with our previously reported average model parameter values of ρ = 9100 kcal/kg, ϵ = 22 kcal/kg/d (4) with assumed BW fluctuations that were normally distributed with SD ≈0.5 kg (7–10), we obtained an estimate of SD(ΔEI) = 180 kcal/d with a 95% CI of ±350 kcal/d. Therefore, daily BW measurements over at least 28-d time intervals will likely be required to provide information about ΔEI that is sufficiently precise to assess diet adherence in a free-living situation.

The 95% CI of the total EI can also be estimated by summing the estimate of the variance of ΔEI (Equation 3) and the variance of the initial energy-balanced value of EI. However, the precision of the total EI is bounded by the precision of the estimate of the initial EI, which is quite poor without DLW measurements. For example, the 95% CI for the baseline EI is >450 kcal/d using Institute of Medicine equations for total energy expenditure (11). All of the calculations to determine ΔEI and its 95% CI can be performed by using simple spreadsheet software, and an example is provided in the supplemental materials under “Supplemental data” in the online issue.

Evaluation of the estimated ΔEI in controlled inpatient feeding studies

We applied our ΔEI method to previously reported daily body weight measurements of 3 obese subjects consuming ≈800 kcal/d in an inpatient setting (12). We used the measured initial body fat mass to calculate ρ and ϵ as described in Appendix A. Because baseline EI was not assessed in this study, we used the Institute of Medicine equations (11) to calculate the baseline energy requirements of each subject assuming light physical activity. This value, along with the measured dietary intake, was used to calculate the ΔEI data for comparison to our estimation method.

Comparison with a computational model prediction of ΔEI

A recent report described a computational model for determining EI in individuals (5) and compared the model predictions with data from the CALERIE phase I study (21). We compared the predictions of this computational model by applying our simple ΔEI method to the individual subject data presented in the supplemental material of this previous report (5).

Evaluation of the estimated ΔEI in simulated free-living virtual study subjects

In contrast to controlled feeding studies, free-living individuals are known to have large day-to-day EI fluctuations with CVs of ≈20–30% (22–26). Corresponding variations in both dietary sodium and carbohydrate can cause rapid changes in extracellular fluid because these nutrients affect renal sodium handling (27, 28). Furthermore, intracellular fluid fluctuations are associated with changes in intracellular glycogen and protein. Thus, daily variations in body fluids underlie the typical day-to-day fluctuations in free-living BW (7–10). Because these rapid fluid fluctuations are a significant component of measured individual BW changes, they confound the estimate of free-living ΔEI based on BW measurements.

To test the ability of our method to estimate ΔEI in free-living conditions, we used simulated BW data from a computational model of human macronutrient balance that included body fluid fluctuations in response to variations in dietary sodium, carbohydrate, and energy (3). This computational model was developed and validated with the use of data that were independent of the data used to develop the ΔEI equations. After 28 d of average energy balance, we simulated a step decrease of EI by 500 kcal/d, which was held constant for 240 d and then returned to the original EI. Over and above these step changes in EI, we simulated 20% random variations in EI, dietary sodium, and dietary carbohydrate to mimic the free-living fluctuations in BW. This same basic diet time course was implemented in all model simulations to test the ΔEI estimation method's ability to recover the known EI change pattern. This strategy allows for the most rigorous evaluation of the methodology because all aspects of the comparisons were controlled for and the EI changes were known.

We also varied the initial conditions of the computational model to represent subjects with different physical activity level (PAL) and varying initial body composition. As a test of the method and of its sensitivity to the parameters, we did not derive new values for the parameters ρ and ϵ. In practice, if information about the initial conditions is available on an individual subject, the parameter values of the ΔEI estimation method should be modified to improve the accuracy of the results.

RESULTS

Estimating ΔEI in controlled inpatient feeding studies

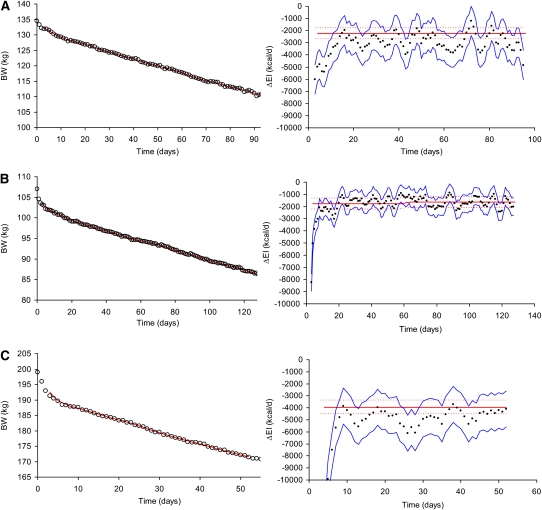
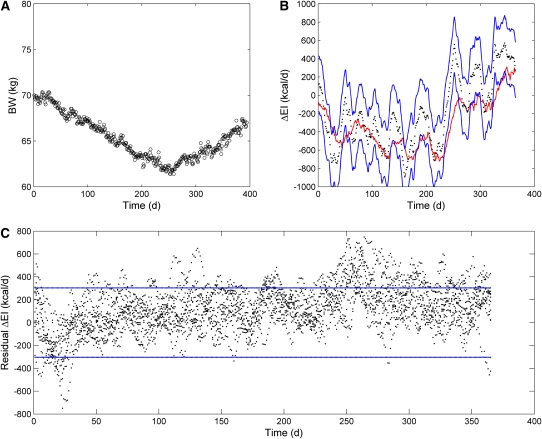
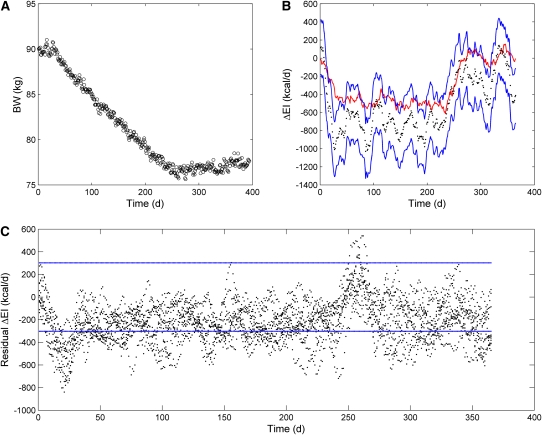
The performance of our ΔEI estimation method in 3 obese subjects during an inpatient controlled feeding study is shown in Figure 1. In all cases, the rapid initial weight-loss led to an overestimation of the magnitude of ΔEI because our simple method does not account for large changes in body water that likely comprised the initial weight-loss. However, the subsequent phase of approximately linear weight-loss resulted in accurate predictions of ΔEI, with the 95% CI of the estimate and the measurements overlapping in all 3 subjects.

FIGURE 1.

Weight changes and estimated changes in energy intake (ΔEI) during 800-kcal/d inpatient controlled diets. A: Results for a 135-kg, 45-y-old woman. The left panel shows daily body weight measurements (circles), and the right panel depicts the ΔEI measurements (red curve) and their 95% CI (dotted red curves) along with our ΔEI estimate (black dots) and its 95% CI (blue curves) (number of data points = 6, time interval between data points = 1 d). B: Results for a 107-kg, 49-y-old woman. C: Results for a 39-y-old, 199-kg man. BW, body weight.

Comparison with a computational model for estimating ΔEI

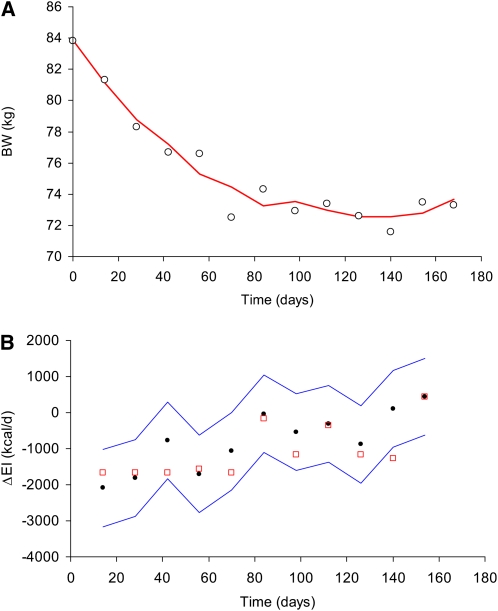
Our simple method for estimating ΔEI was compared with the results of a recently published computational model to determine EI in a 45-y-old, 83.8-kg woman during a 6-mo caloric restriction study shown in Figure 2 (5).The previous computational model prediction of ΔEI (open red squares) agreed reasonably well with our simple estimate and falls within our calculated 95% CI for all but one data point.

FIGURE 2.

Comparison of our simple method for estimating change in energy intake (ΔEI) with a recently proposed computational model for determining individual EI. A: Measured body weight (BW) data from a 83.8-kg, 45-y-old woman (circles) along with the moving linear regression estimate (red curve) (number of data points = 3, time interval between data points = 14 d). B: ΔEI estimated with our simple model (black dots) along with its 95% CI (blue curves) and the computational model prediction for ΔEI (open red squares).

Estimating ΔEI in a computational model of macronutrient balance

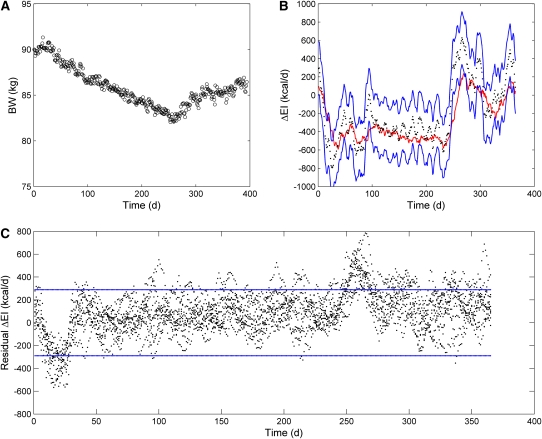
We simulated the free-living BW dynamics using a previously validated computational model of human macronutrient metabolism (3) with initial conditions corresponding to a 90-kg man with body fat mass of 23 kg and PAL of 1.5 (Figure 3A). We added 20% random fluctuations in dietary sodium, carbohydrate, and EI superimposed on the 500-kcal/d step diet changes to mimic realistic free-living BW fluctuations resulting from variations in extracellular and intracellular water (7–10). This computational model was developed with the use of completely independent data from our simple nonlinear energy balance model and thus provides a fair and unbiased assessment of our ΔEI estimation method. That the method accurately tracked the actual changes in ΔEI is shown in Figure 3B, and the residuals in 10 simulated runs of the model with a 95% CI of 290 kcal/d for n = 28 and T = 1 are shown in Figure 3C. The mean value of the residuals was 90 kcal/d. Note that the diet transitions at days 28 and 268 resulted in the largest deviations from the estimated ΔEI, which is due to changes in body fluids unaccounted for by the simple method.

FIGURE 3.

Simulated free-living data from a sedentary 90-kg male virtual study subject generated by using a computational model of macronutrient metabolism. A: Simulated body weight (BW) data for an example run of the model incorporating day-to-day fluctuations in energy intake (EI), dietary sodium, and carbohydrate. B: Estimated changes in EI (ΔEI; black dots) along with the 95% CI (blue lines) and moving average actual EI (red line) for the same example subject as depicted in panel A (number of data points = 28, time interval between data points = 1 d). C: Residuals of the estimated EI changes (black dots) for 10 runs using the same subject. Blue lines denote the calculated 95% CI.

Estimating ΔEI in subjects with varying body composition and physical activity

We next tested the ΔEI estimation method by using simulated subjects who varied in their initial body composition and physical activity. Ideally, we would have information on these parameters to adjust the ΔEI estimation method. However, we decided to test the sensitivity of our method by holding the parameters ρ and ϵ fixed and to examine the effect on the accuracy of the estimated ΔEI.

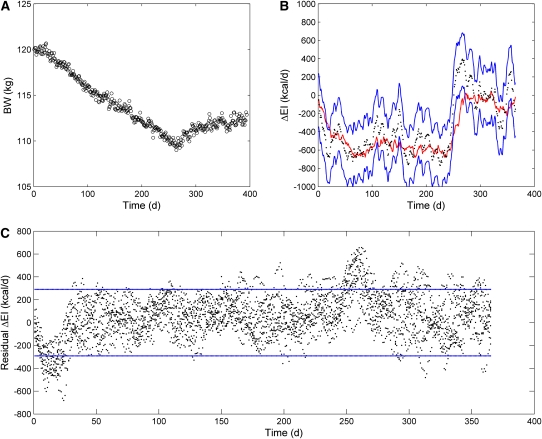
The simulated BW dynamics with initial conditions corresponding to a 120-kg woman with an initial body fat mass of 52.6 kg and PAL of 1.5 with 20% random fluctuations in dietary sodium, carbohydrate, and EI superimposed on the step diet changes are shown in Figure 4A. The estimated ΔEI tracked the actual changes in EI (Figure 4B) despite the significant differences in the initial body-composition variables. The 95% CI was 290 kcal/d, and the mean residual value was 54 kcal/d (Figure 4C). The simulated BW dynamics with initial conditions corresponding to an active 70-kg man with an initial body fat mass of 11.6 kg and PAL of 1.7 are shown in Figure 5A. Again, the estimated ΔEI tracked the actual changes in EI reasonably well (Figure 5B), and the 95% CI was 300 kcal/d with a mean residual of 120 kcal/d (Figure 5C).

FIGURE 4.

Simulated free-living data from a sedentary 120-kg female virtual study subject generated by using a computational model of macronutrient metabolism. A: Simulated body weight (BW) data for an example run of the model incorporating day-to-day fluctuations in energy intake (EI), dietary sodium, and carbohydrate. B: Estimated changes in EI (ΔEI; black dots) along with the 95% CI (blue lines) and moving average actual EI (red line) for the same example subject as depicted in panel A (number of data points = 28, time interval between data points = 1 d). C: Residuals of the estimated EI changes (black dots) for 10 runs using the same subject. Blue lines denote the calculated 95% CI.

FIGURE 5.

Simulated free-living data from an active 70-kg male virtual study subject generated by using a computational model of macronutrient metabolism. A: Simulated body weight (BW) data for an example run of the model incorporating day-to-day fluctuations in energy intake (EI), dietary sodium, and carbohydrate. B: Estimated changes in EI (ΔEI; black dots) along with the 95% CI (blue lines) and moving average actual EI (red line) for the same example subject as depicted in panel A (number of data points = 28, time interval between data points = 1 d). C: Residuals of the estimated EI changes (black dots) for 10 runs using the same subject. Blue lines denote the calculated 95% CI.

Estimating ΔEI during an unknown added exercise program

Addition of an exercise program to a diet intervention is a common prescription for weight-loss, but this confounds the estimation of ΔEI because both the diet and the added exercise contribute to the energy imbalance. We examined the effect of an unknown increase of physical activity on our estimate of ΔEI by combining the usual diet intervention with a relatively vigorous exercise program that increased energy expenditure by 3 kcal ⋅ kg⁻¹ ⋅ d⁻¹ (equivalent to running ≈1.8 miles every day) in a 90-kg man with an initial fat mass of 23 kg and PAL of 1.5. A comparison of Figure 6A with Figure 3A shows that the additional exercise resulted in more weight-loss. As expected, without accounting for the added exercise, these BW data caused a systematic deviation of the estimated ΔEI (Figure 6B), although the actual changes in EI continued to decrease within the calculated 95% CI. The mean of the residuals was −220 kcal/d (Figure 6C), which corresponded with the energy cost of exercise which averaged ≈240 kcal/d.

FIGURE 6.

Simulated free-living data from a sedentary 90-kg male virtual study subject who added an exercise program in addition to the diet. A: Simulated body weight (BW) data for an example run of the model incorporating day-to-day fluctuations in energy intake (EI), dietary sodium, and carbohydrate. B: Estimated changes in EI (ΔEI; black dots) along with the 95% CI (blue lines) and moving average actual EI (red line) for the same example subject as depicted in panel A (number of data points = 28, time interval between data points = 1 d). C: Residuals of the estimated EI changes (black dots) for 10 runs using the same subject. Blue lines denote the calculated 95% CI.

DISCUSSION

We showed the ability of a simple method for estimating ΔEI that has reasonable accuracy and precision and provides a convenient way to monitor the free-living patterns of ΔEI in individuals undergoing a weight-management program. Unlike previous reports (3, 5), our methodology does not require solving a differential equation and provides an explicit calculation of the 95% CI of the estimated ΔEI for each individual, which is required to properly assess compliance. We showed that frequent BW measurements over extended time periods are required to obtain reasonably precise estimates of free-living ΔEI. Recent advances in telemedicine make such BW measurements feasible and relatively inexpensive (29).

All mathematical models of human energy metabolism can be linearized (6) and result in the same ΔEI estimation method, albeit with different parameter values. We showed that the linearized model resulted in accurate ΔEI estimates for realistic ≈10% BW changes that might be expected in clinical weight-management programs. However, a nonlinear method that iteratively updates the energy partitioning rule can be used for very large weight changes and this method is described in Appendix A.

Our method was applied to BW data from 3 obese subjects engaged in an inpatient weight-loss program and provided accurate estimates of ΔEI after the initial period of rapid weight-loss. This transient disagreement was expected because the initial weight-loss was primarily due to reductions of body water that are not captured by our simple method (30). Such body water losses are also unaccounted for by a recent computational modeling method for estimating EI, and we showed that our simple method gave comparable results without the need to solve a differential equation. In addition, our simple method provides the first calculation of the 95% CI of ΔEI, which is needed to properly evaluate an individual's adherence to a prescribed diet change.

To investigate the ability of our method for estimating ΔEI in conditions representative of the free-living situation, we simulated BW data from a variety of “virtual subjects” with the use of a computational model of human macronutrient balance that incorporated realistic day-to-day fluctuations in EI and body water. As a test of the sensitivity of our ΔEI estimation method to the assumed parameter values, we simulated the BW changes in subjects who had substantially different initial BW, body fat, and PAL without adjusting the parameters of our method. Despite this challenge, the method provided reasonably accurate estimates of ΔEI and indicates that knowledge of model parameters is not the main limitation to estimating ΔEI in individuals. Rather, fluctuations in body water and day-to-day variations in EI limit the precision of the calculated ΔEI. This is why averaging the measured BW changes over several subjects significantly improves the precision of the estimated ΔEI for the group (data not shown). Similar to the initial rapid weight-loss in actual obese subjects, we showed that our ΔEI method had difficulty in the days after significant diet transitions due to body fluid shifts not accounted for in the simple model.

Because BW dynamics are affected by changes in both diet and physical activity, we showed that a substantial unknown change i physical activity can negatively affect the accuracy of the ΔEI method. This was the most severe test of our ΔEI estimation method because we fully expected that unaccounted-for changes in physical activity would bias the estimate of ΔEI. Nevertheless, the actual ΔEI remained within the predicted 95% CI, and our method therefore still provided a valid estimate of actual ΔEI even in this extreme example. In the future, it may be possible to incorporate measurements of physical activity changes using pedometers, accelerometers, heart rate monitors, or physical activity logs to adjust model parameters and to improve the ΔEI estimate. Future work will address this possibility and evaluate the effect on the accuracy and precision of the calculated ΔEI.

Estimates of absolute free-living EI in individuals will have very low precision due to the uncertainty of the initial energy-balanced EI. For example, the 95% CI for the baseline EI is >450 kcal/d using the Institute of Medicine equations for total energy expenditure (11), and this calculation requires an estimate of the physical activity of each individual. With the use of DLW measurements from 1399 adults reported in reference 31, the SD of the energy expenditure measurements is ≈500 kcal/d within a 5-kg BW range for both men and women. This very large variance for the initial EI estimate must be added to the calculated variance of our ΔEI estimate. If DLW measurements are performed on each individual before instituting the diet (an expensive and not widely available option), the SD of the initial EI can be substantially reduced but is still ≈100 kcal/d (32). As a result, without a precise estimate of the initial EI at energy balance, the use of BW measurements should be restricted to providing estimates of ΔEI and not absolute EI. Our simple method provides a convenient and inexpensive new tool for estimating free-living ΔEI and its CI using longitudinal BW measurements in individual subjects.

APPENDIX A

Linearized energy balance equation

We previously developed and validated a nonlinear mathematical model of human energy expenditure that included resting metabolic rate, thermic effect of feeding, tissue deposition and turnover costs, and adaptive changes in energy expenditure with over- and underfeeding (4, 13, 14). The linearized version of our model can be written as follows (4):

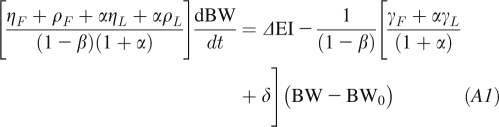where BW is the body weight, ΔEI is the change of EI from its initial energy balanced value, and γ_L = 22 kcal ⋅ kg⁻¹ ⋅ d⁻¹ and γ_F = 3.2 kcal ⋅ kg⁻¹ ⋅ d⁻¹ are the regression coefficients relating resting metabolic rate compared with lean body mass and fat mass, respectively (15). The parameter β = 0.24 accounts for the thermic effect of feeding as well as adaptive changes of energy expenditure during under- and overfeeding (4, 14, 16). The parameters η_F = 180 kcal/kg and η_L = 230 kcal/kg account for the biochemical efficiencies associated with fat and protein synthesis (16, 17), assuming that the change of lean body mass is primarily accounted for by body protein and its associated intracellular water (18). The parameter δ = 7 kcal ⋅ kg⁻¹ ⋅ d⁻¹ represents the physical activity of a relatively sedentary person with a PAL of 1.5. The parameter α represents the relation between changes of lean and fat mass α ≡ dL/dF = C/F (6), where C = 10.4 kg is the Forbes parameter. For modest weight changes, α can be considered to be approximately constant with F fixed at its initial value F₀ (19). An estimate for ΔEI is obtained by rearranging Equation A1:

where a is an estimate of the rate of change of BW over the corresponding time interval t,

and

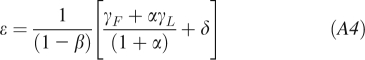Any mathematical model of human energy metabolism can be linearized into the form of Equation A2, and corresponding values for ρ and ϵ can be determined.

The CI of ΔEI

The variance of ΔEI at time t is given by:

where BW refers to the body weight at time t. We estimate parameter a using the ordinary least-squares regression formula 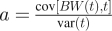to obtain the following:

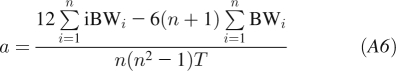where we consider n equidistant time points i with spacing between the points of T and used the identities:

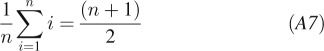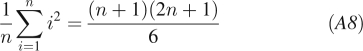The variance in a is given by the standard least squares formula 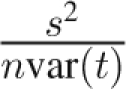, where s² is the residual error of the body weight around the regression line. We can use the empirically determined value of s² or estimate it using the stationary body weight fluctuations var(BW), which then gives

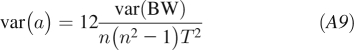We find that this formula and the empirical estimate give similar results. Similarly, the covariance of a and BW is

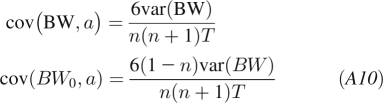Therefore, the ΔEI estimate over a time interval t = nT has a variance of:

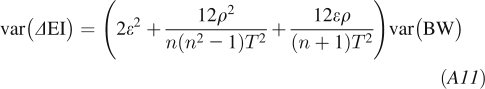The 95% CI is then given by .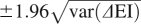

Nonlinear ΔEI estimation method

To account for the nonlinear changes of body composition that occur with large BW changes (19, 20), we rewrite the energy balance equation as follows:

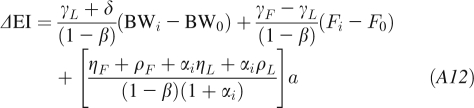where α_i = C/F_i and F_i = F_{i − 1} + (BW_i − BW₀)/(1 + α_{i − 1}).