A Semiparametric Bayesian Approach to Multivariate Longitudinal Data

Summary

We extend the standard multivariate mixed model by incorporating a smooth time effect and relaxing distributional assumptions. We propose a semiparametric Bayesian approach to multivariate longitudinal data using a mixture of Polya trees prior distribution. Usually, the distribution of random effects in a longitudinal data model is assumed to be Gaussian. However, the normality assumption may be suspect, particularly if the estimated longitudinal trajectory parameters exhibit multimodality and skewness. In this paper we propose a mixture of Polya trees prior density to address the limitations of the parametric random effects distribution. We illustrate the methodology by analyzing data from a recent HIV-AIDS study.

1 Introduction

Longitudinal data analysis, in which repeated measurements are taken on subjects at various time points, plays an important role in applied statistics, especially in biomedical research involving clinical trials. Rather than considering a single outcome, it is common nowadays to measure multiple outcomes on a subject to characterize an effect of interest, thus resulting in multivariate longitudinal data. Although statistical methods and estimation techniques are well developed for univariate longitudinal data (Grizzle & Allen, 1969; Khatri, 1966; Pothoff & Roy, 1964; Laird & Ware, 1982; Kleinman & Ibrahim, 1998; Shah et al., 1997; Zhang et al., 1998; Zeger & Diggle, 1994; Diggle et al., 2002), relatively little attention has been concentrated on longitudinal data of a multivariate response. Reinsel (1984) considered a multivariate random intercept covariance structure for balanced data. However, balanced data are quite unlikely in a longitudinal setting. Shah et al. (1997) developed a multivariate longitudinal model for unbalanced data with inference carried out via the EM algorithm. They assumed multivariate longitudinal data with Gaussian random effects and allowed for missing observations. They considered two responses (log CD4 count, log CD8 count) in their example; each was modelled linearly, and so the subject-specific random effect was 4-dimensional. Roy & Lin (2002) also developed a multivariate model for longitudinal data that allows for missing observations, assuming a latent variable approach. Recently, Fieuws & Verbeke (2006) developed a pairwise approach in which all possible bivariate models are fitted.

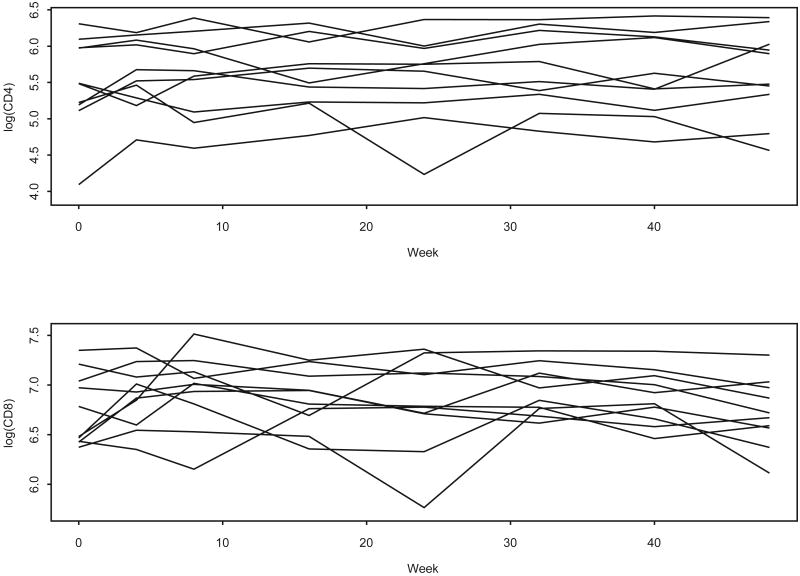
In this paper we take a Bayesian approach to multivariate longitudinal data. Our method generalizes existing methods on several issues. Most of the mixed models above provide a flexible likelihood framework to model continuous correlated outcomes parametrically. However, in practice the parametric assumption on the covariate effects may not always be appropriate; in our example CD4 and CD8 counts vary in a complicated manner over time (see Figure 1). To model longitudinal data of this kind, Zhang et al. (1998) and Zeger & Diggle (1994) considered semiparametric mixed models. In this paper we extend their semiparametric approach to the multivariate setting. We specify fixed covariate effects, but develop a smooth function of time to model the overall mean population effect, and account for the within-subject correlations using random effects. The unknown function is modelled using a linear combination of B-spline basis terms (de Boor, 1978), where the coefficients are modelled using a pairwise shrinkage prior distribution. In multivariate longitudinal data, random effects are usually assumed to have a normal distribution, and it may well happen that this distributions does not correctly fit the data at hand. This is particularly true if the data are multimodal, skewed, have outliers, or consist of diverse populations. Specifically, in our application we consider data on two widely used markers in HIV-AIDS studies: CD4 and CD8 counts. These data are collected from a new AIDS clinical trial (ACTG 398). It is well known that these markers usually have a high amount of between-subject variability (Figure 1). Thus, the normal distribution may not effectively model this extra heterogeneity in the samples. Also, observations from each patient's profile may not have the same distribution. For example, in a clinical study some patients may drop out of the study before the study ends. The longitudinal observations of the patients who left the study may not have the same distribution as those who completed the study (Brown & Ibrahim, 2003). Based on these observations, it is desirable to take the random effects from a sufficiently large class to capture such possibilities. Thus, we consider a model for multivariate random effects which generalizes the parametric normal distributional assumption to include a class of distributions that allows for features such as skewness and multimodality as well as generalizes the parametric models.

Figure 1.

Trajectories of log(CD4) and log(CD8) for 10 randomly selected subjects, ACTG 398 data.

One can use a simple extension of the existing model that employs a finite mixture of normal distributions for random effects. However, determining the number of mixands can be problematic; identifiability issues also arise. In contrast, continuous mixtures alleviate these problems, with nonparametric specification of the mixing distribution being most attractive. Thus, in this paper we assume a multivariate mixture of Polya trees (MPT) prior distribution for q-dimensional random effects. Univariate Polya tree and MPT models have been recently developed (Lavine, 1992, 1994; Walker & Mallick, 1997, 1999; Berger & Guglielmi, 2001; Hanson & Johnson, 2002; Hanson, 2006), but relatively little has been done for the multivariate case. We model the random effects distribution for our multivariate longitudinal data as a mixture of absolutely continuous finite Polya trees in ℝ^q centred at the family of mean-zero q-variate Gaussian distributions. This new framework allows the incorporation of the existing prior information based on the parametric model. This robust generalization has the potential to capture departures from a normal distribution, while having a good performance if the actual distribution is normal. One of the major advantages of using Polya tree prior distributions is that, in contrast to Dirichlet process prior distributions, they can place probability one on the set of absolutely continuous distributions. We perform the analysis within a Bayesian framework, thus providing a coherent means of inference and allowing for easy computation by standard Markov chain Monte Carlo (MCMC) techniques (Gelfand & Smith,1990).

The paper is organized as follows. In the next section we develop a model for multivariate longitudinal data. In Section 3 we develop the Bayesian analysis of the parametric model. We relax the normality assumption with multivariate MPT and Polya tree prior distributions in Section 4. In Section 5 we describe and analyze a clinical trial data set, ACTG 398; Section 6 draws conclusions.

2 Multivariate mixed model

Here we introduce our notation for the form of the multivariate longitudinal model. Let the sample in a longitudinal study consists of K characteristics and m subjects, with the ith subject having n_i measurements over time. Let y_ijk denote the measurement of the ith subject at time t_ij for characteristic k, i = 1, 2, …, m; k = 1, 2, …, K; j = 1, 2, …, n_i. Then the semiparametric mixed model for outcome y_ijk is given by

$$y_{\mathit{ijk}}=x_{\mathit{ijk}}^{\top }{\mathit{\beta }}_k+f_k(t_{ij})+{\mathbf{z}}_{\mathit{ijk}}^{\top }{\mathit{\gamma }}_{ik}+e_{\mathit{ijk}},$$ (1)

where β_k is the p_k × 1 vector of regression coefficients associated with covariates x_ijk (p_k × 1), and f_k(t) is a twice-differentiable smooth function of time for characteristic k. Thus, we allow each characteristic to have a unique nonparametric population mean function in time. The γ_ik are independent q_k × 1 vectors of random effects associated with covariates z_ijk (q_k × 1), and the e_ijk are independent measurement errors.

Let y_ik = (y_i1k, y_i2k, …, y_inik)^⊤. Then we define the following notation:

$${\mathbf{y}}_{ik}={\mathbf{X}}_{ik}{\mathit{\beta }}_k+{\mathbf{N}}_{ik}{\mathbf{f}}_k+{\mathbf{Z}}_{ik}{\mathit{\gamma }}_{ik}+{\mathbf{e}}_{ik}.$$ (2)

We write t⁰ for the vector of the r ordered distinct time points of {t_ij}. N_ik is the incidence matrix for the ith subject and kth characteristic connecting t_i = (t_i1, …, t_ini) to t⁰ such that the (j, h)th element of N_ik is 1 if $t_{\mathit{ij}}=t_h^0$ and 0 otherwise for j = 1, 2, …, n_i, h = 1, 2, …, r. Finally, ${\mathbf{f}}_k={(f_k(t_1^0),\dots ,f_k(t_r^0))}^{\top }$, the subject-specific design matrix X_ik contains the n_i rows ${\mathbf{x}}_{\mathit{ijk}}^{\top }$, and Z_ik contains the n_i rows ${\mathbf{z}}_{\mathit{ijk}}^{\top }$.

We assume that ${\mathit{\gamma }}_i={({\mathit{\gamma }}_{i1}^{\top },{\mathit{\gamma }}_{i2}^{\top },\dots {\mathit{\gamma }}_{iK}^{\top })}^{\top }$, where γ_ij ∈ ℝ^q_j, $q={\sum }_{j=1}^K{q}_j$. For initial model development, γ_i is assumed to have a N_q(0, D) distribution, where D is a symmetric positive definite matrix. The normality assumption for γ_i will be relaxed in Section 4, where we will assume a nonparametric distribution for γ_i. The measurement error e_ik is assumed to be distributed as N(0, R_ik), where ${\mathbf{R}}_{ik}={\sigma }_k^2{\mathbf{I}}_{n_i}$. We also assume independence between γ_i and e_ik.

3 Smoothing spline and priors

Let $\mathit{\theta }=({\mathit{\beta }}_{1:K},{\sigma }_{1:K}^2,{\mathbf{f}}_{1:K},\mathbf{D})$ be the set of parameters for model (2), where we generically write ${\mathbf{v}}_{1:n}={\left\{{\mathbf{v}}_i\right\}}_{i=1}^n$ for any matrices v₁, …, v_n. We assume conditionally conjugate, independent prior distributions that lead to simpler updating schemes in the Markov chain sampling methodology. In particular,

$${\mathit{\beta }}_k\sim N_p({\mathit{\mu }}_k,{\sum }_k^{-1}),{\mathbf{D}}^{-1}\sim \text{Wishart}({\eta }_0,{\sum }_{\eta }),{\sigma }_k^{-2}\sim \text{gamma}({\nu }_{0k}/2,{\delta }_{0k}/2).$$

We model each of the K flexible nonparametric time effects in (2) as a linear decomposition of basis terms. Suppose that ${\mathbf{f}}_k={(f_k(t_1^0),\dots ,f_k(t_r^0))}^{\top }$. Let us suppress the notation k for the moment. Then f is modlled as

$$f(t)=\sum _{l=1}^L{\phi }_l{b}_l(t).$$

Here {b₁, …, b_L} are B-spline basis functions of degree 2 with equidistant knots, and ϕ = (ϕ₁, …, ϕ_L)^⊤ are the associated coefficients. To ensure that the function is flexible, yet smooth, we follow the methodology of Lang & Brezger (2004) and place a first order random walk prior distribution on the coefficients, so that

$$p({\phi }_1)\propto 1,{\phi }_l={\phi }_{l-1}+u_l,l=2,\dots ,L,u_2,\dots ,u_L\mid \tau \stackrel{\mathit{iid}}{\sim }N(0,{\tau }^2).$$

Here the random walk variance τ² can be interpreted as a smoothing parameter. Thus the resulting conditional prior density for ϕ satisfies

$$p(\mathit{\phi }\mid \tau )\propto exp\left(-\frac{1}{2{\tau }^2}{\mathit{\phi }}^{\top }\mathbf{\Omega }\mathit{\phi }\right),$$

with a banded penalty matrix

$$\mathbf{\Omega }=\left(\begin{array}{cccccc}1& -1& 0& \cdots & 0& 0\\ -1& 2& -1& \cdots & 0& 0\\ 0& -1& 2& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & 2& -1\\ 0& 0& 0& \cdots & -1& 1\end{array}\right).$$

Now let us generalize the above prior density for f_k(t). Write the vector of function evaluations ${\mathbf{f}}_k={(f_k(t_1^0),\dots ,f_k(t_r^0))}^{\top }$ as the product f_k = B_kϕ_k, where B_k is an L × r design matrix. Then the prior density on the penalized spline coefficients can be cast into a general form as follows:

$$p({\mathit{\phi }}_k\mid {\tau }_k)\propto exp\left(-\frac{1}{2{\tau }_k^2}{{\mathit{\phi }}_k}^{\top }\mathbf{\Omega }{\mathit{\phi }}_k\right).$$

For the variance parameter we assume an inverse gamma distribution, i.e., ${\tau }_k^2\sim {\text{gamma}}^{-1}(a_k,b_k)$. This prior structure is a Bayesian interpretation of the work of Eilers & Marx (1996), who constructed a difference penalty from the random walk prior and took a penalized maximum likelihood approach.

Because the marginal and joint posterior distributions are analytically intractable, an MCMC sampling scheme is used to produce iterates from the joint posterior distribution, from which the full spectrum of inference can be constructed. Full details of the evaluation of conditional posterior distributions are provided in the Appendix.

4 Nonparametric random effects distribution

We consider a MPT prior distribution for the distribution G on the γ_is in order to relax distributional assumptions. Many authors have investigated nonparametric distributions for random effects. Kleinman & Ibrahim (1998) considered a univariate linear mixed effects model where the random effects γ₁, …, γ_m ∈ ℝ^q arise from a probability measure G assigned a Dirichlet process prior distribution. Zhang & Davidian (2001) considered modelling the random effects distribution in a standard linear mixed model as the square of a polynomial of order K multiplied by a bivariate Gaussian density. Song, Davidian & Tsiatis (2002) extended this approach to the joint modelling of survival and longitudinal data. and modelled a bivariate random effects distribution for CD4 counts in this manner. More recently, Ghidey, Lesaffre & Eilers (2004) considered modelling a bivariate random effects distribution using a mixture of bivariate Gaussian densities with fixed locations.

Lavine (1992) introduced MPT models and noted that random partitions smooth out partitioning effects seen in simple Polya tree models. Berger & Guglielmi (2001) considered a univariate MPT model with a fixed partition to test whether data arise from a parametric family versus a nonparametric alternative. The marginal model is fitted using an importance sampling distribution derived from the parametric family. Hanson & Johnson (2002) considered a median regression model with a univariate MPT prior distribution on the error density centred at a scaled family of Gaussian distributions.

Paddock (1999) and Paddock et al. (2003) considered multivariate Polya trees centred at a multivariate uniform distribution. They randomly jittered the partition, smoothing out the partition effects in a manner similar to an MPT. Hanson (2006) proposed a class of multivariate MPT prior distributions that generalized the multivariate Gaussian family. In either approach, the Polya tree is fully specified up to a finite level J and suffers from an explosion of parameters when the dimension q climbs past 2 or 3. For a q-dimensional MPT prior distribution, the number of 2^q-dimensional Dirichlet vectors needed to define the model is ${\sum }_{j=0}^{J-1}{2}^{jq}=(2^{qJ}-1)/(2^q-1)$. For example, for a finite 4-dimensional tree with J = 5 levels, 69 905 16-dimensional Dirichlet vectors are required, along with the 10 parameters in D. For this reason, we instead develop associated marginal models which have only the parameters in the covariance matrix D.

A random probability measure G given a Polya tree prior distribution is defined by a class of partitions ${\left\{{\Pi }^j\right\}}_{j=1}^J$ and a class of Dirichlet distribution parameters 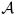. We consider one method to extend the “canonical” partitions of described in Lavine (1992) to multiple dimensions.

The space ℝ^q is partitioned at level j by sets B₀(j; k₁, …, k_q) where k_l = 1, …, 2^j, l = 1, …, q. Define

$$B_0(j;k_1,\dots ,k_q)=({\mathrm{\Phi }}^{-1}((k_1-1)2^{-j}),{\mathrm{\Phi }}^{-1}(k_1{2}^{-j}))\times \cdots \times ({\mathrm{\Phi }}^{-1}((k_q-1)2^{-j}),{\mathrm{\Phi }}^{-1}(k_q{2}^{-j})).$$ (3)

Let ${\Pi }_0^j$ denote the class of partitions at level j, ${\Pi }_0^j=\{B_0(j;k_1,,\dots ,k_q)\}$. The transformed partitions ${\Pi }_{\mathbf{D}}^j$ are obtained from (3) through

$$B_{\mathbf{D}}(j;k_1,\dots ,k_q)=\{{\mathbf{D}}^{1/2}\mathbf{y}:\mathbf{y}\in B_0(j;k_1,\dots ,k_q)\}.$$ (4)

Clearly, if y ∼ N_q(0, D), then Pr(y ∈ B_D(j; k₁, …, k_q)) = 2^−qj.

Let S_j = {1, …, 2^j−1}^q. Define vectors of conditional probabilities C_j;s = (C(j; k₁, …, k_q) : k_l = 2_sl − 1, 2_sl; l = 1, …, q), where s = (s₁, …, s_q)^⊤ ∈ S_j, by

$${\mathbf{C}}_{j,\mathbf{s}}\mid \alpha \sim \text{Dirichlet}(\alpha \rho (j){\mathbf{1}}_{2^q}).$$ (5)

For example, C_2;(1,2) = (C(2; 1, 3), C(2; 1, 4), C(2; 2, 3), C(2; 2, 4))^⊤. These are the conditional probabilities of, respectively, sets B_D(2; 1, 3), B_D(2; 1, 4), B_D(2; 2, 3), B_D(2; 2, 4) given B_D(1; 1, 2). The G-measure of a set in ${\Pi }_{\mathbf{D}}^j$ given 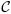= {C_j,s : j = 1, …, J; s ∈ S_j} is defined to be

$$G\{B_{\mathbf{D}}(j;k_1,\dots ,k_q)\}=\prod _{l=1}^{j}C(l;\lceil k_1{2}^{l-j}\rceil ,\dots ,\lceil k_q{2}^{l-j}\rceil ),$$ (6)

where ⌈·⌉ is the ceiling function. On sets at level J, we assume that G follows a N_q(0, D) distribution given D. That is, for A ⊂ B_D(J, k₁, …, k_q), G(A)∣G(B_D(J, k₁, …, k_q)) = 2^qJ Φ_D(A)G{B_D(J, k₁, …, k_q)}.

Denote the prior Polya tree (PT) model on the measure G, given by (4)-(6), as G ∼ PT_q(α, ρ, Φ_D) and further assume the hyperprior D⁻¹ ∼ Wishart(η₀, Σ_η). The random effects model is then

$${\mathit{\gamma }}_1,\dots ,{\mathit{\gamma }}_m\mid G\stackrel{\mathit{iid}}{\sim }G,G\mid \mathbf{D}\sim {\mathrm{PT}}_q\left(\alpha ,\rho ,{\mathrm{\Phi }}_{\mathbf{D}}\right),{\mathbf{D}}^{-1}\sim \text{Wishart}({\eta }_0,{\sum }_{\eta }).$$ (7)

It is easy to verify, given D, for y∣G ∼ G, G ∼ PT_q(c, ρ, Φ_D), that E(y) = 0, cov(y) = D, and Pr(y ∈ A) = ∫_A ϕ_D (x) dx, where ϕ_D(·) is the probability density function (pdf) of a N_q(0, D) vector. The precision α determines how “close” the random probability measure G is to the centering Φ_D, with larger values giving G ≈ Φ_D (Hanson, 2006).

Given a vector y ∈ ℝ^q, we need to know which set k = (k₁, …, k_q)^⊤ in ${\Pi }_{\mathbf{D}}^J$ at level j, B_D(j; k₁, …, k_q), contains it. This is given by

$${\mathbf{k}}_{\mathbf{D}}(j,\mathbf{y})=\left[\begin{array}{c}\mathbf{Int}\{2^j\mathrm{\Phi }(x_1)+1\}\\ ⋮\\ \mathbf{Int}\{2^j\mathrm{\Phi }(x_q)+1\}\end{array}\right],\text{where}\mathbf{x}={\mathbf{D}}^{-1/2}\mathbf{y}.$$

The kth index of k_D(j − 1,w) is recursively given by the ceiling of one half of the kth index of k_D(j, w).

Define n_D(j, s; γ_1:t) to be the 2^q-dimensional vector {# ${\{{\mathit{\gamma }}_i\}}_{i=1}^t$ in B_D(j; k₁, …, k_q)} where each k_l, l = 1, …, q, ranges over the two values 2_sl − 1 and 2_sl. Then the full conditional distribution for C_j,s is given by

$${\mathbf{C}}_{j,\mathbf{s}}\mid \alpha ,{\mathbf{\gamma }}_{1:m},\mathbf{D}\sim \text{Dirichlet}(\alpha \rho (j){\mathbf{1}}_{2^q}+{\mathbf{n}}_{\mathbf{D}}(j,\mathbf{s};{\mathbf{\gamma }}_{1:m})).$$

Let y ∈ ℝ^q. Given 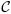and D, the pdf of G is given by

$$g(\mathbf{y}\mid \mathcal{C},\mathbf{D})=2^{J_q}{p}_{\mathcal{C}}\{{\mathbf{k}}_{\mathbf{D}}(J,\mathbf{y})\}{\phi }_{\mathbf{D}}(\mathbf{y}),$$

where p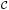(k₁, …, k_q) = G{B_D(J; k₁, …, k_q)}, which is obtained from (6).

Given γ_1:i and D, the expected value of the pdf of G is given by

$$g(\mathbf{y}\mid {\mathit{\gamma }}_{1:i},\mathbf{D})={\phi }_{\mathbf{D}}(\mathbf{y})\prod _{j=1}^J\frac{2^q\alpha \rho (j)+2^q{\mathbf{n}}_{\mathbf{D}}(j,{\mathbf{k}}_{\mathbf{D}}(j,\mathbf{y});{\mathit{\gamma }}_{1:i})}{2^q\alpha \rho (j)+{\mathbf{n}}_{\mathbf{D}}(j-1,{\mathbf{k}}_{\mathbf{D}}(j-1,\mathbf{y});{\mathit{\gamma }}_{1:i})}.$$ (8)

Through (8), the marginal pdf of γ₁, …, γ_m is thus given by

$$\begin{array}{l}g({\mathit{\gamma }}_1,\dots ,{\mathit{\gamma }}_m\mid \mathbf{D})=\left[\prod _{i=1}^m{\phi }_{\mathbf{D}}({\mathit{\gamma }}_i)\right]\left[\prod _{i=2}^m\prod _{j=1}^J\frac{2^q\alpha \rho (j)+2^q{\mathbf{n}}_{\mathbf{D}}(j,{\mathbf{k}}_{\mathbf{D}}(j,{\mathit{\gamma }}_i);{\mathit{\gamma }}_{1:i-1})}{2^q\alpha \rho (j)+{\mathbf{n}}_{\mathbf{D}}(j-1,{\mathbf{k}}_{\mathbf{D}}(j-1,{\mathit{\gamma }}_i);{\mathit{\gamma }}_{1:i-1})}\right]\\ =\left[\prod _{i=1}^m{\phi }_{\mathbf{D}}({\mathit{\gamma }}_i)\right]q_{\mathbf{D}}({\mathit{\gamma }}_{1:m};\alpha ),\text{say.}\end{array}$$

When the vectors ${\{{\mathit{\gamma }}_i\}}_{i=1}^m$ are evenly distributed among sets B_D(j∣k₁,…, k_q) on each level j, q_D(γ_1:m; α) = 1 and the parametric density is obtained. We exploit this fact in the construction of Metropolis-Hastings proposal distributions for sampling D given the remaining parameters as well as sampling the γ₁, …, γ_m.

Assuming the model (7), the full conditional distribution for D given 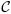and γ₁, …, γ_m is

$$p({\mathbf{D}}^{-1}\mid \mathcal{C},{\mathit{\gamma }}_{1:m})\propto {|{\mathbf{D}}^{-1}|}^{-(m+{\eta }_0-q-1)/2}exp\left\{-0.5tr{\mathbf{D}}^{-1}\left(\sum _{i=1}^m{\mathit{\gamma }}_i{\mathit{\gamma }}_i^{\top }+{\sum }_{\eta }^{-1}\right)\right\}{q}_{\mathbf{D}}({\mathit{\gamma }}_{1:m};\alpha ).$$

By experimenting with various types of Metropolis-Hastings proposal distributions, we have found a Metropolis-Hastings step centred at the current value D⁻¹ updates D⁻¹ fairly well when the estimated random effects are not highly “non-normal.” Updating D⁻¹ proceeds by sampling D*⁻¹ ∼ Wishart(df, D⁻¹/df) and accepting the proposal D*⁻¹ with probability

$$\rho =min\left\{1,\frac{q_{{\mathbf{D}}^{\ast }}({\mathit{\gamma }}_{1:m};\alpha )}{q_{\mathbf{D}}({\mathit{\gamma }}_{1:m};\alpha )}\frac{exp\{-0.5tr({\mathbf{D}}^{\ast -1}({\sum }_{i=1}^m{\mathit{\gamma }}_i{\mathit{\gamma }}_i^{\top }+{\sum }_{\eta }^{-1})+df{\mathbf{D}}^{\ast }{\mathbf{D}}^{-1})\}{|\mathbf{D}|}^{\frac{{\eta }_0+m}{2}-df}}{exp\{-0.5tr({\mathbf{D}}^{-1}({\sum }_{i=1}^m{\mathit{\gamma }}_i{\mathit{\gamma }}_i^{\top }+{\sum }_{\eta }^{-1})+df{\mathbf{DD}}^{\ast -1})\}{|{\mathbf{D}}^{\ast }|}^{\frac{{\eta }_0+m}{2}-df}}\right\}.$$

The random effects γ₁, …, γ_m are also updated via Metropolis-Hastings steps by generating ${\mathit{\gamma }}_i^{\ast }\sim N_q({\mathbf{V}}_i^{-1}[{\mathbf{Z}}_i^{\top }{\mathbf{R}}_i^{-1}({\mathbf{y}}_i-{\mathbf{X}}_i\mathit{\beta }-{\mathbf{N}}_i\mathbf{f})],{\mathbf{V}}_i^{-1})$, where ${\mathbf{V}}_i={\mathbf{Z}}_i^{\top }{\mathbf{R}}_i^{-1}{\mathbf{Z}}_i+{\mathbf{D}}^{-1}$ R_i = diag(R_i1, …, R_iK) and Z_i = diag(Z_i1, …, Z_iK) (see Appendix), and accepting the proposal ${\mathit{\gamma }}_i^{\ast }$ with probability

$$\rho =min\left\{1,\frac{q_{\mathbf{D}}({\mathit{\gamma }}_{1:m}^{\ast };\alpha )}{q_{\mathbf{D}}({\mathit{\gamma }}_{1:m};\alpha )}\right\},$$

where ${\mathit{\gamma }}_{1:m}^{\ast }$ is the set γ_1:m with ${\mathit{\gamma }}_i^{\ast }$ replacing γ_i. When a prior density p(α) is placed on α, the full conditional distribution is given by p(α∣;γ_1:m, D) ∝ p(α)q_D(γ_1:m; α). Updates proceed via Metropolis-Hastings steps as before.

To our knowledge, the random effects model we present is the only direct generalization of the Gaussian model considered in the literature. Under Dirichlet process mixing, a Gaussian model is obtained in the limit as the precision goes to zero, but this is at the boundary of the parameter space. A formal Bayes factor can be computed (see, for example, Basu & Chib, 2003), but the models are not formally nested in the sense that one can test H₀ : θ = θ₀ where θ₀ is an interior point of Θ. Thus, to compare the different models, we follow Geisser & Eddy (1979), who introduced a predictive criterion termed the log pseudo marginal likelihood (LPML). The conditional predictive ordinate (CPO) for the (ijk)th observation is

$${\text{CPO}}_{\mathit{ijk}}=p(y_{\mathit{ijk}}\mid y_{(-\mathit{ijk})})=E\{f(y_{\mathit{ijk}}\mid \mathit{\theta },{\mathit{\gamma }}_{1:m})\mid y_{(-\mathit{ijk})}\},$$

where y_(−ijk) denotes the rest of the data after deleting the (ijk)th observation. The expectation is taken with respect to the posterior distribution of the model parameter given the cross-validated data y_(−ijk). Gelfand & Dey (1994) suggested a particularly simple method to obtain estimates of CPO statistics from MCMC output, which we adapt to the situation at hand.

A useful aggregate measure of predictive model performance is the sum of the log CPO statistics: $\text{LPML}=log{\Pi }_{i=1}^m{\Pi }_{j=1}^{n_i}{\Pi }_{k=1}^K{\text{CPO}}_{\mathit{ijk}}$. The model with the larger LPML value is the better-fitting model from a predictive standpoint. One can compute a pseudo-Bayes factor for comparing model 2 to model 1, defined as PBF₂₁ = exp(LPML₂−LPML₁). Kadane & Lazar (2004) noted that predictive measures, such as the pseudo-Bayes factor, attempt to find “which models give the best predictions of future observations generated from the same process as the original data”.

5 Data Analysis

We illustrate our method using data from a large clinical trial on HIV-AIDS, ACTG 398. All regimens included the following ART drugs: abacavir, a nucleoside reverse transcriptase inhibitor (NRTI); adefovir dipivoxil, another NTRI; efavirenz, a non-NRTI (NNRTI); and amprenavir, a protease inhibitor (PI). In addition, three of the four arms included a second PI: saquinavir, indinavir, or nelfinavir, respectively, whereas the fourth arm received a matched placebo. Thus, three of the treatment arms were similar in that they contained a second PI drug, while the fourth arm had a single PI drug and a matched PI placebo. The results of the primary analysis were reported by Hammer et al. (2002). Based on these results, we combined the three dual PI arms together, versus the single PI arm. Thus, we take two treatment arms in our analysis. The primary objective of the study was to compare the proportion of subjects who had virologic failure after 24 weeks on study between the double-PI arms and the single-PI arm. The subjects in the trial were either NNRTI naive, i.e., they had not previously received drugs from the NNRTI class, or NNRTI experienced, i.e., they had previously received NNRTIs as part of their treatment. NNRTI naive subjects have a better virologic response in the trial. We are interested in analyzing the markers, CD4 and CD8 cell counts of the subjects on the study. These markers were measured at r = 47 distinct time points starting from the 0th week to a maximum 56th week. However, not all subjects have responses at each time point. We discarded patients with two or fewer (n_i ≤ 2) observations and thus our analysis consisted of m = 454 patients with a total of ${\sum }_{i=1}^{454}{n}_i=3172$ observations. The covariates we included in this analysis are: treatment (second PI versus placebo), NNRTI experience, and baseline log₁₀ viral load. We assumed 10 equally-spaced knots between $t_1^0=0$ and $t_{47}^0=56$, so the number of quadratic B-spline basis functions is 11.

We fitted the following bivariate model:

$$y_{\mathit{ijk}}={\beta }_{0k}+{\beta }_{1k}{x}_{\mathit{ijk}1}+{\beta }_{2k}{x}_{\mathit{ijk}2}+{\beta }_{3k}{x}_{\mathit{ijk}3}+f_k(t_{ij})+{\gamma }_{i0k}+{\gamma }_{i1k}{t}_{ij}+e_{\mathit{ijk}},$$ (9)

for i = 1, …, 454; j = 1, …, n_i, and k = 1, 2. Again, y_ijk is the response of the kth marker for the ith subject at the jth time point t_ij (in weeks), k = 1 denotes the log(CD4) count and k = 2 denotes the log(CD8) count. The covariates are fixed for each subject i across the n_i time points: x_ij11 = x_ij21 = log₁₀ baseline HIV RNA, x_ij12 = x_ij22 = treatment arm (1=double-PI and 0=single-PI placebo), and x_ij13 = x_ij23 = NNRT experience (1=experienced and 0=naive). The γ_0ik and γ_1ik are subject i's random effects corresponding to each marker. The longitudinal model can be interpreted as follows. The smooth trajectory f_k(t) is an overall mean response for marker k that anticipates a time-dependent population response, for example a dip following by a levelling off after a subject was initially enrolled in the trial. The ith subject's “intercept” term γ_0ik allows for a global subject deviation in population mean response and the “slope” γ_1ik can be interpreted as the subject-specific difference from the overall population rate of change of the marker at any time t.

More complex subject-specific trajectories are easily modelled in the existing framework. For example, each trajectory could be modelled with a second nonpenalized spline on top of the population trend f_k(t). However given the very limited number of measurements taken on each subject, this would amount to gross overfitting of these data. For example, Brown, Ibrahim & DeGruttola (2005) considered this sort of framework with a normal prior distribution on the subject-specific spline coefficients; their fitted mean trajectories tracked the data quite well, even with measurements totalling as few as n_i = 4.

Prior values were fixed as follows: α = 5, 10, ∞; the μ_ks were zero vectors; Σ_k = 10⁻⁶I₄ (precision matrices for β₁ and β₂); ${\sum }_{\eta }^{-1}=diag(1,0.00015,0.5,0.0001)\times {\eta }_0$ (precision matrix for Wishart prior); η₀ = 4; ν₀₁ = ν₀₂ = δ₀₁ = δ₀₂ = a₁ = b₁ = a₂ = b₂ = 0.001. The matrix Σ_η was chosen to centre D⁻¹ at precision values obtained by Shah, Laird & Schoenfeld (1997) for a different, but similar, data set on (log(CD4), log(CD8)) counts using a Gaussian model. The degrees of freedom (df), df = 3 worked well for α = 10, df = 6 worked for α = 5. However, obtaining reasonable mixing was difficult for α = 1.

Table 1 gives the posterior means and standard deviations (in parentheses) of model parameters along with the LPML values. Predictively, the MPT model with α = 5 is a better model than either α = 10 or the parametric model (α = ∞). The LPML from fitting the model without the splines, but rather an overall population line and with Gaussian random effects is −2024. The LPML assuming a spline rather than a simple linear function in time was −1933, indicating vastly increased predictive utility. The baseline HIV-RNA is a significant covariate for both CD4 and CD8, since the 95% credible intervals do not contain zero across models. However, none of the other covariates are significant in any of the models. These results are similar across the various MPT and the normal models; however, there is a general decreasing trend in both estimated effects and standard deviations as α decreases from ∞ to small values. The estimates of treatment effect are negative for both markers, suggesting a decrease in marker count over the the study period. However, the NNRTI experience was estimated to be negative for CD4 count and positive for CD8 count, although not significant. Hammer et al. (2002) found that, at 48 weeks, there was no significant difference in mean changes in CD4 cell counts relative to baseline in combined double-PI arms versus single-PI placebo, in line with our retaining the hypothesis H₀ : β₁₂ = 0.

Table 1.

Posterior means (standard deviations) of regression effects and LPML values for models (9) and (7), ACTG 398 data. α is the mixture of Polya trees (MPT) and Polya tree (PT) prior distribution precision; higher α values indicate a more parametric model.

	α ∼ Γ(5, 1) PT	α = 5 MPT	α =10 MPT	α = ∞ Parametric
LPML	−1901	−1924	−1930	−1933
β11	−0.294 (0.040)	−0.399 (0.0489)	−0.439 (0.0488)	−0.490 (0.0493)
β12	−0.068 (0.062)	−0.0608 (0.0706)	−0.0246 (0.0744)	−0.00619 (0.0788)
β13	−0.147 (0.054)	−0.125 (0.0679)	−0.136 (0.0710)	−0.145 (0.0743)
β21	−0.064 (0.030)	−0.102 (0.0315)	−0.121 (0.0324)	−0.140 (0.0318)
β22	−0.032 (0.043)	−0.0196 (0.0470)	0.0029 (0.0489)	0.00915 (0.0507)
β23	0.036 (0.043)	0.0323 (0.0461)	0.0325 (0.0468)	0.0330 (0.0480)

As α falls from α = ∞ (parametric model) to α = 10 to α = 5, the overall predictive performance of the model increases according to the LPML measure. For α = 1, reasonable MCMC mixing did not occur even after 100 000 iterations. We instead fitted a simple Polya tree model with D⁻¹ fixed at the posterior mean under the α = 10 model, assigned a prior distribution on α as α ∼ gamma(5, 1). The MCMC mixed very well for this simple PT model. The resulting posterior mean and standard deviation for α were 0.176 and 0.147, a marked shift towards much smaller values than under the prior, and indicating highly “non-normal” random effects. The LPML for the simple PT model increased by about 22, yielding a pseudo Bayes factor of e²² ≈ 10⁹ in favor of the simple PT model with a prior distribution on α. The estimated regression coefficients under this simple Polya tree model are also given in Table 1. Under the MPT model, the correlation between the intercepts is estimated to be 0.61, the correlation between the slopes 0.86. But the correlation between intercept and slope is 0.10 for log(CD4) and −0.13 for log(CD8). Thus, there is a high degree of similarity between CD4 and CD8 counts within a subject over time.

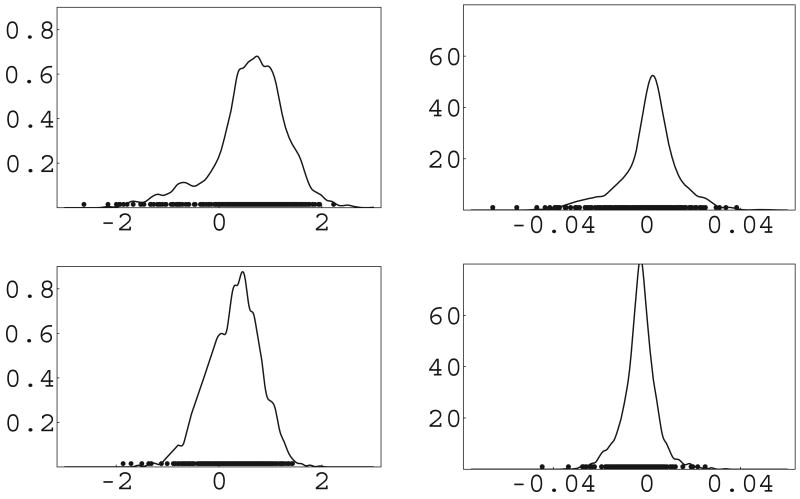
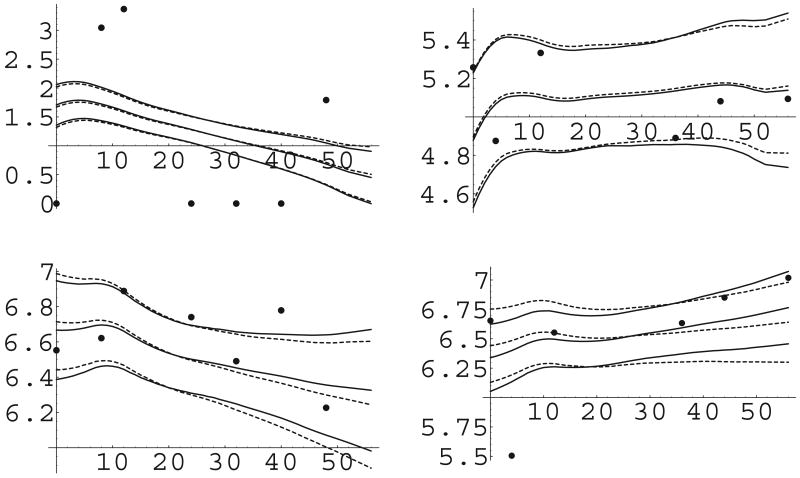
Figure 2 shows the kernel-smoothed estimated posterior densities for the random effects along with the posterior estimates of the m = 454 values from fitting the PT model with α ∼ gamma(5, 1). It is clear from these graphs that the PT ably models the non-normal, skewed characteristics of these densities. Figure 3 shows the estimated mean trajectories for two patients, along with 95% credible intervals; the solid circles represent the observed log CD4 and CD8 counts. The solid line is the parametric model with spline mean, and the dashed line is the simple PT model with spline mean and α ∼ Gamma(5, 1). The trajectories are not wildly different, but some differences are noticeable, especially for the CD8 counts. Differences in predictive (CD4, CD8) counts for subjects not in the study are bound to show more dissimilarities, if interest is rather in predictive inference.

Figure 2.

Estimated marginal densities (lines) and posterior mean random effects (dots) from simple Polya tree model with α ∼ gamma(5, 1), ACTG 398 data. Top panels are intercept (left) and slope (right) for log(CD4), bottom panels are for log(CD8).

Figure 3.

Raw data (dots) and estimated trajectories for two subjects, ACTG 398 data. Solid lines are parametric (α → ∞) model and dashed lines are simple Polya tree model. Columns are subjects and the top panel is log(CD4), bottom log(CD8).

6 Conclusion

Normality of random effects is a routine assumption for linear mixed models, but may be unrealistic. In this paper, we have proposed an approach based on a nonparametric Bayesian method for multivariate longitudinal data, where the random effects are assumed to have a flexible MPT prior distribution that generalizes the standard Gaussian assumption. The model with an MPT prior distribution is shown to outperform the usual Gaussian random effects model. We have found in general that an MPT outperforms a PT with a fixed covariance matrix estimated from either an MPT model or the parametric model, with the same fixed value of α.

Though our model was built from the features of the data at hand, it has general application to situations where multiple responses are measured over time. As pointed out, our model can have more general subject-specific curves such as splines, but due to data limitations, we instead considered a more parsimonious model.

Appendix: Conditional Distributions Under the Gaussian Model

Define matrices X_i = diag(X_i1 …, X_iK), Z_i = diag(Z_i1 …, Z_iK), N_i = diag(N_i1 …, N_iK), R_i = diag(R_i1, …, R_iK), and the vectors ${\mathbf{y}}_i={({\mathbf{y}}_{i1}^{\top },\dots ,{\mathbf{y}}_{iK}^{\top })}^{\top }$, $\mathit{\beta }={({\mathit{\beta }}_1^{\top },\dots ,{\mathit{\beta }}_K^{\top })}^{\top }$, $\mathbf{f}={({\mathbf{f}}_1^{\top },\dots ,{\mathbf{f}}_K^{\top })}^{\top }$. Define ${\mathbf{V}}_k={\sum }_k+{\sum }_i{\mathbf{X}}_{ik}^{\top }{\mathbf{R}}_{ik}^{-1}{\mathbf{X}}_{ik}$, ${\mathbf{P}}_k^{-1}={\tau }_k^{-2}\mathbf{\Omega }+{\sigma }_k^{-2}{\sum }_i{[{\mathbf{N}}_{ik}{\mathbf{B}}_k]}^{\top }[{\mathbf{N}}_{ik}{\mathbf{B}}_k]$, and ${\mathrm{\Delta }}_i={\mathbf{D}}^{-1}+{\mathbf{Z}}_i^{\top }{\mathbf{R}}_i^{-1}{\mathbf{Z}}_i$.

The full conditional distributions under the parametric normal model are:

$$\begin{array}{l}{\mathit{\beta }}_k\sim N_{p_k}\left[{\mathbf{V}}_k^{-1}\left({\sum }_k{\mathit{\mu }}_k+\sum _i{\mathbf{X}}_{ik}^{\top }{\mathbf{R}}_{ik}^{-1}({\mathbf{y}}_{ik}-{\mathbf{N}}_{ik}{\mathbf{f}}_k-{\mathbf{Z}}_{ik}{\mathit{\gamma }}_{ik})\right),{\mathbf{V}}_k^{-1}\right]\\ {\mathit{\gamma }}_i\sim N_q\left[{\mathrm{\Delta }}_i^{-1}{\mathbf{Z}}_i^{\top }{\mathbf{R}}_i^{-1}\left({\mathbf{y}}_i-{\mathbf{X}}_i\mathit{\beta }-{\mathbf{N}}_i\mathbf{f}\right)],{\mathrm{\Delta }}_i^{-1}\right]\\ {\mathbf{D}}^{-1}\sim \text{Wishart}\left({\eta }_0+m,{\left({\sum }_{\eta }^{-1}+\sum _i{\mathit{\gamma }}_i{\mathit{\gamma }}_i^{\top }\right)}^{-1}\right)\\ {\sigma }_k^{-2}\sim \text{gamma}\left(\frac{v_{0k}+{\sum }_i{n}_i}{2},\frac{{\delta }_{0k}+{\sum }_i{\Vert {\mathbf{y}}_{ik}-{\mathbf{X}}_{ik}{\mathit{\beta }}_k-{\mathbf{N}}_{ik}{\mathbf{f}}_k-{\mathbf{Z}}_{ik}{\mathit{\gamma }}_{ik}\Vert }^2}{2}\right)\\ {\mathit{\phi }}_k\sim N_L\left(\frac{1}{{\sigma }_k^2}{\mathbf{P}}_k{\mathbf{B}}_k^{\top }\sum _{i=1}^m{\mathbf{N}}_{ik}^{\top }({\mathbf{y}}_{ik}-{\mathbf{X}}_{ik}{\mathit{\beta }}_k-{\mathbf{Z}}_{ik}{\mathit{\gamma }}_{ik}),{\mathbf{P}}_k\right)\\ {\tau }_k^{-2}\sim \text{gamma}\left(a_k+\frac{L}{2},b_k+\frac{1}{2}{\mathit{\phi }}_k^{\top }\mathbf{\Omega }{\mathit{\phi }}_k\right)\end{array}$$