Stochasticity of Bacterial Attachment and Its Predictability by the Extended Derjaguin-Landau-Verwey-Overbeek Theory

Abstract

Bacterial attachment onto materials has been suggested to be stochastic by some authors but nonstochastic and based on surface properties by others. We investigated this by attaching pairwise combinations of two Salmonella enterica serovar Sofia (S. Sofia) strains (with different physicochemical and attachment properties) with one strain each of S. enterica serovar Typhimurium, S. enterica serovar Infantis, or S. enterica serovar Virchow (all with similar physicochemical and attachment abilities) in ratios of 0.428, 1, and 2.333 onto glass, stainless steel, Teflon, and polysulfone. Attached bacterial cells were recovered and counted. If the ratio of attached cells of each Salmonella serovar pair recovered was the same as the initial inoculum ratio, the attachment process was deemed stochastic. Experimental outcomes from the study were compared to those predicted by the extended Derjaguin-Landau-Verwey-Overbeek (XDLVO) theory. Significant differences (P < 0.05) between the initial and the attached ratios for serovar pairs containing S. Sofia S1296a for all different ratios were apparent for all materials. For S. Sofia S1635-containing pairs, 7 out of 12 combinations of serovar pairs and materials had attachment ratios not significantly different (P > 0.05) from the initial ratio of 0.428. Five out of 12 and 10 out of 12 samples had attachment ratios not significantly different (P > 0.05) from the initial ratios of 1 and 2.333, respectively. These results demonstrate that bacterial attachment to different materials is likely to be nonstochastic only when the key physicochemical properties of the bacteria were significantly different (P < 0.05) from each other. XDLVO theory could successfully predict the attachment of some individual isolates to particular materials but could not be used to predict the likelihood of stochasticity in pairwise attachment experiments.

INTRODUCTION

Bacteria that can attach to and colonize solid surfaces better than other bacteria are more likely to survive and ensure their own propagation (13, 30). Since bacteria with the ability to attach go on to persist better in the environment, it is important from an ecological, industrial, and medical perspective to understand how the attachment process is mediated. One way to understand the attachment phenomenon of bacteria to a surface is to study the force of interaction between the adhering bacterial cell and the substratum. Using measures of these forces, models such as microbial surface thermodynamics model (7) and the classical Derjaguin-Landau-Verwey-Overbeek (DLVO) theory of colloid stability (5) have been used to predict if attachment between bacteria and a surface are likely to occur.

The surface thermodynamic model uses measures of the physicochemical properties of the bacteria, which include cell surface hydrophobicity (CSH) for prediction (8). A number of authors (2, 9, 33) have investigated CSH and used this parameter to predict the attachment of bacteria to different surfaces. Positive correlation between physicochemical properties and bacterial attachment has been observed by some authors (2), but others have found no evidence of such a relationship (11). Furthermore, Thomas et al. (37) and McMeekin and Thomas (27) have investigated factors such as time of immersion, bacterial population density, and nutrient availability to determine if these factors contribute to bacterial attachment onto agar dip slides and chicken skin, respectively. In both of the aforementioned studies, the authors have suggested that the attachment of bacteria to surfaces is a purely stochastic process. The only factor that these authors found to have an effect on attachment was the density of the bacteria. A study conducted by Liao and Cooke (25) came to a similar conclusion after an investigation of the attachment of Salmonella enterica serovar Chester onto green pepper slices.

Marshall et al. (26) were the first researchers to attempt to describe and predict the total interaction energy between bacteria and a surface in a theoretical manner using the DLVO theory. Due to its simplicity and consistency, the DLVO theory has been widely used as not only a qualitative model but also a quantitative method to calculate the free energy changes involved in bacterial attachment (32). While useful in many situations, DLVO is only marginally successful in describing interactions in biological systems (40). Discrepancies are often found between attachment predicted by DLVO calculations and the experimental measurement of attached bacteria. Part of the reason for these discrepancies is that the theory takes into account only the presence of electrostatic double-layer interactions and the Lifshitz-van der Waals forces. In addition, the theory treats bacteria as geometrically uniform stable particles (26), failing to take into account that cell surfaces carry charged polymers such as lipopolysaccharides, proteins, and fimbriae that form a “soft” ion-permeable layer around the cell (10).

In order to overcome the shortfalls of the DLVO theory an “extended” DLVO (XDLVO) theory was suggested by van Oss (39). This author's extension of the theory takes into consideration the Lewis acid-base (AB) forces which are based on electron-donating and electron-accepting interactions between polar moieties in aqueous solutions. Various authors have attempted to use either or both the DLVO and the XDLVO theories to explain bacterial attachment, with positive correlation between predicted and experimental results found by some authors (12, 31) but not by others (34).

The main aim of this study was to use bacteria with different surface characteristics in different pairwise ratios to determine empirically if bacterial attachment to different materials under the conditions of this study is a stochastic or nonstochastic process. The study also aimed to determine if XDLVO theory could be successfully used to predict the attachment of individual isolates to different materials under the conditions used in this study. Furthermore, it also aimed to determine if the theory could also be used to predict whether the attachment of isolates to different materials in different ratios of pairwise combinations is stochastic.

MATERIALS AND METHODS

Bacterial strains, culture conditions, and culture preparation.

Five Salmonella strains (Table 1) were selected for this study based on the differences in their physicochemical properties (8) and their various abilities to attach to a number of different surfaces in pure cultures (9). Isolate S1296a (S. enterica serovar Sofia) was moderately hydrophobic (45%) when measured using the bacterial adherence to hydrocarbon-xylene (BATH-xylene) technique while isolates S1635 (S. Sofia) (28%), ATCC 14028 (S. enterica serovar Typhimurium) (30%), S1677 (S. enterica serovar Infantis) (26%), and S1297a (S. enterica serovar Virchow) (34%) were all found to be hydrophilic (8). Cultures for all experiments were grown in nutrient broth (NB; Oxoid, Basingstoke, United Kingdom) for 18 ± 2 h at 37°C.

Table 1.

Serotypes, attachment to glass, stainless steel, and Teflon, physicochemical properties, and surface free energies of five Salmonella strains^e

Isolate	Serovar	Attachment to the indicated surface (log CFU/cm2)a			Zeta potential (mV)b	Contact angle (°)c			Surface free energy component (mJ/m2)d
		Glass	Stainless steel	Teflon		θB	θF	θw	γbLW	γb+	γb−
S1296a	S. Sofia	3.72 ± 0.28 A	4.54 ± 0.37 B	4.61 ± 0.32 BC	−3.62 ± 0.63	41.03 ± 2.33 A	15.35 ± 1.17 BC	16.51 ± 1.68 BC	34.15 ± 1.04 A	10.58 ± 0.41 B	30.26 ± 0.84 C
S1297a	S. Virchow (PT8)	3.70 ± 0.27 A	3.70 ± 0.19 A	3.52 ± 0.02 A	−6.24 ± 0.55	44.50 ± 0.95 A	15.19 ± 0.49 B	16.40 ± 0.60 C	32.58 ± 0.44 A	11.50 ± 0.28 B	30.17 ± 0.12 C
S1635	S. Sofia	3.59 ± 0.09 A	3.79 ± 0.11 A	3.68 ± 0.15 A	−7.70 ± 1.28	41.27 ± 1.38 A	13.77 ± 1.30 B	20.69 ± 1.91 D	34.05 ± 0.62 A	10.84 ± 0.27 B	28.09 ± 0.82 C
S1677	S. Infantis	3.55 ± 0.23 A	2.74 ± 0.22 D	3.77 ± 0.10 A	−5.77 ± 1.38	42.87 ± 1.55 A	13.58 ± 0.41 B	18.49 ± 1.93 CD	33.33 ± 0.71 A	11.28 ± 0.41 B	28.99 ± 0.76 C
ATCC 14028	S. Typhimurium	3.74 ± 0.08 A	4.04 ± 0.20 AB	4.15 ± 0.11 AB	−5.73 ± 0.72	43.87 ± 2.61 A	15.51 ± 0.58 B	17.18 ± 1.32 BC	32.86 ± 1.20 A	11.30 ± 0.61 B	29.95 ± 0.55 C

^aAttachment of Salmonella isolates to different materials published by Chia et al. (9).

^bZeta potentials determined in 0.75 mM PBS (pH 7.4) published by Chia et al. (8).

^cθ_w, θ_F, and θ_B represent contact angles measured using water, formamide and 1-bromonaphthalene on bacterial lawns respectively. The θ_w values were published by Chia et al. (8).

^dγ_b^LW, γ_b⁺, and γ_b⁻ represent van der Waals, electron acceptor, and the electron donor components for bacterial cell surfaces, respectively.

^eAll results are presented as the means followed by standard deviations for triplicate experiments. Values labeled with the same capitalized letters within columns are not significantly different (P > 0.05).

Cell suspensions for the attachment studies were prepared according to Chia et al. (9). Briefly, cell suspensions were prepared by centrifuging cultures at 13,131 × g for 15 min, washing them once in 15 ml of 150 mmol/liter phosphate-buffered saline ([PBS] 2.7 mmol/liter KCl, 10 mmol/liter Na₂HPO₄, 17 mmol/liter KH₂PO₄, 150 mmol/liter NaCl, pH 7.4), and resuspending the pellet in PBS to an optical density at 600 nm (OD₆₀₀) corresponding to 10⁶ CFU/ml for each isolate (OD₆₀₀ of 0.940 to 0.950 [ATCC 14028], 1.800 to 1.810 [S1296a], 1.085 to 1.095 [S1297a], 1.400 to 1.410 [S1635], and 0.985 to 0.995 [S1677]) at a tolerance of 5%. Three different pairwise ratios (0.428 [30:70], 1 [50:50], and 2.333 [70:30]) of S. Sofia suspension (either S1296a or S1635) with each of the other three Salmonella serovars (S. Typhimurium, S. Infantis, and S. Virchow) were prepared in 50 ml of PBS to provide a total cell density of 10⁶ CFU/ml for the attachment assay. The suspensions were examined microscopically to confirm that the cells were evenly distributed within the suspension and that no clumps or aggregates were present. Malonate agar (MA) [yeast extract, 1 g/liter; (NH₄)₂SO₄, 2 g/liter; K₂HPO₄, 0.6 g/liter; KH₂PO₄, 0.4 g/liter; NaCl, 2 g/liter; C₃H₂Na₂O₄, 4.5 g/liter; dextrose, 1 g/liter; bromthymol blue, 75 mg/liter; agar, 15 g/liter] was used for all plating. Salmonella Sofia, which is able to ferment malonate, produces blue colonies on this medium while S. Typhimurium, S. Infantis, and S. Virchow, which cannot ferment malonate, produce yellowish-green colonies.

Zeta potential measurement of bacteria and materials.

The zeta potential measurement of the bacteria is described in Chia et al. (8). Briefly, cell suspensions were prepared by centrifuging at 13,131 × g for 10 min at 15°C and resuspending the cells in 7.5 mmol/liter PBS (2.7 mmol/liter KCl, 10 mmol/liter Na₂HPO4, 17 mmol/liter KH₂PO₄, 7.5 mmol/liter NaCl, pH 7.4). A 10-ml suspension containing approximately 10⁷ cells/ml was used to obtain measurements using a ZetaSizer (HS3000; Malvern Instruments Ltd., Worcestershire, United Kingdom). Zeta potential measurements for glass, stainless steel, and Teflon were determined as per Khorasani et al. (23) and are presented in Table 2. Briefly, a streaming potential analyzer (Surpass; Anton Paar, Graz Österreich, Austria), with 0.001 M KCl as the electrolyte and HCl and KOH were use to alter the pH. Two pieces of each sample were mounted in the measuring cell, where they were separated by a spacer that introduced a streaming channel with dimensions of 23 by 5 mm. The specimens were soaked in Milli-Q water and stored at 4°C for 24 h prior to streaming potential measurements. The electrolyte solution was pumped through the cell, which consisted of two specimens with a spacer in between; the samples had dimensions of 56 by 26 mm and were placed upon glass plates. The applied pressure difference was set at 0.5 × 10⁴ Pa. The cell potential was measured continuously by two Pt electrodes (data acquisition was facilitated by the instrument software).

Table 2.

Contact angles and surface free energies of glass, polysulfone, stainless steel, and Teflon^d

Material	Contact angle (°)a			Surface free energy components (mJ/m2)b			Zeta potential (mV)c
	θw	θF	θB	γsLW	γs+	γs−
Glass	24.61 ± 1.98 A	17.72 ± 1.31 A	45.78 ± 1.30 A	31.97 ± 0.63 A	11.47 ± 0.58 A	26.48 ± 0.79 A	−23.61 ± 1.52
Polysulfone	30.30 ± 1.95 B	18.39 ± 0.57 B	13.46 ± 0.46 B	43.19 ± 0.08 B	6.05 ± 0.04 B	24.32 ± 1.32 B	−27
Stainless steel	86.83 ± 5.95 C	71.16 ± 3.49 C	29.63 ± 1.57 C	38.78 ± 0.57 C	0.04 ± 0.05 C	3.10 ± 2.06 C	−25.00 ± 1.38
Teflon	105.27 ± 0.45 D	118.29 ± 0.23 D	33.62 ± 1.47 D	37.28 ± 0.58 C	13.21 ± 0.29 D	15.77 ± 1.06 D	−46.07 ± 2.87

^aθ_w, θ_F, and θ_B represent contact angles measured using water, formamide and 1-bromonaphthalene, on substratum surfaces respectively. The contact angle values of glass, stainless steel and Teflon were published by Chia et al. (9).

^bγ_s^LW, γ_s⁺, and γ_s⁻ represent van der Waals, electron acceptor, and the electron donor components for a solid surface, respectively. The surface free energy components of glass, stainless steel, and Teflon were published by Chia et al. (9).

^cRepresents the streaming zeta potential of substratum surfaces measured in this study except the streaming zeta potential of polysulfone which was derived from the literature (44).

^dAll results are presented as the means followed by standard deviations for triplicate experiments. The significance of differences (P < 0.05) between four different substratum surfaces with respect to contact angles and surface free energy components are shown as values (within each column) labeled with different capitalized letters.

Contact angle measurements.

The contact angles for all isolates as well as for glass, stainless steel, and Teflon, used in this study and determined by using water as the solvent, have been presented elsewhere (8). The contact angles for all isolates as well as glass, stainless steel, and Teflon using 1-bromonaphthalene (Sigma) and formamide (Sigma) as the solvents were determined as per Chia et al. (8) with modifications. The contact angles for polysulfone using water, 1-bromonaphthalene, and formamide were also determined as per Chia et al. (8) with modifications. Briefly, the contact angles of the solvents were determined in triplicate using a goniometer (KSV Instruments Ltd., Helsinki, Finland), with the aid of Windows-based KSV CAM software, by the sessile drop method.

Cell suspensions were prepared with sterile distilled water (SDW) as described previously for zeta potential measurements (see “Zeta potential measurement of bacteria and materials” above). Suspensions were adjusted to an OD of 1.0 to 1.4 at 540 nm, giving approximately 10⁹ cells/ml, as determined by spread plating serial dilutions onto nutrient agar and incubation for 18 ± 2 h at 37°C. Lawns of bacteria were prepared by filtering 23 ml of cell suspension onto an HA filter (pore diameter, 0.45 μm; filter diameter, 25 mm [Millipore]) by negative-pressure filtration. Filters were attached to glass slides with double-sided adhesive tape and dried in a desiccator for 30 min. A drop of either 1-bromonaphthalene or formamide was deposited onto the filter using a 1-ml syringe (Hamilton, Reno, NV) fitted with a needle gauge. An image of the drop was captured using a digital video camera (30 frames per s; FireWire IEEE 1394 connection), and the angles were analyzed using the Windows-based KSV CAM software. A minimum of five drops of 1-bromonaphthalene and four drops of formamide was used per bacteria filter. For each material, 10 drops of each solvent was taken on three independently treated surfaces. The contact angles reported in this study were the averages obtained from the three filters or materials.

Attachment assay to different surfaces.

The attachment of bacteria to glass, stainless steel, Teflon, and polysulfone was described by Chia et al. (9). Briefly, glass slides (76 by 25 mm and 1-mm thickness; Sail Brand, China), stainless steel (type 304, number 4 finish, 50 by 20 mm and 0.9-mm thickness) coupons, and Teflon (50 by 20 mm and 0.1-mm thickness; S&D Berg Trading, Victoria, Australia) coupons were prepared by soaking samples in acetone for 30 min to remove grease. Samples were rinsed in water prior to being soaked in 1 N NaOH for at least 1 h. After being soaked in 1 N NaOH, the glass slides and stainless steel and Teflon coupons were rinsed with at least 5 liters of distilled water. Polysulfone membranes (47-mm diameter; Millpore, Billerica, MA) were not treated and were used as provided by the supplier. All materials except polysulfone membranes were sterilized by autoclaving.

All materials were placed into Falcon tubes which contain the cell suspensions (three different ratios) described above and left to stand for 20 min at ∼25°C with swirling for 10 s at 5-min intervals. Glass slides and stainless steel and Teflon coupons were rinsed by being gently dipped up and down in two separate 50-ml aliquots of PBS. As polysulfone membranes were too large to fit inside the Falcon tubes, they were placed into 250-ml sterile jars containing 50 ml of cell suspension (∼10⁶ cells per ml) in PBS for the same length of time (20 min) as the other substrata. The membranes were then rinsed twice for 5 s each, by swirling in 50 ml of sterile PBS.

After membranes were rinsed, each material was placed in a sterile stomacher bag containing 50 ml of buffered peptone water (BPW; Oxoid) containing 1% (vol/vol) Tween 80 and massaged in a stomacher (BagMixer) at speed 9 for 5 min. Beuchat and Scouten (3) demonstrated previously that 1% Tween 80 does not affect the viability of Salmonella. However, we further confirmed that viable bacteria counted were a true reflection of numbers on materials. This was achieved by individual comparison of the numbers of cells of each Salmonella strain attached to stainless steel using epifluorescence microscopy (9) to the numbers recovered using the viable count method. No significant differences were observed (data not shown). After the stomaching step, the glass slides and stainless steel and Teflon coupons were stained with acridine orange (Sigma, St. Louis, MO) and visualized under an epifluorescence microscope (Olympus BH2) using a blue filter. The number of cells per field was counted at a magnification of ×1,000 under oil immersion to ensure that all attached cells were removed. Visualization of the polysulfone was not possible as the material broke into pieces after stomaching.

Salmonella cells that were removed from the materials by stomaching were defined as firmly attached cells. Aliquots of the wash from the stomached material were serially diluted, spread plated on MA, and incubated for 18 ± 2 h at 37°C before enumeration. All experiments were conducted in triplicate.

Energy characteristics of materials and bacteria.

The energy characteristics of the bacteria and materials were calculated according to Minagi et al. (29) and Sinde and Carballo (35) and are shown in Tables 1 and 2, respectively. Briefly, the surface free energies were calculated according to Young's equation, expressed as:

$$\cos \theta =-1+2{\left({\gamma }_s^{\text{LW}}{\gamma }_l^{\text{LW}}\right)}^{1/2}/{\gamma }_l+2{\left({\gamma }_s^{+}{\gamma }_l^{-}\right)}^{1/2}/{\gamma }_l+2{\left({\gamma }_s^{-}{\gamma }_l^{+}\right)}^{1/2}/{\gamma }_l$$ (1)

where γ^LW denotes the Lifshitz-van der Waals component of surface free energy including London, Debye, and Keesom interactions, γ⁺ and γ⁻ are the electron acceptor and the electron donor components, respectively, of surface free energy, θ is the contact angle, and γ_l is the surface tension (mJ m⁻²) of the liquid used for the measurement. The subscript s refers to the solid surface, and l refers to the liquid used for contact angle measurement.

By using three different liquids with known γ_l, γ_l^LW, γ_l⁺, and γ_l⁻, values, for example, water, formamide, and 1-bromonaphthalene, the unknown surface tension components of a solid surface (γ_s^LW, γ_s⁺, and γ_s⁻) or bacterial surface (γ_b^LW, γ_b⁺, and γ_b⁻) can be estimated.

XDLVO calculation.

According to the XDLVO theory, the interaction energy between the bacterial cell surface and the substratum (separated by a distance l) is the sum of Lifshitz-van der Waals [ΔG^LW(l)], Lewis acid-base [ΔG^AB(l)], and electrostatic [ΔG^EL(l)] interaction energies. The total XDLVO interaction energy is given as Bayoudh et al. (1):

$$\Delta G^{\text{XDLVO}}\left(l\right)=\Delta G^{\text{LW}}\left(l\right)+\Delta G^{\text{AB}}\left(l\right)+\Delta G^{\text{EL}}\left(l\right)$$ (2)

The interaction energies for each individual component, LW, AB, and EL, as a function of separation distance are given in Boks et al. (4):

$$\Delta G^{\text{LW}}\left(l\right)=-\frac{A}{6}\left[\frac{2r\left(l+r\right)}{l\left(1+2r\right)}-\text{In}\left(\frac{l\text{+2}r}{l}\right)\right]$$ (3)

where l is the separation distance, r (0.75 μm) (21) is the radius of the bacterium, and A is the Hamaker constant, which can be determined from Boks et al. (4):

$$\Delta G_{slb}^{\text{LW}}=-\frac{A}{12\pi l_0^2}$$ (4)

where ΔG_slb^LW is the Lifshitz-van der Waals component of the free energy of adhesion at contact and is obtained from $-2\left(\sqrt{{\gamma }_b^{\text{LW}}}-\sqrt{{\gamma }_l^{\text{LW}}}\right)\left(\sqrt{{\gamma }_s^{\text{LW}}}-\sqrt{{\gamma }_l^{\text{LW}}}\right)$, and l_o is the minimum separation distance between the outermost cell surface and the substratum (0.157 nm).

The distance dependence of the acid-base interaction energies is given by Boks et al. (4):

$$\Delta G^{\text{AB}}\left(l\right)=2\pi r\Delta G_{slb}^{\text{AB}}\lambda \exp \left(\frac{l_o-1}{\lambda }\right)$$ (5)

where ΔG_slb^AB is the acid-base component of the free energy interaction at contact and is obtained from:

$$2\left[\sqrt{\left({\gamma }_b^{+}-{\gamma }_s^{+}\right)}\sqrt{\left({\gamma }_b^{-}-{\gamma }_s^{-}\right)}-\sqrt{\left({\gamma }_b^{+}-{\gamma }_l^{+}\right)}\sqrt{\left({\gamma }_b^{-}-{\gamma }_l^{-}\right)}-\sqrt{\left({\gamma }_s^{+}-{\gamma }_l^{+}\right)}\sqrt{\left({\gamma }_s^{-}-{\gamma }_l^{-}\right)}\right]$$ (6)

The λ is the characteristic decay length of AB interaction in water (estimated to be 0.6 nm for hydrophilic bacteria) (34).

Electrostatic interaction energy as a function of separation distance was also calculated for the sphere-plane geometry (4),

$$\Delta G^{\text{EL}}\left(l\right)=\pi \epsilon {\epsilon }_{0}r\left({\phi }_b^2+{\phi }_s^2\right)\left\{\frac{2{\phi }_b{\phi }_s}{{\phi }_b^2+{\phi }_s^2}\text{In}\left[\frac{1+\exp \left(-\kappa l\right)}{1-\exp \left(-\kappa l\right)}\right]+\text{In}\left[1-\exp \left(-2\kappa l\right)\right]\right\}$$ (7)

in which εε₀ denotes the dielectric permittivity of the medium, φ_b and φ_s are the surface (zeta) potentials of the bacterial cell surface and collector surface in the surrounding liquid, respectively, and κ is the reciprocal Debye length. Zeta potentials of the materials are shown in Table 2 except for polysulfone, which was derived from Zularisam et al. (44).

Statistical analysis.

Paired t tests (Minitab, version 15; Minitab Inc., Minneapolis, MN) were used to determine significance of differences between the observed cell ratio and the predicted cell ratios, as well as between the predicted cell ratios and attached cell ratios for all materials. An analysis of variance (ANOVA; one way), regression plots, and comparison of means (Tukey's method) were performed on all physicochemical data sets using MINITAB software at a 95% confidence level.

RESULTS

Zeta potential measurement of bacteria and materials.

The zeta potentials of the bacteria are shown in Table 1. The most negative isolate was S1635 (S. Sofia), with a potential of −7.70 mV, and the most positive was isolate S1296a (S. Sofia), with a potential of −3.62 mV. Zeta potentials for the materials are presented in Table 2. The most positive material was glass (−23.61 mV), and the most negative was Teflon (−46.07 mV). The dimension of polysulfone membrane samples (47-mm diameter) used was less than that required by the equipment (56 by 26 mm). The zeta potential value of this material (∼27 mV) was therefore derived from the literature (44).

Contact angle measurements of bacteria and materials.

Vogler (42) considered isolates and materials with water contact angles <65° to be hydrophilic, by which definition all strains used in this study were in the hydrophilic category. However, the strains were separated by a narrow range of contact angle values which were significantly different (P < 0.05) (Table 1). Further, the Vogler (42) definition indicated that glass (24.61°) and polysulfone (30.30°) were hydrophilic, whereas stainless steel (86.83°) and Teflon (105.27°) were hydrophobic.

Attachment to different surfaces.

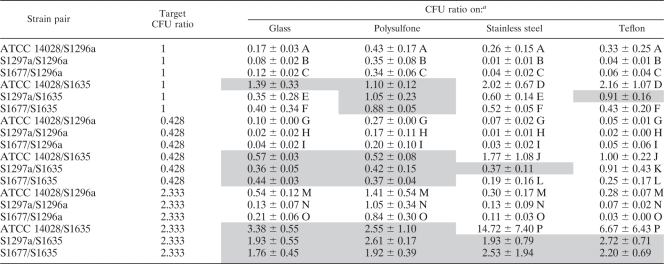
The number of cells still attached to the materials (glass, stainless steel, and Teflon) after stomaching was an average of one cell for each group of 30 fields counted. This equates to 233 CFU/cm², which was deemed too low a number to have an impact on the final count. Hence, in this paper, it is assumed that the number of attached cells is equal to the number of detached cells counted after stomaching. The initial observed inoculum ratios for each individual serovar pair in mixed culture were first compared to the predicted ratios (0.428, 1, and 2.333), and the actual ratios were found not to differ significantly (P > 0.05) from the predicted. All subsequent results were therefore compared to the predicted cell ratio (0.428, 1, or 2.333). Comparison of the attached cell ratios to the predicted ratio of 1 for all materials indicated that ratios ranged from 0.08 to 1.39 for glass, 0.34 to 1.10 for polysulfone, 0.01 to 2.02 for stainless steel, and 0.04 to 2.16 for Teflon. For a predicted ratio of 0.428, ratios of attached cells for each material ranged from 0.02 to 0.57 for glass, 0.17 to 0.52 for polysulfone, 0.01 to 1.77 for stainless steel, and 0.02 to 1.00 for Teflon. For a predicted ratio of 2.333, attached cells ratios ranged from 0.13 to 3.38 for glass, 0.84 to 2.61 for polysulfone, 0.11 to 14.72 for stainless steel, and 0.03 to 6.67 for Teflon (Table 3).

Table 3.

Ratio of CFU numbers of pairwise combinations of Salmonella strain cells detached from four different surfaces

^aUppercase letters indicate values significantly different from the target ratio. Shaded values indicate that the attachment process was stochastic.

In this study we developed a novel protocol to indicate whether the attachment process was stochastic or nonstochastic. If the initial ratio of serovar pairs was not significantly different (P > 0.05) from the ratio after attachment, the process was stochastic. Conversely, if the initial and postattachment ratios were significantly different, a nonstochastic process was indicated. The latter outcome was found for serovar pairs containing S. Sofia following attachment, where greater ratios (P < 0.05) were noted for all substrata tested.

For serovar pairs containing S. Sofia S1635, at a ratio of 0.428, attachment to the different materials was frequently stochastic (Table 3). Seven out of 12 combinations of serovar pairs and surfaces had attachment ratios not significantly different (P > 0.05) from the initial ratios. Similarly, for ratios of 1 and 2.333, 5 out of 12 samples and 10 out of 12 samples, respectively, had attachment ratios not significantly different (P > 0.05) from the initial ratios.

Adhesion predication based on XDLVO theory.

Since the XDLVO theory has been used by various authors (17, 22, 31) to predict the attachment of bacteria onto different surfaces, we compared the predicated ease of attachment of individual strains calculated from the theory to our experimental data. We assumed that more favorable attachment conditions would be indicated by a higher number of attaching cells. The figures show the XDLVO interaction energy profiles for all five strains attaching onto different materials.

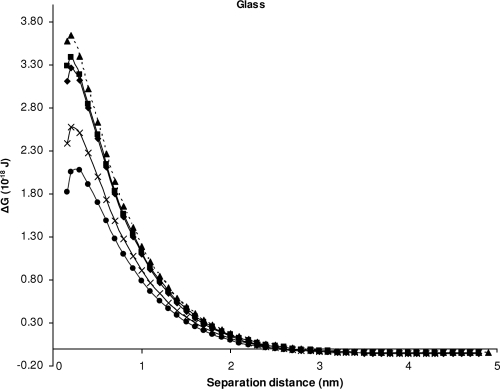
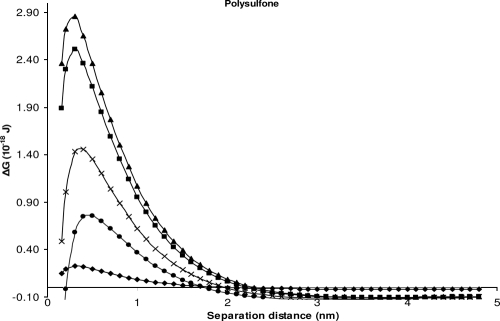
For glass and polysulfone, the model suggests repulsive force between all isolates and glass (Table 4 and Fig. 1) and between most isolates (except S. Sofia isolate S1635 at minimum separation distance) and polysulfone (Table 4 and Fig. 2), but attachment of bacterial cells was observed experimentally.

Table 4.

Interaction energies (10⁻¹⁸ J) between five Salmonella strains and glass, polysulfone, stainless steel, or Teflon and according to the XDLVO theory, at the minimum separation distance^a

Strain	Glass				Polysulfone				Stainless steel				Teflon
	ΔGLW	ΔGAB	ΔGEL	ΔGXDLVO	ΔGLW	ΔGAB	ΔGEL	ΔGXDLVO	ΔGLW	ΔGAB	ΔGEL	ΔGXDLVO	ΔGLW	ΔGAB	ΔGEL	ΔGXDLVO
S1296a	−1.788	5.278	−0.383	3.107	−0.330	0.540	−0.057	0.154	−2.829	−21.287	−0.466	−24.583	−2.608	−7.433	−2.578	−12.6198
S1297a	−1.581	5.124	0.033	3.576	−2.918	5.376	−0.095	2.363	−2.502	−18.910	0.059	−21.352	−2.306	−6.645	−1.722	−10.6730
S1635	−1.775	3.346	0.254	1.825	−3.276	2.489	0.159	−0.628	−2.808	−26.122	0.213	−28.707	−2.589	−8.814	−1.256	−12.6591
S1677	−1.681	4.110	−0.040	2.390	−3.102	3.767	−0.178	0.487	−2.659	−22.532	−0.101	−25.291	−2.451	−7.724	−1.874	−12.049
ATCC 14028	−1.619	4.950	−0.046	3.285	−2.987	5.063	−0.185	1.891	−2.560	−20.023	−0.107	−22.691	−2.361	−6.990	−1.887	−11.237

^aΔG^LW, ΔG^AB, ΔG^EL, and ΔG^XDLVO represent van der Waals, acid-base, electrostatic, and total interaction energy, respectively, at the minimum separation distance (l_o) of 0.157 nm between bacterial cells and substratum surfaces.

Fig. 1.

Changes in the interaction energies as a function of distance between the bacteria and glass, calculated using the XDLVO theory. ■, ATCC 14028; ◆, isolate S1296a; ▴, isolate S1297a; ●, isolate S1635; and ×, isolate S1677.

Fig. 2.

Changes in the interaction energies as a function of distance between the bacteria and polysulfone, calculated using the XDLVO theory. ■, ATCC 14028; ◆, isolate S1296a; ▴, isolate S1297a; ●, isolate S1635; and ×, isolate S1677.

Even though the theory incorrectly predicted repulsion between all bacteria and polysulfone, it correctly predicted that attachment to polysulfone would favor the S. Sofia isolate S1296a over attachment of the S. Typhimurium, S. Infantis, or S. Virchow strains since it has the lowest energy barrier (0.234 × 10⁻¹⁸ J) to overcome (Fig. 2). However, the theory incorrectly predicted that attachment of S. Sofia isolate S1635 to polysulfone was more favorable, a result which was not apparent experimentally. In a similar fashion to the findings for polysulfone, the theory correctly predicted a more favorable attachment of S. Sofia S1296a than S. Virchow S1297a and S. Typhimurium ATCC 14028 to glass (Fig. 1). The theoretical prediction that the attachment of S. Infantis S1677 to polysulfone would be greater than that of S. Sofia S1296a (Fig. 2) was not observed experimentally (Table 3). Similarly, the theoretical prediction that S. Sofia isolate S1635 would attach in greater numbers than the other serovars to glass (Fig. 1) was also not observed experimentally (Table 3).

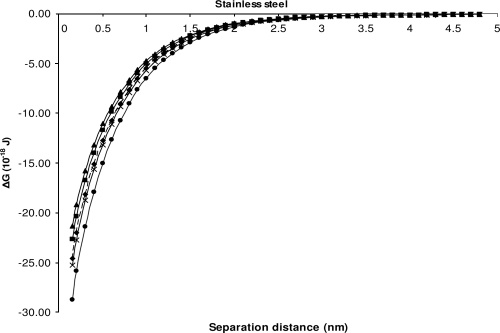
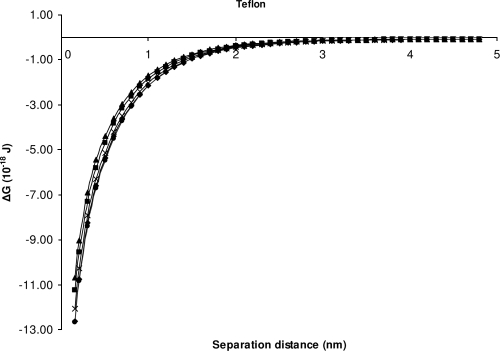
The theory provided good agreement with the experimental data of attachment for S. Sofia S1635 and the other Salmonella serovars for stainless steel. None of the theoretical predictions correlate with the experimental data for attachment of S. Sofia S1296a and the other serovars onto stainless steel (Fig. 3). For Teflon the theory predicts the rate of attachment to be similar for all isolates (Fig. 4). There is therefore a lack of agreement here between the theory and the experimental data for isolate S. Sofia 1296a onto Teflon as, experimentally, this isolate was found to attach in larger numbers than the other serovars (Table 3). Our experimental data agree in part with the model which predicts attachment of all isolates to both stainless steel and Teflon, as indicated by Fig. 3 and 4, where it can be seen that energy barriers cease to exist for these two materials.

Fig. 3.

Changes in the interaction energies as a function of distance between the bacteria and stainless steel, calculated using the XDLVO theory. ■, ATCC 14028; ◆, isolate S1296a; ▴, isolate S1297a; ●, isolate S1635; and ×, isolate S1677.

Fig. 4.

Changes in the interaction energies as a function of distance between the bacteria and Teflon, calculated using the XDLVO theory. ■, ATCC 14028; ◆, isolate S1296a; ▴, isolate S1297a; ●, isolate S1635; and ×, isolate S1677.

As far as we are aware, the XDLVO theory had been used only to predict the attachment of individual isolates to materials. Our next aim was to test if the theory could also be used to predict whether the attachment of isolates to various materials in different ratios of pairwise combinations is stochastic. We assumed that if the XDLVO interaction energy profiles of two isolates closely matched one another, then attachment was predicted to be stochastic. On the other hand, if the XDLVO interaction energy profile of two isolates was not closely matched to one another, then attachment was predicted not to be stochastic. As can be seen by comparing Table 3 to Fig. 1, the near fit of the interaction energy profiles between S. Sofia S1635 and the other three Salmonella serovars for stainless steel and Teflon, for example, demonstrates that the theory is unable to predict the stochasticity of bacterial attachment.

DISCUSSION

This is the first study, to our knowledge, seeking to determine whether attachment to different materials is stochastic by using bacteria with different surface characteristics in different pairwise ratios. We deemed an attachment process to be stochastic when the initial ratio of each serovar pair in the initial inoculum was not significantly different from the ratio of each serovar pair attached to materials. We demonstrated that bacterial attachment to several materials is nonstochastic when the physicochemical properties of the bacteria are significantly different. Polysulfone was the most physicochemically heterogeneous substratum used, a feature making it difficult to interpret an overall contact angle measurement if both hydrophilic and hydrophobic areas were present. This is important because, for example, as pointed out by various authors (6, 20, 14, 36), an increase in the hydrophobicity of bacteria could lead to an increase in the number of bacteria attaching to both hydrophobic and hydrophilic surfaces. However, we reasoned that such heterogeneity would be likely to increase the incidence of stochastic behavior. Likewise, the direct influence of variations in cell surface structure and physicochemical properties on attachment is difficult to predict precisely, and, despite many well-designed and well-conducted studies, the relative importance of significant cell surface features suspected to play key roles in attachment remains obscure. For example, in a study conducted by Ledeboer et al. (24) in which S. Typhimurium mutants with specific fimbrial gene clusters were created, it was found that specific fimbrial groups either increase or decrease its attachment and formation of biofilm onto Hep-2 cells. Heuzenroeder et al. (16) reported that isolates of S. Sofia serovar, which is an S. enterica subspecies II serotype, have 17-kDa thin aggregative fimbriae. Salmonella Typhimurium, S. Infantis, and S. Virchow, which are S. enterica subspecies I serotypes, on the other hand, have specific fimbrial genes such as fim (type 1 fimbriae) and stf (S. enterica serovar Typhimurium fimbriae) (19).

When the XDLVO theory was used to predict both individual and pairwise isolates in different ratios, discrepancies occurred in the predictions of the stochastic attachment of bacteria. The theory is based on calculations of the surface free energies, which were determined from contact angle measurements. We had earlier determined that the contact angle measurements for these isolates were not significantly different (P > 0.05) (8). This could be one of the reasons why the experimental data do not support theoretical predications. Another reason for the discrepancy between predicted and experimental results could be that the theory fails to take into account the surface appendages or the chemical surface heterogeneities of the bacteria, which might influence attachment (4). More specifically, the presence of surface structures prevents the prediction of a precise distance between the substratum and the bacterial surface to allow any accurate calculations or prediction of attachment (28).

However, as pointed out by Hermansson (15), neither the XDLVO theory nor the thermodynamic approach can fully predict experimental attachment; therefore, a better understanding of how bacteria attach is needed. Ong et al. (31), who used the XDLVO to predict the attachment force of Escherichia coli to various materials, suggested that the discrepancies between the theory and the experimental data they observed could be due to the presence of steric interactions in the experimental systems. If the steric effect presents a sufficiently large energy barrier, contact between the interacting surfaces is prevented, and as a result the measured interaction energy will not agree with calculations. Vadillo-Rodriguez et al. (38) further confirmed this by measuring the steric attraction on nine different Streptococcus mitis strains by atomic force microscopy and found that a repulsive force is always present upon approach, even if the XDLVO theory does not show any energy barrier. Another reason for the difference in the theoretical and the experimental results could be related to the surface roughness of the materials. Hoek et al. (18) had found that surface roughness of a membrane could reduce the repulsive energy barrier height, thus rendering rough surfaces more favorable for particle deposition.

Part of the reason why XDLVO theory correctly predicted the attachment to Teflon and stainless steel was the influence and dominance of acid-base interactions. This factor affects the attractiveness or the repulsiveness of the bacteria to a surface (43). On hydrophilic surfaces such as glass and polysulfone, the total free energy of interaction at close approach is positive due to repulsive AB interaction. Conversely, the AB interaction is attractive on stainless steel and Teflon, resulting in a negative total free energy of adhesion at close approach. van Oss (41) pointed out that the acid-base attractive or repulsive nature depends upon the surface hydrophobicity or hydrophilicity of the entities.

In conclusion, this study has demonstrated that bacterial attachment to abiotic surfaces tends to be stochastic in cases in which there are no significant differences with respect to physicochemical characteristics between bacterial strains. This tendency is influenced by the material to which the bacteria are attaching, with attachment to more homogenous materials less likely to be stochastic. The stochasticity of such a process cannot be consistently interpreted using the XDVLO theory, probably because of its reliance on contact angle measurements which do not sufficiently represent the true physicochemical interactions occurring.