Pressure-induced reversible amorphization and an amorphous–amorphous transition in Ge₂Sb₂Te₅ phase-change memory material

Abstract

Ge₂Sb₂Te₅ (GST) is a technologically very important phase-change material that is used in digital versatile disks-random access memory and is currently studied for the use in phase-change random access memory devices. This type of data storage is achieved by the fast reversible phase transition between amorphous and crystalline GST upon heat pulse. Here we report pressure-induced reversible crystalline-amorphous and polymorphic amorphous transitions in NaCl structured GST by ab initio molecular dynamics calculations. We have showed that the onset amorphization of GST starts at approximately 18 GPa and the system become completely random at approximately 22 GPa. This amorphous state has a cubic framework (c-amorphous) of sixfold coordinations. With further increasing pressure, the c-amorphous transforms to a high-density amorphous structure with trigonal framework (t-amorphous) and an average coordination number of eight. The pressure-induced amorphization is investigated to be due to large displacements of Te atoms for which weak Te–Te bonds exist or vacancies are nearby. Upon decompressing to ambient conditions, the original cubic crystalline structure is restored for c-amorphous, whereas t-amorphous transforms to another amorphous phase that is similar to the melt-quenched amorphous GST.

Semiconductor chalcogenides that have a unique behavior of fast reversible phase transition between their crystalline and amorphous forms under pulse-induced heat treatment are prime materials used for phase-change memory. These chalcogenides are hence also referred to as phase-change materials. The principle of phase-change memory is simple: Intense laser or current pulse melts the recording media, which is rapidly quenched to amorphous bits against a crystalline background. Significant differences in optical/electronic properties between the amorphous and crystalline states help to read information. Even though devices of phase-change optical storage, such as rewritable digital versatile disks, were commercially available around twenty years ago, it is only in recent years that significant attention has been paid to understand the atomic-scale mechanism of the reversible phase transition (1–13).

Among the chalcogenide phase-change materials, Ge₂Sb₂Te₅ (GST) exhibits the best performance and hence is the mostly used material in commercial digital versatile disks-random access memory (DVD-RAM) and the ovonic unified memory (14). Furthermore, phase-change random access memory utilizing GST as record media has been demonstrated to be the most promising next-generation memory type (15). The crystalline and amorphous GST is thus extensively studied to unravel the atomic-scale mechanism behind the utilized transition. The crystalline GST has two phases: a low temperature cubic phase and a high temperature trigonal phase. The cubic phase is involved in the phase-change memory, which has been determined to have a distorted rocksalt structure with Te occupying one sublattice and Ge/Sb/vacancies occupying the other sublattice (16). There have been quite some arguments on whether the Ge, Sb, and vacancies are randomly or ordered arranged in this sublattice (2, 11, 16). Nevertheless, the energy difference between the ordered and random cases is small (2).

Very recently, attention is focused on the structure change of GST under high pressures (17–22). This is partially because that very large compressive pressure is momentarily generated in recorded molten bits due to the large density difference between crystalline and amorphous GST. It has been experimentally observed that rocksalt structured GST (referred to as c-GST) transformed to an amorphous phase under a pressure of around 20 GPa at room temperature (17) or under 25 GPa at temperatures from room temperature up to 150 °C (18). Upon decompression the initial cubic structure is not restored at ambient conditions (17) but it is recovered at 145 °C (18). On the other hand, a body-centered cubic polymorph of c-GST with coordination number (CN) 8 has been observed at 30 GPa upon compressing c-GST (19). For the mechanism of pressure-induced amorphization, it has been argued that a strong second nearest-neighbor Te–Te interaction and vacancies play a central role (17). On the other hand, a piece of theoretical work of ab initio molecular dynamics simulations (AIMD) attributed the phase transition to the presence of homopolar Ge/Sb bonds induced by the displacement of Te atoms to fill the voids of neighboring Ge/Sb stoichiometric vacancies (20). In this work we present the direct evidence that the pressure-induced amorphization in c-GST is due to the formation of very strong Te–Te covalent bonds that also results in the Ge/Sb homopolar bonds. Furthermore, we report an amorphous to amorphous phase transition at higher pressures based on ab initio molecular dynamics simulations.

Results and Discussion

The starting structure is c-GST with 324 atoms in the cell where Ge, Sb, and vacancies randomly occupy the same sublattice following the special quasirandom structure (SQS) concept (23). We point out that it is not clear how the random arrangements of Ge, Sb, and vacancies are achieved in the previous theoretical work (20).

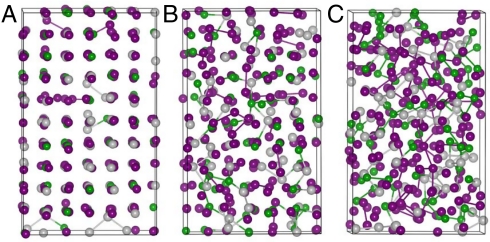
This work provides detailed changes in atomic arrangements and chemical bonding under various pressures up to around 52 GPa (V/V₀ = 0.608). Our simulations show that there is no structure change below 18 GPa (V/V₀ = 0.7878), whereas at 18 GPa, disorder presents at some certain area where starts the collapse of the crystalline structure. The c-GST finally becomes completely disordered at 22 GPa that is in good agreement with previous work (17–20). To give a better understanding of the changes in structures at various pressures, we show in Fig. 1 A–C the snapshot structures at 18, 22, and 33 GPa, respectively. It is clearly seen in Fig. 1A that some Te atoms slip from their original positions to the neighboring vacancy positions, which consequently results in the local distortion of the system and the formation of some homopolar Te–Te, Sb–Sb, Sb–Ge bonds. Fig. 1A also clearly shows that the site selected amorphization of c-GST is due to the large displacements of Te atoms instead of the previous hypothesis of large Ge displacements (1). Upon further compression, the homopolar Ge–Ge appears and the amount of all the homopolar bonds increases with increasing pressures that is also clearly seen in Fig. 1 B and C. Therefore, it is clear that the vacancies and weak second nearest-neighbor Te–Te bonds are the key factors for the pressure-induced amorphization of c-GST. The formation of homopolar Ge/Sb and Te bonds are the results of the amorphization.

Fig. 1.

Structure evolution of cubic GST under various pressures showing the increased amounts of homopolar bonds (A) 18 GPa, (B) 22 GPa, and (C) 33 GPa.

Fig. 2 shows the first nearest-neighbor bond-angle distributions (BAD) around Ge, Sb, and Te in c-GST under various pressures. It is seen that sharp peaks centering at approximately 90° and approximately 172° are still observed at 18 GPa, showing a slightly distorted cubic framework. With increasing the pressure to 22 GPa (V/V₀ = 0.7258), only one broad peak centering at approximately 88° for Ge and Te and at approximately 84° for Sb is obtained for the system. In addition, a very small and broad peak at approximately 60° is observed for around Sb and Te atoms. The results suggest an amorphous structure of cubic framework for GST at 22 GPa (hereafter referred to as c-amorphous). With further increase the pressure to above 33 GPa (V/V₀ = 0.667), the c-amorphous gradually transforms to another amorphous phase of different framework. This amorphous might be in a trigonal framework (hereafter referred to as t-amorphous) as seen by the peaks at approximately 60° and the rather broad angle distribution from approximately 60° up to approximately 130° of the BAD in Fig. 2.

Fig. 2.

Bond-angle distribution around Ge, Sb, and Te in GST under various pressures.

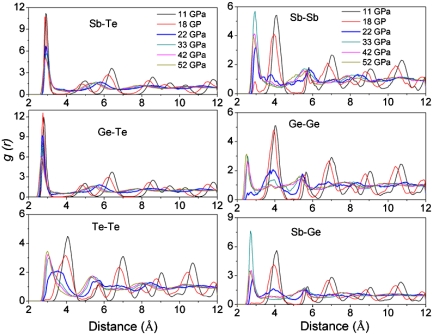
The chemical order of c-GST at various pressures can be obtained by analyzing the partial radial distribution functions (RDF) that is shown in Fig. 3. It is obvious that the system keeps its long range order up to 18 GPa as seen from the rather sharp peaks at long distances in the RDF. Note that there is a very small peak for the Sb–Sb pair at 18 GPa suggesting the onset formation of Sb–Sb homopolar bond. With increase in pressures, the sharp peaks at distances longer than 6 Å gradually disappear showing the collapse of long range order and the formation of amorphous phase. Another obvious feature of the partial RDF is that the originally second nearest-neighbor Ge–Ge, Ge–Sb, Sb–Sb, and Te–Te homopolar interactions turns into the first nearest-neighbor interactions. In other words, the collapse of c-GST is accompanied by the formation of homopolar bonds. The average bond lengths of the Ge–Te and Sb–Te bonds change only slightly with pressures up to 52 GPa (V/V₀ = 0.608) that is clearly seen from the partial RDF of the Ge–Te and Sb–Te bonds. Furthermore, the partial RDF in Fig. 3 indicates that the chemical ordering of the c-amorphous at 22 GPa is very different from that of t-amorphous at above 33 GPa in that the former phase contains much less Ge–Ge and Te–Te homopolar bonds.

Fig. 3.

Partial pair radial distribution functions under various pressures.

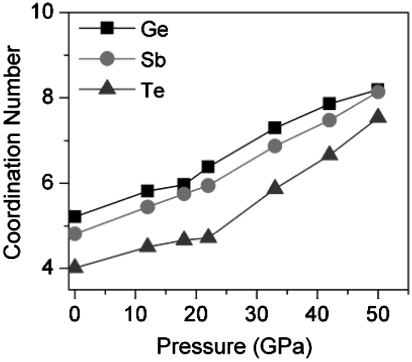
Fig. 4 shows the CNs at various pressures. The CNs for Ge, Sb, and Te in the original SQS structured c-GST are 5.21, 4.81, and 4.00, respectively. Upon compressing, the CNs gradually increases to 6.39, 5.95, and 4.70 for Ge, Sb, and Te at 22 GPa following a linear function. At pressures higher than 22 GPa, the CNs increase rather sharply to 8.19, 8.14, and 7.54 for Ge, Sb, and Te at 52 GPa also following a linear function. The results in Fig. 4 show an obvious turning point for the CNs versus pressures, suggesting the system before and after 22 GPa is quite different. This is in agreement with the above analysis that the c-amorphous has a similar framework as well as similar chemical ordering with c-GST.

Fig. 4.

The distribution of coordination numbers around Ge, Sb, and Te under various pressures.

Further analysis on the electron localization functions (ELF) (24) unravels the mechanism of the pressure-induced amorphization from the chemical bonding point of view. The topological analysis of the ELF is a very useful tool for problems in structure determinations as well as the determination of chemical bonding strength (25). The values of ELF vary between 0 and 1. The ELF value between two bonded atoms shows the type of bonding and bonding strength. For example, ELF = 1 represents perfect covalent bonds and the covalent bonding is the strongest. Any values between 0.5 and 1 reveal covalent bonds of various bonding strength; i.e., the larger the value, the stronger the covalent bond. Whereas 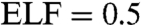gives a metallic system. Fig. 5 A–C give the ELF contour plots showing the typical bonding characters for structures obtained at 18, 22, and 33 GPa, respectively. Fig. 5A shows the ELF in the plane that cuts through the sites where the disorder of Te atoms started as illustrated in Fig. 1A. It is noted in Fig. 5A that some Te atoms (labeled as Te5, Te6, and Te7) diffuse to their neighboring vacant sites forming strong Te–Te covalent bonds. The bond lengths of Te5–Te6 and Te6–Te7 are 3.056 and 2.804 Å, respectively, whose original values are 4.767 and 4.016 Å. Obviously large rearrangements happened between the originally weak second nearest Te–Te bonds. As a consequence, homopolar Ge/Sb bonds form as seen by the Ge–Sb direct bond near Te5 atom, which is weak bonding at this stage. With increasing pressures, Te atoms continue to occupy the nearby vacant positions resulting in large rearrangements and finally the collapse of the crystalline. This is clearly seen in Fig. 5B, which is the ELF contour plot for structure of Fig. 1B. In Fig. 5B we can see the formation of Te square ring consisting of Te1, Te6, Te7, and Te8 bonded by covalent bonding as well as strong covalent bonds of Ge–Sb and Sb–Sb. Furthermore, it is also noted that the amorphous structure obtained at 22 GPa mainly consist of slightly distorted square rings. At 33 GPa, The contour ELF plot reveals different feature. The system contains mainly trigonal rings bonded by relatively weaker covalent bonding compared to that in Fig. 5B. As discussed above, the coordination of this system is approaching to 8 at high pressures. Therefore, the transition from c-amorphous to t-amorphous is due to the release of large Coulomb repulsion force that results in the formation of higher fold coordinated system of weaker covalent bonding. This can be understood by the fact that with increasing pressures or decreasing lattice size, the covalent bond length decrease. Once the bond length in the compressed cell is smaller than the sum of the constitute covalent radii, the original cubic frame work will collapse to release the large repulsion forces, thus results in the phase transition from c-amorphous to t-amorphous.

Fig. 5.

ELF contour plots projected on the (001) planes of c-GST obtained at various pressures: (A) 18 GPa, (B) 22 GPa, and (C) 33 GPa.

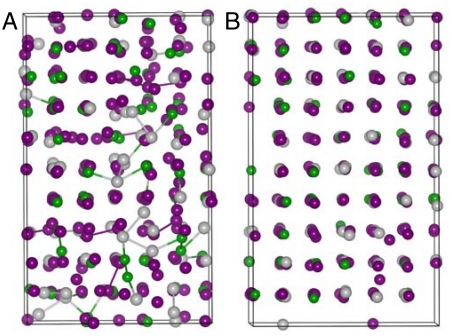
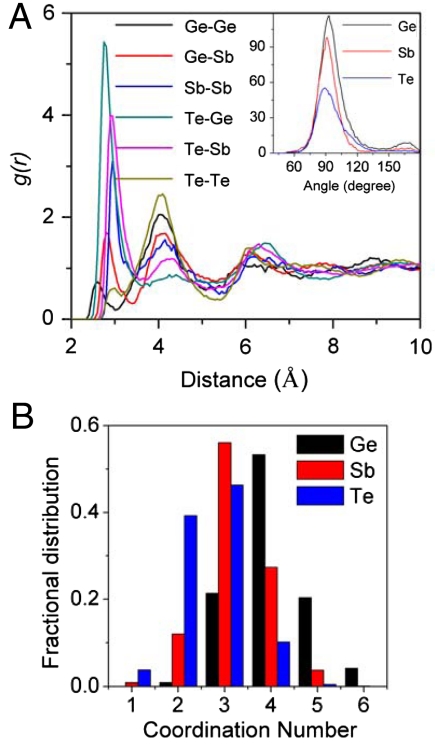
Upon decompressing the c-amorphous structure gradually to ambient pressure, the amount of hompolar bonds decreases and finally the structure restores to the original cubic crystalline structure. This can be seen in Fig. 6 A and B, which illustrate the snapshot structures obtained with decompressing the lattice parameters to 5.56 and 6.02 Å, respectively. The result indicates that reversible amorphization can be achieved in GST by compressing and decompressing the phase in certain pressure range. Whereas by decompressing the t-amorphous phase gradually to the ambient condition, the original crystalline phase is not retrieved, instead the system keeps an amorphous state. Analysis on the amorphous phase reveals that this amorphous structure has a cubic framework as seen by the bond-angle distributions around individual elements inserted in Fig. 7A. Sharp peaks around 93°, 91°, and 89° for around Ge, Sb, and Te atoms as well as the small peak at around 170° clearly show that the structure has a slightly distorted cubic framework. Further analysis on the partial RDF in Fig. 7A shows the medium order of the system. It is also noted in Fig. 7A that the system is dominated by Te–Sb and Te–Ge bonds, with less contributions from Ge/Sb homopolar bonds. In addition, there is no first nearest-neighbor interactions for the Te–Te pairs, which is similar to the crystalline states. Fig. 7B shows the fractional distribution of CNs for this amorphous system. It is seen that Ge is dominated by fourfold coordination, Sb is dominated by threefold coordination and Te is dominated by three- and twofold coordination. The calculated average coordination numbers around Ge, Sb, and Te are 4.06, 3.21, and 2.65 with a cut off distance of 3.1 Å, respectively. Therefore, the feature of the pressured induced amorphous phase is in agreement with that of the melt-quenched amorphous phase (7).

Fig. 6.

Structure evolution of c-amorphous GST upon decompressing with lattice parameters of (A) and (B).

Fig. 7.

The structure features for the amorphous GST obtained by decompressing t-amorphous GST to ambient conditions: (A) The partial radial distribution function where in the Inset figures show the bond-angle distributions around Ge, Sb, andTe, and (B) the fractional distribution of coordination numbers around Ge, Sb, andTe.

Computational Methods

Our AIMD calculations were performed within the framework of density functional theory as implemented in the Vienna ab initio simulation package (VASP) (26). The interatomic forces were computed quantum mechanically using projector augmented wave (PAW) potentials within the local density approximation (27). Gaussian smearing was applied and an energy cutoff of 131.36 eV as well as one gamma point was used for the AIMD simulations. The static ab initio total energy calculations for the ELF also used the VASP code. In this case, the PAW potentials within the generalized gradient approximations of Perdew–Burke–Ernzerhof were used (28).

The initial cell of rocksalt structured GST was constructed following the SQS concept where Te occupy one sublattice and Ge, Sb, and vacancies randomly occupy the other sublattice. The supercell contains 324 atoms with a density of 0.033 atom/ų. The supercell was then thermolized at 300 K by AIMD simulations for 30 ps. The system was then subjected to increasing pressures by gradually reducing the volume in several steps (V/V₀ = 0.8574, 0.7878, 0.7258, 0.667, 0.637, 0.608). Every simulation at fixed volume last 12 to 18 ps. The ion temperature was set at 100 K during compressing and at 300 K for decompressing, where the temperature was controlled using the algorithm of Nosé (29).

Conclusions

By means of AIMD simulations, we observed pressure-induced reversible crystalline-amorphous and polymorphic amorphous transition in c-GST, a technologically important phase-change material. The amorphization of c-GST starts at around 18 GPa and finishes at 22 GPa at 100 K. The amorphous phase obtained at 22 GPa has a cubic framework (c-amorphous) with average CN of 6. With further increasing pressures to above 33 GPa, the c-amorphous transforms to a high density amorphous structure with trigonal framework (t-amorphous) and an average CN of eight. The onset of amorphization is site selective that starts from the site where several vacancies cluster. The collapse of the crystalline phase is due to the large displacement of Te atoms to the nearby vacancy positions that consequently results in very strong Te–Te covalent bonds as well as strong Ge/Sb homopolar bonds. As a consequence, large local distortion forms that result in the unstableness of the crystalline phase and finally the complete amophization. The mechanism of the transition from c-amorphous to t-amorphous is argued to be due to the rearrangements of chemical bonding by the ELF analysis. With increase in the pressure, the bond lengths of the constitute elements decrease and hence the increased bond strength. As the bond lengths are shorter than their corresponding covalent bonds, Columbic repulsion dominates that results in the unstableness of the phase. To release the repulsion forces, the system rearranges into a system with low chemical bonds strength and high coordination numbers. Upon decompressing to normal condition, c-amorphous transforms to the original cubic crystalline structure, whereas t-amorphous transforms to another amorphous state that is similar to melt-quenched amorphous GST. The present results contribute to the understanding of the phase-change mechanism in phase-change materials and hence benefit to tailoring the properties of phase-change materials.