Instant fabrication and selection of folded structures using drop impact

Abstract

A drop impacting a target cutout in a thin polymer film is wrapped by the film in a dynamic sequence involving both capillary forces and inertia. Different 3D structures can be produced from a given target by slightly varying the impact parameters. A simplified model for a nonlinear dynamic Elastica coupled with a drop successfully explains this shape selection and yields detailed quantitative agreement with experiments. This first venture into the largely unexplored dynamics of elastocapillary assemblies opens up the perspective of mass production of 3D packages with individual shape selection.

Capillary forces exerted by a water drop are sufficient to strongly deform thin elastic objects such as carbon nanotubes or biological filaments (1, 2) or even to wrinkle thin polymer sheets (3). Elastocapillary interactions are abundant in nature and are responsible for phenomena such as lung airway collapse (4) and the clustering of insect bristles (5, 6). They are relevant to a number of applications at the micrometer or nanometer scale, such as microelectromechanical systems (7–9), mass production of nonspherical lenses (10), or drug delivery (11). On the other hand, drop impact is one of the most common illustrations of fluid mechanics in everyday life, having practical applications as diverse as pesticide delivery (12) or polymer inkjet printing for flexible electronics (13). Impact and splash of droplets have been studied for more than a century but only a few studies have addressed the case of a compliant substrate, and those are limited to small deformations (14). Here, the impact of a drop on a very flexible target is used to produce millimeter-size three-dimensional structures instantly. We show that impact allows a gain of five orders of magnitude in the fabrication time as compared to a previous method based on evaporation (15); in addition, we unveil the possibility to select the shape of the structure, by tuning the impact parameters. When scaled down and combined with inkjet technology that operates at similar dimensionless numbers, this setup opens up the possibility of mass production of individualized 3D packings at the submillimetric scale.

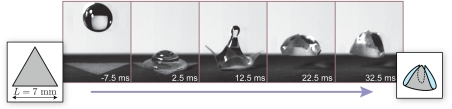
In our experiments, the flexible targets are cut out from thin polydimethylsyloxane (PDMS) sheets. Such polymer films, naturally exhibiting a nonwetting behavior with a water contact angle close to 110°, are treated to enhance contact line pinning (see Materials and Methods for fabrication details). The target is laid down on a superhydrophobic surface, which by repelling water confines the drop onto the target. A water drop of controlled volume is released from a given height, thereby allowing control of the impact velocity. For well-chosen impact parameters, we observe the formation of an instant capillary origami. This concept is demonstrated in the experiment of Fig. 1, where a drop impacts at its center a triangular target of width 7 mm with velocity U = 0.53 m·s^-1. Just after impact, the drop spreads out over the target up to a maximal extent where inertia is balanced by the restoring action of capillarity. Next, surface tension drives a flow toward the center of the drop, causing the rebound of the drop (16) and of the elastic film that sticks to it. While in free fall above the ground, the elastic sheet quickly wraps the drop. An elastocapillary bundle with a tetrahedral shape is formed and falls down to the ground. The whole sequence takes place in 40 ms, which is the typical duration of a hydrophobic rebound (16). When mediated by drop impact, encapsulation is thus considerably faster than when driven by evaporation (15), which typically requires half an hour.

Fig. 1.

Instant capillary origami, obtained with a water droplet of radius R = 1.55 mm impacting a thin triangular polymer sheet with thickness h = 55 μm at velocity 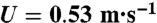. This time sequence reveals that encapsulation results from the interplay between the motion of fluid interface by capillary forces, and the large, dynamic deformations of the film.

Formation of the instant origami is governed by several length scales. Let B = Eh³/[12(1 - ν²)] be the bending modulus of the film, E its Young’s modulus, ν its Poisson’s ratio, h = 55 μm its thickness, L its length, μ = 51.8 × 10^-3 kg·m^-2 its mass per unit area, g the acceleration of gravity, and γ = 72 mN·m^-1 and ρ = 1,000 kg·m^-3 the fluid’s surface tension and density. In all our experiments, the initial drop radius is R = 1.55 mm. Wrapping into a tightly packed structure is made possible by the fact that this radius R is both smaller than the gravitocapillary length ℓ_gc = (γ/ρg)^1/2 ≃ 2.7 mm for the drop to remain spherical and larger than the elastocapillary length ℓ_ec = (B/γ)^1/2 ≃ 0.55 mm above which capillary forces can make slender objects buckle (1, 6, 15). In addition, gravity is important because the size L of the target is millimetric and comparable to the elastogravitational length ℓ_eg = [B/(μg)]^1/3 ≃ 3.5 mm above which gravity bends a cantilever beam. These length scales are all relevant and comparable: Encapsulation results from the mixed effects of gravity, elasticity, and capillarity.

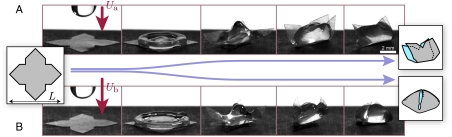
Drop impact, more than just speeding up elastocapillary wrapping, also allows for final shape control. A typical illustration of this shape selection mechanism is presented in Fig. 2 and in Movies S1 and S2.

Fig. 2.

A flower-shaped target reveals the possibility of pattern selection based on impact velocity U. Radius of the drop is R = 1.55 mm in both experiments, target width is L = 10 mm, and U_b > U_a. (A) For low impact velocity, U_a = 0.68 m·s^-1, a cylindrical bundle is formed, having twofold symmetry. (B) At higher velocity, U_b = 0.92 m·s^-1, the drop spreads more widely and almost wets the entire surface of the film; a pyramidal wrap is formed, having fourfold symmetry.

In this experiment, a drop impacts a small flower-shaped film at its center. For a fixed drop radius, different folding scenarios can be observed depending on the impact velocity. At low impact speed, spreading of the drop is limited, and the final pattern is the cylindrical folding of Fig. 2A. At higher speeds, the drop quickly embraces the entire surface of the sheet, and upon retraction a pyramidal wrap is obtained; see Fig. 2B. Different instant origamis can thus be obtained by simply tuning the velocity of impact. A similar selection can be observed with other target shapes. In the case of rectangular films, we observed a competition between two folding modes, one along the length of the rectangle and another one along its width. The pattern can be selected by varying not only the velocity but also the position of impact. The role of these two parameters is investigated in detail next.

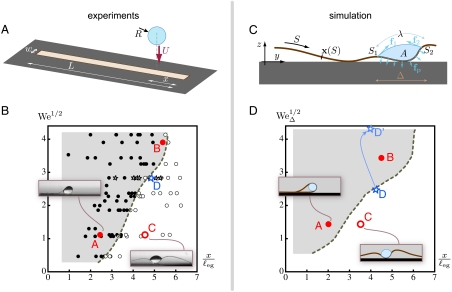
The phenomenon of dynamic elastocapillary encapsulation can be carried over to a 2D geometry where it is considerably simpler to analyze. We carried out a series of systematic experiments using as a target a long and narrow rectangular strip of width w = 2 mm, length L = 5 cm, such that h ≪ w ≪ L. For this narrow strip, L/ℓ_eg = 14.3. This 2D setting, sketched in Fig. 3A, simplifies the geometry by suppressing the 3D aspects of folding such as the formation of singular cones and ridges visible in the final frame in Fig. 2B. Moreover, in this setting, the fluid and solid time scales separate, as we show next.

Fig. 3.

Comparison of experiments (A and B) and simulations (C and D) in a 2D geometry. (A) In these experiments, a drop impacts a long, thin polymer strip laying down on a substrate, at a variable distance x from its end, and with variable impact velocity U. Strip dimensions are L = 5 cm and w = 2 mm, and drop radius is R = 1.55 mm. (B) Phase diagram showing the outcome of the experiment: nonencapsulated drop (○), encapsulated drop (●), or encapsulated drop with the help of a secondary drop obtained by pinch-off (☆). (C) Numerical model of a 2D dynamic Elastica coupled with a quasi-static, incompressible fluid with surface tension. (D) Phase diagram for the Elastica model. In B and D, typical final shapes are shown in inset. The time sequences of a few selected experiments, labeled A, B, C, and D here, are compared in Figs. 4 and 5. During the simulation run labeled D in part D of the figure, the impact parameters are changed to account for the capture of a secondary drop, as shown by the light-blue arrow.

Remarkably, shape selection can still be observed in 2D: The phase diagram in Fig. 3B reveals a competition between wrapped and nonwrapped final configurations. This diagram was obtained by systematically varying the distance x from the point of impact to the end of the strip and the impact velocity U. For the purpose of plotting, the position of impact x was measured in units of ℓ_eg, and U in units of the capillary velocity (γ/ρR)^1/2: The resulting dimensionless velocity is the square root of the Weber number We = ρU²R/γ. In our experiments, the Weber number varies* from 0.21 to 15, which is the typical value at which the inkjet technology operates.

Qualitatively, the process of encapsulation requires passing a gravitational energy barrier with the aid of the initial kinetic energy. The outcome of a particular experiment reflects the efficiency of this energy transfer. Indeed, because both L and R are larger than ℓ_ec, the strip is flexible enough to bend around the drop and the energy is always minimum in the encapsulated state. However, for drops that are too slow, or impact too far from the edge, the barrier associated with lifting up the strip prevents the system from reaching this global minimum. When the drop is deposited near the end (small x), encapsulation involves lifting a short segment of the strip, making the barrier lower. For small enough values of x, encapsulation can even be observed after nearly quasi-static deposition of the drop. For larger values of x, however, the barrier is higher and some amount of kinetic energy is required, which explains the existence of a threshold for the velocity U allowing encapsulation and the increase of this threshold with x. This qualitative reasoning is consistent with the orientation of the boundary obtained in the experimental diagram; see Fig. 3B. It is now turned into a fully quantitative model, which requires to first analyze the time scales.

During the fast initial spreading of the drop, part of the incident kinetic energy is quickly and irreversibly transferred into surface energy. Irreversibility is here a consequence of contact line pinning: Due to the roughness of the substrate, the contact line never recedes; it remains anchored to its maximal extent in all our experiments. This maximal extent, denoted Δ, is directly set by the impact parameters. Δ is a key mechanical quantity that determines how the capillary forces are distributed and how efficiently they bend the film during the subsequent folding. Δ was measured in a separate series of experiments using the same film (see SI Appendix). We found that, in our range of parameters, spreading is well described by the empirical law 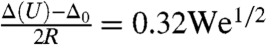. The parameter Δ₀ = Δ(U = 0) represents the amount of spreading for quasi-static deposition, as we are in partial wetting conditions. Note that the exponent 1/2 is consistent with a conversion of kinetic energy ∼ρU²R³ into surface energy ∼γΔ². A simple scaling analysis explains why the spreading takes place on a much faster time scale, denoted τ_c, than the time scale τ_e for the subsequent elastic deformation. The capillary time scale 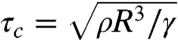is independent of the impact velocity (16). By contrast, the elastic time scale is given by the natural period of vibration of the free end of the strip, 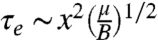. The ratio 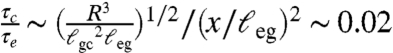is small, when evaluated with the typical value x = 4ℓ_eg of the 2D experiments.

With the aim to predict encapsulation, we consider a mechanical model for the slow folding dynamics of the strip following the initial drop spreading. In this model, the two contact lines are anchored and separated by a prescribed curvilinear distance Δ. The value of Δ captures the initial transfer of kinetic into surface energy, and the rest of the motion is driven solely by capillary forces. The dynamics of the strip is governed by the following potential energy:

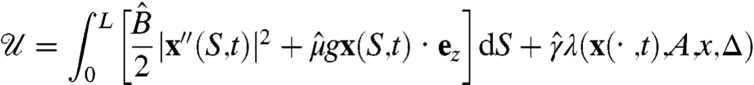[1]

and kinetic energy

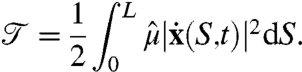[2]

Here, S is the arc length along the strip (0 ≤ S ≤ L), and x(S,t) is the position of the centerline. Deformations take place in the (x,z) plane, and e_z is the unit vector pointing upward. Dots denote derivation with respect to time, and primes with respect to arc length S. The integrals in the potential and kinetic energies 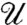and 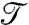are the classical ones for an elastic curve of bending modulus 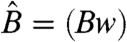and mass per unit length 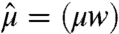, subjected to gravity g: The two first terms in are the elastic energy of bending, proportional to curvature squared, and the potential energy due to gravity. Coupling with the fluid is achieved by the capillary energy 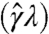, where 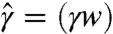is the line tension of the fluid–air interface and λ its perimeter; see Fig. 3C. This interface contacts the strip at points whose arc length coordinates S₁ and S₂ are prescribed in terms of two impact parameters, x and Δ: S₁ = L - x - Δ/2 and S₂ = L - x + Δ/2. Owing to the separation of time scales τ_c ≪ τ_e, the drop is treated quasi-statically. For any configuration of the strip x(S,t), the shape of the drop is found by minimizing the interfacial length λ under the constraint of a prescribed area A. The result is a circular cap attached to the fixed endpoints S₁ and S₂, whose radius and perimeter λ can be computed geometrically in terms of the current configuration of the strip: λ = λ(x(·,t),A,x,Δ) (see SI Appendix).

Our numerical code integrates in time the equations of motion obtained by applying Lagrangian mechanics to our Lagrangian 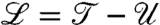. In deriving these equations, we consider the inextensibility constraint |x^′| = 1 and the presence of an impenetrable ground x·e_z≥0. Fluid incompressibility is used during the reconstruction of λ(x(·,t),A,x,Δ). The resulting equations of motion are the classical equations for the dynamics of a 2D Elastica subjected to gravity forces, to frictionless reaction from the ground in the event of contact, and to capillary forces (see SI Appendix for details). The capillary forces tend to make the potential energy 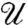lower. They do so by bending the strip around the drop, thereby reducing the interfacial length λ while preserving the imposed area A.

The numerical phase diagram in Fig. 3D has been obtained by varying the impact parameters systematically in a series of simulation runs. The positions of the endpoints S₁ and S₂ of the wet region were sampled, restricted to 0 < S₁ < S₂ < L. In each simulation run, the values of S₁ and S₂ are recorded, as well as the outcome of the numerical experiment, encapsulated or nonencapsulated (the exact criterion for encapsulation is described in Materials and Methods). Each pair of values S₁ and S₂ is translated into impact parameters Δ = |S₂ - S₁| and 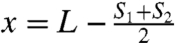. For the purpose of comparison with the experiments, the impact parameter Δ is then converted into an equivalent Weber number using our empirical law 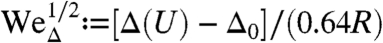capturing the fast initial spreading of the drop. As revealed by the phase diagram in Fig. 3D, the model successfully explains the selection of the final shape by the impact parameters. The essential features of the experimental diagram are reproduced. Any value of the position of the center of impact x is associated with a critical value of the Weber number, which corresponds to a minimal value of the velocity U (or the spreading Δ) for encapsulation to occur. In addition, this critical value of the Weber number is an increasing function of x. The numerical model is based on simplifying approximations such as neglecting the weight and inertia of the drop, as well as three-dimensional effects, capillary waves, and depinning of the contact line. Such a depinning occurs on rare occasions, as in the final frames of Fig. 4 A and B. We obtain nevertheless a close agreement on the boundaries between the encapsulated and nonencapsulated regions. The simulation parameters are set directly from their experimental values and there is no adjustable parameter.

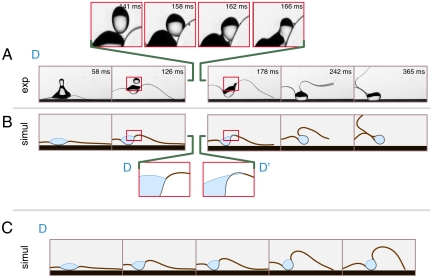
Fig. 4.

Comparison of experimental and simulated time sequences for selected impact parameters shown in Fig. 3. Only a fraction of the strip is shown here. (A) Rigid encapsulation observed when x/ℓ_eg ≲ 1. (B) Floppy encapsulation: For larger values of x/ℓ_eg, the free end of the film folds so as to mitigate the penalization due to gravity. (C) When the drop is deposited too far from the end of the strip, capillary forces cannot overcome the weight of the strip and the drop remains unencapsulated. See also Movie S2.

The model not only predicts the final shape of the strip but also its detailed time evolution. Comparison of typical experimental and numerical time sequences is shown in Fig. 4 for selected values of the impact parameters. An excellent, frame by frame agreement is obtained.

The sets of impact parameters values were chosen so as to illustrate the main regimes of encapsulation. The model perfectly reproduces both the “rigid” mode of encapsulation in sequence A, where the free end of the strip folds about the drop with little deformation, the “floppy” mode in sequence B reminiscent of the Fosbury flop, where bending of the strip helps reduce the height of the gravitational energy barrier, and the absence of encapsulation in sequence C, when impact occurs further from the endpoint of the strip than in A and with a lower velocity U (and spreading length Δ) than in B. To compensate for the slightly different shape of the boundary in the experimental and numerical phase diagrams, the points A, B, and C have been moved by a small amount in the numerical diagram—i.e., we have assigned them the same position relative to the boundary as in the experimental diagram, rather than the same absolute position. Overall, all the details of the dynamic sequence leading to encapsulation are captured with remarkable accuracy.

For a small subset of the experiments, confined to a limited region of the experimental phase diagram and labeled by stars in Fig. 3B, encapsulation takes a special route. In this region, the final state is not always reproducible even for fixed impact parameters. In addition, encapsulation can be observed for anomalously large values of x: The two stars to the right of point D in Fig. 3B clearly stand out to the right of the boundary. This surprising behavior can be explained by looking at the time sequence in Fig. 5A.

Fig. 5.

Encapsulation aided by a topology change of the drop. (A) In the experiments, a secondary drop appears transiently by pinch-off and coalescence when We^1/2 ≈ 2.8. This detachment leads to encapsulation in a region where it would otherwise not be possible: The impact parameters for this experiment are denoted by the star labeled D, located to the right of the boundary in the phase diagram of Fig. 3B. (B) This transient topology change is accounted for by extending the footprint Δ of the drop in the middle of the simulation (Inset D′), by an amount measured from the experimental frames. As a result, simulation correctly predicts encapsulation and matches the experimental movie frame by frame. (C) When this footprint Δ is left unchanged, simulation fails to predict encapsulation.

Shortly after the initial spreading, a vertical jet is formed and a secondary drop detaches. Under the action of gravity, it accelerates downward, catches up with the falling capillary bundle, and coalesces. In some experiments, such as that labeled D in the figure, the bouncing drop lands on the edge of the main drop and coalesces, thereby increasing the wet length Δ, inducing a redistribution of the capillary forces that substantially modifies the subsequent folding dynamics. Because the ejection of a secondary drop is ruled by the Weber number, this view is consistent with the observation that anomalous encapsulation events are all observed when the Weber number is close to a particular value, We^1/2 ≈ 2.8. When the simulation is run as earlier, ignoring the secondary drop, encapsulation is not correctly predicted, as shown in Fig. 5C. The role of the secondary drop is captured by a simple extension of the model. From the experimental movies, we measure the time of ejection of the secondary drop and the position 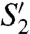of the contact line after coalescence. This shift in position yields virtual impact parameters, labeled D′ in Fig. 3D, which are indeed well inside the region of encapsulation. We run again the simulation, now updating the position S₂ of the contact line to 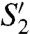at the time of coalescence. As shown in Fig. 5B, the key role of the secondary drop on the final pattern is accurately captured. Encapsulation is correctly predicted and comparison with the experiments reveals an excellent frame-by-frame agreement.

Our system demonstrates one of the interesting and largely unexplored phenomena arising out of the combination of capillarity with large, dynamic deformations of fluid interfaces and flexible bodies. At small scales, viscosity and capillarity are often considered as dominant, and inertia negligible. The impact of a drop is an interesting exception to this rule: Kinetic energy, when initially stored in the form of a rigid-body mode of translation, cannot be dissipated by viscosity. This energy ends up in selecting the final shape among competing equilibria. We studied in detail a 2D setting, where well-controlled experiments were found in quantitative agreement with a tractable model. In this 2D setting, multistability arises from gravity. The dynamical shape selection uncovered here works also at smaller scales, where gravity becomes unimportant. Indeed, there are other sources of multistability, such as nonlinear elasticity of thin films or the follower character of capillary forces. As a matter of fact, numerical experiments confirmed the persistence of shape selection in the absence of gravity (see SI Appendix and Movie S3). Robustness of the selection mechanism opens up the perspective of scaling down the experiment to the size of an inkjet drop.

Materials and Methods

The thin elastic sheets were made of PDMS (RTV615 from General Electric). The polymer was spun on a glass microscope slide at 1,500 rpm for 40 s on a SUSS MicroTec spin-coater (after an initial spreading stage of 10 s at 500 rpm—each change in angular velocity being achieved over 5 s with a linear ramp) and cured at 70 °C for 1 h. The resulting thickness was 55 μm. The thin polymer films were peeled off from the glass using a surgical blade and further cut out to the desired shape. The pattern was then deposited onto a rigid copper substrate warranting a high-restitution coefficient upon impact. To make the copper superhydrophobic we used electroless galvanization (17): The copper was first coated with a textured metallic layer (AgNO₃) and then covered with a low-surface-energy self-assembled monolayer (1H,1H,2H,2H-perfluorodecanethiol). The polymer patterns were powdered with talc to prevent self-adhesion; talc was found to enhance contact line pinning. All sequences were recorded using a high-speed camera Photron SA-5 at 5,000 frames per second.

The numerical simulations are based on the “Discrete Elastic Rods” model of Bergou et al. (18), which have been validated against analytical reference solutions. Here, we used it in a 2D geometry where twist is absent. We used the codebase developed by M. Bergou and E. Grinspun at Columbia University, New York, which has kindly been made available to us. Its robust and efficient treatment of the inextensibility constraint allows for fast simulations, taking typically less than 30 s even at the highest resolution. Details on the implementation of our model are provided in the SI Appendix. 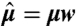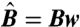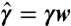In the simulations, we used the experimental values of , , and for the meniscus force, and we set A = V/ℓ_eg. This choice of A reflects the observation that the rounded shape of the drop makes it wider than w; as a result, its width is clearly closer to ℓ_eg than to w. These experimental values were made dimensionless because we used units such that gravity g, lineic mass 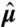, and bending modulus 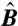all have the value 1. In such units, the line tension 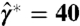and the area of the 2D drop is A^∗ = 0.36.

The criterion for encapsulation used both in experiments and numerical simulations was to test whether the endpoint of the free edge S = L had been moved to the left of the point at the center of impact S = L - x: Encapsulation corresponds to y(L,t = ∞) < y(L - x,t = ∞).