Clinically Constrained Optimization of flexTPI Acquisition Parameters for the Tissue Sodium Concentration Bioscale

Abstract

The rapid transverse relaxation of the sodium magnetic resonance (MR) signal during spatial encoding causes a loss of image resolution, an effect known as T₂-blurring. Conventional wisdom suggests that spatial resolution is maximized by keeping the readout duration as short as possible to minimize T₂-blurring. Flexible twisted projection imaging (flexTPI) performed with an ultra-short echo time, relative to T_2, and a long repetition time, relative to T_1, has been shown to be effective for quantitative sodium MR imaging. A minimized readout duration requires a very large number of projections and, consequentially, results in an impractically long total acquisition time to meet these conditions. When the total acquisition time is limited to a clinically practical duration (e.g., 10 minutes), the optimal parameters for maximal spatial resolution of a flexTPI acquisition do not correspond to the shortest possible readout. Simulation and experimental results for resolution optimized acquisition parameters of quantitative sodium flexTPI of parenchyma and cerebrospinal fluid are presented for the human brain at 9.4T and 3T. The effect of signal loss during data collection on sodium quantification bias and image signal-to-noise ratio are discussed.

Introduction

Quantitative sodium (²³Na) magnetic resonance (MR) imaging measures tissue sodium concentration (TSC) that can be interpreted in terms of sodium ion homeostasis and, therefore, tissue viability (1). The derived map of tissue sodium concentration (TSC) has been termed a bioscale as it is a spatially-resolved quantitative parametric map that has a direct biochemical interpretation, distinct from the term biomarker, which has a more limited implication of risk associated with pathology (2). The TSC bioscale provides insight into diseases that disrupt sodium ion homeostasis (e.g., failure of metabolic energy production in stroke (1)) or cell packing (e.g., cell death in tumors responding to radiation treatment (2–4)). Although the potential clinical importance of ²³Na imaging (5) and a method for quantification of MR signals into molar concentrations (6) have been known for more than two decades, quantitative sodium imaging with acquisition times suitable for humans only became feasible with the introduction of high and ultra-high field advanced MR scanner technology (7), and ultra-short echo-time (UTE) pulse sequences (8–10).

Accurate and precise measurement of the sodium bioscale at a resolution matched to the biological questions and tissue dimensions of human brain is necessary to address issues about regional brain health. Quantitative sodium MR imaging using flexible twisted projection imaging (flexTPI) on a clinical 3 Tesla (T) MR scanner has been described and demonstrated as having acceptable precision and accuracy in human brain (9). This approach calls for a series of ²³Na, or ²³Na and proton, acquisitions to compute the B₀ and B₁ corrected TSC bioscale of the human brain using matched acquisitions performed on a calibration phantom. The calibration phantom is designed to mimic the radiofrequency (RF) coil loading and relaxation characteristics of the human brain while providing compartments of known sodium concentration that can be used to calibrate the arbitrary signal intensity of the MR image into a molar concentration scale. This same quantification approach has also been applied to quantitative sodium and 17-oxygen MR imaging at 9.4 T to compute the cerebral metabolic rate of oxygen consumption (CMRO₂) bioscale (11).

The MR signal of the quadrupolar sodium nucleus has short, bi-exponential transverse relaxation characteristics in human brain tissue (12). An UTE imaging sequence with a short RF pulse and readout duration is required to minimize signal loss during data collection. The most practical and widely used ²³Na acquisition schemes sample k-space using 3-D trajectories that evolve on the surface of nested cones from the center of k-space (8–10). While such sequences are well suited to sodium imaging, the effects of transverse relaxation on the resolution, signal-to-noise ratio (SNR), and accuracy of the final sodium bioscale must be considered within the constraints of acceptable total acquisition times for clinical imaging. In this report, 10 minutes will be considered the upper limit tolerated by cooperative patients in terms of head motion.

The signal loss due to T₂* decay during data acquisition has two effects. First, it constrains the resolution that can be achieved within a fixed total acquisition time. Acquisition parameters that optimize the resolution of ²³Na can be selected, but the impact on the SNR must also be considered to ensure the final images can be reliably quantified. Second, signal loss during data sampling determines the bias of quantitative sodium MR imaging based on the T₂* difference between the sample being measured and the calibration phantom providing the external quantification standard. This report analyzes the impact of T₂* decay on flexTPI (9) for quantitative ²³Na MR imaging to find the acquisition parameters that maximize the resolution of the final TSC bioscale without compromising the SNR required for accurate quantification within a fixed total acquisition time. The analysis is presented in the context of quantitative ²³Na imaging, but could be applied for other short T₂ nuclei (e.g, ¹⁷O) as well.

Materials and Methods

Rapid decay of the MR signal during sampling (readout) in an imaging experiment leads to a loss of image resolution, an effect that is commonly referred to as T₂-blurring (13,14). In conventional proton imaging, the readout duration (T_ADC) is typically much shorter than the transverse relaxation time constant, resulting in a negligible loss of spatial resolution. For short-T₂ species such as sodium, however, the readout duration is often comparable to or longer than the relaxation time constant and the effect of T₂* decay on image resolution is pronounced. Specialized acquisition schemes have been proposed for imaging short-T₂ proton signals, where readout times of 0.81•T₂ and 0.69•T₂ were suggested for 2-D and 3-D projection imaging, respectively (14). In addition to rapid relaxation of the signal, sodium MR imaging has the added difficulties of a low concentration that creates an SNR challenge and a low gyromagnetic ratio that limits the rate at which k-space can be traversed during spatial encoding. These factors must be considered when optimizing any ²³Na imaging protocol.

Intuitively, it follows that the shortest readout duration results in the least T₂-blurring. Among all UTE sequences, 3-D projection imaging (PI) would be optimal to maximize resolution with the shortest readout duration. Unfortunately, 3-D PI requires the largest number of projections to critically sample k-space, resulting in an impractically long acquisition time for quantitative ²³Na MR imaging of human subjects.

Flexible TPI samples k-space with 3-D projections that twist on a set of nested cones that lie within a sphere of radius K_MAX (see Figure 1) rather than sampling a rectangular cuboid as is done for 3-D Cartesian imaging. Sampling a sphere instead of the circumscribed cube effectively limits the full-width at half-max (FWHM) resolution of the final reconstruction to approximately 1.59 times the nominal voxel dimension (14). This follows from the fact that the 3-D continuous Fourier transform of a unit diameter sphere, sometimes referred to as the tinc function (15), has a FWHM of approximately 1.59 Hz. From the time-frequency duality and scaling properties of the Fourier Transform, it follows that the 3-D Inverse Fourier Transform of a sphere of radius K_MAX will be a tinc function with a FWHM of 1.59 (2· K_MAX)=1.59·Δx_nominal, where Δx_nominal is the nominal voxel size. The T₂* decay during data collection will further decrease the resolution of the reconstructed image. For comparison, the FWHM of the 3-D sinc function that corresponds to sampling a 3-D unit cube of k-space is approximately 1.21·Δx_nominal.

Figure 1.

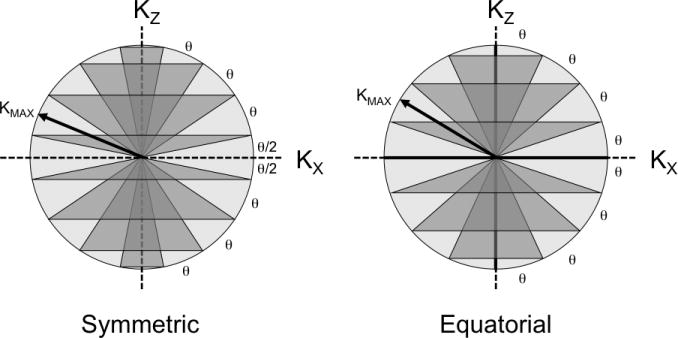
Two schemes (Symmetric, Equatorial) for separating the k-space sphere into nested cones are possible for flexTPI. The nested cones can be symmetrically placed about the K_X-K_Y plane (left, symmetric layout) such that there are no cones of radius K_MAX (“equator” cone in K_X-K_Y plane) or zero (“polar” cones lying along z-axis). Alternatively, the cones can be designed with equatorial and polar cones (right, equatorial layout). The two designs impose slightly different slew rate constraints. K_MAX, the number of cones, and total number of projections depend on the acquisition FOV and matrix size.

In flexTPI, the total number of cones (N_C), total number of projections (NP), and maximum k-space radius (K_MAX) are selected to critically sample k-space to achieve a desired nominal resolution (Δx_nominal) over a specified field of view (FOV), resulting in an effective 3-D matrix size of N_M = FOV/Δx_nominal. Each slew-rate limited flexTPI trajectory begins as a radial projection that continues until the k-space radius equals a specified radial fraction (F_R) of K_MAX (9). Trajectories then change from radial to twisting, thereby reducing the total acquisition time as fewer trajectories are needed to sample each cone (8). The readout duration of each flexTPI projection is the same and is determined by the maximum gradient amplitude (G_MAX), the maximum gradient slew rate (S_MAX), F_R, K_MAX, FOV, and Δx_nominal (or, equivalently, N_M). Optimization of flexTPI for quantitative ²³Na imaging for the best resolution in a fixed total acquisition time is now considered.

True Resolution and SNR of flexTPI Acquisition and Reconstruction

Since flexTPI uses slew-rate-limited twisting trajectories rather than radial projections, the signal intensity from a point source as a function of k-space radius is not the simple exponential of the ideal (non slew-rate limited) 3-D PI (see Figure 2). As the analytical expression for the point-spread function (PSF) of a flexTPI acquisition for a specified T₂* decay profile is not easily derived, a numerical calculation has been used.

Figure 2.

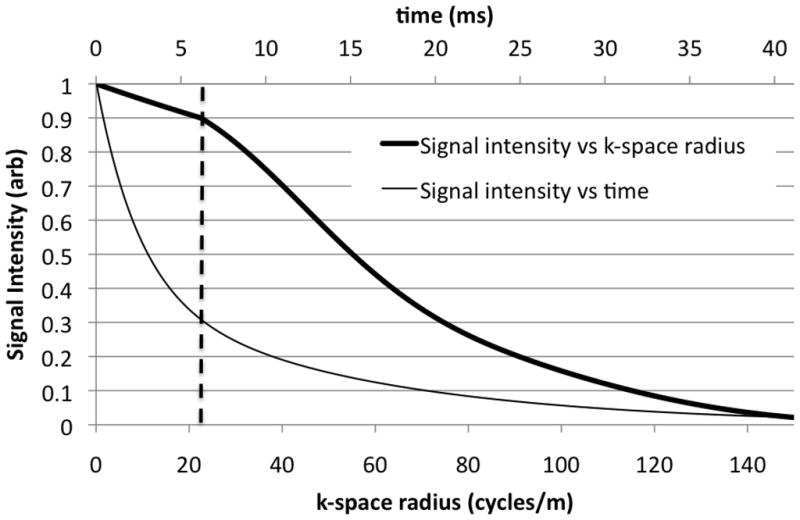
Simulated signal intensity from a unit amplitude point source with a bi-exponential decay (60% T₂=2.5 ms, 40% T₂=14 ms) for a flexTPI acquisition (G_MAX=5 mT/m, S_MAX=200 mT/m/ms, F_R=0.15, FOV=20 cm, N_M=60). The thick line is the signal intensity as a function of k-space radius, which has a non-exponential form (relative to k-space radius). The thin line is the signal intensity as a function of time with the conventional exponential form and corresponds to the signal for a comparable radial acquisition. The vertical dashed line indicates the point at which flexTPI trajectories transition from radial to twisting.

The overall PSF, due to acquisition, T₂* decay, and image reconstruction of flexTPI for the acquisition parameters G_MAX, S_MAX, K_MAX, F_R, N_M, and FOV, was computed by simulating the MR signal from a point-source with a defined T₂* relaxation. The signal from a point-source located at isocenter and with a multi-exponential T₂* decay is

$$S_p(t)=C·\left(\sum _{n=1}^{N_{T_2^{\ast }}}F[n]·e^{-t/T_2^{\ast }[n]}\right)$$ [1]

where $N_{T_2^{\ast }}$ is the number of T₂* relaxation rates and T₂*[n] and F[n] are the relaxation rate and contribution fraction $\left(1={\sum }_{n=1}^{N_{T_2^{\ast }}}F[n]\right)$ of n^th time-constant, respectively. C is a proportionality constant that depends on several factors including the receiver sensitivity, flip angle, and the static magnetic field. The data were reconstructed using a standard gridding-based approach (16) with a Kaiser-Bessel gridding kernel using the known k-space trajectories and sampling density (9) to give the discretely sampled PSF, from which the FWHM was numerically computed and defined as the true resolution (Δx_true) achieved by the acquisition parameters. This approach to determining the PSF is conceptually similar to “gridding ones” (10), except that it incorporates the T₂* decay characteristics to allow the impact of the readout trajectory on resolution (through T₂-blurring) to be evaluated.

The SNR of a flexTPI acquisition was evaluated by comparing the simulated signal from a homogenous cuboid to the result of a simulated noise-only acquisition. The signal from a homogenous cuboid located at isocenter with widths of w_x, w_y, and w_z in the x-, y-, and z-dimensions, respectively, is given by:

$$S_h(t)=C·\left(\sum _{n=1}^{N_{T_2^{\ast }}}F[n]·e^{-t/T_2^{\ast }[n]}\right)·w_x·w_y·w_z·\text{sinc}(k_x(t)·w_x)·\text{sinc}(k_y(t)·w_y)\text{sinc}(k_z(t)·w_z)$$ [2]

Here sinc(x)= sin(πx)πx, and k_x(t), k_y(t), k_z(t) are the k-space positions at time t. The reconstructed image from a simulated cuboid was used to define the signal intensity in a homogenous region (SI_h) as the mean signal intensity over the center 50% of the cuboid in each dimension (i.e., $[-\frac{w_x}{4},\frac{w_x}{4}]\times [-\frac{w_y}{4},\frac{w_y}{4}]\times [-\frac{w_z}{4},\frac{w_z}{4}]$). Using the central region avoided any effects due to the limited resolution that prohibited a sharp transition between the object and the background. For the same acquisition parameters used to compute SI_h, k-space data consisting of unit variance complex white Gaussian noise was reconstructed and the variance of the resulting image-domain standard deviation (σ_n) was computed. The theoretical SNR of a homogenous region was then calculated as:

$${\mathit{SNR}}_h=\frac{{SI}_h}{{\sigma }_n}$$ [3]

Computing the noise standard deviation explicitly incorporated any influence of the flexTPI acquisition and image reconstruction on the noise level. Although the SNR from a single point-source (SNR_p) has previously been used to optimize acquisition of short-T₂ species (14,17), SNR_h is adopted here as it is a more applicable measure for homogenous regions (e.g., white matter of the brain).

Resolution optimized flexTPI acquisition parameters

A naïve resolution optimization of flexTPI for ²³Na imaging results in the trivial, but impractical, result that calls for F_R =1.0 (i.e. flexTPI reduces to 3-D PI) with G_MAX, S_MAX, K_MAX, N_C, and N_P as large as possible. While such an acquisition would indeed have the highest resolution, the total acquisition time would be unrealistically long for human applications. A more practical result is obtained by maximizing the resolution of flexTPI subject to constraints on the total imaging time (T_TOTAL), G_MAX, and S_MAX, the latter two of which are dictated by the scanner hardware performance and the former by the cooperation of the subject. Experience has shown that a total acquisition time longer than 8–10 minutes accumulates artifacts due to head motion for most subjects, although longer acquisitions are possible with motivated subjects.

Quantitative sodium imaging requires a repetition time (T_R) of at least 150–175 ms to achieve the full T₁ recovery necessary for straightforward signal quantification to compute the TSC bioscale. Thus, the maximum number of flexTPI projections that can be used for a single T_TOTAL -length acquisition is:

$${\text{N}}_{\text{P}}=\lfloor \frac{{\text{T}}_{\text{TOTAL}}}{{\text{T}}_{\text{R}}}\rfloor$$ [4]

For a fixed FOV, both N_M and F_R influence the number of projections in a flexTPI acquisition. These two factors must be adjusted simultaneously to maintain the total number of projections. As the N_M is increased (smaller Δx_nominal), more trajectories are required to critically sample k-space. Likewise, when F_R is increased, each trajectory samples a smaller volume of k-space (since there is less twist), also resulting in a larger number of necessary trajectories. This means that for any (T_TOTAL,T_R) pair, there is a collection of (F_R, N_M) pairs that result in the same number of projections. Figure 3 shows example combinations of (F_R, N_M) pairs that satisfy different T_TOTAL constraints for T_R =160 ms.

Figure 3.

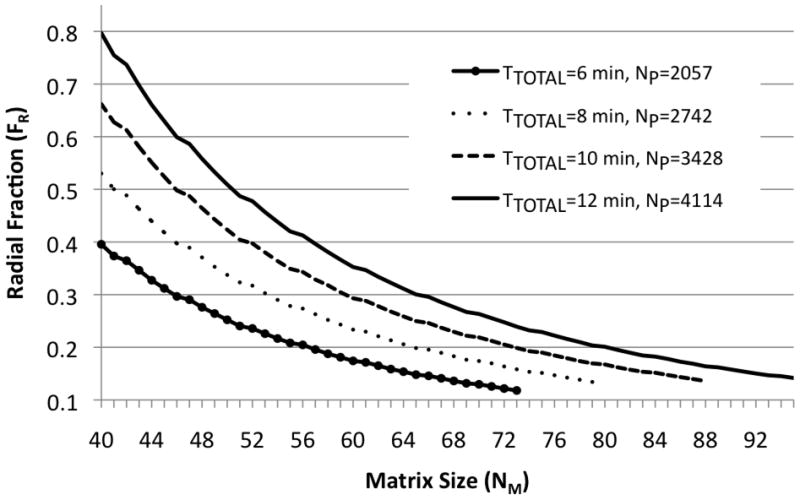
Pairs of (F_R, N_M) satisfying four values of T_TOTAL constraint (6, 8, 10, 12 minutes) for a T_R=160 ms and symmetric k-space cones. For any specified total acquisition time, there is a collection of (F_R, N_M) pairs that must be evaluated for resolution performance.

Figure 3 implies that for any N_P, there are a number of acquisition parameters combinations that must be evaluated to determine which set results in the best final resolution. Even with G_MAX and S_MAX fixed, each combination of (F_R, N_M) has a different readout duration that results in a different amount of T₂-blurring. As N_M is increased, F_R must correspondingly decrease in order to keep N_P constant. This results in an increased T_ADC and, therefore, increased T₂-blurring. However, at the same time that the nominal voxel size is decreased, so the overall impact of the resolution loss due to the tinc function is decreased. These two competing factors contribute to the final true resolution of the reconstructed image.

S_MAX will typically be dictated by the system hardware while a range of G_MAX values will be possible. This raises the question of what maximum gradient amplitude should be used to optimize the resolution of the flexTPI acquisition. The naïve response is to select that largest possible G_MAX so as to minimize T_ADC and the amount of T₂-blurring. However, since flexTPI uses slew-rate limited trajectories (9), use of the maximum gradient amplitude is not necessary. The maximum gradient amplitude that can be achieved during the twist is given by:

$$G_{\mathit{MAX}}^{\mathit{Slew}}=\{\begin{array}{cc}\frac{1}{\gamma }\sqrt{K_{\mathit{MAX}}·\gamma ·S_{\mathit{MAX}}·sin(\theta /2)}& \text{Symmetric}\text{flexTPI}\\ \frac{1}{\gamma }\sqrt{K_{\mathit{MAX}}·\gamma ·S_{\mathit{MAX}}·sin(\theta )}& \text{Equatorial}\text{flexTPI}\end{array}$$ [5]

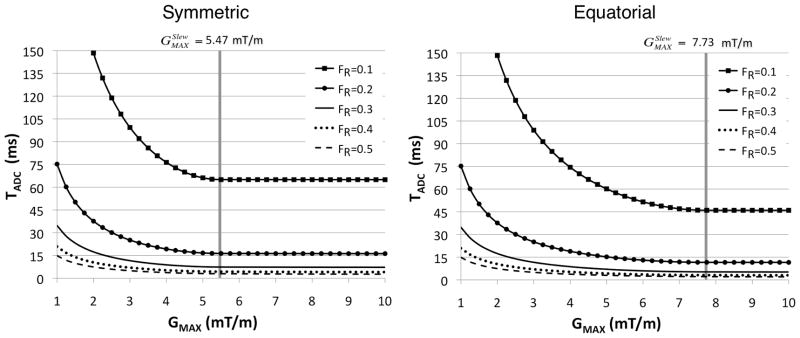
where θ is the angular spacing between cones (see Figure 1). The symmetric and equatorial nesting of k-space cones have different cone configurations and, therefore, produce slightly different slew rate constraints. As shown in Figure 4, choosing $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ will result in a nearly minimal readout duration while using a modest gradient amplitude. When $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$, the duration of the twisted portion of the flexTPI trajectories is minimized. Use of a larger maximum gradient amplitude has minimal impact on the overall readout time since only the radial part of the trajectories, constituting a small fraction of the total readout for F_R < 0.5, can be shortened. For any modern human MR scanner, $G_{\mathit{MAX}}^{\mathit{Slew}}$ is well below the maximum gradient amplitude of the gradient system. This means that the gradient system is conservatively operated during flexTPI acquisitions, which is a potentially valuable property for extending the lifetime of the gradient system at ultra-high field.

Figure 4.

Readout duration for various values of F_R for symmetric and equatorial cone nesting for flexTPI (FOV= 22 cm, N_M=44, S_MAX=150 mT/m/ms. In both cases, $G_{\mathit{MAX}}^{\mathit{Slew}}$ (gray vertical line) achieves nearly the shortest T_ADC among all gradient amplitudes. The difference in minimum T_ADC that can be achieved for the two cone-nesting schemes shown in Figure 1 diminishes as F_R increases.

The true resolution of a ²³Na image acquired with flexTPI for a FOV of 22 cm was evaluated for the T_TOTAL constraints of 4 min and 10 min. The 10 min acquisition time was selected as the maximum time that can be routinely completed without excessive artifacts due to head motion. The 4 min acquisition was selected based on the original flexTPI description (9), which used parameters that resulted in a total acquisition time of approximately 8 minutes by using a 4-minute acquisition and two averages. For each T_TOTAL, the true resolutions in brain parenchyma and in CSF were evaluated separately by numerically finding the FWHM of the PSF computed using the appropriate T₂ relaxation values of each tissue. Brain parenchyma was modeled as having a bi-exponential relaxation of T_2,short = 2.5 ms (60%) and T_2,long =14 ms (40%) and cerebrospinal fluid (CSF) was modeled as having a mono-exponential relaxation of 55 ms. These relaxation rates were selected based on the multiple reports of T_2,short =1–3 ms, T_2,long =12–25 ms, and the T₂ of CSF= 45–60 ms (2, 18–23). All (F_R, N_M) pairs that satisfied each T_TOTAL constraint were evaluated for S_MAX= 90 mT/m/ms and S_MAX=150 mT/m/ms with $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ for both the equatorial and symmetric cone nesting patterns shown in Figure 1. For each (F_R, N_M), the homogeneous signal intensity was found by simulating a unit amplitude 10 × 10 × 10 cm³ cube using Equation [2]. The SNR values of CSF and brain parenchyma were then computed using Equation [3] and normalized by the SNR of the T_TOTAL= 4 min, S_MAX = 90 mT/m/ms, and N_M= 44 acquisition for straightforward comparison. The time of the first sample point in all simulations was 0.3 ms relative to the middle of the RF pulse. This time can be achieved for human imaging at both 9.4 T and 3 T (9,24,25).

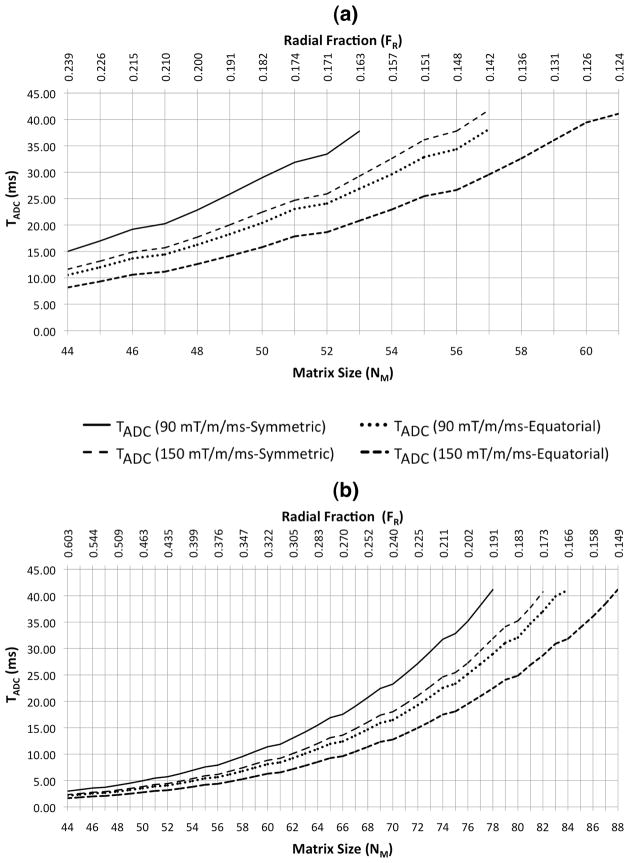
As shown in Figure 5, since flexTPI uses slew-rate limited trajectories, different maximum slew rate constraints and cone nesting schemes result in different readout durations even for the same (F_R, N_M) pair. T_ADC was given an upper bound of 42 ms for all simulations, which is the time at which 5% of the transverse signal from the T_2,long component of brain parenchyma remains. N_M was given a lower bound of 44, which corresponds to a nominal isotropic resolution of 5 mm for the 22 cm FOV.

Figure 5.

Required readout time, T_ADC (ms), as a function of matrix size and radial fraction constrained to total acquisition times of T_TOTAL = 4 (a) and 10 (b) minutes, respectively, for ${\text{G}}_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ and both the symmetric and equatorial patterns of k-space trajectories at two different slew rates (90 mT/m/ms, 150 mT/m/ms).

The impact of choosing $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ was evaluated by computing the true FWHM resolution of brain parenchyma and CSF for symmetric cone nesting with FOV=22 cm and T_R=160 ms. Acquisitions were simulated for $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ and G_MAX= 20 mT/m with (F_R, N_M)=(1.0, 44), (1.0, 63), and (1.0, 82), all of which require T_TOTAL>10 min, to determine whether choosing $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ placed a limitation on the achievable resolution. Changing from $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ to G_MAX= 20 mT/m for F_R=1.0 results in the most significant change in T_ADC as there is no twisted component to the flexTPI trajectories.

PSF analysis of quantification accuracy

The impact of T₂^* decay on quantification accuracy was evaluated by examining the theoretical signal intensity in a homogenous region that would arise from a brain under study and from a quantification phantom with known T₂ characteristics. In the absence of noise, the signal intensity from the homogenous compartment of known sodium concentration ([Na]_true) is simply

$${SI}_{{[Na]}_{\mathit{true}}}={SI}_h\times {[Na]}_{\mathit{true}}$$ [6]

To quantify a signal of unknown concentration measured from a brain under study, a linear calibration function is computed from the signal intensity and known concentrations of the calibration phantom compartments (9). In the absence of noise, this calibration function (f_Q) is simply the inverse of the homogenous signal intensity of the calibration phantom. The quantified ²³Na concentration corresponding to the signal intensity measured in the brain then becomes

$$f_Q({SI}_{{[Na]}_{\text{brain}}})=\frac{{SI}_{{[Na]}_{\text{brain}}}}{{SI}_h^P}=\frac{{SI}_h^B}{{SI}_h^P}{[Na]}_{\text{brain}}$$ [7]

where ${SI}_h^B$ and ${SI}_h^P$ are the homogenous signal intensity of the brain and phantom, respectively. [Na]_brain is the true sodium concentration in the brain and SI_[Na]brain is the signal intensity measured in the brain for that sodium concentration.

From Equation [7], it can be seen that the quantified sodium concentration in a homogenous region is a scaled version of the true concentration. The term ${SI}_h^B/{SI}_h^P$ is termed the quantification bias and depends on the T₂^* difference between the sample and the calibration phantom. Even in the absence of noise, f_Q (SI_[Na]brain)≠ [Na]_brain unless the T₂^* characteristics of the calibration phantom and the brain under study are identical.

The impact of T₂^*-decay on the quantification accuracy was evaluated by examining the quantification bias as a function of readout duration and T₂^* mismatch between brain parenchyma and CSF and the calibration phantom (9). The homogenous signal intensity for the calibration phantom with a mono-exponential T₂^* decay of 12 ms (T₂^* experimentally measured in the calibration phantom) was computed for each parameter set satisfying the T_TOTAL constraints of 4 min and 10 min used for the already described PSF and SNR simulation. A 10 × 10 × 10 cm³ cube was used to compute the homogenous signal intensities ${SI}_h^B$ and ${SI}_h^P$ for Equation [7].

Human Experiments

Sodium MR imaging was performed on healthy normal volunteers at 9.4 T and 3.0 T to demonstrate the impact of acquisition parameters on the true resolution. Human imaging was performed under IRB approved protocols requiring informed consent.

Ultra-high field quantitative sodium MR imaging was performed using a custom-built state-of-the-art 9.4 T MR scanner optimized for human brain imaging (7) and a custom-built quadrature birdcage RF coil tuned to 105.92 MHz. Since this scanner operates above the static magnetic field guideline for insignificant risk set by the United States Food and Drug Administration, the data were collected under an investigational device exemption (IDE). Previous safety evaluations of this MR scanner have revealed no irreversible adverse impact on human health (24,25). Imaging was performed for selected resolutions using the acquisition parameter sets A and B shown in Table 1. For each acquisition parameter set, complementary sodium acquisitions were made for B₀ and B₁ mapping as required for accurate and precise TSC measurement (9). Linear and B0 eddy currents were corrected using previously measured system constants (26).

Table 1.

Acquisition parameters for selected resolutions of human quantitative ²³Na imaging with flexTPI at 9.4 T and 3.0 T.

	B0 (T)	TTOTAL (min)	Matrix	FR	TADC (ms)	Nominal Resolution (mm)	True Resolution1 CSF (mm)	True Resolution1 Brain Parenchyma (mm)
A	9.4	10	44	0.603	2.3	5.00	7.66	7.88
B	9.4	10	76	0.203	27.3	2.89	4.67	5.66
C	3	4	44	0.239	10.5	5.00	7.74	8.65
D	3	4	56	0.148	34.4	3.93	6.32	8.00

¹FWHM of the point spread function

All acquisitions used ${\text{G}}_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ and symmetric k-space cone nesting. Acquisitions A and B were performed at 9.4T and used symmetric k-space cone nesting. Acquisitions C and D were performed at 3.0T and used equatorial k-space cone nesting and two averages (8 minutes to complete both averages).

High-field quantitative sodium imaging was performed using a clinical 3T whole-body scanner (HDx Signa, GE Healthcare, Waukesha, WI) and custom-built birdcage proton and sodium RF coils tuned to 127.8 MHz and 33.8 MHz, respectively. Sodium imaging was performed for selected resolutions using the acquisition parameter sets C and D in Table 1. For efficiency, B₀ mapping was performed at the proton frequency as described by Lu, et al (9) while B₁ mapping was completed using the sodium signal.

The 9.4T and 3.0T data were processed as described in (9) to compute B₀ and B₁ corrected TSC maps. All acquisitions were reconstructed and processed at their nominal voxel sizes. Acquisitions A and C were also reconstructed and processed with voxel sizes matched to acquisitions B and D, respectively. The TSC of white matter and CSF were measured for each acquisition reconstructed at its nominal resolution. White matter voxels were selected from the left and right hemispheres, above the ventricles and away from sulci to avoid bias due to partial volume contributions from CSF and tissue. Similarly, CSF voxels were chosen from within the ventricles but away from all edges. Since flexTPI is a true 3D acquisition the proximity of sulci and ventricle edges were considered in all three planes.

Results

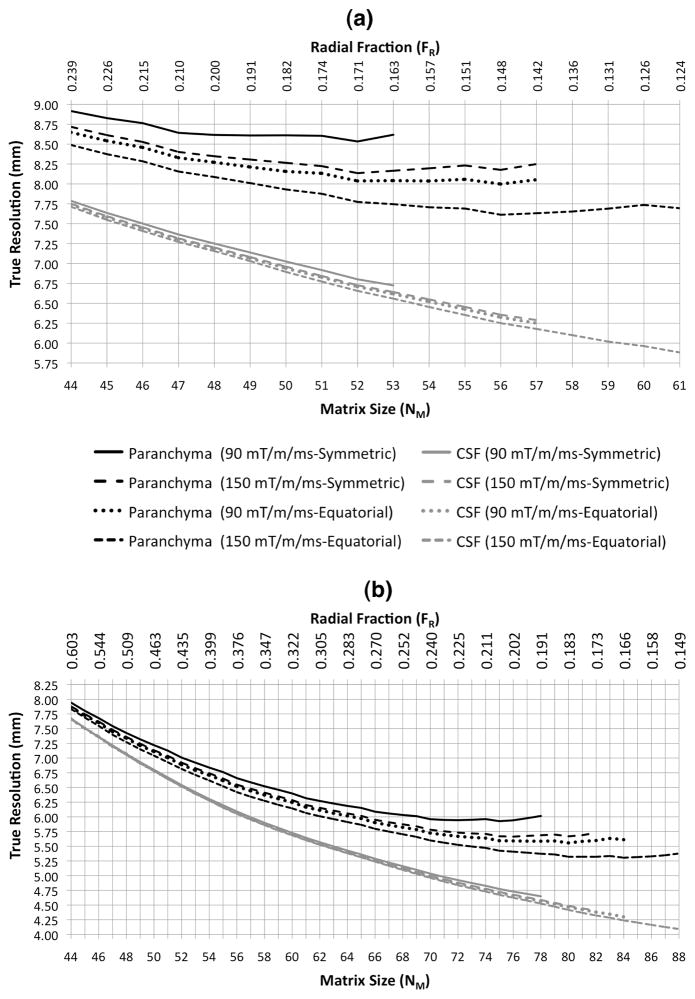
The true FWHM resolutions achieved for flexTPI with T_TOTAL = 4 and 10 min, respectively, are shown in Figure 6. Regardless of total acquisition time and acquisition parameters, the true resolution measured from the FWHM of the PSF is significantly lower than the nominal resolution. The true resolution achieved in brain parenchyma and CSF varies as T_TOTAL and (N_M, F_R) are changed. S_MAX and the cone-nesting scheme also impact the achievable resolution, although the dependence on these factors is most pronounced for T_TOTAL= 4min. Contrary to the conventional view of T₂-blurring, the true resolution of flexTPI generally improves as the readout duration is increased up to approximately 30–35 ms, provided that T_TOTAL is held constant. The exact acquisition parameters that maximize the resolution achieved for brain parenchyma depend on T_TOTAL, S_MAX, and the cone nesting scheme, but in each case there was an (N_M,F_R) pair that produced the optimal resolution in brain parenchyma.

Figure 6.

True resolution (measured as FWHM of simulated PSF) as a function of matrix size as achieved in either brain parenchyma or CSF for a flexTPI acquisition constrained to T_TOTAL = 4 (a) and 10 (b) minutes, respectively, for ${\text{G}}_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ and both the symmetric and equatorial patterns of k-space trajectories at two different slew rates (90 mT/m/ms, 150 mT/m/ms).

Table 2 shows the FWHM resolutions for flexTPI with $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ and G_MAX = 20 mT/m for F_R=1.0 (3-D PI). Increasing G_MAX from $G_{\mathit{MAX}}^{\mathit{Slew}}$ to 20 mT/m significantly reduced the readout duration but only slightly improved the resolution in CSF and brain parenchyma.

Table 2.

Parameters for simulation comparing resolution achieved for $G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ to G_MAX = 20 mT/m.

		$G_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$			GMAX = 20 mT/m
(FR, NM)	TTOTAL (min)	TADC (ms)	True Resolution1 CSF (mm)	True Resolution1 Brain Parenchyma (mm)	TADC (ms)	True Resolution1 CSF (mm)	True Resolution1 Brain Parenchyma (mm)
(1.0, 44)	16.5	1.66	7.59	7.73	0.53	7.58	7.62
(1.0, 63)	33.7	2.36	5.38	5.51	0.73	5.37	5.41
(1.0, 82)	57.0	3.06	4.15	4.28	0.92	4.14	4.18

¹FWHM of the point spread function

All three simulated acquisitions used symmetric cone nesting. These data suggest that the tinc function does not strictly limit resolution. For example, the true parenchymal resolution for (F_R,N_M)=(1.0, 44) is better than the 7.95 mm = 1.59 · 5 mm from the tinc function without any T₂-blurring. This is simply due the very short readout, leading to very little T₂-blurring, and the gridding reconstruction that results in gridded data that extends slightly beyond K_MAX.

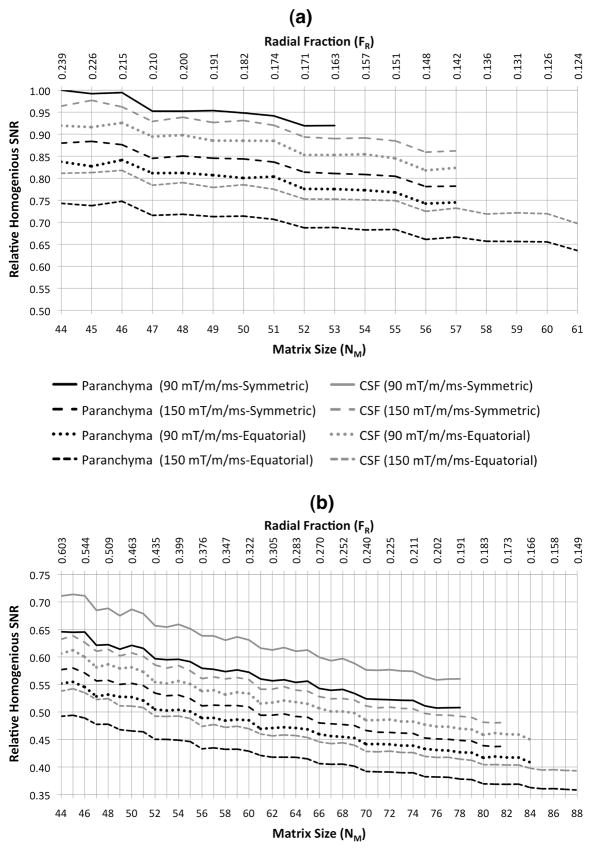
Figure 7 shows the relative SNRs achieved for flexTPI optimized for resolution with T_TOTAL = 4 and 10 min, respectively. The best SNR was achieved by the shortest total acquisition time.

Figure 7.

Relative homogenous SNR as a function of matrix size for flexTPI acquisition with T_TOTAL = 4 (a) and 10 (b) minutes, respectively. SNR values are relative to the homogenous SNR of tissue for T_TOTAL=4 min, N_M=44 and F_R=0.603. Results for ${\text{G}}_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ and both the symmetric and equatorial patterns of k-space trajectories at two different slew rates (90 mT/m/ms, 150 mT/m/ms) are shown.

The quantification bias for brain parenchyma and CSF did not vary substantially as a function of acquisition parameters. TSC of brain parenchyma was underreported by approximately 6.7 +/− 0.2 % across all acquisition parameters while CSF was overreported by 2.5 +/− 0.2 %.

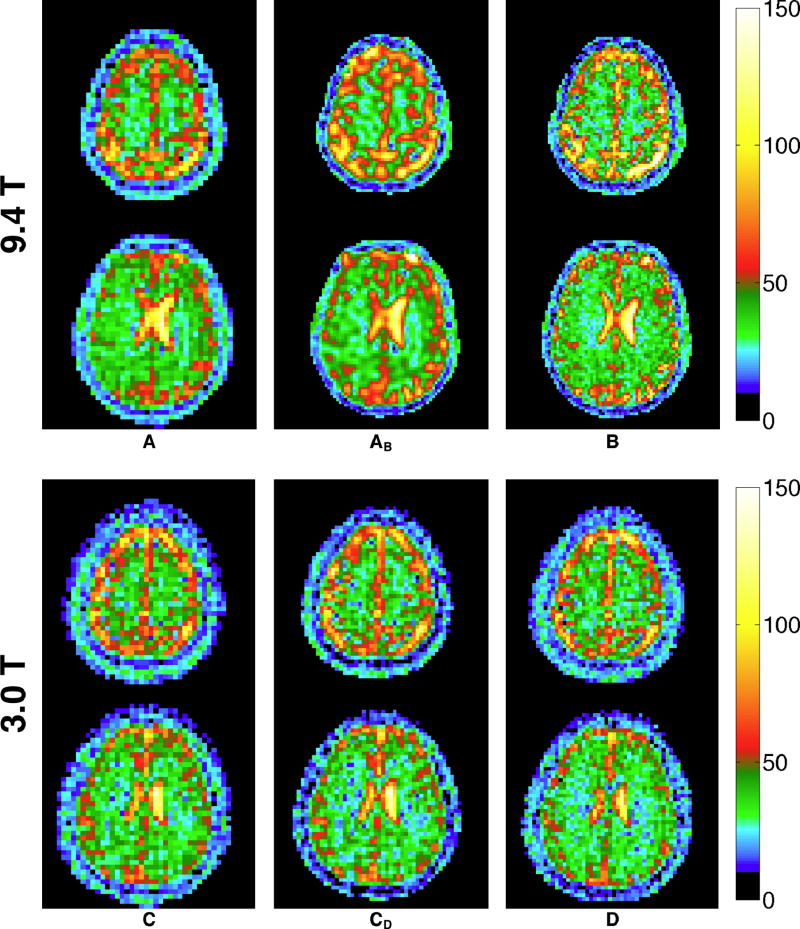
Figure 8 shows representative slices from the TSC bioscales from 9.4 T and 3.0 T acquired with the acquisition parameters in Table 1. In both cases, the short-readout acquisitions (Table 1, A and C) are included twice, first at the nominal acquisition resolution and again with voxels matching the nominal resolution of the resolution optimized acquisition parameters (Table 1, B and D). The resolution difference between the nominal resolution and optimized resolution acquisitions at 9.4T is very significant and easily appreciated visually. The longer readout duration results in significantly improved resolution in brain parenchyma (theoretically 5.66 mm vs 7.88 mm) while maintaining a total acquisition time of 10 min. The difference for TSC data from 3 T is not as striking, which is not surprising given the modest theoretical improvement (8.65 mm to 8.00 mm). The measured TSC values for white matter were 31.4 ± 5.6 mM (A), 30.7 ± 6.2 mM (B), 31.1 ± 6.9 mM (C), and 30.1 ± 7.0 mM (D), respectively. These values are in good agreement with the theoretical TSC of ~33 mM (9), that is reduced to ~30.8 mM by the −6.7% quantification bias found by the simulation. The sodium concentrations in CSF were 127.7 ± 4.6 mM (A), 141.5 ± 6.0 mM (B), 134.9 ± 15.3 mM (C), and 135.5 ± 10.4 mM (D), respectively.

Figure 8.

Two representative slices from quantitative TSC maps in mM acquired at 9.4T (top) and 3T (bottom) on the same subject using the acquisition parameter sets shown in Tables 1 and 2, respectively. Acquisitions A (top, left column) and B (top, right column) were reconstructed at voxel sizes equal to their nominal resolutions of 5 mm and 2.89 mm, respectively. Column A_B (top, center column) is the result of reconstructing acquisition A at the same voxel size as acquisition B. Both A and B have identical acquisition times of 10 minutes. Acquisition B has significantly improved resolution despite the longer readout duration (27.3 ms vs 2.3 ms). This matches the true resolution expected in CSF and brain parenchyma (see Table 1) determined from the PSF simulation. Acquisitions C (bottom, left column) and D (bottom, right column) were reconstructed at voxel sizes equal to their nominal resolutions of 5 mm and 3.92 mm, respectively. Column C_D (bottom, center column) is the result of reconstructing acquisition C at the same voxel size as acquisition D. Both C and D have identical acquisition times of 8 minutes (two averages of a 4-minute acquisition. Acquisition C theoretically has slightly improved resolution in brain parenchyma (8.00 mm vs 8.65 mm), although the difference is difficult to appreciate visually.

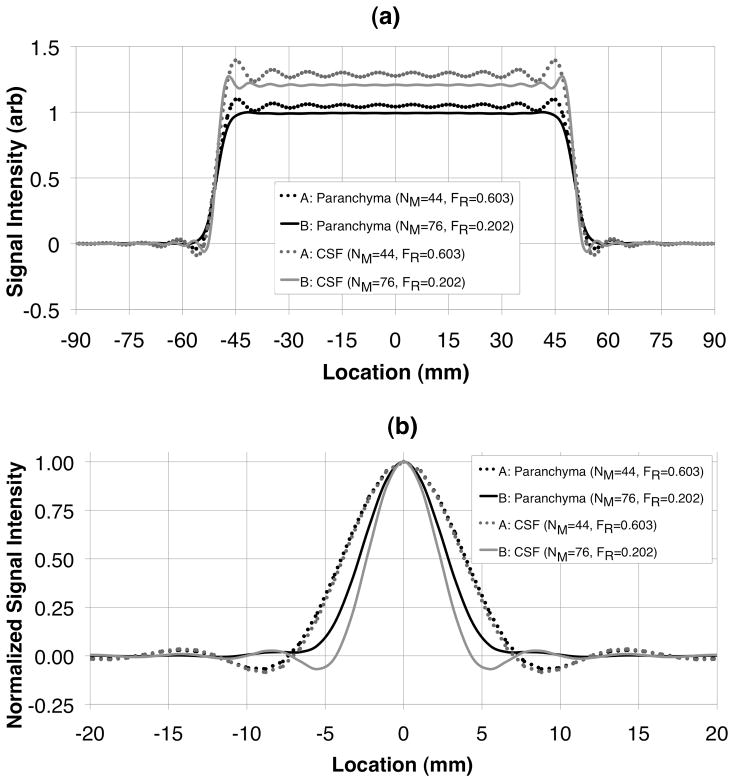
Figure 9 shows the PSF and object cross-sections simulated for acquisition parameter sets A and B for parenchyma and CSF, respectively.

Figure 9.

Cross-sections of simulated 10 cm cube object (a) and point-spread functions normalized to unit amplitude (b) for brain parenchyma and CSF for acquisition parameter sets A and B shown in Table 1. The long readout of acquisition B results in a better FWHM resolution and significantly reduced Gibbs ringing more than the short readout of acquisition A.

Discussion and Conclusion

The resolution and SNR of quantitative flexTPI for clinical ²³Na imaging depends on both acquisition parameters and the T₂* relaxation characteristics of the sample. It is not surprising that the best resolution can be achieved with the longest total acquisition time. However, for a fixed total acquisition time, the resolution can vary more than 30% in brain parenchyma and up to 40% in CSF by simply changing the acquisition parameters. In contrast to previously reported optimizations for short-T₂ species, the optimal true resolution for a fixed total acquisition time is not achieved with the shortest readout duration as has been shown with both simulation and human brain imaging. This non-intuitive result is due to the competing effects of the FWHM of the tinc function and T₂-blurring that combine to produce the overall spatial resolution of the final image. The impact of these two factors can be balanced for a flexTPI acquisition by simultaneously changing the effective matrix size and radial fraction so that the readout trajectory is modified but the total acquisition time remains fixed. Although the changes to (N_M,F_R) are done without modifying G_MAX or S_MAX, the readout duration changes significantly based on the amount of twist and maximum k-space radius required.

The necessary SNR of a TSC bioscale derived from quantitative sodium imaging depends on how the bioscale will be analyzed. Examining the TSC of individual voxels generally requires a higher SNR than interrogating a region of interest. For example, an SNR of 20:1 means that there is a ~0.68 probability (P) of a measured TSC value (TSC_M) in a single voxel falling within ±5% of the true value. For ±10%, the probability is ~0.95. That is, if the true TSC is 30 mM, P(28.5 mM < TSC_M < 31.5 mM) = ~0.68 and P(27 mM < TSC_M < 33 mM) = ~0.95. If the SNR were 10:1, these drop to P(28.5 mM < TSC_M < 31.5 mM) = ~0.38 and P(27 mM < TSC_M < 33 mM) = ~0.68. These values follow directly from the Gaussian approximation to noise in an MR image, which is valid once SNR > ~3:1 (27).

When flexTPI is optimized for resolution, the SNR in a homogenous region is approximately linearly proportional to the matrix size. Even though the nominal voxel volume is proportional to 1/N_M³, the homogenous SNR does not fall that rapidly due to the fact that the noise is proportional to (T_ADC×N_P)^(−1/2)and T_ADC is approximately a fifth-order function of N_M (see Figure 5 and (8)). Thus, the homogenous SNR for a fixed T_TOTAL becomes approximately proportional to 1/N_M^-1/2 as seen in Figure 7. Because of this, performing a T_TOTAL=10min resolution optimized acquisition at high field (e.g, 3 T) will result in a substantial decrease in SNR (approximately 60%—70% lower) compared to a T_TOTAL= 4min acquisition with 2 averages. Even with optimized hardware, the resultant SNR from a 10-min resolution optimized acquisition at 3 T is insufficient for quantification. To achieve a true resolution of less than 6 mm isotropic within a reasonable total acquisition time and with an SNR sufficient for robust quantification, imaging should be performed at ultra-high field. Based on the results presented in Figure 7, achieving sub-6 mm resolution at 3.0 T with an SNR equivalent to that of Acquisition C from Table 1 (see Figure 8) would require at least 4 averages, resulting in an unrealistically long total acquisition time of 40 minutes. The 9.4 T scanner used in this report represents current state-of-the-art in ultra-high field scanner technology and, therefore, provides the best means of achieving the highest true resolution for ²³Na data while maintaining an SNR suitable for robust quantification. Further improvements may be possible from parallel imaging (28) or phased-array (29) configurations not described in this report. For example, the improved SNR from a phased-array receiver may remedy the SNR issue at 3.0 Tesla, provided that the result remains quantitative. At any field strength, a higher resolution could be achieved by increasing the total acquisition time to allow more projections to be collected. However, acquisitions significantly longer than 10 minutes are likely to be tolerated by only the most cooperative and motivated subjects.

When optimizing flexTPI for resolution, the maximum gradient amplitude needed for imaging is dictated by the slew rate capabilities of the scanner as described by Equation [5]. Use of a larger gradient amplitude will have only very minimal impact on the readout duration when F_R < 0.5 but will result in longer gradient ramping times (since a higher G_MAX must be reached) during the radial portion of the trajectories and higher peak current being used to drive the gradient system. These factors may cause heating or additional torque forces, potentially shortening the longevity of the gradient system without any improvement in sodium imaging quality. In addition, the increased acoustic noise and potential for peripheral nerve stimulation may reduce the comfort of the participant. Given the cost of MR gradients and the importance of a positive patient experience, flexTPI has a significant benefit of making only compassionate demand on the gradients without compromising image quality.

For large F_R, choosing ${\text{G}}_{\text{MAX}}>G_{\mathit{MAX}}^{\mathit{Slew}}$ can significantly shorten the readout duration as the majority of the flexTPI trajectory is radial and not slew-rate limited. However, the actual resolution improvement from increasing from ${\text{G}}_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$ to G_MAX= 20 mT/m was found to be very modest (~2% for brain parenchyma and < 0.25% improvement for CSF) for symmetric cone nesting with F_R=1.0.

For moderate radial fractions (0.2< F_R < 0.5), the choice between k-space nesting schemes is largely irrelevant as both can achieve approximately the same resolution, SNR, and quantification bias provided ${\text{G}}_{\text{MAX}}=G_{\mathit{MAX}}^{\mathit{Slew}}$. Equatorial k-space nesting has a slight resolution benefit (e.g., parenchyma: ~ 5.30 mm vs 5.65 mm for T_TOTAL=10min) while the symmetric configuration results in higher homogenous SNR (e.g., parenchyma: ~0.46 vs ~0.37 for T_TOTAL =10min)

The CSF sodium concentrations measured experimentally (see Figure 8) were lower than the expected 144 mM. This was likely due to partial volume effects between CSF and tissue that dilute the measured TSC. Although voxels were selected from inside the ventricles, the wide PSF of tissue made it difficult to choose voxels that are pure CSF, especially at low resolution (e.g., acquisitions A, C, and D) where the ventricles are spanned by only a few voxels. At higher resolution (e.g., acquisition B), there are more voxels within the ventricles and the CSF measurement approached the expected value and the variance of CSF values accordingly dropped.

From the object and PSF cross-sections shown in Figure 9, an additional result of the optimization was observed. The k-space filtering that is common for proton MR imaging is largely unnecessary when imaging short T₂ species, such as ²³Na, with a resolution optimized acquisition. The rapid signal decay effectively windows the data and removes Gibbs-type artifacts. When reconstructed without any k-space filter, the short readout duration (parameter set A, T_ADC= 2.3 ms) shows the characteristic Gibbs artifacts due to the significant side-lobes of the PSF. However, when acquisition parameters B (T_ADC= 27.3 ms) are used, which result in higher spatial resolution with the same total acquisition time, virtually all Gibbs effects are suppressed in brain parenchyma. Windowing k-space data is unnecessary and would only further reduce the true resolution of the data.

In conclusion, quantitative ²³Na imaging with a flexTPI acquisition can be optimized for resolution within an acceptable clinical imaging time. Although T₂*-decay during data acquisition does result in resolution loss due to T₂-blurring, for a fixed total acquisition time, the optimal resolution is not achieved by the shortest readout duration.