Fourier-Bessel Reconstruction of Helical Assemblies

Abstract

Helical symmetry is commonly used for building macromolecular assemblies. Helical symmetry is naturally present in viruses and cytoskeletal filaments and also occurs during crystallization of isolated proteins, such as Ca-ATPase and the nicotinic acetyl choline receptor. Structure determination of helical assemblies by electron microscopy has a long history dating back to the original work on three-dimensional reconstruction. A helix offers distinct advantages for structure determination. Not only can one improve resolution by averaging across the constituent subunits, but each helical assembly provides multiple views of these subunits and thus provides a complete three-dimensional data set. This review focuses on Fourier methods of helical reconstruction, covering the theoretical background, a step-by-step guide to the process, and a practical example based on previous work with Ca-ATPase. Given recent results from helical reconstructions at atomic resolution and the development of graphical user interfaces to aid in the process, these methods are likely to continue to make an important contribution to the field of structural biology.

1. Introduction

The helix is a very utilitarian shape found in all walks of life. Everyday examples include a spring, a circular staircase and a barber pole. Likewise, biological organisms have adopted helices for a wide variety of tasks, ranging from a basic building block for macromolecular structures to higher order assemblies such as the placement of scales on a pine cone. The double-helical arrangement of bases in DNA is perhaps the most famous example, followed by the ubiquitous α-helix used as a structural element of many proteins. Filaments composing the cytoskeleton are composed of globular proteins that are themselves organized on a helical lattice, such as actin, microtubules and myosin. Similarly, extracellular fibers such as flagella and pili on the surface of bacteria and collagen in the extracellular matrix are all based on the helical assemblies of their constituent proteins. These examples demonstrate one of the most important properties of the helix, which is the construction of an extended, fibrous element from a single type of building block. The elastic properties of the fiber are determined by the geometry of the helix and the local interactions between the building blocks. Due to the ubiquity of this molecular design, a great deal of work has gone into understanding the basic geometrical properties of the helix and into developing algorithms for reconstructing the structure of relevant biological assemblies.

2. Basic Principles

2.1. Mathematical description of a helix

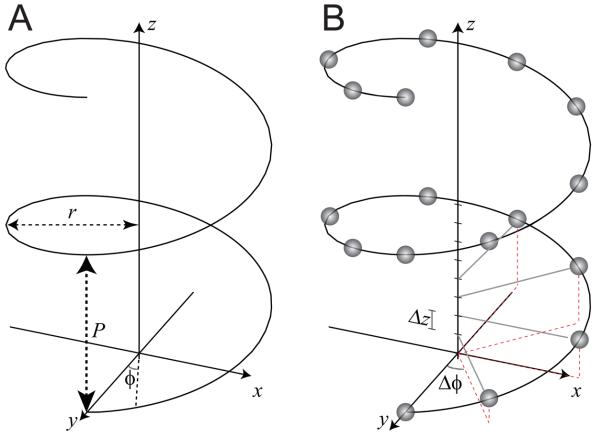
In Cartesian coordinates, a continuous helix can be defined by a set of three equations, x=rcos(2πz/P), y=rsin(2πz/P), z=z; these describe a circle in the x-y plane that gradually rises along the z axis (Fig. 1). The diagnostic parameters of the helix include the radius (r) and the repeat distance along the z axis, or pitch (P). In cylindrical coordinates, which are the most convenient way to describe a helix, these equations become r=r, ϕ=2πz/P, z=z. These equations describe a continuous helix, such as the continuous wire path of a spring (Fig. 1a), but biological assemblies generally involve a discontinuous helix, built with individual building blocks, or subunits, positioned at regular intervals along the helical path. These assemblies are characterized by the angular and axial interval between the subunits, Δϕ, and Δz, or alternatively are characterized by the number of subunits per turn of the helix. Although the helix in Fig. 1b has an integral number of subunits/turn (8), this parameter does not have to be integral, e.g., there are 3.6 amino acids per turn of an α-helix. Generally speaking, the structure repeats at some distance along z and the repeating element can be described as having u subunits in t turns, e.g., 18 subunits in 5 turns for the α-helix. From these values, the repeat distance (c) can be calculated as c = uΔz = tP.

Fig. 1.

Diagrams depicting the geometry of a helix. (A) A continuous helix is characterized by the pitch (P) and the radius (r) adopted by the spiral. Either a Cartesian coordinate system (x,y,z) or cylindrical coordinate system (r,φ,z) can be used. In either case, the z axis corresponds to the helical axis. (B) Helical assemblies are generally composed of identical subunits arranged along the path of a continuous helix. This requires additional parameters, Δφ and Δz, which describe the incremental translation and rotation between the subunits. This helix contains an exact repeat of 8 subunits in one turn, thus, Δφ=45°.

The relationship between a helical assembly and a 2D lattice is useful for understanding the process of 3D reconstruction. To construct a helical assembly, one starts by plotting a planar 2D lattice of points on a sheet of paper (Fig. 2a). To convert this planar lattice into a helix, a vector connecting two lattice points is designated as the “circumferential vector”; that is, a vector in the 2D plane that will be converted into an equator in the helical assembly (Fig. 2b). The sheet of paper is then rolled into a cylinder such that the lattice points at either end of the circumferential vector are superimposed. In 2D crystallography, unit cell vectors are arbitrarily assigned to the (1,0) and the (0,1) directions of the lattice. Based on these assignments, lines drawn through any series of lattice points can be assigned a so-called Miller index (h,k). The corresponding lattice planes produce discrete diffraction spots in the 2D Fourier transform of the lattice. After rolling the sheet into a cylinder, these lines become a family of helices spiraling around the helical axis at a constant radius. Because of the finite lateral extent of the helix, each family of helices crosses the equator (circumferential vector) an integral number of times, and this parameter is defined as the start number (n) of the helical family. DNA is called a double helix because the start number of its fundamental helix is two. The peptide bond of an α-helix generates a one-start helix. Generally, wider cylinders require larger values of n, e.g., a microtubule has13 protofilaments arranged in a 13-start helix. However, just as many different lines can be drawn through a 2D lattice, many different helical families are defined by a helical assembly. This situation is shown in Fig. 2, where the two sets of black lines drawn on the planar lattice can be assigned to the (1,0) and (0,1) lattice planes. Depending on the circumferential vector chosen, the (1,0) lattice planes give rise to 1-start or 4-start helices; the (0,1) lattice planes give rise to 8-start or 10-start helices. Note that the hand of the (1,0) helices is inverted in the two helical assemblies. By convention, left-handed helices have n<0 and, in this case, n=−4.

Figure 2.

Relationship between a planar 2D lattice and a helical assembly. (A) The 2D lattice is characterized by a regular array of points. An infinite variety of lines can be drawn through these points and each set of lines can be assigned a Miller index (h,k). For example, the black lines shown here could be assigned to the (1,0) and (0,1) directions. Two circumferential vectors are shown in green and red and these can be used to generate two unique helical structures shown in panel B. The dashed red and green lines are parallel to the z axes in the resulting helical structures. (B) Helical lattices result from superimposing lattice points on either end of the circumferential vectors shown in panel A. Each set of lines through the 2D lattice are transformed into a family of helices. The start number (n) of each helix corresponds to the number of lines that cross the circumferential vector. The red circumferential vector produces helices with n=1 and n=10. The green circumferential vector produces helices with n=−4 and n=8. For a left-handed helix, n<0.

2.2. Fourier transform of a helix

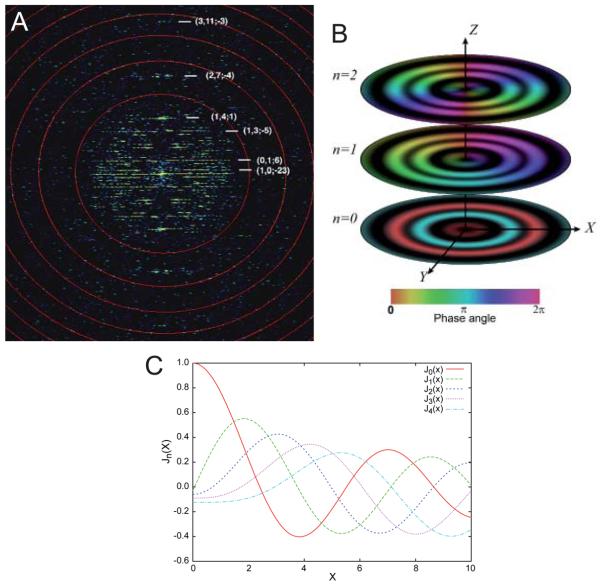
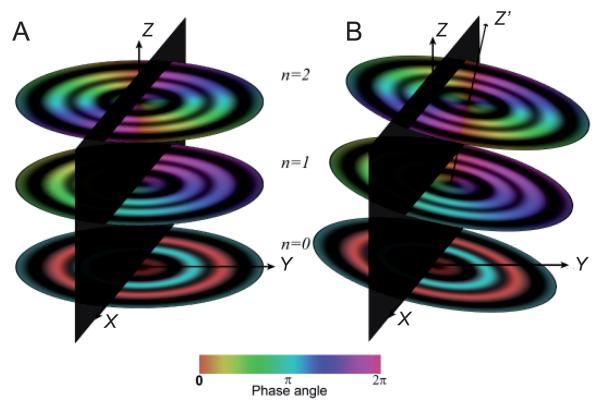
The mathematical derivation for the Fourier transform of a helix was initially described by Cochran et al. (1952) for understanding diffraction patterns from DNA and by Klug et al. (1958) for understanding fiber diffraction from tobacco mosaic virus. Application of these mathematics to electron microscopy was outlined by DeRosier and colleagues (DeRosier and Klug, 1968; DeRosier and Moore, 1970; DeRosier chapter in this volume) and the relevant formulas are presented in the Appendix. The derivation explains why the Fourier transform of a helical assembly (e.g., Fig. 3a) is characterized by a series of horizontal “layer lines”. These layer lines are analogous to the discrete reflections that characterize the Fourier transform of a 2D lattice, in that each layer line corresponds to one of the helical families discussed above, which in turn correspond to one set of lattice planes through the 2D lattice. Thus, each layer line can be assigned a Miller index (h,k). However, the δ function used to describe each reflection from an infinite 2D crystal is convoluted with a Bessel function (J_n(R)) to produce the corresponding layer line in the Fourier transform of a helix. This convolution is a direct consequence of the cylindrical shape of the helix; indeed, Bessel functions are also known as cylinder functions or cylindrical harmonics (Lebedev, 1972). The order, n, of the Bessel function appearing on a given layer line corresponds to the start number for the helical family that produced each layer line. Thus, if the (0,1) family of helices are 10-start, then the J₁₀(R) Bessel function appears on the corresponding layer line, where R represents the radial coordinate of Fourier space.

Fig. 3.

Fourier transform of a helical assembly. (A) The 2D Fourier transform from a Ca-ATPase helical tube (e.g., Fig. 5a) is characterized by discrete layer lines that run horizontally across the transform. Each layer line corresponds to a helical family (c.f., Fig. 2) and can be assigned a Miller index (h,k). The layer line running through the origin is called the equator and has a Miller index of (0,0). The vertical axis is called the meridian and the transform has mirror symmetry across the meridian. The start number of each helix (n) is shown next to each Miller index (h,k; n), and this start number determines the order of the Bessel function appearing on that layer line. The red circles indicate the zeros of the contrast transfer function and the highest layer line (3,11) corresponds to 10 Å resolution. (B) 3D distribution of three layer lines from a hypothetical helical assembly with Bessel orders of 0, 1, and 2, as indicated. The Z axis corresponds to the meridian, the X axis corresponds to the equator, and the Y axis is the imaging direction. Thus, the X-Z plane would be obtained by Fourier transformation of a projection image (e.g., panel A). The amplitude of the 3D Fourier transform is cylindrically symmetric about the meridian, but the phase (depicted by the color table at the bottom) oscillates azimuthally, depending on the Bessel order. Thus, the phase along the n=0 layer line (equator) remains constant; the phase along the n=1 layer line sweeps through one period and the phase along the n=2 layer line sweeps through two periods. (C) Amplitudes of Bessel functions with orders n=0-4. Note that as n increases, the position of the first maximum moves away from the origin.

Bessel functions are oscillating functions that appear in the integral used to express the Fourier transform in cylindrical coordinates (see the Appendix, Fig. 3c). Bessel functions generally have a value of zero at the origin and rise to a maximum at a distance corresponding to ~n+2. The zero-order Bessel function, which typifies the equator of all helices, is an exception in having its maximum at the origin. Thus, the order of the Bessel function appearing on a given layer line can be estimated from the radial position of its first maximum. This estimate is not precise because the values along the layer line are influenced by the Fourier transform of the molecules composing the helix, but it is a reasonable approximation and allows one to “index” the helical diffraction pattern. From a mathematical point of view, data along the layer lines is known as G_n,ℓ(R), where ℓ is the height of the layer line along the Z axis of the Fourier transform.

2.3. Advantages of helical symmetry for 3D reconstruction

Indexing simply means assigning the correct values of n to all of the layer lines composing the Fourier transform. Once accomplished, these indices allow one to calculate a 3D structure by applying an inverse Fourier-Bessel transform to the layer line data. This calculation is a two-step process. In the first step, the Fourier-Bessel transform is applied individually to data from each layer line (G_n,ℓ(R)) to produce a set of g_n,ℓ(r), where r is the radial component in a real space cylindrical coordinate system (see Appendix). The g_n,ℓ(r) are real-space functions that characterize the density wave along the direction of the corresponding helical families. By analogy, the Fourier transform of a single reflection from a planar, 2D lattice would characterize a plane wave along the corresponding direction in real-space. Unlike the situation with planar crystals where density remains in the plane, the helical crystals have cylindrical symmetry. Thus, the g_n,ℓ(r) spiral around the helical axis and by summing them all up, one is able to obtain a 3D structure: ρ(r,ϕ,z). Unlike 2D crystals that must be tilted to produce a 3D structure, full recovery of the 3D Fourier data set is possible from a single image of a helical assembly. This is a major advantage, as the tilting of planar structures inevitably leaves a missing cone of information and, furthermore, the logistics of imaging becomes increasingly difficult as the tilt angle rises (Walz chapter in this volume).

The availability of 3D information from a single projection image of a helical assembly can be appreciated by applying cylindrical symmetry to the layer lines that make up the 2D Fourier transform. Basically, the 3D Fourier transform can be generated by rotating the 2D transform around the helical axis. As the layer lines sweep around this axis, known as the meridian, the amplitude remains constant. This azimuthal invariance of the amplitude imparts mirror symmetry to the Fourier transform, which is an important characteristic in recognizing objects with helical symmetry. On the other hand, the phase varies as a function of the azimuthal angle. Specifically, the phase oscillates through an integral number of periods as the azimuthal angle in the Fourier transform (ψ) varies from 0 to 360°, with the number of periods traversed by a given layer line being equal to its Bessel order, n (Fig. 3b). This behavior explains why it is so important to correctly index the helical symmetry, as an incorrect assignment will completely scramble the phases of the Fourier data. This phase behavior also places an important constraint that aids indexing the Fourier transform of a helical assembly with unknown symmetry. In a projection image, the phases along a layer line on opposite sides of the meridian are constrained to differ by either 0° or 180°. Specifically, if n is even, the phase will have traversed an integral number of periods as it moves half-way around the meridian to the other side of the 2D Fourier transform (i.e., ψ=180°). On the other hand, if n is odd, this phase will be half a period out of sync and will therefore differ by 180°.

3. Step-by-step procedure for helical reconstruction

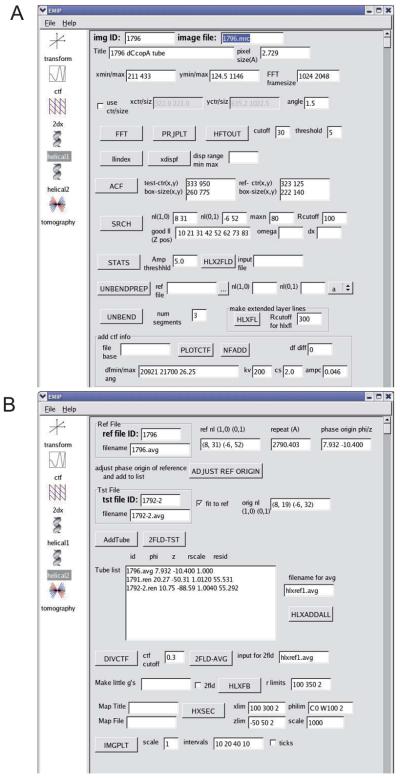
As with all methods of 3D reconstruction, there are many individual steps required for helical reconstruction and a variety of software packages have been developed to manipulate the images and perform the relevant calculations. In particular, the classic paper by DeRosier and Moore (1970) provided a theoretical background and outlined the basic steps provided by the software developed at the Medical Research Council Laboratory of Molecular Biology (the MRC package, Crowther et al., 1996)). This software has been updated and customized by a number of groups, including the DeRosier laboratory (Brandeis package, Owen et al., 1996), the Scripps Research Institute (Phoelix package, Whittaker et al., 1995), the Toyoshima laboratory (Yonekura et al., 2003b), the Kikkawa laboratory (Ruby-Helix package, Metlagel et al., 2007), the Unwin laboratory (Beroukhim and Unwin, 1997) among others. The steps described below represent Unwin's approach and have been implemented in our own Python-based graphical user interface called EMIP, which also provides a platform for a wide variety of image processing tasks, including 2D crystallography and tomography (Fig. 4).

Fig. 4.

Graphical user interface for helical reconstruction. This program (EMIP) collects information from the user and guides him/her through the various steps required for 3D reconstruction. Popup text provides information about each of the steps and a right-click on each button displays relevant log files. (A) Steps in processing individual tubes include masking, Fourier transformation, finding the repeat distance, searching for out-of-plane tilt, unbending and addition of CTF parameters. (B) Steps in averaging Fourier data together and calculation of the 3D map. This user interface was written in Python using the wxPython library for creation of graphical widgets and is available upon request.

3.1. Scanning the film image

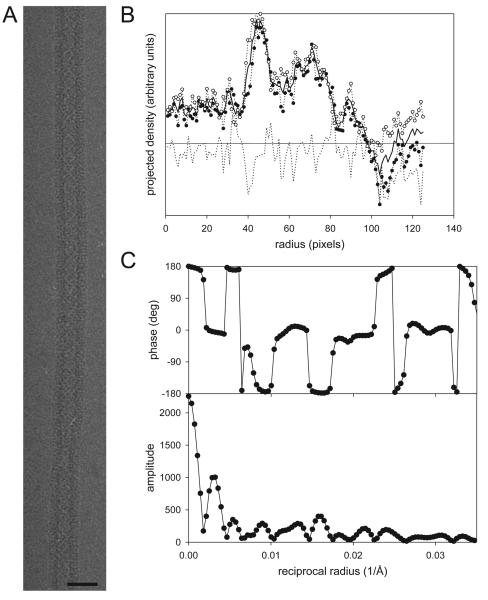
Conventionally, film has been the medium of choice for recording images of helical assemblies. This is because their filamentous shape has made it difficult to encompass an entire assembly with a sufficiently fine sampling interval within the frame of a digital camera. In particular, the membranous tubes produced by ordered arrays of membrane proteins can be very long (5-10 μm) and it is not possible to select a straight, well-ordered portion during low-dose imaging. If recorded on film, a relatively low magnification image can be .screened by optical diffraction and an optimal area can then be digitized with a high precision film scanner at a small sampling interval (e.g., 7 μm) with minimal degradation of the resolution (Henderson et al., 2007). In contrast, current CCD cameras not only have limited numbers of pixels, but the modulation transfer function is significantly worse than film (Sherman et al., 1996; Zhang et al., 2003). As large-format, direct detection digital cameras with better modulation transfer functions become available (Faruqi, 2009), they should also be suitable for imaging. In the meantime, the film should be rotated on the scanner such that the long axis of the helix is parallel to the scan axis (Fig 5a).

Fig. 5.

Masking and centering of an individual helical assembly. (A) An image of a helical tube of Ca-ATPase. Only the straightest part of the assembly would be used for reconstruction, i.e., the upper half. Scale bar corresponds to 60 nm. (B) Plot of density after projecting the image along the helical axis. The origin of the plot corresponds to the center of the tube and density from right (○) and left (●) sides have been plotted together with their average (solid line). The difference between the two sides is plotted as a broken line. The outer radius of this tube is ~115 pixels, which falls just outside the negative density ripple caused by the CTF. (C) Amplitude and phase data from the equator. The fact that phases are close to either 0° or 180° indicates that the tube is well centered.

3.2. Orient, mask and center the helix

Prior to calculating a Fourier transform, the boundaries of the helical assembly are defined in order to mask off peripheral material that would otherwise contribute only noise. The width of the mask should be slightly larger than the apparent width of the helical assembly; the length can be arbitrarily chosen, e.g., 1024 pixels. The masked edge should be apodized and the average density at the edge of the mask should be subtracted from the image in order to minimize Fourier artifacts from this potentially high contrast feature. For the Fourier transform, the box is padded to 512 pixels in the horizontal direction, producing an image with dimensions of 512×1024. The helical assembly must be centered and two alternate methods can be used. The first method involves calculating a projection of the helical assembly along the y axis and comparing the right and left sides of the resulting one-dimensional projection plot; if properly centered, the two sides will show minimal deviations from the average profile (Fig. 5b). This plot is also useful in measuring the radius of the tube, which will be important later. The second method involves examining phases along the equator of the Fourier transform. If properly centered, the equator should be real (Fig. 5c). If a phase gradient exists , the center should be shifted until it is minimized. Finally, the alignment of the helical axis with the scan raster of the image should be refined. This alignment involves an in-plane rotation, which can be evaluated both from the layer lines in the Fourier transform and from the projection plot. The equator and other layer lines that extend to a high radius should be inspected and the tube rotated until they remain aligned with the x axis of the Fourier transform. Also, the relief of the projection plot will be maximal when the helical axis is rotationally aligned.

Some software packages provide a facility for straightening curved helical assemblies (Metlagel et al., 2007). This is typically done by marking points along the helical axis and then using a polynomial fit to model the path of the axis. The image densities are then reinterpolated to straighten the helical assembly. For higher resolution analysis, bent assemblies are generally discarded as this bending most likely produces distortions in the subunits. However, if the radius of curvature is large relative to the repeat distance, then an “unbending” approach, discussed later, can be used to improve resolution.

3.3. Determine repeat distance and interpolate the image

In early work, helical assemblies were relatively short and produced layer lines that spanned multiple pixels in the axial direction of the Fourier transform. Therefore, a one-dimensional plot of the layer line data (G_n,ℓ(R)) was interpolated from the neighboring pixels in the Fourier transform (Bullitt et al., 1988). For longer, better ordered helical assemblies such as those from the nicotinic acetylcholine receptor (Toyoshima and Unwin, 1990) and Ca-ATPase (Toyoshima et al., 1993a), these layer lines were very narrow and, if they fell between the pixels in Fourier space, the observed amplitude was greatly diminished. The alternative of interpolating image densities was therefore developed, not only to align the helical axis with the sampling lattice, but also to ensure that an integral number of repeats was included in the image, thus producing layer lines lying precisely on a pixel in Fourier space. This repeat distance is determined by autocorrelation of a small segment of the helix at one end with the rest of the assembly. This autocorrelation inevitably produces many peaks, indicating the presence of approximate repeats at various sites along the length of the helix. This result reflects the fact that the helix frequently produces an approximate repeat when the azimuthal angle returns to the starting position. Depending on the angular interval of the subunits, some of these repeats are closer than others and an “exact” repeat may never be found within a reasonable length of a given assembly. However, interpolation of the image based on one of these approximate repeats is generally sufficient to place the layer lines very close to integral pixel values in the Fourier transform.

A problem can occur if the helical assembly has a very short repeat distance, such that multiple repeats (say 5) are included in a length of ~1024 pixels. In this case, layer lines are constrained to exist only on multiples of 5 pixels in the transform, creating a situation where layer lines with different Bessel orders fall at the same axial position in the transform. This situation should be avoided, because the corresponding Bessel functions will overlap and produce phase interference. Often, a different repeat distance can be chosen that will resolve this redundancy. From a practical point of view, once a repeat distance has been chosen, the image is stretched along the axial direction such that an integral number of repeats is contained within the fixed box size of the image (typically 2048 pixels). The precise positions of the layer lines depend on the particular repeat distance that has been selected and, because each assembly may be stretched differently, will not necessarily correlate from one image to the next.

3.4. Indexing of layer lines

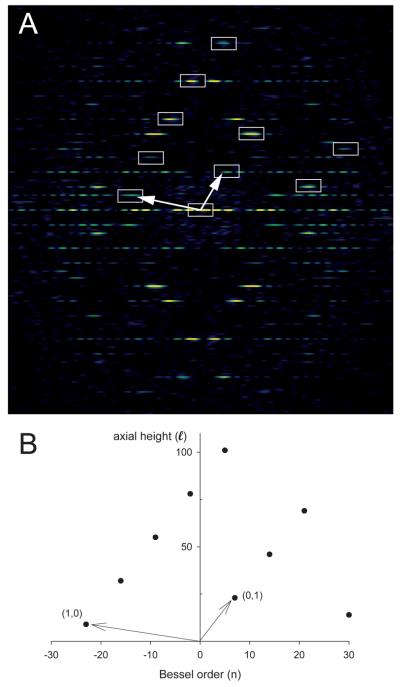
Indexing is perhaps the most vexing of the steps because of the lack of objective measures for verifying the correct answer. This process starts by assigning arbitrary Miller indices to the layer lines in order to define the unit cell, similar to the indexing of a planar, 2D crystal. However, the mirror symmetry in the Fourier transform of a helix creates an ambiguity in this assignment. This mirror symmetry can be thought of as representing two overlapping lattices from the near and far sides of the cylindrical structure. Thus, only one side of the layer line should be considered in the assignment of these Miller indices. In the example in Fig. 6, only the left side of the (1,0) and the right side of the (0,1) are relevant to the indexing. All the other layer lines will correspond to linear combinations of these primary layer lines, e.g., (1,1), (2,0), (1,2). If the (1,0) or (0,1) has been assigned to the wrong side of the meridian, then there will be inconsistency in the locations of the higher order layer lines. Note that although the axial positions of the layer lines fall exactly on the lattice, the radial locations are less exact due to the convolution of 2D lattice points with Bessel functions that extends these points in the radial direction.

Fig. 6.

Indexing of layer lines in the Fourier transform of a helical assembly. (A) Overlay of the near-side lattice on the Fourier transform of Ca-ATPase. (B) Corresponding plot of Bessel order (n) vs. layer line height (ℓ). Assignment of (1,0) and (0,1) layer lines is arbitrary, but once chosen then all of the other visible layer lines should be either a linear combination of these two, or a consequence of mm symmetry in the transform. The radial positions of the layer lines are distorted relative to a planar 2D lattice due to the behavior of Bessel functions, which have a non-linear relationship between the radial position of their first maximum and their order, n. Nevertheless, the axial positions of the layer lines should be accurate.

After assigning Miller indices, the Bessel order for each of the layer lines must be determined. For this process, it is essential to understand the argument of the Bessel function that characterizes the distribution of amplitude: J_n(2πrR), where r is the radius of the helical assembly in real-space and R is the radius along the layer line in Fourier-space. The location of the first maximum of J_n(X) is well established (Fig. 3c) and by noting the value of R for this maximum along a given layer line, one can use a measured value of r to estimate the corresponding value of n. For this estimate, it is wise to use the maximum real-space radius of the helical assembly determined from the projection plot (i.e., beyond the ripple from the contrast transfer function, Fig. 5) and the Fourier-space radius at which the layer line amplitude first starts to rise toward the first maximum. By creating a table containing the measured radii from several layer lines and the Bessel orders determined from the assigned Miller indices (e.g., the Bessel order for the (1,1) layer line is equal to the sum of Bessel orders from the (1,0) and (0,1) layer lines, Fig. 6b), one can strive to achieve an indexing scheme that produces the observed real-space radius of the assembly (Table 1). Higher order layer lines that lie close to the meridian represent important constraints to this procedure, because although the difference between n=−21 and n=−23 for a low-order (e.g. 1,0) layer line may not be distinguishable, the consequent differences to the higher-order layer line (e.g. n=0 or n=−2 for the (1,3)) may be definitive. EMIP aids in the construction of this table or, alternatively, a graphical software tool has been described by Ward et al. (2003) that directs the indexing process.

Table 1.

Indexing layer lines

Miller index (h,k)	Bessel order (n)	Measured Fourier- space radius (pixels−1)	Calculated Real- space radius (pixels)
1,0	−23	36	118.61
0,1	7	12	116.80
1,1	27	27	111.67
0,2	14	22	120.75
1,2	−9	14	125.72
0,3	21	34	115.04
1,3	−2	4	126.31
1,4	5	9	115.89

This indexing procedure leaves an ambiguity with regards to the hand of the structure. A positive Bessel order indicates that the corresponding family of helices are right-handed and the mirror symmetry in the Fourier transform is consistent with the opposite conclusion. In order to resolve this ambiguity, the most straight forward approach is to use rotary shadowing to view the top side of the helical assembly. Alternatively, one can tilt the sample in the electron microscope about an axis normal to the helical axis. At certain angles that depend on the pitch of the helix, this tilt will produce a scalloped appearance along one side of the helix, and a smooth appearance along the other side. As described by Finch (1972), the sense of the tilt and the hand of the helix determine whether the scalloped edge appears on the right or left side of the helical assembly.

3.5. Refine center and determine out-of-plane tilt

The helical axis does not necessarily lie precisely parallel to the imaging plane and the resulting out-of-plane tilt creates systematic shifts to layer line phases that must be taken into account. This situation is illustrated in Fig. 7, which shows how this tilt results in a sampling of the layer line at azimuthal angles (ψ) other than 0 and 180°. As shown in Fig. 3b, the azimuthal dependence of the phase depends on the Bessel function, so once the angle of out-of-plane tilt (Ω) is determined, a correction can be applied to each point along the layer line to recover the phase corresponding to Ω=0. The out-of-plane tilt is determined by comparing phases between the two sides of each layer line for a range of values for Ω. Because this phase relationship is also dependent on the centering of the helical assembly, both Ω and an x-shift (Δx) are refined together. This procedure relies heavily on the correct indexing of the helical symmetry and the magnitude of the phase residual can therefore be used to distinguish between two alternative indexing schemes. This distinction works best when there is a considerable amount of out-of-plane tilt (e.g. a few degrees), thus producing substantial differences in the phase correction on the higher order layer lines.

Fig. 7.

Out-of-plane tilt. These diagrams illustrate the relationship between the 3D Fourier transform and the central section that results from the projection along the viewing direction (Y). Due to this projection layer lines are sampled where they intersect the X-Z plane (black). (A) Untilted helical assembly where the helical axis is coincident with the Z axis of the transform and layer lines are sampled at azimuthal angles (ψ) equal to 0° and 180°. (B) Helical assembly that is tilted away from the viewing direction, causing sampling of layer lines at ψ≠0° and 180°. Z′ corresponds to the helical axis and the angle between Z′ and Z corresponds to the out-of-plane tilt, Ω. This tilt produces systematic phase shifts that are dependent on the order of the Bessel function along each layer line.

3.6. Extract layer line data and calculate phase statistics

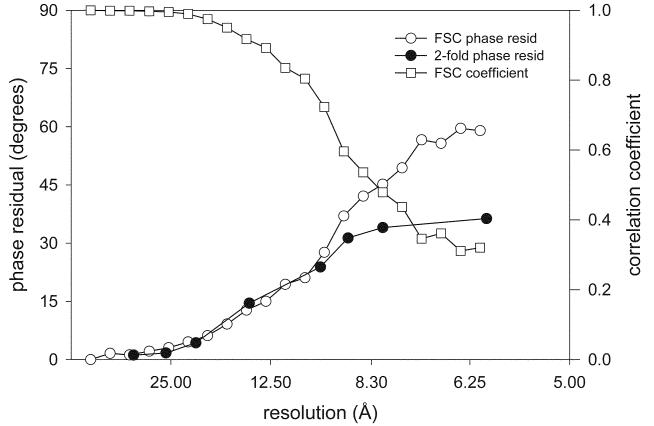
After establishing the helical symmetry and the amount of out-of-plane tilt, amplitude and phase data is extracted along each of the layer lines, producing a list of G_n,ℓ(R). Two redundant sets of data are produced, which are referred to as the near and the far side of the helical assembly and which reflect the two alternative 2D lattices identified during indexing. Phase statistics from this dataset provide a useful measure of the quality of the data. If no symmetry exists, then a simple comparison of near and far data can produce a resolution-dependent phase residual. Two-fold symmetry is common, in which case the near and far data sets are averaged and the two-fold related phase error is plotted as a function of resolution (Fig 10).

Fig. 10.

Evaluation of the resolution of a helical reconstruction. Both the Fourier Shell Coefficient (FSC) and the Fourier Shell phase residual result from comparing masked and aligned molecules obtained from independent halves of the data set. The two-fold phase residual is calculated from averaged G_n,ℓ(R) derived from the entire data set. A two-fold phase residual of 45° is random, whereas a Fourier Shell phase residual of 90° is random. Data reproduced from Xu et al. (2002).

3.7. Determine defocus and apply the contrast transfer function

The contrast transfer function (CTF) of the electron microscope effectively multiplies the Fourier transform by an oscillating function that depends on defocus and the spherical aberration coefficient of the objective lens (Erickson and Klug, 1971). This effect must be corrected, not only because of the aberrations that it produces in the 3D reconstruction, but also because different levels of defocus will alter the period of oscillation and produce destructive interference if uncorrected images are averaged together. Indeed, the accuracy of the correction is critical for recovering high resolution information, because the frequency of the oscillations increase with resolution. A number of excellent programs are available for determining the defocus and astigmatism of an image, such as CTFFIND3 (Mindell and Grigorieff, 2003), PLTCTFX (Tani et al., 1996) and many others (Fernando and Fuller, 2007; Huang et al., 2003; Mallick et al., 2005; Velazquez-Muriel et al., 2003). Once values for the defocus and astigmatism have been determined, the phases along the layer lines are adjusted to eliminate the reversals that characterize the CTF and the amplitudes are multiplied by the magnitude of the CTF to differentially weight data from different images during averaging (Penczek chapter in this volume). These CTF corrections are applied independently to the near and far data sets in order to compensate for astigmatism in the image. Once the CTF corrections are applied, the near and far data sets are averaged to create the final data set for combining with other images.

3.8. Averaging data from multiple images

In order to average data from multiple images in Fourier space, all of the helical assemblies must have the same symmetry. This means that the Bessel orders from all of the corresponding layer lines must be the same. However, layer lines from the various images do not necessarily lie at the same axial positions, because variations in the axial repeat distance cause the layer lines to fall at different axial heights. Ideally, these differences simply reflect a linear scale factor along the helical axis due to the interpolation of images during masking, but in reality, slight distortions in the unit cell cause the layer lines to move slightly with respect to one another. A similar situation occurs with planar, 2D crystals, where the unit cell dimensions and included angle are somewhat variability. As long as this variability is small, the data can be averaged together without significantly reducing the resolution of the reconstruction (Toyoshima and Unwin, 1990).

Prior to averaging, the axial coordinates (ℓ) of each layer line are simply renumbered to match the reference data set and a common phase origin must be found. If two-fold symmetry is present, then the phase origin of a reference image (i.e. the best of the group) is constrained to one of the two-fold axes and the phase origins of the other images are adjusted to match the reference. An amplitude-weighted sum of the CTF-weighted data from all the images can then be produced, together with the sum of the CTF weights. After dividing these averaged amplitudes by the summed CTF weights, this data is suitable for calculating a 3D reconstruction (see below).

3.9. Correcting distortions in the helical assembly (unbending)

As mentioned, one approach to straightening helical assemblies has been to fit a polynomial curve to the helical axis and then to reinterpolate image densities to produce a straighter structure prior to calculating the initial Fourier transform. When combined with cross-correlation to determine the position of the helical axis (Metlagel et al., 2007), this method is analogous to the unbending procedure used for planar 2D crystals (Henderson et al., 1986). Both of these methods compensate for in-plane translation of image densities away from their ideal positions and thus significantly improve the resolution of Fourier data that are then used for 3D reconstruction. However, neither of these approaches considers out-of-plane bending nor more subtle distortions such as stretching in the axial or radial directions. A more sophisticated approach was developed by Bekhouim and Unwin (1997) for their high resolution studies of the helical tubes of acetylcholine receptor. For this method, in-plane and out-of-plane tilt, translation, radial and axial scale factors (stretch) are determined for short segments of the tube. Some of these parameters are determined solely from phase relationships along the layer lines. Other parameters involve comparison of data from the individual segments with reference data produced by averaging together a number of images. The fundamental limitation to the length of the segments is the signal-to-noise ratio that they produce, which must be high enough to allow reliable alignment. Helical assemblies of acetylcholine receptor are ~700 Å in diameter with a wall thickness of ~100 Å, similar to assemblies of Ca-ATPase. In these cases, segments of ~600 Å in length represent the minimum that can be used for this unbending procedure. This places a limit on the range of disorder that can be compensated and continues to require selection of extremely straight or only very slightly bent assemblies. Also, during unbending, data is cut off at the first maximum of the CTF in order to assure maximal reliability of the orientational data, specifically by maximizing signal-to-noise ratio and eliminating the nodes of the CTF. Even though this resolution cutoff limits the precision of the alignments, this precision far exceeds the nominal resolution of the data used for the fits (e.g. 15 Å). This unbending involves many iterative steps of alignment, reboxing and realignment, which have been tied together by a series of scripts, all of which are controlled by the EMIP user interface. Using this strategy on a large number of images, Unwin was able to extend the resolution of the acetylcholine receptor to 4 Å resolution (Miyazawa et al., 2003); Yonekura et al. achieved a similar resolution for bacterial flagella (Yonekura et al., 2003a) and a Ca-ATPase structure was determined at 6.5 Å resolution (Xu et al., 2002).

3.10. Create final averaged data set and correct CTF

The unbending procedure produces data sets for the near and far sides of the individual images that have been weighted by the CTF. Similar to the averaging step above, these near and far data sets (and their respective weights) should be added together to produce an average for each tube, and these should be added together to produce a final averaged data set. The CTF is then corrected by dividing each point along each layer line by the combined sum of the CTF²: the first CTF factor coming from the image formation by the microscope and the second factor from the weight that was applied during the image processing. However, care should be taken in applying this correction to the equatorial data. In particular, the magnitude of the CTF approaches zero at the origin, thus generating very large correction factors for the low resolution amplitudes along the equator. The proportion of amplitude contrast produced by the specimen will greatly influence this correction near the origin, and although Toyoshima has determined the appropriate factor for the acetylcholine receptor (Toyoshima and Unwin, 1988; Toyoshima et al., 1993b), some ambiguity exists for other samples. In most cases, it is necessary to carefully consider the correction applied to the low resolution values along the equator. This is because these values have a large influence over the radial distribution of mass in the final 3D reconstruction. Incorrect handling of the equatorial correction can produce a distorted molecule where, for example, the transmembrane domain is exaggerated relative to the cytoplasmic domain, or visa versa (Fig. 8). One approach is to limit the maximum correction that can be applied along this equator, or to prevent correction to the very lowest resolution terms on the equator. This issue is best handled by trial and error at the very last stages of map calculation.

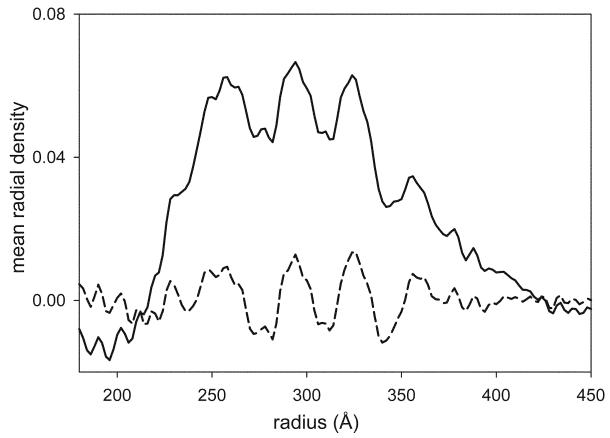
Fig. 8.

Mean radial density distribution derived from the equator of an averaged data set. The solid line corresponds to data that has been appropriately corrected for the CTF, thus producing positive density at radii between 225 and 400 Å. For the dashed line, the CTF correction was limited along the equator. Although the structure at any given radius is unchanged, the overall distribution of mass is dramatically affected, making it impossible to render the molecular surface based on a single density threshold (c.f., Fig. 9c).

3.11. Map calculation and display

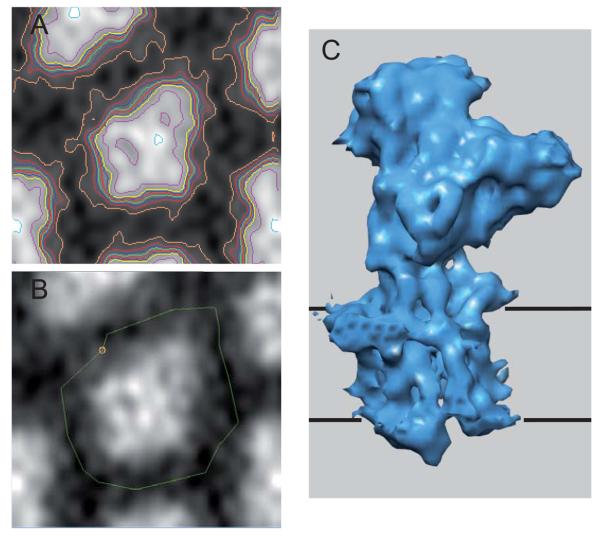
Once an averaged and CTF-corrected data set has been produced, calculation of the 3D map is a two-step operation. The first step involves a Fourier-Bessel transform that converts the Fourier-space layer line data (G_n,ℓ(R)), into real-space density waves (g_n,ℓ(r)). The second step involves summing up these g_n,ℓ(R) functions over the range of r, φ and z required for the final density map (see Appendix). Conventionally, the 3D maps were displayed as a stack of contour plots and programs exist for cutting sections both parallel to and perpendicular to the helical axis. Such contour plots can still be useful in understanding the composition of the asymmetric unit and in delineating individual molecules (Fig. 9). In particular, an individual molecule, or multimer, can be masked from the helical lattice by using IMOD (Kremer et al., 1996). Ultimately, the masked molecules should be rendered as an isodensity surface using a program like Chimera (Pettersen et al., 2004). Such programs also facilitate fitting atomic models to the density, which is a great aid in interpretation and presentation of the structure.

Fig. 9.

Fourier-Bessel reconstruction of Ca-ATPase. (A) Section from the reconstruction with contours superimposed on the densities. Evaluation of contour maps can be useful in delineating the individual molecules composing the structure. (B) Masking of a single molecule from the map, which is useful both for real-space averaging and for display. (C) Surface representation of a single molecule of Ca-ATPase defined by density threshold. The black, horizontal lines correspond to the boundaries of the membrane. In this case, this density threshold corresponds to a volume recovery of ~75% of the expected molecular mass. IMOD (Kremer et al., 1996) was used for panels A and B, and Chimera (Pettersen et al., 2004) was used for panel C.

4. Case Study of Helical Reconstruction of Ca-ATPase

Ca-ATPase is anATP-dependent Ca²⁺ pump found in the sarcoplasmic reticulum and endoplasmic reticulum. Due to its abundance in striated muscle, it has been extensively characterized by biochemical and biophysical methods (Moller et al., 2005). Ca-ATPase in skeletal muscle has a propensity to form 2D crystals within the native membrane (Franzini-Armstrong et al., 1986) and these crystals were studied extensively by electron microscopy in the 1980's and 1990's (Castellani et al., 1985; Dux and Martonosi, 1983; Taylor et al., 1986; Toyoshima et al., 1993a; Zhang et al., 1998). In particular, small vesicles from isolated sarcoplasmic reticulum or from purified, reconstituted Ca-ATPase preparations display 2D lattices predominantly at their highly curved edges. Under the right conditions, Ca-ATPase forms long helical tubes with a diameter of 600-800 Å (Fig. 5. See also chapter by Young in this volume). These lattices are composed of Ca-ATPase dimers that are oriented asymmetrically in the membrane and the intermolecular distance between the cytoplasmic domains on one side of the membrane is greater than the corresponding distance between the luminal domains on the other side of the membrane, thus inducing curvature (Young et al., 1997).

4.1. Variable helical symmetry

Although the diameter of a given tube is generally constant along its length, this diameter is variable from one tube to the next; this variability reflects differences in the helical symmetry adopted by different tubes. For 3D reconstruction, the thinnest tubes were chosen in order to constrain the range of helical symmetries to be analyzed. Even from the thinnest tubes, a series of related, but different symmetries were obtained, which can be characterized by the Bessel orders of the (1,0) and (0,1) layer lines (e.g., −23,6 in Fig. 3). Specifically, tubes with symmetries ranging from (−19,6) to (−27,9) have been used for various 3D reconstructions (Xu et al., 2002; Young et al., 2001a; Young et al., 2001b; Zhang et al., 1998). The underlying unit cell appears to be relatively well conserved in all of these cases and the differing symmetry simply involves use of a different circumferential vector in generating the helical assembly. Inspection of Fig. 2 indicates that the longer circumferential vectors required to generate the larger Bessel orders are strictly correlated with larger diameters of the resulting tubes. In fact, once the basic helical symmetry is understood, simple measurement of the tube diameter using for example the projection plot in Fig. 5, gives a good estimate of the helical symmetry. Any remaining ambiguities can be resolved by checking the even/odd character of the Bessel orders on key layer lines.

4.2. Real-space averaging of different helical symmetries

Well ordered tubes frequently produced visible layer lines at 15 Å resolution and, in exceptional cases a layer line was visible at 10 Å resolution (Fig. 3). Averaging is essential not only for filling in the nodes of the CTF, but also for improving the signal-to-noise ratio at high resolution. By averaging together as few as 12 individual tubes from a single symmetry group, it has been possible to obtain better than 8 Å resolution (Stokes et al., 2005). For higher resolution, structures from multiple symmetry groups were averaged together in real space. For this process, software developed by Toyoshima and colleagues (Yonekura et al., 1997) was used to mask off a single unit cell and then to divide this unit cell in half, which effectively separated the two monomers composing the asymmetric unit. The mean radial density distribution was used to adjust the magnification of the reconstruction and cross-correlation was then used to independently align each of the two monomers from reconstructions of several different symmetry groups (e.g., the −19,6; −20,6; −21,6; −22,6; −23,6 symmetries in Xu et al. (2002)). After averaging the masked monomers, a hybrid unit cell was created. An inverse Fourier-Bessel transform was then calculated to produce a set of layer line data (G_n,ℓ (R)) conforming to the symmetry of the reference data set. Examination of the two-fold related phase residuals revealed a substantial improvement in resolution to 6.5 Å from a total of 70 tubes (Xu et al., 2002). Unwin and colleagues took a similar approach in averaging tubes of acetylcholine receptor with various symmetries (Miyazawa 2003). In this case, 359 tubes falling into 4 different symmetry groups (−16,6; −17,5; −15,7; −18;6) were averaged together. The cylindrical shape of the acetylcholine molecule made it relatively easy to construct a mask around a single pentameric molecule, which was then used for alignment and averaging. The final resolution of 4 Å was verified by dividing the images into two equal halves and calculating an amplitude-weighted phase difference as well as a Fourier shell correlation coefficient.

4.3. Difference maps

A similar strategy of comparing masked molecules in real space has also been used for calculating difference maps from Ca-ATPase crystallized in the presence of various ligands. In particular, the location of the inhibitor thapsigargin (Young et al., 2001a) and of the regulatory protein phospholamban (Young et al., 2001b) was investigated in this way. In addition to aligning the two structures in real space, it was important to optimize the density scaling to minimize the background level of density differences. In order to evaluate the statistical significance of the differences, it is possible to conduct a pixel-by-pixel Student's T-test (Milligan and Flicker, 1987; Yonekura et al., 1997). This involves calculating maps for each of the individual tubes used for the two reconstructions. From these individual maps, a standard deviation can be calculated for each voxel in the averaged reconstruction, which can then be used in calculation of the T statistic. This procedure becomes more complicated when using CTF weighting and real-space averaging. Therefore, in more recent studies, an empirical σ value was used to characterize the significance of the differences, based solely on the Gaussian distribution of densities in the difference map.

4.4. Alternative real-space averaging of g_n,ℓ (r) of different helical symmetries

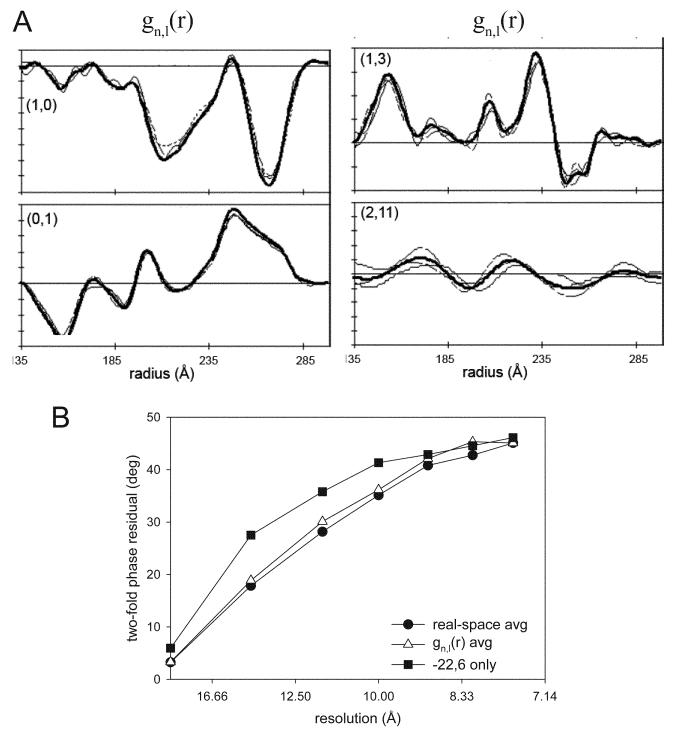
An alternative method for averaging data from different symmetry groups involves the averaging of g_n,ℓ(r) functions rather than the density maps themselves (DeRosier et al., 1999). Although not widely adopted, this elegant method is simpler and more analytically correct than the real space method described above, because it doesn't require the subjective step of masking individual molecules from the maps. The method is based on the fundamental concept that g_n,ℓ(r) functions are derived from individual layer lines and that they correspond directly to F_h,k(r), which are the Fourier coefficients derived from the underlying, planar 2D lattice (Fig. 2). In particular, both g_n,ℓ(r) and F_h,k(r) come from a specific set of planes through this lattice. As long as the molecular packing and geometry of the unit cell is preserved in the different helical symmetries, the different g_n,ℓ(r) derived from particular (h,k) planes can be directly averaged together. Thereafter, the averaged g_n,ℓ(r) can be used to create a 3D map. There are two alignments necessary before averaging g_n,ℓ(r); first is a shift in radius, which reflects the fact that the different symmetries produce helical tubes of different radii. Second, the g_n,ℓ(r) must be adjusted to a common phase origin (e.g. a specific two-fold symmetry axis). These methods were tested on Ca-ATPase tubes from 3 different symmetries and resolution-dependent phase residuals indicate that the improvements in resolution for g_n,ℓ(r) averaging were almost identical to those for real-space averaging (Fig. 11).

Fig. 11.

Averaging of g_n,ℓ(r) from helical assemblies of Ca-ATPase. (A) After alignment, amplitudes from three different symmetry groups are shown (thin, dashed lines), together with the average (thick solid line). (B) Two-fold phase residuals are compared for the Fourier space average from a single symmetry group (−22,6, ■), for the real-space average of the three symmetry groups (●), and for the averaged of g_n,ℓ(r) from these same three symmetry groups (△). The improvements obtained by averaging g_n,ℓ(r) are comparable to those obtained by real-space averaging. Data reproduced from DeRosier et al. (1999).

4.5. Comparison with the Iterative Helical Real-Space Reconstruction method

An alternative to Fourier-Bessel reconstruction of helical assemblies has been developed by Egelman and colleagues and termed the Iterative Helical Real-Space Reconstruction (IHRSR) method (Egelman, 2000, chapter by Egelman in this volume). Initially developed for flexible assemblies of DNA binding proteins (Yu et al., 2001), IHRSR has been used with success for a broad range of structures, including bacterial pili (Mu et al., 2002), actin (Galkin et al., 2003), myosin (Woodhead et al., 2005), and dynamin (Chen et al., 2004). The method is based on matching short segments from the image of a helical assembly to a series of projections from a model using the SPIDER software suite (Frank et al., 1996) in a manner analogous to the single particle analysis of isolated macromolecular complexes. The segments are typically much shorter than for Unwin's unbending methods discussed above and IHRSR is therefore able to compensate for shorter-range disorder. Furthermore, indexing of the layer lines in the Fourier transform is unnecessary, though knowledge of Δφ and Δz for the smallest pitch helix is generally required. Specifically, after using projection matching to determine the relative orientations of all the individual segments along the helical assembly, a 3D structure is generated by backprojection. The helical symmetry of this 3D structure is then determined empirically by examining auto-correlation coefficients after systematically rotating and translating the structure about its helical axis. Once helical parameters (Δϕ and Δz) are determined, the structure is symmetrized and used for the next round of alignment and projection matching.

When applied to images of Ca-ATPase and the related Na,K-ATPase, IHRSR generated a plausible 3D structure, but the resolution-dependent phase residuals were not as good as Fourier-Bessel reconstructions (Pomfret et al., 2007). This was attributed to the fact that Fourier-Bessel reconstruction excludes data that lie between the layer lines, thus filtering out a large amount of noise from the reconstruction and allowing more accurate alignments. On the other hand, IHRSR successfully generated a 3D structure of Ca-ATPase from scallop muscle when Fourier-Bessel methods failed, because these helical tubes were too poorly ordered to successfully complete the necessary alignments based on layer line data. Related real-space methods have been used for very high resolution reconstructions of tobacco mosaic virus, illustrating that if the helical symmetry is well determined and the helical assembly is well ordered, the real-space methods represents a viable alternative to the more conventional Fourier-Bessel analysis (Sachse et al., 2007). However, bacterial flagella are another well ordered helical assembly and it is notable that a Fourier-Bessel reconstruction at 4 Å resolution was reported from only 102 images, comprising ~41000 molecules of the building block, flagellin (Yonekura et al., 2003a). This is a remarkable achievement especially considering the small size of the flagellin molecule (<500 residues). The authors attributed this success to a number of factors, including the high quality of the images, the strict order of molecules in the flagellar filament, and innovative software techniques such as solvent flattening to remove noise from the maps during alignment of individual filaments (Yonekura et al., 2005). Another important factor was the use of optical diffraction to objectively pick the very best helical assemblies for image processing. Specifically, the presence of sharp layer lines extending to high resolution represents a relatively easy basis for selecting the best 60 images from a pool of >1000; the fact that these images came from one of the world's best electron microscopes also improved the odds for a high resolution structure.

5. Conclusions

3D reconstruction of helical assemblies continues to be an important application for electron microscopists. Not only are helical assemblies ubiquitous in nature, but these methods offer advantages for producing a 3D structure. First, the ability to form a regular structure means that individual molecules are likely to adopt a fixed conformation, thus greatly reducing the structural heterogeneity that plagues single particle approaches. Second, the cylindrical symmetry of the helix ensures that all the necessary views of the molecule are present in a single image, thus eliminating the missing cone of information that produces anisotropic resolution in electron crystallography of planar 2D crystals. These advantages have been illustrated by high resolution structures of acetylcholine receptor and bacterial flagella, as well as a medium resolution structure of Ca-ATPase. Additional considerations include the large computational resources that are required for single particle approaches and the potential for combining amplitudes from fiber diffraction with phases derived by the helical reconstruction methods described here. Historically, there has been great variety in the software approaches to Fourier-Bessel reconstructions, making it difficult for a novice to undertake the process of structure determination. However, graphical user interfaces have been recently developed to guide the user through the many complex steps of helical reconstruction, making this process approachable (Yonekura et al., 2003b). Thus, development of biochemical methods to generate ordered helical assemblies, for example during the 2D crystallization of membrane proteins, may be an important area of future development (chapter by Wilson-Kubalek in this volume).

APPENDIX: MATHEMATICAL FOUNDATIONS OF FOURIER-BASED HELICAL RECONSTRUCTION

Definition 1. For an integrable, complex valued function of a real variable (f ∈ C^R), the Fourier transform is defined as

$$\widehat{f}\left(t\right)=F\left[f\right]\left(t\right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f\left(x\right)e^{2\pi \mathit{ixt}}\mathit{dx}.$$

In three dimensions, the scalar domain of the functions becomes a scalar vector product in Euclidean space, and then we have

$$\widehat{f}\left(\mathbf{X}\right)=F\left[f(\mathbf{x}\right]\left(\mathbf{X}\right)=\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}}{\int \int \int }_{{\mathbf{R}}^3}f\left(\mathbf{x}\right)e^{2\pi i\mathbf{x}\cdot \mathbf{X}}{d}^{3}x.$$ (1)

Fourier transform in cylindrical coordinates

A helix is a curve in three-dimensional space, defined in parametric form as a function f : (R³)^R, such that f(t) = (rcos(t), rsin(t), t). Since any point in this helix is equidistant from the z-axis, it is natural to use cylindrical coordinates to take advantage of the symmetries of helices.

Using the cylindrical coordinates defined as x = rcos(ϕ); y = rsin(ϕ); z = z, and X = Rcos(Φ ); Y = R sin(Φ); Z = Z, the scalar product in the exponential term of (1) can be written as,

$$\begin{array}{cc}\hfill \mathbf{x}\cdot \mathbf{X}=\mathit{xX}+\mathit{yY}+\mathit{zZ}& =\mathit{rR}\cos \varphi \cos \mathrm{\Phi }+\mathit{rR}\sin \varphi \sin \mathrm{\Phi }+\mathit{zZ}\hfill \\ \hfill & =\mathit{rR}\cos (\mathrm{\Phi }-\varphi )+\mathit{zZ},\hfill \end{array}$$ (2)

Substituting for the volume element d³x = rdrdϕdz, the Fourier transform in cylindrical coordinates adopts the form

$$\widehat{f}(R,\mathrm{\Phi },Z)=\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}}{\int \int \int }_{{\mathbf{R}}^3}f(r,\varphi ,z)e^{2\pi i(\mathit{rRcost}(\mathrm{\Phi }-\varphi )+\mathit{zZ})}\mathit{rdrd}\varphi \mathit{dz},$$ (3)

with the integration taking place over 0 ≤ r < ∞, 0 ≤ ϕ < 2π and −∞ < z < ∞.

To make this expression more manageable, we can substitute cos(Φ − ϕ) = sin( ϕ + π/2) and use Euler's formula (e^iϕ = cos(ϕ) + isin(ϕ)) to express the sine as a sum of complex exponentials ($\mathit{sin}\left(\theta \right)=\frac{1}{2i}(e^{i\theta }-e^{-i\theta })$. We then have

$$e^{2\pi i\left(\mathit{rRcos}(\mathrm{\Phi }-\varphi )\right)}=e^{2\pi \left(\mathit{rR}\frac{1}{2}(u-u^{-1})\right)}$$ (4)

where u = eⁱ(Φ−ϕ+π/2).

The exponential term can be re-expressed using the formula for generating Bessel functions, (Lebedev, 1972)

$$e^{\frac{1}{2}x(t-t^{-1})}=\underset{n=-\infty }{\overset{\infty }{\Sigma }}{J}_n\left(x\right)t^n,$$ (5)

where J_n(x) are the Bessel functions of the first kind. Thus the exponential term in (3) can be written as

$$e^{2\pi \left(\mathit{rR}\frac{1}{2}(u-u^{-1})\right)}{e}^{2\pi \mathit{izZ}}=\underset{n=-\infty }{\overset{\infty }{\Sigma }}{J}_n\left(2\pi \mathit{rR}\right)e^{\mathit{in}(\mathrm{\Phi }-\varphi +\pi ∕2)}{e}^{2\pi \mathit{izZ}}.$$

Plugging this into (3), we get

$$\begin{array}{cc}\hfill \widehat{f}(R,\mathrm{\Phi },Z)& =\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}}{\int \int \int }_{{\mathbf{R}}^3}f(r,\varphi ,z)\underset{n=-\infty }{\overset{\infty }{\Sigma }}{J}_n\left(2\pi \mathit{rR}\right)e^{\mathit{in}(\mathrm{\Phi }-\varphi +\pi ∕2)}{e}^{2\pi \mathit{izZ}}\mathit{rdrd}\varphi \mathit{dz}\hfill \\ \hfill & =\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}}\underset{n=-\infty }{\overset{\infty }{\Sigma }}{e}^{\mathit{in}(\mathrm{\Phi }+\pi ∕2)}{\int \int \int }_{{\mathbf{R}}^3}f(r,\varphi ,z)J_n\left(2\pi \mathit{rR}\right)e^{-\mathit{in}\varphi }{e}^{2\pi \mathit{izZ}}\mathit{rdrd}\varphi \mathit{dz}.\hfill \end{array}$$

A convenient way to write this expression is achieved by defining a ”helical structure factor” g_n(r, Z) as

$$g_n(r,Z)=\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}}{\int }_0^{2\pi }{\int }_{-\infty }^{\infty }f(r,\varphi ,z)e^{-\mathit{in}\varphi }{e}^{2\pi \mathit{izZ}}d\varphi \mathit{dz},$$ (6)

and thus (3) can be written as

$$\widehat{f}(R,\mathrm{\Phi },Z)=\underset{n=-\infty }{\overset{\infty }{\Sigma }}{e}^{\mathit{in}(\mathrm{\Phi }+\pi ∕2)}{\int }_0^{\infty }{g}_n(r,Z)J_n\left(2\pi \mathit{rR}\right)\mathit{rdr}.$$ (7)

Lastly, if we define

$$\begin{array}{cc}\hfill G_n(R,Z)& ={\int }_0^{\infty }{g}_n(r,Z)J_n\left(2\pi \mathit{rR}\right)\mathit{rdr},\hfill \\ \hfill & ={\int \int \int }_{{\mathbf{R}}^3}f(r,\varphi ,z)J_n\left(2\pi \mathit{rR}\right)e^{-\mathit{in}\varphi }{e}^{2\pi \mathit{izZ}}\mathit{rdrd}\varphi \mathit{dz}.\hfill \end{array}$$ (8)

the Fourier transform in cylindrical coordinates becomes

$$\widehat{f}(R,\mathrm{\Phi },Z)=\underset{n=-\infty }{\overset{\infty }{\Sigma }}{e}^{\mathit{in}(\mathrm{\Phi }+\pi ∕2)}{G}_n(R,Z),$$ (9)

Notice that up to this point, all we have done is to write the Fourier transform for a function f(r, ϕ, z) in cylindrical coordinates. The reason to introduce the ”big G's” and ”little g's”, is that these correspond to data from individual layer lines at particular values of Z in the Fourier transforms of helical particles.

Helical symmetry

In the case that f(r, ϕ, z) represents a density function with helical symmetry, we have a density function that is invariant after a twist of Δϕ and an axial translation Δz, that is,

$$f(r,\varphi ,z)=f(r,\varphi +\mathrm{\Delta }\varphi ,z+\mathrm{\Delta }z).$$ (10)

Similarly, the Fourier transform of these two functions are equal.

Making the transformation ϕ → (ϕ + Δϕ); z → (z + Δz) in (8), we have

$$\begin{array}{cc}\hfill G_n^{\prime }(R,Z)& =\frac{1}{{\left(2\pi \right)}^{3∕2}}{\int \int \int }_{{\mathbf{R}}^3}f(r,\varphi +\mathrm{\Delta }\varphi ,z+\mathrm{\Delta }z)J_n\left(2\pi \mathit{rR}\right)e^{-\mathit{in}(\varphi +\mathrm{\Delta }\varphi )}{e}^{2\pi i(z+\mathrm{\Delta }z)Z}\mathit{rdrd}\varphi \mathit{dz}\hfill \\ \hfill & =\frac{1}{{\left(2\pi \right)}^{3∕2}}{\int \int \int }_{{\mathbf{R}}^3}f(r,\varphi ,z)J_n\left(2\pi \mathit{rR}\right)e^{-\mathit{in}(\varphi +\mathrm{\Delta }\varphi )}{e}^{2\pi i(z+\mathrm{\Delta }z)Z}\mathit{rdrd}\varphi \mathit{dz}\hfill \\ \hfill & =\frac{1}{{\left(2\pi \right)}^{3∕2}}{\int \int \int }_{{\mathbf{R}}^3}f(r,\varphi ,z)J_n\left(2\pi \mathit{rR}\right)e^{-\mathit{in}\varphi }{e}^{2\pi \mathit{izZ}}{e}^{-\mathit{in}\mathrm{\Delta }\varphi }{e}^{2\pi i\mathrm{\Delta }\mathit{zZ}}\mathit{rdrd}\varphi \mathit{dz}\hfill \end{array}$$

In order to satisfy $G_n^{\prime }(R,Z)=G_n(R,Z)$,

$$e^{-\mathit{in}\mathrm{\Delta }\varphi +2\pi i\mathrm{\Delta }\mathit{zZ}}=1$$ (11)

This implies that for a density function with helical symmetry, −nΔϕ + 2π zZ = 2mπ, where m is an arbitrary integer.

The pitch of the helix is defined as the axial displacement of the helix after one full turn. This can be written in terms of the azimuthal and axial displacements between subunits (Δϕ and Δz) as $𝒫=\frac{2\pi \mathrm{\Delta }z}{\mathrm{\Delta }\varphi }$. Then

$$Z=\frac{m}{\mathrm{\Delta }z}+\frac{n}{𝒫}.$$ (12)

In general, a helical structure will not repeat after a single turn, but will require an axial displacement (c) that depends on Δϕ and Δz and that includes several turns. Again, the structure and its transform are invariant after a translation z=c. Applying this fact to (8), we obtain that e²πicZ = 1, which implies that 2πcZ = 2ℓπ, where ℓ is any integer. From this equation, we have that Z = ℓ/c.

This equation implies that the signal in the three-dimensional Fourier transform of an object with helical symmetry will be non-zero only in planes perpendicular to the Z-axis. These planes will be separated by a distance of 1/c.

Selection rule

Substituting the fact that Z = ℓ/c in (12), we get that

$$\ell =c\frac{m}{\mathrm{\Delta }z}+c\frac{n}{𝒫}.$$

Defining u = c/Δz as the number of subunits contained in a single repeat and t = c/P as the number of helical turns in a repeat, this expression becomes

$$\ell =\mathit{um}+\mathit{tn},$$ (13)

which is known as the helical selection rule, based on its resemblance to the selection rules in some quantum mechanical systems.

If the assembly has a cyclic periodicity, that is, if the helical axis is also a k-fold symmetry axis, we have the additional requirement that f(r, ϕ + 2π/k, z) = f(r, ϕ, z). This will add the requirement e^−2πin/k = 1, which implies that n has to be a multiple of k, in addition to the requirements imposed in (13).

Example: Tobacco mosaic virus

Tobacco mosaic virus consists of a coat protein arranged around a single strand of RNA, with a repeat distance of 69Å. In this repeat distance the virus has 49 subunits, and the basic helix makes three turns in a right-handed fashion. Thus, we have that t = 3 and u = 49. Then the selection rule becomes ℓ = 49m + 3n. The equator (ℓ = 0) can always be obtained with m = n = 0. However, in this case it is also consistent with m = 3; n = −49. That is, J₋₄₉(2πrR) also contributes to the equator, although it does so only at rather high spatial frequencies.

For the first layerline (ℓ = 1 = 49m+3n) is consistent with m = 1 then n = 16. The second layerline generates the equation 2 = 49m + 3n, which can be satisfied by m = −1; n = 17. Thus, the first and second layerlines are generated by J₋₁₆ and J₁₇ respectively, which explains their locations relatively far from the meridian in the diffraction patterns. The third layerline generates the equation 3 = 49m + 3n, which is satisfied with the choice of m = 0; n = 1. Therefore the third layerline is characterized by J₁(2πrR), which will have its maximum near the meridian.

It is worth noting that the equation for the first layerline, 1 = 49m + 3n has m = 1; n = −16 as solutions, as well as m = −2; n = 33. That is, this layerline will contain both J₋₁₆ and J₃₃. Although J₃₃ starts contributing at a considerably higher spatial frequencies (~−10 Å), this overlap cannot be ignored, especially if we aim to produce a high resolution three-dimensional reconstruction. In cases like this, there is no established method to deconvolve the Bessel functions as would be required for Fourier-Bessel reconstruction.