A Workflow for Global Sensitivity Analysis of PBPK Models

Abstract

Physiologically based pharmacokinetic (PBPK) models have a potentially significant role in the development of a reliable predictive toxicity testing strategy. The structure of PBPK models are ideal frameworks into which disparate in vitro and in vivo data can be integrated and utilized to translate information generated, using alternative to animal measures of toxicity and human biological monitoring data, into plausible corresponding exposures. However, these models invariably include the description of well known non-linear biological processes such as, enzyme saturation and interactions between parameters such as, organ mass and body mass. Therefore, an appropriate sensitivity analysis (SA) technique is required which can quantify the influences associated with individual parameters, interactions between parameters and any non-linear processes. In this report we have defined the elements of a workflow for SA of PBPK models that is computationally feasible, accounts for interactions between parameters, and can be displayed in the form of a bar chart and cumulative sum line (Lowry plot), which we believe is intuitive and appropriate for toxicologists, risk assessors, and regulators.

Introduction

Current approaches to testing industrial and agricultural chemicals for potential toxicity in people are inefficient, expensive, and reliant on animal experimentation. As a consequence most chemicals in global commerce today have undergone limited or no safety testing at all (Judson et al., 2009).

Over the last few decades alternative methods of evaluating the toxicological hazard of chemical compounds has focused on the potential of in vitro test systems. These are biological systems of a lower level of organization than a complete organism, e.g., isolated organs, cell cultures, and sub-cellular systems. Whilst these systems have been useful in studying the mechanism(s) of toxic action they have been, and perhaps still are, viewed as an alternative means of studying clinically observable toxicity endpoints (Blaauboer, 2010). More recently, the National Research Council (NRC) report, Toxicity Testing in the Twenty-First Century: a Vision and a strategy proposes an ambitious, long-term approach requiring the development of novel in vitro systems (NRC, 2007). This vision is based upon the growing knowledge and elucidation of interconnected pathways composed of complex biochemical interactions of genes, proteins, and small molecules that maintain normal cellular function, control communication between cells and allow cells to adapt to environmental stressors. “Toxicity pathways” are perturbed cellular-response networks that precede and ultimately lead to overt “apical” toxicity. The novel in vitro systems would allow the evaluation of these perturbations of cellular-response pathways. If adopted, the NRC approach would represent a paradigm shift in toxicology and in human and environmental health risk assessment (RA).

The need for alternative approaches to toxicity testing is clear. Whether this involves the development of “traditional,” direct, one to one replacement of animal tests with in vitro systems or “alternative ways” of doing RA, as envisioned in the NRC report, there is a requirement that is common to both: in vitro–in vivo extrapolation. The ability to translate information generated using alternative systems into a reliable predictive toxicity testing strategy is dependent upon a framework into which disparate data can be integrated and utilized. Physiologically based pharmacokinetic (PBPK) models are ideally suited for this and are now recognized as essential tools in the evaluation of in vitro and structure activity relationship-derived data on dose–response relationships in intact organisms (Blaauboer et al., 1996, 1999; DeJongh et al., 1999; Blaauboer 2001,2002,2003a,2003b,2010; Bouvierd’Yvoire et al., 2007).

A PBPK model is an independent, structural model, comprising compartments that correspond directly and realistically to the organs and tissues of the body (e.g., adipose, brain, gut, heart, kidney, liver, lung, muscle, spleen, skin, and bone) and connected by the cardiovascular system. They are mathematical descriptions of biological systems that are translated into computer code and solved computationally. They are frameworks that can capture our understanding of the science underlying the biological processes that lead to disease. A PBPK model is mechanistic because it is specifically formulated to provide insights into the interaction of a foreign chemical(s) with biological processes thought to govern a biological response(s). The principle application of PBPK models is in the prediction of the appropriate form of the target tissue dose, or dose metric, of the parent chemical or its reactive metabolite(s). The dose metric must capture the critical biochemical steps that lead to an effect. Such mechanisms may take place within any compartment, e.g., blood, organ, or sub-cellular compartment. Use of an appropriate dose metric in chemical RA calculations provides a better basis for relating to the observed toxic effects than the external or administered exposure concentration of the parent chemical (Conolly and Butterworth, 1995; Barton et al., 1998; IGHRC, 1999; Johanson et al., 1999; Andersen, 2003; Clewell and Clewell, 2008; Lipscomb and Poet, 2008). Therefore, PBPK models contain knowledge of the system being studied in the form of dozens of parameters and inputs. However, these parameters and inputs are affected by uncertainties, which affect the output of the model.

Sensitivity analysis (SA) allows the model output uncertainty to be ascribed to the source within the model thereby offering a means of evaluating the consistency between internal model structure and the system it tries to emulate (Campolongo and Saltelli, 1997; Campolongo et al., 1999; Saltelli et al., 2004). The many SA methods that exist for the analysis of complex deterministic models can be grouped into two categories: local or one-at-a-time (OAT) methods that consider sensitivities close to a specific set of input parameter values, and global methods, which calculate the contribution of a parameter over the set of all possible input parameters. In a PBPK modeling context a global method would perturb all organ and tissue masses, blood perfusion rates, metabolic parameters, and partition coefficients (PCs) within plausible ranges. The contribution to model output of any single parameter and/or interactions of multiple parameters, e.g., peak venous blood concentration of parent chemical or urinary metabolite is measured yielding useful quantitative information about the overall relative importance of all model parameters. The most commonly applied global method quantifies the importance of parameters as an exact percentage of the total output variance that each factor (or group of factors) is accounting for. This information may be expressed as a bar or pie chart (Campolongo and Saltelli, 1997; Campolongo et al., 1999; Saltelli et al., 2004; Marino et al., 2008) or by the “Lowry Plot” visualizations developed in this paper. In most cases when SA has been conducted on a PBPK model published in the peer-reviewed literature this has been an OAT. This involves the adjustment of individual model parameters, whilst all other parameters are held constant, and observation of the predicted changes in model output, either at a single time or throughout a time course. The results are usually expressed as normalized sensitivity coefficients (SCs), which are the percentage change in the output produced by a fixed and constant percentage (usually 1%) change in the parameter (Plowchalk et al., 1997).

When trying to establish the contribution of a parameter to model predictions, OAT SA techniques are fairly rapid and simple to implement but can give somewhat misleading results if there are substantial interactions among multiple parameters (Campolongo and Saltelli, 1997; Campolongo et al., 1999; Saltelli et al., 2000b, 2004; Loizou et al., 2008). In a model for rat nasal uptake of vinyl acetate the authors conducted an OAT at several exposure concentrations to address the highly non-linear nature of the model and described the SCs as being concentration dependent (Plowchalk et al., 1997). This is inappropriate since the plausible range of the parameters will typically be much wider than this technique allows (and the uncertainty in the parameters should be represented via a joint probability distribution), and as it is OAT results may be unreliable unless the interactions between parameters are negligible, generally this is not true. PBPK models, more often than not, do describe non-linear processes, such as metabolism, and certainly contain interactions between parameters, e.g., tissue and organ masses and blood perfusion rates are related to body mass and cardiac output, respectively. Very often the purpose of the model is to extrapolate beyond the domain of “observation” used to construct and evaluate the model (Andersen and Krishnan, 1994; Andersen, 2003; Barton et al., 2007, 2009; Chiu et al., 2007; Kirman et al., 2008). These model applications and model behaviors along with input variables that are often affected by uncertainties of different orders of magnitude call for a global SA that is independent from assumptions about the model structure (Campolongo and Saltelli, 1997; Campolongo et al., 1999; Saltelli et al., 2004).

Since we are often interested in concentration-time profiles of xenobiotics in biological systems, here we describe an approach for uncertainty and SA adapted to consider sensitivity indices of PBPK model parameters that vary with time. We propose the elements of a workflow for the application of global SA during PBPK model development and evaluation.

Finally, there is a need to develop increased awareness and confidence in the use of PBPK models. Therefore, an important objective underpinning this work is to remain mindful of the need to develop user-friendly tools that shift the emphasis away from mathematical and programming expertise to the biology underlying RA and to present such information in a manner that is acceptable to toxicologists, risk assessors, and regulators. With the future development of intuitive, user-friendly tools, we believe that the workflow we propose does not require in-depth mathematical expertise and could be undertaken by biological scientists. Mathematical equations are included for the interested reader but may be skipped without diminishing the primary objective of this report and we endeavored to provide examples with clear biological relevance. We hope that this work can make a contribution to the development of good PBPK modeling practice and facilitate the dialog between toxicologists and risk assessors and regulators (Kohn, 1995; Clark et al., 2004; Barton et al., 2007; Chiu et al., 2007; Loizou et al., 2008).

Materials and Methods

The PBPK model

A human PBPK model describing a bladder compartment to simulate fluctuations in metabolite concentration in urine caused by micturition (Franks et al., 2006), was adapted to study the inhalation pharmacokinetics of m-xylene (Figure 1). Liver, adipose, richly and slowly perfused tissues, and the bladder represents the body. The model parameter abbreviations and point values, which are similar to previous models, are listed in Table 1 along with the ranges used in the SA (Loizou et al., 1999; MacDonald et al., 2002). Exhalation, metabolism, and renal excretion were the routes of elimination. The amount of unbound 3-methylhippuric acid (MHA) the main metabolite of m-xylene in the blood, was assumed to be available for secretion into the renal tubules via glomerular filtration where no re-absorption takes place but passes directly into the urine (Rowland et al., 1973). The amount of MHA delivered to the kidney and appearing in the urine was described by the following equations,

Figure 1.

Schematic of the PBPK model for m-xylene.

Table 1.

Anatomical, physiological, and kinetic constants and parameters used in the PBPK model.

Parameter	Abbreviation	Value	Range
Molecular mass m-xylene (g/mol)	MWxyl	106.17	–
Molecular mass MHA (g/mol)	MWMHA	193.2	–
Body mass (kg)	BW	75	49–92
Proportion of vascularized tissue (body mass)	VT	0.91	–
Cardiac output (L h−1 BW0.75)	QCC	12	10–20
METABOLISM (LIVER)
In vitro Michaelis constant (mMol L−1)	KM	11.8	9.1–14.6
In vitro maximum rate of metabolism (pmol min−1 mg−1 microsomal protein)	Vmax	895	761–1028
Microsomal protein yield per gram wet weight liver (mg g−1)	MPY	32	18–75
GAS EXCHANGE
Respiratory rate (L h−1 BW0.75)	QPC	12	10–20
Respiratory dead space (proportion respiratory rate)	DS	0.3	0.2–0.33
PARTITION COEFFICIENT
Blood:air partition coefficient	Pba	19	12–26
Rapidly perfused	Prpda	117	50–150
Slowly perfused	Pspda	53	40–80
Adipose	Pfaa	1874	1400–2200
Liver	Plia	279	150–350
TISSUE BLOOD FLOW AS A FRACTION OF CARDIAC OUTPUT
Rapidly perfused	QrpdC	0.48
Slowly perfused	QspdC	0.22	0.2–0.35
Adipose	QfaC	0.05	0.09–0.10
Liver	QliC	0.25	0.2–0.3
TISSUE MASS AS A FRACTION OF BODY MASS
Rapidly perfused	VrpdC	0.09
Slowly perfused	VspdC	0.604
Adipose	VfaC	0.19	0.07–0.28
Liver	VliC	0.0257	0.02–0.031
BLADDER COMPARTMENT
Rate of urine production (L h−1)	Rurine	0.07	0.06–0.115
Urinary creatinine concentration (mmol L−1)	CRE	12.5	7–15
Elimination rate constant (h−1)	K1	10	2–18

$$\begin{array}{l}\frac{d({\text{MHA}}_B)}{dt}=\left(\text{MRLi}\times \frac{{\text{MW}}_{\text{MHA}}}{{\text{MW}}_{\text{xyl}}}\right)-({\text{MHA}}_B\times K_1)\\ \frac{d({\text{MHA}}_B)}{dt}={\text{MHA}}_B\times K_1\\ \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}MRLi}=\frac{V_{\max }\times \text{CVLi}}{K_M+\text{CVLi}}\\ {\text{C}}_{\text{urine}}=\frac{{\text{MHA}}_U}{{\text{Vol}}_U\times \text{Cre}}\end{array}$$

Where, MRLi is the rate of metabolism of m-xylene to MHA in the liver, MW_MHA and MW_xyl are the molecular weights of MHA and m-xylene, respectively, MHA_B is the amount of MHA in the blood, K₁ is a first-order elimination rate constant describing removal of MHA_B from the blood to the urine, V_max is the limiting rate and K_M is the Michaelis–Menten constant for hepatic metabolism of m-xylene, CVLi is the hepatic venous effluent concentration of m-xylene, MHA_U is the amount of MHA in the urine, Vol_U is the volume of urine in the bladder and Cre is the concentration of creatinine. The concentration of MHA in the urine was expressed in millimole/mole creatinine. To imitate micturition, the bladder is assumed to fill with urine at a constant (but adjustable) rate and empty at discrete time intervals (when the volume of urine reduces to zero). This enables comparison to be made between model predictions and experimental observations with timed sampling in human volunteer studies (Franks et al., 2006).

The Michaelis–Menten constant K_M and the in vitro V_max for hepatic metabolism of m-xylene were obtained from the literature (Tassaneeyakul et al., 1996). In vitro –in vivo extrapolation of V_max was obtained by multiplying the in vitro value by a human hepatic microsomal protein yield (MPY) of 32 mg g⁻¹ wet weight liver and the mass of liver (g) (Howgate et al., 2006; Barter et al., 2007).

Global SA techniques

The extended Fourier amplitude sensitivity test (eFAST) method proposed in this paper is one of a suite of methods for a quantitative global SA. Alternative model independent methods for calculating main effect and total effect sensitivity indices include the method of Sobol (1993,2001) and the top marginal variances (TMV) method described in Jansen et al. (1994). The Winding Stairs sampling scheme (Chan et al., 2000) is an efficient method of calculating both these sets of sensitivity indices. Indeed, this sampling scheme can also calculate all interaction variances in addition to main and total effects, and can a handle some dependence between inputs. Whilst Sobol’ or TMV have some advantages over eFAST and are suitable alternatives, they require a greater number of model evaluations.

Some alternative methods for a global SA that require many fewer model evaluations are available. These include a class of methods based upon regression analysis (Helton and Davis, 2000) and include standardized regression coefficients (SRC), Spearman correlation coefficients (SCC) and partial correlation coefficients (PCC). These methods are based upon a linear approximation to the model, therefore results from the SA are only approximate and may be poor for highly non-linear models. As the paper proposes a consistent workflow for SA, model dependent methods were considered to be inadequate. Another alternative is an SA method based upon an emulator, a surface fit that approximates the model (Oakley and O’Hagan, 2004). This is a powerful technique, however it requires a greater understanding of the underpinning mathematics (to assess the quality of fit of the emulator) than the method suggested in the paper.

In this study the two-step approach to SA of large models proposed by Campolongo and Saltelli (1997) was adapted for PBPK models as follows:

1. The Morris test as a preliminary screening exercise to identify the subset of the most potentially explanatory parameters of model output.

2. The eFAST for the quantitative analysis of the selected subset of parameters.

The Morris method is global in the sense that it is obtained by taking average values of local measures throughout the input space and produces two sensitivity measures for each parameter, μ and σ. A high μ indicates a factor with an important overall influence on model output; a high σ indicates either a factor interacting with other factors or a factor whose effects are non-linear. The magnitude of μ and σ for each model parameter is relative, i.e., a parameter has a low μ relative to the parameter with the highest μ. For a screening method to be effective, the probability of not identifying a factor that is important must be low. Previous exercises using the Morris method have satisfied this requirement (Campolongo and Saltelli, 1997; Campolongo et al., 1999; Saltelli et al., 2000a).

The eFAST test is a variance-based global method that is independent of any assumptions regarding model structure (it does not rely on assumptions as to the functional relationship between the model output and its inputs) and is valid for use with non-monotonic models (models that do not give exclusively increasing or decreasing predictions). The method provides a way to estimate the expected value and variance of the dose metric (model output variable) and the contribution of input parameters and their interactions to this variance, given physiologically feasible parameter ranges for inputs. It is important that interactions are identified if the applications of SA are to be fully realized (Campolongo and Saltelli, 1997; Campolongo et al., 1999; Saltelli et al., 1999, 2004; Marino et al., 2008). The eFAST technique can produce two types of sensitivity measure that vary with time: main effects (S_i) and total effects ($S_{T_i}$). The main effect of a parameter represents the reduction in variance if the “true” value of that parameter is known, e.g., the reduction in variation in venous blood concentrations of m-xylene if the real liver mass of an individual is known. The total effect of a parameter represents the proportion of variance remaining if the “true” values of all the other parameters are known, e.g., the variation in venous blood concentrations of m-xylene would be due solely to the variation in liver mass because the true, unique values for all other parameters are known. However, total effects of a given parameter usually have a higher variance when compared to the main effects because although the “true” values of all the other parameters are known, any interactions between these and any number of parameters are unknown. It is useful to think of $S_{T_i}$ as the sum of S_i and interactions.

SA workflow

The workflow comprises the following steps:

1. Perform the screening exercise using the Morris test

2. Identify and select the most important parameters

3. Identify the time period where model output variance is of interest

4. Perform eFAST on the most potentially explanatory subset of parameters

5. Present $S_{T_i}$, S_i and interactions as a Lowry plot

The screening exercise

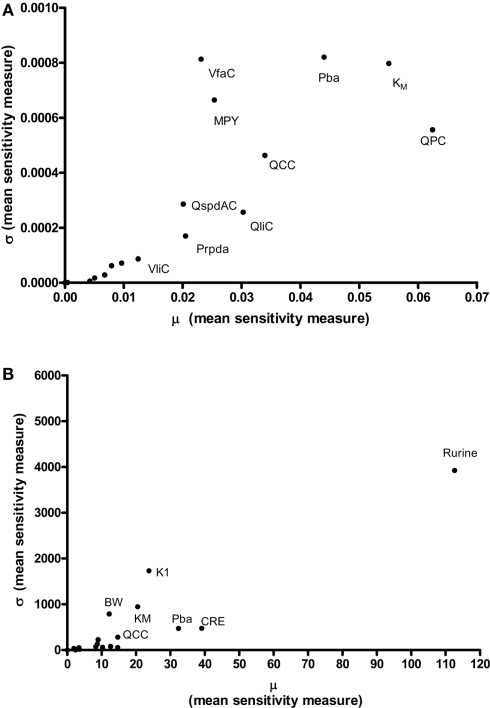
In order to test the validity of the screening exercise as a single initial step for parameter sensitivity measures that change over time, the means of μ and σ were calculated over a period of 0–14 h corresponding to the change in venous blood concentration of m-xylene (CV; Figure 2A) and from 3 to 14 h corresponding to the change in concentration of urinary MHA (C_urine; Figure 2B).

Figure 2.

Simulation of venous blood m-xylene and urinary excretion of methylhippuric acid (expressed against creatinine). The symbols are typical measured values from two volunteers and the solid lines are model predictions using mean point values for anatomical, physiological and biochemical parameters for, (A) CV and (B) C_urine. In panel (A) the lower broken line shows the region of approximate total variance. The upper broken line is the approximate total variance multiplied by 25 in order to show more clearly the relationship to model prediction. The short broken lines at 3 and 5 h in panel (A) and 5 and 8 h in panel (B) show the time slices chosen for eFAST analysis.

The eFAST method

In order to delineate the various steps of a possible workflow the analysis initially was conducted at 40 ppm, the target exposure concentration of the human volunteer studies. For CV eFAST was run at 3–5 h, to investigate parameter sensitivities in the distribution and elimination phases (Figure 2A) and at 5–8 h for C_urine to investigate the early and latter urinary elimination phase (Figure 2B). In order to investigate parameter interactions further analyses were conducted at 0.3, 3, 5, and 8 h at an intermediate concentration of 200 ppm and at 500 ppm, a concentration calculated to generate a hepatic concentration of m-xylene 17% greater than the K_M value for P450 metabolism.

Parameter ranges

Parameter ranges used for both the Morris Screening and eFAST tests were identical and are listed in Table 1. Anatomical and physiological parameter distributions were obtained from the freely available web-based application PopGen, which is a virtual (healthy) human population generator¹. A human population, comprising 50% male and 50% female, white Caucasians, age range 16–65, height range 140–200 cm, body mass indices 18.5–30 was generated to encompass the characteristics of the volunteers that took part in the study described below. In PopGen, organ masses and blood flows are determined for virtual individuals from both a priori distributions of anthropometric parameters such as body mass, height, and body mass index and measured data from existing studies. The algorithms, were derived and evaluated by Willmann et al. (2007).

Parameter ranges were set at the 5 and 95th percentiles of the distributions, with the exceptions of the PCs Prpda, Pspda, Pfaa, and Plia. There were no available distributions for these PCs and therefore the ranges set were considered reasonable assumptions. VspdC and VrpdC, the masses of the slowly and rapidly perfused tissues respectively, were not included in the SA because they are aggregated compartments from which organs and tissues are subtracted when discretely defined during model building. In order to ensure that logical constraints on mass balance and blood flow to the tissues were met the re-parameterizations described in Gelman et al. (1996) were adopted.

The mean value and range for K₁, the first-order elimination rate constant describing removal of MHA_B from the blood to the urine was estimated by simulating the post exposure urinary excretion of methylhippuric acid following exposures at 1–10, 11–20, 21–30, and 31–40 ppm (Engström et al., 1978). The four data sets from were digitized and K₁ estimated using the QuasiNewton algorithm within acslX Libero (see Software).

The data

Venous blood m-xylene and urinary MHA concentrations from a human volunteer study, which will be fully reported in due course, were used to illustrate the SA analysis workflow. Briefly, groups of four volunteers were exposed for 4 h on two separate occasions to a target concentration of 40 ppm m-xylene vapor in the Health and Safety Laboratory controlled atmosphere facility (CAF), a purpose built room 8 m³ in volume (Loizou et al., 1999). Individual body mass, body fat mass, resting alveolar ventilation rate, blood:air PC, urine volumes, and creatinine concentrations were measured. Venous blood samples were taken prior to entering the exposure facility and at hourly intervals during exposure, then every 20 min for the first hour after exiting the exposure facility before returning to hourly intervals for the next 3 h (Figure 2A). Urine samples were taken at 4, 6, 8, 10, 12, 14, 24, 27, 31 h post exposure (Figure 2B).

Software

The numerical solutions to the model equations were obtained using acslX Libero version 3.0.1.6 (AEgis Technologies²). The M functions for the Morris Test and eFAST included with the acslX Optimum suite of tools were adapted for use in this study. Lowry plots were created using R and ggplot2 (Wickham, 2009; R Development Core Team, 2010) with additional code by Takahashi (2010). Data were digitized using Grab It! Graph Digitizer (Datatrend Software, Inc.³). The computer used in this study was a Dell Optiplex 755 Intel Core(TM)2 Duo CPU 3.00 GHz 2.00 GB RAM.

Results

Results of the Morris screening exercise for variance in CV and C_urine are shown in Figures 3A and 3B. The sensitivity indices, μ and σ were plotted for all 19 input parameters but due to lack of space, only 10 in the case of CV, and 7 in the case of C_urine, are annotated. The parameters are ranked in order of importance according to μ for both CV and C_urine in Table 2. The recommended procedure in Campolongo and Saltelli (1997) would be to perform the more computationally expensive eFAST analysis on the most important of the screened parameters. These would certainly include the annotated parameters in Figures 3A and 3B. However, in this study we investigated the correspondence in ranking of the mean values of μ with eFAST indices for every parameter (no parameters were screened out) for both CV and C_urine. Unlike the Morris test mean sensitivity indices, it is not straightforward to take averages of $S_{T_i}$ and S_i. Therefore, to test concordance with the Morris screening, eFAST was conducted on all 19-model parameters at various discrete time points. The two methods were compared by examining the rankings of the μ and $S_{T_i}$ values. Unlike $S_{T_i}$, μ does not include a measure of interactions with other model parameters, therefore strictly speaking, is not a directly comparable sensitivity index. However, since the Morris test has been proposed as a screening method based on ranking μ this comparison is therefore justified (Campolongo and Saltelli, 1997).

Figure 3.

The Morris Screening exercise. Results of the Morris Screening exercise for, (A) the concentration of m-xylene in venous blood (CV) and, (B) the urinary excretion of methylhippuric acid (expressed against creatinine) (C_urine).

Table 2.

Ranking of model parameters: comparison of Morris test screening and eFAST.

Table 2 shows the comparison of ranking of mean values of μ with $S_{T_i}$ values calculated at 3, 5, 8, and 11 h for both CV and C_urine. A tick next to an $S_{T_i}$ value indicates correspondence with the Morris screening across all four time points by being ranked consistently in the top 10 or bottom 9. A cross next to an $S_{T_i}$ value indicates a parameter that may be ranked in the top 10 or bottom 9 at different time points.

The Morris screening test was then conducted at the same time points as the eFAST analysis. Tables 3 and 4 show that there is an improved concordance in the ranking between $S_{T_i}$ and μ for each parameter at 3, 5, 8, and 11 h for CV but less so for C_urine. The rankings are not exactly the same although more parameters are ranked in the top 10 or bottom 9 by both methods. For CV at 3 h BW is ranked in the top 10 most influential parameters and Prpda in the bottom 9 by eFAST in disagreement with the Morris screening. For C_urine the following $S_{T_i}$ indices differ in ranking to the corresponding μ for VliC and Pspda at 3 h, VliC and K₁ at 5 h, VliC, K_M, and K₁ at 8 h (although K₁ was ranked in the top 10 for both methods) and K_M and K₁ at 11 h.

Table 3.

Comparison of ranking of model parameters for variance in CV.

Table 4.

Comparison of ranking of model parameters for variance in C_urine.

The computing time for the Morris screening test for all 19 parameters for both CV and C_urine was approximately 8 s.

The eFAST method

In addition to calculating $S_{T_i}$ and S_i eFAST analysis also produces some useful outputs that can be used to support modeling assumptions. The approximate distribution of total variance of the dose metric with time can be visualized to compare with the domain of experimental observation. Figures 2A and 2B show that the magnitude of approximate total variance over time follows the quantity of substance in blood and urine, respectively. In Figure 2A the lower broken line shows the region of approximate total variance for CV. The upper broken line is the approximate total variance multiplied by 25 in order to show more clearly the relationship to model prediction. Therefore, the profile of the approximate total variance of the dose metric was used to select appropriate time points for detailed eFAST analysis. In contrast to CV, the approximate total variance for C_urine did not require scaling to be graphed. The figures also highlight that variance is very sensitive to the units of measurement and may be only weakly related to the uncertainty in the level of the substance (in blood, urine, or any body compartment of interest) that arises due to uncertainty in the parameters of the model. This does not impact on the functionality of variance-based methods for SA, however the standard deviation (the square root of the variance) is a more appropriate measure of the underlying uncertainty in the model output that results from parameter value uncertainty. Some outputs in the PBPK model may be much more sensitive to the inputs than others. The total variance can be used to compare the sensitivity of model outputs (to the model inputs) provided those outputs have the same units of measurement. For example, if the variance of the substance in the liver was found to be much larger than the variance of the substance in the kidney, one could conclude that the liver parameter value (e.g., mass, perfusion rate, PC) was a much more sensitive parameter than the corresponding kidney parameter.

Figures 4A,B show the Lowry plots of the eFAST quantitative analysis for CV at 3 and 5 h. Let o_i be the main effects (S_i), ordered from largest to smallest.

Figure 4.

Lowry plot of the eFAST quantitative measure. The total effect of a parameter ($S_{T_i}$), is comprised the main effect S_i (black bar) and any interactions with other parameters (grey bar) given as a proportion of variance. The ribbon, representing variance due to parameter interactions, is bounded by the cumulative sum of main effects (lower bold line) and the minimum of the cumulative sum of the total effects (upper bold line), (A) CV at 3 h, (B) CV at 5 h, (C) C_urine at 5 h and (D) C_urine at 8 h.

The amount of variance that is accounted for by including all parameters up to a specified point is bounded below by the cumulative sum of the ordered main effects (the base of the ribbon) and is bounded above by the cumulative sum of the total effects. Note that there is multiple accounting of the interactions associated with each parameter, which causes the total to exceed 100% eventually. In fact, we have an even stricter limit for the upper bound: it cannot exceed 100% minus the sum of the main effects that are not included in the cumulative sum up to that point (the top of the ribbon).

More formally, the lower bound of the included variance for the first k parameters is given by

$$l_k={\displaystyle \sum _{j=1}^k{O}_{i_j}}$$

and the upper bound is given by

$$u_k=\min \left({\displaystyle \sum _{j=1}^k\left(O_{i_j}+i_j\right),}1-{\displaystyle \sum _{j=k+1}^n{O}_{i_j}}\right)$$

where n is the total number of parameters.

Thus, the amount of variance that is accounted for by including all parameters up to a specified point can be determined by taking a cross section of the ribbon above that parameter, i.e., the range from l_k to u_k. For example, in Figure 4A, if you include all parameters up to BW, then the amount of variance accounted for is between approximately 94 and 98%. In this case, to ensure that at least 90% of the model variance is captured you would need to include all terms up to and including MPY, since that is the first point when the lower cumulative frequency line rises above 90%. By including the top 10 parameters, we account for between 95% and 99% of variance at 3 h, and between 90 and 98% at 5 h post exposure.

The contribution of different parameters to variance of CV changes with time. The most notable being Qspdc, the blood perfusion rate of the aggregated slowly perfused compartment, which increases from less than 1.0% (Figure 4A) to 15.3% (Figure 4B). The parameters accounting for most of the variance are similar at both time points except that at 5 h body mass, BW is replaced by Pspda, the blood:air PC for the slowly perfused compartment. MPY, can be seen as representing the contribution of V_max to variance because MPY significantly affects the magnitude of V_max in the in vitro–in vivo scaling calculation. Therefore, both metabolic parameters, K_M and V_max contribute to variance of CV at both time points.

Figures 4C,D show the results of the eFAST quantitative analysis for C_urine at 5 and 8 h. In this case Rurine and CRE are dominant parameters at both time points accounting for about 80–85% variance in C_urine. Beyond Rurine and CRE the parameter rankings differ significantly. At 5 h post exposure Rurine, CRE, and Pba, account for at least 86% of variance due the S_i and approximately 90% including interactions (Figure 4C). At 8 h post exposure the S_i of Rurine, CRE, and VfaC account for at least 90% of variance and almost 95% including interactions (Figure 4D).

Figure 5 is a selection of latticed Lowry plots showing examples of changes in parameter interactions and ordering at various exposure concentrations and time points. There was a broad consistency in the results at the three doses however there were some important differences. The principle differences in results were that (a) the dominance of the most important parameters increased as the dose increased; this was particularly evident at the first two time points (of 0.3 and 3 h) where Pba and QPC accounted for a progressively larger proportion of variance as the dose increased; (b) the results of the SA show that there were some changes in the parameter orderings, in particular MPY became more important as the dose increased; and (c) the Lowry plots clearly indicate that interactions accounted for a larger proportion of variance at all time points for the 200 and 500 ppm doses.

Figure 5.

Selected latticed Lowry plots showing concentration and time-dependent changes in parameter interactions and ordering.

The computing time for the eFAST analysis of 19-model parameters for CV and C_urine was approximately 13 h each.

Discussion

The probability of non-identification of important parameters by the Morris test has been reported to be low (Campolongo et al., 1999). However, previous studies did not involve the calculation of sensitivity measures that change over time and involved models with a larger number of parameters (60+; Campolongo and Saltelli, 1997; Campolongo et al., 1999; Saltelli et al., 1999; Marino et al., 2008). In this study the Morris screening exercise performed well when conducted at the same time points as eFAST. Disagreement with the Morris screening occurred at the 3-h time point for CV where BW was ranked in the top 10 and Prpda in the bottom 9. Quantitatively, BW accounted for 2.3% and Prpda 0.3% of variance. In the case of C_urine disagreement with the Morris screening occurred at each time point. For both CV and C_urine the disagreements in rankings were small and occurred with parameters that accounted for a very small percentage of dose metric variance. It is recommended that the screening phase be performed at the same time points as the eFAST analysis.

The computational cost of performing global SA may be an important criterion for determining whether a screening exercise is required. In this study the eFAST conducted on a PBPK model with 19 parameters took approximately 13 h to complete on a dual core desktop PC. However, the run time increases substantially as the number of parameters is increased. In a preliminary investigation the number of model parameters was increased to 25 (each compartment requires a mass, perfusion rate and PC) by adding a kidney and brain compartment. The run time for eFAST analysis of the 25-parameter model increased to 72 h. Therefore, in the case of PBPK models with modest numbers of parameters, e.g., 19–25, the screening should be used to reduce the number of parameters for quantitative analysis by de-selecting the 10 least important. The run time will still be several hours (this would be substantially reduced on a multicore system).

The eFAST results are consistent with other studies showing that the influence of model parameters on model output follow a Pareto-like distribution (Campolongo et al., 1999; Saltelli et al., 2000a). This is a highly skewed distribution with tails corresponding to extreme values. This means that most of the variance would be described by a few parameters. This is certainly the case with the eFAST data obtained at the early time points for both CV and C_urine. At 3 and 5 h for CV and 3 and 8 h for C_urine, the computation of sensitivity measures occurs in a region of parameter space that corresponds to the time period where the concentration of m-xylene in the system is still substantial. Numerical methods are still able to calculate sensitivity measures even as the variance tends to zero, which occurs at later time points. As this happens the sensitivity measures reflect sampling variability and noise rather than important model structure. It is therefore important to recognize an appropriate point to terminate eFAST, to avoid the region where the variance asymptotes toward zero.

The keys points are that it is important to conduct the SA at a dose within the range of any experimental data as the results from the SA may be sensitive to the dose. However, an advantage of conducting the SA at multiple doses is that the sensitivity of results, in effect the degree of interaction between the parameters of the PBPK model and the dose, can be assessed. Perhaps most importantly, whilst there were some important differences in the most sensitive parameters, there was little change in the ordering of the least important parameters. There was a consistency in the least important parameters at all three doses, therefore the approach suggested in this workflow, of eliminating the least sensitive parameters, was independent of the dose.

The primary objective in the paper was to introduce the elements of a workflow for SA and some of the technical details have been omitted from the methodology for clarity of presentation. One important issue is on the assumed probability distribution for the parameters. In the examples presented in the paper uniform distributions were assumed in all cases. Oakley and O’Hagan (2004) showed that sensitivity indices are influenced by both the relationship between the model output and its inputs, and by the probability distributions for the model parameters. A full treatment of both of these sources of influence is referred to as probabilistic SA. However, this latter source of influence, whilst important, is rarely covered in detail in the literature.

If little information is known about the model parameters it may be reasonable to assume uniform distributions on the inputs (although a robust SA might also examine the results under a variety of assumed probability distributions). However, if it is feasible to obtain reliable probability distributions from sources such as PopGen these should be used in sensitivity analyses. After appropriate transformations of the parameters a variety of distributions can be used in eFAST. Some minor differences in the SA results in this work would have resulted from different probability distributions on the inputs.

In practice there is a balancing act between the availability of a suite of probability distributions and ease of use. The authors consider uniform distributions as a default setting, coupled with a choice of uniform, log-uniform, normal, and log-normal probability distributions for model parameters to be a reasonable compromise.

Despite greater computational cost a number of factors shift the balance in favor of eFAST over OAT techniques. These are: (i) different parameters are affected by different ranges of variation and uncertainty in different regions of parameter space, i.e., different patterns of parameter sensitivity predominate in different regions of parameter space, (ii) the presence of significant interactions between parameters should never be discounted, (iii) presentation of quantitative information on SA in the form of a bar chart is intuitive. Specifically, the presentation of the main effects, S_i with a bar representing the sum total contribution of all interactions ($S_{T_i}$) to variance in the form of a Lowry plot is recommended, (iv) the importance of one parameter rather than another can only be justified if parameter interactions have been quantified.

Conclusion

We have defined the basis of a workflow for SA of PBPK models that is computationally feasible, accounts for interactions between parameters, and can be displayed in an intuitive manner. When used to analyze PBPK models containing up to 25 parameters, Morris screening should be used to identify the 10 least important. However, judgment and experience should guide the user as to the number of parameters to eliminate before performing the more computationally costly eFAST analysis. The results of eFAST analysis can be presented as a bar chart and cumulative sum line that we have named a “Lowry plot” showing the proportional contribution to variance of the most significant parameters and their interactions. We believe the presentation of this kind of data in this form is intuitive and appropriate for toxicologists, risk assessors and regulators.

Appendix

R code for creating Lowry plots

The plots were created using R (R Development Core Team, 2010) and the ggplot2 package (Wickham, 2009).

library(ggplot2)

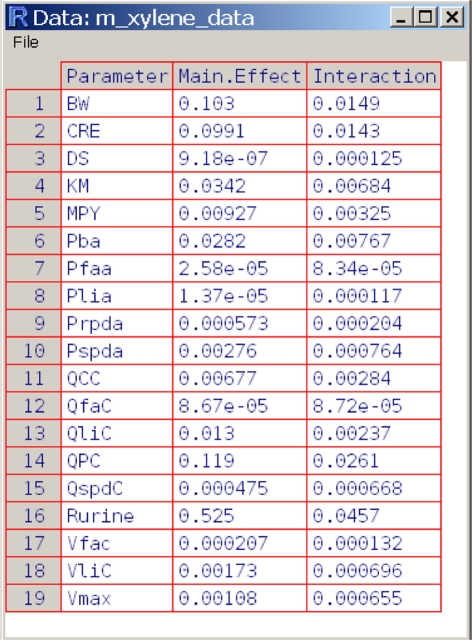
The data are assumed to have three columns:

• • “Parameter,” containing the name of the parameter

• • “Main Effect,” containing the size of the main effects

• • “Interaction,” containing the size of the interactions

In practise, you are likely to read in the data from a file, but for simplicity, here is some code to create sample data.

m_xylene_data <- data.frame(
     Parameter = c(
          "BW", "CRE", "DS", "KM", "MPY", "Pba", "Pfaa",
          "Plia", "Prpda", "Pspda", "QCC", "QfaC", "QliC",
          "QPC", "QspdC", "Rurine", "Vfac", "VliC", "Vmax"),
     "Main Effect" = c(
          1.03E-01, 9.91E-02, 9.18E-07, 3.42E-02, 9.27E-3, 2.82E-2, 2.58E-05,
          1.37E-05, 5.73E-4, 2.76E-3, 6.77E-3, 8.67E-05, 1.30E-02,
          1.19E-01, 4.75E-04, 5.25E-01, 2.07E-04, 1.73E-03, 1.08E-03),
     Interaction = c(
     1.49E-02, 1.43E-02, 1.25E-04, 6.84E-03, 3.25E-03, 7.67E-03, 8.34E-05,
     1.17E-04, 2.04E-04, 7.64E-04, 2.84E-03, 8.72E-05, 2.37E-03,
     2.61E-02, 6.68E-04, 4.57E-02, 1.32E-04, 6.96E-04, 6.55E-04
     )
)

Sometimes it is easier to use the data in wide format, other times in long format. This data fortification process returns both, plus some extra columns.

fortify_lowry_data <- function(data,
     param_var = "Parameter",
     main_var = "Main.Effect",
     inter_var = "Interaction")
{
     #Convert wide to long format
     mdata <- melt(data, id.vars = param_var)


     #Order columns by main effect and reorder parameter levels
     o <- order(data[, main_var], decreasing = TRUE)
     data <- data[o, ]
     data[, param_var] <- factor(
     data[, param_var], levels = data[, param_var]
     )


     #Force main effect, interaction to be numeric
     data[, main_var] <- as.numeric(data[, main_var])
     data[, inter_var] <- as.numeric(data[, inter_var])


     #total effect is main effect + interaction
     data$.total.effect <- rowSums(data[, c(main_var, inter_var)])


     #Get cumulative totals for the ribbon
     data$.cumulative.main.effect <- cumsum(data[, main_var])
     data$.cumulative.total.effect <- cumsum(data$.total.effect)


     #A quirk of ggplot2 means we need x coords of bars
     data$.numeric.param <- as.numeric(data[, param_var])


     #The other upper bound
     #.maximum = 1 - main effects not included
     data$.maximum <- c(1 - rev(cumsum(rev(data[, main_var])))[-1], 1)


     data$.valid.ymax <- with(data,
     pmin(.maximum, .cumulative.total.effect)
     )


     mdata[, param_var] <- factor(
          mdata[, param_var], levels = data[, param_var]
     )


     list(data = data, mdata = mdata)
}

The plot is essentially a bar chart plus a cumulative frequency ribbon, with some minor adjustments to improve appearance of the plot.

lowry_plot <- function(data,
     param_var = "Parameter",
     main_var = "Main.Effect",
     inter_var = "Interaction",
     x_lab = "Parameters",
     y_lab = "Total Effects (= Main Effects + Interactions)",
     ribbon_alpha = 0.5,
     x_text_angle = 25)
{
     #Fortify data and dump contents into plot function environment
     data_list <- fortify_lowry_data(data, param_var, main_var, inter_var)
     list2env(data_list, envir = sys.frame(sys.nframe()))


     p <- ggplot(data) +
     geom_bar(aes_string(x = param_var, y = "value", fill = "variable"),
          data = mdata) +
     geom_ribbon(
     aes(x = .numeric.param, ymin = .cumulative.main.effect, ymax = .valid.ymax),
     data = data,
     alpha = ribbon_alpha) +
     xlab(x_lab) +
     ylab(y_lab) +
     scale_y_continuous(formatter = "percent") +
     opts(axis.text.x = theme_text(angle = x_text_angle, hjust = 1)) +
     scale_fill_grey(end = 0.5) +
     opts(legend.position = "top",
          legend.title = theme_blank(),
          legend.direction = "horizontal"
          )
     p
}


m_xylene_lowry <- lowry_plot(m_xylene_data)
m_xylene_lowry

PBPK model CSL file

! ACSL script Model name: MHA_mict_CH.csl
! This model has a kidney+brain+lung compartment added to base model of
! slowly, rapidly perfused, liver and adipose
! Empirical model describing elimination of metabolite from blood to urine


PROGRAM


INITIAL


ALGORITHM IALG = 2
MAXTERVAL MAXT = 1.0e9
MINTERVAL MINT = 1.0e-9


CONSTANT RMM = 106.17 ! m-xylene molecular mass (g/mol)
CONSTANT MWMHA = 193.2 ! Methylhippuric acid molecular mass (g/mol)
CONSTANT CREmmol = 10.2 ! Urinary creatinine concentration (mmol/L)
CONSTANT BW = 79 ! body mass (kg)
CONSTANT VT = 0.91 ! proportion of vascularised tissue
CONSTANT QCC = 12. ! cardiac allometric constant (L/h/kg^CAE)
CONSTANT QPMC = 350 ! Alveolar ventilation (not scaled for SA analysis)
CONSTANT CAE = 0.75 ! cardiac allometric exponent
CONSTANT RAE = 0.75 ! respiratory allometric exponent
CONSTANT QspdAC = 0.27 ! overall fractional blood flow
CONSTANT VspdAC = 0.794 ! overall fractional volume
CONSTANT Pba = 15.1 ! blood:air partition coefficient
CONSTANT Pspda = 53. ! slowly perfused tissue:air partition coefficient
CONSTANT Prpda = 117. ! rapidly tissue:air partition coefficient
CONSTANT Pfaa = 1874. ! adipose tissue:air partition coefficient
CONSTANT Plia = 279. ! liver tissue:air partition coefficient
CONSTANT Pkia = 70.8 ! Kidney tissue:air partition coefficient
CONSTANT Pbr = 117.6 ! Brain tissue:blood partition coefficient
CONSTANT Plua = 33.4 ! lung tissue:air partition coefficient


CONSTANT QfaC = 0.05 ! adipose fractional blood flow
CONSTANT QspdC = 0.22 ! slowly perfused tissue fractional blood flow
CONSTANT QkiC = 0.19 ! Kidney fractional blood flow
CONSTANT QliC = 0.25 ! liver fractional blood flow
CONSTANT QbrC = 0.12 ! brain fractional blood flow to brain
CONSTANT QluC = 0.025 ! lung fractional blood flow
CONSTANT qrpdc = 0.1450 ! Logical constraint used to re-parameterise flows
CONSTANT VliC = 0.0257 ! liver fractional volume
CONSTANT VfaC = 0.299 ! adipose fractional volume
CONSTANT VspdC = 0.4950 ! slowly perfused tissue fractional volume
CONSTANT VkiC = 0.0044 ! Kidney fractional volume
CONSTANT VbrC = 0.02 ! brain fractional volume
CONSTANT VluC = 0.0167 ! lung fractional volume (both lungs)
CONSTANT vrpdc = 0.0492 ! rapidly perfused logical constraint used to re-parameterise masses
CONSTANT MPY = 32. ! microsomal protein yield (mg microsomal protein/g liver)
CONSTANT Km2E1 = 1.253 ! km (mg/L)
CONSTANT VmaxCivM2E1 = 895 ! vmax (molar; in vitro; microsomal) (pmol/min/mg)
CONSTANT DS = 0.3 ! proportion of dead space
CONSTANT QPC = 14.7 ! respiratory allometric constant (L/h/kg^RAE)
CONSTANT CIppm = 40 ! inhalation exposure concentration (ppm)
CONSTANT tinhon01 = 0. ! inhalation timepoint on (h)
CONSTANT tinhoff01 = 4. ! inhalation timepoint off (h)
CONSTANT K1 = 10 ! First-order elimination rate from blood (/h)


! Logical constraints for mass balance
qfaci = qfac/qcci
qkici = qkic/qcci
qbrci = qbrc/qcci
qluci = qluc/qcci
qlici = qlic/qcci
qspdci = qspdc/qcci
qrpdci = qrpdc/qcci


vrpdci = vrpdc/vti
vspdci = VspdC/vti
vfaci = vfac/vti
vbrci = vbrc/vti
vluci = vluc/vti


! scaling parameters
BWc = BW ** CAE
BWr = BW ** RAE


! Calculated tissue:blood partition coefficient
Pspdb = Pspda / Pba
Prpdb = Prpda / Pba
Pfab = Pfaa / Pba
Plib = Plia / Pba
Pkib = Pkia / Pba
Pbrb = Pbr / Pba
Plub = Plua / Pba


! scaled fractional masses
Vfa = VfaCi * BW
Vki = VkiC * BW
Vbr = VbrCi * BW
Vli = VliC * BW
Vlu = VluCi * BW
Vrpd = VrpdCi * BW
Vspd = VspdCi * BW


Vmax2E1 = VmaxCivM2E1 *1E-12 * Vli * RMM * MPY * 1000000 *60 ! vmax (mg/h)


! Logical constraint (tissue masses re-parameterised for global SA analysis)
vti = vrpdc + vspdc + vbrc + vluc + vkic + vlic + vfac


! Logical constraint (tissue blood perfusion rates re-parameterised for global SA analysis)
qcci =(QrpdC + QSPDC + QbrC + QluC + QkiC + QliC + QFAC)


P = 1 – DS ! proportion of inhaled gas
QC = QCC * BWc ! cardiac output (L/h)
QspdC = QspdAC - QfaC


QPa = QP * P ! alveolar ventilation rate (L/h)
Qspd = QspdCi * QC ! scaled fractional blood flow
Qrpd = QrpdCi * QC ! scaled fractional blood flow
Qfa = QfaCi * QC ! scaled fractional blood flow
Qli = QliCi * QC ! scaled fractional blood flow
Qki = QkiCi * QC ! scaled fractional blood flow to kidney
Qbr = QbrCi * QC ! scaled fractional blood flow to brain
Qlu = QluCi * QC ! scaled fractional blood flow
VspdC = VspdAC – VfaC


! Initial conditions
constant Afa0 = 0.0
constant Ali0 = 0.0
constant AMli0 = 0.0
constant Arpd0 = 0.0
constant Aspd0 = 0.0
constant AX0 = 0.0
constant AEx0 = 0.0
constant dose0 = 0.0
constant Aki0 = 0.0
constant AMki0 = 0.0
constant Abr0 = 0.0
constant Alu0 = 0.0
constant AMHAU0 = 0.0
constant AMHAB0 = 0.0


binexpinh = 0.0;


schedule inhexp.at. tinhon01
schedule inhexp.at. tinhoff01


!************ start 1st set of micturition additions ************


constant RUrine=0.074; ! Rate of Urine Production (l/h)
constant VBladder0 = 0.0 ! Initial volume of liquid in bladder


! Array of micturition timings
parameter(MAX_URINATIONS = 20)
dimension urinationTime(MAX_URINATIONS)
constant urinationTime = 0.0, 4.0, 6.0, 8.0, 10, 12, 14, 13*0.0
integer numUrinations
constant numUrinations = 7


! schedule urination events
     do 10 i = 1, numUrinations
          schedule urination.at. urinationTime(i)
               10: continue


! initialize the concentrations of urine
! inside the bladder and expelled urine
CBladder = 0.0 ! urine still in bladder
CUrine = 0.0 ! urine which has been expelled


!************ end 1st set of micturition additions **************
END ! INITIAL
! ****************************************************************************************
! Model
! ****************************************************************************************
DYNAMIC
!****************************************************************
!************ start 2nd set of micturition additions ************
!****************************************************************
! Discrete event code for urination
! Just reset the amount of liquid and chemical
! in the bladder to zero. Also update the variable
! which contains the concentration of chemical
! in expelled urine.


DISCRETE urination
! concentration of chemical in expelled urine
if(VBladder.gt. 0.0) then
     CUrine = AUCREmmol / (VBladder*CREmmol)
else
      CUrine = 0.0
endif


! reset the bladder liquid volume and amount of chemical
! in the bladder
  VBladder = 0.0
  AMHAU = 0.0
END


!****************************************************************
!************ end 2nd set of micturition additions **************
!****************************************************************

     DISCRETE inhexp
     ! inhalation binary exposure
     if((t.ge. tinhon01).and. (t.lt. tinhoff01)) then
           binexpinh = 1;
  else
     binexpinh = 0;
  endif
END


DERIVATIVE
! inhalation binary exposure
binexpinh = RSW((t.GT.tinhon01).AND.(t.LT.tinhoff01), 1, 0)
IH = CIppm * binexpinh * (RMM / 24450) ! inhalation infusion (mg/L)


! mass in system (mg)
mass = Aspd + Arpd + Afa + Ali + Aki + Abr + Alu + AMli + AX


rel = mass / (dose+1e-10) ! mass balance


Cfa = Afa / Vfa ! fat concentration (mg/L)
Cli = Ali / Vli ! liver concentration (mg/L)
Cki = Aki / Vki ! kidney concentration in kidney (mg/L)
Cbr = Abr / Vbr ! brain concentration in brain (mg/L)
Clu = Alu / Vlu ! lung concentration (mg/L)
Cspd = Aspd / Vspd ! slowly perfused concentration (mg/L)
Crpd = Arpd / Vrpd ! rapidly perfused concentration (mg/L)
CVlu = Clu / Plub ! lung venous organ concentration (mg/L)
CVfa = Cfa / Pfab ! fat venous organ concentration (mg/L)
CVli = Cli / Plib ! liver venous organ concentration (mg/L)
CVbr = Cbr / Pbrb ! Brain venous organ concentration (mg/L)
CVki = Cki / Pkib ! kidney venous organ concentration (mg/L)
CVspd = Cspd / Pspdb ! slowly perfused venous organ concentration (mg/L)
CVrpd = Crpd / Prpdb ! rapidly perfused venous organ concentration (mg/L)


CV = ((CVspd * Qspd) + (CVrpd * Qrpd) + (CVfa * Qfa) + (CVli * QLI) + (CVki * Qki)+(CVbr *
          Qbr)+ (CVlu * Qlu)) / QC ! venous concentration (mg/L)


CVumol = (CV/RMM)*1000 ! Venous concentration (micromoles/L)
CA = ((QC * CV) + (QPMC * IH)) / (QC + (QPMC / Pba)) ! arterial concentration (mg/L)

MRli = (Vmax2E1 * CVli) / (Km2E1 + CVli) ! rate of change of metabolism (mg/h/kg)
Rdose = QPMC * IH ! dose derivative (mg)
RAMli = Mrli ! amount metabolised derivative


CX = CA / Pba ! exhaled concentration (mg/L)
CXPPM = (0.7*CX + 0.3*ih)*(24450.0/RMM) ! exhaled concentration (ppm)
RAfa = Qfa * (CA - CVfa) ! fat compartment derivative (mg/h/kg)
RAli = (QLI * (CA - CVli)) – Mrli ! liver compartment derivative (mg/h/kg)
RAspd = Qspd * (CA - CVspd) ! slowly perfused compartment derivative (mg/h/kg)
RArpd = Qrpd * (CA - CVrpd) ! rapidly perfused compartment derivative (mg/h/kg)
RAki = Qki * (CA - CVki) ! kidney compartment derivative (mg/h/kg)
RAbr = Qbr * (CA - CVbr) ! Brain compartment derivative (mg/h/kg)
RAlu = Qlu * (CA - CVlu) ! lung compartment derivative (mg/h/kg)
RAX = QPMC * CX ! amount exhaled derivative (mg)


RAMHAB = MRli*(MWMHA/RMM)- (K1 * AMHAB) ! amount of methylhippuric acid in blood


RAMHAU = K1 * AMHAB ! amount of methylhippuric acid in bladder compartment
AUCREmmol = AMHAU*1000/MWMHA ! amount in bladder (mmol)


Afa = integ(RAfa, Afa0)
Ali = integ(RAli, Ali0)
AMli = integ(RAMli, AMli0)
Arpd = integ(RArpd, Arpd0)
Aspd = integ(RAspd, Aspd0)
AX = integ(RAX, AX0)
Aki = INTEG (RAki, Aki0)
Abr = INTEG (RAbr, Abr0)
Alu = INTEG (RAlu, Alu0)
AMHAU = INTEG (RAMHAU, AMHAU0)
AMHAB = INTEG (RAMHAB, AMHAB0)
dose = INTEG (Rdose,dose0)



!************ start 3rd set of micturition additions ************
     ! Amount of liquid in bladder
     ! Liquid accumulates in bladder at a constant rate
     VBladder = integ(Rurine, VBladder0)
     ! Concentration of chemical in bladder urine
     if(VBladder.gt. 0.0) then
CBladder = AUCREmmol / (VBladder*CREmmol)
          Else
CBladder = 0.0
     Endif
!************ end 3rd set of micturition additions **************
           CONSTANT TSTOP = 32
          TERMT (T.GE. TSTOP, ’checked on communication interval: REACHED TSTOP’)
     END ! DYNAMIC
     END ! DERIVATIVE
     TERMINAL
          ! code that is executed once at the end of a simulation run goes here
     END ! TERMINAL
END ! PROGRAM

M.file for eFAST analysis

% NOTE: THIS SCRIPT ASSUMES THE SIMULATION HAS ALREADY BEEN COMPILED AND LOADED!!!
% GSA using 2.5th and 97.5th percentiles caculated using PopGen for organ masses and flows and Vmax
% Other ranges based on measured data
% Output partial variances
% Model m-xylene_CLEAN_Megen_1.CSL


seedrnd(45678)

tic
prepare @clear
prepare t cv


% name of response variable
obsName = "Curine";


% names of parameters
factNames = ["RUrine","CREmmol","MPY","QPMC", "BW", "Pba", "VMAXCivM2E1", "Km2E1", "QCC",
                "VfaC", "QliC","Pfaa", "VliC", "Plia", "Pspda", "QfaC", "Prpda", "QspdAC", "K1"];


% ranges over which parameter may vary
parmRanges = [...
0.041, 0.125
9.8, 15.2
20, 50
367, 412
49, 92
11, 30
750, 1031
0.1, 2
10, 20
0.07, 0.28
0.2, 0.3
1400, 2200
0.02, 0.031
150, 350
40, 80
0.087, 0.096
50, 150
0.2, 0.35
2, 18
];
% interference factor, usually 4 or 6 (4 requires less computations)
% see Saltelli 1999 for explanation
M = 4;


% number of resamplings (lower number requires less computation)
% see Saltelli 1999 for explanation
Nr = 1;


% flags, see gsa.m comments for additional info
flags =1;


% call main function to compute sensitivity coeffs
[si, sim, DD]= gsaEFAST(obsName, factNames, parmRanges, M, Nr, flags);


% plot the coeffs computed above
totals = 1 - sum(sim’)’;


%Save all variables in workspace
save("xylene CV full scan GSA results 500ppm.mat")

toc

M.file for generating total and main effects and interaction plotting results

load("xylene CV full scan GSA results 500ppm.mat")
set(@Format = ’Long’)
mainEffectsWithTotals = [sim totals];


h1 = gsaPlotCoefs(obsName, factNames, _t, si);
title(h1, "Total Effects.aps")
h2 = gsaPlotCoefs(obsName, [factNames "totals"], _t, mainEffectsWithTotals);
title(h2, "Main Effects.aps")
h3 = plot(_t, DD);
title(h3, "Approximate Total Variance.aps")


pim = [];
for i = 1:length (factNames)
 pim = [pim, (DD(:,i).* sim(:,i))];
end
h4 = gsaPlotCoefs(obsName, factNames, _t, pim);
title(h4, "Partial Variances.aps")


h5 = gsaPlotCoefs(obsName, factNames, _t, si - sim);
title(h5, "Interactions")


% To evaluate one of your outputs at a specific time, use interp1, e.g.
%totalEffectAtTime5 = interp1(_t, si, 5)
mainEffectAtTime5 = interp1(_t, mainEffectsWithTotals, 5)
%partialVarianceAtTime5 = interp1(_t,pim,5)
interactionsAtTime5 = interp1(_t, si - sim, 5)


%totalEffectAtTime8 = interp1(_t, si, 8)
mainEffectAtTime8 = interp1(_t, mainEffectsWithTotals, 8)
interactionsAtTime8 = interp1(_t, si - sim, 8)


%totalEffectAtTime11 = interp1 (_t, si, 11)
mainEffectAtTim11 = interp1(_t, mainEffectsWithTotals, 11)
interactionsAtTime11 = interp1(_t, si - sim, 11)