An intelligent system based on fuzzy probabilities for medical diagnosis– a study in aphasia diagnosis

Abstract

BACKGROUND:

Aphasia diagnosis is particularly challenging due to the linguistic uncertainty and vagueness, inconsistencies in the definition of aphasic syndromes, large number of measurements with imprecision, natural diversity and subjectivity in test objects as well as in opinions of experts who diagnose the disease.

METHODS:

Fuzzy probability is proposed here as the basic framework for handling the uncertainties in medical diagnosis and particularly aphasia diagnosis. To efficiently construct this fuzzy probabilistic mapping, statistical analysis is performed that constructs input membership functions as well as determines an effective set of input features.

RESULTS:

Considering the high sensitivity of performance measures to different distribution of testing/training sets, a statistical t-test of significance is applied to compare fuzzy approach results with NN results as well as author's earlier work using fuzzy logic. The proposed fuzzy probability estimator approach clearly provides better diagnosis for both classes of data sets. Specifically, for the first and second type of fuzzy probability classifiers, i.e. spontaneous speech and comprehensive model, P-values are 2.24E-08 and 0.0059, respectively, strongly rejecting the null hypothesis.

CONCLUSIONS:

The technique is applied and compared on both comprehensive and spontaneous speech test data for diagnosis of four Aphasia types: Anomic, Broca, Global and Wernicke. Statistical analysis confirms that the proposed approach can significantly improve accuracy using fewer Aphasia features.

As the information age matures, it is becoming clear that human knowledge can and should play a pivotal role in handling the complexities/uncertainties of modern decision making systems. A theory is therefore highly desirable that can systematically formulate human knowledge as well as integrate it with other information systems such as mathematical/statistical models to form more intelligent decisions. Merging these two types of information in system design is therefore essential.

To perform such combination, the main problem is how to represent human knowledge into a mathematical formula. Essentially, fuzzy systems are rulebased systems that aim to achieve this representation. The core of a fuzzy system is a knowledge base composed of the so called fuzzy if-then rules. The first step of designing a fuzzy system is consequently to obtain or define a group of linguistic fuzzy if-then rules (domain knowledge) from human experts. The next step is to merge these rules into a single system.

Various fuzzy systems apply different principles for this merging. From one perspective, fuzzy systems are nonlinear mappings that map an n-dimensional input space to an m-dimensional output space, where certain properties can be defined for this mathematical re-lation. But from a different perspective, fuzzy systems are knowledge-based systems extracted from human knowledge in the form of fuzzy if then rules. Converting a knowledge base into a nonlinear mapping is an outstanding privilege of the fuzzy system theory. This conversion makes the ability to use knowledge based systems (fuzzy systems) in different applications such as signal process-ing, communication systems and medical diagnosis/decision making systems.

Fuzzy systems is one of several ingredients of computational intelligence, or their hybrid combination, such as artificial neural networks,¹,² fuzzy logic and fuzzy clustering,³,⁴ hybrid combinations of artificial neural networks and fuzzy logic,⁵ and geneticfuzzy algorithms,⁶,⁷ which have already been reported in the literature useful for medical diagnosis. Additionally, authors had earlier reported their preliminary success in an application of fuzzy clustering by statistical analysis.^8–10 While there is a great variation to the diagnosis approaches, the above research generally concur on the utility of fuzzy reasoning in dealing with the uncertainty and vagueness, which is typical in the type of diagnosis as well as its symptoms. Furthermore, fuzzy systems are considered attractive due to the transparency of their knowledge base. In other words, the resulting rules and membership functions can be later studied and interpreted by a medical expert for the sake of improvement or training.

In this paper, a different type of fuzzy rule-based structure is proposed for medical diagnosis that is based on fuzzy probability estimators as a key contributor to its inference engine, in contrast to our earlier work¹⁰ that we used a regular product inference engine. The basic premise of fuzzy probabilities here is the in-herent imprecision in probabilities arising out of either lack of sufficiently large data set due to prohibitive cost or inadequate measurements arising out of sensory limitations or environmental uncertainty. Fuzzy probabilities are part of a larger class of decision paradigms in which reasoning with imprecise probabilities is addressed.¹¹ In such a paradigm, fuzzy theory is viewed as a complement rather than a competition to probability theory in its handling of uncertainty.¹² This issue is now addressed more effectively, mainly due to the considerable advances in computing and processing information, making it reasonable to perform computations that are far more complex and less amenable to precise analysis than computations involving precise probabilities. Transition from precise probabilities to imprecise probabilities in probability theory is a form of generalization and as such it enhances the ability of probability theory to deal with real-world problems.¹³

The above paradigm of fuzzy probabilities is proposed here for medical diagnosis in general and aphasia classification in particular. After determining the corresponding fuzzy probabilities for each symptom and aphasia type, a set of rules are constructed that each corresponds to a different aphasia type. Each fuzzy rule represents a mapping between a set of features (antecedents) and a certain type of aphasia (consequent). The set of features is determined by statistical analysis of feature space. By giving a certain set of features, the output of each rule is therefore the diagnosed type of aphasia with a corresponding degree of certainty. Features are sequentially chosen based on how they contribute to improved diagnosis in training space. Unlike our earlier works,⁸,⁹,¹⁰ features that are chosen can be still chosen if they contribute more to improved diagnosis and are not eliminated from the pool of features. Here, we also consider reducing the size of feature space by studying the effectiveness of various features in correct aphasia diagnosis. Furthermore, we consider features from the spontaneous speech as well as the comprehensive model.

This paper is organized as follows. The types of aphasia and the database are introduced in Section 2. The proposed fuzzy probability approach is explained in Section 3. Results of the proposed approach and authors′ earlier work¹⁰ in this field are then statistically compared against those of artificial neural networks in Section 4. Finally, several conclusions are expressed in Section 5.

1) 2.APHASIA DATA BASE

Aphasia is as an acquired impairment of language processes underlying receptive and expressive modalities caused by damage to certain areas of the brain, which are primarily responsible for the language function; Reasons for such brain damage can be stroke, head injury or cerebral tumors. 100,000 new cases of aphasia are caused by stroke every year in the USA alone.¹⁴,¹⁵ Because human brain has large neural networks and various functional cerebral regions, malfunction of these networks can cause different syndromes, and different types of aphasia can be diagnosed. Aphasia diagnosis is a particularly difficult medical diagnostic job because, in addition to the typical complexities of medical diagnosis such as in natural diversity of test objects and expert opinion, there is a significant degree of added complexity by the linguistic uncertainty and vagueness in data, inconsistencies in the definition of aphasic syndromes, large number of interview questions/measurements with im-precision, and hence a natural diversity and subjectivity of opinions of experts who diagnose the disease as well. To reduce diagnostic error in the face of the problem's high com-plexity, Aphasic diagnosis is performed by testing for a large number of empirically cooccurring set of symptoms, rendering aphasic diagnosis a time consuming and error prone process even among multiple experts. The challenge, therefore, is to determine the most consistent and accurate estimation using fewest number of test questions.

Four major types of aphasia syndromes are listed as follows¹⁵:

• Broca's Aphasia (also called Motor or Expressive Aphasia)

• Wernicke's Aphasia (also called Sensory or Receptive Aphasia)

• Global Aphasia (also called Total Aphasia)

• Anomic Aphasia

While the above major types of aphasia may be clearly defined, their classic taxonomy is polytypic in the symptoms′ feature space, i.e. impairments may be part of more than one syndrome.

Furthermore, definition of syndromes is probabilistic rather than crisply defined, and there is great overlap in the boundaries of resulting clusters in the feature space.¹⁵

Major comprehensive language tests in English speaking countries are the Western Aphasia Battery (WAB) and the Boston Diagnostic Aphasia Examination (BDAE). In German speaking countries the Aachen Aphasia Test (AAT) is the commonly used test battery. Because the AAT was used for evaluation of language function in this database, the test has been described in more detail (see table 1).¹⁶

Table 1.

AAT subtests¹⁵

The AAT-test profiles of 265 aphasic patients were gathered since 1986. The database consists of some nominal data, e.g. diagnosis of aphasia type, disease, etc., and quantitative data, i.e. the AAT scores. All patients were examined at a time when no change in the aphasia classification or in the lesion size was expected. In the first time after a brain lesion, the symptoms as well as the size of the lesion can change because parts of the disturbed tissue (penumbra) can recover or can be irreversibly destroyed.¹⁵

From the above 265 AAT scores, 146 patients are diagnosed with one of the four major types of aphasia (Anomic, Broca, Global, and Wernicke), while the rest of the 265 profiles are either other types of aphasia or are undecided profiles. The 146 profiles have been split in two halves here, first half as training set and the second half as testing set.

Database is available online at this address http://fuzzy.iau.dtu.dk/aphasia.nsf.

Two classifiers are designed:

--The first classifier uses the spontaneous speech subtests of the AAT, because these tests are easy to take. Such a classifier is easy to consult, because it needs only a few inputs that are relatively easy to obtain. Inputs to the classifier are selected from the six test scores P0, P1, ..., P5. Diagnosis is the output, which is one of the major aphasia types: Anomic, Broca, Global, Wernicke. The data is processed by the classifier with the highest accuracy, or better to say, with a certain degree of error. The measure of accuracy is the percentage of correct diagnoses when test data set is used as the input of the classifier.

--The second classifier may use all the subtests of the AAT, referred to as the comprehensive model. A major challenge is to select a small but effective set of inputs, as is explained in the following section.

The proposed fuzzy probability classifier

The proposed fuzzy probability classifier approach has three general parts:

--First, statistical parameters for each feature of each type of aphasia are separately calculated from the training set (a set of 73 input-output pairs).

--Second, the calculated statistical parameters are used to construct candidate membership functions for the fuzzy rules. A membership function is defined for each corresponding feature of each aphasia type.

--Third, four fuzzy rules (one for each type of aphasia) are constructed iteratively using the above membership functions. Different combinations of atomic fuzzy propositions are iteratively examined/selected to gain the best possible fuzzy rule-base. The rule construction procedure considers the contribution of all available features one at a time in order to avoid the time consuming alternative of an exhaustive search. The rule base uses a fuzzy probability estimator as inference engine. For calculation MATLAB software version 7.0 is used.

A. Calculating Statistical Parameters

For each aphasia type in the training set and for each feature, mean and standard deviation σ_i^l are calculated as below, where I = 1,…, 30 is index of features, l = 1,…, 4 is index of aphasia types.

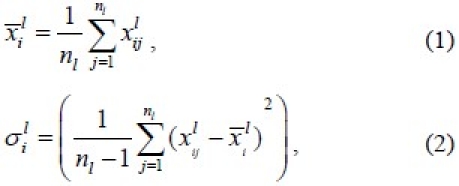
And where j = 1,… n₁ is index of patient re-cord, and n₁ is the total number of patients for each aphasia type l.

B. Membership Function Definition

The above statistical parameter pairs are then used to define trapezoid fuzzy set A_i^l as below:

Where, d_i^l, c_i^l, b_i^l, a_i^l are defined as follows:

Figure 1 illustrates the histogram of a typical feature N4 (Compound words) from feature space for patients with the four Aphasia types. As can be seen, it is difficult to determine the optimal general shape for the fuzzy probabilities due to the small available dataset. Authors implemented both trapezoid and Gaussian forms in the earlier stages of their research and confirmed that, as will be shown in the following sections, the trapezoid form provides a good performance as well as reasonable “fit” to the distribution of patient records.

Figure 1.

Histogram of a typical feature N4 (Compound words) from feature space which shows thedistribution of patients scores. There are respectively 24, 42, 33 and 47 patients for Anomic, Broca, Global and Wernicke.

C. Obtaining Fuzzy Rule-base

For each type of aphasia, a general fuzzy rule is defined as:

Where degree of truth for each atomic fuzzy proposition (x_i is A_i^l) is defined by 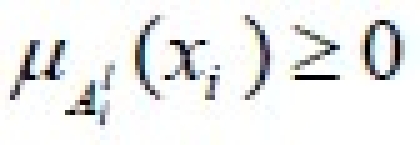. A composition of these atomic terms makes up the fuzzy rule's antecedent. The degree of certainty for l^th rule, u^l, is calculated by using fuzzy probability estimator.¹⁷ Zadeh¹² defines the probability of a fuzzy event A by

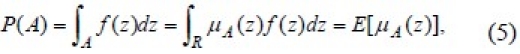
where z is a random variable, f (z) the density of z, u_A (z) the membership function for the fuzzy event A, and E[.] the expected value. On this basis, the probability of the fuzzy output event C is

An estimator fot the probability P(C)¹⁸

which is interpreted as average membership degrees and is implemented as a part of the inference engine as follows:

Where m ≤ 30 is the total number of features that are actually used as input in the antecedent part of the rule. During testing stages, u¹ is interpreted as the degree of affinity of a given patient to a particular aphasia type l during testing.

Rule generation algorithm aims to gain the highest accuracy with fewest inputs by recursively and exhaustively examining all possible first order combination of inputs. For all Aphasia classes, the same set of features is used in the rule-base. In other words, features are the same in all rules, differing only in their definition of membership functions for different aphasia types (classes). The search algorithm is stated as follows. At start, algorithm begins with only one feature, i.e. one atomic term in the antecedent. All available features and their corresponding atomic fuzzy propositions are substituted one at a time in the rule structure and the feature with the best performance is selected. The algorithm then keeps this feature's corresponding atomic proposition in the rule but doesn't omit it from the set of features; this means that a feature can be reselected in next stages. This is unlike our previous work¹⁰ and also Huang and Gedeon's²⁰ in which the same search algorithm was used but the selected feature form set of features was omitted and couldn't be reselected after its first selection. In second stage, it appends another atomic term from the set of features to the rule's antecedent, choosing the feature which produces the best accuracy in combination with previously chosen feature. This process is repeated until no further classification improvement is gained by adding a feature.

In this application, the search algorithm has been started with one feature in each rule. Following the iterative rule generation algorithm, the best accuracy is found by a combination of three features for comprehensive model (feature x₆ has been selected twice in the first and third stages of search algorithm) and two features for spontaneous speech. It is observed that increasing the number of features any further will either has no effect on it or decrease the accuracy.

For instance, below rules are obtained with comprehensive model data.

The Matrix U=[u^l] is the output of rules Where u^l represents the degree of belonging to each l^th type of aphasia, and is calculated as indicated in (8). Finally, maximum value of u^l is considered as final diagnosis for aphasia type T:

Figure 2 shows the fuzzy probability classifier as a diagram.

Figure 2.

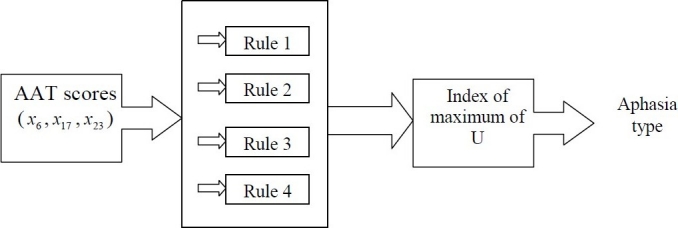
Fuzzy classifier diagram.

Results

The above fuzzy classifier approach is applied to two sets of data, first set is data from spontaneous speech interview, while the second is from comprehensive model data as explained in Section 2. For comparative purposes, a back-propagating neural network (NN), with network characteristics similar to those reported in¹,² has been tested on both sets of data. More-over, we compared the results with a hierarchical fuzzy rule based approach. The hierarchical rule based approach here is similar to Akbarzadeh-T and Moshtagh-K¹⁰ with a difference on method of feature selection. Since feature selection based on nonelimination yields better results, the results of the hierarchical fuzzy rule based approach are also updated in this paper. Furthermore, in order to reach reliable conclusions, a 50 fold cross validation on 50 random distributions of training sets and testing sets are considered. For the NN, the design choices are as follows:

Network topology: A multilayer perceptron with an input layer, a hidden layer, and an output layer.

Inputs: Test scores P1, P5, N0, and C1.

Outputs: The four classes A, B, G, and W.

Neurons: 4-5-4 neurons, read layerwise from input layer to output layer, with sigmoid-sigmoid-linear activation functions.

Learning method: Back-propagation with momentum.

Software: MATLAB version 7.0

Table 2 shows the features used as inputs for the networks of both classifiers.

Table 2.

Features for ANN classifiers¹,²

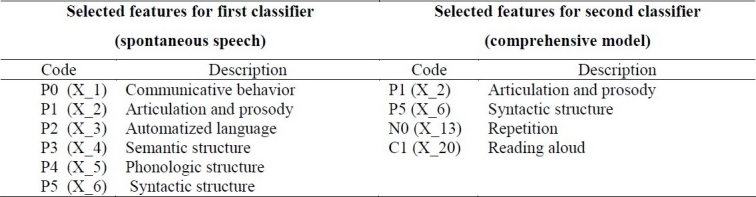
The detailed results of applying NN for 50 random distributions are presented in our previous paper,¹⁰ respectively for both spontaneous speech and comprehensive model feature space.

The results are comparable to those reported earlier in some studies¹,²; although the results of these studies only mentioned one specific distribution, i.e. the best result for NN with spontaneous speech is 87% and for comprehensive model is 92% correct diagnosis for all four major types of aphasia. The best result that was obtained in Akbarzadeh-T and Moshtagh-K¹⁰ for classification with spontaneous speech is 90.82%, and with comprehensive model is 91.89%.

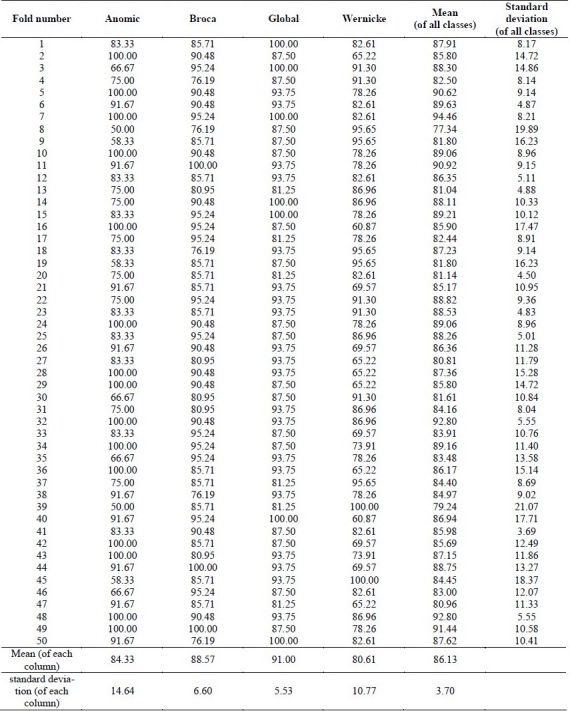
Next, the proposed fuzzy approach is ap-plied. Table 3 shows the features used as inputs for the obtained rules in both classifiers. A 50-fold cross validation of the fuzzy approach is presented in Table 4 and Table 5, respectively, for first classifier (with spontaneous speech) and second classifier (with comprehensive model). The best result for first classifier is 96.74% and for second classifier is 94.46% correct diagnosis, as mean of correct diagnosis for the four classes.

Table 3.

Selected features for fuzzy classifiers

Table 4.

Fuzzy probability estimator results for test sets (first classifier (spontaneous speech) features: test scores P0 and P5)

Table 5.

Fuzzy probability estimator results for test sets (second classifier (comprehensive model) features: test scores P5, N4, B0)

The results of applying hierarchical fuzzy rule based approach on aphasia database as explained in Akbarzadeh-T and Moshtagh-K's work,¹⁰ for a 50 fold cross validation of training sets and test sets, are presented in Table 6 and Table 7, respectively, for first classifier (with spontaneous speech) and second classifier (with comprehensive model). The best result for first classifier is 91.30% and for second classifier is 95.55% correct diagnosis, as mean of correct diagnoses for the four classes.

Table 6.

Fuzzy hierarchical method results for test sets (first classifier (spontaneous speech) features: test scores P0 and P5)

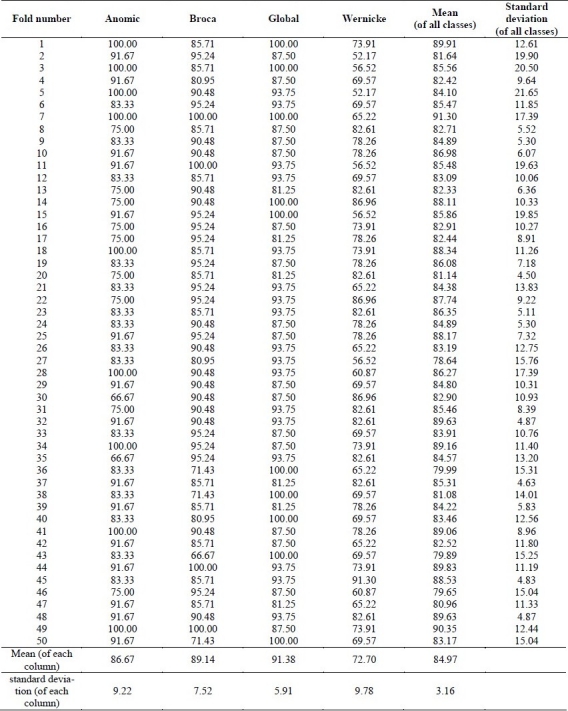
Table 7.

Fuzzy hierarchical method results for test sets (second classifier (comprehensive model) features: test scores P5, N4, B0)

Finally, we compare the proposed fuzzy probability estimator approach here with neural networks and our previous fuzzy hierarchical approach as explained in Akbarzadeh-T and Moshtagh-K's work.¹⁰ We should indicate that, for a fair comparison, we applied the search algorithm which is explained in section 3 to our previous fuzzy hierarchical approach as well.¹⁰ Considering the high sensitivity of performance measures to different distribution of testing/training sets, a statistical t-test of significance is applied here to compare both fuzzy approaches results with NN results. The proposed fuzzy probability estimator approach clearly provides better diagnosis for both classes of data sets. Specifically, for the first and second type of fuzzy probability classifiers, i.e. spontaneous speech and comprehensive model, p values are 2.24E-08 and 0.0059, respectively, strongly rejecting the null hypothesis. While the change in feature selection improved performance of our previous fuzzy hierarchical approach,¹⁰ the significance of statistical results did not change. It can also be deduced that both hierarchical fuzzy and fuzzy probabilities perform comparatively better when there is more uncertainty, i.e. fewer test data as in spontaneous speech model. It should be also noted that the fuzzy probability estimator approach is able to reach this level of performance using significantly fewer number of features than NN, but the number of measurements are the same in both fuzzy approaches (see table 8). It should also be mentioned that the fuzzy probability estimator calculates quicker than neural networks and fuzzy hierarchical method. The total execution time for one training/testing simulation is 12.53 seconds for the neural networks and 2.60 seconds for the fuzzy probability estimator approach, also in our previous work it was 4.35 seconds for hierarchical fuzzy rule based method. Fuzzy probability estimator approach is about five times quicker than neural networks and about 1.7 times quicker than our previous work, the hierarchical fuzzy rule based method.

Table 8.

Comparing fuzzy approaches with neural networks

Conclusion

Fuzzy probability estimator can be considered as a type of perception based probability the-ory. In perception based probability theory everything and especially truth and possibility is or is allowed to be a matter of degree. This is in contrast to standard probability theory where only likelihood is a matter of degree. In this paper, we proposed the use of fuzzy probabilities for better medical classification and implemented it on Aphasia diagnosis. While Aphasia presents a particularly challenging medical diagnosis due to various complexities such as in linguistic uncertainty and vagueness in measurement data as well as inconsistencies in the definition of aphasic syndromes themselves, this paper concludes that fuzzy probabilities are an appropriate decision making paradigm to reach good accuracy in its prediction and classification.

The proposed fuzzy probability approach begins with statistical analysis of the input feature space for defining the membership functions and reducing the size of the feature space. The fuzzy system performs the diagnosis by detecting the affinity of a new data set to the previously trained clusters of data. The clusters are defined by membership functions that are chosen after statistical analysis of the feature space. The proposed method is then applied to the aphasia database at AAT and results are compared with those of previously reported neural networks. Statistical analysis reveals that the proposed fuzzy approach has a better performance for accuracy while also using fewer features as compared with artificial neural networks. In fact, due to the high level of conflict and vagueness in the data set, it is observed that using more inputs will not necessarily produce better accuracy, while the choice of features will significantly influence classification performance. It is also observed that proposed fuzzy probability estimator has a better performance than our previously proposed hierarchical fuzzy rule based approach.

Authors’ Contributions

MMKh carried out the design and coordinated the study, participated in all of different parts of this study and prepared the manuscript.

MRAT provide assistance in the design of the study and participated in manuscript preparation.

NJ and MKh provides assistance for all other non engineering parts of the study.

All authors have read and approved the content of the manuscript.