Abstract
Tropomyosin (Tm) plays a critical role in regulating the contraction of striated muscle. The three-state model of activation posits that Tm exists in three positions on the thin filament: “blocked” in the absence of calcium when myosin cannot bind, “closed” when calcium binds troponin and Tm partially covers the myosin binding site, and “open” after myosin binding forces Tm completely off neighboring sites. However, we recently showed that actin filaments decorated with phosphorylated Tm are driven by myosin with greater force than bare actin filaments. This result cannot be explained by simple steric hindrance and suggests that Tm may have additional effects on actin-myosin interactions. We therefore tested the hypothesis that Tm and its phosphorylation state affect the rate at which single actin-myosin bonds form and rupture. Using a laser trap, we measured the time necessary for the first bond to form between actin and rigor heavy meromyosin and the load-dependent durations of those bonds. Measurements were repeated in the presence of subsaturating myosin-S1 to force Tm from the closed to the open state. Maximum bond lifetimes increased in the open state, but only when Tm was phosphorylated. While the frequency with which bonds formed was extremely low in the closed state, when a bond did form it took significantly less time to do so than with bare actin. These data suggest there are at least two closed states of the thin filament, and that Tm provides additional points of contact for myosin.
Keywords: Actin, Contractile Protein, Myosin, Protein Phosphorylation, Skeletal Muscle, Tropomyosin
Introduction
The actin-binding protein tropomyosin (Tm)2 is thought to operate in opposing roles as an inhibitor or an activator in the cross-bridge cycle by sterically hindering myosin binding to actin in the absence of calcium and, conversely, promoting the cooperative relief of inhibition over the span of one regulatory unit when an initial myosin binds (1–3). Data suggest that the transition of Tm from an inhibitory to a permissive state proceeds through at least one intermediate step. The three-state model of cooperative activation suggests that Tm exists in three positions on the thin filament: 1) blocked, in the absence of calcium when myosin cannot bind; 2) closed, when calcium binds troponin and Tm still partially covers the myosin binding site; and 3) open, after initial myosin binding forces Tm completely off neighboring myosin binding sites (4, 5).
These state changes are thought to be propagated to neighboring regulatory units on the thin filament. Tm polymerizes in a head-to-tail manner with neighboring Tm dimers (6), and evidence suggests that Tm can transmit conformational changes over long distances via end-to-end interactions (7–9). In the α isoform of Tm found in striated muscle, there is a phosphorylation site near the carboxyl terminus at Ser-283 (10). This phosphorylation site is in the head-to-tail overlap between neighboring Tm dimers, and we showed previously that Tm phosphorylation is necessary to extend cooperative activation beyond one regulatory unit (11). We also found that actin filaments decorated with phosphorylated Tm (A+Tm.P) produced greater isometric force at intermediate densities of myosin than bare actin filaments or actin filaments decorated with dephosphorylated Tm (A+Tm.DP) (11). This increase in force suggests that phosphorylated Tm may augment actin-myosin interactions.
To test the hypothesis that Tm phosphorylation has effects on binding kinetics at the level of single cross-bridges, we used a laser trap to measure the rate of heavy meromyosin (HMM) binding to actin in the rigor state, as well as the load-dependent bond lifetimes of rigor HMM unbinding from actin. We performed these measurements using bare actin filaments, A+Tm.P, and A+Tm.DP. To control the activation state of the filament, we used myosin-S1 to force Tm from the closed to the open state. Our data suggest that Tm exists in at least two “closed” states, and that it provides additional points of contact for myosin on the thin filament that modify both the rate of actin-myosin bond formation and the intrinsic lifetime of the bond.
EXPERIMENTAL PROCEDURES
Proteins
HMM was prepared from rat skeletal muscle as described in Guo and Guilford (12). Myosin subfragment 1 (S1) was prepared according to Margossian and Lowey (13) and modified with N-ethylmaleimide (NEM). All proteins were stored in liquid nitrogen in small aliquots containing 50% glycerol. F-actin was prepared from rat skeletal muscle according to Pardee and Spudich (14), biotinylated with N-hydroxysuccinimide biotin according to Rao et al. (11), and stabilized with phalloidin. Tm was also prepared from rat hind leg skeletal muscle as described by Smillie (15) and reconstituted with F-actin according to Rao et al. (11). The level of Tm phosphorylation in both the reconstituted and free state was assumed to reflect the native level as reported by Rao et al. (11) using a similar preparation. Free Tm and Tm-decorated actin filaments were dephosphorylated with calf intestine alkaline phosphatase (Calbiochem) as described by Rao et al. (11).
Actin filaments, A+Tm.P, and A+Tm.DP were coupled to 0.97-μm (diameter) streptavidin-coated microspheres (Bangs Laboratories, Fishers, IN). A suspension containing ∼4 × 108 beads was combined with a 2 μm final concentration of biotinylated actin filaments with and without Tm.P or Tm.DP (a significant excess to occupy all available streptavidin sites) and allowed to couple with overnight mixing at 4 °C. Beads were washed and resuspended with actin buffer (25 mm KCl, 25 mm imidazole, 1 mm EGTA, 4 mm MgCl2 (pH 7.4)). The actin-coated beads were blocked with 1 mg/ml BSA to reduce nonspecific interactions. HMM rather than myosin was used for all experiments to reduce nonspecific interactions and to limit binding events to those with single heads (16). NEM-S1 was used to transition Tm from the closed to the open state on actin filaments.
Site Densities and Contact Areas
Site densities from HMM-coated pedestals were calculated from previously published values from the lab (12). The number of available myosin binding sites on the actin-coated beads was determined fluorescently by binding saturating concentrations of myosin-S1 modified with Alexa Fluor 488 C5-maleimide (Invitrogen). Alexa Fluor 488 C5 maleimide (AF) was added to S1 at a 10-fold molar excess and reacted at room temperature in the dark for 1 h. The reaction was stopped by adding 25 mm DTT to quench the excess AF. The reaction mixture was then dialyzed (10,000 kDa molecular mass cutoff) with two buffer changes overnight in 1 liter of actin buffer. An actin-coated bead population of 1.2 ± 0.09 × 106 beads/μl was mixed with the AF-S1 over a range of concentrations (150 nm AF-S1 to 1 μm AF-S1), and fluorescence intensity was measured using a FluoStar Optima plate reader (excitation, 480 nm; emission, 520; BMG, Durham, NC) to determine at what concentration AF-S1 saturably binds the beads. These fluorescence values were compared with an AF-S1 standard curve over a range of 1–20 nm to determine the concentration of AF-S1 bound to a population of actin-coated beads. The density of myosin binding sites (μm−2) was subsequently calculated.
Laser Trap
The laser trap used in these studies was described in detail in Guilford et al. (17). Back focal plane interferometry was used to measure the position of trapped beads relative to the trap center, from which measurements of displacement and force were calculated. The sensitivity of the interferometer and the trap stiffness were calibrated by the step response method (18, 19) and by fits to the power spectral density (20).
Nitrocellulose-coated coverslips with 3–10-μm pedestals were prepared as described (16). 20 μg/ml rat skeletal HMM in actin buffer was incubated in a flow cell for 1 min at room temperature. The flow cell was then blocked with 1 mg/ml BSA in actin buffer for 1 min. A suspension of actin-coated, A+Tm.P, or A+Tm.DP beads was then introduced. For A+Tm.P and A+Tm.DP, 500 nm free Tm.P or Tm.DP was included. For time to bond formation and bond lifetime experiments, NEM-S1 was added to the bead suspension at a range of 10–20 nm to force the closed-to-open transition of Tm (Fig. 1D). An oxygen scavenger system (0.125 mg/ml glucose oxidase, 0.0225 mg/ml catalase, 2.87 mg/ml glucose) was also included in the bead suspension. All solutions contained 10 mm DTT. For control experiments, 1 mm Na4P2O7 (pyrophosphate) was included in the bead suspension (16).
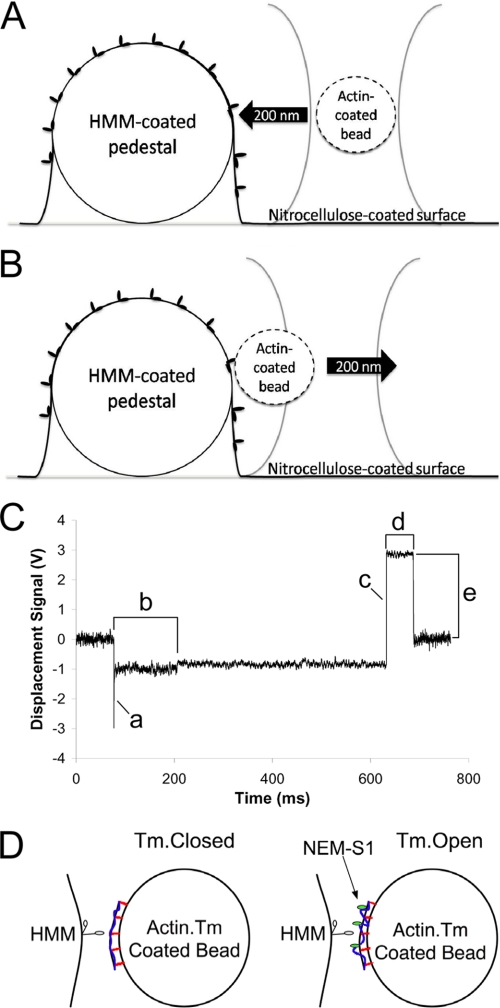
FIGURE 1.
Experimental Setup. A, an actin-coated bead is captured in the laser trap and moved rapidly into contact with an HMM molecule adhered to an immobilized glass pedestal coated with nitrocellulose. A bond is allowed to form. B, the actin-HMM bond is loaded by rapidly moving the laser 50–200 nm away from the pedestal. C, a representative force trace collected from bare actin-coated beads making contact with an HMM-coated pedestal. The actin-coated bead was stepped 200 nm toward the HMM-coated pedestal (a). The tb was characterized by a slight decrease in the variance in the trap signal and a significant shift in the baseline of the trap signal (b). The laser was moved 200 nm away from the HMM-coated pedestal to load the actin-HMM bond (c). The resulting bond lifetime (d) and the load experienced by the bond (e) were subsequently calculated based on the laser trap stiffness. D, biotinylated actin filaments (black curved line with red lines perpendicular to the bead surface) decorated with Tm (blue line) and bound to streptavidin-coated beads were preactivated by adding NEM-S1 (green ovals) at subsaturating concentrations to the bead mixture. If Tm is present, NEM-S1 should shift Tm from the closed state to the open state, exposing more myosin binding sites on the actin filaments bound to the bead. Bond formation and dissociation were measured with Tm in the closed state (no NEM-S1) and Tm in the open state (10–20 nm NEM-S1). Note that Tm motions are exaggerated in this figure for effect and that the figure is not drawn to scale.
The flow cell was placed onto a piezoelectric microscope stage. A bead was captured in the laser trap and brought into contact with an HMM-coated pedestal on the surface. Details of individual laser trap experiments are given under “Results.”
The contact area between the actin-coated and HMM-coated beads was estimated as reported previously (21). We assumed the bond length, l, to be 30.5 nm, assuming 20 nm for the length of an HMM molecule protruding normally to the nitrocellulose-coated surface, 7 nm for actin, and 3.5 nm for streptavidin bound on the microsphere. The mean radius of the HMM-coated pedestals and the actin-coated beads was 1.5 and 0.485 μm, respectively. The resulting contact areas were 6.9 × 10−2 μm2 for HMM-coated pedestals and 7.1 × 10−2 μm2 for actin-coated beads.
RESULTS
Shifting Tm from the Closed to the Open State
Myosin binding to actin is necessary to shift Tm from the closed state to the open state and completely expose myosin binding sites. We used NEM-S1, which binds tightly to actin, to shift Tm-decorated actin from the closed to the open state. Thus, the frequency with which bonds form would be expected to increase with increasing NEM-S1 concentration up to a point and then decrease as the myosin binding sites on the actin filaments become fully occupied.
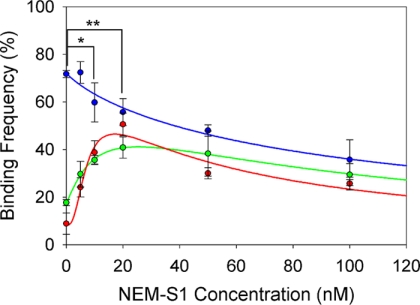
To determine the NEM-S1 concentration necessary for maximum HMM binding to occur, we measured the frequency of bond formation for single HMM-actin interactions as a function of NEM-S1 concentration. Actin-coated beads were captured in a laser trap and brought into contact with an HMM-coated target (Fig. 1A). Whether or not a bond had formed was determined by moving the laser trap away from the HMM-coated target (Fig. 1B). If a bond had formed, the trapped bead would remain in contact with the target until the actin-myosin bond ruptured (Fig. 1C). Bond frequency was defined as the ratio of the number of bonds formed to the total number of trapped- and target-bead contacts. Bond frequency was measured as a function of NEM-S1 concentration. Other factors such as contact area, protein density, and contact time were not included because they were constant throughout the experiments (22).
The results of these experiments are shown in Fig. 2. As expected, bare actin-coated beads exhibited the highest binding frequency (70 ± 1%) when no NEM-S1 was present and declined in binding frequency because of competitive inhibition of binding as NEM-S1 concentration was increased. Overall, bare actin produced the highest binding frequencies at all concentrations of NEM-S1. In contrast, the binding frequencies of beads coated with A+Tm.P and A+Tm.DP produced the lowest binding frequencies when no NEM-S1 was present. This implies steric hindrance by Tm in the absence of any initial myosin binding. As the concentration of NEM-S1 was increased to ∼20 nm, the binding frequencies of the A+Tm.P and A+Tm.DP beads reached maxima of 50 ± 5% and 40 ± 5% respectively. At higher NEM-S1 concentrations, binding frequencies for both A+Tm.P and A+Tm.DP steadily declined, presumably because of competition for binding sites by NEM-S1 and some remaining steric hindrance by Tm.
FIGURE 2.
Binding frequency was measured over a range of NEM-S1 concentrations (0–100 nm) for actin beads (blue circles), A+Tm.P beads (red circles), and A+Tm.DP beads (green circles). Equation 1 (blue line) was fitted to the actin bead data, and Equation 2 was fitted to the A+Tm.P and A+Tm.DP bead data (red line and green line, respectively). The mean step loads applied for bond frequency measurements ranged from 12–15 pN. The mean number of trapped- and target-bead contacts was 752 per data point. *, significance between A+Tm.P versus bare actin; **, significance between A+Tm.DP versus bare actin (p < 0.05).
The binding frequency between HMM with bare actin-coated beads was modeled as competitive inhibition and was fit by a Hill equation as a function of myosin-S1 concentration
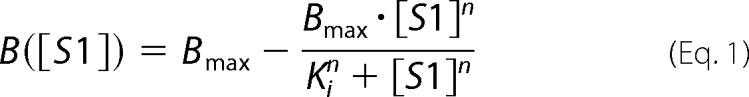 |
where B is the bond frequency, [S1] is the NEM-S1 concentration, Bmax is the bond frequency of HMM when exogenous NEM-S1 is absent, Ki is [S1] at 50% inhibition, and n is the Hill coefficient of inhibition. Inhibition of binding with bare actin filaments was non-cooperative with a Hill coefficient of 0.85 ± 0.1 (Fig. 2). This is consistent with previous findings suggesting that myosin binding to actin filaments is non-cooperative (23). 50% inhibition occurred at [S1] = 99 ± 19 nm.
In the case of A+Tm.P and A+Tm.DP, the addition of NEM-S1 is expected to shift the position of Tm from the closed conformation to the open conformation and expose myosin binding sites. Thus the bond frequency data of A+Tm.P and A+Tm.DP was analyzed as the difference of two Hill equations, one that describes the rise in bond frequency (closed-to-open activation) and one that describes fall in bond frequency (competitive inhibition). Non-zero binding frequency in the absence of NEM-S1 is assumed to arise from incomplete reconstitution of Tm onto the actin filament. In this simple model we do not attempt to model the low rate of myosin binding in the closed state that occurs as Tm diffuses across the actin filament.
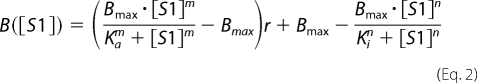 |
Ka is [S1] at 50% activation, m is the Hill coefficient of activation, and r is the fraction of filaments regulated by Tm. Fitted values of r suggest that A+Tm.P and A+Tm.DP filaments were regulated by 87 and 76%, respectively, as evidenced by the nonzero binding frequencies in the absence of NEM-S1. These data are consistent with the fractional binding of Tm to actin predicted from the binding kinetics of Tm.P and Tm.DP (11) (88 and 95%, respectively). The balance of events without NEM-S1 are presumably because of a small frequency of binding in the closed state.
This simple model also assumes that Bmax is the same in both Tm-regulated and unregulated actin filament units. If we fit Equation 2 allowing these Bmax to differ between the states, the two fitted estimates of this parameter do not differ significantly from one another (although with large error).
A+Tm.P activation by NEM-S1 was cooperative with a Hill coefficient of activation of 2.3 ± 0.7, whereas with A+Tm.DP filaments it was non-cooperative (m = 1.2 ± 0.1). These manifest as bond frequencies that increase rapidly with NEM-S1 in A+Tm.P, whereas the rise in bond frequency in A+Tm.DP is less abrupt (see Fig. 2). These Hill coefficients are consistent with our previous evidence suggesting that phosphorylated Tm extends cooperative activation beyond one thin filament regulatory unit (11).
The Hill coefficients of inhibition for A+Tm.P and A+Tm.DP did not differ significantly from 1.0 and are not suggestive of cooperativity (n was 1.1 ± 0.7 and 1.2 ± 0.1 for A+Tm.P and A+Tm.DP, respectively). Therefore, the data were fit using n = 1 for A+Tm.P and A+Tm.DP to reduce fitting error. [S1] at 50% inhibition was significantly lower for A+Tm.P compared with actin. This implies that A+Tm.P increases the affinity of the thin filament for myosin compared with bare actin filaments. This is consistent with earlier findings with (24) and without (25) troponin present. In the presence of Ca2+ as well, the affinity of S1 for Tm/troponin-decorated filaments is higher than that of bare actin (26).
Tropomyosin Phosphorylation Accelerates Formation of the First Actin-Myosin Bond
To determine whether Tm phosphorylation affects actin-myosin on-rates, we measured the time to bond formation (tb) between single HMM and myosin binding sites on actin-coated beads. Formation of the first bond between actin on the trapped bead and HMM on the target was accompanied by a small shift in bead position and a decrease in Brownian motion of the trapped bead. tb was defined as time elapsed between bead-target contact and the initial formation of a bond (Fig. 1C). We previously reported this method for studying selectin-ligand bonds (27), and a similar method has been reported using a biomembrane force probe (28). This measurement differs from the frequency of bond formation because tb is only measured when a bond actually forms.
We used our measured tb to calculate specific 2D on-rates (μm2/s) using the equation
where mr is the site density of HMM molecules on the nitrocellulose-coated pedestals, ml is the density of available myosin binding sites on our actin-coated beads, and Ac is the effective contact area between the pedestal and the trapped bead. mr was determined to be 1255 heads/μm2 using previously published data collected using the NH4-ATPase method (12). An ml of 637 myosin binding sites/μm2 of bead surface was determined by binding AF-NEM-S1 to the actin-coated beads and calculating the available myosin binding sites. Ac between the HMM-coated pedestal and actin-coated bead was estimated (21) at 0.14 μm2.
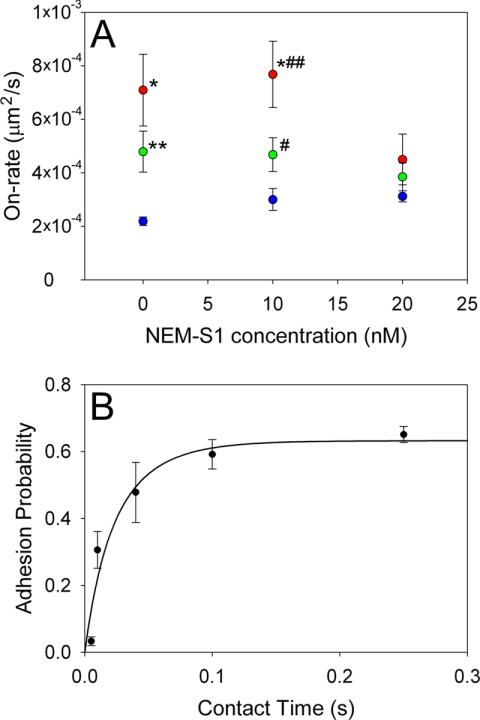
Specific 2D on-rates for each experimental condition are shown in Fig. 3A. To test how tb changed as Tm is shifted from the closed to the open state, NEM-S1 was applied at subsaturating concentrations of 10 and 20 nm. 20 nm was chosen because it corresponds to the highest degree of activation of the reconstituted filament (Fig. 2). Surprisingly, when no NEM-S1 was present (the presumed closed state of Tm) the on-rates of both A+Tm.P and A+Tm.DP were ∼3 times and ∼2 times greater than bare actin, respectively. As Tm shifted from the closed state to the open state, on-rates decreased significantly in A+Tm.P (p = 0.04) and converged toward that of bare actin filaments (see Fig. 3A). Thus, Tm in the closed state accelerates the stereospecific binding of myosin to the filament. Moreover, the degree of acceleration of actin-myosin binding by Tm seems to be dependent on phosphorylation, as kon0 is highest in A+Tm.P at all concentrations of NEM-S1. While it is tempting to argue that the addition of NEM-S1 simply blocks available myosin binding sites resulting in lower on-rates, half-maximal inhibition of bare actin occurs at much higher concentrations (50–100 nm NEM-S1).
FIGURE 3.
The specific 2D on-rates of actin, A+Tm.P, and A+Tm.DP with HMM are plotted as function of NEM-S1 concentration to alter the state of Tm (A). Specific 2D on-rates (kon0) were calculated from Equation 3. The mean number of on-rate measurements per data point was 175. *, p = 0.0003 compared with actin beads. B, adhesion probability was plotted as a function of contact time for actin-coated beads making contact with HMM-coated pedestals. Adhesion probability was defined as the number of bonds formed divided by the total number of attempts. Equation 3 was fit (black line) to the data to determine the kon0. The mean number of steps per data point was 632. **, p = 0.0009 compared with actin beads; #, p = 0.02 compared with actin beads; ##, p = 0.03 compared with A+Tm.DP.
While specific 2D on-rate results cannot be directly compared with the rate of S1 association with actin as measured by classical methods such as stopped-flow, certain characteristics of myosin-S1 binding to actin still hold true. Consistent with previous studies using stop flow techniques (29), our data show that in the presence of increasing concentrations of myosin-S1, the binding rates of bare actin, actin-Tm.P, and actin-Tm.DP are essentially the same. However, our results are the first to demonstrate that actin-myosin rates are significantly increased when Tm is in the closed state in both the phosphorylated and dephosphorylated state.
We validated our 2D on-rate measurements using an alternate technique in which we estimated 2D on-rates by measuring the probability of bond formation as a function of fixed contact times between the actin-coated bead and the HMM-coated pedestal. Similar to Chesla et al. (22), we determined adhesion probability as a function of contact time, p(t), between two surfaces by repeatedly stepping an actin-coated bead into contact with a stationary HMM-coated pedestal and counting the number of bonds formed for a fixed number of contacts. This process was repeated over a range of contact times (5–250 ms), and adhesion probabilities were plotted as a function of contact time (Fig. 3B). The resulting data were fitted as in Chesla et al. (22) to determine a kon for bare actin beads of 2.6 ± 0.6 × 10−4 μm2/s. This value is in close agreement with our time to bond formation data (2.2 ± 0.2 × 10−4 μm2/s) under the same experimental conditions.
Tropomyosin Phosphorylation Increases the Lifetime of the Actin-Myosin Rigor Bond
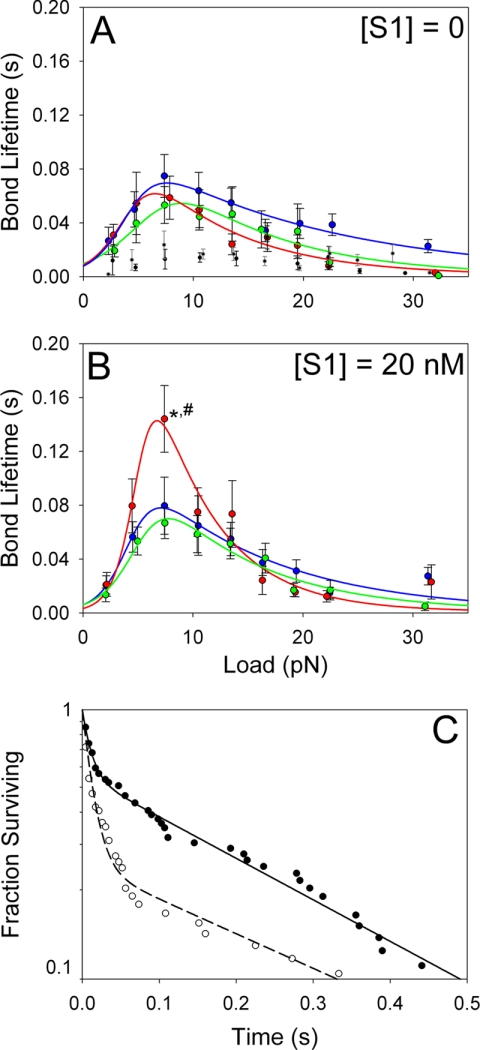
A range of step loads (2.5–31.5 pN) was applied to actin-HMM bonds using the laser trap, and the bond lifetimes were measured as illustrated in Fig. 1, B and C. All loading experiments were performed with rigor HMM (no nucleotide present), and data were collected with either 0 or 20 nm NEM-S1. The actin-HMM bond behaved as a catch-slip bond under all experimental conditions, first increasing in bond lifetime to a maximum and subsequently decreasing in bond lifetime with increasing force. The critical force (fcr) at which bond lifetime is maximal was consistent with previous studies (16) and ranged from 6.5–8.9 pN, with the lowest fcr values occurring in A+Tm.P, to the highest fcr values occurring in A+Tm.DP. This corresponds roughly to the maximum unitary force produced by a single myosin head.
In the absence of NEM-S1, the load-dependent bond lifetimes were similar for actin, A+Tm.P, and A+Tm.DP (Fig. 4A). However, at 20 nm NEM-S1, which shifts Tm to the open conformation, the maximum bond lifetime of A+Tm.P-HMM bonds, and only these bonds, increased significantly by about 2-fold (Fig. 4B). These data show that phosphorylated Tm changes the load-dependent dissociation rate of the A+Tm-HMM bond, but only when Tm is in the open state. This implies a structural difference at the A+Tm.P-myosin binding interface as compared with actin alone. Control measurements were performed in the absence of HMM and also in the presence of 1 mm pyrophosphate, which locks myosin in a weak binding state. In both cases, bond lifetimes were low and independent of force (Fig. 4A). Nonspecific bonds in the absence of HMM formed with a 13% frequency. Bonds in the presence of pyrophosphate, however, formed with 2-fold greater frequency than blank targets, suggesting that while these bonds were short-lived, they were specific in nature.
FIGURE 4.
Bond lifetime as function of applied load was measured for actin (blue circles), A+Tm.P (red circles), and A+Tm.DP (green circles) following bond formation with an HMM-coated pedestal. In A, no NEM-S1 was present, and in B, 20 nm NEM-S1 was present. The data were fit as described in Ref. 16 by a two-pathway model (51). The mean number of bonds measured per force bin was 50. Consistent with previous studies (16), when bond lifetimes were measured using blank targets and actin beads (black circles), bond lifetimes were independent of applied force and were significantly lower than in the presence of HMM on the targets. To capture bond ruptures with actin-HMM in the weak binding state, 1 mm sodium pyrophosphate (Na4P2O7) was added to the flow cells (16). The bond lifetimes in the presence of pyrophosphate (gray circles) were similar to those in the absence of HHM but occurred at a ∼2 times higher frequency than blank targets. This indicates that specific bonds between actin-HMM were still being formed. C, representative bond survival probability data of A+Tm.P preactivated with 20 nm NEM-S1. Bond survival at 7.5 pN load (●, 63 bonds) and 4.5 pN load (○, 74 bonds). A double exponential decay was fit to the data (solid and dashed lines). At 4.5 pN, 75% of bonds were in a short-lived state and 25% in a long-lived state. The exponential time constants for the two states were 0.013 ± 0.009 s and 0.323 ± 0.234 s, respectively. At 7.5 pN, 44% of bonds were in a short-lived state and 56% in a long-lived state. The exponential time constants for the two states were 0.011 ± 0.004 s and 0.270 ± 0.382 s, respectively. *, p = 0.0477 compared with actin beads; #, p = 0.0047 compared with A+Tm.DP beads.
DISCUSSION
Tm phosphorylation has been shown in a variety of models to be associated with increased contractile function (30–33). Our data show that Tm phosphorylation has significant effects on single cross-bridge interactions that are not purely inhibitory. These effects vary depending on the position of Tm on the actin filament, accelerating actin-myosin binding in the closed state, and slowing load-dependent bond rupture in the open state.
NEM-S1 as a Thin Filament Activator
The position of Tm on the filament was controlled through NEM-S1, which has a binding constant of 1.4 × 106 m−1 with bare actin and 6.3 × 106 m−1 with Tm-actin (34) and should result in 11% of the binding sites on the Tm-actin filament being occupied at 20 nm NEM-S1. This value corresponds to about 1 regulatory unit per bound NEM-S1. To explain the cooperativity evident in A+Tm.P (Fig. 2), this suggests that when phosphorylated, Tm polymerizes with at least one neighboring dimer, allowing cooperative activation.
More Than One Closed State
The data in Figs. 2 and 3 seem at odds. With no added NEM-S1, Tm begins in the closed state, and the frequency with which bonds form is extremely low. This is exactly what one would intuit from the three-state model. However, when a bond does form, it does so at a considerably higher rate than with bare actin.
The obvious interpretation of these data is that there is more than one closed state. Consider a pair of closed states in equilibrium with one another as illustrated in Fig. 5. One (closed1) is more like the blocked state in that the on-rate for myosin is low relative to bare actin, whereas in the second closed state (closed2), it is high relative to bare actin. This may be envisioned as the Tm molecule diffusing across the myosin binding sites on actin within a range of angles defining the closed state. More than half of the time it is in state 1, and myosin binding is reduced. For the fraction of time Tm is in state 2, Tm becomes a “guide” to myosin binding on actin, enhancing the on-rate. Thus, two closed states explain both the reduced frequency of bond formation and the higher rate with which an initial bond forms. That we observe these two distinct states experimentally tells us something about the timescale of the motion of Tm motion. Tm must be diffusing at such a rate that the two closed states are discernable by HMM. If Tm was diffusing faster, the two states would appear as one indistinct range of positions, and myosin would be unable to bind to the actin-Tm complex. The observed time to bond formation of actin and HMM in the presence of Tm suggests an upper limit to the time scale of diffusion of the Tm between the two states is 50–100 s−1. When the filament reaches the open state, myosin binds at rates characteristic of bare actin.
FIGURE 5.
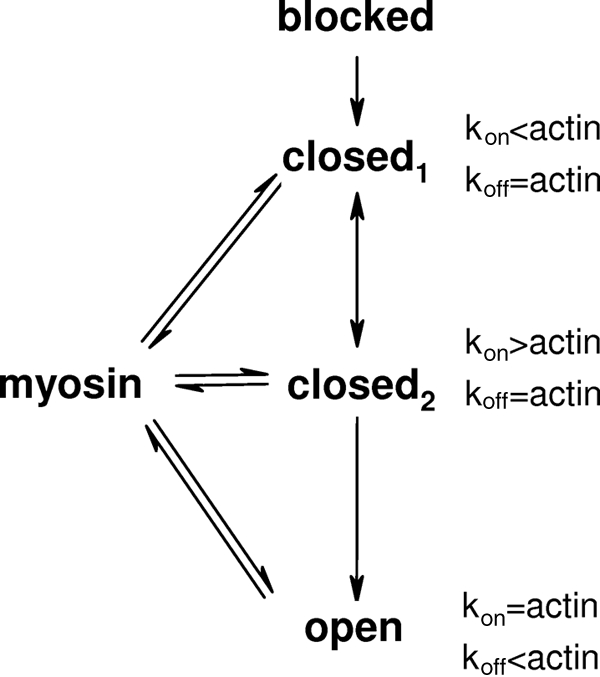
A revised “three-state” model of thin filament activation. To explain our experimental data, we propose two closed states of the thin filament, here designated as closed1 and closed2. Closed1 would be characterized by an actin-myosin bond formation rate (kon) that is below that of bare actin. In contrast, closed2 would be characterized by a rate of bond formation higher than that of bare actin. Bond formation in the open state is indistinguishable in rate from bare actin but the rate of bond rupture (koff) is lower.
This model appears to be consistent with the work of Craig and Lehman (35), showing that actively cycling myosin heads bind to a different location on the thin filament than do rigor heads. Although our data were collected solely with rigor myosin, it may capture the functional manifestations of the binding sites of Craig and Lehman. Structural studies have also shown that the position of Tm on actin is not static but rather remains in dynamic equilibrium with subpopulations of Tm in the closed state in both calcium-containing and calcium-free buffers (36).
Tm in the closed state partially blocks critical amino acid residues on actin that are a part of the myosin-binding site (35, 37). However, steric hindrance in and of itself cannot explain the force enhancements (11, 23) and increased ATPase rates (38) that have been observed with the addition of Tm. Thus Tm must have other effects on single cross-bridge kinetics to account for those changes and the data presented here. Our model explains this as Tm providing additional binding interfaces for myosin. As a result, the rate with which the actin-myosin bond is formed is increased (in the proposed closed2 state), as is the intrinsic duration of the actin-myosin bond (in the open state). The rate of bond formation is presumably the more relevant of the two because attached times at cellular [ATP] are much shorter than the intrinsic duration of the actin-myosin bond.
One might argue that the disconnect between the rate of bond formation and the probability of bond formation could be the result of a mixed population of beads, some with actin and some without. This is clearly not the case. In two-dimensional bond kinetics there is a positive relationship between the density of binding sites and the frequency of bond formation and also between the density of binding sites and the apparent on-rate (22, 27, 28). However, with bare actin, our measured rate of bond formation remained constant even while the bond frequency decreased with increasing NEM-S1 concentration. Thus, the observed changes must be attributed with factors other than the density of actin on beads.
Effects of Tm Phosphorylation
Effects on bond lifetime were observed only when Tm was phosphorylated. However, we argue that the effects on single cross-bridge interactions by Tm that we observed are phosphorylation-independent at the single cross-bridge level. The simplest interpretation is that Tm phosphorylation causes a greater fraction of Tm to shift to the open state when myosin binds, this shift being driven by long-range transmission of the closed-to-open transition in Tm through enhanced end-to-end interactions. As a result, bond lifetimes on average are longer when Tm is phosphorylated because on average myosin (or NEM-S1) binding shifts more Tm dimers to the open state. Enhanced end-to-end interactions may also be responsible for maintaining a greater amount of Tm in the closed state in the absence of myosin binding, leading to faster on-rates when Tm is phosphorylated.
Myosin as an Allosteric Catch Bond
A number of models have been proposed to explain catch-slip bonds, but the allosteric model (39) (two bound states with different bond dissociation rates, the ratio between them being dependent on applied force (40, 41)) is particularly attractive for myosin. Integrins, for example, undergo an allosteric shift that is characterized by a shift from a bent to a straightened conformation with differing ligand affinities (42–44). Further, the hinge between the epidermal growth factor and lectin domains of selectins (45, 46), and between the lectin and pilin domains of FimH (41, 47) have been shown to be vital for catch-bond behavior in those molecules. The implication is that a structural hinge coupled to the binding interface is necessary to catch bond behavior (48). Myosin too contains a hinge region between the motor domain and the light chain-binding domain and an actin-binding cleft that opens and closes to modulate actin-binding affinity (49, 50). When we plotted bond survival probabilities for each of our experimental conditions, in every case the data were best fit by double exponential decays suggestive of allosteric catch-slip behavior (Fig. 4C). We also see that phosphorylated Tm changes the behavior of actin-myosin allosteric catch bonds. At present we cannot discern what, if anything, Tm is doing to the structure of the actin-binding interface of myosin to change its allosteric regulatory properties and extend the bond lifetime. Taken as a whole, though, our data suggest that Tm provides additional points of interaction for myosin on the thin filament.
This work was supported, in whole or in part, by National Institutes of Health NSF Graduate Training Grant MCB0718430 (to the University of Virginia), National Institutes of Health Biophysics Graduate Training Grant GM080186 (to the University of Virginia), and National Institutes of Health Cardiovascular Graduate Training Grant HL07284 (to the University of Virginia).
- Tm
- tropomyosin
- A+Tm.P
- actin filaments decorated with phosphorylated tropomyosin
- A+Tm.DP
- actin filaments decorated with dephosphorylated tropomyosin
- HMM
- heavy meromyosin
- S1
- myosin subfragment 1
- NEM
- N-ethylmaleimide
- AF
- Alexa Fluor 488 C5 maleimide
- tb
- time to bond formation
- 2D
- two-dimensional.
REFERENCES
- 1. Greene L. E., Eisenberg E. (1980) Proc. Natl. Acad. Sci. U.S.A. 77, 2616–2620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Hill T. L., Eisenberg E., Greene L. (1980) Proc. Natl. Acad. Sci. U.S.A. 77, 3186–3190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Bremel R. D., Weber A. (1972) Nat. New Biol. 238, 97–101 [DOI] [PubMed] [Google Scholar]
- 4. McKillop D. F., Geeves M. A. (1993) Biophys. J. 65, 693–701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Maytum R., Lehrer S. S., Geeves M. A. (1999) Biochemistry 38, 1102–1110 [DOI] [PubMed] [Google Scholar]
- 6. McLachlan A. D., Stewart M. (1975) J. Mol. Biol. 98, 293–304 [DOI] [PubMed] [Google Scholar]
- 7. Edwards B. F., Sykes B. D. (1978) Biochemistry 17, 684–689 [DOI] [PubMed] [Google Scholar]
- 8. Edwards B. F., Sykes B. D. (1980) Biochemistry 19, 2577–2583 [DOI] [PubMed] [Google Scholar]
- 9. Edwards B. F., Sykes B. D. (1981) Biochemistry 20, 4193–4198 [DOI] [PubMed] [Google Scholar]
- 10. Mak A., Smillie L. B., Bárány M. (1978) Proc. Natl. Acad. Sci. U.S.A. 75, 3588–3592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Rao V. S., Marongelli E. N., Guilford W. H. (2009) Cell Motil. Cytoskeleton 66, 10–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Guo B., Guilford W. H. (2004) Cell Motil. Cytoskeleton 59, 264–272 [DOI] [PubMed] [Google Scholar]
- 13. Margossian S. S., Lowey S. (1982) Methods Enzymol. 85, 55–71 [DOI] [PubMed] [Google Scholar]
- 14. Pardee J. D., Spudich J. A. (1982) Methods Enzymol. 85, 164–181 [DOI] [PubMed] [Google Scholar]
- 15. Smillie L. B. (1982) Methods Enzymol. 85, 234–241 [DOI] [PubMed] [Google Scholar]
- 16. Guo B., Guilford W. H. (2006) Proc. Natl. Acad. Sci. U.S.A. 103, 9844–9849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Guilford W. H., Tournas J. A., Dascalu D., Watson D. S. (2004) Anal. Biochem. 326, 153–166 [DOI] [PubMed] [Google Scholar]
- 18. Dupuis D. E., Guilford W. H., Wu J., Warshaw D. M. (1997) J. Muscle Res. Cell Motil. 18, 17–30 [DOI] [PubMed] [Google Scholar]
- 19. Svoboda K., Block S. M. (1994) Annu. Rev. Biophys. Biomol. Struct. 23, 247–285 [DOI] [PubMed] [Google Scholar]
- 20. Allersma M. W., Gittes F., deCastro M. J., Stewart R. J., Schmidt C. F. (1998) Biophys. J. 74, 1074–1085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Rinko L. J., Lawrence M. B., Guilford W. H. (2004) Biophys. J. 86, 544–554 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Chesla S. E., Selvaraj P., Zhu C. (1998) Biophys. J. 75, 1553–1572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. VanBuren P., Palmiter K. A., Warshaw D. M. (1999) Proc. Natl. Acad. Sci. U.S.A. 96, 12488–12493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Cassell M., Tobacman L. S. (1996) J. Biol. Chem. 271, 12867–12872 [DOI] [PubMed] [Google Scholar]
- 25. Eaton B. L. (1976) Science 192, 1337–1339 [DOI] [PubMed] [Google Scholar]
- 26. Korman V. L., Hatch V., Dixon K. Y., Craig R., Lehman W., Tobacman L. S. (2000) J. Biol. Chem. 275, 22470–22478 [DOI] [PubMed] [Google Scholar]
- 27. Snook J. H., Guilford W. H. (2010) Cell Mol. Bioeng 3, 128–138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Chen W., Evans E. A., McEver R. P., Zhu C. (2008) Biophys. J. 94, 694–701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Trybus K. M., Taylor E. W. (1980) Proc. Natl. Acad. Sci. U.S.A. 77, 7209–7213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Heeley D. H., Watson M. H., Mak A. S., Dubord P., Smillie L. B. (1989) J. Biol. Chem. 264, 2424–2430 [PubMed] [Google Scholar]
- 31. Houle F., Rousseau S., Morrice N., Luc M., Mongrain S., Turner C. E., Tanaka S., Moreau P., Huot J. (2003) Mol. Biol. Cell 14, 1418–1432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Rao V. S., La Bonte L. R., Xu Y., Yang Z., French B. A., Guilford W. H. (2007) Am. J. Physiol. Heart Circ. Physiol. 293, H654–H659 [DOI] [PubMed] [Google Scholar]
- 33. Gaffin R. D., Gokulan K., Sacchettini J. C., Hewett T. E., Klevitsky R., Robbins J., Sarin V., Zawieja D. C., Meininger G. A., Muthuchamy M. (2006) Am. J. Physiol. Heart Circ. Physiol. 291, H552–H563 [DOI] [PubMed] [Google Scholar]
- 34. Nagashima H., Asakura S. (1982) J. Mol. Biol. 155, 409–428 [DOI] [PubMed] [Google Scholar]
- 35. Craig R., Lehman W. (2001) J. Mol. Biol. 311, 1027–1036 [DOI] [PubMed] [Google Scholar]
- 36. Pirani A., Xu C., Hatch V., Craig R., Tobacman L. S., Lehman W. (2005) J. Mol. Biol. 346, 761–772 [DOI] [PubMed] [Google Scholar]
- 37. Vibert P., Craig R., Lehman W. (1997) J. Mol. Biol. 266, 8–14 [DOI] [PubMed] [Google Scholar]
- 38. Lehrer S. S., Morris E. P. (1984) J. Biol. Chem. 259, 2070–2072 [PubMed] [Google Scholar]
- 39. Yakovenko O., Sharma S., Forero M., Tchesnokova V., Aprikian P., Kidd B., Mach A., Vogel V., Sokurenko E., Thomas W. E. (2008) J. Biol. Chem. 283, 11596–11605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Thomas W., Forero M., Yakovenko O., Nilsson L., Vicini P., Sokurenko E., Vogel V. (2006) Biophys. J. 90, 753–764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Tchesnokova V., Aprikian P., Yakovenko O., Larock C., Kidd B., Vogel V., Thomas W., Sokurenko E. (2008) J. Biol. Chem. 283, 7823–7833 [DOI] [PubMed] [Google Scholar]
- 42. Takagi J., Petre B. M., Walz T., Springer T. A. (2002) Cell 110, 599–611 [DOI] [PubMed] [Google Scholar]
- 43. Xiao T., Takagi J., Coller B. S., Wang J. H., Springer T. A. (2004) Nature 432, 59–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Vinogradova O., Velyvis A., Velyviene A., Hu B., Haas T., Plow E., Qin J. (2002) Cell 110, 587–597 [DOI] [PubMed] [Google Scholar]
- 45. Phan U. T., Waldron T. T., Springer T. A. (2006) Nat. Immunol. 7, 883–889 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Lou J., Yago T., Klopocki A. G., Mehta P., Chen W., Zarnitsyna V. I., Bovin N. V., Zhu C., McEver R. P. (2006) J. Cell Biol. 174, 1107–1117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Aprikian P., Tchesnokova V., Kidd B., Yakovenko O., Yarov-Yarovoy V., Trinchina E., Vogel V., Thomas W., Sokurenko E. (2007) J. Biol. Chem. 282, 23437–23446 [DOI] [PubMed] [Google Scholar]
- 48. Sokurenko E. V., Vogel V., Thomas W. E. (2008) Cell Host Microbe 4, 314–323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Rayment I., Rypniewski W. R., Schmidt-Bäse K., Smith R., Tomchick D. R., Benning M. M., Winkelmann D. A., Wesenberg G., Holden H. M. (1993) Science 261, 50–58 [DOI] [PubMed] [Google Scholar]
- 50. Rayment I., Holden H. M., Whittaker M., Yohn C. B., Lorenz M., Holmes K. C., Milligan R. A. (1993) Science 261, 58–65 [DOI] [PubMed] [Google Scholar]
- 51. Pereverzev Y. V., Prezhdo O. V., Forero M., Sokurenko E. V., Thomas W. E. (2005) Biophys. J. 89, 1446–1454 [DOI] [PMC free article] [PubMed] [Google Scholar]