The Timing of Vision – How Neural Processing Links to Different Temporal Dynamics

Abstract

In this review, we describe our recent attempts to model the neural correlates of visual perception with biologically inspired networks of spiking neurons, emphasizing the dynamical aspects. Experimental evidence suggests distinct processing modes depending on the type of task the visual system is engaged in. A first mode, crucial for object recognition, deals with rapidly extracting the glimpse of a visual scene in the first 100 ms after its presentation. The promptness of this process points to mainly feedforward processing, which relies on latency coding, and may be shaped by spike timing-dependent plasticity (STDP). Our simulations confirm the plausibility and efficiency of such a scheme. A second mode can be engaged whenever one needs to perform finer perceptual discrimination through evidence accumulation on the order of 400 ms and above. Here, our simulations, together with theoretical considerations, show how predominantly local recurrent connections and long neural time-constants enable the integration and build-up of firing rates on this timescale. In particular, we review how a non-linear model with attractor states induced by strong recurrent connectivity provides straightforward explanations for several recent experimental observations. A third mode, involving additional top-down attentional signals, is relevant for more complex visual scene processing. In the model, as in the brain, these top-down attentional signals shape visual processing by biasing the competition between different pools of neurons. The winning pools may not only have a higher firing rate, but also more synchronous oscillatory activity. This fourth mode, oscillatory activity, leads to faster reaction times and enhanced information transfers in the model. This has indeed been observed experimentally. Moreover, oscillatory activity can format spike times and encode information in the spike phases with respect to the oscillatory cycle. This phenomenon is referred to as “phase-of-firing coding,” and experimental evidence for it is accumulating in the visual system. Simulations show that this code can again be efficiently decoded by STDP. Future work should focus on continuous natural vision, bio-inspired hardware vision systems, and novel experimental paradigms to further distinguish current modeling approaches.

Introduction

Our visual system is continuously challenged with various types of tasks, such as recognizing other people or objects, searching for a friend in a crowd, or determining the direction and speed of other cars while driving. To solve these different tasks, it has been hypothesized that visual information arriving in the primary visual area (V1) of the cortex is further processed via two specialized pathways: first, the ventral stream associated with forms and colors mostly involved in “what” tasks like object recognition, and, second, the dorsal stream which is mostly processing “where” information and motions. In general, however, the visual areas form a complex network, and the two main processing pathways are strongly interconnected. It is therefore hardly possible to derive anatomically the neural dynamics – that is, neural activity evolution over time – underlying visual processing. Nevertheless, different visual tasks such as recognition, search, and motion detection, not only vary with respect to “what” has to be processed, they also differ in “how fast” and “how accurate or detailed” the respective perception can (or must) be accomplished. The diverse temporal dynamics of visual processing can motivate and help distinguishing feedforward, feedback, and top-down influences during specific visual tasks. In turn, computational models that account for reaction times, and the time course of neural activity during visual tasks, can offer mechanistic explanations for internal cortical processes such as activity accumulation, attentional effects, and information transfer.

Here, we review some of our recent models based on spiking neural networks (SNN) that describe neuronal correlates of several visual tasks at multiple timescales. These models are all biologically plausible, reproduce a broad range of experimental observations, and predict others. They help to understand the neural dynamics underlying visual processing, and in particular visual processing times. More specifically, feedforward models can account for the phenomenal speed of object recognition (see Fast Feedforward Processing, Latency Coding, and STDP). This type of rapid processing presumably depends on the ability of the visual system to learn how to recognize familiar visual primitives in an unsupervised manner. Spike timing-dependent plasticity (STDP) may play a key role here. Feedforward processing is usually sufficient to extract the glimpse of a visual scene in 100–200 ms. Recurrent connectivity, however, allows accumulating evidence over longer timescales (several hundreds of milliseconds) whenever a finer visual discrimination is needed (see Slower Visual Decision Making). Such recurrent connections, in combination with bottom-up and top-down connections between brain areas, are also crucial to mediate attentional mechanisms through biased-competition (see Top-Down Attention), and can account for both “pop out” and serial modes in visual search. Attention not only up-modulates the firing rates of the neurons encoding the attended features, but also enhances their synchrony, enabling faster reaction times, dynamic information routing, and phase-of-firing coding (PoFC; see Oscillations Format Visual Processing). The phase patterns may be decoded thanks to STDP. Finally, we evoke important unsolved questions and future directions in Section “Unsolved Questions and Future Directions.”

Fast Feedforward Processing, Latency Coding, and STDP

Vision can be extremely fast. There is now considerable behavioral and electrophysiological evidence showing that the primate visual system can achieve high-level object recognition in just 80–100 ms after stimulus onset (see Thorpe's review in this Special Topic). This phenomenal speed imposes severe constraints on the underlying neural processes. Given that about 10 neuronal layers are involved in that sort of processing, the time window available for each neuron to perform its computation is only of about 10 ms. As the firing rates in the visual system are barely above 100 Hz, such a small window will consequently contain at most one spike (Thorpe and Imbert, 1989). A classical rate coding scheme, where individual neurons encode information in their mean firing rate, is thus ruled out. Instead, the information has to be encoded by which of the afferents were recruited, and possibly additionally by the relative recruiting times. This scheme is referred to as “rank order coding” (Thorpe and Gautrais, 1998). Note that if computation is restricted to one spike per neuron, the use of feedback loops is also ruled out. This implies that the first spike wave after stimulus onset probably does much more than conventionally assumed (VanRullen and Thorpe, 2002). Simulations have confirmed that it is indeed possible to perform fast and robust object recognition even in cluttered natural images, using only one spike per neuron, and feedforward connectivity (VanRullen et al., 1998; Delorme and Thorpe, 2001; Masquelier and Thorpe, 2007; Weidenbacher and Neumann, 2008).

In this section, we focus on how STDP may shape this kind of processing. STDP is a physiological mechanism of activity-driven synaptic regulation, where an excitatory synapse is reinforced when it receives a spike before a postsynaptic one is emitted (long-term potentiation, LTP). In the opposite case, its strength is weakened (long-term depression, LTD), when the postsynaptic spike precedes the presynaptic one. STDP has been observed both in vivo and in vitro in many species (from insects to mammals) and in many brain areas, including the visual cortex (see Caporale and Dan, 2008 for a review). Note that STDP is in agreement with Hebb's (1949) postulate because it reinforces the connections with those presynaptic neurons that fired slightly before the postsynaptic neuron, which are the ones that “took part in firing it.”

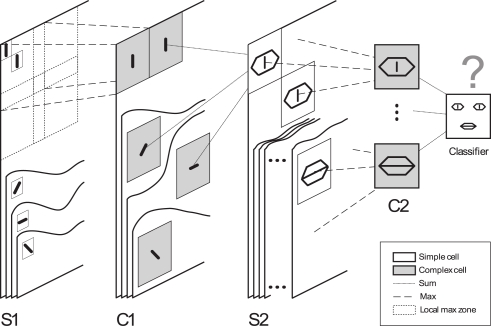
What happens if such a rule is at work in a hierarchical neuronal network crossed by waves of spikes generated by visual stimuli? In Masquelier and Thorpe (2007), we assessed this question using a model inspired by HMAX (HMAX stands for “Hierarchical Model And X” – where X is a highly non-linear maXimum operation; Riesenhuber and Poggio, 1999; Serre et al., 2007). In an attempt to model the increasing complexity and invariance observed along the ventral pathway, we used a four-layer hierarchy (S1–C1–S2–C2) in which simple cells (S) gained their selectivity from a linear sum operation, while complex cells (C) gained invariance from a non-linear max pooling operation (see Figure 1). However, our network operates in the temporal domain: when presented with an image, the first layer's S1 cells, emulating V1 simple cells, detect edges with four preferred orientations, and the more strongly a cell is activated, the earlier it fires a first spike. There is evidence for this so-called “intensity-to-latency conversion” in V1, where response latency decreases with stimulus contrast (Gawne et al., 1996; Albrecht et al., 2002), and also with the proximity between the stimulus orientation and the cell's preferred orientation (Celebrini et al., 1993). These S1 spikes are then propagated asynchronously through the subsequent layers, where STDP takes place. Interestingly, within this time-to-first-spike coding framework, the maximum operation of complex cells simply consists of propagating the first spike emitted by a given group of afferents (Rousselet et al., 2003). This can be achieved efficiently by one spiking neuron with low threshold that has synaptic connections from all neurons in the group [such “low threshold” relay cells are found in both the lateral geniculate nucleus (LGN), Rathbun et al., 2010 and the cortex, Swadlow and Gusev, 2002].

Figure 1.

Overview of the five layer feed forward spiking neural network used in Masquelier and Thorpe, 2007. As in HMAX (Riesenhuber and Poggio, 1999; Serre et al., 2007), we alternate simple cells that gain selectivity through a sum operation, and complex cells that gain shift and scale invariance through a max operation (which in our framework simply consists of propagating the first received spike). Cells are organized in retinotopic maps until the S2 layer (inclusive). S1 cells detect edges. C1-maps subsample S1-maps by taking the maximum response over a square neighborhood. S2 cells are selective to intermediate complexity visual features, defined as a combination of oriented edges (here, we symbolically represented an eye detector and a mouth detector). There is one S1–C1–S2 pathway for each processing scale (not represented). Then C2 cells take the maximum response of S2 cells over all positions and scales, and are thus shift- and scale-invariant. Finally, a classification is done based on the C2 cells’ responses (here we symbolically represented a face/non-face classifier). In the brain, equivalents of S1 cells may be in V1, S2 cells in V1–V2, S2 cells in V4–PIT, C2 cells in AIT, and the final classifier in PFC. Here STDP shapes the C1-to-S2 connectivity. Figure 2 shows an example of resulting selectivities after exposing the network to face images. Figure modified from Masquelier and Thorpe (2007).

When we exposed the network to natural images, we observed that the neurons equipped with STDP gradually became selective to prototypical patterns that were both salient, and consistently present in the images. During the convergence process, synapses compete with each other (Song et al., 2000), and the winning synapses are those through which the earliest spikes arrive (on average; Song et al., 2000; Guyonneau et al., 2005). Interestingly, these earliest spikes, which correspond to the most salient regions of an image, are typically the most informative (VanRullen and Thorpe, 2001). Furthermore, the resulting effect of this “early input selection” is to make the postsynaptic neuron respond more quickly (Song et al., 2000; Gerstner and Kistler, 2002; Guyonneau et al., 2005).

Figure 2 shows an example, in which we exposed the network to face images, and where the STDP neurons indeed became selective to face features. Note that we used unsegmented images, but the background was not learned since backgrounds are too different from one image to another for the STDP process to converge. It is important to note that up to this point, the learning was fully unsupervised. No external teacher's signal or previous knowledge was given to the model. For example, in Figure 2, the system obviously had no idea it was going to see faces. The features were only learned due to statistical regularities in the training dataset. However, the output of the STDP neurons can be fed into a supervised classifier, leading to robust object categorization, even with few (∼10) STDP-learned features (Masquelier and Thorpe, 2007).

Figure 2.

Preferred stimulus reconstructions of three C2 cells after 0, 50, 150, and 500 presentations. At the top of each frame, the input image is shown with red, green, or blue squares, indicating the receptive fields of the cells that fired (if any). At the bottom, we reconstructed the preferred stimuli of the three cells: the left cell gradually becomes selective to foreheads, the middle one to noses and left eyes, and the right one to a global view of a face. Above each reconstruction, the number of postsynaptic spikes emitted is shown with the corresponding color. Figure modified from Masquelier and Thorpe (2006). See also the videos available online at: http://dx.doi.org/10.1371/journal.pcbi.0030031

It is well known that the visual system is plastic and can learn frequently encountered visual features or feature contingencies (Jiang and Chun, 2001). The model predicts that frequently occurring features are not only more likely to be learned, but will also be processed and recognized faster than unfamiliar ones (recall that postsynaptic latencies decrease with training). Consistent with this, psychophysical experiments show that familiar categories such as faces are processed faster (Crouzet et al., 2010), and that processing times can be speeded up with experience (Masquelier et al., 2008).

One important limitation in our study is that we used a noise-free deterministic model, while real neuronal responses are known to be variable. Future work will assess its robustness to neuronal noise. One can distinguish two kinds of response variability, or lack thereof: reliability and precision (Tiesinga et al., 2008). When a neuron fires approximately the same number of spikes on each trial, it is said to be reliable, whereas, when the spikes occur almost at the same time across trials, it is said to be precise. We have recently demonstrated that STDP-based pattern learning needs a precision of 10–20 ms, when in fact it is relatively insensitive to a lack of reliability, providing the input patterns involves a sufficient number of afferents (Gilson et al., unpublished observation). It would be interesting to quantify this number for the kind of rapid visual processing exposed in this section.

Finally, it is worth mentioning that STDP-based unsupervised learning is not restricted to natural image statistics. In fact, any arbitrary spike pattern that consistently repeats in the input can be learned (Masquelier et al., 2008, 2009a).

Slower Visual Decision Making

As we have seen in the previous section, feedforward processing of the first spike wave can be sufficient to rapidly extract the glimpse of a visual scene. Being so reactive is obviously advantageous in numerous emergency situations, such as obstacle/projectile avoidance or prey/predator/friend identification. But when reactivity is less crucial, integrating the visual information over time will generally improve perception, especially when visual evidence is noisy, moving, and ambiguous.

A psychophysical paradigm, designed to study the time course of slow perceptual decision making, is the random-dot motion (RDM) discrimination task (Roitman and Shadlen, 2002; Palmer et al., 2005; Churchland et al., 2008). Subjects performing this task have to decide on the net direction of motion in a patch of randomly moving dots. The quantity of the sensory evidence and thus, the task difficulty, is controlled by the amount of coherent motion. In the free response version, as soon as the subjects have gathered enough evidence to make a choice, they usually indicate their decision by a saccade to a target located in the corresponding direction. Reaction times in the RDM task are typically long, in the order of several 100 ms, with faster responses to more coherent motions. A decision criterion is needed to determine how much evidence is “enough” to terminate the accumulation process, and to initiate the corresponding saccade. In theory, there are several possible decision criteria, such as relative or absolute thresholds (or “bounds”). Neurophysiological evidence from different cortical areas so far suggests a fixed firing rate threshold independent of reaction times (see below; Roitman and Shadlen, 2002; Schall et al., 2002; Churchland et al., 2008).

To identify possible neural correlates of this accumulation-to-bound concept, the psychophysical RDM task was combined with simultaneous recordings of decision-related activity from several brain areas along the dorsal visual stream [middle temporal (MT) and lateral intra-parietal (LIP) area, prefrontal cortex (PFC), and the superior colliculus (SC)]. All of them form part of the cognitive link between visual sensation and saccadic movement (reviewed in Schall, 2003; Smith and Ratcliff, 2004; Opris and Bruce, 2005). Particularly single neuron activity in area LIP of behaving monkeys has been found to increase gradually during motion viewing, dependent on task difficulty and according to choice behavior (Shadlen and Newsome, 2001; Roitman and Shadlen, 2002), while upstream of LIP in area MT neurons fire monotonically as a function of motion coherence (Britten et al., 1993). Area MT might thus provide the sensory evidence that is passed on to LIP for integration. Besides, the recorded LIP activity suggests a fixed firing rate threshold, as it reaches a uniform level, independent of response time or difficulty (about 40–80 ms prior to the saccade). Apart from these 40–80 ms for motor preparation, the rather long latency between signal onset and the onset of build-up activity in LIP (∼190 ms) has to be subtracted from the measured reaction times to arrive at an estimate of the pure decision time, i.e., the actual time during which evidence is accumulated (Roitman and Shadlen, 2002; Churchland et al., 2008).

Decision-related activity build-up was also found downstream of LIP, in the dorsolateral PFC (Kim and Shadlen, 1999) and SC (Horwitz and Newsome, 1999). Interestingly, all neurons that exhibit ramping activity characteristically show persistent neural firing in delayed memory or decision tasks (Gnadt and Andersen, 1988; Shadlen and Newsome, 2001). This observation has inspired the application of a biophysically based model of working memory (Brunel and Wang, 2001) on decision making (Wang, 2002). In the model, strong recurrent connections generate attractor states, which facilitate sustained spiking activity in excitatory subpopulations of the neural network (Figure 3A, S1 and S2), while global inhibitory feedback leads to competition between these subgroups, and thus enables categorical decision making. In the following, the basic network shown in Figure 3A serves as a building block to model particular brain regions that participate in the processing of competitive features. The spiking neuron models of visual-attention mechanisms and information transfer, which are described in the subsequent sections, involve multiple cortical areas, and hence consist of several of these basic decision units. Here, in the case of the RDM task, the network can be viewed as a representation of a local microcircuit in area LIP, where one neural subpopulation is selective for each of the possible motion directions (see Albantakis and Deco, 2009 for multiple choices).

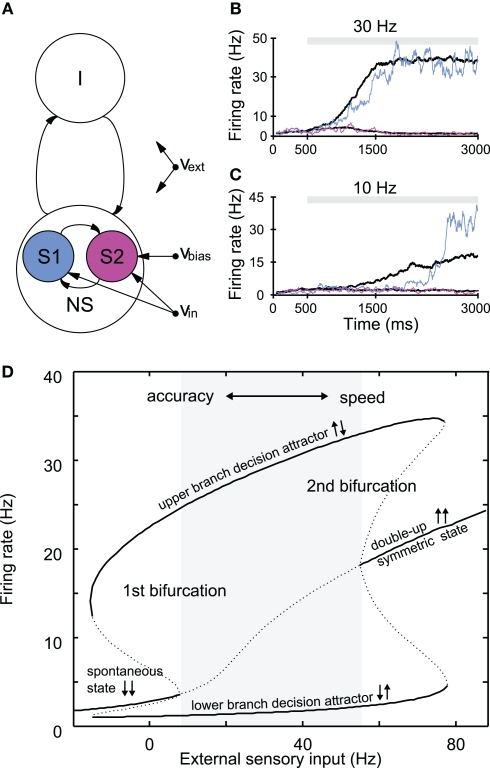
Figure 3.

Attractor network of slow perceptual decision making. (A) Schematic representation of the network, which consists of excitatory and inhibitory spiking neurons, with full synaptic connectivity. All neurons receive external inputs as (poissonian) spike trains characterized by their rate. The excitatory neurons are organized in three pools: the non-specific neurons (NS) and the two selective pools (S1, S2) that receive the inputs encoding each stimulus (with rate ν_in). An additional bias (ν_bias) can be applied to one of the two selective pools. All neurons also receive an input (ν_ext) that simulates the spontaneous activity in the surrounding cerebral cortex. (B,C) Single trial (colored traces) and mean firing rate evolution (black) of the selective pools for different inputs. Mean traces are the average over 20 trials for 0% coherence (ν_bias = 0). (B) In the case of high inputs, the transition from the spontaneous state to the decision state is evidence-driven and slow even for single trials. (C) For low inputs, the switch is induced by noise fluctuations, and rather sharp in a single trial. Yet, the mean activity builds up slowly. (D) Stable (solid lines) and unstable (dotted lines) attractor states, dependent on the external sensory input obtained from a mean-field approximation of the network (Brunel and Wang, 2001). The gray area depicts the evidence-driven regime, where the spontaneous state is no longer stable. Increasing the external inputs to both selective populations increases reaction time and decreases accuracy. Thus, a speed–accuracy trade-off might be implemented through the inputs to the neural populations (see text). Left of the first bifurcation, transitions are induced by noise. (B–D) Simulations were performed with a synaptic strength of 1.68 within selective populations; all other parameters were taken from Wang (2002).

Decision formation corresponds to the transition from the spontaneous state of the network (where all neurons fire at low firing rates) to a decision state [where one selective population (the “winner”) fires at high rates (Figures 3B,C)]. If the connection strengths are fixed, the input strength determines whether particular attractor states are stable or not (Figure 3D). For sufficient external inputs, the spontaneous state becomes unstable (>10 Hz in Figure 3D), and the system “relaxes” into one of the two possible decision states driven by sensory evidence. The transition time increases the closer the system is to this bifurcation point. In addition to the attractor configuration, the network's long synaptic time-constant, generated by a high NMDA to AMPA receptor ratio, is crucial for a slow transition and for the model's ability to accumulate inputs.

Note that, although individual spiking neurons are simulated, the decision outcome is determined by the pooled activity of the selective neural populations, consistent with a rate-code, and not by individual spikes, as opposed to the feedforward network for object recognition described in Section “Fast Feedforward Processing, Latency Coding, and STDP.” Also, in contrast to the feedforward model, the decision making model is inherently stochastic, as every neuron in the network receives its own individual background inputs in the form of Poisson spike trains. As there are a finite number of neurons in the network, the resulting output spike rate of each neural population also fluctuates in time around the noise-free value, or, equivalently, the firing rate obtained for an infinite number of neurons. The neural noise plays an important role in the model's decision making. First, it is responsible for the probabilistic outcome of the decision process when faced with ambiguous evidence for both alternatives (as in Figures 3B,C). Moreover, we showed that in the case of low sensory input, where the spontaneous state is still stable (left to the bifurcation), fluctuations due to the network's finite size noise can cause transitions to the decision state (Martí et al., 2008). Without noise (corresponding to an infinite amount of neurons), the network would stay indefinitely in the spontaneous state for small external inputs. If the number of neurons in the network is small, fluctuations that are large enough to induce a transition to the decision state are more probable. These noise-driven decisions exhibit rather sharp switches in activity on single trials with long, exponentially distributed decision times. Nevertheless, averaging across trials with different decision times in the noise-driven condition results in a gradual build-up of activity (Figure 3C), consistent with the experimentally observed neural firing rates, which are trial-averaged single neuron activity.

As mentioned above in the evidence-driven regime, the transition times of the model depend on the common external input to the selective populations, with faster transients and lower accuracy for higher sensory inputs. Even if both selective populations receive the same input (no bias), the average (chance level) decision time will thus be shorter if this common input is higher (Figure 3D). This model characteristic arises through the non-linearity of the attractor landscape, and offers an interesting alternative mechanism to control the speed–accuracy trade-off (Roxin and Ledberg, 2008), apart from adapting the decision threshold, as suggested by conceptual models of decision making (Ratcliff and Smith, 2004; Palmer et al., 2005). In this context, we recently showed that the attractor model is capable of reproducing changes of mind that emerged through speed–pressure in a slightly altered RDM task (Resulaj et al., 2009), if the decision threshold is set low and, in addition, the external inputs applied to both selective populations are high (Albantakis and Deco, 2011). Specifically, changes of mind in the model became more frequent, the closer the system was to the second bifurcation, where the symmetric state returns to be stable.

Another implication of the non-linearity inherent to the attractor model is the violation of the so-called time-shift invariance: evidence occurring earlier during the accumulation process will have a greater effect on the decision outcome than later evidence, which happens only when the transient is already converging toward one of the decision attractors (Wong et al., 2007). This prediction was indeed observed in a RDM experiment, where brief pulses of motion added to the random-dot stimulus affected the final choice more at earlier onset times (Huk and Shadlen, 2005). To produce this effect with a linear accumulator model, additional time-dependent features like collapsing decision bounds or an urgency signal need to be superimposed on the conceptual model.

In general, most models of perceptual decision making so far focused exclusively on sensory evidence accumulation. In that sense, the non-linear attractor model is a notable exception, as it is further able to account for other modalities of decision making neurons, like persistent activity and their responses to visual target signals (Wong and Huk, 2008). Nevertheless, not much is yet known about the physiological mechanisms of the various internal states, which can play a significant role in the decision making process, such as speed–accuracy trade-off, urgency, reward expectation, or attention.

Top-Down Attention

Another situation where pure fast feedforward processing of spiking information is insufficient to perform the required computation, arises when a task demands the evaluation of a crowded and/or complex visual scene. In this case, the visual system is unable to simultaneously evaluate the immense amount of information conveyed in a complex scene just by the initial fast feedforward sweep of information transfer. Precisely to cope with this problem, attentional mechanisms are required to account for the selection of relevant scene information. In addition to the local recurrent connections treated in the previous section, intercortical recurrent connections between different brain areas shape the focus of attention.

Biased-competition mechanisms can account for the attentional spotlight

Attentional mechanisms optimize the processing of bottom-up relevant aspects of the sensory signal by adding top-down influences. These top-down signals bias the system to concentrate on only a small proportion of the incoming information relevant for the behavioral task under consideration. Top-down and bottom-up processing result from intercortical connections between the different brain areas. Indeed, one quarter of all possible connections between areas is realized in the human brain, most of which being of recurrent nature (Salin and Bullier, 1995). Thus, partial representations held in different cortical areas might be integrated by mutual cross communication, mediated by the inter-area neuronal fibers. The role of recurrent processing is central to modern perspectives on hierarchical inference in the brain. Modern accounts (e.g., predictive coding) see the brain as actively constructing predictions of its sensorium that are mediated by top-down connections, and tested against sensory evidence to provide a prediction error (Spratling, 2008; Friston and Kiebel, 2009; Hesselmann et al., 2010). This error is then propagated through the system, and accumulated to optimize representations of the causes of sensory input. This view is based upon Helmholtzian ideas, and regards the brain as testing hypotheses about the causes of sensations. In this spirit, perception could be handled as an inverse inference problem, whose goal is to estimate the factors that have generated the particular percept. Indeed, this can be formalized in the framework of Bayesian Decision Theory (Friston and Kiebel, 2009; Hesselmann et al., 2010).

Further neurophysiological evidence gives rise to the assumption that each cortical area is capable of representing a set of alternative hypotheses encoded in the activities of different cell assemblies [similar to the selective populations (S1, S2) in the decision making network (Figure 3A)]. Representations of different conflicting hypotheses inside each area compete with each other for activity and representation (Desimone and Duncan, 1995). However, each area represents only a part of the environment and/or internal state. In order to achieve a coherent global representation, different cortical areas bias each other's internal representations by communicating their current states to other areas through inter-area connections. They favor thereby certain sets of local hypotheses over others. For example, different objects present in the visual field could compete for representation in one brain area (Wolfe, 1994). This competition might be resolved by a bias given to one of them from another area, as obtained from this other area's local view-encoding. For example, it could favor the behaviorally relevant location in the visual field, and thus the object corresponding to that location to be represented in the first area (Rolls and Deco, 2002, 2010). Each brain area might thus act like the decision network described in Figure 3A, with multiple competing alternatives. By recurrently biasing each other's competitive internal dynamics, the global neocortical system dynamically achieves a global representation in which each area's state is maximally consistent with those of the other areas. This view has been referred to as the “biased-competition” hypothesis (Desimone and Duncan, 1995).

In parallel to this competition-centered view, a cooperation-centered picture of brain operation has been formulated, where global representations find their neuronal correlate in assemblies of co-activated neurons (Hebb, 1949). Co-activation of neurons induces stronger mutual synaptic connections between themselves, which leads to assembly formation. Reverberatory communication between assembly members then results in persistent neuronal activation, and gives rise to a representation extended in time, as described in Section “Slower Visual Decision Making” for visual decision making. The concept of neuronal assemblies was later formalized in the framework of statistical physics (Hopfield, 1982; Amit and Brunel, 1997; Brunel and Wang, 2001), where assemblies of co-activated neurons form attractors in the phase space of the recurrent neuronal dynamics (patterns of co-activation can represent fixed points from which the dynamical system evolves). In summary, the formalism of attractor dynamics, including biased competition and cooperation, offers a unifying principle for the “slow” recurrent integration and segregation of information in multi-area neurocognitive modeling of brain functions (Deco and Rolls, 2005a,b; Deco et al., 2009; Mavritsaki et al., 2011).

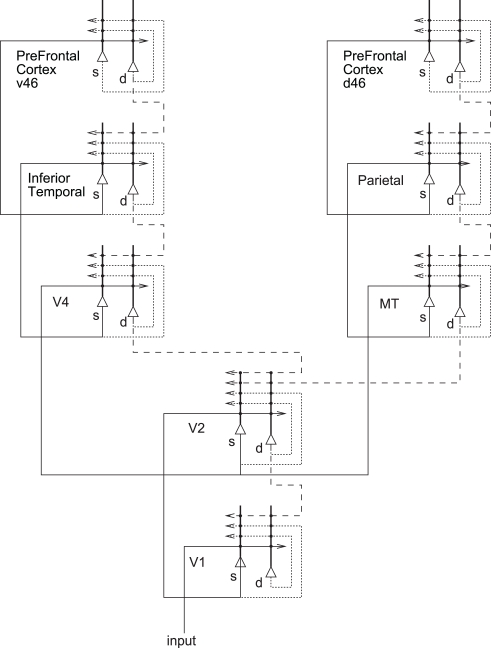
A cortical architecture that implements the principles of visual-attention described above is shown in Figure 4 (see Deco and Rolls, 2005a,b) for more details). The figure shows how the dorsal “where” visual stream (reaching the posterior parietal cortex, PP) and the ventral “what” visual stream (via V4 to the inferior temporal cortex, IT) interact through early visual cortical areas (such as V1 and V2) to account for many aspects of visual-attention. The system is composed of six modules [V1 (the primary visual cortex), V2–V4, IT, PP, ventral PFC v46, and dorsal PFC d46], reciprocally connected according to anatomical data. This multi-area neurodynamical model implements the principle of biased-competition (presented above) at the local and global brain area level. Information from the retina reaches V1 via the LGN. The attentional top-down signal biasing the intra- and intercortical competition is assumed to come from PFC area 46 (modules d46 and v46). In particular, feedback connections from area v46 with the IT module could specify the target object in a visual search task. The feedback connections from area d46 with the PP module generate the bias to a targeted spatial location in an object recognition task given a spatial attentional cue. Each brain area consists of mutually coupled neuronal populations, whose dynamics are described by conductance-based synaptic and spiking neuronal models. The equations describing the detailed neuronal dynamics can be further reduced using mean-field techniques. The mean-field approximation consists of replacing the temporally averaged discharge rate of a neuron with the instantaneous ensemble average of the activity of the neuronal population (see Rolls and Deco, 2010). The dynamical evolution of activity at the level of a cortical area can be simulated in the framework of the present model by integrating the population activity in a given area over space and time. An explicit spiking neuron simulation of two coupled brain regions (V2 and V4) engaged in biased-competition, with each population acting according to the network shown in Figure 3A, is described in (Deco and Rolls, 2005b), and revealed further insights into the non-linear interactions between bottom-up and attentional top-down effects.

Figure 4.

System-level architecture of a model of the cortical mechanisms of visual-attention and memory. The system is essentially composed of six modules which model the two known main visual pathways of the primate visual cortex. Forward connections are indicated by solid lines; back-projections (which could implement top-down processing) by dashed lines, and recurrent connections within an area by dotted lines. s, Superficial pyramidal cells; d, deep pyramidal cells. Figure modified from Deco and Rolls (2005a).

Attention in visual search

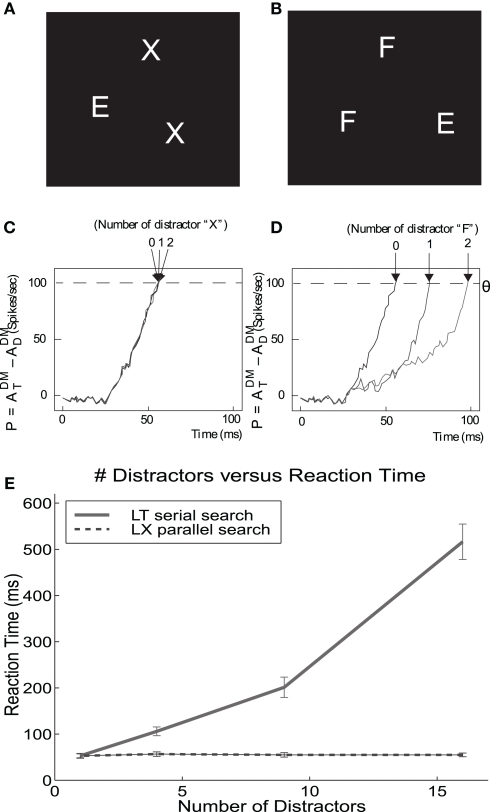
One source of evidence for attentional mechanisms in visual processing comes from psychophysical experiments using visual search tasks. This was proposed by Treisman and Gelade (1980); see also (Pashler, 1998) for other types of experiments evidencing attention. There, subjects examine a display containing randomly positioned items in order to detect a previously defined target. All other items in the display, which are different from the target, play the role of distractors. The main phenomenology can be understood from the dependence of the measured reaction time as a function of the number of items in the display. There are two main types of searching displays, namely: feature search or “pop out,” and conjunction or serial search. In a feature search task, the target differs from the distractors in a single feature, (e.g., only in its color). In this case, search times are independent of the number of distractors. In a conjunction search task, the target is defined by a conjunction of features, and each distractor shares at least one of those features with the target. The conjunction search experiments show that search time increases linearly with the number of distractors, implying a serial process.

The computation of a visual search works as follows. An external top-down bias from prefrontal area v46 to the IT module drives the competition in IT in favor of the population encoding the target object. Then, the intermodular back-projected attentional modulation IT–V4–V1 enhances the activity of the populations in V4 and V1, which encode the component features of the target. Only the locations in V1 matching the back-projected target features are up-regulated. The enhanced firing of the neuronal populations encoding the particular location of the target in V1 lead to increased activity in the spatially mapped forward pathway from V1 to V2–V4 to PP. This results in an increased firing in the PP module in the location that corresponds to the target. Consequently, these cascades of biased-competitions compute the location of the target, and are made explicit by the enhanced firing activity of neuronal populations at the location of the target in the spatially organized PP module. (Deco and Lee, 2004) showed that the properties of feature and conjunction search are both reproduced by this attentional architecture, as shown in Figure 5.

Figure 5.

Serial and parallel search emerge from the same mechanism. (A,B) Parallel and serial search stimuli, respectively. (C,D) Difference in the activation at the target location relative to the distractor locations as time evolves. The time required for this signal to cross threshold is assumed to be related to the time required by humans to find the target. The time required to find the E in X's is constant while the time required to find the E in F's increases linearly with the number of F's. (E) The visual search experiment is repeated for other stimuli with a large number of distractors. Finding the L in X's requires constant time (parallel), while finding the L in T's increases linearly with the number of T's (serial). DM, dorsal stream module. Figure modified from Deco and Lee (2004).

The implication of these computational results is that, while the network searches the visual field in parallel, there are differences in the latencies of the neural responses in the different conditions, related to how easily the dynamical system can perform the constraint satisfaction for the different conditions (see also Heinke and Backhaus, 2011).

Oscillations Format Visual Processing

As we have seen above, communication between higher and lower level brain areas is crucial to direct attention in visual search or complex visual scenes. Information transfer mediated by local and intercortical recurrent connections is generally associated with oscillatory activity. Particularly in the visual system, oscillatory activity has been widely reported experimentally, especially in the gamma frequency range. Yet, whether oscillations have a major functional role or, instead, would only be a by-product of neuronal information processing, is still debated. In this section, we argue that some of our recent modeling studies suggest at least three main functions for oscillatory activity:

Oscillations and attention

The biased-competition theory claims that the neuronal response – in terms of firing rate – to simultaneously presented stimuli is a weighted average of the response to isolated stimuli, and that attention biases the weights in favor of the attended stimulus (Desimone and Duncan, 1995). Thus, a neuron's firing rate increases when its preferred stimulus is attended, but decreases when the non-preferred one is attended. More recently, it has been shown that attention has also an effect on synchrony: selective attention to a visual stimulus specifically enhances the gamma-band synchronization among neurons in monkey's extrastriate visual cortex driven by that stimulus (Fries et al., 2001b, 2008; Bichot et al., 2005; Taylor et al., 2005; Womelsdorf et al., 2006). In humans, several EEG and MEG studies have found similar effects (Jensen et al., 2007; Tallon-Baudry, 2009). Although rate and gamma synchrony modulations occur simultaneously, it is not clear if and how they are mechanistically related.

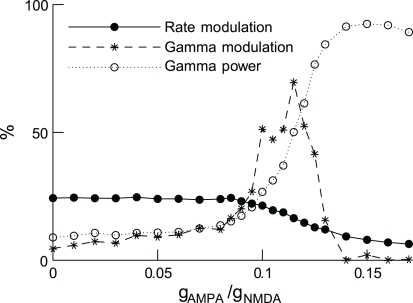
To investigate this issue, we recently extended the analysis of the above-mentioned model (Deco and Rolls, 2005b), in which biased-competition is implemented in a network of excitatory and inhibitory spiking neurons (as in Figure 3A), and attention is modeled as an additional input to the neurons encoding the attended stimulus. We looked at the effect of this input on both firing rates and gamma synchronization (Buehlmann and Deco, 2008). In order to allow oscillations; we increased the ratio of excitatory synaptic conductivities g_AMPA/g_NMDA. Indeed, when the shorter AMPA latencies dominate over the long-lasting NMDA ones, the latency of the excitatory components is smaller than the one of the inhibitory GABA components, resulting in the generation of oscillations (Brunel and Wang, 2003).

In accordance with the experiments, a stimulus generates correlated neural activity in the gamma frequency band, and its power is stronger for the neurons encoding the attended stimulus than for the neurons encoding the unattended stimulus. As the g_AMPA/g_NMDA conductance ratio increases, the attentional rate modulation decreases monotonically but the gamma modulation first increases up to a maximum and then decreases (Figure 6). These results imply that rate and gamma modulations can occur independently of each other, and are therefore not concomitant effects. Furthermore, gamma modulations are desirable because they were found to decrease the reaction times, in line with experimentation in monkeys (Womelsdorf et al., 2006). This suggests an optimal g_AMPA/g_NMDA conductance ratio.

Figure 6.

In attention, rate and gamma modulations are not concomitant effects. Rate modulation (solid curve) and gamma modulation (dashed curve) as a function of the excitatory synaptic conductance ratio g_AMPA/g_NMDA. Increasing this ratio increases rhythmic gamma-band power (dotted curve), decreases the rate modulation monotonically while gamma modulation has a peak. Either of the two modulations can be dominant, depending on the gamma power. Figure modified from (Deco et al., 2011).

Communication through coherence

Another desirable effect of rhythmic synchronization is that it allows the flexible routing of information between neuron pools. Consider two pools, A and B, oscillating at the same frequency. A projects on B, but A's spikes will significantly influence B if, and only if, they arrive during a critical period of excitability. Thus, by shifting the phase between the pools, one can virtually activate or deactivate the communication link between the pools. This is known as the “communication through coherence” (CTC) hypothesis (Fries, 2005). Direct physiological evidence for it is found in cat and monkey visual systems (Womelsdorf et al., 2007). In humans, the fact that a near-threshold visual stimulus can be perceived or not, depending on the phase of ongoing EEG oscillations at stimulus onset (Busch et al., 2009; Mathewson et al., 2009), is consistent with CTC.

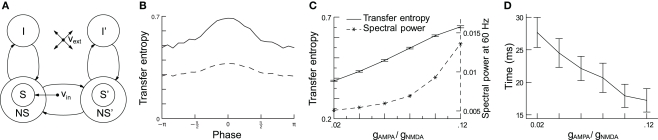
Recently, we quantified the effect of phase shifting on the communication between two oscillating neuronal pools (Figure 7A) using transfer entropy (TE; Buehlmann and Deco, 2010). TE is an information theoretical measure that quantifies the statistical coherence between systems, and is able to distinguish between shared and transported information (Schreiber, 2000). In accordance with the experiments, we found that (i) there is an optimal phase relation at which TE is highest between the two groups of neurons (Figure 7B), that (ii) TE increases as a function of the gamma power (Figure 7C), and (iii) the speed of information transfer increases as a function of the gamma power, measured from the time required to reach 50% of the TE after stimulus onset (Figure 7D). Taken together, these findings support the CTC hypothesis and, as rhythmic neuronal synchronization makes information transport more efficient and flexible, they suggest that it has an important functional role.

Figure 7.

Increasing network gamma frequency band power leads to mean transfer entropy (TE) increase and time for information transfer decrease. (A) Schematic representation of the network, which consists of two parts: in each part, there are excitatory (S, NS) and inhibitory (I) spiking neuron pools, which are interconnected. The connectivity is full. The selective pool (S) receives the external input (ν_in) and has strong recurrent connections. The two parts of the network are connected via the selective pools by both feedforward and feedback connections. All neurons also get an input (ν_ext) that simulates the spontaneous activity in the surrounding cerebral cortex. (B) TE as a function of phase shifts and directionality. TE is highest for a 0 phase shift and gets lower the more it differs from it. The solid line represents TE from neuronal pool 1 to pool 2 (forward), the dashed line from pool 2 to pool 1 (backward). Forward TE is clearly stronger than backward TE. (C) When the conductance ratio g_AMPA/g_NMDA increases, both gamma power (dashed line) and TE (solid line) increase. (D) Rise times of TE as a function of the conductance ratio. Information starts flowing after stimulus onset when, consequently, TE starts rising. The plot shows the time required to reach 50% of the average TE. TE clearly rises faster for higher gamma-band power. In both graphics, error bars indicate 95% confidence intervals; averaged over 100 trials. Figure modified from (Buehlmann and Deco, 2010).

Phase-of-firing coding, and STDP-based decoding

Communication through coherence suggests that there is an optimal time window for a neuron pool A to send spikes to another pool B, so that they have a significant impact on B. But how can information be encoded in those spikes? Recent experiments have established that information can be encoded in the spike phases with respect to a background oscillation in the local field potential (LFP) – a phenomenon referred to as PoFC. Evidence for such coding has been seen in the visual system, in particular in V1 (König et al., 1995; Fries et al., 2001a; Montemurro et al., 2008; Vinck et al., 2010) and V4 (Lee et al., 2005). These firing phase preferences could result from combining an oscillatory drive with a stimulus-dependent current that would produce the variations in preferred phases (Hopfield, 1995). This mechanism is supported by direct physiological evidence in vitro (Schaefer et al., 2006; McLelland and Paulsen, 2009). However, it remains unknown if such a firing activity can be decoded, that is if downstream neurons can respond selectively to patterns of phases in their inputs, and if this behavior can be learned.

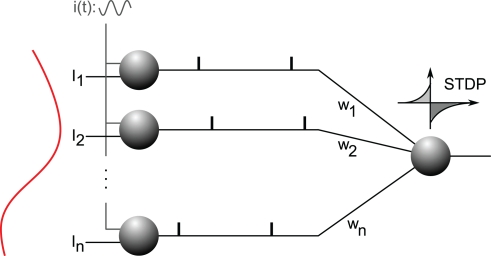
We have shown recently that STDP can solve the problem efficiently (Masquelier et al., 2009b). Specifically, a single neuron equipped with STDP (Figure 8) can robustly detect a hidden pattern repeating at random intervals, which involves only a subset of its afferents, and is automatically encoded in their firing phases (Figure 9). The oscillatory drive improves the spike time precision by decreasing their sensitivity to initial conditions, and avoiding jitter accumulation, so that they depend mainly on the current input values (Brette and Guigon, 2003; Hasenstaub et al., 2005; Schaefer et al., 2006; Markowitz et al., 2008). The ability of STDP to detect repeating spike patterns had been noted before in continuous activity (Masquelier et al., 2008, 2009a), but it turns out that oscillations greatly facilitate learning, which is possible even when only a small fraction of the afferents (∼10%) exhibits PoFC. A benchmark with more conventional rate-based codes demonstrated the superiority of oscillations and PoFC for both STDP-based learning and speed of decoding, which only takes one oscillatory cycle.

Figure 8.

Analog-to-phase conversion. Excitatory afferents 1…n are shown on the left. They receive static input currents I₁…I_n. (plotted on the left) and a common oscillatory drive i(t), which leads to a current-to-phase conversion: the stronger the current, the earlier the afferent fires during the oscillation cycle. All the afferents are connected through plastic synapses with weights w₁…w_n, to one downstream neuron equipped with STDP. This neuron will gradually become selective to the spike wave corresponding to the repeating current pattern (see Figure 9). Figure is modified from Deco et al. (2011).

Figure 9.

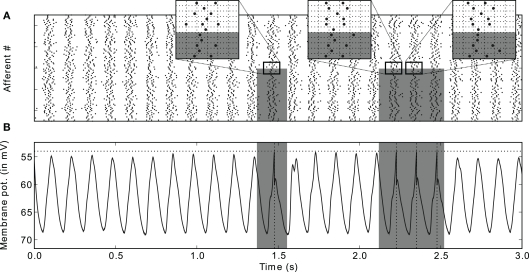
Downstream neuron's input and response after learning (A) Input spike trains. Spikes come in waves because of the oscillatory drive. Gray rectangles designate the periods where the pattern is presented, and the afferents that are involved in it (bottom half here). Three insets [horizontal grid size = 1 rad (in phase) = 20 ms] zoom on adequate periods to illustrate that the spike phases of the afferents involved in the pattern are the same (except for the noise) for different pattern presentations, which is not true for other afferents (top half). It is this repeating “spike wave” that STDP detects and learns. (B) Postsynaptic membrane potential as a function of time: it oscillates, but reaches the threshold if and only if the pattern is presented. Figure is modified from Deco et al. (2011).

The oscillatory drive formats the spike times into waves (Figure 9A) that are similar to the first spike waves after visual stimulus onset described in Section “Fast Feedforward Processing, Latency Coding, and STDP.” It is thus not so surprising that neurons equipped with STDP can also detect and learn repeating patterns in the spike waves caused by the oscillatory drive. This new oscillation-based scheme, however, can account for continuous vision, when no external time reference such as a stimulus onset is available. The scheme is particularly appealing for the processing of static, or slowly changing visual stimuli, which, without oscillations, would not generate precisely timed spikes (eye movements may be an alternative, see Continuous Vision). Consistent with our proposal, a growing body of experimental evidence in animals and humans demonstrates that successful long-term memory encoding correlates with increased oscillatory activity across a broad range of frequencies (from theta to gamma), in particular in the visual modality (Jensen et al., 2007; Klimesch et al., 2008; Tallon-Baudry, 2009). Interestingly, beyond mere oscillation power, what seems to be a prerequisite for successful visual memory formation is that single units should be phase-locked to the oscillation (Rutishauser et al., 2010) – a result consistent with our model.

Unsolved Questions and Future Directions

Continuous vision

In Section “Fast Feedforward Processing, Latency Coding, and STDP,” we focused on the transient activity generated when a stimulus suddenly appears at a given time from the dark, a paradigm extensively studied in the lab but rather unnatural. A more natural situation is that an image is formed on the retina at t = t₀ after a body or head movement, a saccade, or a micro-saccade (all of these are referred to as “movement” below). In that case, the “intensity-to-latency conversion” hypothesis we made is questionable for several reasons, in particular in the retina. First, the input current to a retinal ganglion cell (RGC) is a spatiotemporally filtered version of the luminance signal, as opposed to a spatially filtered version [among other things the surround signal is delayed (Enroth-Cugell et al., 1983; Cai et al., 1997)], and this spatiotemporal filtering does not stop during the movements. This means that the RGC input currents at t = t₀, and slightly after, depend not only on the current image, but also on what happened during the movement, and possibly even before. Furthermore, these currents are integrated and converted into spikes. This introduces another dependence on history (the same input current does not lead to the same spike latencies, depending on when the last spike was emitted). For all these reasons, the times-to-first-spikes with respect to t₀ are probably poor encoders of the current image. However, because the history of neighboring cells is likely to be similar, it seems reasonable to assume that this history will typically have a similar effect on their spike times, and thus a weak effect on their relative spike times – but this should be confirmed by simulations. Consistent with this idea, relative latencies are found to be more reliable than absolute ones in the retina (Gollisch and Meister, 2008).

We feel it is time to build models able to deal not only with “stimulus onset paradigms,” as the ones reviewed in Section “Fast Feedforward Processing, Latency Coding, and STDP,” but also with continuous vision, including body, head, and eye movements and moving stimuli. Such models could also simulate, unlike the current ones, the experimental protocols of rapid serial visual presentation (RSVP) and visual masking. The timescales involved in natural continuous vision processing are fast (∼10 ms; Butts et al., 2007), and individual neurons’ firing rates are not well defined at such a fine temporal resolution. Spiking neuron models should be preferred. STDP, which is able to detect consistently repeating spike patterns even in continuous activity (Masquelier et al., 2008, 2009a), probably plays a key role in continuous vision as well. Last but not least, continuous vision involves feedback loops, which should thus be included in those models. These should generate – among other things – self-sustained oscillations (Gray and Singer, 1989), and their desirable consequences reviewed in Section “Oscillations Format Visual Processing.”

Hardware implementations

As we have seen in this review, encoding and processing information with spike patterns is an efficient strategy which is probably extensively used in the visual system. Software simulation of these mechanisms is time consuming though, which can reduce their relevance for technology. Silicon hardware implementations, however, could be several orders of magnitude faster than the biological hardware (which is incredibly slow: neurons cannot fire more than a few hundred spikes per second, and those impulses propagate on axons between neurons with a velocity of 1–2 m/s). This means that an artificial vision system based on biological algorithms implemented on silicon hardware could, in principle, clearly outperform animals including humans.

One appealing technology to implement spike-based processing is the so-called address event representation (AER), where the spikes are carried as addresses of sending or receiving neurons on a digital bus. Time “represents itself” as the asynchronous occurrence of the event. AER was first proposed in 1991 by Mead's Lab at the California Institute of Technology (Sivilotti, 1991), and has been used since then by a wide community of hardware engineers. Furthermore, the recently discovered memristive nanoscale devices (Strukov et al., 2008) provide an appealing implementation of the STDP functionality (Linares-Barranco and Serrano-Gotarredona, 2009).

Together with Linares’ group, we are building hardware self-learning models of the visual cortex, which combine both AER and memristor technologies. In a first attempt to simulate the early visual system, we used a simple set up combining an AER artificial retina (Lichtsteiner et al., 2007) and a SNN mimicking V1 (the LGN was ignored). The artificial retina sensed the external world in a continuous (frame-free) manner, and generated spikes that were asynchronously propagated, as they flowed in, until they reach the V1 SNN. In this network, neurons were equipped with memristor-based STDP (for now simulated). This enabled them to gradually become orientation selective, as the system was exposed to natural stimuli (Zamarreño-Ramos et al., 2011). These results are still preliminary, but very encouraging. We speculate that this line of research will yield revolutionary results in the next decade.

Distinguishing decision making model approaches

Models on the accumulation of noisy evidence, as for instance during continuous motion viewing, come in a huge variety of flavors, which may be very difficult to distinguish on the basis of just behavioral data or even mean firing rates. Finding new analytical methods and intelligently designed experiments to distinguish the different approaches is thus a major future challenge in the field of perceptual decision making. Several recent studies have acknowledged this objective with a particular emphasis on multiple alternatives (Ditterich, 2010; Leite and Ratcliff, 2010; Purcell et al., 2010; Churchland et al., 2011).

Analyzing higher-order statistical properties (i.e., a variance and within-trial correlation measure) of neurophysiological data from a two- and four-alternative RDM task, (Churchland et al., 2011) could help distinguish between models categorized by their different sources of variability. Models with just one source of variability [either with a randomly varying slope but no within-trial noise (Carpenter and Williams, 1995), or a fixed slope with a random distribution of firing rates at each time-step (Cisek et al., 2009)] failed to account for the higher-order measures, although they agreed with behavior and mean firing rates. On the other hand, all different implementations of a stochastic accumulation to threshold, the drift–diffusion model (Ratcliff and Rouder, 1998) – a model based on probabilistic population codes (Beck et al., 2008) – and a recurrent attractor model (Wong et al., 2007) – a reduction of the model described in Section “Slower Visual Decision Making” – also matched the experimental data in variance and correlation.

Based on human behavioral data from a RDM task with three alternatives and three motion components, (Ditterich, 2010) intended to distinguish more detailed aspects of conceptual accumulation-to-bound models with regard to their goodness of fit and their neurophysiological predictions. Perfect integrators were compared to leaky, saturating integrators, with either feedback or feedforward inhibition. Note that most of the discussed models were found equivalent for certain parameter ranges (Bogacz et al., 2006). Hence, it might not be too surprising that none of the models could be excluded based only on the fits to the behavioral data. However, they differ substantially in their neurophysiological predictions on how the integrator states should evolve over time (see Table 2 in Ditterich, 2010). Invasive neural recordings from monkeys performing the same task will hopefully soon settle the dispute. Moreover, feedforward and feedback inhibition respectively suggest either negative or positive correlation between the integrator units, which might be tested with multi-electrode recordings.

Finally, for equal coherences in all three motion directions, (Niwa and Ditterich, 2008) measured faster mean reaction times for higher coherence levels, consistent with the predictions from the non-linear recurrent attractor network for increasing external inputs to all selective populations (see Slower Visual Decision Making). While models with feedforward inhibition require a scaling of the variance of the sensory signals in order to account for this effect, conceptual models with feedback inhibition could explain the result just with a change of the mean input (Ditterich, 2010). In that context, the predictions of the biophysically based attractor model on reaction times and changes of mind could also be tested more rigorously in a change of mind RDM experiment with two directionally opposite motion components (see Albantakis and Deco, 2011).

Conclusion

With this review we aimed to outline, within the frame of SNNs, the various ways in which different processing timescales imply and connect to different neural dynamics in the visual system. For object recognition, the high processing speed excludes extensive crosstalk between neural populations, and feedforward connectivity seems sufficient to explain experimental observations. However, recurrent connections are crucial for any non-linear operation, such as data integration or shaping the focus of attention, in tasks where higher level processing is beneficial in spite of consequently longer reaction times. Moreover, oscillatory activity might act as a higher-order mechanism for routing and encoding the exchanged information. Depending on which particular task the visual system is currently engaged in, the amount of information that is transmitted back and forth within and between the relevant brain areas thus varies substantially. Nonetheless, not only the amount of information exchanged between neural populations is task-dependent, the way the information is encoded also differs for the different processing modes. In fact, with the four modes of temporal processing, we have presented four distinct ways of how information might spread through the visual pathways: during object recognition for the fast feedforward sweep of activity along the ventral pathway, which consists of only one or a few spikes at each processing level, “rank order coding” (Thorpe and Gautrais, 1998) allows to convey information despite the low number of spikes, which excludes the classic rate coding scheme. Rate coding does still play the dominant role in visual discrimination tasks, where information is accumulated in decision-related brain areas along the dorsal visual stream. If the interplay between top-down and bottom-up signaling contributes to solving task-specific challenges to the visual system (such as directing attention or visual search), information may be routed via oscillatory activity, as described in the CTC theory (Fries, 2005). Finally, background oscillations in the LFP could serve as an internal substitute for an external temporal reference frame, which allows temporal encoding of information through the spike phases. This PoFC (Montemurro et al., 2008) provides a possible temporal code that is applicable even in the absence of external time frames, as in continuous vision or for long-lasting stimuli.

To conclude, we have shown that all these different coding schemes can be implemented in biologically inspired spiking neuron models with the associated neural dynamics determined by their network connectivity. The connection weights in the respective models were assumed to have formed according to Hebbian rules. Synapses that implement STDP can further shape the spiking network to perform temporal coding, and also to decode the information again. It remains to be investigated how robust the temporal codes are when faced with real, noisy sensory inputs, and to what extend the brain actually takes functional advantage of the various hypothetical neural codes. Yet, with our review, we want to emphasize the complementary nature and common basic principles of the different encoding schemes and neural dynamics that might operate alternatively in the visual system through a switch procedure, or even simultaneously, through multiplexed temporal scales (Victor, 2000; Panzeri et al., 2010).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.