Self-heating in piezoresistive cantilevers

Abstract

We report experiments and models of self-heating in piezoresistive microcantilevers that show how cantilever measurement resolution depends on the thermal properties of the surrounding fluid. The predicted cantilever temperature rise from a finite difference model is compared with detailed temperature measurements on fabricated devices. Increasing the fluid thermal conductivity allows for lower temperature operation for a given power dissipation, leading to lower force and displacement noise. The force noise in air is 76% greater than in water for the same increase in piezoresistor temperature.

Piezoresistive transduction is an alternative to optical detection for sensing the tip motion of atomic force microscope cantilevers.¹ The additional fabrication and implementation complexity of piezoresistive cantilevers is worthwhile in applications where optical access is limited or inconvenient.^{2, 3} In the past decade, the design optimization of piezoresistive cantilevers has been widely investigated.^{4, 5, 6, 7} Measurement resolution generally improves as power dissipation increases⁵ until the piezoresistor temperature becomes substantially greater than the ambient temperature, since increasing temperature corresponds to decreasing piezoresistive coefficient and increasing noise.^{8, 9}

In general, published research on piezoresistive cantilever design has either ignored Joule heating or set a power budget that is decoupled from cantilever design.^{4, 6} However, many applications are limited by cantilever temperature rather than power dissipation, such as biological force measurements,¹⁰ and the temperature increase for a given power varies with cantilever design. This letter considers how the temperature-dependence of piezoresistive cantilever performance can be included in cantilever design and operation.

Figure 1 shows the cantilever geometry, thermal conduction model, and a fabricated device. The overall length, width, and thickness of the cantilever are l, w, and t, respectively. The piezoresistor extends length l_pr from the base, encompasses the full cantilever width, and has a narrow slit to electrically isolate the loop. During operation, the resistor is electrically biased and Joule heating power W is distributed along its length.

Figure 1.

(a) The cantilever geometry and simulated power dissipation density, (b) 1D finite differences simulation used to calculate the temperature profile, and (c) scanning electron micrograph of a typical cantilever used here.

We fabricated piezoresistive cantilevers from single crystal silicon. The fabrication details have been presented previously.¹¹ Briefly, silicon-on-insulator wafers were phosphorus doped using 800 °C POCl₃ diffusion. Subsequently the piezoresistor and cantilever were patterned and etched, aluminum was sputtered and patterned for electrical contacts, and the cantilever was released using deep reactive ion etching. The dopant concentration profile was measured using spreading resistance analysis and the electrically active surface concentration was 2×10²⁰ cm⁻³.

We focus on two cantilever designs whose dimensions are summarized in Table 1. The piezoresistor constitutes 90% and 59% of the total resistance for designs A and B, respectively, and all experimental powers refer to the power dissipated in the released cantilever. The excess resistance was measured using the transfer length method and is primarily due to the silicon interconnect resistance.

Table 1.

Summary of cantilever dimensions and measured parameter values (μ±σ).

	Design A	Design B
l (μm)	890	124
w (μm)	10	10
t (μm)	2	0.34
lpr (μm)	212	32
kc at 300 K (W∕m K)	128.2	98.9
$G_f^{\prime }$ (mW∕m K)	32.8±3.3	43.4±2.7
Gbase (μW∕K)	41.9±16.3	17.7±8.4
Λ (μm)	287.1±20.7	104.6±25.0

The steady-state temperature is calculated by considering thermal conduction along the length of the beam and directly into the fluid; radiation is neglected but is small by comparison.¹² A one-dimensional (1D) approximation remains valid as long as the Biot number is much less than 1. For our cantilevers, Bi<10⁻⁵. The temperature profile, T(x), is calculated from $G_f^{\prime }\left[T\left(x\right)-T_0\right]-\nabla \left[A{k}_c\left(x\right)\nabla T\left(x\right)\right]={\dot{q}}^{\prime }\left(x\right)$, where $G_f^{\prime }$ is the cantilever-fluid thermal conductance per unit length, T₀ is the ambient temperature, A is the cross-sectional area, k_c is the average thermal conductivity of a cross-section, and ${\dot{q}}^{\prime }$ is the Joule heating per unit length. The temperature profile is simulated using finite differences by imposing an isothermal boundary condition at the silicon die (T₀) and adiabatic conditions at the cantilever tip. The thermal conductance between the cantilever and die, G_base, is finite. The values for k_c(x) consider temperature dependent phonon-impurity and phonon-boundary scattering.¹³ Boundary scattering is calculated from the beam thickness while impurity scattering is calculated from the dopant concentration profile. We calculate ${\dot{q}}^{\prime }\left(x\right)$ from 4I²R_s(T)∕w, where I is the current flow, and R_s is the temperature dependent sheet resistance.¹⁴ The average heating per unit length is W∕l_pr.

The cantilever temperature profile was measured using Raman thermometry.^{15, 16} The cantilever was biased to induce self-heating and the temperature was measured from the wavelength shift of the Stokes peak. The laser wavelength, power, and spot diameter were 488 nm, 45 μW and 1 μm, respectively. The adjustable parameters in the model, $G_f^{\prime }$ and G_base, were simultaneously fit to each temperature profile by minimizing the sum of the squared relative temperature residuals.

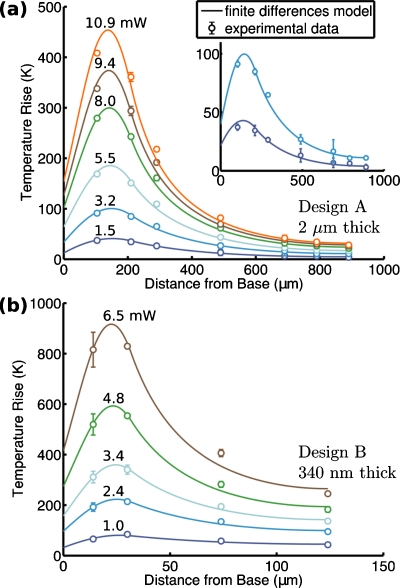
Figures 2a, 2b show the experimental and predicted temperature profiles for designs A and B operating in air. Table 1 summarizes the fitted model parameters. The temperature reaches a maximum approximately $\frac{2}{3}{l}_{pr}$ from the base and then decreases exponentially with thermal healing length $\Lambda ={\left(k_{c}A∕G_f^{\prime }\right)}^{1∕2}$.¹⁷ While we found $G_f^{\prime }$ to be insensitive to power dissipation, G_base and Λ vary considerably because they directly depend on k_c, which changes with temperature. The cantilever tip temperature increases linearly with power dissipation by 2.5 and 36.7 K∕mW for designs A and B, respectively. The 15-fold difference in ∂T_tip∕∂W is primarily due to surface area and distance from the piezoresistor to the cantilever tip (2.4Λ versus 0.9Λ), because the thermal conductance from the piezoresistor to the cantilever base varies less than 20% between the designs.

Figure 2.

[(a)–(b)] Comparison between Raman thermometry results and the finite differences model over a range of power dissipations in air. Error bars represent the standard deviation and are smaller than some of the symbols. The average model residual for both cantilever designs is 2%. (inset) Detail of the 1.5 and 3.2 mW data for design A. Error bars represent the standard deviation.

Although the heat transfer mechanism through the fluid is thermal conduction, an effective convection coefficient can be calculated from $h_{eff}=G_f^{\prime }∕2\left(w+t\right)$.^{18, 19} The measured effective convection coefficients in air are 1366±139 and 2098±131 W∕m² K for designs A and B, respectively, which are comparable to recent simulation results.¹²

The maximum and tip temperatures can be analytically approximated. The thermal conductance from the piezoresistor to the cantilever base, neglecting conduction to the fluid, is G_pr≈2wtk_c∕l_pr. Assuming that most of the heat is conducted to the cantilever base and not into the fluid, T_max≈W(G_base+G_pr)∕G_baseG_pr and T_tip≈T_maxe^{−(l−(2∕3)l_pr)∕Λ}. The error in calculating the tip temperature using the analytical model is <10 K using the parameters in Table 1.

As the thermal conductivity of the surrounding fluid increases, the temperature increase for a given power dissipation decreases. Piezoresistive cantilever measurement resolution scales as $1∕\sqrt{W}$,⁵ so an increase of k_f should improve the cantilever performance envelope. We measured the force resolution of cantilever design B in air and deionized water to explore this effect.

The cantilever stiffness was calibrated as 4.1±0.4 mN∕m from its dimensions and resonant frequency in air (22.3 kHz) before being passivated by 170 nm of parylene N to prevent electrochemical corrosion, increasing the stiffness by ≈12%. The cantilever sensitivity and noise were measured over a 10 to 10 kHz bandwidth using a temperature compensated Wheatstone bridge with a 0.5 to 4 V dc bridge bias and low noise instrumentation amplifier (TI INA103). The average temperature increase in the piezoresistor during experiments (ΔT_pr) was calculated from its electrical resistance using the temperature coefficient of resistance measured during Raman temperature calibration (1130±66 ppm∕K, 95% confidence interval). Displacement sensitivity was measured by deflecting the cantilever against a glass slide using a capacitively sensed piezoelectric stage (PI P-733) over a 5 μm deflection range and calculating the linear regression. We observed no detectable difference in force sensitivity between air and water. However, increased electromagnetic noise pickup in water increased the integrated noise by 10%. Thermomechanical force noise remained smaller than the piezoresistor Johnson noise in water.

The measured force noise in air was 76% greater than in water for a constant ΔT_pr [Fig. 3a]. Substantially greater heating was observed in air than in water [Fig. 3b], and the best fit $G_f^{\prime }$ values were 40.0 and 1129 mW∕m K in air and water, respectively. The temperature beyond the piezoresistor decays more quickly in water than in air, leading to an even greater improvement in force resolution when measured against the tip temperature. For 500 μW of total power dissipation (2.6 pN in air and 2.9 pN in water), the simulated ΔT_tip in air is 20 K while in water it is only 0.05 K. The thermal advantage of water is slightly offset by water’s increased density and viscosity which reduce the cantilever resonant frequency.²⁰ Both the thermal and physical properties of the fluid need to be accounted for in cantilever design.

Figure 3.

(a) Experimental force resolution in a 10 to 10 kHz bandwidth for cantilever design B in air and water. The force noise in air is 76% greater than in water for the same average piezoresistor temperature increase. (b) Average piezoresistor temperature as a function of total power dissipation calculated from current-voltage curves in air and water. Error bars represent the standard deviation.

Piezoresistive cantilever design and performance change significantly when self- heating is considered. First, the optimal piezoresistor length is shorter because the thermal conductance from the piezoresistor to the cantilever base is inversely proportional to piezoresistor length. Second, while narrow and thin cantilevers are advantageous for decreasing stiffness and increasing force sensitivity, wider and thicker cantilevers can dissipate more power. Third, the optimal cantilever dimensions and doping vary with k_f, and larger k_f improves sensing resolution. Finally, the resolutions of optical and piezoresistive sensing tend to converge in liquid due to the increase in thermomechanical noise and piezoresistor power dissipation.

In conclusion, we have investigated piezoresistive cantilever self-heating in air and water and provided design guidance for temperature-rise constrained applications. Force resolution measurements demonstrate that operation in water, usually considered a hindrance, can actually enhance performance. The results show that both the thermal and physical properties of the surrounding fluid should be considered in cantilever design.