Frailty Modelling for Survival Data from Multi-Centre Clinical Trial

Summary

Despite the use of standardized protocols in, multicentre, randomised clinical trials (RCTs), outcome may vary between centres. Such heterogeneity may alter the interpretation and reporting of the treatment effect. Below, we propose a general frailty modelling approach for investigating, inter alia, putative treatment-by-centre interactions in time-to-event data in multi-centre clinical trials. A correlated random effects model is used to model the baseline risk and the treatment effect across centres. It may be based on shared, individual or correlated random-effects. For inference we develop the hierarchical-likelihood (or h-likelihood) approach which facilitates computation of prediction intervals for the random effects with proper precision. We illustrate our methods using disease-free time-to-event data on bladder cancer patients participating in an European Organization for Research and Treatment of Cancer (EORTC) trial, and a simulation study. We also demonstrate model selection using h-likelihood criteria.

1. Introduction

In this paper we focus on multi-centre trials with time to event endpoints. We are interested in investigating potential heterogeneity in outcomes between centres. In this context, the use of proportional hazards (PH) frailty models with random effects, rather than PH models with fixed (centre) effects, are useful [1–4].

Our approach is to model: (a) the between-centre variation in the baseline risk and (b) the treatment effect across centres [2, 5], using random effects. Thus, our model incorporates a random centre effect and a random treatment-by-centre interaction. These two random components (or frailty terms) have usually been assumed to be independent [2, 5]. However, independence may be un-necessarily restrictive [6–8]. In particular, Legrand et al. [4] has recommended using correlated random effects. Furthermore, our approach also models individual-specific frailty terms [9–11], because covariates specified in the protocol, or involved in the minimization procedure [12, p.71], may not account for all prior differences between patients. Thus, by deploying classical frailty concepts, we hope to improve conventional strategies for analyzing RCTs trials.

Usually, inference in frailty models requires a marginal-likelihood approach, whereby the random effects are integrated out of the joint density consisting of response variables and random effects. This may involve the evaluation of analytically intractable integrals over the random effect distributions. To avoid these difficulties, several methods (e.g. Monte Carlo EM and Markov chain Monte Carlo) have been suggested [13, 14], but these remain computationally intensive, particularly when the number of random components is large or when their correlation structure is modelled [15–19].

Another important issue is that of estimating the standard errors for the prediction of random effects, which is required in order to construct 100(1 − α)% prediction intervals. Plots based on these intervals are useful, especially when investigating the heterogeneity of random centre and treatment effects. However, estimating the standard errors of random effects using “plug-in” methods, such as empirical Bayes (EB, [13, 20]), may underestimate the true variability of the estimated random effects. Thus, the development of an integral method of inference for frailty models is required.

Accordingly, we propose a unified method of inference within the h-likelihood framework [21–23]. The h-likelihood consists of data, parameters and unobserved random effects, and obviates integration over the random-effect distributions. Thus, the h-likelihood can be used directly for inference on random effects, while the marginal likelihood cannot because it eliminates them by integration. The h-likelihood approach also gives a statistically efficient estimation procedure for various random-effect models [11, 19, 24–26]. We derive, via the h-likelihood approach, improved methods for estimating the standard errors of the predictor of the random effects and the frailty parameters. In particular, we emphasize inference on the random effects rather than on just estimating the frailty parameters. Predictions and their intervals are useful in investigating heterogeneity over centers. We illustrate the methodology by analyzing time to first recurrence in patients with bladder cancer from an EORTC trial [27] and by a simulation study. We also employ the data to illustrate model selection using criterion [11] based on h-likelihood.

The paper is organized as follows. In Section 2 we review a formulation of frailty models, present an extension, and show how to interpret the random-effect terms. The h-likelihood estimation procedure for fitting the model is derived and an improved method for estimating the standard-error of the frailty parameters is proposed. Next, a new prediction method for random effects is proposed in Section 3. The new method is illustrated using the bladder cancer data set in Section 4. A simulation study is conducted to evaluate the performance of the proposed method in Section 5. And, finally, we discuss the approach in Section 6. The technical details are given in Appendices.

2. The model and estimation

2.1. Model formulation and interpretation

In general, suppose that data consist of right censored time-to-event observations collected from q centres. Let T_ij (i = 1, …, q, j = 1, …, n_i, n = Σ_i n_i) be the survival time for the jth observation in the ith centre (or cluster) and let C_ij be the corresponding censoring time. Then observable data become y_ij = min{T_ij, C_ij} and δ_ij = I(T_ij ≤ C_ij), where I(·) is the indicator function.

Denote by v_i a s-dimensional vector of unobserved log-frailties (random effects) associated with the ith cluster. Given v_i, the conditional hazard function of T_ij is of the form

$${\lambda }_{ij}(t\mid v_i)={\lambda }_0(t)exp({\eta }_{ij}),$$ (1)

where λ₀(·) is a unknown baseline hazard function,

$${\eta }_{ij}=x_{ij}^T\beta +z_{ij}^T{v}_i$$

is the linear predictor for the hazards, and x_ij = (x_ij1, …, x_ijp)^T and z_ij = (z_ij1, …, z_ijs)^T are p × 1 and s × 1 covariate vectors corresponding to fixed effects β = (β₁, …, β_p)^T and log-frailties v_i, respectively. Here z_ij is often a subset of x_ij. Alternatively, it may be the constant (unity) representing a cluster effect on the baseline hazard [13]. In this paper, we assume the normal distribution for v_i:

$$v_i\sim N_s(0,{\mathrm{\sum }}_i),$$

which is useful for modelling multi-component [11, 28] or correlated frailties [13, 29]. Here the covariance matrix Σ_i = Σ_i(θ) depends on θ, a vector of unknown parameters. We note that the formulation of model (1) is actually the same as that of Vaida and Xu [13] but that their covariance matrix for Σ_i is diagonal [8].

Equation (1) includes some well-known models. Let v_i0 be a random baseline intercept (representing the random baseline risk) and let v_i1 be a random slope (i.e. random treatment effect or random treatment-by-center interaction). If in model (1) z_ij = 1 and v_i = v_i0 for all i, j, it becomes a random intercept or shared model [30, 31] with

$${\eta }_{ij}=x_{ij}^T\beta +v_{i0},$$ (2)

where v_i0 ~ N (0, Σ_i) with ${\mathrm{\sum }}_i\equiv {\sigma }_0^2$ for all i. Let β₁ be the effect of primary covariate x_ij1 such as the main treatment effect and let β_m (m = 2, …, p) be the fixed effects corresponding to the covariates x_ijm. Our two random components lead to a bivariate model [8, 32] with

$${\eta }_{ij}=v_{i0}+({\beta }_1+v_{i1})x_{ij1}+\sum _{m=2}^p{\beta }_m{x}_{\mathit{ijm}},$$ (3)

which is easily derived by taking z_ij = (1, x_ij1)^T and v_i = (v_i0, v_i1)^T in (1). Here

$$\left(\begin{array}{c}{v}_{i0}\\ v_{i1}\end{array}\right)\sim N\left\{\left(\begin{array}{c}0\\ 0\end{array}\right),{\mathrm{\sum }}_i\equiv \left(\begin{array}{cc}{\sigma }_0^2& {\sigma }_{01}\\ {\sigma }_{01}& {\sigma }_1^2\end{array}\right)\right\}.$$

Model (3) allows a correlation term, ρ = σ₀₁/(σ₀σ₁), between two random effects (v_i0 and v_i1) within a centre and potentially extends the independent frailty model in which ρ = 0 [2, 5].

Furthermore, we note the model (1) may be asymmetric (or unbalanced) as it does not contain a generic individual-specific frailty term, v_ij to match the individual-level fixed effects, x_ij. Following Ha et al. [11], the one-component model (1) with ${\eta }_{ij}=x_{ij}^T\beta +z_{ij}^T{v}_i$ can be extended easily to a two-component model with

$${\eta }_{ij}=x_{ij}^T\beta +z_{ij}^{(1)T}{v}_i^{(1)}+z_{ij}^{(2)T}{v}_{ij}^{(2)},$$ (4)

where $v_i^{(1)}$ and $v_{ij}^{(2)}$ are independent, and $z_{ij}^{(1)}$ and $z_{ij}^{(2)}$ are random-covariate vectors corresponding to $v_i^{(1)}$ and $v_{ij}^{(2)}$, respectively. In fact, the model (4) can be written as in (1) by taking $z_{ij}={(z_{ij}^{(1)T},z_{ij}^{(2)T})}^T$ and $v_i={(v_i^{(1)},v_{ij}^{(2)})}^T$. Thus, the extension of results from one-component model (1) to two-component model (4) is straightforward [11, 21].

In order to interpret the fixed and random effects, we consider model (3) with a single binary-treatment indicator, x_ij. Then,

$${\lambda }_{ij}(t\mid v_{i0},v_{i1};x_{ij})={\lambda }_0(t)exp\{v_{i0}+({\beta }_1+v_{i1})x_{ij}\}.$$

Now, the time-dependent relative risk for treatment becomes

$${\psi }_{ij}(t\mid x=1,x=0)=\frac{{\lambda }_0(t)exp\{v_{i0}+({\beta }_1+v_{i1})·1\}}{{\lambda }_0(t)exp\{v_{i0}+({\beta }_1+v_{i1})·0\}}=exp({\beta }_1+v_{i1}),$$

which is free of time t and holds for all patients in centre i. Here exp(β₁) is the usual expression for the relative risk in a standard PH model. Thus, ψ_ij(t|x = 1, x = 0), represents a random multiplicative divergence from the standard relative risk in a PH model which is homogeneous with respect to centres. Note that exp(β₁ + v_i1) is often called the treatment hazard ratio in the ith centre [2, 5]. We also have that

$$\frac{exp({\beta }_1+v_{i1})}{exp({\beta }_1)}=exp(v_{i1}).$$

Thus v_i1 means the random deviation of the ith centre from the overall treatment effect. Similarly, in order to interpret v_i0 we consider the model without the covariate x_ij

$${\lambda }_{ij}(t\mid v_{i0})={\lambda }_0(t)exp(v_{i0})$$

whence,

$${\phi }_{ij}(t)=\frac{{\lambda }_0(t)exp(v_{i0})}{{\lambda }_0(t)exp(0)}=exp(v_{i0})$$

which is free of time t and holds for all patients in centre i, and v_i0 represents the random deviation of the ith centre from the overall underlying baseline risk.

2.2. H-likelihood estimation

We now show how to derive the h-likelihood estimation procedure for fitting a correlated semiparametric model (1) and also propose how to obtain valid standard-error estimates for frailty parameters (i.e. dispersion parameters).

Since the functional form of λ₀(t) is unknown, following Breslow [33], we approximate the baseline cumulative hazard function ${\mathrm{\Lambda }}_0(t)={\int }_0^t{\lambda }_0(u)du$ by a step function with jumps at the observed death times [23, 34];

$${\mathrm{\Lambda }}_0(t)=\sum _{k:y_{(k)}\le t}{\lambda }_{0k},$$

where y_(k) is the kth (k = 1, …, D) smallest distinct death time among the y_ij’s, and λ_0k = λ₀(y_(k)).

Following Ha et al. [23], the hierarchical log likelihood (h-likelihood) for frailty models (1) is defined by

$$h=h(\beta ,v,{\lambda }_0,\theta )=\sum _{ij}{\ell }_{1ij}+\sum _i{\ell }_{2i},$$ (5)

where

$$\begin{array}{l}\sum _{ij}{\ell }_{1ij}=\sum _{ij}{\delta }_{ij}\{log{\lambda }_0(y_{ij})+{\eta }_{ij}\}-\sum _{ij}\{{\mathrm{\Lambda }}_0(y_{ij})exp({\eta }_{ij})\}\\ =\sum _k{d}_{(k)}log{\lambda }_{0k}+\sum _{ij}{\delta }_{ij}{\eta }_{ij}-\sum _k{\lambda }_{0k}\left\{\sum _{(i,j)\in R_{(k)}}exp({\eta }_{ij})\right\},\end{array}$$

ℓ_1ij = ℓ_1ij(β, λ₀; y_ij, δ_ij|v_i) is the logarithm of the conditional density function for y_ij and δ_ij given v_i,

$${\ell }_{2i}={\ell }_{2i}(\theta ;v_i)=-\frac{1}{2}[logdet\{2\pi {\mathrm{\sum }}_i(\theta )\}]-\frac{1}{2}{v}_i^t{\mathrm{\sum }}_i{(\theta )}^{-1}{v}_i$$

is the logarithm of the density function for v_i with parameters θ, Λ₀(·) is the baseline cumulative hazard function, and ${\eta }_{ij}=x_{ij}^T\beta +z_{ij}^T{v}_i$. Here β = (β₁, …, β_p)^T, $v={(v_1^T,\dots ,v_q^T)}^T$, λ₀ = (λ₀₁, …, λ_0D)^T, d_(k) is the number of deaths at y_(k) and R_(k) = R(y_(k)) = {(i, j) : y_ij ≥ y_(k)} is the risk set at y_(k). In (5) log likelihood of the ith cluster is the logarithm of the joint density of (y_i, δ_i) and v_i, where y_i = (y_i1, …, y_ini)^T and δ_i = (δ_i1, …, δ_ini)^T. As the number of λ_0ks can increase with the number of events, the function λ₀(t) is potentially of high dimension. Accordingly, for estimation of (β, v) Ha et al. [23] proposed the use of the profiled h-likelihood h^* from which λ₀ is eliminated:

$$h^{\ast }=h{\mid }_{{\lambda }_0={\widehat{\lambda }}_0}=\sum _{ij}{\ell }_{1ij}^{\ast }+\sum _i{\ell }_{2i},$$ (6)

where

$${\widehat{\lambda }}_{0k}(\beta ,v)=\frac{d_{(k)}}{{\sum }_{(i,j)\in R_{(k)}}exp({\eta }_{ij})},$$

are solutions of the estimating equations, ∂h/∂λ_0k = 0, for k = 1, …, D. Note here that ${\sum }_{ij}{\ell }_{1ij}^{\ast }={\sum }_{ij}{\ell }_{1ij}{\mid }_{{\lambda }_0={\widehat{\lambda }}_0}={\sum }_k{d}_{(k)}log{\widehat{\lambda }}_{0k}+{\sum }_{ij}{\delta }_{ij}{\eta }_{ij}-{\sum }_k{d}_{(k)}$ does not depend on λ₀. Thus Lee and Nelder’s [21–22] h-likelihood procedure for hierarchical generalized linear models (HGLMs) can be extended to the frailty models based on h^* [11, 19]. Here, for the estimation of frailty parameters θ we use an adjusted profile h-likelihood [18, 35], p_β,v(h^*) defined in (A2); the details for estimation procedure are given in Appendix A.

We have shown that the approximated standard-error estimates for β̂ are obtained from the inverse of −∂²h^*/∂(β, v)², given in (7) [18, 23]. In this paper we propose that the approximated standard-error estimates for θ̂ are directly obtained using the inverse of −∂²p_β,v(h^*)/∂θ²; the technical details are given in Appendix B. We also show the performance of these estimates by simulation below. Some conceptual differences between h-likelihood and other estimation methods for frailty models (1) are described in Appendix C.

3. Prediction of random effects

In HGLMs location parameters and dispersion parameter are asymptotically orthogonal [21]. Thus, very recently Lee and Ha [36] showed that a proper standard-error (SE) estimate for the prediction interval of random effects v can be computed from the inverse of the information matrix for (β, v) based on the h-likelihood. Here, the SE becomes the squared root of the approximation of the conditional mean-square error of prediction (CMSEP) of Booth and Horbert [37]. This is a general measure of predictive uncertainty and, following Lee and Ha [36], its extension to frailty models is straightforward as shown below.

In frailty models (1), as in HGLMs, location parameters (β, λ₀, v) and frailty parameters θ are asymptotically orthogonal. For a moment, assume that θ is known. Accordingly, we need only focus on (β, v) after eliminating λ₀ i.e. by using h^*. Following Ha et al. [23] and Ha and Lee [18], the asymptotic covariances for β̂ and v̂ − v are obtained from the inverse of information matrix, J(h^*; β, v) = −∂²h^*/∂(β, v)², of β and v based on h^*:

$$J(h^{\ast };\beta ,v)=-\left(\begin{array}{cc}{\partial }^2{h}^{\ast }/\partial \beta \partial {\beta }^T& {\partial }^2{h}^{\ast }/\partial \beta \partial v^T\\ {\partial }^2{h}^{\ast }/\partial v\partial {\beta }^T& {\partial }^2{h}^{\ast }/\partial v\partial v^T\end{array}\right)=\left(\begin{array}{rr}\hfill X^T{W}^{\ast }X& \hfill X^T{W}^{\ast }Z\\ \hfill Z^T{W}^{\ast }X& \hfill Z^T{W}^{\ast }Z+U\end{array}\right),$$ (7)

where X and Z are the n × p and n × q model matrices for β and v whose ijth row vectors are $x_{ij}^T$ and $z_{ij}^T$, respectively, $U=-{\partial }^2{\ell }_2/\partial v^2={\mathrm{\sum }}^{-1}=\text{BD}({\mathrm{\sum }}_1^{-1},\dots ,{\mathrm{\sum }}_q^{-1})$, and the weight matrix W^* = W^*(β, v) is given in (B4). Here, BD(·) denotes a block diagonal matrix. This means that the SEs of v̂ − v can be computed from the information matrix, J in (7), of the profile h-likelihood h^*.

Let y_o = (y^T, δ^T)^T and $\psi ={({\beta }^T,{\lambda }_0^T)}^T$. Here y and δ are the vectors of y_ij’s and δ_ij’s, respectively. Following Booth and Horbert [37], the CMSEP based on y_o and ψ is defined by

$$\text{CMSEP}=E_{\psi }[\{\widehat{v}(\widehat{\psi })-v\}{\{\widehat{v}(\widehat{\psi })-v\}}^T\mid y_o],$$

where v̂ (ψ̂) ≡ v̂ (ψ)|_ψ=ψ̂ and v̂ (ψ) is the solution to ∂h/∂v = 0 for a given ψ. Note here that v̂ (ψ) = E(v|y_o) asymptotically. Along the lines of Lee and Ha [36], J(h^*; β̂, v̂)⁻¹ ≡ J(h^*; β, v)⁻¹|_{β=β̂, v = v̂} gives the first-order approximation to the CMSEP, leading to a SE for v̂ − v:

$$\begin{array}{l}\text{CMSEP}={var}_{\psi }(v\mid y_o)+D(\psi )\\ \approx \{{(-{\partial }^{2}h/\partial v\partial v^T)}^{-1}+(\partial \widehat{v}/\partial \psi )var(\widehat{\psi }){(\partial \widehat{v}/\partial \psi )}^T\}{\mid }_{\psi =\widehat{\psi },v=\widehat{v}}\end{array}$$ (8)

$$\begin{array}{l}=\text{bottom}\text{right}\text{hand}\text{corner}\text{of}J{(h^{\ast };\widehat{\beta },\widehat{v})}^{-1}\\ ={\{(Z^T{W}^{\ast }Z+U)-(Z^T{W}^{\ast }X){(X^T{W}^{\ast }X)}^{-1}(X^T{W}^{\ast }Z)\}}^{-1}{\mid }_{\beta =\widehat{\beta },v=\widehat{v}},\end{array}$$ (9)

where var_ψ(v|y_o} = E[{v̂ (ψ) − v}{v̂ (ψ) − v}^T|y_o] and D(ψ) = E[{v̂ (ψ̂) − v̂ (ψ)}{v̂(ψ̂) − v̂ (ψ)}^T|y_o] is a nonnegative correction that accounts for the variability of parameter estimates ψ̂. Here ∂v̂/∂ψ = − (−∂²h/∂v∂v^T)⁻¹ (−∂²h/∂v∂ψ^T)|_{v= v̂}. For the SE of prediction of random effects Vaida and Xu [13] and Othus and Li [20] used the EB method based on conditional posterior distribution of v given y_o, leading to

$${var}_{\psi }(v\mid y_o)\approx {(-{\partial }^{2}h/\partial v\partial v^T)}^{-1}{\mid }_{\psi =\widehat{\psi },v=\widehat{v}},$$ (10)

which corresponds to the first term on the right hand side of (8) [21, 37]. The EB method can underestimate the SE of v̂ − v because it ignores the term above, D(ψ), which accounts for the inflation of the CMSEP caused by estimating $\psi ={({\beta }^T,{\lambda }_0^T)}^T$ [36, 37]. Following Lee and Ha [36], for the 95% h-likelihood and EB prediction intervals for v we use

$$\{\widehat{v}-1.96\text{SE}(\widehat{v}-v),\widehat{v}+1.96\text{SE}(\widehat{v}-v)\},$$

where v̂ are obtained from (A1). Here the estimated h-likelihood and EB standard errors, SE(v̂ − v), are also obtained from the square roots of (9) and (10), respectively.

4. Practical example

4.1. The data and correlated model

The duration of the Disease Free Interval (DFI) in non muscle invasive bladder cancer patients, treated in various centres in Europe, is analysed. The DFI is defined as the time from randomization to the date of the first recurrence. Patients without recurrence at the end of the follow-up period were censored at their last date of follow-up. Patients were enrolled in 7 studies conducted by the EORTC [27]. For simplicity of analysis, we consider only 410 patients from 21 centres included in EORTC trial 30791 (Table 1). The two covariates of interest are: CHEMO x_ij1 (0=No, 1=Yes) and TUSTAT x_ij2 (0=Primary, 1=Recurrent). Notice that x_ij1 is the main treatment covariate. Patients with missing values for x_ij2 were excluded. The numbers of patients per centre varied from 3 to 78, with mean 19.5 and median 15. Of the 410 patients, 204 patients (49.8 per cent) without recurrence were censored at the date of last follow up.

Table 1.

Numbers of patients and recurrences per centre in the bladder cancer data

Centre	np	ne	rc	Centre	np	ne	rc
1	3	1	0.67	12	15	11	0.27
2	3	2	0.33	13	18	8	0.56
3	4	4	0	14	18	9	0.50
4	5	2	0.60	15	21	10	0.52
5	5	5	0	16	27	17	0.37
6	6	4	0.33	17	28	15	0.46
7	7	3	0.57	18	30	12	0.60
8	8	4	0.50	19	42	13	0.69
9	11	5	0.55	20	52	18	0.65
10	14	8	0.43	21	78	46	0.41
11	15	9	0.40

n_p = No. of patients in centre; n_e = No. of events; r_c = 1 − (n_e/n_p); Centres ordered by increasing n_p.

For the purpose of analysis, we consider the three submodels of (3):

• M1 (Cox): Cox model without frailties (basic hazard),

• M2 (Indep): Cox models, with two independent frailty terms (ρ = 0),

• M3 (Corr): Cox models, with two correlated frailty terms (ρ ≠ 0).

Models M2 and M3 contain the random baseline risk v_i0 and the random treatment-by-centre interaction term, v_i1x_ij1. The models were fitted using SAS/IML. The results are summarized in Table 2. In all three models the two fixed effects (β_j, j = 1, 2) are significant. In particular, the use of chemotherapy (CHEMO = 1) significantly prolongs the time to first recurrence as compared to patients who do not receive chemotherapy (CHEMO = 0): see also [4]. The two nested models (M1 and M2) ignoring random components or their correlation show similar results for β_j (j = 1, 2). However, the absolute magnitude and SE of the estimate for the main treatment effect β₁ in M1 and M2 are smaller than those for the correlated model (M3). In M2 and M3, the variances ( ${\sigma }_0^2$ and ${\sigma }_1^2$) indicate the amount of variation between centres in the baseline risk and in the treatment effect, respectively. Here, the estimate of ${\sigma }_0^2$ is relatively larger than that of ${\sigma }_1^2$. This does not seem surprising since differences in outcome according to treatment effect are typically smaller than differences due to patient characteristics which often vary across centres. However, care may be necessary in comparing the two variances because these two values should not be interpreted on the same scale.

Table 2.

Results for fitting the four models to the bladder cancer data

Model	β̂1 (SE)	β̂2 (SE)	${\widehat{\sigma }}_0^2$ (SE)	${\widehat{\sigma }}_1^2$ (SE)	σ̂01 (SE)	[ρ̂]
M1 (Cox)	−0.667 (0.170)	0.509 (0.144)	–	–	–
M2 (Indep)	−0.695 (0.175)	0.544 (0.149)	0.070 (0.058)	3 × 10−12 (1 × 10−4)	–
M3 (Corr)	−0.757 (0.191)	0.532 (0.150)	0.161 (0.178)	0.036 (0.170)	−0.068 (0.149)	[−0.893]
M4 (B)	−0.695 (0.175)	0.544 (0.149)	0.070 (0.058)	–	–

M1: Cox model without frailties; M2: independent frailty model with ρ = 0;

M3: correlated frailty model with ρ ≠ 0; M4: shared frailty model with random baseline risk (B) only; β₁ and β₂, effects of treatment and tumor status, respectively; ${\sigma }_0^2$ and ${\sigma }_1^2$, the variances of random baseline risk and random treatment effect, respectively; σ₀₁ and ρ, the corresponding covariance and correlation with ρ = σ₀₁/(σ₀σ₁);

SE, the estimated standard error for parameters.

Moreover, the correlated model M3 explains the degree of dependency between the two random components (i.e. the random centre effect v₀ and the random treatment-by-centre interaction v₁). The estimate of ρ (ρ̂ = −0.893) gives a large negative value, indicating that the two predicted random components (v̂₀ and v̂₁) have a strong negative correlation. It is clear from the plot (not shown) of v̂₁ against v̂₀ that as v_i0 increases (i.e. the baseline risk increases), v_i1 decreases. Note here that exp(v_i1) represents the ratio of treatment hazard rate in the ith centre (i.e. exp(β₁ + v_i1)) to overall hazard rate (i.e. exp(β₁)). In particular, the estimate of β₁ in M3 is negative; we see that a decreasing value of v_i1 corresponds to an increased treatment effect. Thus, the negative correlation leads to the conclusion that treatment confers more benefit in centres with a higher baseline risk. This is consistent with the findings by Turner et al. [6] and Rondeau et al. [8] in the context of meta-analysis.

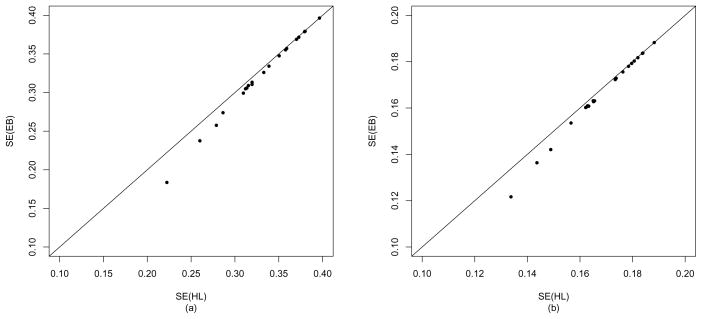
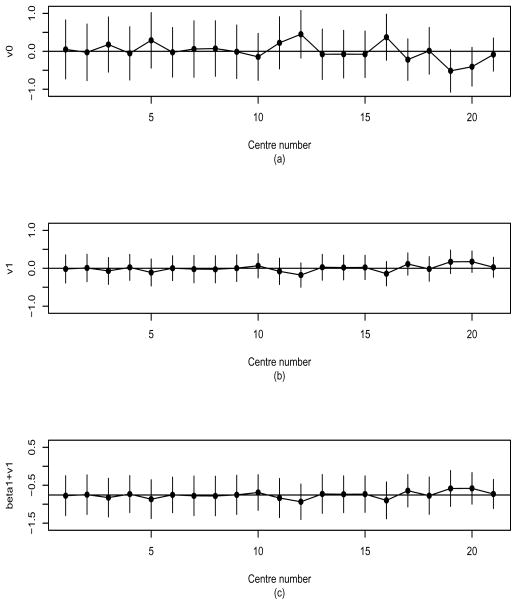
Figure 1 compares SE estimates of h-likelihood (HL) versus EB under M3. As expected, the EB estimates are smaller than HL estimates in both v_i0 and v_i1, leading to a lower coverage probability of prediction interval than the nominal level. Accordingly, below, we conduct detailed analyses of the random effects using HL. Figure 2 shows the estimates and 95% prediction intervals for the random effects in the 21 centres using M3. It shows the variations of the two random components (v_i0, v_i1) over centres, ordered by the number of patients entered. In particular, Figure 2(a) shows that centres 12 and 19 provide the highest and the lowest baseline risk, respectively. From Figure 2(b) we see that the corresponding centres give lowest and highest treatment hazards, respectively, which leads in this case to a negative correlation (ρ̂ = −0.893), as shown in Table 2.

Figure 1.

Standard error (SE) estimates of empirical Bayes (EB) versus h-likelihood (HL) analyses for random effects in the bladder cancer data; (a) v₀ and (b) v₁ in correlated model (M3).

Figure 2.

Random effects of 21 centres in the bladder cancer data and their 95% prediction intervals, under correlated model (M3); (a) baseline risk (v_i0); (b) treatment-by-centre interaction (v_i1); (c) log treatment hazard ratio (b_i1 = β₁ + v_i1). Centres are sorted in increasing order of number of patients.

Figures 2(a) and 2(b) also give the prediction intervals for the random baseline risk (v_i0) and the random treatment-by-centre interaction (v_i1), respectively. Overall, the lengths of the intervals are seen to decrease as the number of patients per centre increases, particularly for Figure 2(a): see also [13]. Figure 2(a) indicates substantial variation in the baseline risk across centres. However, Figure 2(b) shows overall homogeneity in the effect of treatment across centres, that is, there is little treatment-by-centre interaction in this data set. Thus, in this multicentre trial there is little difference in the treatment effects across centres and the treatment is shown to be effective, while there appears to be substantial variation in the baseline risk of DFI across centres. These results suggest that the treatment effect may be generalized to a broader patient population as in the findings by Yamaguchi and Ohashi [2].

In addition, the prediction intervals for the log treatment hazard rates (i.e. b_i1 = β₁ + v_i1) in the different centres are also useful to check the variations over centres. Similarly, the 95% prediction interval of b_i1 is given by

$$\{{\widehat{b}}_{i1}-1.96\text{SE}({\widehat{b}}_{i1}-b_{i1}),{\widehat{b}}_{i1}+1.96\text{SE}({\widehat{b}}_{i1}-b_{i1})\},$$

where b̂_i1 = β̂_i1 + v̂_i1 and $\text{SE}({\widehat{b}}_{i1}-b_{i1})=\sqrt{var({\widehat{b}}_{i1}-b_{i1})}$. Here var(b̂_i1 − b_i1) = var(β̂₁) + var(v̂_i1 − v_i1) + 2cov(β̂₁, v̂_i1 − v_i1) is obtained from J⁻¹ in (7). Figure 2(c) shows wider interval lengths than in Figure 2(b) due to the additional variance and covariance terms, but again confirms there is little difference in the treatment effects over centres.

4.2. Model selection

A thorough analysis will involve us in enlarging the potential model space beyond M1, M2 or M3. We consider a number of extensions below and show how to select an appropriate model using a Akaike information criterion (AIC) [11] based on the focussed extended restricted likelihood (ERL, [35]);

$$\mathit{AIC}(T_d^{\ast })=T_d^{\ast }+2p_T.$$

Notice that $T_d^{\ast }=-2p_{\beta ,v}(h^{\ast })$ is a deviance based on the ERL p_β,v(h^*) in (A2) which eliminates (β, v) from h^*, the profile h-likelihood from which the nuisance function λ₀(t) has already been eliminated. Thus, $T_d^{\ast }$ is a function only of the frailty parameters θ and $\mathit{AIC}(T_d^{\ast })$ is used to select the frailty structure best supported by the data. Here p_T is the number of frailty parameters (i.e. the parameters governing the frailty distribution), not the number of all fitted parameters or frailties. Notice that the focussed $\mathit{AIC}(T_d^{\ast })$ is a sharper model selection tool than the more usual unfocussed AIC [11].

Recall that v_i0 and v_i1 are the random baseline risk and random treatment effect of the ith centre, respectively. For the purpose of analysis, we consider the following five models including M1–M3, λ_ij(t|v) = λ₀(t) exp(η_ij) with η_ij allowing several frailty structures in models M2–M5: Here (v_i0, v_i1) ~ BN means that $v_{i0}\sim N(0,{\sigma }_0^2),v_{i1}\sim N(0,{\sigma }_1^2)$ and ρ = Corr(v_i0, v_i1); (v_i0, v_i1) ~ IN also means BN with ρ = 0.

$$\begin{array}{l}\text{M}1(\text{Cox}):{\eta }_{ij}={\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2},\\ \text{M}2(\text{Indep}):{\eta }_{ij}=({\beta }_1+v_{i1})x_{ij1}+{\beta }_2{x}_{ij2}+v_{i0},\text{with}(v_{i0},v_{i1})\sim IN.\\ \text{M}3(\text{Corr}):{\eta }_{ij}=({\beta }_1+v_{i1})x_{ij1}+{\beta }_2{x}_{ij2}+v_{i0},\text{with}(v_{i0},v_{i1})\sim BN.\\ \text{M}4(\text{B}):{\eta }_{ij}={\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+v_{i0},\text{with}{v}_{i0}\sim N(0,{\sigma }_0^2),\\ \text{M}5(\text{T}):{\eta }_{ij}={\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+v_{i1}{x}_{ij1},\text{with}{v}_{i1}\sim N(0,{\sigma }_1^2),\end{array}$$

where B and T denote random baseline risk and random treatment effect, respectively. Here M3 is our full model and the others are various simplifications of it by assuming null components, i.e. M1 (v_i0 = 0, v_i1 = 0), M2 (ρ = 0), M4 (v_i1 = 0) and M5 (v_i0 = 0). For ease of comparison and ranking of candidate models, we have set the smallest AIC to be zero and the other AIC values are shifted accordingly. In Table 3 we report the AIC differences, not the AIC values themselves. The deviance from model M2 is very similar to that obtained in M4 because in M2 the variance of the v_i1 is very small, i.e. ${\widehat{\sigma }}_1^2\approx 0$ in Table 2. If the AIC difference is larger than 1 the choice can be made [38, p.84]. Under this empirical criterion, we note that $\text{AIC}(T_d^{\ast })$ selects M4 as an appropriate model; its estimation results are also presented in Table 2. In particular, it clearly rejects more complex models M2 and M3 than M4, indicating that it reflects model complexity properly [11].

Table 3.

Deviance results: AICs for selecting frailty structures in the bladder cancer data

Model	$T_d^{\ast }$	pT	$\text{AIC}(T_d^{\ast })$
M1 (Cox)	2196.2	0	1.2
M2 (Indep)	2193.0	2	2.0
M3 (Corr)	2192.7	3	3.7
M4 (B)	2193.0	1	0
M5 (T)	2194.2	1	1.2
M6 (I)	2195.6	1	2.6
M7 (B+I)	2192.3	2	1.3
M8 (T+I)	2193.5	2	2.5
M9 (Indep+I)	2192.3	3	3.3
M10 (Corr+I)	2192.1	4	5.1

AIC, differences where the smallest AIC is adjusted to be zero; T, random treatment effect (v_i1); I, individual random effect (v_ij); Indep, B & T are independent; Corr, B & T are correlated; $T_d^{\ast }=-2\{p_{\tau }(h^{\ast })\};p_T$, the number of frailty parameters.

However, the T_ij may also depend on the individual-specific random effects as in Ha et al. [11]. If this is the case, some of the observed variation between centres is attributable to the heterogeneity between patients. We account for this properly, by introducing an appropriate patient-specific frailty component. Let v_ij be the random effects of the jth patient in the ith centre, satisfying v_ij ~ N (0, σ²). The extra random term v_ij, which is matched with individual-level event time T_ij and fixed effect x_ij, can be viewed as modelling heterogeneity between patients at the individual patient level [9]. Accordingly, we consider the following additional models:

$$\begin{array}{l}\text{M}6(\text{I}):{\eta }_{ij}={\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+v_{ij},\text{with}{v}_{ij}\sim N(0,{\sigma }^2),\\ \text{M}7(\text{B}+\text{I}):{\eta }_{ij}={\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+v_{i0}+v_{ij},\text{with}{v}_{i0}\sim N(0,{\sigma }_0^2)\text{and}{v}_{ij}\sim N(0,{\sigma }^2),\\ \text{M}8(\text{T}+\text{I}):{\eta }_{ij}={\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+v_{i1}{x}_{ij1}+v_{ij},\text{with}{v}_{i1}\sim N(0,{\sigma }_1^2)\text{and}{v}_{ij}\sim N(0,{\sigma }^2),\\ \text{M}9(\text{Indep}+\text{I}):{\eta }_{ij}=({\beta }_1+v_{i1})x_{ij1}+{\beta }_2{x}_{ij2}+v_{i0}+v_{ij},\text{with}(v_{i0},v_{i1})\sim IN\text{and}{v}_{ij}\sim N(0,{\sigma }^2),\\ \text{M}10(\text{Corr}+\text{I}):{\eta }_{ij}=({\beta }_1+v_{i1})x_{ij1}+{\beta }_2{x}_{ij2}+v_{i0}+v_{ij},\text{with}(v_{i0},v_{i1})\sim BN\text{and}{v}_{ij}\sim N(0,{\sigma }^2),\end{array}$$

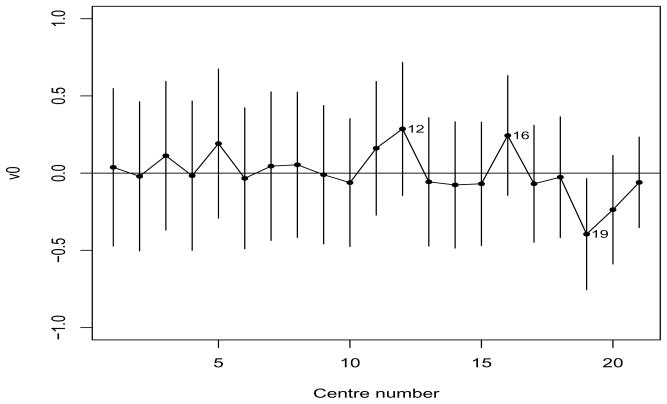
where I denotes individual random effect. Now, M10 is the full model which combines models M3 and M6 and the others are various simplifications of it as before, i.e. M9 (ρ = 0), M8 (v_i0 = 0), M7 (v_i1 = 0) and M6 (v_i0 = 0, v_i1 = 0). Note that M6 has independence between the survival times within centres. However, comparing model M6 with M4, M6 is rejected. We also see that additional random effects v_ij for B, T, Indep and Corr do not lead to any improvement in deviances. Here, the $\text{AIC}(T_d^{\ast })$ again rejects the additional complexity implied by models M7–M10. Thus, for the bladder-cancer data set the focussed AIC chooses M4 as the best model among those considered. Under M4 the predicted random effects (i.e. random baseline risks) and 95% prediction intervals for each centre are plotted in Figure 3. It shows substantial variations in the baseline risk over centre as evident in Figure 2(a). In particular, the three centres (12, 16) and 19 stand out as having the highest and lowest baseline risks, respectively. Note that although we report the SEs of the σ²s, one should not use them for testing σ² = 0 [13]. Now we are also interested in testing the hypothesis $H_0:{\sigma }_0^2=0$, no centre effect (i.e. no variation in random-baseline risk). Such a null hypothesis is on the boundary of the parameter space, so that the critical value of an asymptotic $({\chi }_0^2+{\chi }_1^2)/2$ distribution is 2.71 at 5% significant level [25, 39, 40]. The difference in deviance (−2p_τ (h^*) in Table 3) between M1 and M4 is 3.2(> 2.71), indicating that the centre effect is significant, i.e. ${\sigma }_0^2>0$.

Figure 3.

Random baseline risks (v_i0) of 21 centres in the bladder cancer data and their 95% prediction intervals, under the final model (M4). Centres are sorted in increasing order of number of patients.

5. Simulation study

Numerical studies, using 200 replications of simulated data, were conducted to evaluate the performance of the proposed method. Here we consider the two interesting models (2) and (3), which correspond to M4 and M3, respectively. The structure of bladder-cancer data in Table 1 is assumed in order to generate the data from each model. That is, the simulated data structures consist of the total patients n = 410 coming from 21 centres, with the number (n_i) of different patients.

Firstly, data are generated from the model (2) with λ₀(t) = 1 and the two different binary covariates, the main treatment x_ij1 and x_ij2;

$${\lambda }_{ij}(t\mid v_{i0})=exp\{{\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+v_{i0}\}.$$

Here x_ij1 and x_ij2 are generated from a Bernoulli distribution with success probability 0.5, respectively. The corresponding true parameters are β₁ = −0.5 and β₂ = 0.5. The random effects v_i0 are also generated from $N(0,{\sigma }_0^2)$ with ${\sigma }_0^2=0.2$ and 1.0. The corresponding censoring times were, respectively, generated from exponential distribution with parameter values empirically determined to achieve approximately the right censoring rate in each centre of Table 1.

For the 200 replications we computed the mean, standard deviation (SD), the mean of the estimated SE for β̂_j (j = 1, 2) and ${\widehat{\sigma }}_0^2$, respectively. The corresponding SEs are, respectively, obtained from J⁻¹ in (7) and {−∂²p_τ (h^*)/∂θ²}⁻¹ in (B2). The results of fitting the model (2) are summarized in Table 4. Here, to save space we report only the results about ${\sigma }_0^2=1$ which give similar results to ${\sigma }_0^2=0.2$. Overall, the h-likelihood estimates of β_j and ${\sigma }_0^2$ perform well even though the simulated data consist of somewhat high censoring. In Table 4 SD is the estimates of the true {var(ξ̂)}^1/2, and SEM is the average of SE estimates for ξ̂, where $\xi ={({\beta }_0,{\beta }_1,{\sigma }_0^2)}^T$. Our SE estimates work well as judged by the very good agreement between SEM and SD.

Table 4.

Simulation results for the estimation of fixed parameters over 200 replications under random baseline (M4) and correlated frailty models (M3) when the true distribution of log-frailty is correctly specified or misspecified (i.e. a mixture of two bivariate normals).

Fitted model	Setting	Parameter	True	Mean	SD	SEM
M4	Correct	${\sigma }_0^2=1$
		β̂1	−0.5	−0.505	0.150	0.150
		β̂2	0.5	0.504	0.156	0.149
		${\widehat{\sigma }}_0^2$	1	1.005	0.426	0.418
M3	Correct	${\sigma }_0^2={\sigma }_1^2=0.2$, σ01 = −0.1
		β̂1	−0.5	−0.506	0.191	0.186
		β̂2	0.5	0.494	0.153	0.148
		${\widehat{\sigma }}_0^2$	0.2	0.211	0.138	0.138
		${\widehat{\sigma }}_1^2$	0.2	0.212	0.221	0.209
		σ̂01	−0.1	−0.104	0.135	0.133
		ρ̂	−0.5	−0.493	–	–
	Correct	${\sigma }_0^2={\sigma }_1^2=1$, σ01 = −0.5
		β̂1	−0.5	−0.480	0.261	0.283
		β̂2	0.5	0.502	0.155	0.153
		${\widehat{\sigma }}_0^2$	1	1.021	0.472	0.457
		${\widehat{\sigma }}_1^2$	1	1.029	0.569	0.559
		σ̂01	−0.5	−0.519	0.398	0.397
		ρ̂	−0.5	−0.506	–	–
	Misspecified	${\sigma }_0^2={\sigma }_1^2=0.2$, σ01 = −0.1
		β̂1	−0.5	0.502	0.198	0.185
		β̂2	0.5	0.488	0.155	0.148
		${\widehat{\sigma }}_0^2$	0.2	0.209	0.140	0.144
		${\widehat{\sigma }}_1^2$	0.2	0.208	0.211	0.205
		σ̂01	−0.1	−0.102	0.139	0.138
		ρ̂	−0.5	−0.490	–	–
	Misspecified	${\sigma }_0^2={\sigma }_1^2=1$, σ01 = −0.5
		β̂1	−0.5	−0.476	0.309	0.293
		β̂2	0.5	0.512	0.156	0.153
		${\widehat{\sigma }}_0^2$	1	1.048	0.483	0.461
		${\widehat{\sigma }}_1^2$	1	1.089	0.600	0.588
		σ̂01	−0.5	−0.525	0.415	0.404
		ρ̂	−0.5	−0.491	–	–

SD, standard deviation of estimates over 200 simulations, is defined by {Σ_i (κ̂⁽ⁱ⁾ − κ̄)²/199}^1/2, where κ̂⁽ⁱ⁾ is the estimate of κ in the ith replication and κ̄ = Σ_i κ̂⁽ⁱ⁾/200 is the mean of κ̂⁽ⁱ⁾’s, and $\kappa ={\beta }_1,{\beta }_2,{\sigma }_0^2,{\sigma }_1^2$, or σ₀₁.

SEM, the mean of estimated standard errors over 200 simulations.

Next, data were generated from the model (3) with λ₀(t) = 1:

$${\lambda }_{ij}(t\mid v_{i0},v_{i1})=exp\{{\beta }_1{x}_{ij1}+{\beta }_2{x}_{ij2}+v_{i0}+v_{i1}{x}_{ij1}\}.$$ (11)

The random effects v_i0 and v_i1 are generated from the bivariate normal distribution with four combinations of frailty parameters; $({\sigma }_0^2,{\sigma }_1^2,\rho )=(0.2,0.2,-0.5),(1.0,1.0,-0.5),(0.2,0.2,0.5)$ and (1.0, 1.0, 0.5), leading to σ₀₁ = −0.1, −0.5, 0.1, 0.5, respectively. The remaining simulation schemes including (x_ij1, x_ij2) and (β₁, β₂) are the same as before. The results of fitting the model (3) with ρ = −0.5 are also given in Table 4. Though not reported here, we found the similar results for ρ = 0.5. Overall, our approach again works well. However, the estimates of the frailty parameters ( ${\sigma }_0^2,{\sigma }_1^2$, σ₀₁) are slightly biased when the variances are large as in $({\sigma }_0^2,{\sigma }_1^2)=(1.0,1.0)$.

In addition, we investigated the performance of our h-likelihood procedure when the normal assumption of log-frailties v_i0 and v_i1 in (11) is violated. For linear mixed models Ha et al. [41] and Verbeke and Lesaffre [42] have shown that misspecifying the normal random-effect distribution has little effect on the fixed effects estimates. Following Verbeke and Lesaffre [42], for simplicity we consider a mixture (Johnson and Kotz, [43, p.73]) of two bivariate normal distributions. That is, v_i = (v_i0, v_i1)^T are generated from one of the following two cases:

$$\begin{array}{l}\text{Case}1:\frac{1}{2}N\left\{\left(\begin{array}{r}\hfill -0.3\\ \hfill 0.1\end{array}\right),\left(\begin{array}{cc}0.11& -0.07\\ -0.07& 0.19\end{array}\right)\right\}+\frac{1}{2}N\left\{\left(\begin{array}{r}\hfill 0.3\\ \hfill -0.1\end{array}\right),\left(\begin{array}{cc}0.11& -0.07\\ -0.07& 0.19\end{array}\right)\right\},\\ \text{Case}2:\frac{1}{2}N\left\{\left(\begin{array}{r}\hfill -0.8\\ \hfill 0.4\end{array}\right),\left(\begin{array}{cc}0.36& -0.18\\ -0.18& 0.84\end{array}\right)\right\}+\frac{1}{2}N\left\{\left(\begin{array}{r}\hfill 0.8\\ \hfill -0.4\end{array}\right),\left(\begin{array}{cc}0.36& -0.18\\ -0.18& 0.84\end{array}\right)\right\}.\end{array}$$

Two non-normal distributions with Cases 1 and 2 have been chosen such that E(v_i) = 0 and such that var(v_i) equals the random-effect variance-covariance parameters in the first and second settings given in M3 of Table 4, respectively. Note that Cases 1 and 2 produce unimodal and bimodal distributions, respectively (not shown). The results in the third and fourth settings given in M3 of Table 4 again confirm that the h-likelihood method gives robust results for the estimation of parameters, particularly for β, when the distribution of frailty is misspecified.

The SAS/IML program for a correlated model (11) with a simulated data set is available from the website: http://stat.snu.ac.kr//hglmlab.

6. Discussion

We have shown that the proposed method provides a unified framework for the inference. The data-directed simulation results have demonstrated that our procedure performs well for the estimation of parameters, including the estimated SEs. Using h-likelihood, we have also shown how to investigate potential sources of the heterogeneity related to treatment effect over centres in multi-centre clinical trial. The proposed method can be also employed when studying such heterogeneity in a meta-analysis [8] which combines survival data from different clinical trials.

The heterogeneity of treatment effect could also arise in other situations besides treatment-by-centre interaction. For example, it could arise in the case that the treatment effect affects the variances of the frailty terms [44]; a simple dispersion model is a model (2) with $v_{i0}\sim N(0,{\sigma }_{i0}^2)$ allowing a regression model for ${\sigma }_{i0}^2$, given by $log{\sigma }_{i0}^2={\gamma }_0+{\gamma }_1{x}_{ij1}$ where x_ij1 is a main treatment covariate. Pan and MacKenzie [45, 46] have developed appropriate structural dispersion methods for testing this hypothesis in the repeated measures setting with Gaussian response variables and with and without random effects. Thus, we are currently working on an extension of our method to models with structural dispersion.

In the data set in Section 4 we coded the main treatment as x_ij1 = 0, 1 to indicate control or treatment group. However, the coding of $x_{ij1}=\pm \frac{1}{2}$ may give a flexible covariance structure for the random effects [6, 8]. Though not reported here, both codings give similar estimation results for all random-effect models (M2–M10) considered and select M4 as the best model. Furthermore, we investigated how the small size (e.g. n_i = 3) of some centres in Table 1 influences the inference results. Here, the centres, centre numbers 1 and 2, with less than 4 patients were combined into one new centre. We have also observed (not shown) that the results obtained from fitting a correlated model (M3) under the combined data set are very similar to those of M3 in Table 2.

The focussed $\text{AIC}(T_d^{\ast })$ in Section 4.2 is a criterion for the frailty parameters only and it cannot be used for model selection involving the β parameter because the restricted likelihood $T_d^{\ast }$ eliminates the β. However, if β is the subject of the model selection process we may use the AIC based upon an adjusted profile h-likelihood p_v(h_p) in (C1) [11]. Thus, there is clearly scope for further research on the development of a criterion for selecting the best model globally. We have ignored missing covariates in the data set analysed because their frequency is too small (i.e. 4/414=1%), but the original data set with 7 studies includes more missing covariates. The development of h-likelihood methods for frailty models allowing for missing covariates would be an interesting topic for future work.

Appendix A

H-likelihood estimation procedure

With h^* in (6) we estimate the fixed parameters (β, θ) and random effects v as follows. Ha et al. [23] further showed that given θ the estimation of τ = (β^T, v^T)^T is obtained by solving

$$\frac{\partial h^{\ast }}{\partial \tau }={\frac{\partial h}{\partial \tau }|}_{{\lambda }_0={\widehat{\lambda }}_0}=0.$$ (A1)

Here the first partial derivatives, ∂h/∂τ, are given by the simple forms:

$$\frac{\partial h}{\partial \beta }=\sum _{ij}({\delta }_{ij}-{\mu }_{ij})x_{ij}\text{and}\frac{\partial h}{\partial v_i}=\sum _j({\delta }_{ij}-{\mu }_{ij})z_{ij}-{\mathrm{\sum }}_i^{-1}{v}_i(i=1,\dots ,q),$$

where μ_ij = Λ₀(y_ij) exp(η_ij). Next, for the estimation of the frailty parameters θ, we use Lee and Nelder’s [21] adjusted profile h-likelihood [18] which eliminates (β, v) from h^*, defined by

$$p_{\tau }(h^{\ast })={\left[h^{\ast }-\frac{1}{2}logdet\left\{\frac{J(h^{\ast };\tau )}{(2\pi )}\right\}\right]|}_{\tau =\widehat{\tau }},$$ (A2)

where τ̂ = τ̂(θ) = (β̂^T(θ), v̂^T(θ))^T and J(h^*; τ) = −∂²h^*/∂τ² is an information matrix for τ with a detailed form in (7). The restricted maximum likelihood (REML) estimator for θ are obtained by solving iteratively

$$\frac{\partial p_{\tau }(h^{\ast })}{\partial \theta }=0.$$ (A3)

Note here that

$$\frac{\partial p_{\tau }(h^{\ast })}{\partial \theta }=-\frac{1}{2}\text{tr}\left({\mathrm{\sum }}^{-1}\frac{\partial \mathrm{\sum }}{\partial \theta }\right)-\frac{1}{2}{\widehat{v}}^T\left(\frac{\partial {\mathrm{\sum }}^{-1}}{\partial \theta }\right)\widehat{v}-\frac{1}{2}\text{tr}\left({\widehat{J}}^{-1}\frac{\partial \widehat{J}}{\partial \theta }\right),$$

where Σ = BD(Σ₁, …, Σ_q) is the q × q block diagonal matrix and Ĵ = Ĵ(θ) = J(h^*; τ)|_τ=τ̂(θ). Note also that in implementing (A3) we allow the ∂v̂/∂θ term [18, 24, 26]; the computations of the ∂Ĵ/∂θ term including the ∂v̂/∂θ term are given in Appendix B.

In summary, the estimates of τ and θ are obtained by alternating between the two estimating equations (A1) and (A3) until convergence is achieved [18, 23]. The two equations are, respectively, solved using the Newton-Raphson method with the corresponding Hessian matrices, −∂²h^*/∂τ² and −∂²p_τ (h^*)/∂θ². After convergence, we directly compute the estimates of var(τ̂ − τ) and var(θ̂) using the inverses of −∂²h^*/∂τ² and −∂²p_τ (h^*)/∂θ², respectively.

Appendix B

The computation of −∂²p_τ (h^*)/∂θ²

The adjusted profile h-likelihood in (A2) can be expressed as

$$p_{\tau }(h^{\ast })=\widehat{h}-\frac{1}{2}logdet(\widehat{J})+\frac{(p+q)}{2}log(2\pi ),$$

where τ = (β^T, v^T)^T, ĥ = h^*|_{τ= τ̂ (θ)} = h^*(τ̂(θ), θ) and Ĵ = J(h^*; τ)|_{τ= τ̂(θ)} = J(τ̂ (θ), θ). Since

$$\frac{\partial p_{\tau }(h^{\ast })}{\partial {\theta }_r}=\frac{\partial \widehat{h}}{\partial {\theta }_r}-\frac{1}{2}\text{tr}\left({\widehat{J}}^{-1}\frac{\partial \widehat{J}}{\partial {\theta }_r}\right),$$ (B1)

we have

$$-\frac{{\partial }^2{p}_{\tau }(h^{\ast })}{\partial {\theta }_r\partial {\theta }_s}=-\frac{{\partial }^2\widehat{h}}{\partial {\theta }_r\partial {\theta }_s}+\frac{1}{2}\text{tr}\left(-{\widehat{J}}^{-1}\frac{\partial \widehat{J}}{\partial {\theta }_r}{\widehat{J}}^{-1}\frac{\partial \widehat{J}}{\partial {\theta }_s}+\frac{{\partial }^2\widehat{J}}{\partial {\theta }_r\partial {\theta }_s}\right).$$ (B2)

We now show how to compute equation (B2). Following Lee and Nelder [22] and Ha and Lee [18], we allow for ∂v̂/∂θ_r in computing the two equations, (B1) and (B2), but not for ∂β̂/∂θ_r. Then we have

$$\begin{array}{l}\frac{\partial \widehat{h}}{\partial {\theta }_r}={\left\{\left(\frac{\partial h^{\ast }}{\partial {\theta }_r}\right)+\left(\frac{\partial h^{\ast }}{\partial v}\right)\left(\frac{\partial \widehat{v}}{\partial {\theta }_r}\right)\right\}|}_{v=\widehat{v}}\\ ={\frac{\partial h^{\ast }}{\partial {\theta }_r}|}_{v=\widehat{v}}\end{array}$$

since (∂h^*/∂v)|_{v = v̂} = 0: see also Appendix 2 of Ha et al. [23]. Along the lines of Appendix C of Lee and Nelder [21], we can show that

$$\begin{array}{l}\frac{\partial \widehat{v}}{\partial {\theta }_r}={-{\left(-\frac{{\partial }^2{h}^{\ast }}{\partial v^2}\right)}^{-1}\left(-\frac{{\partial }^2{h}^{\ast }}{\partial v\partial {\theta }_r}\right)|}_{v=\widehat{v}}\\ =-{(Z^T\widehat{W}Z+U)}^{-1}{U}_r^{\prime }\widehat{v},\end{array}$$

where Ŵ is given in (B3), U = Σ⁻¹ and $U_r^{\prime }=\partial {\mathrm{\sum }}^{-1}/\partial {\theta }_r=-{\mathrm{\sum }}^{-1}(\partial \mathrm{\sum }/\partial {\theta }_r){\mathrm{\sum }}^{-1}$. From these results the first term on the right hand side (RHS) of (B2) becomes

$$\begin{array}{l}-\frac{{\partial }^2\widehat{h}}{\partial {\theta }_r\partial {\theta }_s}={\left\{\left(-\frac{{\partial }^2{h}^{\ast }}{\partial {\theta }_r\partial {\theta }_s}\right)-\left(\frac{{\partial }^2{h}^{\ast }}{\partial {\theta }_r\partial v}\right)\left(-\frac{\partial \widehat{v}}{\partial {\theta }_r}\right)\right\}|}_{v=\widehat{v}}\\ =-\frac{1}{2}\text{tr}\left({\mathrm{\sum }}^{-1}\frac{\partial \mathrm{\sum }}{\partial {\theta }_r}{\mathrm{\sum }}^{-1}\frac{\partial \mathrm{\sum }}{\partial {\theta }_s}-{\mathrm{\sum }}^{-1}\frac{{\partial }^2\mathrm{\sum }}{\partial {\theta }_r\partial {\theta }_s}\right)+\frac{1}{2}{\widehat{v}}^T{U}_{rs}^{″}\widehat{v}+{\widehat{v}}^T{U}_s^{\prime }\left(\frac{\partial \widehat{v}}{\partial {\theta }_r}\right),\end{array}$$

where $U_{rs}^{″}={\partial }^{2}U/\partial {\theta }_r\partial {\theta }_s=-U_s^{\prime }(\partial \mathrm{\sum }/\partial {\theta }_r){\mathrm{\sum }}^{-1}-{\mathrm{\sum }}^{-1}(\partial \mathrm{\sum }/\partial {\theta }_r)U_s^{\prime }-{\mathrm{\sum }}^{-1}({\partial }^2\mathrm{\sum }/\partial {\theta }_r\partial {\theta }_s){\mathrm{\sum }}^{-1}.$. From (7) we have

$$\widehat{J}=\left(\begin{array}{rr}\hfill X^T\widehat{W}X& \hfill X^T\widehat{W}Z\\ \hfill Z^T\widehat{W}X& \hfill Z^T\widehat{W}Z+U\end{array}\right),$$ (B3)

where Ŵ = W^*|_{τ= τ̂(θ)} = W ^*(τ̂(θ), θ). Note here that following Appendix B of Ha and Lee [18], W^* = W^*(β, v) is given by

$$W^{\ast }=W_1-W2,$$ (B4)

where W₁ = diag{Λ̂_0ij exp(η_ij)} is the n × n diagonal matrix with Λ̂_0ij = Λ̂₀(y_ij) and W₂ = (W₃M)C⁻¹(W₃M)^T is the n × n symmetric matrix. Here W₃ = diag{exp(η_ij)}, $C=\text{diag}\{d_{(k)}/{\widehat{\lambda }}_{0k}^2\}$ is the D × D diagonal matrix, and M = (M₁, …, M_D)^T is the n × D indicator matrix whose (ij, k)th element is 1 if y_ij ≥ y_(k) and 0 otherwise. Notice that Λ̂_0ij and λ̂_0k also depend on (β, v) only and that the corresponding matrix forms are available in Ha and Lee [18]. Thus, the two derivatives in the second term on the RHS of (B2) are computed as follows:

$$\frac{\partial \widehat{J}}{\partial {\theta }_r}=\left(\begin{array}{rr}\hfill X^T{W}_r^{\prime }X& \hfill X^T{W}_r^{\prime }Z\\ \hfill Z^T{W}_r^{\prime }X& \hfill Z^T{W}_r^{\prime }Z+U_r^{\prime }\end{array}\right)\text{and}\frac{{\partial }^2\widehat{J}}{\partial {\theta }_r{\theta }_s}=\left(\begin{array}{rr}\hfill X^T{W}_{rs}^{″}X& \hfill X^T{W}_{rs}^{″}Z\\ \hfill Z^T{W}_{rs}^{″}X& \hfill Z^T{W}_{rs}^{″}Z+U_{rs}^{″}\end{array}\right).$$

Here $W_r^{\prime }=\partial \widehat{W}/\partial {\theta }_r$ and $W_{rs}^{″}={\partial }^2\widehat{W}/\partial {\theta }_r\partial {\theta }_s$ are calculated by the following procedures.

$$\frac{\partial \widehat{W}}{\partial {\theta }_r}={\left\{\left(\frac{\partial W^{\ast }}{\partial {\theta }_r}\right)+\left(\frac{\partial W^{\ast }}{\partial v}\right)\left(\frac{\partial \widehat{v}}{\partial {\theta }_r}\right)\right\}|}_{v=\widehat{v}}={\left\{\left(\frac{\partial W^{\ast }}{\partial v}\right)\left(\frac{\partial \widehat{v}}{\partial {\theta }_r}\right)\right\}|}_{v=\widehat{v}}$$

since ∂W^*/∂θ_r = 0, and

$$\frac{{\partial }^2\widehat{W}}{\partial {\theta }_r\partial {\theta }_s}={\left\{\left(\frac{\partial \widehat{v}}{\partial {\theta }_r}\right)\left(\frac{{\partial }^2{W}^{\ast }}{\partial v^2}\right)\left(\frac{\partial \widehat{v}}{\partial {\theta }_s}\right)+\left(\frac{\partial W^{\ast }}{\partial v}\right)\left(\frac{{\partial }^2\widehat{v}}{\partial {\theta }_r\partial {\theta }_s}\right)\right\}|}_{v=\widehat{v}},$$

where

$$\frac{{\partial }^2\widehat{v}}{\partial {\theta }_r\partial {\theta }_s}=-{(Z^T\widehat{W}Z+U)}^{-1}\left\{(Z^T{W}_r^{\prime }Z+U_r^{\prime })\frac{\partial \widehat{v}}{\partial {\theta }_s}+U_s^{\prime }\frac{\partial \widehat{v}}{\partial {\theta }_r}+U_{rs}^{″}\widehat{v}\right\},$$

and ∂W^*/∂v and ∂²W^*/∂v² can be calculated by repeatedly differentiating (B4) with respect to v.

Appendix C

Comparison of different estimation methods

Ha et al. [19, 23] have showed that the profile h-likelihood h^* in (6) is proportional to the penalized partial likelihood h_p [PPL, 17], which uses the partial likelihood [47–48] for ℓ_1ij in h; h^* = h_p + constant. The h-likelihood and PPL procedures are the same for the estimation of β and v, given frailty parameters θ, but are different for that of θ. For the estimation of θ, the h-likelihood method uses the restricted likelihood p_β,v(h^*), whereas the PPL method uses an adjusted profile h-likelihood

$$p_v(h_p)={\left[h_p-\frac{1}{2}logdet\left\{\frac{J(h_p;v)}{(2\pi )}\right\}\right]|}_{v=\widehat{v}},$$ (C1)

where J(h_p; v) = −∂²h_p/∂v², which is a Laplace approximation to the marginal likelihood [19]; notice that p_v(h_p) − p_v(h^*) = constant. However, the PPL ignores the ∂v̂/∂θ term in solving the score equations ∂p_v(h_p)/∂θ = 0; this leads to an underestimation of the parameters and/or SEs, particularly when the cluster size n_i is small [14, 18, 19].

Recently, the penalized maximum likelihood approach [8], which penalizes the baseline hazard λ₀(t) in marginal likelihood, has been proposed for the inference of parameters, but it can not directly use for inference of frailties because it eliminates them by integration as in standard marginal-likelihood approach [13, 34]. Furthermore, Bayesian approaches [4, 7] have been also suggested. Legrand et al. [4] proposed a Bayesian approach using a Laplace integration technique to approximate the marginal posterior density, π(θ|y, δ); it can be shown that under uniform priors (i.e. flat priors) for β and θ, log{π(θ|y, δ)} ≃ p_β,v(h^*). Thus, we see that the h-likelihood method is equivalent to Legrand et al.’s method under uniform priors - a choice, however, which is unlikely to be adopted in practice by Bayesians. Komarek et al. [7] also proposed to use a Markov chain Monte Carlo algorithm but in an accelerated failure time model with Gaussian random effects.