Hepatic Blood Perfusion Measured by 3-min Dynamic ¹⁸F-FDG PET in Pigs

Abstract

There is an unmet clinical need for an imaging method for quantification of hepatic blood perfusion. The purpose of the present study was to develop and validate a PET method using blood-to-cell clearance (K₁) of 2-[¹⁸F]fluoro-2-deoxy-D-glucose (¹⁸F-FDG), 3-O-[¹¹C]-methylglucose (¹¹C-MG) or 2-[¹⁸F]fluoro-2-deoxy-D-galactose (¹⁸F-FDGal) as a measure of hepatic blood perfusion without the need of portal venous blood samples. We aimed to make the method as simple as possible with the perspective of future application to clinical studies. For this purpose, we examined the possibility of using 3-min data acquisition and a model-derived dual-input calculated from measurements of radioactivity concentrations in a peripheral artery.

Methods

Pigs (40 kg) underwent dynamic PET of the liver with ¹⁸F-FDG, ¹¹C-MG or ¹⁸F-FDGal with simultaneous measurements of time-activity curves (TAC) in blood sampled from a femoral artery and the portal vein (PV); blood flow rates were measured in the hepatic artery (HA) and portal vein (PV) by transit-time flow-meters. Two input functions were compared: A measured dual-input and a model-derived dual-input, the latter with the PV TAC estimated from the measured arterial TAC and a previously validated one-parametric PV-model. K₁ was estimated for each tracer by fitting compartmental models to the data comparing 3-min and 60-min data acquisitions and the two dual-input TACs.

Results

Agreement between K₁ estimated using the measured and the model-derived dual-input was good for all 3 tracers. For ¹⁸F-FDG and ¹¹C-MG, K₁ (3-min data acquisition, model-derived dual-input and one-tissue compartmental model) correlated to the measured blood perfusion (P = 0.01 and P = 0.07, respectively). For ¹⁸F-FDGal the correlation was not significant.

Conclusion

A simplified method for quantification of hepatic blood perfusion using 3-min dynamic ¹⁸F-FDG PET or ¹¹C-MG PET with blood sampling from only a peripheral artery was developed. Parametric K₁ images were constructed and showed homogeneous blood perfusion in these normal livers.

Total hepatic blood flow can be measured in terms of volume pr. time unit (e.g. mL blood/min) by various methods for example using infusion of indocyanine green (1) or direct flow-meter measurements (2). Studies have shown that the hepatic blood flow tends to be increased in patients with liver cirrhosis (3) but it is not known to what extent the large heterogeneity in liver tissue histopathology (4,5) and intrahepatic portal vein pressure (6) may be reflected in intrahepatic variations in the liver tissue blood perfusion (mL blood/mL liver tissue/min). This is relevant for understanding liver pathophysiology and when planning local treatment of patients with liver diseases, inclusive cancer in the liver. Compared to other organs, in vivo measurements of the hepatic blood perfusion is, however, challenging due to the special blood supply to the liver with the major proportion coming from the portal vein (PV) which is inaccessible to blood sampling in humans and only a minor part coming from the hepatic artery (HA). A simplified method for quantification of regional variations in the hepatic blood perfusion is thus needed. Positron emission tomography (PET) is an attractive technique for this purpose since it can provide high resolution 3D-images of kinetic parameters and we can build on experience from previous studies of the dual-input of tracer to the liver (7–13).

We and others previously found that PET-estimates of hepatic blood-to-cell clearance (K₁) of 2-[¹⁸F]fluoro-2-deoxy-D-glucose (¹⁸F-FDG) (7,8), 3-O-[¹¹C]-methylglucose (¹¹C-MG) (7) and 2-[¹⁸F]fluoro-2-deoxy-D-galactose (¹⁸F-FDGal) (9) are comparable with the hepatic blood perfusion measured simultaneously by surgically placed ultrasound transit-time flow-meters in pigs. Since the estimation of K₁ is determined by the initial time-activity curves (TACs) in tissue and input (7) this requires blood sampling from an artery and the PV in order to calculate the correct dual-input TAC to the liver. Because the PV is inaccessible to blood sampling in humans various approaches have attempted to overcome this problem. Using dynamic H₂¹⁵O PET (10) and ¹⁸F-FDG PET (11) Kudomi et al. developed a non-invasive method to extract tissue-derived hepatic input functions in pigs. The authors modeled the arterial input function by assuming a rectangular tracer administration and a three-compartmental whole-body model. The PV input function was described by a one-tissue compartmental model and hepatic tracer kinetics was analyzed by compartmental models. The combined set of models was fitted to multiple liver tissue TACs using several constrained and fixed parameters. The estimated input functions were shown to compare well with measured dual-input TACs of H₂¹⁵O and ¹⁸F-FDG from Iozzo et al. (10).

The purpose of the present study was to develop a simplified method using a model-derived dual-input TAC calculated from arterial TAC with only two fixed parameters, namely β (min), which reflects the tracer-specific mean splanchnic transit time (12), and the mean hepatic arterial flow fraction (13). We have previously validated the replacement of the measured dual-input function with the model-derived dual-input using simulated tissue TACs (13). In the present study we estimated K₁ of ¹⁸F-FDG, ¹¹C-MG and ¹⁸F-FDGal from liver PET data of anaesthetized pigs (TACs) using measured and model-derived dual-input. We compared the K₁ estimates with direct measurements of the hepatic blood perfusion and evaluated the use of 3-min data acquisition instead of the traditional 60-min data acquisition since K₁ is determined by the initial data.

MATERIALS AND METHODS

The material comprised raw data from previous PET studies of six pigs that underwent both ¹¹C-MG and ¹⁸F-FDG PET (9) and nine pigs that underwent ¹⁸F-FDGal PET (11). Data included dynamic PET recordings of the liver and measurements of tracer concentrations in blood samples collected manually from a femoral artery and the PV. The blood flow rates in the HA and PV were continuously recorded by surgically placed ultrasound transit-time flow-meters. In (9) ¹¹C-MG PET was performed before ¹⁸F-FDG PET due to the radioactive half-lives of the two tracers. All studies were performed using an ECAT EXACT HR-47 PET camera (CTI, Knoxville,TN; Siemens Medical Systems, Inc., Hoffman Estates, IL).

Liver tissue blood perfusion (Q; mL blood/mL liver tissue/min) was calculated as the sum of the average flow-meter-measured HA and PV blood flow rates during the initial 3 minutes after tracer administration (mL blood/min) divided by the wet liver weight (g) corrected for liver tissue density (1.07 g/mL tissue).

Kinetic Analysis

PET emission data were reconstructed using filtered back projection resulting in images with 128 × 128 × 47 voxels of 2.4 mm × 2.4 mm × 3.1 mm and a central spatial resolution of 6.7 mm full width at half maximum (FWHM). The dynamic recording included 35 time frames: 18 × 10 s, 4 × 30 s, 5 × 1 min, 6 × 5 min, and 2 × 10 min (total 60 min). A volume-of-interest (VOI) (107–143 mL) was drawn in the liver keeping a distance of 1.5–2 cm to the edge of the liver and avoiding the central area where the large vessels are present and used to generate a liver tissue TAC (C_liver(t)), corrected for radioactive decay back to start of the PET recording.

The measured dual-input TAC, C_dual(t), was calculated as the flow-weighted mean of the TACs measured in arterial blood, C_A(t) and PV blood, C_PV(t), corrected for radioactive decay back to start of the PET recording, and the measured blood flow rates in the hepatic artery, F_HA, and in the PV, F_PV (7):

$$C_{\mathit{\text{dual}}}(t)=f_{\mathit{\text{HA}}}{C}_A(t)+(1-f_{\mathit{\text{HA}}})C_{\mathit{\text{PV}}}(t);f_{\mathit{\text{HA}}}=F_{\mathit{\text{HA}}}/(F_{\mathit{\text{HA}}}+F_{\mathit{\text{PV}}})$$ Eq. 1

Since the blood sampling sites were close to the liver, no time delay was needed. The model-derived PV TAC (C̃_PV(t)) was calculated from the arterial TAC (C_A(t)) by applying a PV-model for the transfer of tracer from the arterial system to the PV (12) and using population means of a tracer-specific parameter for the transfer, β̅, being 0.50 minutes for ¹⁸F-FDG, 0.57 minutes for ¹¹C-MG and 0.82 minutes for ¹⁸F-FDGal (13):

$${\tilde{C}}_{\mathit{\text{PV}}}(t)={\displaystyle {\int }_{\mathit{0}}^{t}h(t-\tau )C_A(\tau )d\tau ;h(t)=\overline{\beta }/{(t+\overline{\beta })}^2}$$ Eq. 2

Using C̃_PV(t) and a mean HA blood flow fraction f_HA of 0.25 (13), a model-derived dual-input TAC (C̃_dual(t)) was calculated as (13):

$${\tilde{C}}_{\mathit{\text{dual}}}(t)=\overline{f_{\mathit{\text{HA}}}}{C}_A(t)+(\mathit{1}-\overline{f_{\mathit{\text{HA}}}}){\tilde{C}}_{\mathit{\text{PV}}}(t)$$ Eq. 3

The kinetic analysis was performed as VOI-based kinetic analysis followed by construction of parametric images of K₁ of ¹⁸F-FDG and ¹¹C-MG. The VOI-based data analysis focused on the estimation of K₁ and its correlation with Q, measured by the flow-meters, i.e. verifying that K₁ can be used as a measure of Q. For ¹⁸F-FDG and ¹⁸F-FDGal, we used a two-tissue compartmental model of tracer distribution and metabolism for 60-min data acquisition with the parameters K₁ (mL blood/mL liver tissue/min), rate constant for backflux of tracer from cell-to-blood (k₂; /min), rate constant for intracellular phosphorylation of the tracer (k₃; /min), rate constant for intracellular dephosphorylation (k₄; /min), and a vascular distribution volume (V₀; mL blood/mL liver tissue). Because ¹¹C-MG is not metabolized in the liver (14), we used a one-tissue compartmental model of tracer distribution for 60-min data acquisition for this tracer with the parameters K₁, k₂, and V₀ (7). Next, a one-tissue compartmental model with the parameters K₁, k₂, and V₀ was fitted to all three tracer using data from the initial 3-min of the PET recordings. The kinetic parameters were estimated by non-linear fitting of the respective model to the VOI-based liver tissue TAC (C_liver(t)) with the use of C_dual(t) and C̃_dual(t).

For the construction of parametric images of hepatic blood perfusion in terms of K₁ for ¹⁸F-FDG and ¹¹C-MG, noise was reduced by applying an additional Gaussian filter (8 mm FWHM) to the images thereby reducing the central spatial resolution to 10.5 mm FWHM corresponding to a volumetric resolution of around 1 mL. The image of K₁ was generated by fitting a linearized one-tissue compartmental model (15) with the parameters K₁, k₂, and V₀ (16) to the initial 3 minutes of the ¹⁸F-FDG and ¹¹C-MG PET recordings using C̃_dual(t) as input. V₀ was fixed to 0.40 mL blood/mL liver tissue (Winterdahl, unpublished observations, similar to values reported by Iozzo et al. (8)).

Statistical analysis

Data are expressed in terms of the mean ± standard error of the mean (SEM). Differences between K₁ values estimated using C̃_dual(t) or C_dual(t) were tested by a paired two-sample t-test; differences with a P value < 0.05 were considered statistically significant. Correlation between K₁ and Q was tested by the Pearson product-moment correlation coefficient, r; P < 0.05 was considered to indicate statistically significant correlation. Mean relative deviations of K₁ from Q, i.e. (K₁ − Q)/ Q, were tested by a one-sample t-test; deviations with a P value < 0.05 were considered statistically significant. The mean relative deviation was interpreted as the accuracy of the PET-method and SEM of the deviation as the precision. Differences between variables between animals versus within animals were assessed by ANOVA.

RESULTS

The agreement between K₁ estimated using C̃_dual(t) or C_dual(t) was good for all combinations of models, tracers and data acquisition periods using the VOI-based liver tissue TACs (C_liver(t)) (paired t-tests, all P > 0.1).

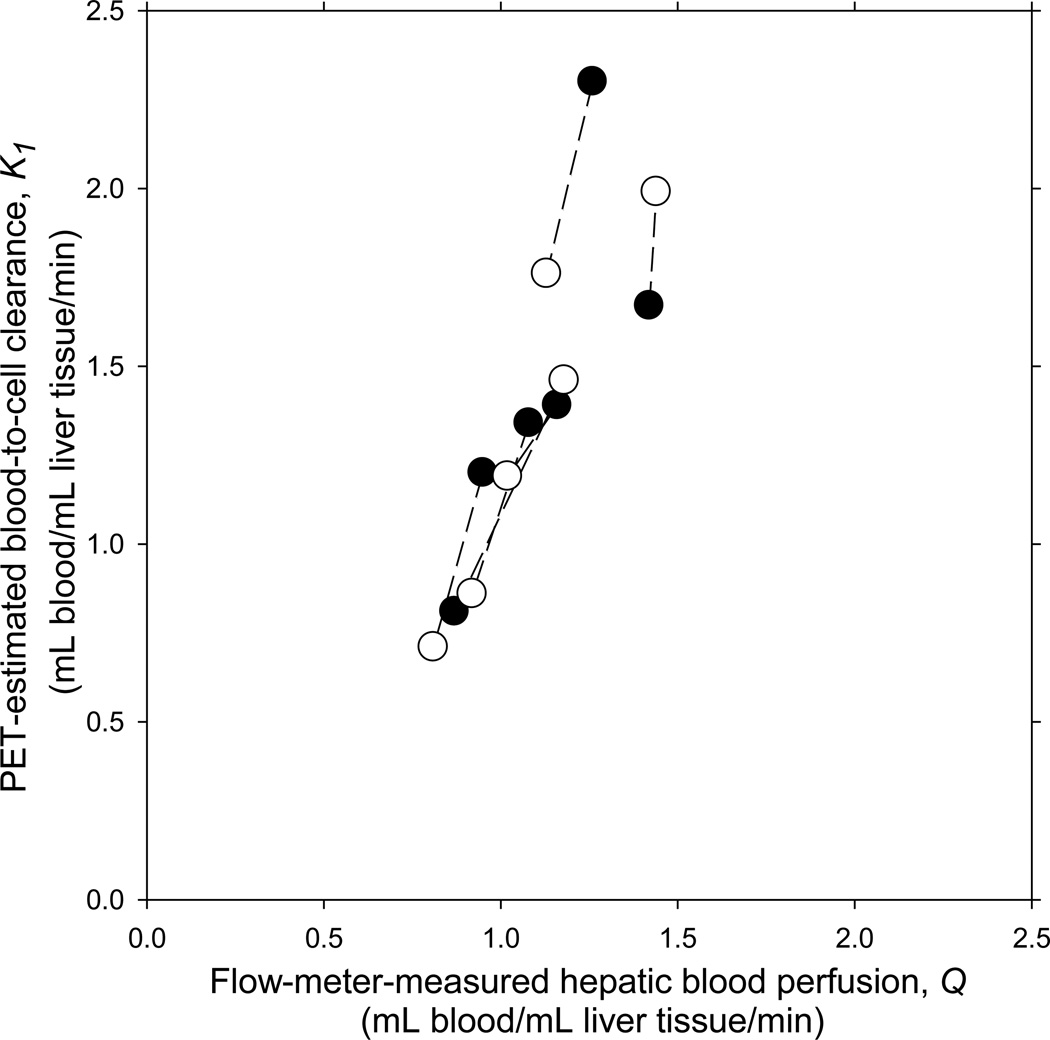
The correlations between K₁ for ¹⁸F-FDG and Q and between K₁ for ¹¹C-MG and Q were not statistically significant when using the 60-min analyses and C_dual(t) (Table 1). The correlation coefficient for 60-min ¹⁸F-FDG was similar to a correlation coefficient of 0.57 (P = 0.03) found by Iozzo et al. using 180 min acquisition (8). The use of 3-min acquisition period, a one-tissue compartmental model and C_dual(t) resulted in better correlation for both tracers; this was further improved by the use of C̃_dual(t), and the correlation was statistically significant for ¹⁸F-FDG using C̃_dual(t) (Table 1). The mean relative deviation of K₁ from Q for both ¹⁸F-FDG and ¹¹C-MG, i.e. (K₁ − Q)/ Q, was positive in all cases but not statistically significantly different from zero except for ¹¹C-MG using 3-min acquisition and C_dual(t) (Table 1). Fig. 1 shows the significant correlations between Q and K₁ for ¹⁸F-FDG as well as between Q and K₁ for ¹¹C-MG (3-min, one-tissue compartmental model, C̃_dual(t)). The tendency for K₁ to overestimate Q for both tracers (Fig. 1) was not statistically significant in agreement with the accuracy estimates (Table 1).

TABLE 1.

Blood-to-cell Clearance of ¹⁸F-FDG and ¹¹C-MG as a Measure of Hepatic Blood Perfusion in Pigs

	18F-FDG (n = 6)		11C-MG (n = 6)
	Correlation between K1 and Q, r	Relative deviation of K1 from Q	Correlation between K1 and Q, r	Relative deviation of K1 from Q
Measured Cdual(t), 60-min; two-tissue compartmental model for 18F-FDG, one-tissue compartmental model for 11C-MG	0.60 (P = 0.14)	0.08 ± 0.09 (P = 0.43)	0.26 (P = 0.61)	0.11 ± 0.10 (P = 0.28)
Measured Cdual(t), 3-min; one-tissue compartmental model for both 18F-FDG and 11C-MG	0.88 (P = 0.02)	0.10 ± 0.04 (P = 0.08)	0.58 (P = 0.23)	0.32 ± 0.08 (P = 0.01)
Model-derived C̃dual(t), 3-min; one-tissue compartmental model for both 18F-FDG and 11C-MG	0.94 (P = 0.01)	0.19 ± 0.11 (P = 0.13)	0.77 (P = 0.07)	0.27 ± 0.12 (P = 0.07)

K₁, PET-estimated blood-to-cell clearance of tracer (mL blood/mL liver tissue/min). Q, blood perfusion of liver tissue measured by ultrasound transit-time flow-meters (mL blood/mL liver tissue/min). C_dual(t), measured dual-input TAC (kBq/mL blood). C̃_dual(t), estimated dual-input TAC (kBq/mL blood). r, Pearson’s correlation coefficient for correlation between individual pairs of K₁ and Q. P < 0.05 was considered to indicate statistically significant correlation. Relative deviation of K₁ from Q is presented as mean ± SEM (mean deviations with P < 0.05 were considered statistically significantly different from zero; one-sample t-test).

FIGURE 1.

Relationship between VOI-based blood-to-cell clearance, K₁, for ¹⁸F-FDG (●) and ¹¹C-MG (○) and hepatic blood perfusion, Q, measured simultaneously by ultrasound transit-time flow-meters in six 40-kg pigs. K₁ was estimated from dynamic PET of the liver using a model-derived dual-input, C̃_dual(t) (see text), 3-min data acquisition period and a one-tissue compartmental model. Measurements from same animal are connected by a straight line.

For ¹⁸F-FDGal, there was very little or no correlation between K₁ and Q for any of the analyses and we did not proceed with examining the use of ¹⁸F-FDGal as a flow tracer.

For both ¹⁸F-FDG and ¹¹C-MG, the model fit underestimated the initial rise of C_liver(t) when using the compartmental 60-min models but not when using the 3-min model. In agreement with this, the estimates of K₁ for ¹⁸F-FDG were on average 5% (range −3% to +23%) higher for the 3-min than for the 60-min data acquisition for both C_dual(t) and C̃_dual(t) and for ¹¹C-MG, K₁ was on average 20% (range +11% to +29%) higher for 3-min than for 60-min data acquisition, for both C_dual(t) and C̃_dual(t).

For the six animals that underwent both ¹⁸F-FDG and ¹¹C-MG PET, 2.4% of the variance of the relative deviation of K₁ from Q was due to variation within individual animals; 72% of the variance was due to inter-individual variations. This high reproducibility of the K₁ estimates allowed us to regard the ¹⁸F-FDG and ¹¹C-MG studies as double determinations within the same animal. In three animals normal physiological variations in the hepatic blood perfusion gave Q values that were higher during the ¹¹C-MG PET than during the ¹⁸F-FDG PET and opposite in the other three animals. The correlation between changes in Q and changes in K₁ was highly significant (r = 0.924; P = 0.008). K₁ was accordingly able to detect the direction of the changes in the perfusion within each animal (Fig. 1). These results are noticeable because changes in Q were only 1–36%.

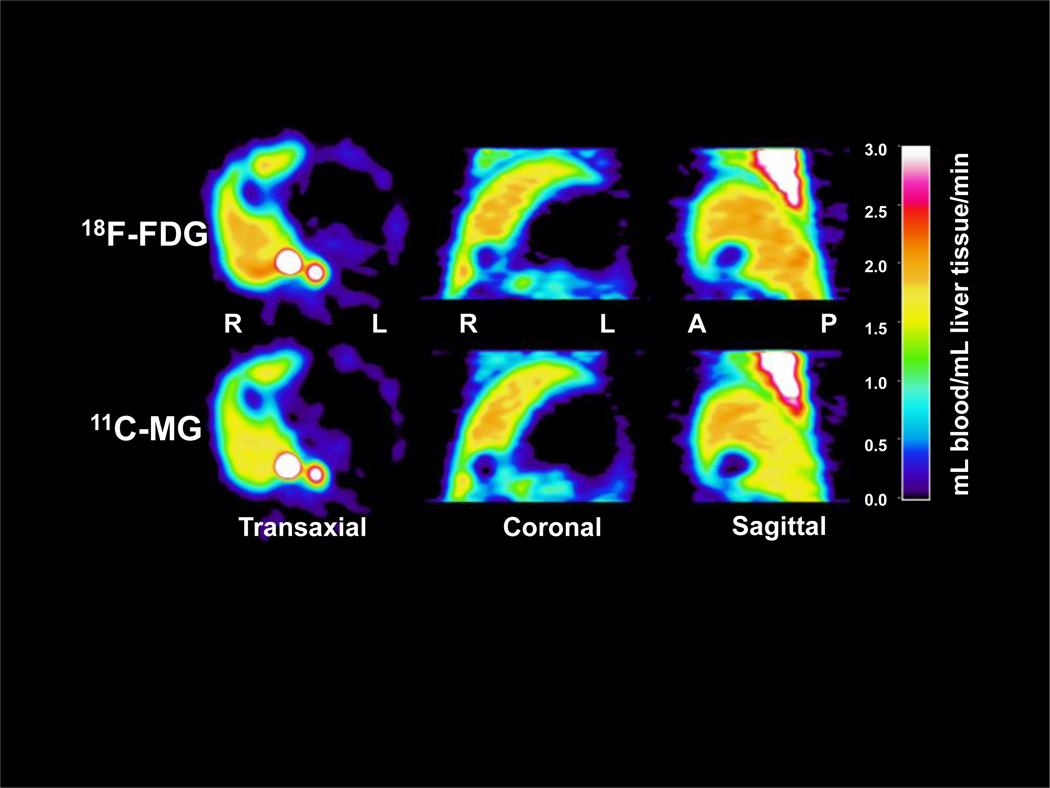
Examples of parametric images of K₁ for ¹⁸F-FDG and ¹¹C-MG are shown in Fig. 2. As the dual-input applies only for the liver, it should be noted that the estimates of K₁ are only valid for the liver, not for other organs or structures seen in the image. The figure illustrates how the two tracers gave very similar images of the liver tissue blood perfusion and that the blood perfusion in the normal pig liver is homogeneous. The coefficient of variation of the mean perfusion estimate was 13% for ¹⁸F-FDG and 14% for ¹¹C-MG.

FIGURE 2.

Hepatic blood perfusion (mL blood/mL liver tissue/min) in a 40-kg pig estimated as blood-to-cell clearances, K₁ of ¹⁸F-FDG (upper panel) and ¹¹C-MG (lower panel) from dynamic PET using a model-derived dual-input, C̃_dual(t), calculated from the arterial TAC, 3-min data acquisition period and a linearized one-tissue compartmental model. R, right side of the pig; L, left side; A, anterior; P, posterior.

DISCUSSION

The main results of the present pig study are that the measured dual-input TAC could successfully be replaced by the model-derived input TAC, based on a measured arterial TAC, for both ¹⁸F-FDG and ¹¹C-MG. The use of 3-min data acquisition gave K₁ values which correlated better with the measured blood perfusion than the use of 60-min acquisitions for both tracers.

The physiological basis for using K₁ as an estimate of hepatic blood perfusion is founded in a fast blood-to-cell transfer of glucose and ¹⁸F-FDG and ¹¹C-MG. In contrast to capillaries in other organs, the liver sinusoids are lined by highly fenestrated endothelial cells. This means that most blood-borne substances come in close contact to the hepatocyte plasma-membrane which has a huge surface area and contains facilitative glucose transporters (17,18) yielding a large permeability-surface area product (PS-product) (18,19). A reason for the poor correlation between K₁ for ¹⁸F-FDGal and Q in spite of equally high permeability for ¹⁸F-FDGal (9) could be that the rate constant for hepatocellular metabolism of ¹⁸F-FDGal, k₃ (9) is much higher that for the metabolism of ¹⁸F-FDG which may influence the estimation of the K₁ but the present data do not allow us to draw any conclusions on this.

In all fitting procedures we used a uniform weighting according to Yaqub et al. (20) and this could explain the tendency to underestimation of the initial rise of the fitted liver TAC for ¹⁸F-FDG and ¹¹C-MG when using 60-min data acquisition compared to 3-min data acquisition. The accuracy of the K₁ estimates is probably more affected by the weighting schemes when analyzing data with long acquisition periods than short acquisition periods because the determination of K₁ is particularly sensitive to the initial measurements following tracer injection (7). In agreement with this, for both ¹⁸F-FDG and ¹¹C-MG, the use of a one-tissue compartmental model of distribution and 3-min data acquisitions yielded robust estimation of K₁.

It is unlikely that the tendency for K₁ to overestimate Q for both ¹⁸F-FDG and ¹¹C-MG (3-min, C̃_dual(t)) (Fig. 1) is due to underestimation of Q by the flow-meter measurements since these are highly accurate and precise (21,22). Another explanation is that intrahepatic blood vessels are unavoidably included in the drawing of the VOI which may influence the VOI-based analysis. Combination of dynamic PET with visualization of intrahepatic vessels by contrast-enhanced CT is likely to minimize this problem but we did not have access to PET/CT at the time of the experiments.

When regarding ¹⁸F-FDG and ¹¹C-MG as double determinations in the six pigs that underwent PET with both tracers, we found a highly significant correlation between changes in the hepatic blood perfusion, Q, and changes in K₁ (Fig. 1). In each case, the change in blood perfusion between the two PET studies resulted in a corresponding change in the VOI-based K₁. Even minor physiological variations in the blood perfusion (1–36%) were thus detectable by the simplified PET method and this may have potential for detection of flow changes in small volumes (1-mL) using parametric images, which could for example be important for early tumor detection.

Compared to the VOI-based analysis, the parametric images tended to give higher estimates of K₁. Despite this, the parametric images yielded information about regional variations in the hepatic blood perfusion and is thus a useful supplement to the VOI-based analysis. In general, parametric images are often noisy and biased as a result of large statistical uncertainties of kinetic parameters in individual voxels. In the present study we reduced the noise in the K₁ images by applying a filter that reduced the spatial resolution. Future applications may improve the statistical properties using direct parametric image reconstruction techniques that allow for the kinetic model to be applied as part of the image reconstruction including an appropriate weighting scheme (23).

A crucial point for the transfer of this simplified PET method to humans is the estimation of the model-derived dual-input TAC, C̃_dual(t), from measured arterial TAC. This includes estimation of the model-derived PV TAC, C̃_PV(t), based on a population mean tracer-specific parameter β̅, which reflects the tracer-specific mean splanchnic transit time (12), and a mean HA blood flow fraction of 0.25 (13). In terms of mean HA flow fraction and mean transit time for the PET tracer ¹⁵O-carbon monoxide through the splanchnic circulation, human splanchnic circulation (2) is very similar to that in pigs. We have previously shown that the estimation of K₁ for ¹⁸F-FDG and ¹¹C-MG are insensitive to minor variations in β̅ and the HA blood flow fraction and it is therefore likely that the method quite readily can be transferred to humans even in spite of minor differences in the two key parameters (13). This is important for the potential clinical use of the method in patients in whom the liver structure is partially altered by cirrhosis, cancer, steatosis, or other disease as it indicates that only in cases with profoundly changed model parameters (e.g. end-stage cirrhosis), the use of population means may not be valid, but this needs to be quantified and validated in detail in future prospective clinical studies.

An interesting clinical perspective of the present simplified method is that an ¹⁸F-FDG bolus injection can be utilized to combine measurements of hepatic blood perfusion (in terms of K₁ from the initial 3-min data) using C̃_dual(t) and studies of hepatic glucose metabolism if the PET recording is continued for 45–60 minutes. Combination of parametric images of the hepatic blood perfusion and quasi-steady state metabolism of ¹⁸F-FDG using single arterial input (24,25) allows for simultaneous assessment of regional variations in liver blood perfusion and glucose metabolism. This may be clinically useful for early distinction between residual tumor tissue and changes of the parenchymal perfusion and metabolism after local treatment of tumors such as radiofrequency ablation of colorectal liver metastases. For ¹¹C-MG, the short radioactive half-life of 20 min enables repeated measurements for example before and after administration of a drugs with effects on regional hepatic hemodynamics.

Liver tumors are characterized by a predominantly arterial blood perfusion, viz. increased f_HA. If nevertheless ¹⁸F-FDG PET data are analyzed for the whole liver using the dual-input TAC, the use of this incorrect and less dynamic input to the tumor will give rise to an artificially too high K₁ in the tumor as compared with the correctly estimated blood perfusion in the surrounding non-malignant tissue. The tumor-to-background on a parametric image of K₁ will be enhanced. This has to be validated in prospective studies once the present method has been transferred to humans.

CONCLUSION

We have developed and validated a simplified method to quantify and image blood perfusion of normal pig livers using 3-min dynamic PET recording after intravenous injection of ¹¹C-MG or ¹⁸F-FDG, the latter being a commonly available PET tracer. The method does not require sampling of PV blood or measurements of blood flow in the HA or PV, it only requires measurements of arterial TAC and calculation of the model-derived dual-input. Despite the simplicity of the method, the estimated hepatic blood perfusion was highly correlated with independently measured hepatic blood perfusion. Parametric images were constructed allowing for the assessment of regional variations in the hepatic blood perfusion which was homogeneous in normal pig livers. Similarities between the splanchnic circulation in humans and pigs are promising for the transfer to humans and moreover the 3-min perfusion measurement can be an integrated part of a routine clinical ¹⁸FDG PET/CT examination without additional tracer administration and radiation burden to the patient.

List of symbols and their units

¹⁸F-FDG

2-[¹⁸F]Fluoro-2-deoxy-D-glucose

¹¹C-MG

3-O-[¹¹C]-Methylglucose

¹⁸F-FDGal

2-[¹⁸F]Fluoro-2-deoxy-D-galactose

HA

Hepatic artery

PV

Portal vein

VOI

Volume-of-interest (mL liver tissue)

TAC

Time-activity curve (kBq/mL tissue or blood versus time)

β

Tracer-specific parameter of the PV model (min)

β̅

Population mean of tracer-specific β (min)

f_HA

HA blood flow fraction

f_HA

Mean HA blood flow fraction

C_A(t)

Arterial TAC (kBq/mL blood)

C_PV(t)

Portal vein TAC (kBq/mL blood)

C_dual(t)

Measured dual-input TAC (kBq/mL blood)

C̃_dual(t)

Model-derived dual-input TAC (kBq/mL blood)

C_liver(t)

Liver tissue TAC (kBq/mL liver tissue)

K₁

Blood-to-cell clearance of tracer (mL blood/mL liver tissue/min)

Q

Blood perfusion of liver tissue (mL blood/mL liver tissue/min)

F_PV

Portal venous blood flow (mL blood/min)

F_HA

Hepatic arterial blood flow (mL blood/min)