linkcomm: an R package for the generation, visualization, and analysis of link communities in networks of arbitrary size and type

Abstract

Summary: An essential element when analysing the structure, function, and dynamics of biological networks is the identification of communities of related nodes. An algorithm proposed recently enhances this process by clustering the links between nodes, rather than the nodes themselves, thereby allowing each node to belong to multiple overlapping or nested communities. The R package ‘linkcomm’ implements this algorithm and extends it in several aspects: (i) the clustering algorithm handles networks that are weighted, directed, or both weighted and directed; (ii) several visualization methods are implemented that facilitate the representation of the link communities and their relationships; (iii) a suite of functions are included for the downstream analysis of the link communities including novel community-based measures of node centrality; (iv) the main algorithm is written in C++ and designed to handle networks of any size; and (v) several clustering methods are available for networks that can be handled in memory, and the number of communities can be adjusted by the user.

Availability: The program is freely available from the Comprehensive R Archive Network (http://cran.r-project.org/) under the terms of the GNU General Public License (version 2 or later).

Contact: kalinka@mpi-cbg.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The advent of high-throughput technologies in the biological sciences has resulted in a large amount of data that can often be represented as systems of interacting elements, such as genes or proteins. To understand how the nodes in these networks relate to one another and how the topologies of the networks influence how they work, an extremely useful analytical approach is to identify sets of related nodes, known as communities (Radicchi et al., 2004).

Until recently, this was conducted by clustering nodes in the network, however, a major drawback to this approach is that each node can belong to only a single community and in densely-connected networks, subnetworks may often overlap to such an extent that this approach becomes unsuitably restrictive. A superior method that circumvents this constraint is to cluster the links between nodes, thereby allowing nodes to belong to multiple communities and consequently revealing the overlapping and nested structure of the network (Ahn et al., 2010; Evans and Lambiotte, 2009). We implement the algorithm outlined by Ahn et al. (2010), which employs the Jaccard coefficient for assigning similarity between links, e_ik and e_jk, that share a node, k,

(1)

where n₊(i) refers to the first-order node neighbourhood of node i. After assigning pairwise similarities to all of the links in the network, the links are hierarchically clustered and the resulting dendrogram is cut at a point that maximizes the density of links within the clusters normalizing against the maximum and minimum numbers of links possible in each cluster, known as the partition density.

2 IMPLEMENTATION

We extend the algorithm so that it can handle networks that are weighted, directed and both weighted and directed using the Tanimoto coefficient suggested by Ahn et al. (2010),

(2)

where a_i refers to a vector describing the weights of links between node i and the nodes in the first-order neighbourhoods of both nodes i and j (equal to 0 in the event of an absent link). For directed networks, links to nodes shared by both node i and j are given a user-defined weight below 1 if they are in the opposite orientation.

For networks that have numbers of edges that can be comfortably handled in memory (adjustable to suit the resources available to each user), several different hierarchical clustering algorithms can be chosen. For networks that are too large to be handled in memory, single-linkage clustering is used to enhance performance (see Supplementary Material).

To facilitate analysis of the communities generated by the algorithm, we have included a suite of functions that allow the user to explore the structure of the communities as they relate to each other. Included in this are functions to extract the nested structure of communities and to further cluster the communities themselves using the Jaccard coefficient and the numbers of nodes shared by pairs of communities, thereby allowing the user to visualize the structure of the network across multiple scales (see Fig. 1D). In addition to this, we provide functions that calculate a novel community-based measure of node centrality. This measure weights the number of communities a node belongs to by the average pairwise similarity between the communities,

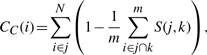(3)

where the main sum is over the N communities to which node i belongs, and S(j,k) refers to the similarity between community j and k, calculated as the Jaccard coefficient for the number of shared nodes between each community pair, and this is averaged over the m communities paired with community j and in which node i jointly belongs.

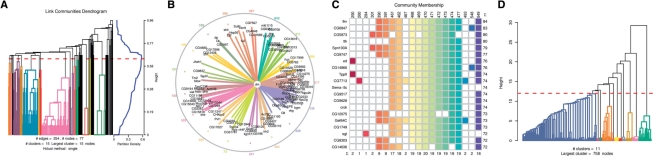
Fig. 1.

Visualizing link communities. (A) Example output from the link clustering algorithm in the R package ‘linkcomm’. The plot shows the link communities that result from cutting the dendrogram at a point where the partition density is maximized. (B) The network of interactions between the transcription factor diminutive (dm) and its targets visualized using a novel graph layout algorithm (see text) (C) A community-membership matrix showing colour-coded community membership for nodes that belong to the most communities. (D) A hierarchical clustering dendrogram showing clusters of link communities (meta-communities) which are based on the numbers of nodes shared by pairs of communities (see text).

We also provide several visualization methods for representing the link communities (Figs 1A–C). Foremost here is an implementation of a novel method for visualizing link communities (Fig. 1B) (http://scaledinnovation.com). This algorithm anchors communities evenly around the circumference of a circle in their dendrogram order (to minimize crossing over of links) and positions nodes within the circle according to how many links they possess in each of the communities. Thus, nodes that have links to a lot of communities will get pushed into the centre of the circle making this method well suited for representing ego networks where one or a small number of nodes belong to multiple communities (Fig. 1B).

3 RESULTS AND DISCUSSION

We ran the algorithm on a large gene co-expression network derived from Drosophila melanogaster embryonic in situ expression data (Tomancak et al., 2007). This weighted network contains 106 357 links, 1031 nodes, and an average degree of 206. Links between genes indicate that the genes are co-expressed in at least one tissue during the final stages of embryonic development, and the weights attached to the links refer to the similarity of expression patterns for pairs of genes, calculated using the Jaccard coefficient (based on the numbers of shared tissues).

The algorithm produced 873 non-trivial communities (composed of more than two edges). Further clustering of these communities allowed us to extract 11 meta-communities, where again nodes may appear multiple across different meta-communities (Fig. 1D).

Using our measure of community centrality (3) we find that genes expressed in the gut, epidermis and pharynx structures tend to appear in many communities and hence tend to be expressed in many different tissues. Conversely, genes expressed in the yolk, fat body, eye, brain and ventral cord tend to be expressed in fewer tissues (Supplementary Tables S1 and S2). These results allow us to identify genes that may have more or less specific roles during the final stages of embryonic development.

In future versions of the package we aim to implement a visualization method that will allow the user to zoom interactively into the network so that large networks can be plotted in their entirety without losing access to information at the local scale (Saalfeld et al., 2009).