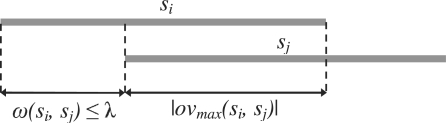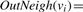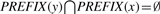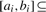A memory-efficient data structure representing exact-match overlap graphs with application for next-generation DNA assembly

Abstract

Motivation: Exact-match overlap graphs have been broadly used in the context of DNA assembly and the shortest super string problem where the number of strings n ranges from thousands to billions. The length ℓ of the strings is from 25 to 1000, depending on the DNA sequencing technologies. However, many DNA assemblers using overlap graphs suffer from the need for too much time and space in constructing the graphs. It is nearly impossible for these DNA assemblers to handle the huge amount of data produced by the next-generation sequencing technologies where the number n of strings could be several billions. If the overlap graph is explicitly stored, it would require Ω(n²) memory, which could be prohibitive in practice when n is greater than a hundred million. In this article, we propose a novel data structure using which the overlap graph can be compactly stored. This data structure requires only linear time to construct and and linear memory to store.

Results: For a given set of input strings (also called reads), we can informally define an exact-match overlap graph as follows. Each read is represented as a node in the graph and there is an edge between two nodes if the corresponding reads overlap sufficiently. A formal description follows. The maximal exact-match overlap of two strings x and y, denoted by ov_max(x, y), is the longest string which is a suffix of x and a prefix of y. The exact-match overlap graph of n given strings of length ℓ is an edge-weighted graph in which each vertex is associated with a string and there is an edge (x, y) of weight ω=ℓ−|ov_max(x, y)| if and only if ω≤λ, where |ov_max(x, y)| is the length of ov_max(x, y) and λ is a given threshold. In this article, we show that the exact-match overlap graphs can be represented by a compact data structure that can be stored using at most (2λ−1)(2⌈logn⌉+⌈logλ⌉)n bits with a guarantee that the basic operation of accessing an edge takes O(log λ) time. We also propose two algorithms for constructing the data structure for the exact-match overlap graph. The first algorithm runs in O(λℓnlogn) worse-case time and requires O(λ) extra memory. The second one runs in O(λℓn) time and requires O(n) extra memory. Our experimental results on a huge amount of simulated data from sequence assembly show that the data structure can be constructed efficiently in time and memory.

Availability: Our DNA sequence assembler that incorporates the data structure is freely available on the web at http://www.engr.uconn.edu/~htd06001/assembler/leap.zip

Contact: hdinh@engr.uconn.edu; rajasek@engr.uconn.edu

1 INTRODUCTION

An exact-match overlap graph of n given strings of length ℓ each is an edge-weighted graph defined as follows. Each vertex is associated with a string and there is an edge (x, y) of weight ω=ℓ−|ov_max(x, y)| if and only if ω≤λ, where λ is a given threshold and |ov_max(x, y)| is the length of the maximal exact-match overlap of two strings x and y. τ=ℓ−λ≤|ov_max(x, y)| is called the overlap threshold. The formal definition of the exact-match overlap graph is given in Section 2.

Storing the exact-match overlap graphs efficiently in term of memory becomes essential when the number of strings is very large. In the literature, there are two common data structures to store a general graph G=(V, E). The first data structure uses a 2D array of size |V|×|V|. We refer to this as an array-based data structure. One of its advantages is that the time for accessing a given edge is O(1). However, it requires Ω(|V|²) memory. The second data structure stores the set of edges E. We refer to this as an edge-based data structure. It requires Ω(|V|+|E|) memory and the time for accessing a given edge is O(logΔ), where Δ is the degree of the graph. Both these data structures require Ω(|E|) memory. If the exact-match overlap graphs are stored using these two data structures, we will need Ω(|E|) memory. Even this much of memory may not be feasible in cases when the number of strings is over a hundred million. In this article, we focus on data structures for the exact-match overlap graphs that will call for much less memory than |E|.

1.1 Our contributions

We show that there is a compact data structure representing the exact-match overlap graph that needs much less memory than |E| with a guarantee that the basic operation of accessing an edge takes O(logλ) time, which is almost a constant in the context of DNA assembly. The data structure can be constructed efficiently in time and memory as well. In particular, we show that

• The data structure takes no more than (2λ−1)(2⌈logn⌉+⌈logλ⌉)n bits.

• The data structure can be constructed in O(λℓn) time.

As a result, any algorithm that uses overlap graphs and runs in time T can be simulated using our compact data structure. In this case, the memory needed is no more than (2λ−1)(2⌈logn⌉+⌈logλ⌉)n bits (for storing the overlap graph) and the time needed is O(Tlogλ). If λ is a constant or much smaller than n, our data structure will be a perfect solution for any application that does not have enough memory for storing the overlap graph in a traditional way.

Our claim may sound contradictory because in some exact-match overlap graphs the number of edges can be Ω(n²) and it seems like it will require Ω(n²) time and memory to construct them. Fortunately, because of some special properties of the exact-match overlap graphs, we can construct and store them efficiently. In Section 3.1, we will describe these special properties in detail.

Briefly, the idea of storing the overlap graph compactly is from the following simple observation. If the strings are sorted in the lexicographic order, then for any string x the lexicographic orders of the strings that contain x as a prefix are in a certain integer range or integer interval [a, b]. Therefore, the information about out-neighborhood of a vertex can be described using at most λ intervals. Such intervals have a nice property that they are either disjoint or contain each other. This property allows us to describe the out-neighborhood of a vertex by at most 2λ−1 disjoint intervals. Each interval costs 2⌈logn⌉+⌈logλ⌉) bits, where 2⌈logn⌉ bits are for storing its two bounds and ⌈logλ⌉ bits are for storing the weight. We have n vertices so the amount of memory required by our data structure is no more than (2λ−1)(2⌈logn⌉+⌈logλ⌉)n bits. Note that this is just an upper bound. In practice, the amount of memory may be much less than that.

1.2 Application: DNA assembly

The main motivation for the exact-match overlap graphs comes from their use in implementing fast approximation algorithms for the shortest super string problem which is the very first problem formulation for DNA assembly. The exact-match overlap graphs can be used for other problem formulations for DNA assembly as well.

Exact-match overlap graphs have been broadly used in the context of DNA assembly and the shortest super string problem where the number n of strings ranges from thousands to billions. The length ℓ of the strings is from 25 to 1000, depending on the DNA sequencing technology used. However, many DNA assemblers using overlap graphs are time and memory intensive. If an overlap graph is explicitly stored, it would require Ω(n²) memory which could be prohibitive in practice. In this article, we present a data structure for representing overlap graphs that requires only linear time and linear memory. Experimental results have shown that our preliminary DNA sequence assembler that uses this data structure can handle a large number of strings. In particular, it takes about 2.4 days and 62.4 GB memory to process a set of 660 million DNA strings of length 100 each. The set of DNA strings is drawn uniformly at random from a reference human genome of size of 3.3 billion base pairs.

1.3 Related work

Gusfield et al. (1992) and Gusfield (1997) consider the all-pairs suffix-prefix problem which is actually a special case of computing the exact-match overlap graphs when λ=ℓ. They devised an O(ℓn+n²) time algorithm for solving the all-pairs suffix-prefix problem. In this case, the exact-match overlap graph is a complete graph. So the run time of the algorithm is optimal if the exact-match overlap graph is stored in a traditional way.

Although the run time of the algorithm by Gusfield et al. is theoretically optimal in that setting, it uses the generalized suffix tree which has two disadvantages in practice. The first disadvantage is that the space consumption of the suffix tree is quite large (Kurtz, 1999). The second disadvantage is that the suffix tree usually suffers from a poor locality of memory references (Ohlebusch and Gog, 2010). Fortunately, Abouelhoda et al. (2004) have proposed a suffix tree simulation framework that allows any algorithm using the suffix tree to be simulated by enhanced suffix arrays. Ohlebusch and Gog (2010) have made use of properties of the enhanced suffix arrays to devise an algorithm for solving the all-pairs suffix-prefix problem directly without using the suffix tree simulation framework. The run time of the algorithm by Ohlebusch and Gog is also O(ℓn+n²). Please note that our data structure and algorithm can be used to solve the suffix-prefix problem in O(λℓn) time. In the context of DNA assembly, λ is typically much smaller than n and hence our algorithm will be faster than the algorithms of Gusfield (1997) and Ohlebusch and Gog (2010).

Exact-match overlap graphs should be distinguished from approximate-match overlap graphs which is considered in Myers (2005), Medvedev et al. (2007) and Pop (2009). In the approximate-match overlap graph, there is an edge between two strings x and y if and only if there is a prefix of x, say x′, and there is a suffix of y, say y′, such that the edit distance between x′ and y′ is no more than a certain threshold.

2 BACKGROUND

Let Σ be the alphabet. The size of Σ is a constant. In the context of DNA assembly, Σ={A, C, G, T}. The length of a string x on Σ, denoted by |x|, is the number of symbols in x. Let x[i] be the i-th symbol of string x, and x[i, j] be the substring of x between the i-th and the j positions. A prefix of string x is the substring x[1, i] for some i. A suffix of string x is the substring x[i, |x|] for some i.

Given two strings x and y on Σ, an exact-match overlap between x and y, denoted by ov(x, y), is a string which is a suffix of x and a prefix of y (notice that this definition is not symmetric). The maximal exact-match overlap between x and y, denoted by ov_max(x, y), is the longest exact-match overlap between x and y.

Exact-match overlap graphs: informally, an exact-match overlap graph is nothing but a graph where there is a node for each read and two nodes are connected by an edge if there is a sufficient overlap between the corresponding reads.

To be more precise, given n strings s₁, s₂,…, s_n and a threshold λ, the exact-match overlap graph is an edge-weighted directed graph G=(V, E) in which there is a vertex v_i∈V associated with the string s_i, for 1≤i≤n. There is an edge (v_i, v_j)∈E if and only if |s_i|−|ov_max(s_i, s_j)|≤λ. The weight of the edge (v_i, v_j), denoted by ω(v_i, v_j), is |s_i|−|ov_max(s_i, s_j)|. See Figure 1.

Fig. 1.

An example of an overlap edge.

If all the n input strings have the same length ℓ, then τ=ℓ−λ is called the overlap threshold. If there is an edge (v_i, v_j) in the graph, it implies that the overlap between s_i and s_j is at least τ.

The set of out-neighbors of a vertex v is denoted by OutNeigh(v). The size of the set of out-neighbors of v, |OutNeigh(v)|, is called the out-degree of v. We denote the out-degree of v as deg_out(v)=|OutNeigh(v)|.

For simplicity, we assume that all the strings s₁, s₂,…, s_n have the same length ℓ. Otherwise, let ℓ be the length of the longest string and all else works.

The operation of accessing an edge given its two endpoints: given any two vertices v_i and v_j, the operation of accessing the edge (v_i, v_j) is the task of returning ω(v_i, v_j) if (v_i, v_j) is actually an edge of the graph, and returning NULL if (v_i, v_j) is not.

3 METHODS

3.1 A memory-efficient data structure representing an exact-match overlap graph

In this section, we present a memory-efficient data structure to store an exact-match overlap graph. It only requires at most (2λ−1)(2⌈logn⌉+⌈logλ⌉)n bits. It guarantees that the time for accessing an edge, given two end points of the edge, is O(logλ). This may sound like a contradictory claim because in some exact-match overlap graphs the number of edges can be Ω(n²) and it seems like it should require at least Ω(n²) time and space to construct them. Fortunately, because of some special properties of the exact-match overlap graphs, we can construct and store them efficiently. In the following paragraphs, we will describe these special properties.

The graph representation we envision is one where we store the neighbors of each node. The difference between the standard adjacency lists representation of a graph and ours lies in the fact that we only use O(λ) memory to store the neighbors of any node. We are able to do this since we sort the input strings in lexicographic order and employ a data structure called PREFIX defined below.

Another crucial idea we employ is the following: let x be any string and let the input reads be sorted in lexicographic order. If we are interested in identifying all the input strings in which x is a prefix, then these strings will be contiguous in the sorted list. If we use the sorted position of each read as its identifier, then the neighbors of any node can be specified with O(λ) intervals (as we show next).

Without loss of generality, we assume that the n input strings s₁, s₂,…, s_n are sorted in lexicographic order. We can assume this because if they are not sorted, we can sort them by using the radix sort algorithm which runs in O(ℓn/w) time, where w is the word length of the machine used, assuming that the size of the alphabet is a constant. If the alphabet is not of size O(1), the sorting time will be O(nℓlog(|Σ|)/w).

We associate an identification number with each string s_i and its corresponding vertex v_i in the exact-match overlap graph. This identification number is nothing but the string's lexicographic order i. We will access an input string using its identification number. Therefore, the identification number and the vertex of an input string are used interchangeably. Also, it is not hard to see that we need ⌈logn⌉ bits to store an identification number. We have the following properties.

Given an arbitrary string x, let PREFIX(x) be the set of identification numbers of all the input strings for which x is a prefix. Formally, PREFIX(x)={i|x is a prefix of s_i}.

PREFIX enables us to specify the neighbors list of any node in the graph compactly. In PROPERTY 3.1, PROPERTY 3.2, PROPERTY 3.3, and Lemma 3.1, we prove certain properties of PREFIX and finally show that we can represent the neighbors list of any node as 2λ−1 intervals.

Property 3.1. —

If PREFIX(x)≠∅, then PREFIX(x)=[a, b], where [a, b] is some integer interval containing integers a, a+1,…, b−1,b.

Proof. —

Let a=min_{i∈PREFIX(x)}i and b=max_{i∈PREFIX(x)}i. Clearly, PREFIX(x)⊆[a,b]. On the other hand, we will show that [a,b]⊆PREFIX(x). Let i be any identification number in the interval [a,b]. Since the input strings are in lexicographically sorted order, s_a[1, |x|]≤s_i[1, |x|]≤s_b[1, |x|]. Since a∈PREFIX(x) and b∈PREFIX(x), s_a[1, |x|]=s_b[1, |x|]. Thus, s_a[1, |x|]=s_i[1, |x|]=s_b[1, |x|]. Therefore, x is a prefix of s_i. Hence, i∈PREFIX(x).

For example, let

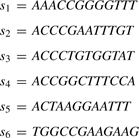If x=AC, then PREFIX(x)=[2, 5]. Similarly, if x=ACCC, then PREFIX(x)=[2, 3].

Property 3.1 tells us that PREFIX(x) can be expressed by an interval which is determined by its lower bound and its upper bound. So we only need 2⌈logn⌉ bits to store PREFIX(x). In the rest of this article, we will refer to PREFIX(x) as an interval. Also, given an identification number i, checking whether i is in PREFIX(x) can be done in O(1) time. In the Subsection 3.2.1, we will discuss two algorithms for computing PREFIX(x), for a given string x. The run times of these algorithms are O(|x| log n) and O(|x|), respectively.

Property 3.1 leads to the following property.

Property 3.2. —

for each vertex v_i. In the other words, OutNeigh(v_i) is the union of at most λ non-empty intervals.

Proof. —

Let v_j be a vertex in OutNeigh(v_i). By the definition of the exact-match overlap graph, 1≤|s_i|−|ov_max(s_i, s_j)|=ω(v_i, v_j)≤λ. Let ω(s_i, s_j)=ω. Clearly, ov_max(s_i, s_j)=s_i[ω+1, |s_i|]=s_j[1, |ov_max(s_i, s_j)|]. This implies that v_j∈PREFIX(s_i[ω+1, |s_i|]).

On the other hand, let v_j be any vertex in PREFIX(s_i[ω+1, |s_i|]), it is easy to check that v_j∈OutNeigh(v_i). Hence, .

From Property 3.2, it follows that we can represent OutNeigh(v_i) by at most λ non-empty intervals, which need at most 2λ⌈logn⌉ bits to store. Therefore, it takes at most 2nλ⌈logn⌉ bits to store the exact-match overlap graph. However, given two vertices v_i and v_j, it takes O(λ) time to retrieve ω(v_i, v_j) because we have to sequentially check if v_j is in PREFIX(s_i[2, |s_i|]),PREFIX(s_i[3, |s_i|]),…, PREFIX(s_i[λ+1, |s_i|]). But if OutNeigh(v_i) can be represented by k disjoint intervals then the task of retrieving ω(v_i, v_j) can be done in O(logk) time by using binary search. In Lemma 3.1, we show that OutNeigh(v_i) is the union of at most 2λ−1 disjoint intervals.

Property 3.3 —

For any two strings x and y with |x|<|y|, either one of the two following statements is true:

• PREFIX(y)⊆PREFIX(x)

• 

Proof. —

There are only two possible cases that can happen to x and y.

Case 1: x is a prefix of y. For this case, it is not hard to infer that PREFIX(y)⊆PREFIX(x).

Case 2: x is not a prefix of y. For this case, it is not hard to infer that .

Lemma 3.1. —

Given λ intervals [a₁,b₁],[a₂,b₂]…[a_λ,b_λ] satisfying Property 3.3, the union of them is the union of at most 2λ−1 disjoint intervals. Formally, there exist p≤2λ−1 disjoint intervals [a′₁,b′₁],[a′₂,b′₂]…[a′_p,b′_p] such that .

Proof. —

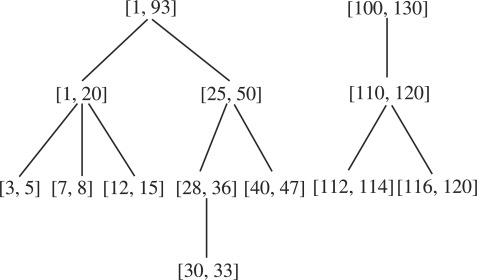
We say interval [a_i,b_i] is a parent of interval [a_j,b_j] if [a_i,b_i] is the smallest interval containing [a_j,b_j]. We also say interval [a_j,b_j] is a child of interval [a_i,b_i]. Since the intervals [a_i,b_i] are either pairwise disjoint or contain each other, each interval has at most one parent. Therefore, the set of the intervals [a_i,b_i] form a forest in which each vertex is associated with an interval. See Figure 2. For each interval [a_i,b_i], let I_i be the set of maximal intervals that are contained in the interval [a_i,b_i] but disjoint from all of its children. For example, if [a_i,b_i]=[1,20] and its child intervals are [3,5], [7,8] and [12,15], then I_i={[1,2],[6,6],[9,11],[16,20]}. If the interval [a_i,b_i] is a leaf interval (i.e. an interval having no children), I_i is simply the set containing only the interval [a_i,b_i]. Let . We will show that A is the set of the disjoint intervals [a′_i,b′_i] satisfying the condition of the lemma.

First, we show that . By the construction of I_i, it is trivial to see that . Conversely, it is enough to show that for any 1≤i≤λ. This can be proved by induction on vertices in each tree of the forest. For the base case, obviously each leaf interval [a_i,b_i] is in A. Therefore, for any leaf interval [a_i,b_i]. For any internal interval [a_i,b_i], assume that all of its child intervals are subsets of . By the construction of I_i, [a_i,b_i] is a union of all of the intervals in I_i and all of its child intervals. Therefore, .

Secondly, we show that the intervals in A are pairwise disjoint. It is sufficient to show that any interval in I_i is disjoint with every interval in I_j for i≠j. Obviously, the statement is true if [a_i,b_i]∩[a_j,b_j]=∅. Let us consider the case where one contains the other. Without loss of generality, we assume that [a_j,b_j]⊂[a_i,b_i]. Consider two cases:

Case 1: [a_i,b_i] is the parent of [a_j,b_j]. By the construction of I_i, any interval in I_i is disjoint from [a_j,b_j]. By the construction of I_j, any interval in I_j is contained in [a_j,b_j]. Therefore, they are disjoint.

Case 2: [a_i,b_i] is not the parent of [a_j,b_j]. Let [a_j,b_j]=[a_i0,b_i0]⊂[a_ii,b_ii]…⊂[a_ih,b_ih]=[a_i,b_i], where [a_it,b_it] is the parent of [a_it−1,b_it−1]. From the result in Case 1, any interval in I_it is disjoint from [a_it−1,b_it−1] for 1≤t≤h. So any interval in I_i is disjoint from [a_j,b_j]. We already know that any interval in I_j is contained in [a_j,b_j]. Thus, they are disjoint.

Finally, we show that the number of intervals in A is no more than 2λ−1. Clearly, |A|=∑_i=1^λ|I_i|. It is easy to see that the number of intervals in I_i is no more than the number of children of [a_i,b_i] plus one, which is equal to the degree of the vertex associated with [a_i,b_i] if the vertex is not a root of a tree in the forest, and equal to the degree of the vertex plus one if the vertex is a root. Let q be the number of trees in the forest. Then, |A|=∑_i=1^λ|I_i|≤∑_i=1^λd_i+q=2|E|+p, where d_i is the degree of the vertex associated with [a_i,b_i] and E is the set of the edges of the forest. We know that in a tree the number of edges is equal to the number of vertices minus one. Thus, |E|=λ−q. Therefore, |A|≤2λ−q≤2λ−1. This completes our proof.

Fig. 2.

A forest illustration in the proof of Lemma 3.1.

The above proof yields an algorithm for computing the disjoint intervals starting from the forest of intervals. Once the forest is built, outputting the disjoint intervals can be done easily at each vertex. However, designing a fast algorithm for constructing the forest is not trivial. In the Subsection 3.2.2, we will discuss an O(λlogλ)-time algorithm for constructing the forest. Thereby, there is an O(λlogλ)-time algorithm for computing the disjoint intervals [a′_i,b′_i] in Lemma 3.1, given λ intervals satisfying Property 3.3. Also, from Property 3.3 and Lemma 3.1, it is not hard to prove the following theorem.

Theorem 3.1. —

OutNeigh(v_i) is the union of at most 2λ−1 disjoint intervals. Formally, where p≤2λ−1, for 1≤m≠m′≤p. Furthermore, ω(v_i,v_j)=ω(v_i,v_k) for any 1≤m≤p and for any v_i,v_k∈[a_m,b_m].

Theorem 3.1 suggests a way of storing OutNeigh(v_i) by at most (2λ−1) disjoint intervals. Each interval takes 2⌈logn⌉ bits to store its lower bound and its upper bound, and ⌈logλ⌉ bits to store the weight. Thus, we need 2⌈logn⌉+⌈logλ⌉ to store each interval. Therefore, it takes at most (2λ−1)(2⌈logn⌉+⌈ log λ⌉) bits to store each OutNeigh(v_i). Overall, we need (2λ−1)(2⌈logn⌉+⌈logλ⌉)n bits to store the exact-match overlap graph. Of course, the disjoint intervals of each OutNeigh(v_i) are stored in sorted order of their lower bounds. Therefore, the operation of accessing an edge (v_i,v_j) can be easily done in O(logλ) time by using binary search.

3.2 Algorithms for constructing the compact data structure

In this section, we describe two algorithms for constructing the data structure representing the exact-match overlap graph. The run time of the first algorithm is O(λℓnlogn) and it only uses O(λ) extra memory, besides ℓn⌈log|Σ|⌉ bits used to store the n input strings. The second algorithm runs in O(λℓn) time and requires O(n) extra memory. As shown in Section 3.1, the algorithms need two routines. The first routine computes PREFIX(x) and the second one computes the disjoint intervals described in Lemma 3.1.

3.2.1 Computing interval PREFIX(x)

In this subsection, we consider the problem of computing the interval PREFIX(x), given a string x and n input strings s₁,s₂,…, s_n of the same length ℓ in lexicographical order. We describe two algorithms for this problem. The first algorithm takes O(|x|logn) time and O(1) extra memory. The second algorithm runs in O(|x|) time and requires O(n) extra memory.

The first algorithm runs in phases. In each phase, it considers one of the symbols in x. In the first phase, it considers x[1] and obtains a list of input strings for which the first symbol is x[1]. Since the input strings are in sorted order, this list can be represented as an interval [a₁,b₁]. Followed by this, in the second phase the algorithm considers x[2]. From out of the strings in the interval [a₁,b₁], it identifies strings whose second symbol is [x₂]. These strings will form an interval [a₂,b₂]; and so on. The interval that results at the end of the k-th phase (where k=|x|) is PREFIX(x). In each phase, binary search is used to figure out the right interval.

In the second algorithm, a trie is built for all the input strings. Each node in the trie corresponds to a string u and the node will store the interval for this string (i.e. the node will store a list of input strings for which u is a prefix). For any given x, we walk through the trie tracing the symbols in x. The last node visited in this traversal will have PREFIX(x) (if indeed x is a string that can be traced in the trie).

A binary search based algorithm: let [a_i,b_i]=PREFIX(x[1, i]) for 1≤i≤|x|. It is easy to see that PREFIX(x)=[a_|x|,b_|x|]⊆[a_|x|−1,b_|x|−1]⊆…⊆[a₁,b₁]. Consider the following input strings, for example.

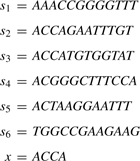Then, [a₁,b₁]=[1,5], [a₂,b₂]=[2,5], [a₃,b₃]=[2,3] and PREFIX(x)=[a₄,b₄]=[2,3].

We will find [a_i,b_i] from [a_i−1,b_i−1] for i from 1 to |x|, where [a₀,b₀]=[1,n] initially. Thereby, PREFIX(x) is computed. Let Col_i be the string that consists of all the symbols at position i of the input strings. In the above example, Col₃=ACCGTG. Observe that the symbols in string Col_i[a_i,b_i] are in lexicographical order for 1≤i≤|x|. Another observation is that [a_i,b_i] is the interval where the symbol x[i] appears consecutively in string Col_i[a_i−1,b_i−1]. Therefore, [a_i,b_i] is determined by searching for the symbol x[i] in the string Col_i[a_i−1,b_i−1]. This can be done easily by first using the binary search to find a position in the string Col_i[a_i−1,b_i−1] where the symbol x[i] appears. If the symbol x[i] is not found, we return the empty interval and stop. If the symbol x[i] is found at position c_i, then a_i (respectively b_i) can be determined by using the double search routine in string Col_i[a_i−1,c_i] (respectively, string Col_i[c_i,b_i−1]) as follows. We consider the symbols in the string Col_i[a_i−1,c_i] at positions c_i−2⁰, c_i−2¹,…, c_i−2^k, a_i−1, where k=⌊log(c_i−a_i−1)⌋. We find j such that the symbol Col_i[c_i−2^j] is the symbol x[i] but the symbol Col_i[c_i−2^j+1] is not. Finally, a_i is determined by using binary search in string Col_i[c_i−2^j, c_i−2^j+1]. Similarly, b_i is determined. The pseudo-code is given as follows.

Analysis: as we discussed above, it is easy to see the correctness of the algorithm. Let us analyze the memory and time complexity of the algorithm. Since the algorithm only uses binary search and double search, it needs O(1) extra memory. For time complexity, it is easy to see that computing the interval [a_i,b_i] at step i takes O(log(b_i−1−a_i−1))=O(logn) time because both binary search and double search take O(log(b_i−1−a_i−1)) time. Overall, the algorithm takes O(|x|logn) time because there are at most |x| steps.

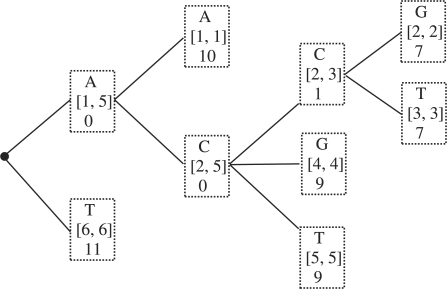
A trie-based algorithm: as we have seen in Subsection 3.2.1, to compute the interval [a_i,b_i] for symbol x[i], we use binary search to find the symbol x[i] in the interval [a_i−1,b_i−1]. The binary search takes O(log(b_i−1−a_i−1))=O(logn) time. We can reduce the O(logn) factor to O(1) in computing the interval [a_i,b_i] by pre-computing all the intervals for each symbol in the alphabet Σ and storing them in a trie. Given the symbol x[i], to find the interval [a_i,b_i] we just retrieve it from the trie, which takes O(1) time. The trie is defined as follows (Fig. 3). At each node in the trie, we store a symbol and its interval. Observe that we do not have to store the nodes that have only one child. These nodes form chains in the trie. We will remove such chains and store their lengths in each remaining node. As a result, each internal node in the trie has at least two children. Because each internal node has at least two children, the number of nodes in the trie is no more than twice the number of leaves, which is equal to 2n. Therefore, we need O(n) memory to store the trie. Also, it is well known that the trie can be constructed recursively in O(ℓn) time.

Fig. 3.

An illustration of a trie for the example input strings in Subsection 3.2.1.

It is easy to see that once the trie is constructed, the task of finding the interval [a_i,b_i] for each symbol x[i] takes O(1) time. Therefore, computing PREFIX(x) will take O(|x|) time.

3.2.2 Computing the disjoint intervals

In this subsection, we consider the problem of computing the maximal disjoint intervals, given k intervals [a₁,b₁],[a₂,b₂],…, [a_k,b_k] which either are pairwise disjoint or contain each other. As discussed in Section 3.1, it is sufficient to build the forest of the k input intervals. Once the forest is built, outputting the maximal disjoint intervals can be done easily at each vertex of the forest.

The algorithm works as follows. First, we sort the input intervals in non-decreasing order of their lower bounds a_i. Among those intervals whose lower bounds are equal, we sort them in decreasing order of their upper bounds b_i. So after this step, we have (i) a₁≤a₂≤…≤a_k and (ii) if a_i=a_j then b_i>b_j for 1≤i<j≤k. Since the input intervals are either pairwise disjoint or contain each other, for any two intervals [a_i,b_i] and [a_i+1,b_i+1] (for 1≤i<k) the following statement holds. Either [a_i,b_i] contains [a_i+1,b_i+1] or they are disjoint. Observe that if [a_i,b_i] contains [a_i+1,b_i+1], then [a_i,b_i] is actually the parent of [a_i+1,b_i+1]. If they are disjoint, then the parent of [a_i+1,b_i+1] is the smallest ancestor of [a_i,b_i] that contains [a_i+1,b_i+1]. If such an ancestor does not exist, then [a_i+1,b_i+1] does not have a parent. Let A_i={[a_i1,b_i1],…,[a_im,b_im]} be the set of ancestors of [a_i,b_i], where i₁<…<i_m. It is easy to see that [a_i1,b_i1]⊂…⊂[a_im,b_im]. Therefore, the smallest ancestor of [a_i,b_i] that contains [a_i+1,b_i+1] can be found by binary search, which takes at most O(logk) time. Furthermore, assume that [a_ij,b_ij] is the smallest ancestor, then the set of ancestors of [a_i+1,b_i+1] is A_i+1={[a_i1,b_i1],…,[a_ij,b_ij]}. Based on these observations, the algorithm can be described by the following pseudo-code.

Analysis: as we argued above, the algorithm is correct. Let us analyze the run time of the algorithm. Sorting the input intervals takes O(klogk) time by using any optimal comparison sorting algorithm. It is easy to see that finding the smallest interval from the set A dominates the running time at each step of the loop, which takes O(logk) time. Obviously, there are k steps so the run time of the algorithm is O(klogk) overall. Notice that the sorted list of the intervals is actually a pre-order traversal of the forest. So the time complexity of the algorithm after sorting the intervals can be improved to O(k). However, the improvement does not change the overall time complexity of the algorithm since sorting the intervals takes O(klogk) time.

3.2.3 Algorithms for constructing the compact data structure

In this subsection, we describe two complete algorithms for constructing the data structure. The algorithms will use the routines in Subsections 3.2.1 and 3.2.2. The only difference between these two algorithms is the way of computing PREFIX. The first algorithm uses the routine based on binary search to compute PREFIX and the second one uses the trie-based routine. The following pseudo code describes the first algorithm.

An analysis of the time and memory complexity of the first algorithm follows. Each computation of PREFIX in line 3 takes O(ℓlogn) time and O(1) extra memory. So the loop of line 2 takes O(λℓlogn) time and O(λ) extra memory. Computing the disjoint intervals in line 5 takes O(λlogλ) time and O(λ) extra memory. Since λ≤ℓ, the run time of loop 2 dominates the run time of each step of loop 1. Therefore, the algorithm takes O(λℓnlogn) time and O(λ) extra memory in total.

The second algorithm is described by the same pseudo code above except for line 3 where the routine of Subsection 3.2.1 for computing PREFIX(s_i[j, |s_i|]) is replaced by the trie-based routine of Subsection 3.2.1. Let us analyze the second algorithm. Computing PREFIX in line 3 takes O(ℓ) time instead of O(ℓlogn) as in the first algorithm. With a similar analysis to that of the first algorithm, the loop of line 2 takes O(λ ℓ) time and O(λ) extra memory. Constructing the trie in line 1 takes O(ℓn) time. Therefore, the algorithm runs in O(λℓn) time. We also need O(n) extra memory to store the trie. In many cases, n is much larger than λ. So the algorithm takes O(n) extra memory.

It is possible to develop a third algorithm by revising the step in line 2 to line 4 in the pseudo code that computes the set of intervals of the suffixes of each input string s_i. The revision is based on suffix trees and the binary search-based algorithm given in Subsection 3.2.1. The idea is to build a suffix tree for every input string s_i. Note that every leaf in the suffix tree corresponds to a suffix of the input string s_i. After building the suffix tree, we populate every leaf in the suffix tree with the corresponding interval by traversing the suffix tree and computing the interval for each node in the suffix tree given the interval for its parent. Finally, we output the intervals for those suffixes whose lengths are no less than the overlap threshold τ=ℓ−λ. It is easy to see that the time needed to determine the interval for any node in the suffix tree is O(logn) given the interval for its parent. Because the suffix tree has O(ℓ) nodes, it takes O(ℓlogn) time to compute intervals. In addition, it takes O(ℓ) time to build the suffix tree and O(λlogλ) time to find the disjoint intervals. Since λ≤ℓ≤n, we will spend O(ℓlog n) time for each input string s_i. As a result, the entire algorithm will run in time O(ℓnlogn). Also, the entire algorithm will take O(ℓ) extra memory because each of the suffix trees takes O(ℓ) memory. In practice, logn is smaller than λ and hence this algorithm could also be of interest.

4 RESULTS

We have implemented a DNA sequence assembler named Large-scale Efficient DNA Assembly Program (LEAP) that incorporates our data structure for the overlap graphs. The assembler has three stages: preprocess input DNA sequences, construct overlap graph and assemble. In the context of DNA sequence assembly, the input DNA sequences are called reads. In the first stage, we add the reverse complement strings of the reads. Then we sort them and remove contained reads. The second stage is the main focus of our article, constructing the data structure of the overlap graph. The last stage basically analyzes the overlap graph, then retrieves unambiguous paths and outputs the contigs accordingly.

We tested our assembler on simulated data as follows. First, we simulated a genome G. Then each read of length ℓ is drawn from a random location in either G or the reverse complement of G. Reads drawn from the genome are error-free reads. The number n of the drawn reads is determined by the coverage depth, c, by the equation . We considered three datasets with the same read length ℓ=100, the same coverage depth c=20 and different genome sizes: 238 Mb, 1 GB and 3.3 GB. The number of reads in the datasets is 47.6 million, 200 million and 660 million, respectively. The size of the first genome is approximately the size of human chromosome 2. The size of the third genome is approximately the whole human genome size. For the first and the second dataset, we have run our assembler with varying values of the overlap threshold τ: 30, 40, 50, 60 or 70. We only tried the overlap threshold τ=30 for the last dataset because the run time was quite long, about 2.4 days. To assess the quality of the contigs, we aligned them to the reference genome and found that all the contigs appeared in the reference genome. We have run our assembler on a Ubuntu Linux machine of 2.4 GHz CPU and 130 GB RAM. To save memory usage, we choose the binary search-based algorithm to construct the overlap graph in the second stage. The details are provided in Tables 1 and 2.

Table 1.

The detail results for the first dataset

Genome size (Mb)	238	238	238	238	238
Number of read (M)	47.6	47.6	47.6	47.6	47.6
Overlap threshold (bp)	30	40	50	60	70
Overlap time (h)	0.68	0.57	0.46	0.36	0.26
Intervals (M)	551	472	392	312	232
Edges (M)	1298	904	668	471	286
Overlap memory (GB)	5.4	4.5	3.7	3	2.2
Assembly N50 (Kb)	19 376	3171	429	50	5
Longest contig (Kb)	49 835	8326	1847	262	43
Total time (h)	0.84	0.71	0.61	0.5	0.4

Table 2.

The detail results for the second and the third datasets

Genome size (Gb)	1	1	1	1	1	3.3
Number of read (M)	200	200	200	200	200	660
Overlap threshold (bp)	30	40	50	60	70	30
Overlap time (h)	5.1	4.2	3.5	2.7	1.9	48.5
Intervals (B)	2.91	2.48	2.06	1.64	1.22	6.58
Edges (B)	5.43	4.35	3.12	2.18	1.45	14.7
Overlap memory (GB)	28.1	23.5	20	15.7	11.8	62.4
Assembly N50 (Kb)	2713	646	168	32	5	771
Longest contig (Mb)	103	82	35	14	6	381
Total time (h)	6.1	5.3	4.5	3.7	2.9	57.3

The DNA sequence assembler developed by Simpson and Durbin (2010) also employs the overlap graph approach. Their assembler, named String Graph Assembler (SGA), uses the suffix array and FM-index for the entire read set to construct the overlap graph. This article reported that the bottleneck in terms of time and memory usage was in constructing the suffix array and FM-index that required 8.5 h and about 55 GB of memory on the first dataset. The total processing time was 15.2 h. On the third dataset, they estimated by extrapolation that the step of constructing the suffix array and FM-index would require about 4.5 days and 700 GB of memory. The total processing time on the third dataset would be more than that. However, SGA has been improved in terms of memory efficiency since its first version was released. Unfortunately, while the second version of SGA improves memory usage, its run time increases. We were able to run the latest version of SGA on the same machine on the datasets. The source code of the latest version of SGA can be found at https://github.com/jts/sga. Table 3 provides the time and memory comparison between the assemblers. For all of the datasets, we have run the two assemblers with the same overlap threshold τ=30. The contigs output by the two assemblers were almost the same.

Table 3.

Time and memory comparison between the assemblers

Dataset	LEAP		Latest SGA		Old SGA
	Time	Memory (GB)	Time (days)	Memory (GB)	Time	Memory (GB)
238 Mb	0.8 h	5.4	1.1	7.9	15.2 h	55
1 GB	6.1 h	28.1	5.6	38.5	–	–
3.3 GB	2.4 d	62.4	–	–	≥4.5 d	700

5 CONCLUSION

We have described a memory-efficient data structure that represents the exact-match overlap graph. We have shown that this data structure needs at most (2λ−1)(2⌈logn⌉+⌈logλ⌉)n bits, which is a surprising result because the number of edges in the graph can be Ω(n²). Also, it takes O(logλ) time to access an edge through the data structure. We have proposed two fast algorithms to construct the data structure. The first algorithm is based on binary search and runs in O(λℓnlogn) time and takes O(λ) extra memory. The second algorithm, based on the trie, runs in O(λℓn) time, which is slightly faster than the first algorithm, but it takes O(n) extra memory to store the trie. The nice thing about the first algorithm is that the memory it uses is mostly for the input strings. This feature is very crucial for building an efficient DNA assembler.

We are also developing our assembler LEAP that incorporates the data structure for the overlap graph. The experimental results show that our assembler can efficiently handle datasets of size equal to that of the whole human genome. Currently, our assembler works for error-free reads. In reality, reads usually have errors. If the error rate is high, our assembler may not work well. However, with improving accuracy in sequencing technology, the error rate has been reduced. If the error rate is low enough, we will have many error-free reads, which means that our assembler will still work in this case. Also, an alternative way to use our assembler is to first correct the reads before feeding them to our assembler. In future, we would like to adapt our assembler to handle reads with errors as well.