Birefringence measurement of the retinal nerve fiber layer by swept source polarization sensitive optical coherence tomography

Abstract

A Swept Source Polarization-Sensitive Optical Coherence Tomography (SS-PS-OCT) instrument has been designed, constructed, and verified to provide high sensitivity depth-resolved birefringence and phase retardation measurements of the retinal nerve fiber layer. The swept-source laser had a center wavelength of 1059 nm, a full-width-half-max spectral bandwidth of 58 nm and an A-line scan rate of 34 KHz. Power incident on the cornea was 440 µW and measured axial resolution was 17 µm in air. A multiple polarization state nonlinear fitting algorithm was used to measure retinal birefringence with low uncertainty. Maps of RNFL phase retardation in a subject measured with SS-PS-OCT compare well with those generated using a commercial scanning laser polarimetry instrument. Peak-to-valley variation of RNFL birefringence given here is less than values previously reported at 840nm.

1. Introduction

Optical Coherence Tomography (OCT) was first introduced as a time domain (TD) technique in 1991 [1] with frequency domain (FD) techniques introduced in 1995 [2,3]. Frequency domain techniques increased in use after 2003 when FD-OCT was shown to provide an advantage over TD-OCT in terms of signal-to-noise ratio and acquisition speed [3–5]. With FD-OCT, high speed and high resolution clinical 3-D imaging has become possible [6,7].

Polarization-sensitive OCT (PS-OCT), being a functional extension of OCT, can measure polarimetric properties of birefringent samples [8–13]. PS-OCT provides additional contrast to standard OCT by making use of interference fringe intensity and relative phase of two detected orthogonal polarization states. The first PS-OCT system reported in literature was described in 1992 [8], with the first polarization sensitive images presented in 1997 [9]. Early PS-OCT systems utilized bulk optics [8–10], but later, fiber-based systems were developed and demonstrated [11–13]. Fiber-based systems are smaller in size and more convenient to align compared to free space systems. However, free space systems’ polarization state at the reference and sample paths is easier to control and reference to a fixed laboratory frame. Controlling the polarization state of light in single mode fiber-based systems is more difficult because of uncontrolled polarization changes that can occur in single mode optical fiber [14].

Several different polarization sampling and analysis methods have been introduced to deduce polarimetric properties of birefringent samples. Using TD-PS-OCT Saxer et al used a Stokes formalism to determine the rotation axis of Stokes vectors on the Poincare sphere [11]. Roth et al used an algebraic method and polarization sensitive free space components in the sample arm to measure birefringence [15]. Cense et al demonstrated the first phase retardation and birefringence measurements in a human subject using TD-PS-OCT [16]. Park et al developed a Jones matrix approach with sequential polarization modulation to measure the four elements of the Jones matrix representing sample polarimetric properties [17]. Jiao et al used two superposed light sources [18], and later demonstrated continuous polarization modulation [19]. Davé et al used polarization maintaining (PM) fiber to characterize a birefringent plate retardance and axis orientation with a single A-scan [20].

More recently, FD-PS-OCT was developed to obtain high sensitivity and fast acquisition speeds [21–25]. Oh et al was able to measure sample birefringence with only one wavelength scan without depth limitation but using additional frequency shifters [23]. Yamanari et al used a modulated input polarization state, requiring only one A-scan to calculate sample retardation at the expense of a factor of three reduction in measurement depth [25]. Al-Qaisi et al was able to record an image of biological tissue free of ghost lines using PM fiber [26].

Previously, OCT imaging of the posterior eye was performed solely using light sources centered about the 840 nm spectral range where water absorption is minimal. A number of groups have reported RNFL phase retardation and birefringence measurements at 840 nm using spectral domain (SD)-PS-OCT systems [27–29]. At 840 nm light penetration into the retina is limited by high absorption and scattering at the retinal pigment epithelium (RPE). Recently, OCT retinal imaging has migrated to the 1 micron range because of reduced scattering and deeper penetration well into the choroid [30,31]. Several groups have demonstrated PS-OCT at 1 µm using FD techniques [21–24]. Yamanari et al demonstrated retinal imaging using a SS-PS-OCT system at 1 micron that allowed visualization of birefringence in the sclera [24]. Schmoll et al was able to perform retinal scans using SD-PS-OCT using PM fibers [32]. The setup was successful when stationary, but applications requiring fiber movement presented operational problems.

A promising clinical application of PS-OCT retinal imaging is early detection of glaucoma. Huang and Knighton showed that microtubules within retinal ganglion cells (RGCs) are the main contributor to RNFL birefringence [33]. In glaucoma patients, measurements of RNFL birefringence show a reduction compared to normal eyes [28,29]. Standard OCT systems cannot detect this compositional change in the RNFL as glial content in healthy eyes varies significantly [34]. On the other hand, PS-OCT can be used to measure birefringence in the RNFL and distinguish from non-birefringent elements [12], making earlier detection and quantification of the level of RGC degeneration in the RNFL possible [35,36]. In glaucoma, degenerate RGC axons are replaced by non-birefringent glial cells, so birefringence is believed to decline earlier and at a faster rate than RNFL thickness [36]. If more accurate birefringence measurement is possible, RGC axon degeneration might be detected earlier, and therefore glaucoma can be detected at an earlier stage. Accurate RNFL birefringence measurements in primate retinas were obtained using a time-domain bulk optics PS-OCT system and a multiple-state non-linear fitting algorithm [37,38].

In this paper, we present a single mode fiber-based SS-PS-OCT clinical system for retinal imaging operating at 1060 nm. The SS-PS-OCT system uses hardware dispersion compensation, achieves real-time display at 34 frames per second, and utilizes a frequency-quadrupled k-space clock to acquire interference fringe signals in orthogonal polarization modes without the need for spectral recalibration. The fiber based SS-PS-OCT system is constructed on a wheeled cart with a slit-lamp interface similar to that routinely used at ophthalmologists’ offices. We present results of a preliminary study comparing RNFL measurements on a human subject with the SS-PS-OCT system and a commercial scanning laser polarimetry instrument.

2. Methods

2.1 SS-PS-OCT instrumentation

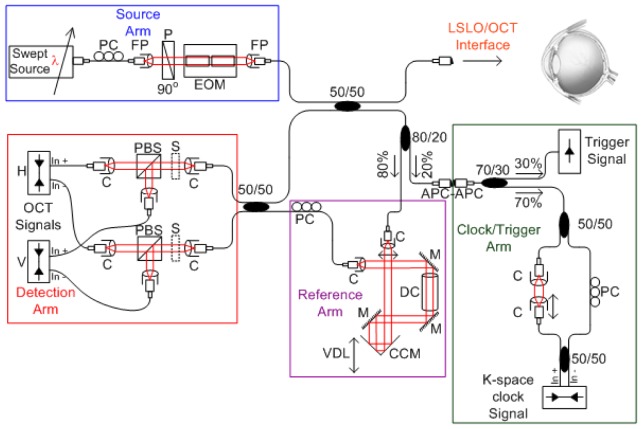
The SS-PS-OCT system (Fig. 1 ) is comprised of a swept laser source (HSL-1000 by Santec Corp., Komaki, Aichi, Japan) with a 34 KHz sweep repetition rate, $f_R$, a 1059 nm center wavelength, ${\lambda }_0$, a 58 nm full-width-half-max (FWHM) spectral bandwidth, $\Delta \lambda$, a 2.9 mW average output power and 0.64 duty cycle. Laser light travels through single mode optical fiber (HI1060 by Corning Inc., Corning, NY). A polarization controller (FPC560 by Thorlabs Inc., Newton, NJ) at the source transforms light polarization to a vertical linear state (0°). Light is then collimated into free space using a fiberport (PAF-X-2-1064 by OFR Inc., Caldwell, NJ) and propagates through a Glan-Thompson linear prism polarizer (MGT25E8-HEAR1000-1600 by Karl Lambrecht Corp., Chicago, IL) with polarization axis vertically oriented (0°). Light then propagates through a modified broadband bulk electro-optic phase modulator. The modulator consists of two matched 20mm long MgO doped LiNbO₃ crystals arranged in series, with the second crystal oriented at 90 degrees relative to the first. Applied voltage to the second crystal is equal in magnitude but opposite in polarity to that applied to the first crystal so phase retardation is doubled and effects of intrinsic birefringence are balanced.

Fig. 1.

SS-PS-OCT system schematic, PC: polarization controller, FP: fiberport, P: polarizer, EOM: broadband electro-optic modulator, C: collimator, CCM: corner cube mirror, PBS: polarizing beam splitter. S: solenoid, VDL: variable delay line, DC: dispersion compensation glass rod, M: silver coated mirror.

Ideally, the fast axes of the two crystals in the modulator should be oriented at precisely 90 degrees. Unfortunately, relative orientation of fast axes in off-the-shelf modulators is frequently slightly misaligned from 90 degrees. Small angular misalignments (δθ) between the two crystals cause a ‘self interference’ or ‘ghost line artifact’ with amplitude proportional to sin(δθ). In the case of 20mm long LiNbO₃ crystals utilized in the study reported here, path length mismatch is equal to $\Delta n\cdot L=0.08175*20=1.635mm$ single pass, which is manifest as an undesirable image artifact at an interferometer pathlength mismatch of 817.5 μm. Eliminating ghost line artifacts is crucial for successful operation of optical interferometric systems because image field of view and signal-to-noise ratio (SNR) may otherwise be reduced. Some OCT researchers have tried to remove these artifacts from recorded images by treating as fixed-pattern noise. In these approaches, an additional reflection path is needed to successfully subtract the ghost line artifact [24]. Though this method can potentially reduce or eliminate a ghost line artifact, lost light is not recovered, residual features of the artifacts can remain, and a reduction in modulation depth occurs. We modified the off-the-shelf modulator using a cantilever rotation mount of one of the LiNbO₃ crystals in the modulator. The rotation mount allowed precise angular adjustment of one LiNbO₃ crystal and effective elimination of the ghost line artifact while achieving high modulation depth. Using a wavelength dependent voltage drive waveform enabled accurate, constant phase retardation across the entire laser sweep [39].

Light exiting the modulator is coupled back into optical fiber using a fiber port (PAF-X-2-1064) before being split to reference and sample paths using a 50/50 non-polarizing broadband fiber splitter (WP 10500202B2100 by AC Photonics Inc., Santa Clara, CA). An 80/20 splitter is used to tap 20% of the reference light into the clock/trigger path. Light in the reference path is collimated into free space. A set of three mirrors (10Z40ER.2 by Newport) steer light to reduce the footprint and provide sufficient pathlength in air to match sample arm pathlength. A corner cube retro reflector (UBBR1-1I by Newport) mounted on a motorized stage (KT-LSR75A by Zaber) is used to adjust pathlength in the reference arm. A glass rod was designed using optical design software (ZEMAX by Zemax corp., Bellevue, WA) to balance dispersion mismatch between reference and sample paths. One mirror in the reference arm was adjusted to set reference arm power to optimize signal-to-noise ratio [40]. A polarization controller is used after light is coupled back into fiber to control reference arm polarization state. In the clock/trigger path a 70/30 splitter is used. The 30% segment is connected to a photoreceiver which serves as an intensity-based global trigger for system acquisition and control. The 70% segment is directed to a fiber-based Mach-Zehnder interferometer (MZI) with a total path length that matches that of the sample arm. The MZI interferometer acts as the linear k-space clock signal generator. The laser has a 6 mm coherence length (1.5 mm image field of view) and as such the MZI signal frequency was dialed down to obtain high visibility interference fringe signals. The resultant signal was then quadrupled using real-time analog circuitry to achieve a longer scan depth (~3.2 mm) with low phase noise errors. The sample path is interfaced directly into a commercial line scanning laser ophthalmoscope (LSLO) (PSI corp., Andover, MA). The setup is mounted on a modified slit lamp (SL-130 by Zeiss Meditec). Average incident power on the cornea was 440 μW (1.15 mW at the peak output wavelength).

Light returning from sample and reference paths recombine and interfere at the 50/50 coupler before being collimated into free space. Two bulk-optic polarization beam splitters split the light into horizontal and vertical polarization components (PSCL-B by OFR Inc., Caldwell, NJ). Light is then coupled into single mode fiber and detected by two 80-MHz balanced fiber-coupled photoreceivers (1817-FC by NewFocus). A solenoid was placed before each polarization beam splitter to allow blocking one detection arm and detecting light without balanced detection using the balanced photoreceivers. We experimentally measured SNR and sensitivity of our system by passing light from the sample arm through a neutral density filter (NDF) then focusing on a mirror. With a total attenuation of 42.6 dB, SNR was measured to be 49.7 dB at a depth of 0.2 mm with 5.3 dB/mm rolloff. System sensitivity at DC is then equivalent to 93.4 dB. With higher laser power and more asymmetric coupling to the source arm one can increase SNR even further. Axial resolution (17.4 μm) was determined by computing the Fourier transform of the non-Gaussian optical power spectrum to give full width at half maximum (FWHM) of the point spread function (PSF). The value matched the experimental axial resolution of about 17.1 μm measured when a single reflector was positioned in the sample arm. The measured axial resolution in air corresponds to a resolution of about 12.4 μm in tissue (assuming an average index of refraction of 1.38).

2.2 Acquisition and processing

When performing SS-PS-OCT measurements, input polarization state is varied step-wise at the source arm such that for every three consecutive laser sweeps the input polarization state is S₀: −2π/3, S₁: 0, and S₂: 2π/3 respectively. At the exit of the electro-optic modulator, the three input polarization states (S₀, S₁, and S₂) are equally spaced on the QU great circle of the Poincare sphere [41,42].

Horizontal and vertical components of detected reference light must have equal amplitudes for all three input polarization states in order to accurately measure birefringence properties. Fiber segment lengths were kept short throughout the system to minimize polarization mode dispersion (PMD) so that a single polarization controller was positioned in the reference arm. Since placement of a single polarization controller in both detection arm inputs was not possible, polarimetric measurements were recorded in an unbalanced mode with one arm. Although stress-type polarization controllers require shorter segments of fiber these devices can introduce substantial PMD and hence were not utilized.

A Hanning window is applied to the raw detected real-valued vertical, ${\Gamma }_v(z)$, and horizontal, ${\Gamma }_h(z)$, fringe intensities to enhance SNR. An optimized fast Fourier transform (FFT) algorithm based on the Intel^® C primitives is applied to obtain depth-resolved horizontal E_h(z) and vertical E_v(z) electric field amplitudes, and relative phase difference [φ_diff(z) = φ_v(z) – φ_h(z)]. A phase of −2π/3 is added to φ_diff(z) for S₀, and 2π/3 for S₂ to account for the input polarization states in the reference path.

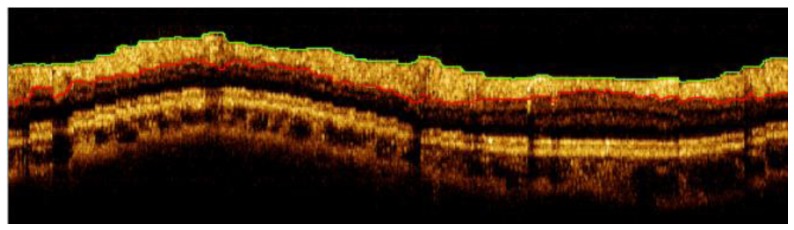
A fully automatic boundary detection algorithm was developed to segment the RNFL. The boundary detection algorithm is intensity based and operates on individual A-scans. In a first step, a rectangular Wiener filter is applied to B-scan images to reduce speckle noise along the boundary axis while maintaining edges. A bisquare fit is then applied to each de-speckled A-scan to further remove speckle influence and give a smooth curve. A threshold is applied to the curve fit to detect anterior and posterior RNFL boundaries. Anterior and posterior edges are independently filtered to remove outliers and then overlaid on acquired images (Fig. 2 ).

Fig. 2.

A clustered ring scan acquired about the optic nerve head. Acquired image diameter is 3.5 mm and consists of 36 clusters of 100 A-lines/cluster.

Given the posterior and anterior boundaries of the RNFL we cropped E_h(z), E_v(z), and φ_diff(z) and computed the normalized Stokes vector, S(z), to fully represent depth-resolved polarization data for each respective cluster.

$$S(z)\equiv \left[\begin{array}{c}Q(z)\\ U(z)\\ V(z)\end{array}\right]=\left[\begin{array}{c}{E}_v{(z)}^2-E_h{(z)}^2\\ 2E_v(z)E_h(z)\cos ({\phi }_{diff}(z))\\ 2E_v(z)E_h(z)\sin ({\phi }_{diff}(z))\end{array}\right]/(E_v{(z)}^2+E_h{(z)}^2)$$ (1)

To determine double pass phase retardation per unit depth (DPPR/UD) with high accuracy, we adopted the multiple-state nonlinear fitting algorithm reported previously [38]. The multiple-state nonlinear fitting algorithm is a powerful tool to determine tissue polarimetric parameters since all recorded noise-free model polarization arcs are constrained to rotate about the same eigen-axis ( $\widehat{\beta }$) by the same phase-delay (equal to the round-trip or double-pass retardation angle 2δ(z)). The constraint allows fitting a large number of data points (100’s) with a few parameters. Uncertainty in any polarization state’s arc is compensated for by the constraints placed on the other arcs and hence a priori knowledge of the eigen-axis is unnecessary. The multiple-state nonlinear fitting algorithm has the advantage that all depth-resolved points are utilized simultaneously to measure polarimetric properties of a specimen unlike other methods that only consider start and end points [43–45].

Uncertainty or asymptotic standard parameter errors of the multiple-state nonlinear fitting algorithm are calculated from the sum of squares of distances between measured and fitted data. Uncertainty values are calculated for each cluster as a measure of fit quality. For clusters with uncertainty higher than a specified threshold a second fit to the data is computed so that the new posterior RNFL boundary is reevaluated to be the mean cluster thickness. If after the repeat measurement, DPPR/UD is still larger than a specified threshold, the cluster is flagged for manual RNFL segmentation. If the manually selected RNFL clusters have an uncertainty higher than a specified threshold they may be removed from further consideration.

2.3 Description of measurements

Since no generally accepted turbid birefringence standard exists, SS-PS-OCT system calibration is difficult. Although quarter-wave-plates have been used to measure system accuracy, the procedure is problematic since data from only two axial points is obtained. To verify birefringence measurements of our SS-PS-OCT system, we measured phase retardation (δ) and birefringence (Δn) of a thin (150 μm) weakly birefringent turbid film (NewFocus model 5842). 100 A-lines were recorded on a 66 μm × 42 μm rectangular grid area that we refer to as a cluster. The weakly birefringent turbid film was previously measured with a bulk optics PS-OCT system.

Two retinal scanning schemes were employed, a raster scan and a clustered ring scan. The raster scan is comprised of 500 polarization-diverse A-lines per B-scan and 160 B-scans that cover a 6 mm × 6 mm square area centered on the optic nerve head. The clustered ring scan consists of 36 clusters of 100 A-lines per ring, corresponding to an angular separation of 10 degrees (π/18 radians) and 10 concentric rings about the optic nerve head with equidistant diameters from 2 mm to 5 mm. Each cluster of 100 A-lines is acquired in a sinusoidal pattern (3 input polarization states per A-line for a total of 300 laser sweeps per cluster) covering a 66 μm × 52 μm area at the innermost ring and 66 μm × 130 μm at the outermost ring. 100 A-lines per cluster were found to offer a good compromise between polarimetric signal-to-noise ratio (PSNR) improvement and reduced acquisition time [46]. To ensure speckle fields are uncorrelated, A-line separation was set at 10 μm - 14 μm, equivalent to system speckle size. Averaging $N_A=100$ uncorrelated A-lines increases PSNR by approximately $\sqrt{N_A}=10$ [46].

The raster scan is acquired in balanced detection mode and used to obtain high contrast fundus image of the retina and utilized to automatically obtain a vascular fingerprint of the retina. The raster scan is acquired before each clustered ring scan. The clustered ring scan is used to obtain high resolution peripapillary RNFL thickness [Z_RNFL (x,y)], phase retardation [δ_RNFL(x,y)], and birefringence [Δn _RNFL(x,y)] maps. An LSLO image is simultaneously acquired with each of the OCT scans. The LSLO image allows determination of the blood vasculature with less contrast than the raster fundus OCT image but is sufficient to obtain relative registration between the raster and clustered ring scans. The high contrast blood vessel signature from the raster scan is then superimposed on the clustered maps obtained from the clustered ring scans. The blood vessel vasculature is also used to co-register the SS-PS-OCT retinal scan maps with the phase retardation map obtained from a commercial scanning laser polarimeter (GDx-VCC, Karl Zeiss Meditec).

We present scans from a healthy 25-year-old volunteer’s right- (OD) and left- (OS) eyes. The subject had vision 20/20 OU with normal visual field, optic nerve head, and retinal exams performed at a local ophthalmologic clinic. SS-PS-OCT and GDx imaging were performed in the Biomedical Engineering laser laboratory at the University of Texas at Austin. Informed consent was obtained from all subjects participating in the study prior to examination. Imaging protocols were approved by the Institutional Review Board of the University of Texas at Austin (IRB protocol # 2007040101) and are registered NCT # 01222065.

3. Results

3.1 Birefringent film measurement

We measured single pass phase retardation (SPPR) for a 150 μm thick turbid birefringent film to be δ = 41.06 +/− 0.51 degrees, corresponding to single pass phase retardation per unit depth (SPPR/UD) of 27.22 °/100 μm or a birefringence of 8.01⋅10⁻⁴ at 1060 nm. Park et al measured single pass phase retardation δ = 24.76° +/− 0.62° for the same birefringent film in 80 μm thickness, which corresponds to SPPR/UD of 30.95°/100 µm or Δn = 7.14⋅10⁻⁴ at 840 nm [47]. The variance in birefringence values between our SS-PS-OCT measurement and that obtained by Park et al may be due to instrument measurement uncertainty (axial resolution = 17µm; phase resolution = +/− 2°), different measurement sites or different wavelengths employed in the two instruments (1060 nm vs. 840 nm). The turbid weakly birefringent film is an excellent retardation calibration since magnitude of Δn is comparable to retinal birefringence values (~3.2⋅10⁻⁴). The calibration film also exhibits scattering, though less than that exhibited in a healthy RNFL, and exhibits similar SNR to the RNFL of elderly patients (the highest risk population for glaucoma).

3.2 In vivo eye measurements

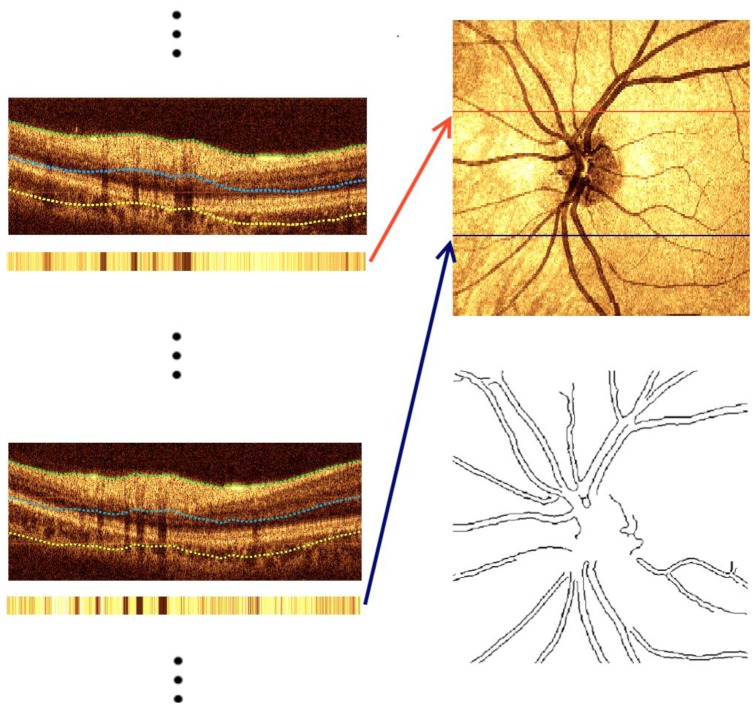
Retinal vasculature directly visualized from LSLO images had low contrast and high speckle noise, which made accurate automatic blood vessel detection difficult. However, the high contrast fundus image derived from OCT raster scans allows for easy automatic detection of the retinal vasculature. The raster fundus-like image at each retinal position is constructed by averaging signal intensity of 50 depth pixels starting at an offset of 50 pixels from the anterior nerve fiber layer boundary from each B-scan (Fig. 3(a) ). Juxtaposing averaged signals from all B-scans produces a fundus-like image of the retina centered about the optic nerve head (Fig. 3(b)). Speckle in the derived image (Fig. 3(b)) is reduced by applying a two-dimensional (2-D) Wiener filter, followed by a 2-D median filter, and adaptive histogram equalization. Blood Vessel edges are detected using a Canny edge detection algorithm (Fig. 3(c)). Only blood vessels with a minimum apparent size were retained to reduce the number of false positives.

Fig. 3.

Steps for reconstructing fundus-like image from raster scan data. (a) B-scans from different locations and corresponding averaged signal intensity from an offset from the upper boundary to a certain depth of each B-scan. (b) Juxtaposed averaged signals from each B-scan to form a fundus like image of the retina. (c) Automatically reconstructed blood vessels.

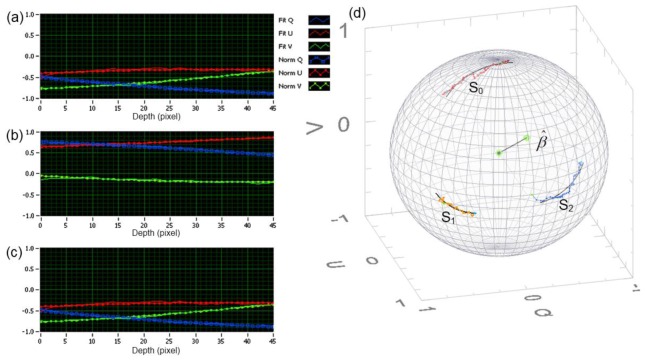
Figures 4(a) , 4(b), and 4(c) show evolution of the noise corrupted normalized Stokes parameters (Q, U, V) and their fits for a 158μm thick RNFL cluster in the inferior region of the OD for the three incident polarization states S₀ = −120°, S₁ = 0°, and S₂ = 120° respectively. Figure 4(d) shows the polarimetric speckle noise corrupted arcs, S_m(z) and their noise-free fits, P_m(z) on the Poincare sphere where m = 0, 1, and 2. All three incident polarization states on the Poincare sphere are fit to the same eigen-axis and phase-delay.

Fig. 4.

158μm thick cluster from the inferior RNFL region of the OD. Evolution of the polarimetric speckle noise corrupted normalized Stokes parameters (Q_n, U_n, and V_n) for the 3 incident polarization states (solid lines) and their noise-free fits (dotted lines) (a): S₀ = −120°, (b): S₁ = 0°, and (c): S₂ = 120°. (d) Polarimetric speckle corrupted arcs, S_m(z) and their noise-free fits, P_m(z) such that m = 0, 1, 2. All three states are fit to the same eigen-axis, $\widehat{\beta }$.

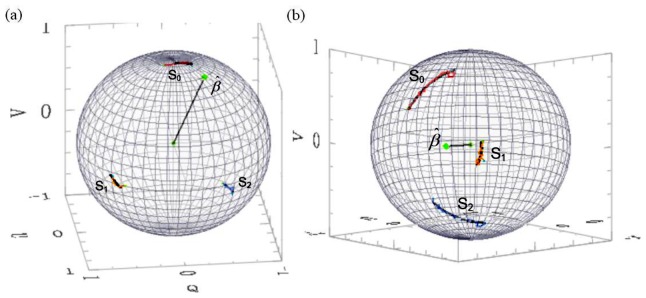
Figure 5 shows fits on the Poincare sphere to polarimetric speckle noise corrupted data from a healthy volunteer’s OD. Figure 5(a) corresponds to a 44 μm thick cluster with measured DPPR of 11.33°, equivalent to DPPR/UD of 25.76°/100μm, with 1.95°/100μm (7.57%) DPPR/UD uncertainty. Figure 5(b) is a 155 μm thick cluster with measured DPPR of 43.7°, equivalent to DPPR/UD of 28.22°/100μm, with 0.35°/100μm (1.24%) DPPR/UD uncertainty.

Fig. 5.

Poincare sphere polarimetric noise corrupted arcs for the three polarization states and their noise free fits about the eigen-axis $\widehat{\beta }$. (a) 44 μm thin RNFL cluster in the temporal OD region. (b) 155 μm thick RNFL cluster in the inferior OD region.

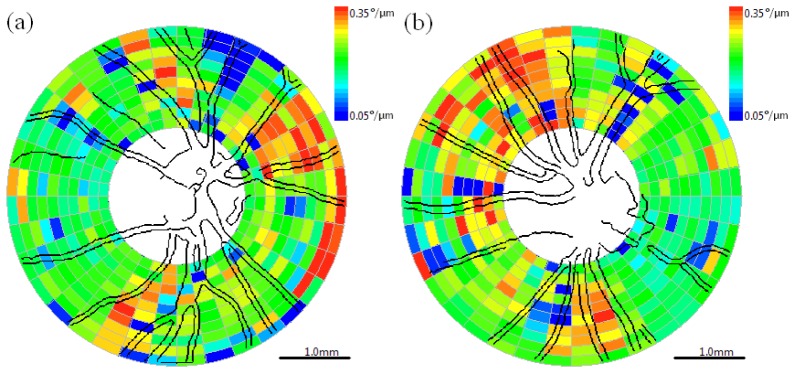
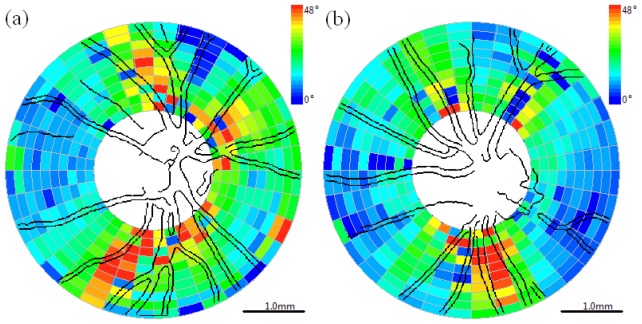
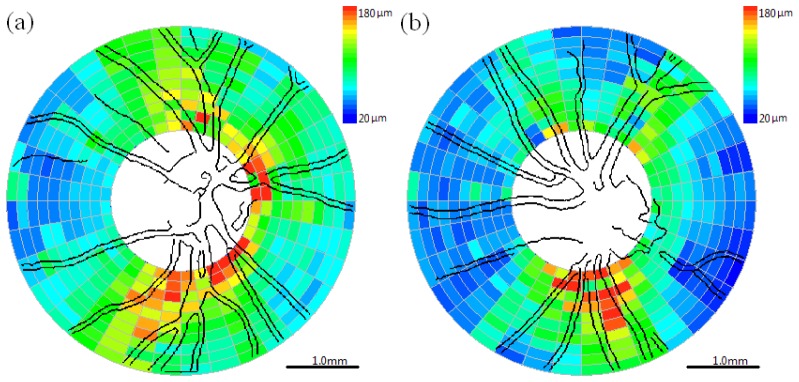
Discrete clustered data sets (Figs. 6 –8 ) recorded from a control subject enrolled in a clinical study are provided for right (OD) and left (OS) eyes. The non-linear fitting algorithm discussed above determines birefringence or DPPR/UD (°/μm, Fig. 6). RNFL thickness (μm, Fig. 7 ) is obtained using the boundary detection algorithm. Double pass phase retardation (°, Fig. 8) is obtained by multiplying RNFL thickness by DPPR/UD. Blood vessel maps for both OD and OS eyes acquired from a raster scan recorded immediately before acquisition of the clustered data are superimposed on the clustered DPPR/UD, RNFL thickness, and DPPR maps for registration and serve as a landmark for future longitudinal studies.

Fig. 6.

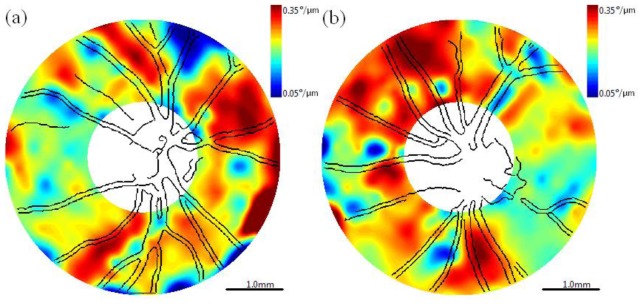
Cluster map with superimposed blood vessels detected from fundus-like raster scans of birefringence or DPPR/UD (°/μm). (a) Right eye (OD) and (b) left eye (OS). Color bar: 0.05°/μm (Δn = 7.35∙10⁻⁵) – 0.35°/μm (Δn = 5.16∙10⁻⁴). Scale bar is 1.0mm on the retina.

Fig. 8.

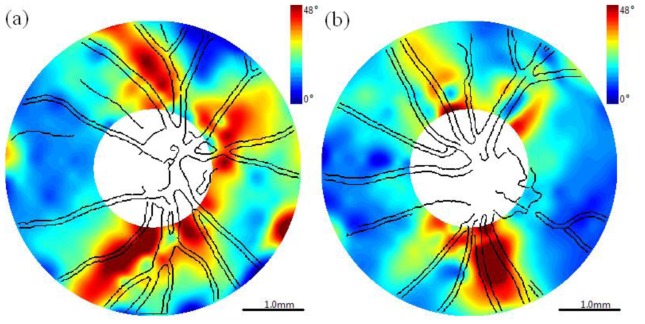
Cluster map with superimposed blood vessels detected from fundus-like raster scans of DPPR (°). (a) Right eye (OD) and (b) left eye (OS). Color bar: (0° - 48°). Scale bar is 1.0mm on the retina.

Fig. 7.

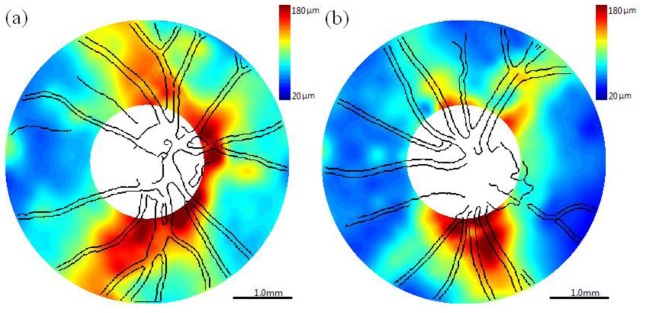
Cluster map with superimposed blood vessels detected from fundus-like raster scans of retinal nerve fiber layer thickness (RNFLT, μm). (a) Right eye (OD) and (b) left eye (OS). Color bar: 20-180 μm. Scale bar is 1.0mm on the retina.

Smooth maps (Figs. 9 –11 ) corresponding to the clustered maps (Figs. 6–8) were generated using the Matlab® gridfit function. Figure 9 depicts the birefringence or DPPR/UD (°/μm) maps. Figure 10 depicts the RNFL thickness (μm) maps. Figure 11 depicts DPPR maps (°).

Fig. 9.

Birefringence or DPPR/UD (°/μm) maps with superimposed blood vessels detected from fundus-like raster scans. (a) Right eye (OD) and (b) left eye (OS). Color bar: 0.05°/μm (Δn = 7.35·10⁻⁵) – 0.35°/μm (Δn = 5.16·10⁻⁴). Scale bar is 1.0mm on the retina.

Fig. 11.

DPPR (°) maps with superimposed blood vessels detected from raster scan. (a) Right eye (OD) and (b) left eye (OS). Color bar: 0° – 48°. Scale bar is 1.0mm on the retina.

Fig. 10.

Retinal nerve fiber layer thickness (RNFLT, μm) maps with superimposed blood vessels detected from fundus-like raster scans. (a) Right eye (OD) and (b) left eye (OS). Color bar: 20 μm – 180 μm. Scale bar is 1.0mm on the retina.

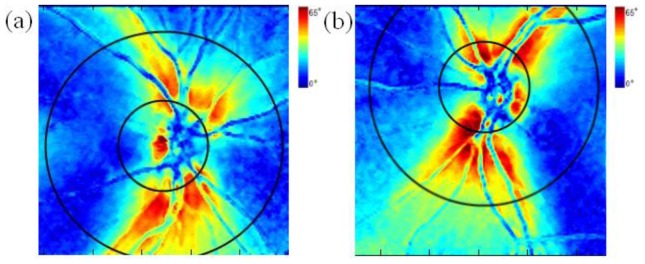
Phase retardation maps recorded using the commercial scanning laser polarimeter (Fig. 12 ) depicts overlaid rings corresponding to the region of interest where the SS-PS-OCT measurements were acquired. Maximum phase retardations in phase maps recorded by SS-PS-OCT and scanning laser polarimetry are selected so that maximum path length difference (corresponding to birefringent phase delay) is equivalent. The maximum value in the color bar of Fig. 12 (65°) corresponds to the maximum value in the color bar of Fig. 11 (48°) multiplied by the center wavelength of the SS-PS-OCT system (1060 nm) divided by center wavelength of the scanning laser polarimetry instrument (780 nm).

Fig. 12.

DPPR maps obtained from GDx-VCC with superimposed rings corresponding to the SS-PS-OCT clustered scan region. (a) Right eye (OD) and (b) left eye (OS). Color bar: 0° – 65°.

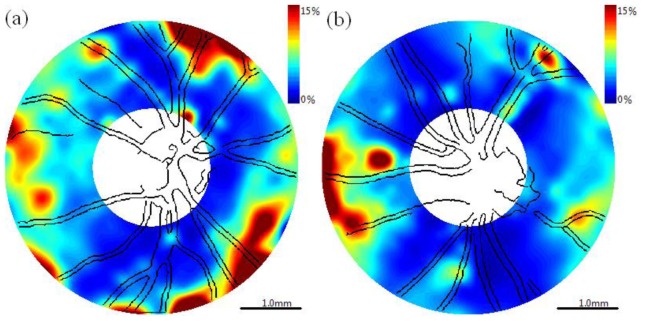
Percent uncertainty of DPPR/UD values determined for SS-PS-OCT images (Fig. 13 ) suggest that regions with low uncertainty correlate with thicker RNFL regions with higher phase retardation. DPPR/UD uncertainty maps can also help identify clusters with unreliable fits.

Fig. 13.

DPPR/UD uncertainty maps with superimposed blood vessels detected from raster scan. (a) Right eye (OD) and (b) left eye (OS). Color bar: 0% – 15%.

4. Discussion

Polarization mode dispersion (PMD) has been investigated extensively in optical telecommunications [14]. In single-mode fiber (SMF), core ellipticity, noncircular symmetric stresses, and tight bends give rise to random birefringence and the two orthogonal polarization states, in the presence of PMD, travel through fiber at different speeds. This differential phase delay and differential group delay can cause a broadening of the OCT point spread function. Higher orders of PMD can degrade performance of PS-OCT systems. Fiber length of the SS-PS-OCT signal interferometer reported here was kept to less than 3 meters, and routed in a 10 inch diameter circular-shaped polyvinyl chloride track. The construction and packaging of the PS-OCT signal interferometer helped minimize deleterious PMD effects.

Many factors can contribute to errors in birefringence and phase retardation measurements. Anterior RNFL boundary has a sharp edge and is easy to detect automatically unlike the posterior boundary. Variations in detected posterior boundary can significantly influence measured birefringence and phase retardation especially in the presence of blood vessels. If detected posterior boundary is too deep (overestimated), blood vessels may be included in measurement which increases birefringence fitting error. Blood vessels introduce an optical phase shift and degrade SNR. If detected posterior boundary is too shallow, the number of axial data points is too small and may result in high uncertainty and potentially missing RNFL tissue underneath blood vessels. Thresholds for the boundary detection algorithm were selected so that the posterior RNFL boundary is at the top of the blood vessel when large blood vessels are present, but includes the whole RNFL when no blood vessel or only small blood vessels are present. Another important factor is system axial resolution (about 12 μm in the retinal nerve fiber layer). Better axial resolution can lead to more accurate measurements. Uncertainty in the group refractive index of the RNFL (assumed to be n = 1.38) alone can introduce up to a 4% error.

DPPR measurements recorded with the SS-PS-OCT system are similar in magnitude and spatial extent with the DPPR measurements made with the commercial scanning laser polarimeter. In images recorded by both instruments, amplitude of the phase retardation is highest in the superior and inferior bundles where the major retinal arteries exit the optic nerve head. Retinal arteries provide a good landmark to register the images. Inasmuch as the marginal cost of adding polarization sensitivity to standard ophthalmologic OCT instrumentation is relatively low, PS-OCT may provide some clinical advantages compared to purchase and operation of two distinct OCT and scanning laser polarimetry instruments.

Polarimetric OCT imaging at 840 nm may have certain advantages over 1060 nm since phase retardation measurement for the same birefringent specimen is about 26% greater at 840 nm (1060/840 ≈1.26). Greater phase retardation may give higher PSNR and more accurate birefringence measurements. A number of groups have reported RNFL birefringence measurements at 840nm [27–29]. Mujat et al reported RNFL birefringence measurements in a normal eye at 840nm with a peak-to-valley variation of Δn = 4.5⋅10⁻⁴ – 1.75⋅10⁻⁴. Yamanari et al reported RNFL birefringence measurements in a normal eye at 840nm with a peak-to-valley DPPR/UD variation of 0.5 – 0.15 °/μm. Gotzinger et al reported RNFL birefringence measurements in a normal eye at 840nm with a peak-to-valley SPPR/UD variation of 0.11 – 0.02 °/μm. Results here suggest that peak-to-valley RNFL birefringence variation is Δn = 4.71⋅10⁻⁴ – 2.94⋅10⁻⁴. Peak-to-valley RNFL birefringence variation for each reported study is given in Table 1 .

Table 1. Peak-to-Valley RNFL Birefringence Variation.

Author (Year)	λ      (nm)	Δn      (Superior-Inferior)	Δn      (Nasal-Temporal)	Variation
Mujat (2007)	840	4.5⋅10−4	1.75⋅10−4	2.75⋅10−4
Yamanari (2008)	840	5.83⋅10−4	1.75⋅10−4	4.08⋅10−4
Gotzinger (2008)	840	2.57⋅10−4	0.47⋅10−4	2.1⋅10−4
Present	1060	4.71⋅10−4	2.94⋅10−4	1.77⋅10−4

Inasmuch as form birefringence is dependent on the refractive indices of the constituents (i.e., water and protein), wavelength variation of Δn is expected to be small. For example, refractive index variation of water between 840nm and 1060nm is 0.002. RNFL birefringence in the superior-inferior region given here is most similar to values reported by Mujat et al. RNFL birefringence in the nasal-temporal region given here (Δn = 2.94⋅10⁻⁴) are substantially greater than values given in Table 1 at 840nm. For example, compared to Mujat and Yamanari, birefringence in the nasal and temporal region given here is 68% greater. Inspecting DPPR/UD uncertainty maps (Fig. 13) suggests that the discrepancy is not due to the multiple-state nonlinear fitting algorithm. Relative uncertainty in birefringence in most regions is less than 8%. Moreover, visual inspection of arc-fits on the Poincare sphere in the nasal and temporal regions further supports our confidence in the reliability of the multiple-state nonlinear fitting algorithm. Further studies are required to investigate differences in computed birefringence values in thin RNFL regions determined using the multiple-state nonlinear fitting algorithm and other computational approaches.

5. Conclusion

We constructed a high sensitivity swept source polarization sensitive optical coherence tomography (SS-PS-OCT) system operating at 1 micron to obtain thickness, birefringence, and phase retardation measurements of the RNFL about the optic nerve head in healthy individuals. Double pass phase retardation (DPPR) measurements of a 150 μm thick turbid birefringent film gave a birefringence of $\Delta n=7.48\cdot {10}^{-4}$ consistent with values reported previously. Application of a multiple-state nonlinear fitting algorithm suggests that RNFL birefringence maps in healthy individuals may be determined with an uncertainty less that 15%. Maps of RNFL phase retardation in a subject measured with SS-PS-OCT compare well with those generated using a commercial scanning laser polarimetry instrument. Peak-to-valley variation of RNFL birefringence given here is less than values previously reported at 840nm. Notably, RNFL birefringence in the nasal-temporal region given here is greater than previously reported values at 840nm.