Number-Space Mapping in Human Infants

Abstract

Mature representations of number are built on a core system of numerical representation that connects to spatial representations in the form of a mental number line. The core number system is functional in early infancy, but little is known about the origins of the mapping of numbers onto space. In this article, we show that preverbal infants transfer the discrimination of an ordered series of numerosities to the discrimination of an ordered series of line lengths. Moreover, infants construct relationships between numbers and line-lengths when they are habituated to unordered pairings that vary positively, but not when they are habituated to unordered pairings that vary inversely. These findings provide evidence that a predisposition to relate representations of numerical magnitude to spatial length develops early in life. A central foundation of mathematics, science, and technology therefore emerges prior to experience with language, symbol systems, or measurement devices.

The mapping of number to space is fundamental to measurement, mathematics, and science, and is evident whenever processing of number occurs (de Hevia, Vallar, & Girelli, 2008; Hubbard, Piazza, & Pinel, 2005). In adults, this mapping takes the form of a mental number line: an analogue continuum in which numerical magnitude is represented along an oriented axis (Dehaene, 1992; Restle, 1970). Number lines appear to be universal across humans, although there is cultural variability in their direction (oriented left to right in most Western cultures; Dehaene, Bossini, & Giraux, 1993) and spacing (typically equal intervals for Western adults, but logarithmically spaced intervals for children and adults who reside in remote communities and lack formal education; Dehaene, Izard, Spelke, & Pica, 2008; Siegler & Opfer, 2003). Number lines are activated even when adults perform a task with no numerical relevance, and this activation enhances their responses to number stimuli whose values accord with the spatial position of the response (the SNARC, Spatial Numerical Association of Response Codes, effect; Dehaene et al., 1993).

Although adults’ numerical and spatial representations build on systems of number and geometry that are functional in early infancy (Brannon, 2002; Newcombe & Huttenlocher, 2000; Xu & Spelke, 2000), little is known about the developmental origins of the capacity to relate these representations to one another. Some evidence suggests that number-space mappings develop through the acquisition of culture-specific skills and formal education: Children show evidence of an oriented (e.g., left-to-right) number line only some years after they begin schooling (Berch, Foley, Hill, & Ryan, 1999; van Galen & Reitsma, 2008), and the orientation of this representation is modulated by the orientation of the culture’s writing system (Zebian, 2005). Nevertheless, humans may be predisposed to treat space and number as intrinsically related. Adults with little or no formal education map numbers onto space when asked to place quantities on a horizontal line, revealing that their internal organization of magnitude includes a relationship to space (Dehaene et al., 2008; though see Cantlon, Cordes, Libertus, & Brannon, 2009; Dehaene, Izard, Pica, & Spelke, 2009). Moreover, Western preschool children spontaneously map numbers onto space when presented with a visuospatial task (de Hevia & Spelke, 2009), and they even display an intuition of the left-to-right organization of numerical magnitude that is favored in Western culture (Opfer, Thompson, & Furlong, in press).

We hypothesized that the number-space connection originates in an early-developing predisposition to relate these two dimensions. We tested this hypothesis by using three methods to assess 8-month-old infants’ responses to numerical and spatial magnitudes.

Experiment 1

The first experiment used a habituation/novelty preference method to probe infants’ sensitivity to relationships between sequences of increasing or decreasing numbers (presented as visuospatial arrays) and sequences of increasing or decreasing lengths (presented as horizontal lines). First, infants were habituated to repeating sequences of arrays of visual elements that successively doubled or halved in number (from 4 to 64 or the reverse), while the nonnumerical properties of item size, array size, and envelope size were controlled. Density was allowed to vary with number during habituation, as this cue was absent at test. The spatial lengths therefore were not related to any spatial properties of the numerical displays. After the time infants spent looking at the numerical sequences declined, infants were presented with the test, which consisted of alternating trials in which sequences of horizontal lines successively doubled or halved in length (Fig. 1a). If infants naturally map representations of number to space, they should detect the direction of magnitude change in both numerical and spatial dimensions and generalize habituation from sequences with increasing numbers to sequences with increasing lengths, or from sequences with decreasing numbers to sequences with decreasing lengths.

Fig. 1.

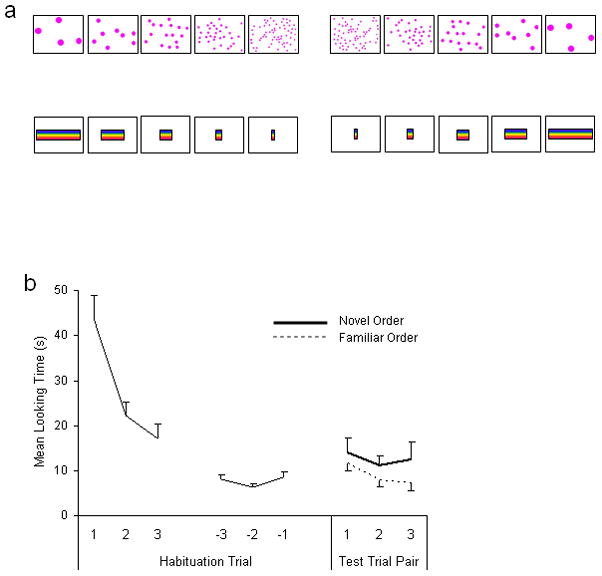
Infants’ generalization of habituation from increasing number to increasing length or from decreasing number to decreasing length. The illustrations in (a) show the numerical and line displays presented in Experiment 1. The examples include the numerical displays used during habituation (top) and the arrays of line lengths used during testing (bottom); sequences of increasing magnitude are shown on the left, and sequences of decreasing magnitude are shown on the right. The graph (b) shows mean looking times for the first three and last three habituation trials and for the test trials, which varied in whether novel or familiar orderings of lengths were displayed. Error bars represent standard errors of the mean.

Method

Participants

Participants were 24 full-term infants (13 female and 11 male; mean age = 8 months, range: 7 months 16 days to 8 months 15 days). Fifteen other infants were eliminated because of crying (8), experimenter error (3), equipment failure (2), or test-trial looking times more than 3 standard deviations from the overall group mean (2).¹

Materials

Numerical displays were composed of colored circles, squares, or equilateral triangles. For each trial, only one type of figure and one color were presented. The summed area occupied by the figures and the total envelope area were controlled because these continuous variables could serve to relate the numerical displays to the line displays. Summed area was equated across displays by varying item size inversely to number: For arrays of 4, 8, 16, 32, and 64, respectively, circle diameters were 3.8°, 2.7°, 1.9°, 1.3°, and 0.9° visual angle; square sides were 3.4°, 2.4°, 1.7°, 1.2°, and 0.8° visual angle; and triangle sides were 4.8°, 3.4°, 2.4°, 1.7°, and 1.2° visual angle. We held envelope area constant across displays by positioning items randomly within a fixed area. Test displays consisted of centrally positioned rainbow-colored rectangles of constant height (1.2° visual angle) and varying length (1.3°, 2.7°, 5.3°, 10.5°, and 20.4° visual angle). These rectangles changed symmetrically in five successive steps by either doubling or halving.

Each numerical trial consisted of a repeating cycle (9 s in total) that began with the image of a dog moving while noise was played (1,000 ms). Following a blank screen (500 ms), a series of five numerical displays (1,200 ms each) was presented. Each numerical display was followed by a blank screen (300 ms; total sequence length = 7,500 ms). Line-length trials were identical to the numerical trials, except that the displays consisted of the line lengths.

Design

Prior to the habituation trials, infants were familiarized with both increasing and decreasing line lengths, in order to avoid a general novelty response during the test trials due to the introduction of displays with new colors and shapes. During this phase, all infants were presented with two familiarization trials showing the same increasing and decreasing line lengths that would be presented later at test. Half of the infants were then randomly assigned to each of the two habituation conditions: They were habituated to either an ascending numerical sequence (ascending condition) or a descending numerical sequence (descending condition). The order of the two familiarization trials (increasing vs. decreasing sequences) and of the test trials (familiar first vs. novel first) was counterbalanced across infants within each habituation group.

Procedure

Infants were seated on a parent’s lap in a softly illuminated room and faced a screen surrounded by black surfaces and curtains. Parents were instructed to refrain from interacting with their infants and to close their eyes during the test sequences. A video camera below the screen was directed at the infant’s face, and a second video camera (display camera) was placed behind the infant to record the displays. The footage from the two video cameras was sent to a TV monitor and a VCR in a separate room, where one or two observers recorded the infant’s looking times. During this coding process, the display footage was occluded to ensure that the observer was blind to the habituation and test conditions. For each infant, two observers coded the data live or from videotape; average intercoder reliability was 91%.

At the beginning of each trial, a black occluder was lifted to reveal a white screen (57 cm× 48 cm) on which images were projected from behind; the total display area measured 21.4°× 25.4° of visual angle at a viewing distance of about 60 cm. First, infants were presented with two familiarization trials; on each trial, one of the two line-length (test) displays was visible until the infant had looked for 20 s. For the habituation and test trials, each display remained visible until the infant looked for at least 0.5 s, and ended when the infant looked away for 2 s continuously (or looked for a maximum of 120 s). Habituation trials continued until the infant either received 14 trials or reached the criterion of a 50% decline in looking time across 3 consecutive trials relative to the total looking time on the first 3 consecutive trials that had summed to at least 12 s. If an infant did not meet this criterion after the minimum possible 6 trials, the displays were cycled in the same order until habituation was achieved or the 14-trial limit was reached. Following habituation, all infants were shown 6 trials in which the two test displays appeared in alternation.

Analyses

Infants’ looking times during test trials were submitted to an analysis of variance (ANOVA) with habituation condition (increasing vs. decreasing) and test order (familiar first vs. second) as between-subjects variables, and test-trial type (familiar vs. novel) as a within-subjects variable. All other tests were two-tailed.

Results and discussion

Infants spent more time looking at the test trials with the novel (reversed) ordering of lines (12.7 s), relative both to the test trials with the familiar (congruent) ordering of lines (8.9 s), t(23) = 2.37, p = .03, d = 0.52, and to the final three habituation trials, t(23) = 2.65, p = .01 (Fig. 1b). This novelty preference was shown by 18 of the 24 infants (sign test: z = 2.24, p = .02; Wilcoxon signed-rank test: z = 2.48, p = .01) and influenced infants’ test-trial preferences, F(1, 20) = 4.65, p = .04, η_p² = .19, independently of the ordering of numbers presented during habituation (F < 1, n.s.). No other effects or interactions were significant. Infants therefore generalized their habituation to an increment or decrement in number to an increment or decrement in length, respectively.

Because the first experiment presented numbers and lines that halved or doubled repeatedly in a predictable order, it is possible that these sequences called infants’ attention to the numerical and spatial orderings, yielding an amodal transfer of ordinal meaning from one dimension to the other. We conducted Experiment 2 in an attempt to replicate and extend the findings from Experiment 1 under conditions that precluded such ordinal transfer. We tested whether infants would learn a specific, positive relationship between numbers and lengths and generalize the relationship to new numerical and spatial values.

Experiment 2

Infants viewed a series of familiarization displays in a quasi-random, unordered sequence. Each display comprised an array of visual elements (e.g., dots) above a horizontal line. Across trials, the dots varied in number and the line varied in length such that longer lines accompanied greater numbers of dots. Following familiarization, infants were shown two test trials presenting sequences with new numbers and line lengths that were paired either positively (as in familiarization) or inversely (e.g., shorter lines accompanying greater numbers of dots; Fig. 2a). To ensure that infants learned relations between lengths and numbers rather than between lengths and item sizes, array sizes, or filled display area, we controlled these spatial variables (as described in the Materials section). If infants extracted the rule that higher number was related to increasing line length (positive relationship), they should have applied that rule to the test exemplars and should have displayed a preference for new pairings conforming to the extracted rule over new pairings that did not conform to the rule. This preference would be expected despite the absence of any correlated spatial variable common to the familiarization and test displays.

Fig. 2.

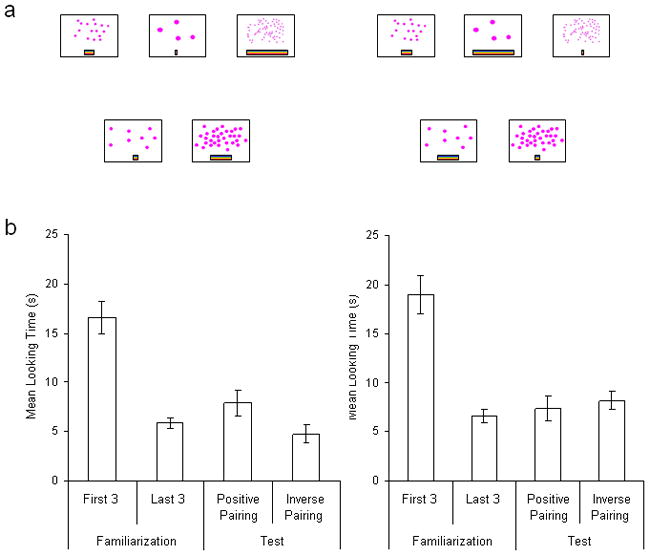
Infants’ learning of positive versus inverse relationships of number to length. The illustrations (a) show the displays presented in Experiments 2 and 3. The examples include numerical and line pairings used during familiarization (top) and test (bottom). Positive pairings are shown on the left, and inverse pairings on the right. The graph (b) shows mean looking times for the first three and last three familiarization trials and for the two kinds of test trials (positive and inverse pairings). Results are shown separately for Experiment 2 (left) and Experiment 3 (right). Error bars represent standard errors of the mean.

Method

Participants

Participants were 20 infants (5 female and 15 male; mean age = 8 months 3 days, range: 7 months 18 days to 8 months 19 days). Twelve other infants were eliminated because of crying (5), parental interference (2), or test-trial looking times more than 3 standard deviations from the overall group mean (5).

Materials

The familiarization displays were made by combining three of the lines and three of the element arrays used in Experiment 1: the displays corresponding to the largest (64), smallest (4), and middle (16) numerical values. In the numerical arrays, the total overall area of the visual elements was kept constant across numerosities, at half the size of the elements in Experiment 1. Summed area was equated across arrays by varying item size inversely to number; number was therefore correlated with item size during familiarization.

To ensure that infants responded to number, we changed the spatial properties of the numerical displays between familiarization and test. In the test displays, dot size was the same for all array sizes; number therefore was correlated only with summed area, a dimension that did not covary with length during familiarization. The test displays consisted of the remaining lines and array numerosities used in Experiment 1: an array of 8 dots and an array of 32 dots each paired with a line 2.7° long or with a line 10.5° long. The dots were altered to keep their size constant (i.e., the dots’ diameters for numerosities 8 and 32 was 1.3° visual angle). Therefore, the numerical and spatial values presented during test were novel but lay within the range of the values presented during familiarization.

For each familiarization trial, three different images for each number-line pairing were presented in a pseudorandom order, so that consecutive numerosities did not follow any predictable order (e.g., 16, 64, 4, 16, 4, 64, 16, 4, 64). For each test trial, three different images for each of the two number-line pairings were presented in alternation, starting with 8 (i.e., 8, 32, 8, 32, 8, 32). The positions of the elements varied across trials. Each familiarization trial and test trial consisted of a repeating cycle: A numerical array, centered in the upper half of the screen (1,000 ms), was subsequently joined by a line centered on the lower half of the screen (1,000 ms); this stimulus was followed by a blank screen (500 ms) and then the next display. Each cycle lasted 22.5 s during familiarization and 15 s during the test; cycles were looped until the end of each trial.

Design

Infants were familiarized with the number-line pairings that were positively related, and then were tested with the positive and inverse number-length pairings. Half the infants were tested on the positive pairings first, and the other half were tested on the inverse pairings first.

Procedure and analyses

Once the infants were seated, the familiarization trials began, following the same procedure as in Experiment 1. After familiarization, all infants were given two test trials. For 19 of the 20 infants, two observers coded the data live or from videotape; average intercoder reliability was 95%. Test-trial looking times were submitted to an ANOVA with trial order (positive vs. inverse pairing first) as the between-subjects variable and trial type (positive vs. inverse pairing) as the within-subjects variable. All other tests were two-tailed.

Results and discussion

Infants received an average of 8.3 familiarization trials, exhibiting habituation from the first 3 trials (16.6 s) to the last 3 trials (5.9 s), t(19) = 7.8, p < .0001. Relative to their performance in the last 3 familiarization trials, infants showed no dishabituation to the positive, t(19) = −1.51, n.s., or inverse, t(19) = 1.28, n.s., test displays. Nevertheless, infants looked longer at the positive test display (7.9 s) than at the inverse test display (4.8 s), t(19) = 3.12, p = .005, d = 0.77 (Fig. 2b). This effect was found in 15 of the 20 infants (1 infant looked equally to the two kinds of test displays and 4 looked longer at the inverse pairing; sign test: z = 2.29, p = .02; Wilcoxon signed-rank test: z = 2.77, p = .005,) and was the only tested variable that affected looking times, F(1, 18) = 9.48, p = .006, η_p² = .34.

These findings provide evidence that infants learned the number-length relationship in the familiarization displays and generalized this relationship to the new numbers and lengths in the test displays. Because all the spatial variables that can covary with number in visual arrays were equated either in the familiarization displays or in the test displays, infants’ generalization must have depended on abstraction of a relationship between line length and element number. Thus, infants were sensitive to the positive number-length mapping.

Experiment 3

Experiment 2 revealed that infants detect a positive relationship between number and length, but it does not indicate whether this relationship is favored over an equally consistent inverse relationship. From birth, infants are able to learn arbitrary relationships between events (Fiser & Aslin, 2002; Siqueland & Delucia, 1969). Thus, Experiment 3 used the same method and displays as in Experiment 2, except that numbers and lengths were inversely related during familiarization, with longer lines accompanying smaller numbers of visual elements (Fig. 2a).

Method

The method was the same as in Experiment 2, except as follows. Participants were 20 infants (8 female and 12 male; mean age = 8 months 2 days, range: 7 months 17 days to 8 months 26 days). Nine other infants were eliminated because of crying (6), parental interference (1), or excessive test-trial looking times (2). The familiarization arrays from Experiment 2 were presented in a consistent inverse relationship, such that the shortest line accompanied the largest numerosity. For 18 of the 20 infants, two observers coded the data live or from videotape; average intercoder reliability was 95%.

Results and discussion

Infants received an average of 7.9 familiarization trials and exhibited habituation from the first 3 trials (19 s) to the last 3 trials (6.6 s), t(19) = 7.5, p < .0001. Again, no dishabituation effects were observed for the new displays showing the positive pairing, t(19) < 1, n.s., or for the test displays showing the inverse pairing, t(19) = −1.24, n.s., relative to the familiarization displays. Infants also showed no preference between the test displays with positive pairings (7.4 s) and the test displays with inverse pairings (8.2 s), t(19) = −0.55, n.s. (Fig. 2b). The rule-congruent preference was shown by only 11 of the 20 infants (1 infant looked equally to the two kinds of test displays and 8 preferred to look at the displays with positive pairings; sign test: z = 0.45, n.s.; Wilcoxon signed-rank test: z = 0.56, n.s.), and did not affect infants’ test-trial looking times (F < 1). Thus, infants did not generalize the inverse mapping between number and length to the new test displays.

Further analyses compared infants’ looking patterns across Experiments 2 and 3. Infants showed similar looking times on the first three and last three familiarization trials across the two experiments, each t(38) < 1, n.s., and they reached the habituation criterion after similar numbers of trials, t(38) < 1, n.s. In contrast, on the test trials, the interaction between experiment and test display (positive vs. inverse pairing) was significant, F(1, 38) = 5.03, p = .03, η_p² = .12. Looking times for the positive test pairing in Experiment 2 (7.9 s) were comparable to those for both the positive and the inverse pairings in Experiment 3 (7.4 and 8.2 s, each t < 1, n.s.).

Might infants have a baseline preference for positive number-length pairings? Such a preference could have masked their successful learning of the inverse relation and boosted their apparently successful learning of the positive relation.² The final experiment tested for this possibility.

Experiment 4

Method

Participants were 20 infants (11 female and 9 male; mean age = 8 months 6 days, range: 7 months 16 days to 8 months 21 days). Three additional infants were excluded for excessive looking. The method was the same as in Experiments 2 and 3 except that no familiarization sequences were presented, and the two test displays appeared three times in alternation for a total of six test trials. Looking times were analyzed by an ANOVA with test-trial pair (first, second, or third pair) and test display (positive vs. inverse pairing) as within-subjects variables and test order (positive pairing first vs. second) as a between-subjects variable. Additional ANOVAs and two-tailed t tests compared looking patterns across Experiments 2 through 4.

Results

Infants looked longer at positive pairings than at the inverse pairings, F(1, 18) = 12.95, p = .002, η_p² = .32, but this effect was complicated by a significant three-way Test-Trial Pair × Test Display × Test Order interaction, F(2, 36) = 8.61, p < .001, η_p² = .32. Least significant difference post hoc tests revealed a preference for the positive pairings over the inverse pairings only on the first trial pair among infants who received the positive pairing first (p < .0001; all other ps > .13). Thus, infants looked longest on the first trial and at the positive pairings.

Next, we compared the average percentage of looking time for the positive pairings (i.e., the percentage of time infants spent looking at the positive pairing out of all time spent looking at test pairings) in Experiment 4 (baseline) with the average percentage of looking time for the positive pairings in Experiments 2 and 3. Because of the order effect, we conducted a separate one-way ANOVA for each test-trial pair in Experiment 4. The difference in looking preferences across experiments was only marginally significant in the analysis for the first test-trial pair in Experiment 4, F(2, 57) = 2.84, p = .06, η_p² = .09, but was reliable in the analysis for the second test pair, F(2, 57) = 3.14, p = .05, η_p² = .10, and the third test pair, F(2, 57) = 3.87, p = .02, η_p² = .12. Looking preferences in Experiment 2 differed significantly from those for the third test pair of the baseline experiment, t(38) = 2.59, p = .01. Looking preferences in Experiment 3 did not differ from looking preferences in the baseline experiment on any test-trial pair (all ps > .14; Fig. 3).

Fig. 3.

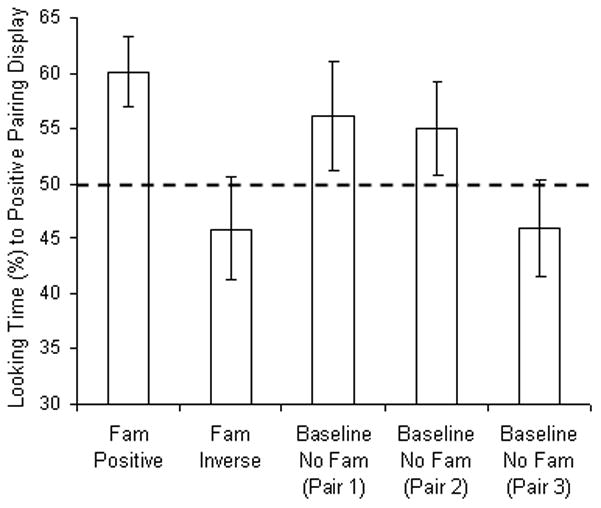
Percentage of looking time for positive pairings among infants familiarized to the positive rule (Experiment 2), familiarized to the inverse rule (Experiment 3), and tested without familiarization on three pairs of trials (Experiment 4, the baseline).

Discussion

Experiment 4 revealed that infants have an intrinsic preference for positive pairings over inverse pairings of numbers and lengths. Nevertheless, this preference does not account for either the positive findings of Experiment 2 or the negative findings of Experiment 3. When infants saw positive and inverse mappings without previous familiarization to any pairing, they showed significantly less preference for the positive pairing (once the long looking times observed in the early test trials had diminished) than did infants in Experiment 2. This result indicates that the infants in Experiment 2 showed successful learning and generalization of the positive pairing between numbers and lengths. Moreover, the looking preferences of infants in Experiment 4 (baseline) never differed from those of the infants in Experiment 3, who were given the opportunity to learn the negative pairing. Infants therefore learned to relate numbers to lengths when they varied positively, but not when they varied inversely.

General Discussion

Human infants are sensitive to relationships between number and length, and they manifested this sensitivity in three ways in our experiments. First, infants generalized from an increasing (or decreasing) sequence of numbers to an increasing (or decreasing) sequence of line lengths. Second, infants abstracted a specific positive relationship (but not an inverse relationship) between number and length from a small number of examples, and they generalized this relationship to new values. Third, infants showed an intrinsic preference for numbers and lengths that were positively related rather than inversely related.

These abilities were revealed through three contrasting patterns of looking time. When infants were habituated to an increasing or decreasing sequence of numbers, their interest in the sequence declined, so that they exhibited shorter looking times at new line lengths that exhibited the same ordinal change (Experiment 1). When infants were allowed to learn a specific relation between number and length from a few randomly ordered examples, they generalized the relation to new examples and showed heightened interest in new numbers and lengths that exhibited the same relation (Experiment 2). Finally, when infants were presented with numbers and lengths without previous familiarization, they spent more time looking at positive pairings than at inverse pairings (Experiment 4). All three tendencies reflect (and likely enhance) infants’ predisposition to relate number to space in a productive way.

An ongoing controversy concerns the mechanisms of number-space mappings: Do these mappings reflect the intrinsic cognitive architecture of numerical and spatial representations (Dehaene et al., 2008, 2009) or domain-general processes of analogical reasoning (Cantlon et al., 2009)? Adults can use space to represent similarity relations among nonnumerical entities such as faces or colors (Munsell, 1912; Shepard, 1987; Valentine, 1991; see Stevens & Marks, 1965); it is possible that infants also can map spatial variables to a variety of entities. Nevertheless, infants’ mapping of number to space has a specific direction: Infants who viewed an increasing sequence of numbers related that series to a sequence of lengths that increased rather than decreased (Experiment 1), and infants who were exposed to randomly ordered number-length pairings learned the pairing rule when greater numbers accompanied longer lengths (Experiment 2), but not when they accompanied shorter lengths (Experiment 3). Thus, the ability to relate representations of number and space has a privileged structure, with larger numbers corresponding to greater horizontal lengths for infants, as for adults (de Hevia, Girelli, Bricolo, & Vallar, 2008; Restle, 1970). Nevertheless, it is possible that infants would be able to learn an inverse mapping if they were given longer or more varied exposure to the mapping.

Although important aspects of the number-space relation are modulated by experience and education (Dehaene et al., 1993, 2008; Siegler & Opfer, 2003; Zebian, 2005), the present findings reveal that the human brain is predisposed to treat number and space as related. Human infants form and use relationships between number and space prior to the acquisition of language and counting, and prior to encounters with visual symbols, rulers, or other measurement devices. Mathematics, science, and technology therefore build in part on a cognitive propensity with deep roots in human development.