Abstract
Children take years to learn symbolic arithmetic. Nevertheless, non-human animals, human adults with no formal education, and human infants represent approximate number in arrays of objects and sequences of events, and they use these capacities to perform approximate addition and subtraction. Do children harness these abilities when they begin to learn school mathematics? In 2 experiments in different schools, kindergarten children from diverse backgrounds were tested on their non-symbolic arithmetic abilities during the school year, as well as on their mastery of number words and symbols. Performance of non-symbolic arithmetic predicted children’s mathematics achievement at the end of the school year, independent of achievement in reading or general intelligence. Non-symbolic arithmetic performance was also related to children’s mastery of number words and symbols, which figured prominently in the assessments of mathematics achievement in both schools. Thus, non-symbolic and symbolic numerical abilities are specifically related, in children of diverse socio-economic backgrounds, near the start of mathematics instruction.
Core Numerical Abilities and Learning of School Mathematics
Learning symbolic arithmetic is difficult for most children (Baroody & Dowker, 2003), especially those who are economically disadvantaged (Case, Griffin, & Kelly, 1999; Sirin, 2005). Nevertheless, representations of approximate number are available to adults with no formal education (Pica, Lemer, Izard, & Dehaene, 2004), human infants (McCrink & Wynn, 2004), non-human primates (Flombaum, Junge, & Hauser, 2005), and preschool children (Barth, LaMont, Lipton, & Spelke, 2005), who compare and add non-symbolic numbers with a ratio limit on accuracy (Feigenson, Dehaene, & Spelke, 2004). Children can use these capacities to perform approximate symbolic addition and subtraction prior to learning arithmetic (Gilmore, McCarthy, & Spelke, 2007), but do they harness these abilities when they learn school mathematics?
Recent research has provided mixed evidence concerning the relation of non-symbolic numerical abilities to learning of symbolic arithmetic. On one hand, correlations have been found between the accuracy of performance on a non-symbolic numerical comparison task, presented to students at 14 years of age, and school mathematics performance from kindergarten to sixth grade (Halberda, Mazzocco, & Feigenson, 2008). In contrast, the school mathematics performance of 6- to 7-year-old children was found not to be related to the magnitude of the numerical distance effect exhibited by the children on a comparison task involving non-symbolic numerical displays (Holloway & Ansari, 2009), although such a relation was obtained on a similar comparison task with symbolic numbers in two studies (Holloway & Ansari, 2009; De Smedt, Verschaffel, & Ghesquière, 2009). These divergent findings could stem either from differences in the aspect of non-symbolic number processing assessed in the different studies or from differences in the age at which children’s non-symbolic abilities were tested: Relationships between non-symbolic abilities and formal mathematics may only be observed when non-symbolic abilities are tested in older children, who have had years of experience with symbolic mathematics. Further research is needed to distinguish these possibilities and clarify the relationship between early developing, non-symbolic numerical abilities and learning of school mathematics.
To investigate whether non-symbolic numerical abilities are associated with success at the first steps of school mathematics instruction, we presented a test of non-symbolic numerical ability to 5- to 6-year old children during their first year of school, and related their performance to their mastery of their school’s mathematics curriculum at the end of that year. Our test focused on non-symbolic addition (after Barth et al., 2005; Barth, La Mont, Lipton, Dehaene, Kanwisher, & Spelke, 2006) rather than numerical comparison, for two reasons. First, non-symbolic addition requires not only that children detect and compare numerical magnitudes but that they transform them by means of operations that will stand at the center of their later mathematics curriculum. For this reason, tests assessing children’s non-symbolic arithmetic ability may be more sensitive indicators of the types of numerical ability that could theoretically enhance children’s performance in later years of the school math curriculum. Second, the mathematics curriculum pursued by the children in our sample included considerable work comparing symbolic, small numbers but little work with large numbers and little or no material pertaining to addition (see Appendix). If mastery of this curriculum is associated with performance of large-number non-symbolic arithmetic, it is highly unlikely that such a correlation would stem from extraneous similarities between the tests in these two domains, such as the fact that both focus on operations of comparison (see Holloway & Ansari, 2008). An experiment that correlates large-number non-symbolic addition with mastery of this curriculum therefore provides a strong test of the association between children’s non-symbolic numerical abilities and their mastery of the first steps of school mathematics.
Our experiments addressed further questions concerning the nature of the relationship between non-symbolic addition performance and school mathematics achievement. Children’s performance on the mathematics achievement tests likely is affected by numerous factors, including children’s motivation and attentiveness and their general intelligence as well as their numerical abilities. To investigate the specificity of the relation between non-symbolic numerical abilities and school mathematics, we considered not only children’s achievement in school mathematics but also their achievement in literacy (Experiments 1 and 2) and their verbal intelligence (Experiment 2), and we performed hierarchical regression analyses to investigate whether non-symbolic numerical abilities predicted school mathematics performance after variations in intelligence and literacy achievement were controlled.
When non-symbolic numerical abilities were found to be related specifically to mathematics achievement by this analysis in Experiment 1, further questions were addressed in Experiment 2 concerning the underlying school skills that are associated with non-symbolic performance. The mathematics achievement tests administered in both schools assessed a host of numerical abilities, including the generation and ordering of number words and symbols, the enumeration and comparison of small sets of objects, and the recognition of geometrical forms; variation in any of these abilities might correlate with children’s proficiency at non-symbolic arithmetic. In a preliminary effort to specify further the relation of non-symbolic numerical abilities to mastery of school mathematics, we asked, in Experiment 2, whether children’s non-symbolic arithmetic abilities are related to their mastery of number words and symbols, and whether this relation accounts for the association between non-symbolic numerical abilities and school mathematics achievement.
Finally, we compared the performance of children at a range of socioeconomic levels. Numerous studies (e.g. Griffin & Case, 1996; Jordan, Huttenlocher, & Levine, 1992) have demonstrated an achievement gap in children’s success with school arithmetic: Children from lower socio-economic backgrounds fail to reach the achievement levels of their more advantaged peers. Do these varying achievement levels stem from differences in children’s core numerical abilities, from differences in their mastery of the symbolic number system, or from other factors? We addressed this question in two experiments. In Experiment 1, we compared the non-symbolic abilities and school mathematics performance of a group of children from lower- and middle-economic backgrounds to data on the non-symbolic abilities and school mathematics performance of more advantaged children. In Experiment 2, we compared the non-symbolic abilities, knowledge of verbal numbers and Arabic numerals, verbal IQ, literacy and school mathematics performance of a new sample of children from lower- and middle-economic backgrounds. We also compared the performance of these children on the non-symbolic task and school mathematics test with the performance of a new group of children from a more advantaged socioeconomic background.
Experiment 1
In the first experiment, we presented a group of kindergarten children from a low- to middle-class community with the test of non-symbolic addition developed by Barth et al. (2005) and previously tested on children of the same age, from a middle-to upper-class community. Following Barth et al. (2005) and in accord with past literature using non-symbolic arithmetic tasks on children and adults (e.g., Pica et al., 2004; Barth, Kanwisher & Spelke, 2003; Barth et al., 2006; McCrink, Dehaene & Dehaene-Lambertz, 2007), we measured the accuracy of the performance of this sample of children and compared their accuracy to the previously reported performance of more advantaged children who were tested with the same materials and following the same procedures (Barth et al., 2005). At the end of the school year, the new sample of children was given tests of achievement in mathematics and literacy. To investigate associations between the children’s non-symbolic numerical abilities and their learning of school mathematics, we tested for relationships between their non-symbolic addition performance and their performance on the two school tests. To test for effects of social class on school mathematics achievement, we presented the same test of mathematics achievement to a new group of children from the more advantaged community of the children tested by Barth et al. (2005).
Method
Participants in the main experiment were children attending public kindergarten in a low- to middle-class community in which about 40% of children qualified for economic subsidies (n = 41; mean age = 5.8 years; range = 5.3–6.3 years; 19 males, 22 females). On the basis of their qualification for free and reduced lunch, children were either classified as low-SES (n =19; mean age = 5.8 years; range = 5.3–6.3 years; 8 male) or middle-SES (n =22; mean age = 5.7 years; range = 5.3–6.3 years; 11 male). The experimenter was blind to the income level of the students. Parents of all children provided informed consent to take part.
Participants in the comparison study of non-symbolic addition were children in a middle- to upper-income community (n = 17; mean age = 5.3 years; range = 5.0–5.7 years). Data from these children were previously reported by Barth et al. (2005). Participants in the comparison study of school mathematics achievement were a new group of children drawn from the same higher socio-economic community as Barth et al. (2005) (n = 21; mean age = 6.0 years; range = 5.5–6.3 years).
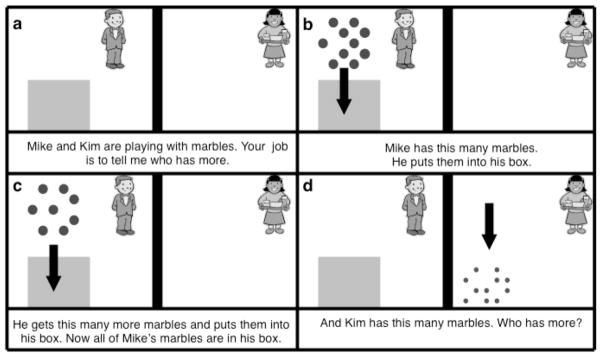
During March of their kindergarten year, participants in the main experiment were given a test previously administered to children in the socio-economically privileged community (Barth et al., 2005), requiring approximate addition of two arrays of dots and comparison of the sum to a third dot array (Figure 1; see video at www.lsri.nottingham.ac.uk/ckg/materials). On each test trial, children saw a computer-animated event, narrated by an accompanying adult, in which arrays of dots appeared and moved behind a screen. After viewing two sets of blue dots that moved in succession behind the screen, children were shown a set of red dots and judged whether the blue or red dots were more numerous. Across trials, the sum and comparison arrays differed by varying ratios (4:5, 4:6, 4:7); each was larger on half the trials. To prevent children from relying on strategies based on continuous quantity variables, dot size, array size, and density were positively correlated with number on half of the trials and negatively correlated with number on the other half. Children completed 24 test problems; the size of the addends and comparison arrays ranged from 5–58 in each array. Children in the main experiment were tested individually by a female experimenter in a quiet area in the school. Children in both the comparison studies were tested individually by a female experimenter in a quiet area in the lab.
Figure 1.
The non-symbolic addition test for a sample problem in Exp. 1.
Following Barth et al., (2005), we measured accuracy at each ratio and computed for each child an overall accuracy score on the test. To test whether children across the achievement spectrum focused on numerical magnitudes in performing this task, we quantified for each child the effect of comparison ratio on children’s performance by calculating the relative increase in accuracy for easy ratios compared to more difficult ratios (ratio 4:7 accuracy - ratio 4:5 accuracy / ratio 4:7 accuracy, following Hollowasy & Ansari, 2009), and then correlated this measure against children’s mathematics achievement.
Two months later, toward the end of the academic year, the school conducted tests of achievement in literacy and mathematics. The mathematics test involved 43 questions assessing children’s counting skills and knowledge of Arabic numerals, as well as elementary geometrical abilities such as halving a circle (see Appendix). Because the kindergarten curriculum included no arithmetic instruction or large numbers, no mathematics test items presented addition problems or numbers as large as those that appeared in the non-symbolic test. The literacy assessment included items examining rhyming, alphabet recognition, letter sounds, high frequency words and hearing and recording sounds in words. Both achievement tests were administered by teachers, who were unaware of children’s earlier performance on the non-symbolic addition task. Children completed the first part of the mathematics test in small groups; the second part of the mathematics test was administered individually, as was the complete test of literacy.
Results and Discussion
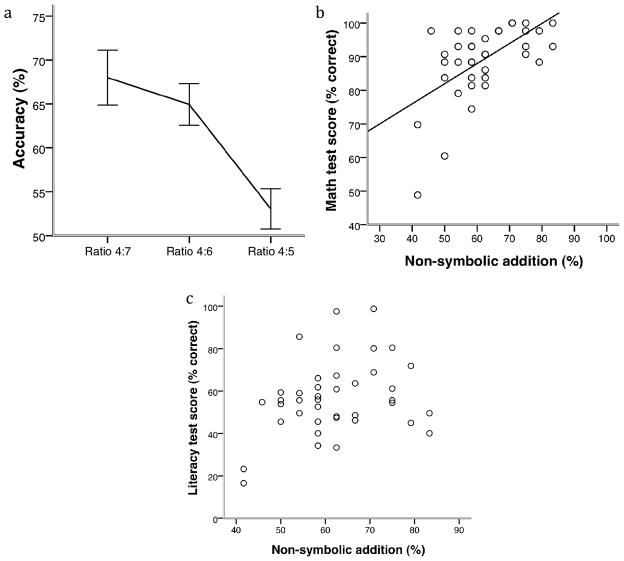
Children in the main experiment succeeded at the non-symbolic addition task (62.0%, chance = 50%, t(40) = 7.20, p < .001), showing the characteristic ratio effect (F(1, 40) = 15.37, p < .001; Figure 2a) and without resort to guessing strategies or reliance on non-numerical properties of the displays (see analyses in the Appendix). There were no effects of gender on this task.
Figure 2.
Performance of the children from the school population in Exp. 1 a) Accuracy on the non-symbolic addition task (error bars represent s.e.m.) b) Correlation between performance on the non-symbolic addition task and on the mathematics achievement test.
The literacy and mathematics test scores also showed no effects of gender and were highly correlated with one another (r = .484, df = 38, p = .002). Nevertheless, children’s performance of non-symbolic addition only correlated significantly with their performance on the mathematics test (r = .587, df = 38, p < .001; Figure 2b), not with their performance on the literacy test (r = .297, df = 38, p = .063; Figure 2c). The correlation with mathematics test performance remained after correction for differences in literacy performance (r = .530, df = 37, p = .001). These findings provide evidence for a specific relationship between non-symbolic numerical abilities and mastery of school mathematics.
A similar relationship was observed, however, when children’s ratio effect scores were considered. Ratio effect scores from the non-symbolic addition task were correlated significantly with performance on the mathematics test (r = .544, df = 38, p < .001; controlling for literacy score r = .406, df = 37, p = .01), raising the possibility that high-achieving children focused on number more than low-achieving children in this task.
Next we compared the performance of the children at different socioeconomic levels. For the test of non-symbolic addition, there was no effect of socioeconomic status on children’s performance, either between two economic subgroups in the school (t(39) < 1) or between the children in this community and those in the more privileged community drawn on in the past research (F(1, 55) = 2.00, p = .164, with age as a covariate). There was no difference in performance on the school mathematics achievement test between the two economic subgroups in the school (t(38)<1). Nevertheless, the group of children drawn from the wealthier community performed better on the mathematics achievement test than their less advantaged peers, (F(1,58) = 5.45, p = .023, with age as covariate; Table 1, top), consistent with the widespread gap in mathematics achievement between wealthy and poor children.
Table 1.
Children’s performance on the school mathematics test and literacy test in each Experiment.
| Experiment | Group | School math test scores (%) | School literacy test scores (raw) | ||
|---|---|---|---|---|---|
| Mean | Range | Mean | Range | ||
| 1 | Low-Mid SES | 89.2 | 48.8 – 100.0 | 185.7 | 54 – 323 |
| High SES | 95.1 | 86.1 – 100.0 | - | - | |
| 2 | Low-Mid SES | 88.4 | 52.0 – 100.0 | 138.2 | 9 – 234 |
| High SES | 91.7 | 84.0 – 98.8 | - | - | |
Although performance of non-symbolic addition and achievement in school mathematics were specifically correlated, the meaning of this correlation is not clear. Like Halberda et al. (2007), we hypothesized that children who performed better at symbolic school mathematics would show greater sensitivity to non-symbolic numerical magnitudes. In the present experiment, however, achievement in school mathematics also was correlated with the magnitude of the ratio effect obtained on the non-symbolic addition task: high achieving children showed a greater ratio effect than low achieving children. This correlation is consistent with a different account of our primary findings: high and low-achieving children may be equally sensitive to number in non-symbolic arrays, but the former children may be more motivated to attend to number in non-symbolic addition tasks.
Nevertheless, interpretation of the correlation between the ratio effect and mathematics achievement is complicated, because children performed at chance on the most difficult ratio that we tested. It is possible that the high-achieving children indeed were more sensitive to non-symbolic numerical magnitudes than the low-achieving children and not simply more motivated to attend to them. Because all children were at chance on the problems testing the most difficult ratio, however, children with greater sensitivity to number also showed a greater ratio effect. In order to distinguish between these possibilities, we conducted a further experiment with a new sample of school children, in which we presented children with non-symbolic addition problems at three ratios that all should elicit above-chance performance.
If non-symbolic numerical abilities are related to children’s learning of symbolic mathematics, why is symbolic arithmetic so hard to learn? Given that non-symbolic numerical abilities were similar for children at different socio-economic levels, moreover, what accounts for the superior mathematics achievement of wealthy children? The findings of a previous experiment (Gilmore et al., 2007), performed on children from the same two communities, provided suggestive answers to both questions. Prior to instruction in arithmetic, kindergarten children from the two communities were given problems in symbolic, approximate addition using the procedures of Experiment 1, but with numbers presented verbally and in Arabic notation. Children succeeded at this task, and their performance showed the same ratio effect as in the present studies, suggesting that they recruited their non-symbolic number knowledge spontaneously to perform symbolic arithmetic. Nevertheless, children in the wealthier community outperformed the less advantaged children on the symbolic arithmetic task, consistent with past research (Griffin & Case, 1996; Jordan et al., 1992). Thus, mastery of symbolic mathematics may have two sources: non-symbolic numerical abilities that are present prior to schooling in arithmetic and exist across a broad economic spectrum, and symbol mastery that is acquired during childhood and is accelerated for advantaged children. The next experiment tests this suggestion further.
The findings of Experiment 1 also raise the question whether, and how children’s non-symbolic numerical abilities contribute to their school mathematics performance. The school mathematics achievement test given to children focused prominently on number word and symbol mastery, but it also included tests of skills outside the numerical domain such as identifying geometric figures or ordering shapes by size. In the next experiment, we investigate further whether non-symbolic numerical abilities specifically relate to kindergarten children’s mastery of symbolic numbers, by separately measuring children’s mastery of number words and Arabic symbols and then testing for relationships between symbol mastery, non-symbolic arithmetic, and performance on a different test of school mathematics.
Experiment 2
In Experiment 2, a new group of kindergarten children from a different low- to middle-class community was given a new test of non-symbolic addition, using easier ratios and presenting problems in a more engaging format. In addition, these children were given tests of verbal number knowledge, Arabic number knowledge, verbal intelligence, as well as school-administered tests, given at the end of the academic year, of achievement in reading and mathematics. We tested for interrelationships among children’s performance on these tasks, and we compared the mathematics performance of these children to that of a new sample of children from the more advantaged community tested in Experiment 1.
Method
Participants were two new groups of kindergarten children. One group (n = 62; mean age = 5.9 years; range = 5.3–6.4 years; 24 males, 38 females) was composed of kindergarten children from a public school in a different lower-middle socioeconomic community. Students on free and reduced lunch were classified as low-SES (n= 16; mean age = 6.0 years; range = 5.3–6.4 years; 10 male) and all other students from the school were classified as middle-SES (n = 46, mean age = 5.9 years; range = 5.3 –6.4 years; 14 male). The second group (n = 21, mean age = 5.8 years; range = 5.5–6.3 years; 12 males, 9 females) were kindergarten children from diverse public and private schools from the same high socioeconomic community as in Experiment 1. Parents of all children provided informed consent to take part.
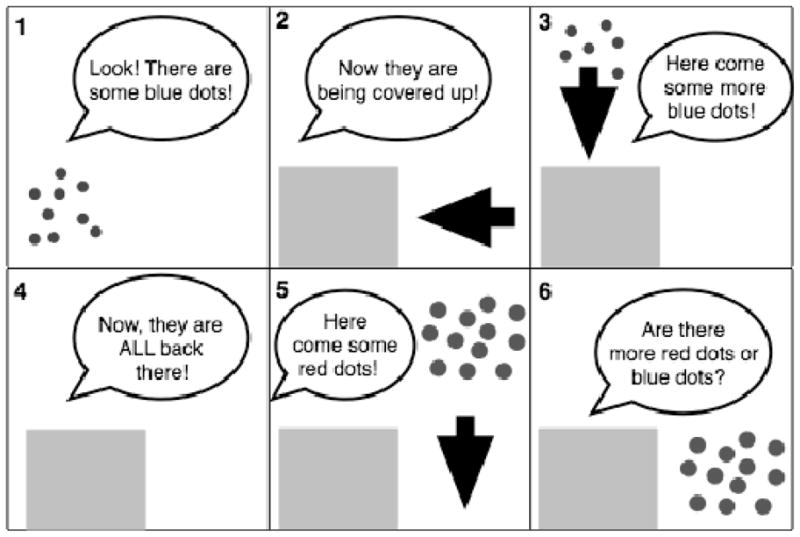
During April and early May of their kindergarten year, children in the less advantaged school community were given a new test of non-symbolic addition (Figure 3; see video at www.lsri.nottingham.ac.uk/ckg/materials), modified from that used in Experiment 1. This test comprised 24 problems where the sum and comparison arrays varied by three new ratios (5:7, 5:8 and 5:9). Verbal number knowledge was assessed by asking children which of two verbally presented numbers was larger (16 trials, half one-digit and half two-digit numbers). Arabic number knowledge was assessed by asking children to name an Arabic numeral shown on the computer screen (16 trials, half one-digit and half two-digit numbers). One-digit and two-digit trials were intermixed and numbers ranged from 1 to 92. Children were tested individually by a female experimenter in a quiet area in the school. In one session children completed the non-symbolic addition task followed by the Arabic numeral test and in a second session they completed the symbolic addition task followed by the verbal number test.
Figure 3.
The non-symbolic addition test for a sample problem in Exp. 2.
Two months later, at the end of the school year, children’s mathematics achievement was assessed using a different mathematics test, administered by teachers who were unaware of students’ performance on the experimental tasks, consisting of 49 questions assessing counting skills, knowledge of Arabic numerals, shapes and coins (see Appendix). All questions involved quantities less than 10. The test was administered by teachers to small groups of children. Teachers also administered the DIBELS standardized literacy test (Good & Kaminski, 2002) and the PPVT-III test of verbal intelligence (Dunn & Dunn, 1997).
The children in the more advantaged community were given the same two tests of non-symbolic addition and of school mathematics performance in a single session in the summer. They were tested individually by a female experimenter in a quiet area in the lab.
Results and Discussion
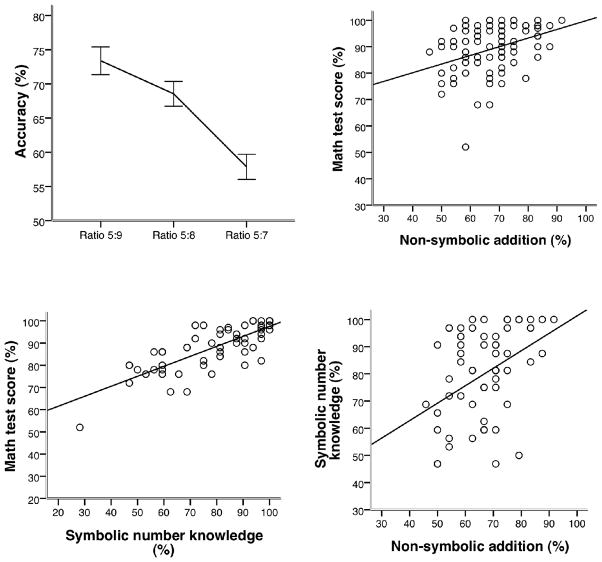
Children in the school population again performed the non-symbolic addition task well above chance (66.6%, t(61) = 12.12, p < .001), with a ratio effect on accuracy (F(1, 61) = 45.80, p < .001; Figure 4a), and without resort to strategies that are alternatives to addition (see analyses in the Appendix). There were no sex differences on this task, or on the tests of mastery of number words and symbols. Children showed knowledge of both number words (mean accuracy = 80.3%, SD = 16.4%) and Arabic numerals (mean accuracy = 79.4%, SD = 22.2%). Most importantly, performance of non-symbolic addition again was correlated with academic achievement in mathematics (r = .376, df = 59, p =. 003; Figure 4b), and the correlation remained after controlling for verbal intelligence and achievement in literacy (r = .276, df = 57, p = .034).
Figure 4.
Children’s performance in Experiment 2. (a) Accuracy on the non-symbolic addition task (error bars represent s.e.m.) (b) Correlation between children’s performance on non-symbolic addition task and scores on the school’s mathematics test (c) Correlation between children’s performance on tests of symbol mastery and performance on the school’s mathematics test. (d) Correlation between children’s performance of non-symbolic addition and performance on tests of symbol mastery.
In contrast to Experiment 1, there was no relationship between children’s ratio effect scores on the non-symbolic addition task and their achievement in mathematics (r = .007, n.s.). Thus, students across the achievement spectrum focused on number in the non-symbolic addition task, and the superior performance of children with high math achievement stemmed from their greater sensitivity to non-symbolic numerical magnitudes. Because the comparison ratios used in Experiment 2 were easier than those in Experiment 1, these findings suggest that the correlation of the ratio effect to school math achievement in Experiment 1 also reflected the greater numerical sensitivity of high-achieving children in that experiment, rather than individual differences in task orientation.
Children’s achievement in mathematics also was associated with their mastery of number words and symbols (respectively, r = .738 and .713, p < .001; combined, r = .788, p < .001, all dfs = 59; Figure 4c), and these correlations also survived correction for verbal intelligence and literacy (combined, r = .505, df = 57, p < .001). Finally, children’s non-symbolic arithmetic performance was correlated with their symbolic number knowledge (respectively, r = .370 and .351, p < .01; combined, r = .391, p = .002, all dfs = 60; Figure 4d), and again this correlation survived correction for verbal intelligence and literacy (combined r = .313, df = 57, p = .016).
To examine the relationship between non-symbolic abilities and school mathematics performance, we performed three hierarchical regression analyses (see Table 2). The first analysis tested whether non-symbolic numerical abilities are associated with school mathematics performance after controlling for both school achievement in literacy and verbal intelligence, and whether mastery of number words and symbols also contributed to school mathematics achievement, above and beyond the effects of non-symbolic numerical abilities. For this analysis, non-symbolic addition, and a combined measure of number word and symbol mastery, were entered into the hierarchical regression analysis after verbal intelligence and school achievement in literacy, in the order in which they arise developmentally. Both these factors were found to contribute to children’s achievement in school mathematics (Table 2, model 1), consistent with the suggestions from our past research (Gilmore et al., 2007).
Table 2.
Hierarchical regression models for children’s performance in Experiment 2.
| Model | DV | Predictor | R2 change | Significance of R2 change |
|---|---|---|---|---|
| 1 | School Mathematics Test | Age | .015 | p = .344 |
| Verbal IQ | 0.227 | p < .001 | ||
| Literacy | 0.323 | p < .001 | ||
| Non-symbolic addition | 0.033 | p = .036 | ||
| Symbolic number knowledge | 0.084 | p < .001 | ||
| 2 | Symbolic number knowledge | Age | .017 | p = .322 |
| Verbal IQ | .237 | p < .001 | ||
| Literacy | .326 | p < .001 | ||
| Non-symbolic addition | .041 | p = .017 | ||
| 3 | School Mathematics Test | Age | .015 | p = .344 |
| Verbal IQ | .227 | p < .001 | ||
| Literacy | .323 | p < .001 | ||
| Symbolic number knowledge | .111 | p < .001 | ||
| Non-symbolic addition | .007 | p = .286 |
Nevertheless, mastery of number symbols cannot be considered as an independent predictor of school mathematics achievement, because at least half the items on the test of achievement in school mathematics focused on these very abilities (see Appendix). In an initial attempt to investigate whether the association between non-symbolic addition performance and school mathematics achievement depended specifically on these items, rather than on children’s mastery of other aspects of the mathematics curriculum such as words for geometric shapes, two further hierarchical regression analyses were performed. First, we asked whether non-symbolic addition performance is specifically related to mastery of number words and symbols, through an analysis in which the combined measure of number symbol mastery replaced school achievement as the predicted variable. For this analysis, non-symbolic addition performance was entered into the hierarchical regression analysis after verbal intelligence and school achievement in literacy. Non-symbolic addition performance strongly predicted number symbol mastery in this analysis (Table 2, model 2), consistent with the hypothesis that individual differences in learning of number symbols underlies the relationship between non-symbolic addition and school achievement.
To test that hypothesis further, a third hierarchical regression analysis was performed, in which number word and symbol mastery was entered first into the analysis before non-symbolic addition performance (but after literacy achievement and verbal intelligence). In this analysis, non-symbolic numerical performance no longer contributed significantly to children’s school mathematics achievement (Table 3, model 3). Children’s non-symbolic numerical abilities therefore appear to contribute to their achievement in mathematics primarily because they are associated with children’s successful learning of number words and symbols, which figures prominently in both the kindergarten mathematics curriculum and the assessments of mathematical learning administered by both schools.
As a preliminary test for socio-economic differences in mathematical ability and achievement, we compared the performance of the two economic subgroups at the school. Within the school population, low- and middle-class children performed equally on the tests of non-symbolic addition, verbal and Arabic number knowledge, and school mathematics achievement (respectively, t(60) = 1.56, p = .124, t(60) = 1.39, p = .168, and t(60) < 1). We next compared performance on the tests of non-symbolic addition and school mathematics achievement in the school population to that of the separate group of children from a high-income community. As in Experiment 1, children in the more advantaged community performed better on the test of mathematics achievement (t(76.9) = 2.06 p =.043; ; Table 1, bottom), but not significantly better than their less advantaged peers on the test of non-symbolic addition (t(81) =1.60, p = .114).
General Discussion
At the start of formal instruction, children’s successful mastery of their school’s mathematics teaching is associated with their performance of non-symbolic, approximate arithmetic. Children who performed better on a test of non-symbolic, large-number addition showed greater mastery of the kindergarten mathematics curriculum, even though that curriculum involved no large numbers or addition. This relationship, obtained in two experiments with different schools and achievement tests, was not a byproduct of general intelligence or academic aptitude but was specific to mathematics. Moreover, this relationship did not reflect high-performing children’s greater tendency to focus on number in the non-symbolic addition task: When tested with ratios that prevented floor effects, children across the achievement spectrum showed an effect of numerical distance on the non-symbolic addition task, providing evidence that they understood the task and performed it by focusing on number. Nevertheless, children with higher achievement in mathematics showed greater abilities to perceive, remember, and operate on non-symbolic numerical magnitudes.
Finally, the hierarchical regression analyses revealed that the influence of non-symbolic approximate arithmetic on school mathematics performance was driven largely by the association of non-symbolic abilities and mastery of number words and symbols, rather than any association of non-symbolic abilities to other aspect of kindergarten mathematics such as recognizing and labeling geometric figures or ordering objects by size. These findings provide the first evidence that children’s non-symbolic number abilities are associated with learning of the symbolic number system at the center of children’s first instruction in school mathematics.
Educated adults perform mental arithmetic, in part, by drawing on non-symbolic representations of approximate numerosity (Dehaene, 1997). Symbolic and non-symbolic number representations share a common neural substrate (Piazza, Pinel, Le Bihan, & Dehaene, 2007) and symbolic arithmetic suffers when non-symbolic numerical abilities are impaired by injury or temporary deactivation of their associated brain regions (Lemer, Dehaene, Spelke, & Cohen, 2003; Cappelletti, Barth, Fregni, Spelke, & Pascual-Leone, 2007). After children have received 8 years of instruction in symbolic mathematics, non-symbolic abilities are correlated with symbolic mathematics assessed many years prior (Halberda et al., 2008). The present experiments extend these findings by revealing a linkage between non-symbolic arithmetic and symbolic mathematics achievement at the beginning of formal instruction, across children from a wide socio-economic spectrum. Non-symbolic numerical abilities therefore predict children’s mastery of their first-year mathematics curriculum.
Because our findings show that non-symbolic abilities are associated with formal mathematical performance very early in the course of mathematics instruction, and prior to the introduction of instruction in arithmetic, they reveal that the association between non-symbolic and abilities and formal mathematics found by Halberda and colleagues (2008) is not solely the product of lengthy instruction in mathematics. Because this association survives controls for intelligence and school achievement in other domains, we can conclude that it is not an artifact of individual differences in general cognitive aptitude or motivation. Instead, there is a specific relationship between children’s developing non-symbolic arithmetic performance and their symbolic numerical abilities at the start of schooling and prior to any formal instruction in arithmetic.
The first-year school mathematics curriculum is multifaceted, and so the present findings raise the question whether children’s non-symbolic numerical abilities enhance their school mathematics learning across the board or only in some areas. The present findings cannot answer this question conclusively, but the findings of Experiment 2 reveal one aspect of the mathematics curriculum that is clearly associated with children’s non-symbolic abilities: their mastery of the symbolic number systems--number words and Arabic notation--on which both schools’ assessments of mathematics achievement largely focus. These findings are consistent with two distinct hypotheses concerning the causes of children’s success in the early mathematics curriculum. On one hypothesis, the non-symbolic numerical abilities that arise in infancy support children’s learning of the number words and symbols that are the primary focus of their mathematics curriculum. On the other hypothesis, children’s learning of number words and symbols, both prior to and during the first year of school instruction, sharpens their non-symbolic numerical abilities. At present, there is mixed evidence concerning the relationship between non-symbolic numerical abilities and number word mastery (c.f. LeCorre & Carey, 2007; Huang, Spelke & Snedeker, in press). Further research with younger children is needed to distinguish these possibilities.
Regardless of the causal mechanisms relating non-symbolic to symbolic numerical abilities, our findings provide evidence that performance of non-symbolic arithmetic is predictive of success in kindergarten mathematics. Although such non-symbolic tests focus on numbers larger than children are studying, and on an operation that plays little or no role in their curriculum, children find these problems engaging and motivating. Training studies are needed to explore the educational benefits of curricula that build explicitly on non-symbolic numerical knowledge and the effectiveness of interventions that enhance children’s non-symbolic numerical abilities (e.g. Wilson & Dehaene, 2007).
Our findings raise questions concerning the achievement gap between children from different socio-economic backgrounds. Some analysts have speculated that in meritocratic societies, economic differences come to reflect, and are perpetuated by, genetic differences in cognitive ability (Herrnstein & Murray, 1996). Thus, economically disadvantaged children’s lesser achievement in school mathematics could stem from a genetic predisposition to lesser aptitude in this domain, inherited from parents whose economic success was diminished by their low mathematical ability. Although we cannot exclude the possibility that wealthy and poor children differ subtly in their intrinsic aptitude for mathematics, we have found no evidence of such a difference. The mathematics achievement gap between wealthy and poor children more likely stems from well-known differences in preschool children’s exposure to conventional symbol systems (Griffin & Case, 1996; Jordan et al., 1992). Because socio-economic differences in numerical symbol learning can be erased by targeted preschool interventions (Griffin, Case & Siegler, 1994; Siegler & Ramani, 2008), achievement gaps in school mathematics may be eliminable.
Acknowledgments
We thank Jennie Sheiman for her help with the data collection, and Hilary Barth for her help with the task in Experiment 1.
This work was supported by a grant (#REC 0337055) from the National Science Foundation (to E.S.S.) and a British Academy Postdoctoral Fellowship (to C.K.G.).
Appendix
Alternative Strategy Analyses
The children’s performance on the approximate non-symbolic addition tasks was examined for evidence that children were using alternative non-arithmetical strategies to solve the problems. The first set of analyses examined whether children showed a tendency to choose the sum of the addends or the comparison set. Children who relied on this strategy would score 50% overall and because performance was above 50% in all experiments, this strategy cannot account for children’s performance. As shown in Table A1 children performed significantly above chance both for problems in which the correct answer was the sum of the addends and for problems in which the correct answer was the comparison set on the non-symbolic addition task in both Experiments 1 and 2.
Table A1.
| Experiment | Trials / subject | Accuracy | p Value | > Chance (50%) |
|---|---|---|---|---|
| E1 | Addends > Foil (12) | 61.0% | p = .003 | Yes |
| Addends < Foil (12) | 63.0% | p = .002 | Yes | |
| E2 | Addends > Foil (12) | 66.4% | p < .001 | Yes |
| Addends < Foil (12) | 66.8% | p < .001 | Yes |
The second set of analyses examined whether children based their answers on the range of values tested across the sets of trials. For example, children may answer that there are more red dots when the number of red dots is large. To test for children’s use of this strategy, the problem set for each experiment involved two sets of 12 problems with non-overlapping ranges of values. On half of the problems at each ratio, the size of the addends predicted the correct answer and on half of the problems the size of the comparison set predicted the correct answer. Use of either of these strategies therefore would predict the correct answer on half of the trials and the incorrect answer on the remaining trials. As shown in Table A2, children performed significantly above chance in each experiment on the problems for which these strategies predicted the incorrect answer, and thus use of these strategies cannot account for children’s performance.
Table A2.
| Experiment | Trials / subject | Accuracy | p Value | > Chance (50%) |
|---|---|---|---|---|
| E1 | Foil size not predictor (12) | 57.9% | p = .001 | Yes |
| Addend size not predictor (12) | 66.1% | p = .001 | Yes | |
| E2 | Foil size not predictor (12) | 64.5% | p < .001 | Yes |
| Addend size not predictor (12) | 68.7% | p < .001 | Yes |
The third set of analyses examined whether children based their answers on a comparison of values within each trial. If the difference between the larger addend and the comparison set is particularly small then the correct answer is always that the sum of the addends is larger. Conversely if the difference between the larger addend and the comparison set is particularly large then the correct answer is always that the comparison set is larger. If children were basing their answers on this type of comparison then they would perform at chance for problems with a medium difference and for which the correct answer cannot be predicted in this way. As shown in Table A3, children performed above chance on this critical subset of problems in Experiment 2, although not in Experiment 1.
Table A3.
| Experiment | Trials /subject | Accuracy | p Value | > Chance (50%) |
|---|---|---|---|---|
| E1 | 7 | 54.7% | p = .162 | No |
| E2 | 8 | 62.1% | p < .001 | Yes |
The fourth set of analyses examined whether children were relying on continuous quantity information to solve the task. As shown in Table A4, children performed above chance, though not significantly, for all the subsets of problems in both Experiments 1 & 2 in which density, array size, element size, and summed area and contour length failed to predict the correct outcome. Although children did not perform significantly above chance, their performance in these experiments cannot be explained through reliance on continuous quantity variables, because this strategy would have resulted in children scoring significantly below chance for one subset of problems (A or B). Because children were not below chance on any subset, they must have been basing their answers at least in part on the numerosity of dots in the arrays, rather than correlated continuous quantities such as dot size, area, or density.
Table A4.
| Experiment | Trials / subject | Accuracy | p Value | > Chance (50%) |
|---|---|---|---|---|
| E1 | A* (12) | 51.4% | p = .534 | No |
| B (12) | 72.6% | p < .001 | Yes | |
| E2 | A (12) | 46.5% | p = .174 | No |
| B (12) | 86.7% | p < .001 | Yes |
Continuous Quantity Type: (A) Dot size, summed dot area, total contour length, and density are positively correlated with number while array size is negatively correlated with number; (B) Dot size, summed dot area, total contour length, and density are negatively correlated with number while array size is positively correlated with number.
Table A5.
The set of problems used in the non-symbolic addition task for Experiment 1 with the characteristics of each problem in relation to possible alternative strategies.
| Ratio | Addends | Comparison number | Range strategy predictor* | Difference | CQ Type # |
|---|---|---|---|---|---|
| 4:7 | 16 + 17 | 58 | Foil | Large (41) | B |
| 4:7 | 16 + 16 | 56 | Foil | Large (40) | A |
| 4:7 | 6 + 6 | 21 | Addend | Medium (15) | B |
| 4:7 | 6 + 7 | 23 | Addend | Medium (16) | A |
| 4:7 | 27 + 31 | 33 | Addend | Small (2) | B |
| 4:7 | 30 + 26 | 32 | Addend | Small (2) | A |
| 4:7 | 10 + 11 | 12 | Foil | Small (1) | B |
| 4:7 | 11 + 12 | 12 | Foil | Small (1) | A |
| 4:6 | 15 + 15 | 45 | Foil | Large (30) | B |
| 4:6 | 15 + 19 | 51 | Foil | Large (32) | A |
| 4:6 | 5 + 5 | 15 | Addend | Medium (10) | B |
| 4:6 | 8 + 6 | 21 | Addend | Medium (13) | A |
| 4:6 | 25 + 20 | 30 | Addend | Small (5) | B |
| 4:6 | 21 + 30 | 34 | Addend | Small (4) | A |
| 4:6 | 9 + 6 | 10 | Foil | Small (1) | B |
| 4:6 | 9 + 12 | 14 | Foil | Small (2) | A |
| 4:5 | 20 + 16 | 45 | Foil | Large (25) | B |
| 4;5 | 15 + 25 | 50 | Foil | Large (25) | A |
| 4;5 | 6 + 6 | 15 | Addend | Small (9) | B |
| 4:5 | 7 + 9 | 20 | Addend | Medium (11) | A |
| 4;5 | 25 + 20 | 36 | Addend | Medium (11) | B |
| 4;5 | 20 + 30 | 40 | Addend | Medium (10) | A |
| 4;5 | 9 + 6 | 12 | Foil | Small (3) | B |
| 4:5 | 12 + 8 | 16 | Foil | Small (4) | A |
Continuous Quantity Type: (A) Dot size, summed dot area, total contour length, and density are positively correlated with number while array size is correlated negatively with number; (B) Dot size, summed dot area, total contour length, and density are negatively correlated with number while array size is positively correlated with number.
Indicates whether the addend or foil predicts the correct answer according to the range strategy tested above (see Table A2).
Table A6.
The set of problems used in the non-symbolic and symbolic addition tasks for Experiment 2 with the characteristics of each problem in relation to possible alternative strategies.
| Ratio | Addends | Comparison number | Range strategy predictor* | Difference | CQ Type# |
|---|---|---|---|---|---|
| 5:9 | 31+29 | 33 | Addend | Small (2) | A |
| 5:9 | 34+31 | 36 | Addend | Small (2) | B |
| 5:9 | 12+13 | 14 | Foil | Small (1) | B |
| 5:9 | 11+11 | 12 | Foil | Small (1) | A |
| 5:9 | 16+17 | 60 | Foil | Large (43) | A |
| 5:9 | 18+18 | 65 | Foil | Large (47) | B |
| 5:9 | 9+5 | 25 | Addend | Medium (16) | B |
| 5:9 | 5+7 | 22 | Addend | Medium (15) | A |
| 5:8 | 33+28 | 38 | Addend | Small (5) | B |
| 5:8 | 30+26 | 35 | Addend | Small (5) | A |
| 5:8 | 10+11 | 13 | Foil | Small (2) | B |
| 5:8 | 11+13 | 15 | Foil | Small (2) | A |
| 5:8 | 20+18 | 61 | Foil | Large (41) | B |
| 5:8 | 17+18 | 56 | Foil | Large (38) | A |
| 5:8 | 5+8 | 21 | Addend | Medium (13) | B |
| 5:8 | 8+7 | 24 | Addend | Medium (16) | A |
| 5:7 | 27+25 | 37 | Addend | Medium (10) | A |
| 5:7 | 28+31 | 42 | Addend | Medium (11) | B |
| 5:7 | 10+8 | 13 | Foil | Small (3) | B |
| 5:7 | 12+12 | 17 | Foil | Small (5) | A |
| 5:7 | 21+16 | 52 | Foil | Large (31) | A |
| 5:7 | 18+24 | 59 | Foil | Large (35) | B |
| 5:7 | 7+6 | 18 | Addend | Medium (11) | B |
| 5:7 | 8+9 | 24 | Addend | Medium (15) | A |
Continuous Quantity Type: (A) Dot size, summed dot area, total contour length, and density are positively correlated with number while array size is correlated negatively with number; (B) Dot size, summed dot area, total contour length, and density are negatively correlated with number while array size is positively correlated with number.
Indicates whether the addend or foil predicts the correct answer according to the range strategy tested above (see Table A2).
Kindergarten tests
Experiment 1 - Mathematics test
Part 1 (30 questions): Students recorded responses on worksheets while sitting in groups of 6–8 students.
| Questions | Description |
|---|---|
| 1–3 | Count 7–10 objects and write the correct Arabic number. |
| 4–6 | Recognize Arabic numbers 5–8 and draw the correct number of items. |
| 7 | Identify two sets with equal amounts by counting. |
| 8 | Fill in the missing number 8 on a calendar. |
| 9–10 | Count items in a box and circle a set of items that contains one more/less. |
| 11 | Draw a line to cut a picture in half. |
| 12 | Equal parts of a whole—identify something cut in half. |
| 13 | Count6 pennies. |
| 14 | Compare two sets (pictures and Arabic numeral) identify which picture had one more. |
| 15 | Draw a group of objects that were one less than the original group. |
| 16 | Understand word problem (e.g. recognize a teddy bear wearing stripes). |
| 17 | One to one correspondence. |
| 18–20 | Number sequence: fill in a missing number from a set order (e.g. 6, ?, 8). |
| 21–24 | Comparing size: circle the larger/more voluminous/taller/heavier item. |
| 25 | Comparing objects that are the same: circle two items that were the same length. |
| 26 | Comparing the shortest: circle the shortest picture. |
| 27 | Correctly order a set of objects by size |
| 28–30 | Interpreting graphs: pick item that was chosen most/least. |
Part 2 (13 questions): Teachers administered individually to students.
| Questions | Description |
|---|---|
| 1–3 | Copy, extend, and create a pattern using manipulatives. |
| 4 | Describe the pattern created. |
| 5–7 | Ordinals: point to the 1st–5th shape in a pattern. |
| 8 | Conservation of number: identify 6 objects in a set, then identify without counting, 2 sets of 3 objects. |
| 9 | Measure an item using cubes. |
| 10 | Sort items by an attribute. |
| 11–13 | Name a circle, triangle, rectangle. |
Experiment 1 - literacy assessment
Teachers administered a literacy assessment individually at the end of the school year, in ignorance of our findings. The test consisted of 5 parts: rhyming (10 questions), alphabet recognition (54 questions), letter sounds (26 questions), high frequency words (200 questions) and hearing and recording sounds in words (37 questions). Children were given a raw score on the literacy assessment by adding their correct answers together on all parts of the test.
Experiment 2 - Mathematics test
This test consisted of 49 questions and was administered by teachers to students in small groups.
| Questions | Description |
|---|---|
| 1–5 | Identify a circle (2 sizes), triangle, or square (2 sizes) |
| 6–8 | Extend a pattern |
| 9–10 | Knowledge of “Left” and “Right” |
| 11 | One to one correspondence |
| 12–15 | Concept of “one more” and “one less” |
| 16–24 | Recognize sets of 3–9 objects and circle the Arabic numeral |
| 25–28 | Recognize 3D objects by their forms (cube, sphere, cone, cylinder) |
| 29–34 | Knowledge of verbal terms for quantity (e.g., “shortest,” “heaviest”) |
| 35 | Translate analog time to digital time |
| 36–38 | Counting of small numbers (e.g., shown a picture of two people each with two objects, the child is asked “How many in all?”) |
| 39 | Circle the picture that matches the addition sentence “2 + 1 = 3” |
| 40–42 | Counting of small numbers and identification of Arabic numbers (e.g., shown a picture of 3 bees with one bee crossed out, the child is asked to circle the correct Arabic numeral. |
| 43 | Circle the picture that matches the subtraction sentence “4−2 = 2” |
| 44–47 | Recognize pictured sets of 1–7 pennies and circle the correct Arabic numeral (with cents sign). |
| 48–49 | Recognition of a nickel and dime. |
Contributor Information
Camilla K. Gilmore, Learning Sciences Research Institute, University of Nottingham
Shannon E. McCarthy, Department of Psychology, Harvard University
Elizabeth S. Spelke, Department of Psychology, Harvard University
References
- Baroody AJ, Dowker A. The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise. Mahwah, NJ: Erlbaum; 2003. [Google Scholar]
- Barth H, La Mont K, Lipton J, Dehaene S, Kanwisher N, Spelke E. Non-symbolic arithmetic in adults and young children. Cognition. 2006;98:199–222. doi: 10.1016/j.cognition.2004.09.011. [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke ES. Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences. 2005;102:14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth H, Kanwisher N, Spelke ES. The construction of large number representations in adults. Cognition. 2003;86:201–221. doi: 10.1016/s0010-0277(02)00178-6. [DOI] [PubMed] [Google Scholar]
- Cappelletti M, Barth H, Fregni F, Spelke ES, Pascual-Leone A. rTMS over the intraparietal sulcus disrupts numerosity processing. Experimental Brain Research. 2007;179:631–642. doi: 10.1007/s00221-006-0820-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case R, Griffin SA, Kelly WM. Social class gradients in mathematical ability and their responsiveness to compensatory education. In: Keating D, Hertzman C, editors. Tomorrow’s society, today’s children: The health and developmental wealth of nations. New York: Guilford; 1999. pp. 125–150. [Google Scholar]
- De Smedt B, Verschaffel L, Ghesquière P. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology. 2009;103:469–479. doi: 10.1016/j.jecp.2009.01.010. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The Number Sense: How the Mind Creates Mathematics. Oxford: Oxford University Press; 1997. [Google Scholar]
- Dunn LM, Dunn LM. Peabody Picture Vocabulary Test – III. Circle Pines, MN: American Guidance Service; 1997. [Google Scholar]
- Feigenson L, Dehaene S, Spelke ES. Core systems of number. Trends in Cognitive Sciences. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Flombaum JI, Junge JA, Hauser MD. Rhesus monkeys (Macaca mulatta) spontaneously compute addition operations over large numbers. Cognition. 2005;97:315–325. doi: 10.1016/j.cognition.2004.09.004. [DOI] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke ES. Symbolic arithmetic knowledge without instruction. Nature. 2007;447:589–591. doi: 10.1038/nature05850. [DOI] [PubMed] [Google Scholar]
- Good RH, Kaminski RA. Dynamic indicators of basic early literacy skills. 6. Longmont, CO: Sopris West; 2002. [Google Scholar]
- Griffin S, Case R. Evaluating the breadth and depth of training effects when central conceptual structures are taught. Monographs of the Society for Research in Child Development. 1996;61:83–102. doi: 10.1111/j.1540-5834.1996.tb00538.x. [DOI] [PubMed] [Google Scholar]
- Griffin SA, Case R, Siegler RS. Rightstart: Providing the central conceptual prerequisites for first formal learning of arithmetic to students at risk for school failure. In: McGilly K, editor. Classroom lessons: Integrating cognitive theory and classroom practice. Cambridge, MA: MIT Press; 1994. pp. 25–49. [Google Scholar]
- Halberda J, Mazzocco MMM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455:665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Herrnstein R, Murray C. The Bell Curve: Intelligence and Class Structure in American Life. New York: Free Press; 1996. [Google Scholar]
- Holloway ID, Ansari D. Domain-specific and domain-general changes in children’s development of number comparison. Developmental Science. 2008;11:644–649. doi: 10.1111/j.1467-7687.2008.00712.x. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children’s mathematics achievement. Journal of Experimental Child Psychology. 2009;103:17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Huang YT, Spelke ES, Snedeker J. When is four far more than three? Children’s generalization of newly acquired number words. Psychological Science. doi: 10.1177/0956797610363552. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Huttenlocher J, Levine SC. Differential calculation abilities in young children from middle- and low-income families. Developmental Psychology. 1992;28:644–653. [Google Scholar]
- LeCorre M, Carey S. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition. 2007;105:395–438. doi: 10.1016/j.cognition.2006.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemer C, Dehaene S, Spelke E, Cohen L. Approximate quantities and exact number words: dissociable systems. Neuropsychologia. 2003;41:1942–1958. doi: 10.1016/s0028-3932(03)00123-4. [DOI] [PubMed] [Google Scholar]
- McCrink K, Dehane S, Dehane-Lambertz G. Moving along the number line: The case for operational momentum. Perception and Psychophysics. 2007;69:1324–1333. doi: 10.3758/bf03192949. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Large number addition and subtraction by 9-month-old infants. Psychological Science. 2004;15:776–781. doi: 10.1111/j.0956-7976.2004.00755.x. [DOI] [PubMed] [Google Scholar]
- Piazza M, Pinel P, Le Bihan D, Dehaene S. A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron. 2007;53:293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306:499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Ramani GB. Playing linear numerical board games promotes low-income children’s numerical development. Developmental Science. 2008;11:655–661. doi: 10.1111/j.1467-7687.2008.00714.x. [DOI] [PubMed] [Google Scholar]
- Sirin SR. Socioeconomic status and academic achievement: A meta-analytic review of research. Review of Educational Research. 2005;75:417–453. [Google Scholar]
- Wilson AJ, Dehaene S. Number sense and developmental dyscalculia. In: Coch D, Fischer K, Dawson G, editors. Human Behavior and the Developing Brain. 2. New York: Guilford; 2007. pp. 212–238. [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]