Assessing protein loop flexibility by hierarchical Monte Carlo sampling

Abstract

Loop flexibility is often crucial to protein biological function in solution. We report a new Monte Carlo method for generating conformational ensembles for protein loops and cyclic peptides. The approach incorporates the triaxial loop closure method which addresses the inverse kinematic problem for generating backbone move sets that do not break the loop. Sidechains are sampled together with the backbone in a hierarchical way, making it possible to make large moves that cross energy barriers. As an initial application, we apply the method to the flexible loop in triosephosphate isomerase that caps the active site, and demonstrate that the resulting loop ensembles agree well with key observations from previous structural studies. We also demonstrate, with 3 other test cases, the ability to distinguish relatively flexible and rigid loops within the same protein.

1 Introduction

A great deal of effort has been directed towards the development of computational methods for predicting the conformations of protein loops, which is a critical task in comparative protein modeling and in computational protein design^1–4. The success of these methods has been evaluated primarily by comparing the results of the loop predictions with the loop conformations observed in crystal structures. That is, the focus is predicting the structure of the loop—a specific conformation—rather than the ensemble of conformations populated at biologically relevant conditions. Although these loop prediction methods can be used to identify multiple low-energy conformations, it is challenging to determine populations of the conformations, i.e., to relate energies of individual conformations to free energies of micro or macrostates in the ensemble, although significant progress in this regard has been made by Meirovitch and coworkers^5–7.

The flexibility of loops, i.e., the ability to adopt multiple conformations at relevant temperatures, is often critical to biological function, by playing an important role in molecular recognition. For example, the active site loop of the triosephosphate isomerase (TIM barrel) changes its conformation from an open to a closed state after binding of ligands^{8, 9}. In kinases, two critical loops near the active site are flexible, with important implications for drug discovery: the glycine-rich loop (also called the P-loop) and the activation loop, including the DFG motif, which can adopt at least 2 major conformations in some kinases, referred to as ‘out’ and ‘in’. For example, while c-Src generally adopts the DFG-in conformation, the unfavorable DFG-out conformation can be induced by binding small molecules¹⁰. Loop flexibility can also play an important role in antibody-antigen recognition. The H3 loop in the complementarity-determining region of antibodies, which has the most diversity in sequence and is the most critical loop for antigen affinity and specificity, frequently demonstrates evidence of conformational flexibility^11–13.

More broadly, there are many cases where loops adopt different conformations in different crystal structures, e.g., holo vs. apo, or even different crystal unit cells for the same protein¹⁴. Although the B-factors in crystal structures provide some information about conformational flexibility, each structure is best viewed as a snapshot from the equilibrium ensemble. NMR experiments can provide some direct information about conformational equilibria, but generally cannot provide complete information about the ensemble of interconverting structures.

Molecular dynamics (MD) has been widely used to study protein flexibility, including loop dynamics^{15, 16}. The main liability of MD is that the timescales for interconverting between loop conformations can be long relative to the femtosecond time steps used, such as the millisecond timescale for the TIM capping loop to interconvert between the open and closed states¹⁷. Although such timescales may soon become accessible by MD simulation, they will remain extremely computationally expensive. Methods like replica exchange MD can be used to accelerate convergence but are likewise computationally expensive.

Here we describe a Monte Carlo method for generating ensembles of loop conformations and cyclic peptides. It is related to classes of loop prediction methods that use torsion-angle sampling of backbone and side chain degrees of freedom (DoF), which makes it possible to make large conformational moves that cross energy barriers. Specifically, it builds on loop prediction methods that exploit “inverse kinematics” methods for creating move sets that do not ‘break’ the loop^18–24. The new contribution here is implementing these moves in a Monte Carlo scheme that also samples side chain DoF²⁵. We apply the method to a number of proteins with flexible loops, including the well-known case of TIM. We also evaluate our ability to distinguish between (relatively) rigid and flexible loops within the same protein.

2 The Move Set: Torsional Perturbations via Inverse Kinematics

2.1 Torsions and Sterics

It is widely accepted that the essential dynamics of a protein backbone can be captured by moves involving only the torsions ϕ, ψ with the other internal variables (bond lengths, bond angles and ω torsions) being kept close to their canonical values, although not necessarily rigid^{19, 23, 24}.

Compared to the high energy associated with ω angle deformation, ϕ and ψ angles are relatively free to rotate but their range is restricted by steric interactions. Ramachandran regions in the (ϕ, ψ) coordinates for each peptide ensure intra-peptide steric avoidance, and additional restrictions are imposed by more distant clashes. Clashes involving backbone atoms (or atoms bonded to them) are completely determined from the backbone angles. On the other hand, atoms further along sidechains (from the γ position out) are not completely determined from the backbone, although their placement may be restricted by it. Significantly, sidechains may interact with other sidechains so that their placement must be accomplished as a whole. Given a backbone conformation, a separate search is required to determine sterically acceptable or otherwise energetically viable sidechain conformations. Reciprocally, backbone moves may be restricted by fixed sidechain geometry.

2.2 MC move and state variables

To design a Monte Carlo move for reversibly exploring the torsion space, we must therefore consider the state space as the set of all torsions, {t_i; χ_j} where the t_i are backbone torsions and χ_j are sidechain torsions, with the indices running respectively over all the backbone and sidechain DoF. A chain of {N, Cα, C} triplets (a standard backbone) is one possibility but chains through e.g. cysteine bridges, or other macromolecules, such as nucleic acids, could also be considered. In the following, we will assume the standard case (protein backbone loops) exclusively. For the case of a loop of N residues bridging two fixed ends the essential backbone DoF would be M = 2N − 6. Here, 6 backbone DoF are involved in placing the end of the loop in a fixed rotation/translation relationship to the beginning. We call these DoF, labeled arbitrarily as t_i, (i = 1, …, 6) the compensators. The remaining M DoF, labeled as t_i, (i = 7, …, 2N) are the controls. This separation in controls and compensators is arbitrary and may change from one move to the next. We could assume that the end residues 0 and N + 1 act as hinges, i.e. the ϕ₀ and ψ_N+1 torsions are fixed, but ψ₀, ϕ_N+1 are free, adding two DoF to the backbone. The treatment is essentially the same, replacing M by M + 2 and redefining some indices. We will only discuss the first case (no hinge mobility). It will be assumed that there are K sidechain DoF in the set 𝖲 of sidechains interacting with the loop; we may only wish to include in 𝖲 those sidechains on the loop and hinges. The placement for those depends on the loop conformation. We may also include sidechains on residues in some sphere of influence about the loop. Or we may simply include all the sidechains in the protein. We make no distinction at this stage.

Then, to design a reversible MC move that involves only the loop backbone DoF as well as the selected group 𝖲 of sidechains coupled to the loop we must establish the Metropolis criterion for acceptance of a move of the form

$$\{t_i,{\chi }_j\}\to \{t_i+\delta t_i;{\chi }_j+\delta {\chi }_j\},i\in [7,2N],j\in [1,K]$$ (1)

The shape space geometry accessible via our formulation characterizes our moves: assume that the L (= 2N) torsions for a loop kinematic chain are divided into the L − 6 controls and 6 compensators. The method used here employs the ϕ, ψ pairs of 3 amino acids (the pivots). These can be chosen at arbitrary locations along the loop, breaking it into three subfragments for kinematic purposes. To each value of the L − 6 controls there correspond up to 16 distinct conformations satisfying the closure conditions, each characterized by a unique set of values of the compensators. As discussed in our earlier work²⁶, the 16 alternative solutions represent different orientations of the 3 subfragments between successive pivots in a reference frame attached to the 3 pivot Cα atoms about the 3 axes joining each pair of pivots. Thus we refer to the method as Triaxial Loop Closure (TLC). The basic idea in the TLC method (discussed more in detail in the next section) is to construct a loop with arbitrary internal degrees of freedom, taking advantage of the fact that the inverse kinematic problem can be solved by determining appropriate values of six torsions. Thus any variation in the remaining DoF’s — other torsions, including omegas, bond angles and even bond lengths — can be considered, if so desired. Here we treated only ϕ − ψ variations as these are the most ”flexible” DoF’s, but we could have included all other DoF’s in the MC scheme in any combination desired. The conformational variability of the constitutive pieces for loop closure, i.e. the three subfragments, is of course an important factor for solving the closure problem. We see that this variability can be decomposed in two types: the end-to-end variability of the individual fragments, and the inherent variability of the loop closure problem, i.e. relative locations and orientations of the ends of the loop as well as the environment in the loop vicinity.

The first is a direct problem: compute the fragment (in practice we do not check that the fragment is indeed sterically feasible until the assembly is successful). The individual fragment assembly, being subject to no end constraints, is only limited by the Ramachandran and other steric restrictions. However, for purposes of assembling the three subfragments into a self consistent loop, each individual fragment of length L_i residues with i = 1, 2, 3, is encoded by 4 variables: the overall geometric length of the virtual bond joining first and last atoms, d_i; the angles θ_i, ξ_i made by the two end bonds to the virtual bond; and the torsion of the two end bonds about the virtual bond, δ_i. The variability of the closure problem is governed by these twelve parameters (d_i, θ_i, ξ_i, δ_i), i = 1, 2, 3. The equations expressing closure depend on these parameters smoothly; small changes cause usually small changes in the number and disposition of solutions except that, for certain arrangements, solutions could spontaneously appear or disappear (pairs of polynomial roots may join and become complex, or the converse, see the discussion of the Inverse Kinematic problem below).

We now search the nearby conformation space by perturbing one of the control torsions. This will result in perturbing the overall structure of one of the chains, leading to a perturbed set of solutions. These changes may lead to overall large motions, see e.g. Ref.²⁷ for a discussion of the end conditions and their constraining of various inner DoF. However, a reasonable acceptance ratio for the method can be more or less guaranteed by varying the controls and restricting the stepsize. Below we discuss a two stage scheme, splitting the move into a pure backbone and a pure sidechain stage.

2.3 Solving the Inverse Kinematic problem

Many methods for finding solutions that satisfy the closure conditions have been proposed, both exact^{18, 22, 26, 28–32}and approximate^{6, 21, 33–37}. Exact methods address the Inverse Kinematic problem by searching for the values of a certain torsion, say τ, in terms of which all other torsions can be determined. Go and Scheraga¹⁸ pursued a direct solution in the original angle variables. This involves finding the zeros of a certain transcendental expression, a process that may require substantial computation to adequately resolve the entire domain. Subsequent works employ standard techniques from the robotics literature to convert to a more tractable polynomial form in the variable u = tan τ/2. All the real roots of this 16th degree polynomial can be found efficiently and stably by the use of the method of Sturm chains³⁸. All other torsions can be recovered readily and therefore such methods are capable of finding all backbone solutions for any given combination of control torsion values. On the other hand, approximate methods typically use an iterative procedure to find a solution. As a result they are not guaranteed to find all solutions consistent with a given set of control values, and the same is true for the approach in Ref.¹⁸, which is also followed in Refs.^{20, 23, 24}, although for this class of methods the issues are mainly related to the computational sensitivity of multiple roots.

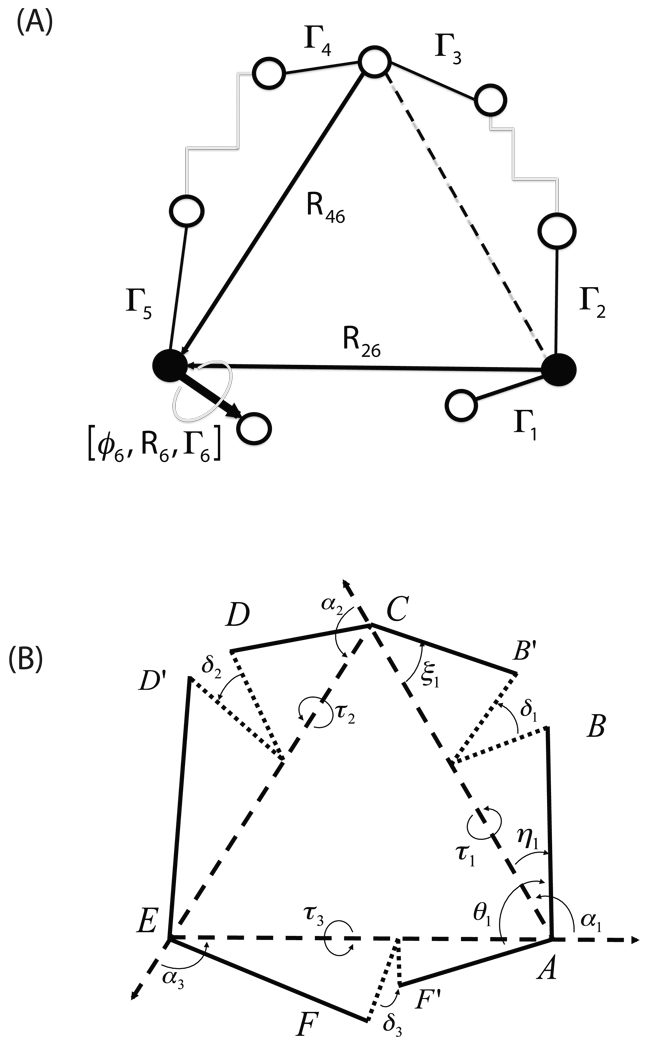
In previous applications the conrot algorithm has been used²⁰. It places the rotatable bonds on 6 consecutive bonds plus a driver. A generalization by Wu and Deem²² uses one driver on either end. A weakness of the conrot approach is that a change on either side of the short compensator segment may make the closure problem unsolvable²⁴. A generalization from robotics removes that restriction²⁹. Our own method for solving the tripeptide closure problem, explained in detail in Ref.²⁶, has the advantage of mathematical simplicity, speed and robustness. It also allows for a straightforward generalization for longer chains of arbitrary geometry. Its simplicity comes from taking advantage of the natural pairing up of rotatable bonds in amino acids to reduce the closure problem to three rotations, and we refer to this as the TLC method²⁶. Referring to Fig. 1(b) we note that each Cα, C, N, Cα unit is identified by four variables: the overall geometric length of the virtual bond joining first and last atoms, d_i; the angles θ_i, ξ_i made by the two end bonds to the virtual bond; and the torsion of the two end bonds about the virtual bond, δ_i (actually, the formulation uses the angles α_i of the triangle formed with edges d_i). These definitions remain unchanged even if arbitrary structure exists between the two end pairs (Fig. 1(a)). We may produce multiple conformations for a long closed chain by partitioning into 3 subsegments and mapping each to a simple kinematic generalization of the tetrad Cα, C, N, Cα (Fig. 1(a)(b)).

Fig. 1.

(A) The atoms and parameters defining triaxial loop closure (TLC). (B) The generalized 6R/3A kinematic chain.

In brief, three Cα atoms are selected (the pivots). The chain between any two of these, containing L atoms including the endpoints is determined to within a rotation/translation (i.e. in its own body frame) by its own internal coordinates: L − 3 torsions, L − 2 angles, L − 1 lengths. With fixed (to any prescribed value) bond-lengths and bond-angles, each chain can be completely described by its L − 3 internal torsions. Below, we will index the residues of the three pivots as 1, 2 and 3 and we will index their backbone atoms as N_i, Cα_i and C_i, i = 1, 2, 3 accordingly. Below we use the atom names interchangeably with their cartesian coordinates, e.g. N₁ can be thought of as equivalent to the vector R₁, etc (see eq. 5).

As is explained in Ref.²⁶ and somewhat more at length in Ref.³⁹ (see also the supplementary material discussion in Ref.⁴⁰), the three fragments, respectively between pivots 1–2, 2–3 and 3−1, form a triangle with edges d_i, i = 1, 2, 3. The parameters necessary for setting up and solving the TLC equations can be extracted from knowledge of only the first two and last two atoms of each chain (Fig. 2). Once the three 4-atom fragments have been assembled into a triangle, the relative rotation of each fragment about the triangle must place the end-atoms relative to those on each neighboring fragment so that the angles (N_iCα_iC_i, i = 1, 2, 3 assume prescribed values (Fig. 1). In this way, loop closure is accomplished when an appropriate rotation for each piece has been found. It turns out that the problem overlays the solution of a 16th degree polynomial, so that to each real root there corresponds a possible backbone loop geometry (subject, of course, to overall steric viability) to a total of, at most, 16 solutions possible for a given collection of state variables, the control 2N − 6 torsions.

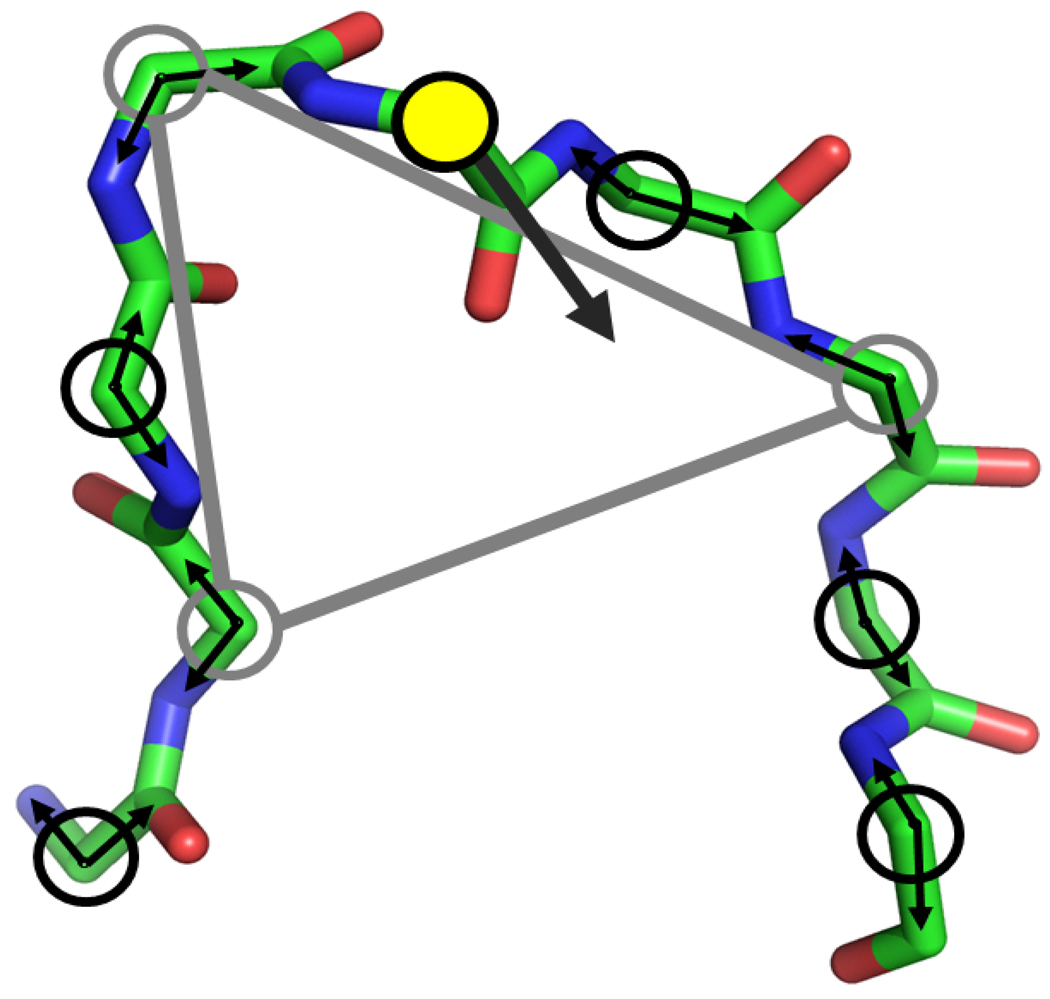
Fig. 2.

Construction of a tripeptide move. A node consists of a ϕ/ψ pair at each alpha carbon of the loop (with only backbone shown). The yellow filled circle is the alpha carbon whose dihedral angle servers as a driver angle (the wide black arrow). A randomly constructed triaxial closure is shown as the grey triangle in which each grey circle represents the randomly selected pivot.

2.4 Jacobian

Since fixing the end of the chain (the Closure Conditions) implies relationships among the torsions, we seek solution of these relationships such that specifying M torsions along the loop leads to complete determination of all 2N torsions and unambiguous Cartesian coordinates for all loop backbone atoms that are sterically self-consistent. In general, for any feasible value of the controls there may exist multiple sets of compensators that allow the loop to close. They are functions of the controls and their values solve the loop closure problem.

As a result, the element of volume in torsion space, initially uniform in these variables

$$d𝒱=d{\varphi }_{1}d{\psi }_1\dots d{\varphi }_{N}d{\psi }_{N}d{\chi }_1\dots d{\chi }_K$$

will need to be modified by

$${\mathit{\text{dt}}}_1\dots {\mathit{\text{dt}}}_6=\frac{\partial (t_1,\dots ,t_6)}{\partial ({\mathbf{R}}_6,{\mathbf{\Gamma }}_6,t_6)}d{\mathbf{R}}_{6}d{\mathbf{\Gamma }}_6{\mathit{\text{dt}}}_6$$

leading to the well known expression (e.g. see formula 23 in²³) for the inverse of the above Jacobian:

$$J_i=\text{det}\frac{\partial ({\mathbf{R}}_6,{\mathbf{\Gamma }}_6,t_6)}{\partial \mathbf{t}}=\left|\begin{array}{cccccc}\hfill \frac{\partial {\mathbf{R}}_6}{\partial t_1}\hfill & \hfill \frac{\partial {\mathbf{R}}_6}{\partial t_2}\hfill & \hfill \frac{\partial {\mathbf{R}}_6}{\partial t_3}\hfill & \hfill \frac{\partial {\mathbf{R}}_6}{\partial t_4}\hfill & \hfill \frac{\partial {\mathbf{R}}_6}{\partial t_5}\hfill & \hfill \frac{\partial {\mathbf{R}}_6}{\partial t_6}\hfill \\ \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_1}·e_1\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_2}·e_1\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_3}·e_1\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_4}·e_1\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_5}·e_1\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_6}·e_1\hfill \\ \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_1}·e_2\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_2}·e_2\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_3}·e_2\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_4}·e_2\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_5}·e_2\hfill & \hfill \frac{\partial {\mathbf{\Gamma }}_6}{\partial t_6}·e_2\hfill \\ \hfill \frac{\partial t_6}{\partial t_1}\hfill & \hfill \frac{\partial t_6}{\partial t_2}\hfill & \hfill \frac{\partial t_6}{\partial t_3}\hfill & \hfill \frac{\partial t_6}{\partial t_4}\hfill & \hfill \frac{\partial t_6}{\partial t_5}\hfill & \hfill \frac{\partial t_6}{\partial t_6}\hfill \end{array}\right|.$$

Since

$$\frac{\partial {\mathbf{R}}_k}{\partial t_j}={\mathbf{\Gamma }}_j\times {\mathbf{R}}_{\mathit{\text{jk}}},\frac{\partial {\mathbf{\Gamma }}_6}{\partial t_j}={\mathbf{\Gamma }}_j\times {\mathbf{\Gamma }}_6,\frac{\partial t_i}{\partial t_j}={\delta }_{\mathit{\text{ij}}}$$ (2)

this Jacobian can assume the simpler, 5 × 5 form

$$J_i≔\mathbf{J}({\mathbf{R}}_6,{\mathbf{\Gamma }}_6,t_6;t_1,\cdots ,t_6)=\left|\begin{array}{ccccc}\hfill {\mathbf{\Gamma }}_1\times {\mathbf{R}}_{16}\hfill & \hfill {\mathbf{\Gamma }}_2\times {\mathbf{R}}_{26}\hfill & \hfill {\mathbf{\Gamma }}_3\times {\mathbf{R}}_{36}\hfill & \hfill {\mathbf{\Gamma }}_4\times {\mathbf{R}}_{46}\hfill & \hfill \mathbf{0}\hfill \\ \hfill ({\mathbf{\Gamma }}_1\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill & \hfill ({\mathbf{\Gamma }}_2\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill & \hfill ({\mathbf{\Gamma }}_3\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill & \hfill ({\mathbf{\Gamma }}_4\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill & \hfill ({\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill \\ \hfill ({\mathbf{\Gamma }}_1\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill & \hfill ({\mathbf{\Gamma }}_2\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill & \hfill ({\mathbf{\Gamma }}_3\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill & \hfill ({\mathbf{\Gamma }}_4\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill & \hfill ({\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill \end{array}\right|$$ (3)

Here

$${\mathbf{R}}_{\mathit{\text{ij}}}={\mathbf{R}}_j-{\mathbf{R}}_i,{\mathbf{\Gamma }}_i=\frac{{\mathbf{R}}_i^{\prime }-{\mathbf{R}}_i}{\Vert {\mathbf{R}}_i^{\prime }-{\mathbf{R}}_i\Vert }$$ (4)

and e_i, i = 1, 2, 3 are the usual unit vectors along axes x, y, z of an arbitrary reference frame (the Lab frame). The atoms associated with closure are

$${\mathbf{R}}_{2k-1}=N_k,{\mathbf{R}}_{2k}=C{\alpha }_k(={\mathbf{R}}_{2k-1}^{\prime }),{\mathbf{R}}_{2k}^{\prime }=C_k;k=1,2,3$$ (5)

We note that the term Γ₅ × R₅₆ = 0 and was omitted. In the general case, the three pivot residues are indexed by 1 ≤ n₁ < n₂ < n₃ ≤ N, and this reindexing will be implied where appropriate.

It is well known²² that the Jacobian in the form first proposed by Dodd et al.²⁰ is incomplete, and lacks frame invariance. In a rigorous derivation of the Jacobian from the configuration integral, Wu and Deem²² show that the correct, frame invariant form is

$$J^{-1}=\frac{1}{{\mathbf{\Gamma }}_6·{\mathbf{e}}_3}{J}_i$$ (6)

However, since the acceptance criterion involves ratios of Jacobians computed at the same frame, the additional factors cancel and the relative probabilities remain unchanged.

Although the latter form (6) is indeed invariant if all vectors are changed by an arbitrary affine transformation, it has the undesirable feature that it involves a projection to an arbitrary frame. Consequently, the factor Γ₆ · e₃ may accidentally vanish (in which case J_i will also vanish) necessitating a random reorientation of the frame to break the degeneracy. Thus it is desirable to eliminate this superuous dependence and derive a form that depends only on intrinsic (body frame) coordinates, for which invariance is easily seen. This can be accomplished by carrying out an expansion of this determinant in complementary minors; indeed, the top 3 rows are expressed in terms of intrinsic coordinates, while the last two involve projections to the space frame. We thus expand the determinant as

$$J_i={\displaystyle \sum _{i=1}^4}{(-1)}^i\left|\begin{array}{cc}\hfill ({\mathbf{\Gamma }}_i\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill & \hfill ({\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill \\ \hfill ({\mathbf{\Gamma }}_i\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill & \hfill ({\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill \end{array}\right||{\mathbf{\Gamma }}_j\times {\mathbf{R}}_{j6}{\mathbf{\Gamma }}_k\times {\mathbf{R}}_{k6}{\mathbf{\Gamma }}_l\times {\mathbf{R}}_{l6}|$$ (7)

where the indices (i, j, k, l) are a cyclic permutation of (1, 2, 3, 4).

Applying the well known identity (e.g.,⁴¹, Eq.(25), p.76)

$$\left|\begin{array}{cc}\hfill \mathbf{A}·\mathbf{C}\hfill & \hfill \mathbf{B}·\mathbf{C}\hfill \\ \hfill \mathbf{A}·\mathbf{D}\hfill & \hfill \mathbf{B}·\mathbf{D}\hfill \end{array}\right|=\mathbf{A}·\mathbf{C}\mathbf{B}·\mathbf{D}-\mathbf{B}·\mathbf{C}\mathbf{A}·\mathbf{D}=(\mathbf{A}\times \mathbf{B})·(\mathbf{C}\times \mathbf{D})$$ (8)

to the first of the 2 × 2 minors in Eq.(7) we have:

$$\left|\begin{array}{cc}\hfill ({\mathbf{\Gamma }}_1\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill & \hfill ({\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_1\hfill \\ \hfill ({\mathbf{\Gamma }}_1\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill & \hfill ({\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_2\hfill \end{array}\right|=({\mathbf{\Gamma }}_1\times {\mathbf{\Gamma }}_6)\times ({\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)·{\mathbf{e}}_3=({\mathbf{\Gamma }}_1·{\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)({\mathbf{\Gamma }}_6·{\mathbf{e}}_3)$$ (9)

The remaining 2 × 2 minors result in analogous expressions. Substituting these into Eq.(7) we have

$$\frac{J_i}{{\mathbf{\Gamma }}_6·{\mathbf{e}}_3}={\displaystyle \sum _{i=1}^4}{(-1)}^i({\mathbf{\Gamma }}_i·{\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)|{\mathbf{\Gamma }}_j\times {\mathbf{R}}_{j6}{\mathbf{\Gamma }}_k\times {\mathbf{R}}_{k6}{\mathbf{\Gamma }}_l\times {\mathbf{R}}_{l6}|$$ (10)

(as above, the indices (i, j, k, l) are a cyclic permutation of (1, 2, 3, 4)), which can be recombined to give the expression for the inverse Jacobian

$$J^{-1}=\frac{1}{{\mathbf{\Gamma }}_6·{\mathbf{e}}_3}{J}_i=\left|\begin{array}{cccc}\hfill {\mathbf{\Gamma }}_1\times {\mathbf{R}}_{26}\hfill & \hfill {\mathbf{\Gamma }}_2\times {\mathbf{R}}_{26}\hfill & \hfill {\mathbf{\Gamma }}_3\times {\mathbf{R}}_{46}\hfill & \hfill {\mathbf{\Gamma }}_4\times {\mathbf{R}}_{46}\hfill \\ \hfill ({\mathbf{\Gamma }}_1·{\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)\hfill & \hfill ({\mathbf{\Gamma }}_2·{\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)\hfill & \hfill ({\mathbf{\Gamma }}_3·{\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)\hfill & \hfill ({\mathbf{\Gamma }}_4·{\mathbf{\Gamma }}_5\times {\mathbf{\Gamma }}_6)\hfill \end{array}\right|$$ (11)

where we took advantage of the fact that Γ_i × R_i6 = Γ_i × R_i+1,6 with i = 1, 3 due to the fact that the axes Γ_i, Γ_i+1, i = 1 or 3 are coterminal. Fig.(1(a)) shows all quantities that enter in the Jacobian.

This 4 × 4 determinant is the frame invariant form of the inverse Jacobian for the TLC method. It has the advantage that it is expressed entirely in terms of body coordinates, and thus it is free from degeneracies and can be evaluated without projecting to an ad hoc coordinate system. It is numerically equivalent to the Wu and Deem form (6), when the latter is defined. The Jacobian (11) can be easily expressed in terms of the intrinsic parameters (d_i, θ_i, ξ_i, δ_i), i = 1, 2, 3 entering in the TLC algorithm⁴², a feature that it shares with reduced Jacobians derived by other authors^{22, 43}. However such expressions lack the simplicity and geometrical appeal of (11).

2.5 Backbone Perturbation Procedure

The loop closure algorithm described in the previous section, while perfectly general, is currently implemented as a strategy for perturbing only the backbone coordinates. The sidechain coordinates perturbation procedure, as well as the strategy for combining these perturbations in a way such that detailed balance is maintained, will be outlined in the two sections. An important design feature of this approach is that the backbone and sidechain perturbations are generated independently.

An important feature of both the backbone selection probability and the sidechain selection probability is that they are reversible, or

$$\alpha (\mathbf{t}\to \mathbf{t}\prime )=\alpha (\mathbf{t}\prime \to \mathbf{t})$$ (12)

where t′ = t + δt is the trial move starting from the torsion state t and δt is the perturbation vector to the loop of interest. For the purposes of this work, we require the selection probability to be uniform to enforce equation 12. For this to be true, we need to establish the procedure which ensures that a uniform distribution of torsions over the entire loop can be generated.

The procedure for generating a trial move δt closely follows that of Ref.^{20, 22, 23, 29}. Since the algorithm currently solves for 2N − 6 torsions, and we wish to have a procedure that is valid for loops of arbitrary length, we must select a subset of 2N − 6 torsions. There is some flexibility in how this could be done, but the present implementation is as follows (see Fig. 2):

1. From the designated loop torsions, a single torsion angle i is selected uniformly and identified as a driver angle coordinate (the yellow circle in Fig. 2), as has been described in previous work²⁶.

2. For torsion t_i, a random variate δt_i is generated, with a maximum value of up to π.

3. A randomly constructed triaxial closure is generated by randomly selecting 3 α carbons as pivots from the loop (excluding the α carbon on which the driver angle resides), and assigning the ϕ/ψ angles as the torsions (the grey triangle in Fig. 2).

4. A set of torsions for the stationary solution t_k, k ∈ [1, K] is generated, resulting in up to K = 16 solutions. For this case, only the alternative sets of pivot coordinates are considered, with the driver angle held at t_i. For each solution, a Jacobian term J(t_k) is computed.

5. A set of torsions for the perturbed solution t_l, l ∈ [1, L] is similarly generated, with associated J(t_l) terms.

6. A trial solution t′ is selected from the solutions (t_k, t_l) with the following probability:

   $$\alpha (\mathbf{t}\to \mathbf{t}\prime )=\frac{J(\mathbf{t}\prime )}{{\displaystyle {\sum }_{k=1}^K}J({\mathbf{t}}_k)+{\displaystyle {\sum }_{l=1}^L}J({\mathbf{t}}_l)}$$ (13)

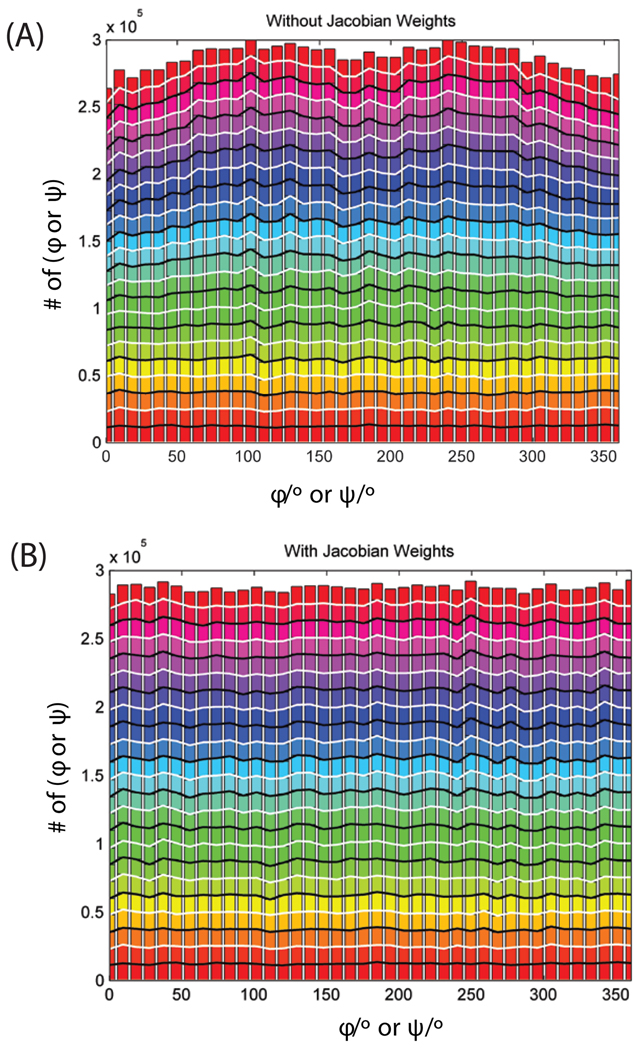
   To show that this procedure generates a uniform distribution, the phi/psi angles of an 11 residue polypeptide is sampled with no potential. Half of the time, the loop closure procedure is applied as described above, and the other half of the time, only a driver angle is perturbed uniformly, with the remaining Cartesians updated accordingly (with no closure condition enforced). The second procedure is required so that the full space of dihedral angles is accessible. Every move is accepted, with no potential applied or steric exclusion. This procedure generates a uniform distribution of torsions, as is shown in Fig. 3. It shows a distribution of an 11-residue peptide sampled with the loop closure procedure described above. Only backbone DoF are sampled, and no forcefield is applied. The endpoints are constrained to fixed positions. This control closely follows previous work^{20, 23}. Fig. 3(a) shows the distribution of angles with no Jacobian selection term applied, and Fig. 3(b) shows the distribution with the reweighting term applied. The Jacobian term clearly improves the uniformity of the sampling.

Fig. 3.

Distribution of ϕ/ψ angles without (A) and with (B) Jacobian weighting of selection for an 11-residue peptide. A Total of 4.5 × 10⁵ trial moves were generated. No forcefield is used the selection probability, and all trial moves are accepted.

2.6 Sidechains

The efficient sampling of sidechains²² is important since sidechain conformations often determine the biological function of proteins. In the current work, the sidechain χ angles are not taken from the rotamer library due to their nonuniform distribution. Instead, to generate the sidechain trial moves, a single sidechain is randomly selected and each χ angle is perturbed by a value which is randomly and uniformly distributed in a defined domain [−d/2, d/2]^{25, 44}. The polar hydrogens for the selected residue are sampled as well over the domain [−π, π].

To improve the sampling efficiency, no energy is computed for the states with steric clashes, which are defined based on the distances between heavy atoms. Specifically, a steric clash is defined when pairs of heavy atoms are closer than 0.7 times the sum of their Lennard-Jones radii. Rapid identification of steric clashes (using neighbor lists) avoids computationally expensive energy evaluations, for conformations that will result in very high energies and negligible acceptance probabilities.

The most expensive term in energy evaluation is the solvation energy in which the time consuming step is the computation of Born radii. Since the Born radii and the long range energy terms generally vary slowly for relatively small, local conformational changes, less frequent evaluation of these terms will contribute more to the sampling performance. For this purpose the Multiple Time-Step Monte Carlo sampling (MTSMC) procedure⁴⁵ is incorporated in the present method, in a scheme based on that in Ref.⁴⁴. The Born radii and the long range interactions are held fixed at the latent state of the original coordinates during the inner loop sampling, and only updated in every outer loop calculation. The final configuration from the inner loop is then taken to be a trial move and subjected to the MTSMC acceptance criterion (see Eq. 20 in Ref.²⁵)

2.7 The POSH Monte Carlo Method

Both the TLC method for determining the backbone moves of loop residues and the sidechain sampling via perturbation have been incorporated in the POSH (port out, starboard home) Monte Carlo method introduced in a previous work²⁵. The application of this method on small peptide systems has shown reasonable agreement with experiments²⁵. In the present work, we are interested in its performance in more complicated protein systems with flexible loops.

Briefly, the move sets in this approach consist of two steps: an initial trial (1 → 2) move with large perturbation followed by a series of annealing moves consisting of smaller perturbation within the inner loop of length N_I (2 → 3). The generalized Metropolis acceptance probability for this series of moves is given by:

$$\mathit{\text{acc}}(1\to 3)=\mathit{\text{min}}(1,\frac{p_3{T}_{41}}{p_1{T}_{23}})$$ (14)

where p₁ and p₃ are the probabilities of being in the original and final trial state, respectively. T₄₁ and T₂₃ are transition probabilities. T₂₃ is the normal forward transition probability, as would be given in the usual derivation of detailed balance, but T₄₁ is a reverse transition probability that is constructed using an alternative reverse path through configuration space that is constructed by taking the final state (state 3) and subtracting the perturbation (1 → 2) from state 3 to arrive at state 4. Further details are given in Ref.²⁵.

The trial moves are generated by a perturbation that uniformly varies over some domain [−d/2, d/2] with a different magnitude for the initial and annealing steps. In this work, for both types of trial moves, either backbone or sidechain is allowed to be perturbed with equal probability. For backbone perturbations, the ϕ or ψ dihedral angle can vary over the domain of [−2π, 2π] for initial steps and [−π/4, π/4] for annealing steps. For sidechain χ angles, the domain is [−π, π] and [−π/9, π/9], respectively, for the initial and inner step trial moves. The number of inner steps N_I is set to 20 which was reported as the upper bound of inner steps for generating precise distribution. For all protein systems studied in this work, a mixture of 50% POSH and 50% standard MC sampling, followed by the MTSMC procedure, is used due to its better performance as studied in the previous work²⁵.

3 Simulations

We applied the loop Monte Carlo method described above to several proteins with flexible loops. The first is the enzyme triosephosphate isomerase (TIM) which has been used as a model system for studying loop flexibility, primarily by NMR. This enzyme catalyzes the reversible isomerization of dihydroxy-acetone phosphate (DHAP) to D-glyceraldehyde 3-phosphate (GAP). The active site loop 6 (residues 167–176) undergoes conformational changes upon ligand binding, and is believed to be flexible in the absence of ligand binding, transitioning between ‘open’ and ‘closed’ states. To assess the capability of our method to capture the dynamical properties of this flexible loop, three sets of simulations were performed. The first one started from the apo yeast TIM (PDB ID 1YPI) with open loop conformation (we call this SIM1), and the second started from the 2-phosphoglycolate (PGA)-bound TIM (PDB ID 2YPI) with closed loop conformation (SIM2), and the third is the same as the second except that the ligand PGA was removed from the initial structure (SIM3).

The titratable residues in the starting structures were predicted according to the experimental conditions. Specifically, in all simulations, His95 was treated as neutral, and protonated on the Nε2. Glu165 is protonated in SIM2 in order to maintain the strong interaction with ligand PGA⁹, but was unprotonated in the other simulations. Residues within 8 Å of the active site loop were included for the side chain sampling and the flexible loop was extended to include residues 165–178 in the simulations for both the backbone and side chain sampling. The force field OPLS-AA^{46, 47} was used for the protein TIM and ligand PGA except that the partial charges for the phosphate group of PGA were adjusted based on the previous work by Wong et al.⁴⁸ The Surface Generalized Born (SGB)^{49, 50} model was used for implicit solvent with the treatment of nonpolar term⁵⁰. To prevent the sampling from being trapped in local minima, all simulations were performed at the temperature of 600K. Each simulation has a length of N_o = 2 × 10⁵ up to 5 × 10⁵ outer steps. Data analyses were performed over the equilibrium simulations (roughly after 10⁵ outer steps) during which the potential energy is relatively stable.

The same protocol was also applied to other protein systems which have been studied by NMR experiments, specifically those with PDB ID 1H2O, 1XWE, and 1Q9P. By choosing NMR structures, we eliminate any concerns about crystal packing influencing the loop conformation or flexibility. These specific proteins were chosen because each has two loops consisting of 5–8 residues, one of which has multiple conformations with large variation among the various NMR models (flexible loop) and the other has a narrow range of loop conformations among the NMR models (rigid loop). Both the flexible and rigid loops were simulated using the same sampling protocol and the same parameter settings in order to compare with the experimental data since both loops within the same protein were measured in the same experimental conditions. The titratable residues in the starting structures were protonated at the experimental pH = 7.0 for 1H2O, 6.0 for 1XWE and 5.8 for 1Q9P. The flexible loops consist of residues 59–64 for 1H2O, 1609–1616 for 1XWE and 48–53 for 1Q9P; the residues in the rigid loops are 46–51 for 1H2O, 1536–1540 for 1XWE and 78–82 for 1Q9P.

4 Results and Discussion

As an initial illustration of the utility of our loop MC method for sampling conformation space of protein loops, we applied this method to the well-studied enzyme triosephosphate isomerase (TIM). The active site loop undergoes large-scale motions interconverting between open and closed conformations. This conformational transition occurs on the time scale of milliseconds¹⁷, making it a challenge for molecular dynamics simulations in previous studies^{51, 52}.

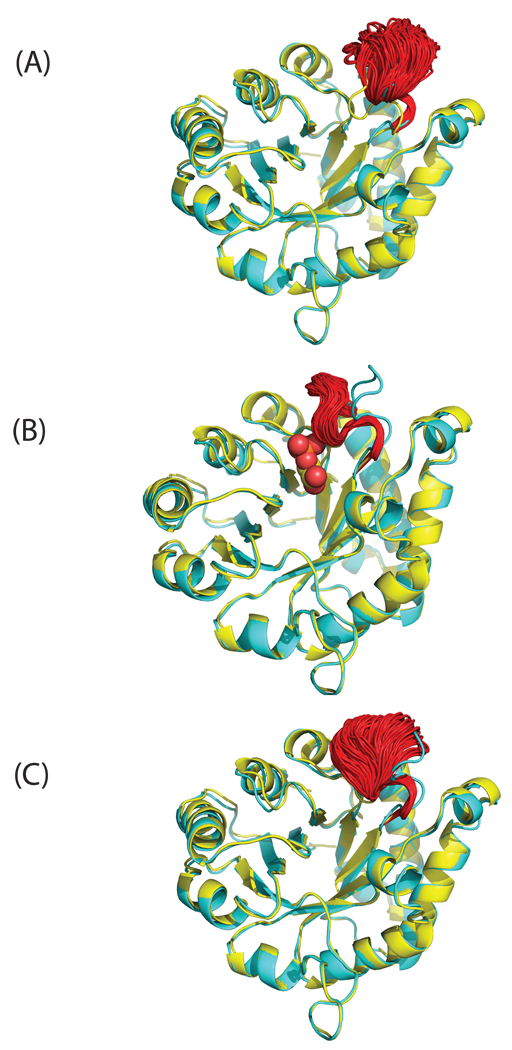
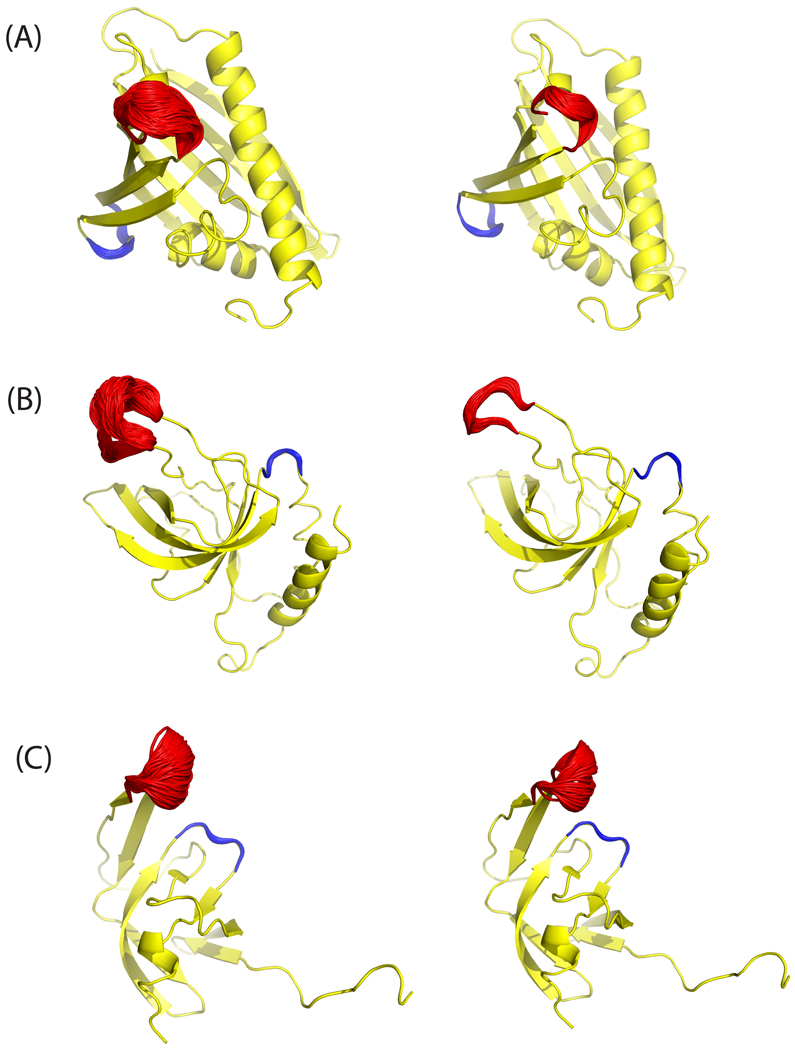
In the current work, multiple transitions between open and closed loop conformation of yeast TIM have been observed in the simulation of the apo protein, but only at 600 K (vide infra). Figure 4 (a) and (c), which start from the open and closed state, respectively, show sampled loop conformations from the equilibrium ensemble, spanning both open and closed form. In the simulation with the ligand PGA bound, the active site loop stays in the closed conformation, as can be seen in Fig. 4(b). These results agree qualitatively with NMR experiments which found that the loop samples open and closed conformations whether or not a ligand was bound, but that ligand binding shifted the equilibrium strongly towards the closed conformation^{17, 53}. Upon PGA binding, the carboxylate of the ligand protonates residue Glu165 making it hydrogen bonded with PGA instead of with Ser96 in the apo structure, such that the closed loop conformation is preferred in the presence of ligand.

Fig. 4.

The ensemble structures (red) for the flexible loop (residues 165–178) of yeast TIM were taken from the equilibrium simulation with initial structures of (A) apo (open) conformation, (B) bound (closed) conformation and (C) the closed conformation with the ligand PGA removed. The X-ray structure of apo yeast TIM (PDB 1YPI) is shown in yellow and bound state (PDB 2YPI) in cyan. The ligand PGA is depicted by spheres.

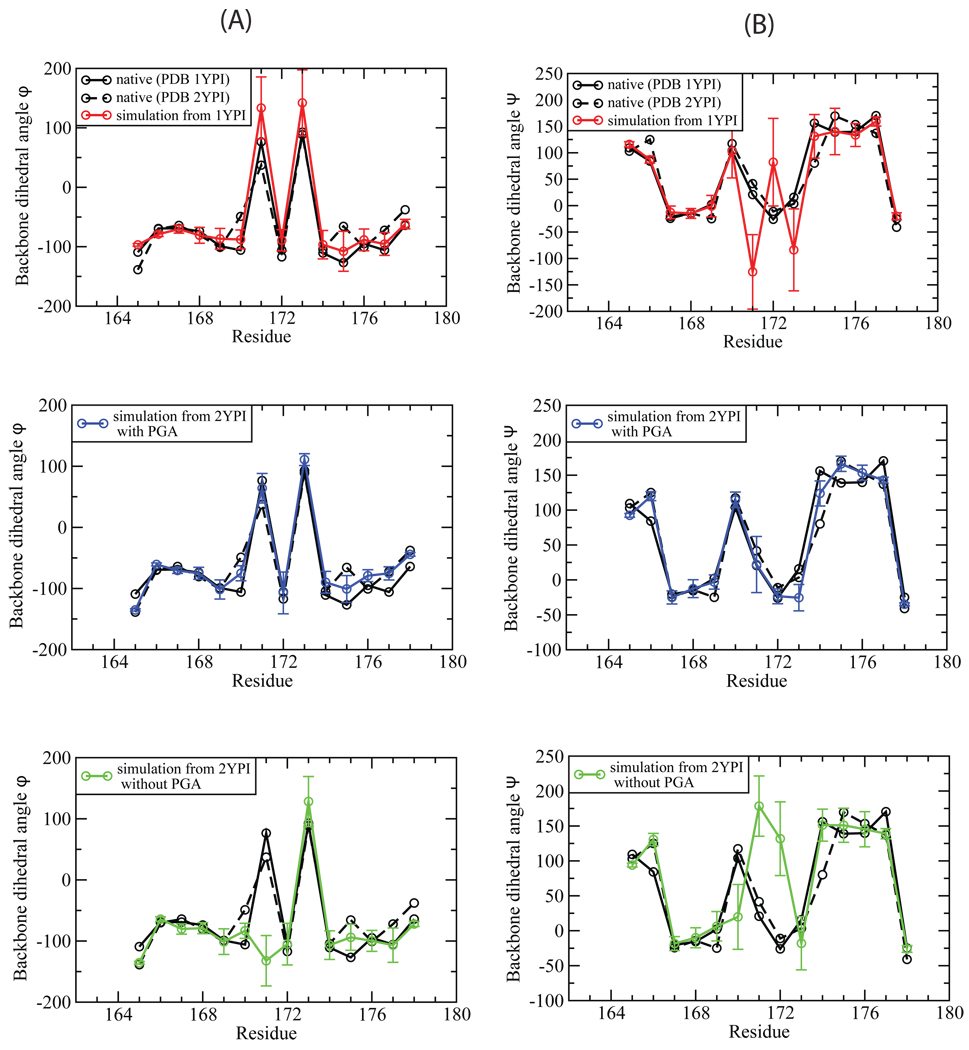
It has been known that the active site loop of TIM moves largely as a rigid unit^{51, 54}. Figure 5 shows that the backbone dihedral angles of the flexible loop in the X-ray structure of apo TIM are very similar to those in the structure of ligand-bound TIM. The ensembles generated by the loop MC method largely agree with the experimental data in this regard. We calculated the backbone ϕ and ψ angles and averaged them over the equilibrium ensemble for each of the three simulations. For the holo simulations, the ensemble averaged ϕ and ψ angles agree well with those measured in the X-ray structures, as shown in Fig. 5 (a) and (b) (blue lines). Similar agreement was also found for the apo simulations started from both the open and closed conformation, except that residues 170–173 have relatively large deviation and fluctuation, which is consistent with the findings in previous simulation studies^{17, 52} (red and green lines in Fig. 5 (a) and (b)).

Fig. 5.

The comparison of the calculated backbone dihedral angles, ϕ (A) and ψ (B), with those measured in the X-ray structures. The black solid line is for apo TIM (PDB 1YPI) and the dashed line for the ligand-bound TIM (PDB 2YPI). The calculated dihedral angles were averaged over the equilibrium ensemble simulated from the initial structure of apo (red), ligand-bound (blue), and closed form with the ligand PGA removed (green).

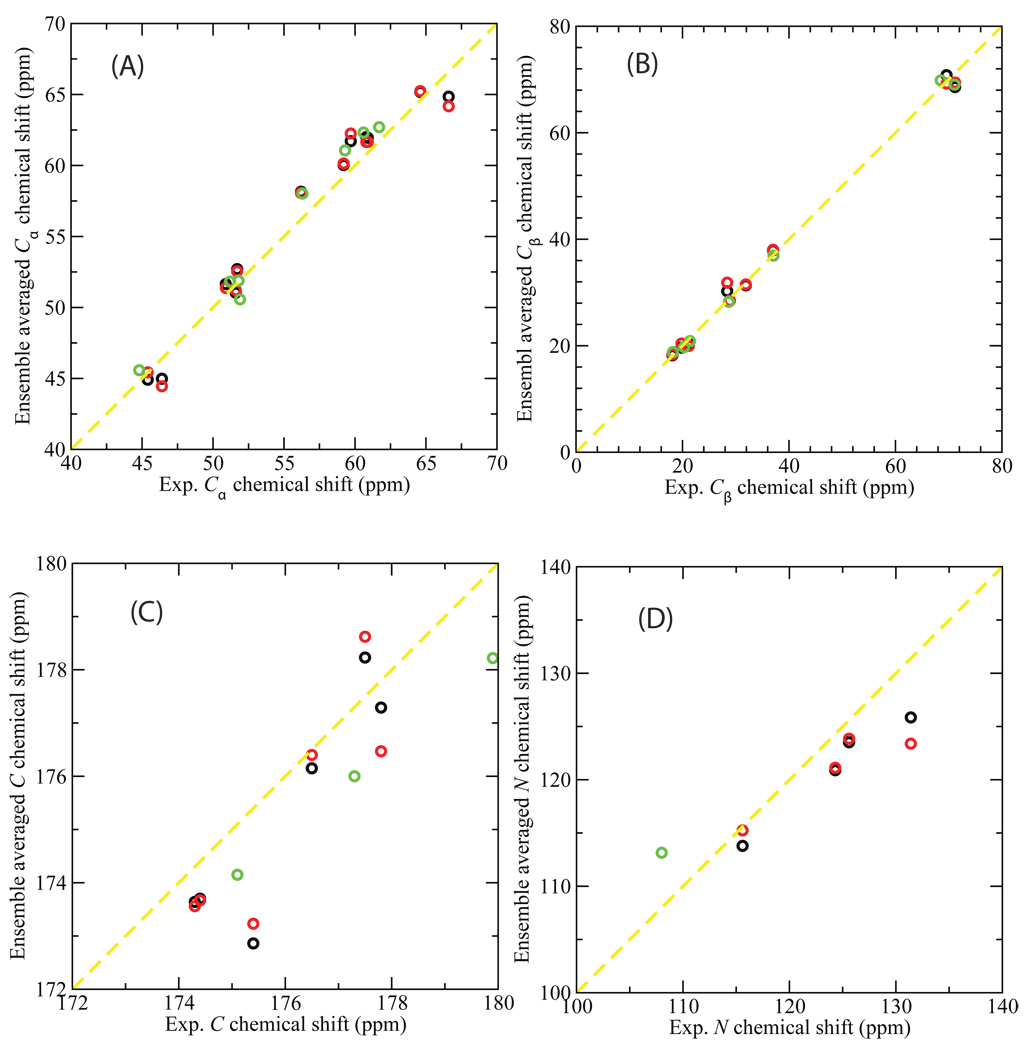
NMR spectroscopy can provide information on both the structure and dynamics of proteins in physiologically relevant environments⁵⁵. The chemical shift is NMR’s most ubiquitous parameter, the variation of nuclear magnetic resonance frequencies of the same kind of nucleus due to variations in the electron distribution. To directly compare with the experimental data, ensemble averaged chemical shifts were calculated for each equilibrium ensemble by using SHIFTX⁵⁶ to calculate chemical shifts for the residues of the flexible loop in each conformation and then averaging over all the conformations in the ensemble. For the apo simulations, starting from either the open or closed structures, the ensemble-averaged chemical shifts were compared with NMR measurements of apo yeast TIM⁵⁷. For the simulation of the ligand-bound, closed structure, NMR data measured for G3P-bound yeast TIM⁵⁷ were used. [The chemical shifts for the closed loop of the enzyme bounded with G3P and GPA are very similar (Yimin Xu, personal communication)]. A strong linear correlation was found between the ensemble-averaged and experimentally measured chemical shifts for C_α (Fig. 6 (a)) and C_β (Fig. 6 (b)) atoms with the correlation coefficient r of 0.98 or higher in all cases. For carbonyl C and amide N atoms of the flexible loop, although there are fewer experimental chemical shifts available, the calculated ensemble averages have small variations from experimental values (Fig. 6 (c) and (d)). The agreement with the NMR chemical shifts provides additional evidence that the ensembles generated by the loop MC sampling are reasonable.

Fig. 6.

Ensemble-averaged chemical shifts (ppm) versus the NMR experimental measurements for C_α (A), C_β (B), carbonyl C (C), and amide N (D) atoms of the flexible loop 6 of yeast TIM. SHIFTX⁵⁶ was used to calculate chemical shifts which were then averaged over an ensemble of 1000 structures from the equilibrated MC simulations. The starting PDB structures for the simulations are: 1YPI (black); 2YPI with the ligand PGA removed (red); and 2YPI with PGA bound (green). The experimental chemical shift data are those for apo yeast TIM in NMR experiment⁵⁷ (for comparison with the apo simulations), and for yeast TIM with ligand G3P⁵⁷ (for comparison with the holo simulation). Experimental chemical shifts are not available for some atoms and these are omitted.

We note that the experimental chemical shifts were measured at 300 K, while our simulations were performed at 600 K. This is because at 300 K it is difficult to observe the conformational transitions between the open and the closed state. We suspect, but cannot prove, that this occurs in part due to 1) the well-known tendency of generalized Born implicit solvent models to over-stabilize salt-bridges, 2) the effect of constraining the omega angles, as well as the bond angles and lengths, in addition to the loop closure condition, and 3) sampling only the loop and not the remainder of the protein. Using a higher temperature overcomes all of these effects and reasonable ensembles are generated which agree with the NMR chemical shifts. Because the Monte Carlo sampling scheme does not perturb degrees of freedom outside the loop, such that the overall structure is preserved, a higher temperature sampling protocol can still provide physical insights. The efficiency gained by sampling a lower dimensional space, while still obtaining a reasonable estimate of ensemble properties, motivates the use of this set of approximations.

As a second initial application, we also applied our sampling method to other protein structures, solved by NMR, which have loops with differing flexibility in order to evaluate our ability to distinguish the flexible and rigid loops within the same protein. The conformational ensembles from equilibrium simulations for both the flexible and rigid loops are shown in Fig. 7 for three proteins with PDB ID 1H2O (a), 1XWE (b), and 1Q9P (c) sampled at 600 K (left) and 300 K (right). These results clearly show that the loop residues which are flexible in the experimentally derived structures consistently are more floppy in the sampled ensemble at either temperature than the loop residues which are relatively rigid in the same NMR structures. To further quantify these results, root mean square fluctuation (RMSF) of the heavy atoms in both loops were calculated for the sampled and NMR models as shown in Table 1. We recognize that the set of NMR models for each protein cannot be viewed as a true ensemble, but the qualitative agreement is nonetheless encouraging. Thus, for studying protein loop flexibility, our method is a viable alternative to molecular dynamics simulations, which have also been used successfully to obtain ensembles in quantitative agreement with NMR data. In the cases examined here, the differences in rigidity appear to be related simply to the level of solvent exposure, i.e., floppy loops are more solvent exposed and have less interaction with their neighbors. For simulations of all studied protein systems, three NMR targets and TIM, the average acceptance ratio is about 14%.

Fig. 7.

Ensembles of loop structures from equilibrium simulations using MC sampling for proteins with PDB ID: (A) 1H2O, (B) 1XWE and (C) 1Q9P sampled at T=600 K (left) and T=300 K (right). The sampled flexible loops (‘floppy’) which have large fluctuation in the NMR models are shown in red and the rigid loops with very small fluctuations are in blue. The structures in yellow are taken from MODEL 1 of the PDB file.

Table 1.

Root-mean-squared fluctuation (RMSF) (Å) of heavy atoms of both floppy and rigid loops in the equilibrium ensemble simulated by POSH MC method with initial structure of the first model of NMR structures. For comparison, the RMSF over all NMR models for each protein are also computed at both 600 K and 300 K.

Heavy atom RMSF	1H2O			1Q9P			1XWE
	NMR	POSH		NMR	POSH		NMR	POSH
		600 K	300 K		600 K	300 K		600 K	300 K
Flexible loop	2.75	1.64	0.75	3.51	1.27	1.06	4.83	2.50	1.10
Rigid loop	0.49	0.40	0.15	1.25	0.38	0.18	1.03	0.50	0.31

Our current approach only varies phi-psi angles as they are most flexible, but actually it is possible to include all other DoF in the MC scheme in any desired combination. We are working on a further version of the algorithm that will incorporate sampling which allows omega angles, as well as bond lengths and angles, to fluctuate more freely, which may allow for lower temperature sampling of systems of this type. Although in the present study we have considered solvation effects implicitly only, including water molecules explicitly in the simulation is possible in principle. However, water molecules in the immediate vicinity of a loop would lead to steric clashes whenever a large backbone move is attempted, which would reduce the efficiency of the present approach.