Determinants of valve gating in collecting lymphatic vessels from rat mesentery

Abstract

Secondary lymphatic valves are essential for minimizing backflow of lymph and are presumed to gate passively according to the instantaneous trans-valve pressure gradient. We hypothesized that valve gating is also modulated by vessel distention, which could alter leaflet stiffness and coaptation. To test this hypothesis, we devised protocols to measure the small pressure gradients required to open or close lymphatic valves and determine if the gradients varied as a function of vessel diameter. Lymphatic vessels were isolated from rat mesentery, cannulated, and pressurized using a servo-control system. Detection of valve leaflet position simultaneously with diameter and intraluminal pressure changes in two-valve segments revealed the detailed temporal relationships between these parameters during the lymphatic contraction cycle. The timing of valve movements was similar to that of cardiac valves, but only when lymphatic vessel afterload was elevated. The pressure gradients required to open or close a valve were determined in one-valve segments during slow, ramp-wise pressure elevation, either from the input or output side of the valve. Tests were conducted over a wide range of baseline pressures (and thus diameters) in passive vessels as well as in vessels with two levels of imposed tone. Surprisingly, the pressure gradient required for valve closure varied >20-fold (0.1–2.2 cmH₂O) as a passive vessel progressively distended. Similarly, the pressure gradient required for valve opening varied sixfold with vessel distention. Finally, our functional evidence supports the concept that lymphatic muscle tone exerts an indirect effect on valve gating.

lymph propulsion is determined by the interplay of active and passive forces that combine to propel lymph centrally against a pressure gradient (28, 44, 58). Active lymph propulsion is achieved by the spontaneous, rhythmic contractions of collecting lymphatic vessels (21, 30, 38, 55). Passive factors influencing lymph flow include Starling forces that favor net fluid reabsorption at the level of the lymphatic capillaries, tissue compression from the contractions of nearby skeletal muscle fibers (19, 45), respiratory movements (7, 41, 43), and gravitational forces (45, 50).

Lymphatic valves are essential for minimizing backflow of lymph, and two systems of valves have been described previously (50). Primary lymphatic valves are composed of the overlapping, but discontinuous, junctions of endothelial cells in lymphatic capillaries (8, 9, 40), which function to facilitate preferential movement of interstitial fluid into initial lymphatics. In contrast, secondary lymphatic valves are typically bicuspid structures, spaced every few millimeters along collecting lymphatic vessels. Valve location and development closely correspond with the presence of a muscle cell layer in the vessel wall. Each semilunar valve cusp is lined on both sides by a layer of endothelial cells and anchored at its base by collagen fibers in the wall. The downstream insertion point of a valve leaflet is anchored to the wall by collagen and elastin (1, 26, 54), forming a buttress to prevent inversion when output pressure is elevated (50). Competent secondary valves are essential for ensuring the net proximal flow of lymph toward the heart. A series of dysfunctional valves would exacerbate lymphedema by allowing lymph reflux into peripheral networks of lymphatic vessels, thus promoting elevated hydrostatic pressure in the initial lymphatics, which, in turn, would retard fluid absorption from the interstitium. The consequences of insufficient or malformed secondary valves are readily apparent in genetic conditions involving lymphatic valve malformation (6, 47).

Secondary lymphatic valves are thought to gate passively according to the instantaneous luminal pressure gradient (36, 50), opening and closing with each lymphatic contraction cycle, as fluid is transferred from upstream to downstream lymphangions (18, 59). In some species, a role for active force development by specialized smooth muscle cells or actin filament extensions from these cells into the leaflets (4, 34) has been postulated to facilitate valve closure (5, 31); however, this view is based almost exclusively on structural rather than functional evidence (50). Studies of lymphatic valve ultrastructure abound (1, 26, 54), but we are unaware of published measurements of the forces required to gate secondary lymphatic valves. A passive mechanism for gating is inferred from assumptions based on structure (“funnel-like” shape) and size (37, 50), in which a very low Reynolds number for lymph flow predicts that valve closure is strictly controlled by pressure and viscous forces. Passive movements of the valve leaflets are consistent with the results of micropipette occlusion and fluid injection protocols (27, 29, 52, 53).

Although there is no reason to question the basic assumptions regarding passive lymphatic valve gating (50), several observations in isolated, pressurized collecting lymphatic vessels from rat mesentery led us to suspect that other factors significantly influence this process. First, the valves in passive, single-valve segments are open when pressures in the two cannulation pipettes are equal. A valve can remain open even during a spontaneous contraction because the intraluminal pressure spike associated with systole is blunted by the low access resistance created by the cannulation pipettes. Second, for strongly pumping segments with two valves, in which intraluminal pressure in the lymphangion is measured with a servo-null system, the output valve is often observed to open at the peak of systole even when peak systolic pressure does not reach or exceed the pressure in the output pipette (unpublished observations), as would be predicted if only the pressure gradient determined valve opening; moreover, the discrepancy between the two pressures appears to depend on the degree to which the vessel is distended.

For these reasons, we hypothesized that the gating of secondary lymphatic valves is governed primarily by the passive, trans-valve pressure gradient but is also influenced by leaflet stiffness or other mechanical factors related to vessel distention. To test this hypothesis, we devised protocols to measure the small pressure gradients required to open or close lymphatic valves under carefully controlled conditions and to determine whether those pressure gradients vary as a function of vessel diameter.

An additional goal of our study was to determine the valve gating patterns during the active, lymphatic contraction cycle. Surprisingly, these patterns have not been documented in detail previously but are assumed to be similar to those observed for heart valves during the cardiac cycle. However, at least two studies have noted the apparent absence of a period of isovolumic systole in spontaneously contracting lymphatic segments (2, 18), when closure of both valves of a lymphangion should be required for intraluminal pressure development (38). Thus we sought to measure valve gating patterns during active lymphatic contractions in relation to pressure and diameter. We predicted that the patterns would be more complex than those of cardiac valves because 1) lymphatic preload and afterload can vary independently or simultaneously depending on the prevailing local pressure conditions, and 2) there are differences in the flow regimes in lymphatic vessels (low Reynolds numbers and highly viscous flow) vs. the heart (large Reynolds numbers and important inertial effects).

METHODS

Vessel isolation.

All animal protocols were approved by the University of Missouri Animal Care and Use Committee and conformed to the Public Health Service Policy for the Humane Care and Use of Laboratory Animals (PHS Policy, 1996).

Male Sprague-Dawley rats (150–300 g) were anesthetized with sodium pentobarbital (60 mg/kg ip), and a loop of intestine from each animal was exteriorized. Lymphatic vessels (80–180 μm inner diameter) were dissected from mesenteric arcades and placed in physiological saline solution (PSS) with albumin (APSS) at room temperature. The animal was subsequently euthanized with Nembutal (120 mg/kg ic). APSS contained the following (in mM): 145.0 NaCl, 4.7 KCl, 2.0 CaCl₂, 1.2 MgSO₄, 1.2 NaH₂PO₄, 0.02 EDTA, 5.0 glucose, 2.0 sodium pyruvate, 3.0 3-(N-morpholino) propanesulfonic acid, and 0.5 g/100 ml purified BSA (pH = 7.4 at 37°C). APSS was used for initial dissection and to fill the cannulation pipettes, whereas PSS was used for the regular bath solution in protocols studying spontaneous contractions. High K⁺-PSS (KPSS) was used in some protocols to impose a higher level of tone and was made with the same composition as PSS except for equimolar substitution of K⁺ for Na⁺. The passive properties of the vessel, including most valve gating tests and passive pressure-diameter curves, were assessed in Ca²⁺-free PSS, which was identical to PSS except that 3.0 mM EDTA was substituted for CaCl₂. All chemicals were obtained from Sigma (St. Louis, MO) except albumin (no. 10856; U.S. Biochemicals, Cleveland, OH).

Cannulation, pressurization, and imaging methods.

After removal of fat and loose adventitia, a segment of lymphatic vessel with one or two valves was transferred to a 3-ml chamber, filled with PSS, and cannulated at each end with a glass micropipette held in a Lucite holder mounted on a Burg-style V-track system (17). The entire apparatus was transferred to the stage of an inverted microscope (an inverted Zeiss ACM equipped with Zeiss ×3.2 and ×6.3 Neofluor objectives). Input and output pressures (P_in and P_out, respectively) were initially set from standing reservoirs, and the axial length of the vessel was adjusted so that there was no slack in the vessel with P_in and P_out temporarily set to ∼13 cmH₂O; this was necessary to prevent axial buckling of the vessel at high pressures, which otherwise interfered with accurate diameter tracking. A continuous flow of heated PSS (2 ml/min) prevented changes in osmolarity associated with evaporation.

The vessel image was digitized using a fire-wire CCD camera (model A641FM; Basler, Ahrensburg, Germany). Camera resolution was 1,624 × 1,236 pixels (14 frames per second, monochrome, 12 bits/pixel), but the progressive scan settings were adjusted to acquire a custom video format of 1,624 × 510 pixels at 30 Hz. The effective resolution was 0.53 and 0.99 μm/pixel using Zeiss 6.3 × and 3.2 × objectives, respectively. Inner diameter was continuously tracked using a custom computer algorithm (10). P_in and P_out were measured using low-pressure transducers (CyberSense model 104; Nicholasville, KY) and digitized in synchrony with diameter data at 60 Hz using an A-D card (model PCI 6030e; National Instruments, Austin TX). Video images were captured in AVI files along with embedded pressure and diameter data, so that all the measured parameters could be replayed offline (using LabVIEW; National Instruments); this method also permitted diameter tracking to be performed at additional sites along the vessel, if needed. The video was compressed (5:1) without degrading the image quality, using a lossless video codec (Lagarith).

After initial equilibration, pressure control was switched from standing reservoirs to a custom-made, analog servo-control system (Cardiovascular Research Institute, Texas A&M University) in which servo-null style pumps (model V102; Ling Dynamic Systems, Royston, UK) were connected to the pipettes and powered by a hardware-based servo-controller through unitary-gain power amplifiers. The controller compared the output signal from the pressure transducers to reference voltages specified by a computer (running LabVIEW) and adjusted the pump voltages accordingly (57). Pressure steps between 0 and 50 cmH₂O could be achieved within 50 ms, and combinations of step- or ramp-pressure waveforms could be applied to the input and/or output ends of the isolated lymphatic segment.

Servo-null pressure recording.

In segments with two valves, the servo-null method was used to directly measure intraluminal pressure (P_L). Servo-null micropipettes were pulled from borosilicate glass (1.0/0.5 mm outer diameter/inner diameter, Omega-dot; Frederick Haer, Bowdoin, ME) using a Sutter P-97 puller (Sutter Instrument, Novato, CA). The tips were either gently broken or beveled to an outer diameter of ∼2 μm. The pipettes were back-filled with 2 M NaCl and connected to a servo-null micropressure system (model 4A; IPM, La Mesa, CA) to monitor intraluminal pressure in the central lymphangion. Positioning was achieved using a hydraulic micromanipulator (model MO-102; Narishige, East Meadow, NY). The servo-null pump incorporated the same type of low-pressure transducer used in the servo-controller. The system was calibrated using a water manometer along with the other pressure transducers before each experiment. The output signal was filtered at 50 Hz (model LPBF-01G; NPI Electronic; Tamm, Germany).

After cannulation, but before the bath temperature was raised to 37°C, the vessel was passive; micropuncture was typically performed during this time to minimize trauma to the vessel. The servo-null system was zeroed with the micropipette positioned just outside the vessel wall. Successful micropuncture left the pipette tip free from obstruction in the vessel lumen. Servo-null measurements of P_L were made immediately downstream from the input valve (see image montage in Fig. 1A) to protect the central lymphangion from changes in axial length that occurred upon penetration of the micropipette through the vessel wall. The success rate, without subsequent impairment of contractions after warming, was ∼80%. The criteria used to assess valid servo-null pressure recordings were the same as described previously (33). The calibration of each micropipette was adjusted after bath temperature reached 37°C and checked periodically during the experiment if pipette plugging was suspected; the test involved simultaneously raising P_in and P_out and adjusting the calibration gain and offset as appropriate to match the pipette pressures.

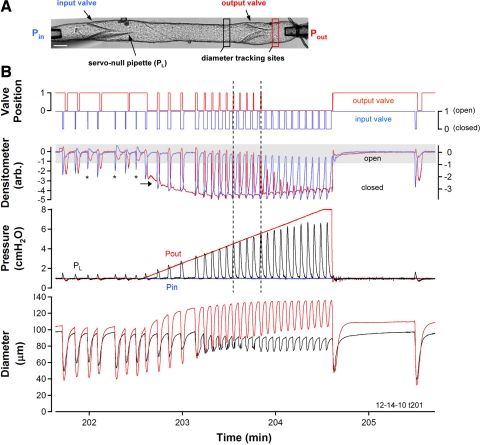
Fig. 1.

A: video montage of the isolated lymphatic vessel preparation, showing the positions of the input, output, and servo-null pipettes relative to the 2 valves. Black and red rectangles indicate the approximate positions of the diameter tracking windows in the central and output segments, respectively. Shadow at bottom left is caused by the servo-null pipette. P_in, input pipette pressure; P_out, output pipette pressure; P_L, intraluminal pressure in the central segment; arb., arbitrary units. Calibration bar = 100 μm. B: representative record of the lymphatic response to ramp-wise elevation in P_out. Initially, P_in and P_out were both set to 1 cmH₂O and, after 7 spontaneous contractions, a P_out ramp to 8 cmH₂O (at 4 cmH₂O/min) was imposed. Bottom trace: time course of the inner diameter changes in the central segment (black) and the output segment (red). Pressure traces show P_in (blue), P_out (red), and P_L (black) superimposed on a common scale. As the P_out ramp progressed, greater intraluminal systolic pressures were developed by the central segment during each contraction cycle but diastolic pressure returned to 1 cmH₂O each cycle. Top two traces: net densitometer signals recorded from pairs of windows positioned over the midlines of each valve region (see methods for details and representative window positions in Supplemental Fig. S1), where blue is position of the input valve leaflets and red is position of the output valve leaflets. Top traces: open and closed positions of the respective valves obtained after applying a threshold window to the densitometer traces (any signal below the lower edge of the window corresponds to a closed valve). *Contraction cycle in which the output valve did not transiently close. This experiment represents the response of 9 different vessels.

After micropuncture, the vessel was equilibrated for 30–60 min at 37°C and 3 cmH₂O until a stable pattern of spontaneous contractions developed. Subsequently, P_in and P_out were lowered to a baseline pressure of 1 cmH₂O for an additional 5- to 10-min equilibration period before pressure ramps were imposed. All vessels, even those with two valves (consisting of 1 complete lymphangion surrounded by 2 partial lymphangions), showed nearly synchronized contractions of the entire cannulated segment.

Valve timing protocols.

The movements of the input and output valve leaflets relative to changes in diameter and intraluminal pressure were determined at various levels of P_in and P_out. Initially, P_out was set to the same level as P_in and several spontaneous contractions were recorded. Subsequently, a slow, ramp-wise elevation in P_out was imposed, with the final pressure being just beyond the level at which the vessel failed to eject during systole. The P_out level at which this occurred was quite variable (4–20 cmH₂O), as detailed in a separate study (unpublished observations). During these protocols, the video, along with associated analog data, was saved periodically into an AVI file at 28–30 Hz. Movements of the lymphatic valves were detected upon replay of the AVI files, in synchrony with the extracted diameter and pressure data, using a custom computer algorithm (in LabVIEW) to measure the change in image intensity in a region of interest overlaying the base and/or midpoint of a valve leaflet.

The most accurate recordings of valve gating were made in vessels in which closed valve leaflets were oriented perpendicular to the image plane; most output valves were intentionally positioned in this way when the vessel was cannulated to optimize valve tracking. Two densitometric windows were positioned along the midline of the vessel, with the mean pixel intensity of one window used to detect the amount of overlap between the leaflets when the valve was closed or partially closed (Supplemental Fig. S1, window 4; Supplemental Material for this article is available online at the Am J Physiol Heart Circ Physiol website); this signal was highest when the valve was completely open (Supplemental Fig. S1A) and lowest when it was completely closed. However, pixel intensity within the vessel lumen was also influenced by vessel constriction and/or lateral movements associated with constriction. Therefore, a second window was positioned in the vessel midline (Supplemental Fig. S1, window 3) and used to monitor the change in lumen intensity associated with contraction. The difference between the mean pixel intensities of the two windows (after both were normalized to their control values in diastole) yielded a net densitometer signal that more closely reflected only the movements of the valve leaflets. The baseline level of the net densitometer trace also reflected the backward bulging of the output valve as P_out was progressively elevated (e.g., Supplemental Fig. S1, B–E, red trace). The degree to which the densitometer output accurately reflected the valve positions was confirmed by replaying the video (at ∼1/3 real time) and manually toggling a button to denote whether the valve was open or closed in each frame; the resulting manual and automated traces were virtually identical. A thresholding method was then applied to the net densitometer trace to convert it to a digital recording of valve position, where 1 was open and 0 was closed.

Valve closure and opening tests.

To determine the trans-valve pressure gradient required to open or close a valve, single valves were studied in isolation (see Fig. 4B). Initial valve gating tests were performed in Ca²⁺-free solution to prevent interference from intraluminal pressure spikes associated with spontaneous contractions. Only one densitometer window was needed under these conditions, with the window positioned along the midline of the closed leaflets.

Fig. 4.

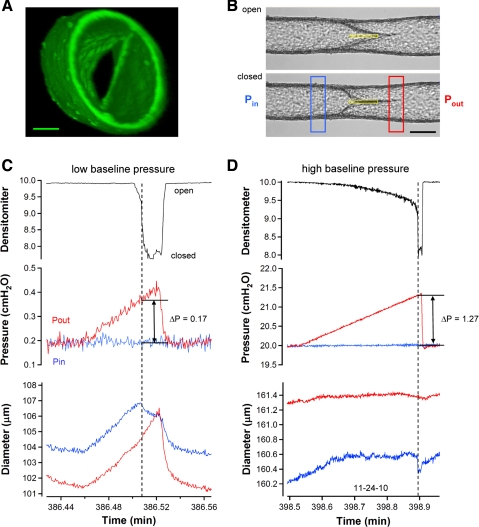
Valve closure tests performed on a single-valve vessel in Ca²⁺-free solution. A: confocal reconstruction of a secondary valve in a rat mesenteric lymphatic obtained in Ca²⁺-free solution to prevent contractions. View is taken from downstream, looking back (against normal flow) into the valve. Structures at 1 o'clock and 7 o'clock at the inner edge of the lumen are the valve insertion points, or buttresses. Calibration bar = 40 μm. B: images of a representative vessel with the valve in the open (top) and closed (bottom) positions. Single densitometer window used to detect valve leaflet position is shown in yellow. Calibration bar = 120 μm. C and D: densitometer, pressure, and diameter traces are similar to those described in previous figures (no P_L recordings were necessary under these conditions because all pressures could be controlled). Tests begin with P_in (red trace) and P_out (blue trace) equal in which case the valve is open. A ramp-wise increase in P_out is imposed until the valve closes. P_out and P_in levels at the instant of closure are recorded and the difference (P_out − P_in) is the minimal pressure gradient required for closure. Diameter traces on both sides of the valve are recorded at sites corresponding to the colored windows in B. Test in C starts at the lowest baseline pressure level used (0.2 cmH₂O), whereas the test in D starts at the highest level of baseline pressure used (20 cmH₂O). Both recordings are from the same vessel. Note the difference in the diameter and pressure scales between C and D.

For valve closure tests, pressures were initially set to equal “baseline” values (typically 3 cmH₂O), and the leaflet positions were monitored as P_out was slowly ramped (4 cmH₂O/min) to a higher value, with P_in held constant, until the valve closed. The point of valve closure was evident by a rapid decline in the densitometer signal and also by a smaller but simultaneous drop in upstream diameter. This procedure was repeated three times at each baseline pressure while the video was saved to an AVI file. The baseline pressure was then set to another level, either 0.2, 0.5, 1, 2, 3, 5, 7, 11, 15, or 20 cmH₂O for 1–2 min, and the ramp test was repeated in triplicate. A complete set of measurements at all of the above pressures was typically obtained.

For valve opening tests, P_out was set to a level higher than the baseline P_in required to close the valve; P_in was then ramped up to a higher level, while P_out was held constant, until the valve opened. Valve opening was evident by an abrupt increase in the densitometer signal. This procedure was repeated in triplicate for each of the baseline pressures while the video was recorded.

Because the valve tests under passive conditions might not accurately reflect the behavior of the valves under physiological conditions, the closure test was repeated in the presence of imposed basal tone. A number of different agonists potentially could have been used to impose tone (13, 39), but accurate measurement of the small pressure gradients required to test valve gating also required elimination of spontaneous contractions. After several different methods were attempted for simultaneously imposing tone and inhibiting contractions, the one that worked most consistently was to exchange the bath for KPSS + substance P (SP). Elevated [K⁺] led to cessation of spontaneous contractions and produced a transient constriction, while the simultaneous addition of SP led to the development of stable tone, at least at low pressures (see Supplemental Fig. S2). The SP dose was adjusted to induce various levels of tone, from ∼10% tone at 5 × 10⁻⁸ M to ∼80% tone at 1 × 10⁻⁶ M. Tone was calculated as the percent diameter decrease at 3 cmH₂O compared with that of the passive vessel.

Particle tracking.

In a few vessels, we sought to confirm that a valve indeed remained open in the face of an adverse pressure gradient by tracking particles that flowed backwards through the valve. For particle tracking, the cannulation pipettes were filled either with unfiltered APSS containing some particulate matter (2 experiments) or with a dilute suspension of red blood cells (1:8 in APSS; 2 experiments) obtained by cardiac puncture of the same rat. When particles or cells exited the output pipette at defined pressure gradients, sequences of AVI images were captured showing the particles moving retrograde through the valve toward the input pipette (Supplemental Fig. S3). Frame subtraction was used to generate a 32-bit image in Image J (National Institutes of Health; http://rsb.info.nih.gov/ij) to give a middle-gray image with bright spots indicating the position to which the particle had moved and dark spots to indicate the position from which the particle had moved. This subtracted image was then overlaid onto the average of the two images used for the subtraction and the particle positions were pseudocolored.

Confocal microscopy.

Vessel segments were observed at ×40–50 magnification using a Leica AOBS SP2 Confocal Multiphoton Microscope System. The cells were loaded with CellTracker Green (5 μM in PSS; Molecular Probes). Images were acquired at 0.3-μm intervals in the z-axis (vertically through the lumen) using 489 nm excitation and 508 nm emission wavelengths. The image stacks were reconstructed using Leica confocal software to produce various three-dimensional projections.

Data analysis.

Custom analysis programs written in LabVIEW were used to extract embedded data from the AVI files, detect valve leaflet movements, and detect diameter and pressure changes off-line. Data were compiled and plotted in Excel (Microsoft, Redmond, WA) and Igor (Wavemetrics, Lake Oswego, OR) and/or Photoshop (Adobe, Mountain View, CA). Typically, one vessel was used for data analysis from each animal. Curve fitting was performed using Igor. Supplemental video files were made using custom LabView programs to crop the video sequences, overlay the embedded data traces, and add appropriate labels. The files were converted from AVI to MP4 format using Aiseesoft Converter Suite (Beijing, China).

RESULTS

Valve gating during the lymphatic contraction cycle.

To determine the sequence of changes in valve position relative to changes in inner diameter and intraluminal pressure, two-valve lymphatic segments were subjected to different combinations of P_in and P_out. A typical recording is shown in Fig. 1B. With P_in and P_out initially set to equal levels, P_out was slowly elevated from 1 to 8 cmH₂O at a standard ramp rate of 4 cmH₂O/min. P_in was held constant as P_out was elevated. Typical diameter and pressure responses to a P_out ramp are represented by the two bottom traces. The second trace from the top is the net densitometer signal (red is output valve, axis at left; blue is input valve, axis at right) with the shaded area over the densitometer trace representing the range of that signal corresponding to an open valve. The top traces show the binary valve positions (using the same color scheme). Progressive elevation of P_out was associated with a progressive decrease in the open times of both valves and a progressive increase in the closed time of the input valve; in this example, the output valve stopped opening halfway through the ramp, as noted below.

Vessel diameter was measured on both sides of the output valve to illustrate the effect of increasing P_out on the diameters of the respective segments. As P_out increased, the vessel distended progressively on the output (downstream) side of the valve (red trace), as reflected by increases in both end diastolic diameter and end systolic diameter (ESD). In contrast, end diastolic diameter in the central chamber, on the upstream side of the output valve (black trace), decreased slightly as P_out increased, reflecting a modest myogenic constriction. Myogenic constriction was a very typical response during P_out ramp protocols and will be described in more detail a separate study. In Fig. 1B, bottom, pressures in the input pipette (blue trace), output pipette (red trace), and central lymphangion (black trace) are overlaid on a common y-axis scale. As P_out was raised from 1 to 3 cmH₂O, P_L transiently increased during each contraction such that peak systolic P_L exceeded P_out; when this occurred, the output valve opened, as indicated on the “valve position” trace, and partial emptying of the luminal contents resulted. At P_out levels from 4–6 cmH₂O (denoted by vertical dotted lines), the output valve opened during each spontaneous contraction and some ejection occurred, even though peak P_L did not clearly exceed P_out. This phenomenon is discussed in subsequent figures and was not due to unequal calibrations of the two transducers. At P_out levels >6 cmH₂O, the lymphangion continued to contract spontaneously and generated a rise in P_L sufficient to close the input valve, but the peak systolic pressure was insufficient to open the output valve (as was evident by the closed state of the output valve in the valve position trace). Contraction frequency increased by ∼70% during this particular P_out ramp, followed by rate-sensitive inhibition (12) that was evident by a long delay before contractions resumed after termination of the ramp. The video sequence is available as Supplemental Video S1.

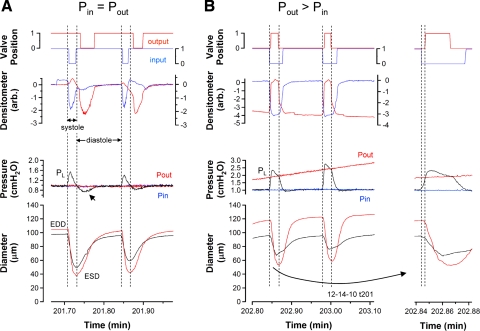
Expanded views of the timing of valve leaflet positions relative to diameter and intraluminal pressure are shown in Fig. 2 when P_in = P_out (A) and later in the ramp when P_out > P_in (B). There were significant differences in the patterns of valve gating under these two conditions. In Fig. 2A, both valves were open before the first period of systole began (systole and diastole are denoted by vertical dotted lines). When systole was initiated, the fall in diameter and rise in P_L essentially coincided. Closure of the input valve coincided with the period in which P_L exceeded P_in. The input valve then returned to the open position at the end of systole. In early diastole, when the rate of the diameter change was relatively high, P_L dipped transiently below P_in (and P_out). This negative pressure, relative to P_in, observed previously in isolated bovine mesenteric lymphangions under similar conditions (24) and that we hereafter call the “suction effect,” pulled the output valve leaflets backward into the closed position, as indicated in the densitometer trace and the valve position trace. This phenomenon was observed in ∼75% of vessels when P_in and P_out were equal and at a low level (≤3 cmH₂O); diameter typically decreased by ≥50% in systole under these conditions, as evident in this example (see also the examples in Supplemental Figs. S4 and S5). The suction effect was diminished somewhat during the second contraction, was only present in four of the seven contractions before the ramp (missing in contractions marked by asterisk in Fig. 1B), and was essentially absent in Fig. 2B when the systolic periods were characterized by smaller amplitude changes.

Fig. 2.

Expanded views of selected contractions from the recording in Fig. 1 show the timing of the input and output valves at different levels of P_out. Traces are the same as described in Fig. 1. A: lymphatic contraction cycle when P_in = P_out (1 cmH₂O). Vertical lines denote the periods of systole, as determined from the diameter recordings. B: lymphatic contraction cycle when P_out > P_in. Vertical lines denote the periods of systole, as determined from the diameter recordings. B, inset: first contraction with an expanded time scale; here the dotted vertical lines denote a period of isovolumic systole. ESD, end systolic diameter; EDD, end diastolic diameter.

When P_out was higher than P_in, the valve gating pattern was much more consistent with the pattern observed for ventricular valves during the cardiac cycle (56), as illustrated in Fig. 2B. The output valve was closed throughout diastole. At the initiation of systole, the input valve closed, permitting a greater rise in P_L than could be recorded when P_in and P_out were equal (due to partial shunting of the P_L spike through an open output valve into the output cannula). When P_L exceeded P_out, the output valve opened. Pressure development in the central lymphangion during the time that both valves were closed implies that a brief period of isovolumic systole occurred (Fig. 2B, inset with expanded time scale at right). During this time, diameter was decreasing at the site immediately upstream from the output valve but the effect on volume was apparently balanced by an increase in diameter at the more proximal end (near the sinus) of the central lymphangion (data not shown); indeed, diameter increases near the sinus were typical during systole when P_out was elevated (data not shown). In midsystole, peak systolic P_L clearly exceeded P_out, but this was not the case at higher levels of P_out (see Fig. 3). Systolic P_L peaked before the point in time when ESD was reached. At ESD, P_L was essentially equal to P_out, at which point the output valve began to close. The input valve remained open until P_L fell below P_in. Note the slightly longer open time for the input valve and its correspondence with the P_L trace in the second contraction of Fig. 2B, presumably because P_out and thus peak P_L were higher so that the fall to P_in required more time.

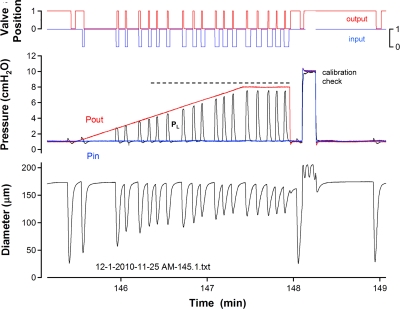
Fig. 3.

Example recording from a vessel that was able to eject for every contraction during a P_out ramp. Horizontal dotted line corresponds to contractions that resulted in opening of the output valve without peak systolic P_L equaling or exceeding P_out. At the end of the ramp, P_in and P_out were elevated simultaneously to 10 cmH₂O to check the calibration of the pipette used to measure P_L.

Discrepancy between the level of peak systolic P_L and P_out during ejection.

A common observation during P_out ramps is illustrated in Fig. 3. Peak systolic P_L clearly did not exceed or even match P_out after P_out was greater than ∼3 cmH₂O; nonetheless, the output valve opened transiently during each contraction (red valve position trace), as indicated by the horizontal dotted line. At first we suspected transducer drift or partial plugging of the servo-null pipette, which would have altered the P_L calibration. However, a quick calibration test following the P_out ramp (at time = 148.1 min) verified that neither of these problems occurred. It is still possible that the frequency response of the servo-null pipette was not sufficient to accurately detect the P_L peak; however, this behavior was observed in a number of vessels with varying degrees of discrepancy between peak systolic P_L and P_out. This difference in the two pressures in the face of continued ejection, along with the “bias” of the valves to be open in the absence of a pressure gradient, led us to more carefully examine the pressure gradients required to close or open a valve at different levels of vessel distention.

Valve closure test using a P_out ramp.

A three-dimensional reconstruction of a valve in a rat mesenteric lymphatic vessel, obtained using confocal microscopy, is shown in Fig. 4A. The view is taken from downstream, looking back against the normal flow direction into the valve. Both the valve leaflets and their downstream insertion points are visible, and the bicuspid appearance of the valve is evident. A video that rotates through a 360° view is available as Supplemental Video S2. Based on areas calculated from this image, the ratio of the valve opening to the lumen is 1:7.

A typical valve used for a closure test is shown under brightfield illumination in Fig. 4B, with the valve viewed from the side so that the insertion points lie at the top and bottom surfaces of the vessel. Figure 4, C and D, shows the data obtained during the closure test. Initially, pressures in the cannulation pipettes were equal (in Fig. 4, C and D, middle traces) and the valves were open (densitometer signals were high). As P_out slowly increased, the valve closed (denoted by a vertical dotted line). At this time, diameter decreased because pressure on the upstream side of the valve dropped to P_in (from approximately half-way between P_out and P_in) at the moment of closure. The magnitude of the diameter change depended on the degree to which the vessel was distended initially.

At the low baseline pressure used for the test in Fig. 4C, the minimal pressure gradient (P_out − P_in) required to close the valve was 0.17 cmH₂O. In contrast, when the closure test was repeated on the same valve, at a higher baseline pressure (Fig. 4D), a minimal pressure gradient of 1.27 cmH₂O was required for closure. The set of three closure tests for this vessel at the lower pressure level are available as Supplemental Video S3.

Particle tracking during the imposition of an adverse pressure gradient confirmed that valves with the morphology shown in Fig. 4B, top, were indeed open. Supplemental Fig. S3A shows a vessel segment with an apparently open valve when P_in = P_out = 5 cmH₂O. As P_out was elevated ramp wise from 5 to ∼6.7 cmH₂O, with P_in held constant, a single particle emerged from the “output” pipette (point #1) and moved backwards through the valve, down the prevailing pressure gradient, until it exited the “input” pipette at point #17. The positions of the particle at sequential times in the AVI file are shown by the yellow dots (1–17). Supplemental Fig. S3B shows particle velocity as a function of the relative position, and Supplemental Fig. 3C shows the diameter, pressure and densitometer data during the P_out ramps associated with this test. The times at which the movements of this particle were recorded correspond to AVI frame numbers (1,156–1,295, with total duration = 4.8 s) in the second ramp; the pressure gradient was ∼1 cmH₂O when this particle moved across the field of view. In other experiments (see Supplemental Video S4), red blood cells introduced into the pipette system were observed to move in the same direction through an open valve and to stop abruptly the instant the valve closed.

Valve opening test using a P_in ramp.

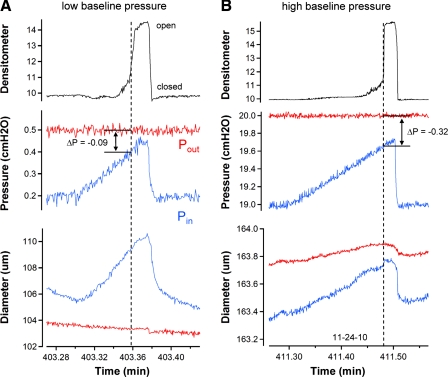
An example of the test devised to measure the minimal pressure gradient required to open a valve is shown in Fig. 5. With P_out held constant, P_in was raised ramp wise until the valve opened and the difference between P_in and P_out at the point of opening was recorded as the minimal pressure gradient required to open the valve. Figure 5A shows a recording of the valve opening test at a low baseline pressure, where P_in − P_out was −0.09 cmH₂O at the moment the valve opened, indicating that the valve opened before the pressures were equal. The red and blue diameter traces are the diameter changes on the output side and input sides of the valve, respectively. The test was repeated two more times at the same baseline pressure (the full sequence is available as Supplemental Video S5). At a higher baseline pressure and diameter (Fig. 5B), the same valve opened when P_in was 0.32 cmH₂O below P_out. These tests suggest that vessel distention has an effect on the pressure gradient required for valve opening but that the influence of vessel distention on the trans-valve pressure gradient is smaller than that for valve closure at a comparable baseline pressure.

Fig. 5.

Valve opening tests performed on a single-valve vessel in Ca²⁺-free solution. A: valve opening test at a low baseline pressure. Densitometer, pressure, and diameter traces are similar to those described in previous figures. Blue traces are the respective recordings on the input side of the valve, and red traces are the respective recordings on the output side of the valve. Test begins with P_out sufficiently higher than P_in to maintain a closed valve. A ramp-wise increase in P_in is imposed until the valve opens. P_out and P_in levels at that instant are recorded and the difference (P_in − P_out) is the minimal pressure gradient required for opening. This value was typically negative as shown here. B: valve opening test is repeated at the highest level of P_out used (20 cmH₂O). Both A and B are from the same vessel. Note the difference in the diameter and pressure scales between the 2 panels.

Summary analyses for valve gating tests.

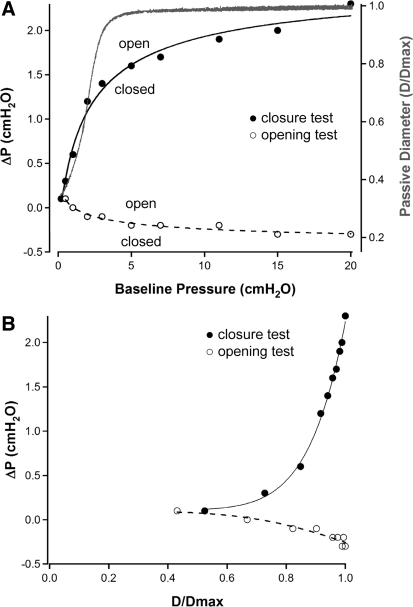
The data sets from the valve closure and opening tests, performed at 10 different baseline pressures, were analyzed in two different ways. In Fig. 6A, the pressure gradient required for valve closure (filled circles, axis at left) is plotted as a function of baseline pressure. The reference pressure was designated as the side on which the pressure ramp was imposed (output); thus ΔP was calculated as P_out − P_in for the valve closure test. Over the lower end of the baseline pressure range from 0.1 to 3 cmH₂O, the pressure gradient required for valve closure increased from 0.1 to 1.4 cmH₂O. However, as baseline pressure increased from 3 to 20 cmH₂O, the pressure gradient required for valve closure increased only an additional 30% (1.4 to 2.1 cmH₂O). Interestingly, the change in slope of the curve fitting these data roughly corresponded to the “elbow” in the passive pressure-diameter relationship for the same vessel (red), which is plotted on the axis at right in Fig. 6A. The data from the valve opening tests on the same vessel are also plotted in Fig. 6A (open circles). The reference pressure was designated as the side on which the pressure ramp was imposed (input); thus ΔP was calculated as P_in − P_out for the valve opening test.

Fig. 6.

Summary of valve closure and opening tests for one lymphatic vessel. A, left axis: pressure gradient required for valve closure (P_out − P_in; ●) or opening (P_in − P_out; ○) plotted as a function of baseline pressure. Each point is the average ΔP (P_out − P_in) for 3 trials. Right axis: continuous pressure diameter relationship for the same vessel determined from a simultaneous P_in + P_out ramp from 0.2 to 20 cmH₂O in Ca²⁺-free PSS after valve gating tests were completed; data were normalized to the passive diameter at 20 cmH₂O. B: pressure gradient required for valve closure (P_out − P_in; ●) or opening (P_in − P_out; ○) plotted as a function of normalized diameter. All measurements were made in Ca²⁺-free PSS. All curve fits are power functions. D/D_max, passive diameter/maximum passive diameter.

Although the general shapes of ΔP-baseline pressure curves were fairly representative of those for most vessels, plotting data sets from multiple vessels in this manner resulted in substantial scatter in the data along the baseline pressure axis. Because baseline pressure determined the passive vessel diameter, the data were expressed as a function of vessel diameter. In Fig. 6B, the pressure gradient required for valve closure (closed circles) and valve opening (open circles) for the same vessel are plotted as a function of the normalized passive diameter (D/D_max), where D_max is the maximum passive diameter in Ca²⁺-free PSS at 20 cmH₂O. Here the ΔP for each test is defined as in Fig. 6A. It is evident that the pressure gradient required for valve closure increased 23-fold (0.1 to 2.3 cmH₂O) as the diameter approached the maximal passive diameter. The data set for the valve opening tests on the same vessel show a similar trend in that the passive vessel diameter altered the pressure gradient required for valve opening; however, the magnitude of the effect was much smaller (4-fold) over the baseline pressure range of 0.2 to 20 cmH₂O.

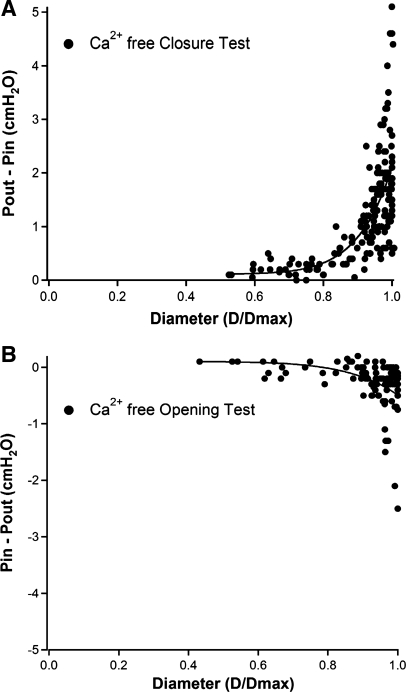
The results of valve closure tests performed on 17 vessels and valve opening tests performed on 10 vessels are summarized in Fig. 7. All tests were performed in Ca²⁺-free solution with the x-axis representing normalized diameter. Higher baseline pressures are associated with progressive distention of the vessel up to the maximum diameter recorded at 20 cmH₂O, and it is apparent that a valve in a highly distended vessel can remain open in the face of a substantial adverse pressure gradient (on average 2.2 cmH₂O, but as high as 5 cmH₂O; Fig. 7A). Likewise, the opening tests in Fig. 7B show that valve opening occurs at a progressively more negative pressure gradient (P_in − P_out) as a vessel distends. However, the range of the pressure gradient required for valve opening changes only approximately sixfold with vessel diameter compared with the >20-fold range of the pressure gradient required for valve closing (only one vessel required a pressure gradient more negative than −1 cmH₂O for valve opening). The data sets in Fig. 7 were fit with the power functions listed in Supplemental Table S1. We impute no physiological or mathematical significance to the power functions; they merely provided better fits of the data sets than exponential or third order polynomial functions.

Fig. 7.

Summary of measurements describing the pressure gradient required for valve closure (A; n = 17) or valve opening (B; n = 10) as a function of normalized diameter.

Effect of vessel tone on valve closure.

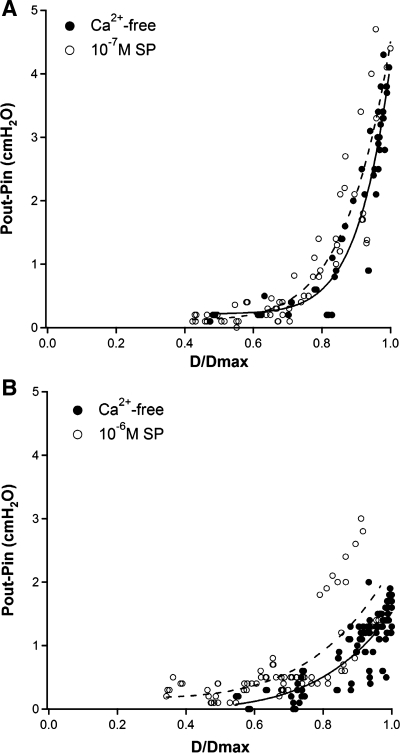
We were concerned that valve gating tests under passive conditions might not accurately reflect the behavior of the valves under physiological conditions; e.g., that the relationships in Fig. 7 might be altered by the presence of spontaneous vessel tone. An effect of tone on gating would be predicted if smooth muscle cells directly or indirectly controlled tension of the valve leaflets. The graph in Fig. 8A shows the results of valve closure tests in four vessels using KPSS + 1 × 10⁻⁷ M SP to impose tone (open circles), along with tests performed subsequently on the same valves in Ca²⁺-free solution (closed circles). The tone induced by this dose of SP (20.4 ± 2.2%) slightly exceeded the upper limit of basal tone observed under several physiological conditions (11, 13, 22, 23). Tone was relatively stable at low pressures but did not completely recover after tests at baseline pressures >10 cmH₂O. Thus, at some pressures, tone changed during the set of three closure tests at each baseline pressure. For this reason, all of the data points (rather than only the average of 3 trials at each baseline pressure) were plotted in Fig. 8. There appeared to be slight difference in the curves fitting these data sets, with the curve for the SP data shifted slightly to the left of the Ca²⁺-free curve. Curve fits of the individual (paired) data sets (not shown) confirmed that the SP and Ca²⁺-free curves essentially overlapped in three of the four vessels.

Fig. 8.

Summary of valve closure measurements (○) after imposing a moderate (A) or high (B) level of tone using high K⁺ physiological saline solution (KPSS) + substance P (SP). Concentration of SP was 10⁻⁷ M for all vessels in A, 6 × 10⁻⁷ M for 2 vessels in B and 1 × 10⁻⁶ M for the other 2 vessels in B. Measurements in same vessels at same baseline pressures in Ca²⁺-free PSS are shown (●). Dotted lines are curve fit for SP data; solid lines are curve fit for Ca²⁺-free data (n = 4 for A and B); curve fit parameters are listed in Supplemental Table S1.

The valve closure tests were repeated on four additional vessels in which the SP dose was adjusted (from 6 × 10⁻⁷ M to 1 × 10⁻⁶ M) to impose ∼50% tone (51.3 ± 1.6%). In this case, the curve that fit the aggregate closure test data for SP was more noticeably shifted to the left compared with the curve for the aggregate data in Ca²⁺-free solution (Fig. 8B). Curve fits of the individual (paired) data sets (not shown) confirmed that three of four vessels showed substantial leftward shifts in the curves fitting the SP data relative to the curves fitting the Ca²⁺-free data. The data sets in Fig. 8 were fit to power functions, with coefficients listed in Supplemental Table S1. A leftward shift in the ΔP vs. D/D_max relationship suggests that the induction of tone increases the pressure gradient necessary to close the valve at any given baseline pressure, compared with a passive vessel.

DISCUSSION

Valve gating patterns during the contraction cycle.

This study is, to our knowledge, the first detailed description of the timing of lymphatic valve movements relative to pressure and diameter changes during the lymphatic contraction cycle. Thus Fig. 2 is the equivalent of the “Wigger's diagram” (32) for the lymphangion. In the rat, the timing of lymphatic valve leaflet movements during the contraction cycle closely resembles that of cardiac valves if, and only if, P_out > P_in (Fig. 2B). At the onset of systole, the input valve closes first, allowing pressure in the chamber to rise during contraction, after which the output valve opens when P_L exceeds P_out (at low pressures). At higher pressures, the output valve will typically open even though P_L does not reach P_out, according the relationship defined in Fig. 7B. In either case, once open the output valve closes at the end of systole when P_L falls sufficiently below P_out. Finally, the input valve reopens after diastolic P_L has returned to the baseline level. If diastolic P_L does not return to baseline before the next contraction is initiated, the input valve remains closed and a slow rise in diastolic P_L ensues, as can be observed just before the onset of valve insufficiency (unpublished observations).

Flow measurements are usually included in cardiac cycle diagrams (32). Unfortunately, we were not able to measure lymphangion flow accurately under conditions in which diameter, pressure, and valve movements were simultaneously measured. Although centerline velocity can be measured using red blood cells introduced into the input pipette (see Supplemental Video S4), velocity during much of systole is often too high (15, 16) to be accurately determined at ∼30 frames per second with the camera used in the present experiments. Flow measurements in conjunction with valve gating tests could increase our understanding of some aspects of valve behavior but would not likely result in highly detailed flow information such as the presence of secondary flow structures near the valve leaflets. This kind of information is currently better obtained from carefully constructed computational flow simulations, such as we have performed for the straighter regions of lymphangions (49). The outcomes of those simulations may then be used to attempt to design better experimental approaches to measure flow patterns around the valves.

Unlike the heart, where P_out always exceeds P_in, lymphatic valves can exhibit multiple gating patterns depending on the prevailing P_in and P_out (see Figs. 1–2). When P_in = P_out, the input valve typically closes at the onset of systole and opens at the end of systole. Because the output valve is open when the trans-valve pressure gradient is zero (Fig. 7), it can occasionally remain open throughout the entire contraction cycle (e.g., contractions marked by asterisk in Fig. 1). More typically, the output valve closes transiently in early diastole as P_L dips below the level of P_in and P_out (Fig. 2A). The dip in intraluminal pressure is associated only with contractions of large amplitude that typically occur at low baseline pressure levels (<3 cmH₂O) and is the subject of another study (14). In the heart, isovolumic systole is a brief period of time when both input and output valves of the ventricle are closed, allowing pressure development during ventricular contraction. This phase may or may not occur in a lymphatic vessel. Benoit et al. (2) noted, from in vivo observations of lymphatics in the rat mesentery, that there was no discernable period of isovolumic systole. The vessels in their experiments, which were performed in supine animals without an externally imposed afterload, most likely exhibited valve gating patterns resembling those shown in Fig. 2A rather than Fig. 2B. Experiments with single, isolated bovine mesenteric lymphangions studied at equal diastolic P_in and P_out also demonstrated the absence of a period of isovolumic systole (20). In contrast, our recordings (Fig. 2B, inset) clearly show a brief period of isovolumic systole when P_out > P_in. Differences in the level of afterload possibly could reconcile the apparent discrepancy between the observations of Benoit et al. (2) and Gashev (20) with those of McHale and Roddie (38, 39) with respect to resolving a period of isovolumic systole in the lymphangion contraction cycle.

Still other valve gating patterns can occur in lymphatic vessels under conditions where P_in and P_out change, conditions never experienced by the heart. For example, in edematous tissues, lymphatic P_in may exceed P_out and the lymphangion may behave more as a conduit, with continuous forward flow, than as a pump (23, 48); similar behavior may occur normally in intestinal lymphatics during high levels of lymph formation. We are able to simulate this condition by setting P_in higher than P_out and thereby imposing a favorable gradient for flow (23, 25). When P_in is increased ramp wise while P_out is held constant, both valves typically remain open throughout the ramp (see Supplemental Fig. S4). In contrast, when P_in and P_out are simultaneously elevated, both valves will gate sequentially during each contraction cycle until P_in and P_out exceed a certain level (Supplemental Fig. S5). The simultaneous P_in + P_out ramp might simulate a condition where a lymphatic vessel would be pumping against a gravitational load in the face of developing edema.

Effect of vessel distention on valve gating.

Our measurements of valve gating in single-valve segments verify previous predictions that the gating of lymphatic valves is primarily (or solely) determined by the trans-valve pressure gradient. Predictions about passive valve gating have been made largely on the basis of valve ultrastructure, which show that the leaflets are composed of two thin endothelial cell sheets containing elastin and collagen fibers (26). Schmid-Schönbein (50) noted that the small size of the vessel and low Reynolds numbers for lymph flow support the concept that valve leaflet movements are dictated solely by trans-valve pressure gradients and viscous forces. Although such gradients are predicted to be small, we could find no published measurements to validate this assumption, apart from the work of Lobov (35) in an unpublished Russian thesis. Lobov reported that an adverse pressure gradient of ∼0.4 cmH₂O was sufficient to close secondary valves in bovine mesenteric lymphatic vessels at a baseline pressure of 3 cmH₂O; although a direct comparison with our results is not possible without knowing D/D_max for bovine vessels in those particular experiments, the absolute value is well within the range of the pressure gradients for closure of rat mesenteric lymphatic valves shown in Fig. 7A.

A novel and important finding from our study is that the trans-valve pressure gradient required for valve closure (and to a lesser extent for valve opening) depends strongly on vessel distension, the level of which is determined by the baseline pressure at which the test is performed. At low pressures (<2 cmH₂O) that are within the physiological range of rat mesenteric vessels (2), ∼0.1 cmH₂O pressure gradient (P_out > P_in) is required for valve closure, whereas at higher pressures (e.g., >10 cmH₂O), a trans-valve gradient of 2.2 cmH₂O (and in some cases >5 cmH₂O; Fig. 7A) is required. Thus there is a >20-fold range in the pressure gradient determining valve closure over the range of pressures the vessel would experience normally and under conditions of edema (44, 46). The baseline pressure at which the ΔP for closure substantially increases (typically 2–3 cmH₂O) corresponds approximately to the “elbow” in the passive pressure-diameter curve of the vessel (Fig. 6A) and suggests that the increase in the pressure gradients required for opening/closing may be determined by tensioning of the valve leaflets as the vessel progressively distends. The ΔP-diameter relationship (Fig. 7A) explains why valves do not always close when a vessel segment with a single-valve contracts under conditions where P_in = P_out (as occurs in Fig. 1 before the P_out ramp begins). At baseline pressures >2 cmH₂O, the small fluctuations in intraluminal pressure associated with contraction are insufficient to generate even a transient backpressure large enough to close the valve, since the pressure spikes are largely shunted out the open cannulation pipettes. The graph in Fig. 7A also explains why reverse flow (through an open valve) can sometimes be observed in vivo (Supplemental Video S7). The graph in Fig. 7B explains why an output valve can open even if internal (developed) pressure does not exceed output pressure (Fig. 3).

There was a distinct lack of symmetry in the ranges of pressure gradients necessary to open (6-fold) and close (20-fold) the valve leaflets as transmural pressure increased (Fig. 6). This is perhaps related to the bias of the valves to remain in the open position. Furthermore, increasing the transmural pressure likely results in less contact area between the leaflets and makes coaptation more difficult. This would further bias the valve to the open position. We occasionally noted that there appeared to be less contact area between the leaflets at larger vessel diameters, but the imaging techniques used here did not allow for accurate assessment of contact area. It is also possible that, like the vessels themselves (Fig. 6A), the valve leaflets become stiffer with increasing diameter as the wall distends and pulls radially on the base and/or buttress of the leaflets. While direct measurements of stiffness in this setting would be extremely difficult to make, we can qualitatively visualize leaflet behavior under various flow conditions. In some experiments, the leaflets exhibit measureable “flutter” in response to rapid pressure oscillation at both low and high baseline transmural pressures (Supplemental Video S6), suggesting that they remain reasonably compliant even when a vessel is near maximally distended. A fuller assessment of this phenomenon through high resolution three-dimensional imaging and computational modeling would be beneficial. In the meantime, the findings of our study should provide valuable information for models of lymphatic function such as the recent model developed by Bertram et al. (3).

Influence of vessel tone on valve gating.

The idea that active force generation by muscle cells in the lymphatic wall can control valve gating is controversial. In bovine lymphatics, some anatomical evidence exists for the presence of muscle cells or muscle cell extensions into the valve leaflets (4, 5), yet no functional data are available to support the concept that muscle contraction per se can initiate valve closure/opening. In this regard, we never observed valves to close without the imposition of an appropriate trans-valve pressure gradient, even in the presence of tone. However, the relationships described in Fig. 8 and Supplemental Fig. S6 clearly demonstrate that tone has an influence, albeit an indirect one, on valve closure. The reciprocal implication is that high levels of tone will lead to enhanced valve opening when P_in < P_out (Fig. 7B), i.e., in the presence of high tone an output valve will open well before P_L reaches P_out, meaning that active force developed by lymphatic muscle during systole would facilitate valve opening. It should be noted that “tone” in this context reflects the effect of steady-state stimulation of the vessel with KPSS + SP in our protocols. Whether the same principle also applies to the transient, active force development by lymphatic muscle during the contraction cycle will be difficult to determine using methods similar to the ones we employed. Nevertheless, our results (Fig. 8) are partially consistent with the idea of an active muscle component previously proposed to be involved in the gating of bovine lymphatic valves (4, 5, 42), although we anticipate that this is an indirect effect transmitted possibly through collagen fibers at the base or buttress of the valve leaflets rather than by muscle cells within the leaflets.

Physiological implications.

The lymphatic system typically works against an opposing standing pressure gradient to move lymph from a low pressure environment (the interstitium) to a higher pressure environment (outflow into the venous network). An important conclusion from the present study is that, despite the pressure gradient against which the lymphatic network works, secondary lymphatic valves in rat mesenteric lymphangions nevertheless have a “bias” to be in the open position (Figs. 1, 2, 6, and 7). However, the extent of this “open bias” is strongly influenced by the hydrodynamic conditions that the valve experiences on a moment-to-moment basis. When lymph pressures are low and there is little or no adverse pressure gradient (e.g., P_in = P_out = 1 cmH₂O), the valves are open the majority of the contractile cycle, ∼85 and 75% of the duty cycle for the input and output valves, respectively (Figs. 1 and 2A). However, when the vessel must work against a pressure gradient, the amount of time the valve spends in the open position significantly declines, to ∼75 and 15% of the duty cycle for the input and output valves, respectively, when P_out = ∼2 cmH₂O and P_in = 1 cmH₂O (Figs. 1 and 2B). When the opposing pressure gradient exceeds the limit of the pump, the output valve does not open and the duty cycle of the input valve falls substantially (to ∼30% in the example shown in Fig. 1).

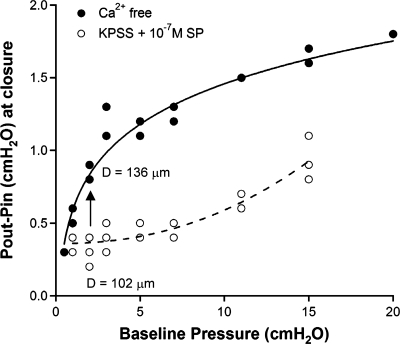
The open bias of the valve potentially could translate into several physiological advantages to enhance the efficiency of lymphatic function, including the predominant role of the valve to minimize backflow of lymph. We have also demonstrated that valve gating is different at low vs. high pressures (Figs. 6 and 7). When pressure is low, the vessel has a relatively small diameter and the trans-valve pressure difference needed to close the valve is relatively small. However, when the pressure is high, the vessel is distended and the ΔP required for closure significantly increases. Additionally, we have shown that this relationship is altered by lymphatic tone (Fig. 8). Thus a potential benefit of the residual lymphatic muscle tone between contractions could be to help maintain the vessel at a relatively small diameter (compared to the passive diameter at the same pressure), thereby allowing the valve to close properly during diastole under a small adverse pressure gradient. This is illustrated clearly in Fig. 9, which depicts the ΔP required to close a valve at different baseline pressures in a single vessel with high tone (KPSS + 10⁻⁶M SP) and in the same vessel with no tone (Ca²⁺ free PSS). With loss of tone (vertical arrow), a larger ΔP is required for valve closure. For example, at a baseline pressure of 2 cmH₂O, the ΔP required to close the output valve in the vessel with high tone (∼102 μm average diameter) is ∼0.3 cmH₂O, whereas in the same vessel with no tone (∼136 μm average diameter), the ΔP required to close the output valve is approximately threefold higher. Figure 9 illustrates this relationship for a single vessel where the effect is easier to see, but the entire data set shows a similar relationship (see Supplemental Fig. S6), both for moderate and high levels of tone.

Fig. 9.

Plot of the trans-valve pressure gradient at the moment of valve closure as a function of baseline (initial) pressure. Graph represents an alternative way to express the closure test data for 1 of the 4 vessels used in Fig. 8B (∼50% tone group). Complete data sets for all 4 vessels are plotted in a similar manner in Supplemental Fig. S6. Arrow indicates the increase in the adverse pressure gradient required to close the valve if the vessel were to lose all tone at a constant lumenal pressure of 2 cmH₂O. Diameters indicated are the averages calculated from the respective trials (with and without tone) at 2 cmH₂O.

An extension of the idea described in the preceding paragraph is that valves will become more susceptible to becoming insufficient in distended vessels, because a greater ΔP is required for closure. Thus, if diastolic pressure rises, pressure will be more likely to equalize through an open valve, rendering that valve insufficient. Indeed, we have observed this sequence of events frequently under conditions that mimic those seen in lymphedema (a simultaneous ramp increase in P_in and P_out, with P_out > P_in; unpublished observations) and insufficient valves have been reported to be associated with distended lymphatic vessels in vivo, including vessels in patients with lymphedema (44, 51). A potential means to combat this problem and minimize lymph reflux could be to increase the resting tone of the collecting lymphatic vessels.

In summary, our findings provide several new insights into the function of secondary lymphatic valves. 1) We have documented in detail for the first time the temporal sequence of events among diameter, pressure, and valve gating during the lymphatic contraction cycle. The timing of the lymphatic valve movements is similar to that of cardiac valves only under the specific condition where lymphatic afterload is elevated. 2) We find that lymphatic vessel distention exerts a profound influence on the pressure gradient required for valve opening/closing. 3) We provide an explanation for why lymphatic valves in mesenteric vessels have a natural tendency to remain open when the trans-valve pressure gradient is zero or near zero. 4) Finally, we present functional evidence to support the concept that lymphatic muscle tone exerts at least an indirect effect on valve gating.

GRANTS

This work was supported by National Institutes of Health Grants HL-089784 (to M. J. Davis), AG-030578 (to A. A. Gashev), HL-070308 (to D. C. Zawieja), and HL-094269 (to J. E. Moore, Jr.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).