Abstract
Brain functional connectivity (FC) refers to inter-regional synchrony of low frequency fluctuations in blood oxygenation level dependent (BOLD) functional MRI (fMRI). FC has been evaluated both during task performance and in the “resting” state, yielding reports of FC differences correlated with behavior and diagnosis. Two methodologies are widely used for evaluating FC from BOLD fMRI data: Temporal correlation with a specified seed voxel or small region of interest; and spatial independent component analysis (ICA). While results from seed-based and ICA methodologies are generally similar, they are conceptually different. The present study is intended to elucidate and illustrate, qualitatively and quantitatively, the relationship between seed and ICA derived measures of FC. Seed-based FC measures are shown to be the sum of ICA-derived within network connectivities and between network connectivities. We present a simple simulation and an experiment on visuomotor activity that highlight this relationship between the two methods.
Keywords: BOLD fMRI, functional connectivity, seed-based connectivity, ICA, within network connectivity, between network connectivity
Introduction
Functional connectivity (FC) refers to inter-regional synchrony of low frequency1 fluctuations in blood oxygenation level dependent functional magnetic resonance imaging (BOLD fMRI). FC has been evaluated in the absence of an explicit task (“resting state”)1–4 as intrinsic FC (IFC). Reports of differences in IFC correlated with behavior2,5,6 and diagnosis7–12 are abundant. The utility of functional connectivity should not be surprising, given the biological basis of this description in terms of the organization of the brain into functional networks. A functional network may be broadly defined as a set of brain regions that are consistently synchronous. Functional connectivity between any two brain regions may be due to connectivity within a network or between networks. In the context of functional neuroimaging, the framework of functional connectivity provides researchers opportunities to formulate and to test hypotheses about functional networks.
FC between brain regions has been estimated primarily using one of two methods: (a) seed-based correlation1,2 or (b) spatial independent component analysis (ICA)13 typically implemented using group ICA by temporal concatenation14. Several measures of FC have been estimated using the two methods. Typically, FC has been used to visualize task activated ensembles15–17 and resting state functional networks7,9,13,18–20. Recently, FC has been computed between networks12. ICA derived network maps have been compared to seed-based connectivity maps and shown to be similar, though not identical21. To our best knowledge, a quantitative analysis of the similarities and differences among these measures of FC has never been made. The principal purpose of this paper is to elucidate the relationship between FC measures estimated using seed-based correlation and spatial ICA. We derive the relationship and present a simple simulation and an experimental example to illustrate the similarities and differences between the two approaches. We show that the functional connectivity of the brain as measured using seed-based methodology is expressible as the sum of connectivities within and between ICA derived networks. While the seed based method provides a single metric of connectivity for each pair of regions, ICA method provides three measures of connectivity: total connectivity, connectivity within networks and connectivity between networks.
Direct comparison of ICA-derived and seed-based connectivity measures is nontrivial. ICA for resting state BOLD fMRI is typically implemented using group ICA by temporal concatenation14. Group ICA requires specific preprocessing steps such as prewhitening and dimensionality reduction, that are typically not performed while using seed-based methods. In addition, statistical tests for functional connectivity on the two methods are driven by different underlying theories, which complicates quantitative comparisons. Here we derive and then validate a novel theoretical relationship between the two methods with simulation and experiments using both typical and equivalent preprocessing and testing methods.
Theory
Seed-based functional connectivity between any voxel x1 and seed voxel x2 can be defined as
| [1] |
where S(x,t) is the demeaned BOLD fMRI signal from voxel x at time t and T is the number of time points in the experiment. The denominator of Eq (1) is a normalization factor that can be ignored for the purpose of this theory.
Spatial ICA decomposes BOLD signal into components (or functional networks), each comprising a spatial map and a corresponding time course22, which can be written as
| [2] |
where K is the number of spatially independent components, Mk is the spatial map of component or “network” k, and Ak is the timecourse of component k.
Substituting Eq (2) in Eq (1) yields:
| [3] |
where CICA is the ICA-derived correlation between voxel x1 and x2.
Rearranging the terms for k = l and k ≠ l yields:
| [4] |
where the first term is the representation of the sum over within network connectivities (total WNC), and the second term is the representation of the sum over between network connectivities (total BNC). Hence, total connectivity
| [5] |
Within network connectivity (WNC) of network k between voxel x1 and x2 is
| [6] |
and between network connectivity (BNC) between networks k and l is
| [7] |
Application of ICA for multiple subjects (or sessions) is typically done using group ICA14. Group ICA may be implemented using temporal concatenation14 or using a tensor approach23. The temporal concatenation ICA method assumes identical component spatial distribution across subjects (and runs) but does not impose any restriction on the time course from different runs/participants, while the tensor ICA assumes that the time courses of each run are identical. Since the spatial distributions of networks are found to be robust18,19,24 across subjects (and tasks), the temporal concatenation method is preferred when resting state or differing tasks are combined in a group, and inter-task differences of WNC and BNC are only impacted by component time courses. Hence, inter-task difference in WNC for network k reduces to inter-task difference in
| [8] |
and inter-task difference in BNC between network m and n reduces to inter-task difference in
| [9] |
Generalizing Eq (8) and (9) for the whole brain, inter-task differences in WNC can be approximated by the difference in the power of the network time courses, and the inter-task difference in BNC can be approximated by the difference in the correlation of the network time courses.
Methods
Simulation
Simple BOLD fMRI-like data were simulated in 2 mm isotropic voxels in an MNI-space normalized brain. Noise throughout the brain was simulated by sampling from a gaussian distribution. Intrinsic connectivity was added within the visual and motor cortices by adding samples from a filtered (0.01 to 0.1 Hz) random gaussian distribution. Besides the rest paradigm, task modulation was added in the visual and motor cortices to obtain two 260-second task paradigms: 1. Visual paradigm: A block design (6 blocks of 20 sec off 20 sec on, 20 sec off at the end) visual activation and 2. Visuo-motor paradigm: A block design (6 blocks of 20 sec on 20 sec off, 20 sec off at the end) concurrent visual and motor cortex activation. Each of the three tasks were simulated fifteen times to provide data similar to fifteen runs for each task. Simulated fMRI data at voxel x at time t
| [10] |
where M is the spatial mask for visual cortex (Mv), motor cortex (Mm) or whole brain (Mb)), T is the block design task activation amplitude at time t calculated by convolving the canonical hemodynamic response function with the boxcar stimulus timecourse, ι is the simulated intrinsic activity, γ is the simulated noise and βtm, βim, βtv, βiv and βn are the weights of motor task, intrinsic motor activity, visual task, intrinsic visual activity and noise respectively.
The visual mask was created by including BA 17, 18 and 19 from an atlas and the motor mask was created by including BA 3,4 and 6 from an atlas. The weights used for the three tasks are listed in Table 1. Task weight for the visual activation was chosen to be higher than the task weight for motor activation based on observations from experiment. The noise weight was chosen to obtain an SNR of five.
Table 1.
Weights used for fMRI simulation of the three paradigms
| Parameter | Visual Task | Visuomotor Task | Resting State |
|---|---|---|---|
| β tm | 0 | 1 | 0 |
| β im | 1 | 1 | 1 |
| β tv | 2 | 2 | 0 |
| β iv | 1 | 1 | 1 |
| β n | 0.2 | 0.2 | 0.2 |
βtm is the weight for motor task activation; βim is the weight for motor intrinsic fluctuations; βtv is the weight for visual task activation; βiv is the weight for visual intrinsic fluctuation; βn is the weight for noise fluctuation.
Analysis of simulated data
Simulated data was smoothed using a 6 mm guassian kernel. Typical BOLD-fMRI preprocessing steps such as slice-time correction, motion correction, normalization were not performed since the data was simulated in normalized MNI space without slice time delays or motion artefacts.
Seed based connectivity
BOLD signal correlation of individual voxels from the entire brain to the primary visual cortex (MNI coordinates −2, −82, 4) and the primary motor cortex (MNI coordinates −38, −22, 60) were computed during visual, visuo-motor and rest conditions. Correlation scores were converted to z-scores using the Fisher Z-transform25 and cluster-size thresholded to obtain effective p-value of 0.05 or better.
ICA-based connectivity
Using GIFT (http://icatb.sourceforge.net) a group independent component analysis (ICA) toolbox, group ICA using temporal concatenation14 with Infomax algorithm implementation was performed on the entire dataset (pooling all visual runs, all visuo-motor runs and all rest runs). Automatic dimensionality estimation using MDL yielded a mean of 3 components. Inspection of spatial distribution of the components by weighting distribution in gray matter to white matter, yielded a visual component, a motor component and a spatially non-specific noise component.
Similarity between the connectivity maps obtained by ICA and seed-based methods was computed using weighted spatial correlation on unthresholded connectivity maps.
Differences in within-network connectivity (WNC) between conditions were calculated as the difference in power of the network time courses and tested using Student's t-test. Between-network connectivity (BNC) was calculated, for each pair of networks, as the Pearson correlation of the networks' time courses12. No temporal lags in the timecourses were used to compute this correlation. This Pearson correlation coefficient was converted to a z-score using the Fisher transform25, and then contrasted between conditions using the Students t-test. For WNC and BNC measures, significance was determined (for effective p< 0.05) using Bonferroni correction for multiple comparisons. To quantitatively validate Eq (4), the sum of BNC and sum of within-network connectivity (WNC) were calculated between the motor seed and the visual seed, as per Eq (4), using individual run network time courses and the group ICA network maps as per Eq (2).
Experimental paradigm and fMRI data acquistion
Twenty healthy volunteers (11 male) age 24–61 years (mean=32) participated after giving informed consent to this IRB-approved study. BOLD fMRI data were acquired at 3.0 Tesla (Philips Medical Systems) using SENSE-2D-EPI (TR/TE = 2000/30 ms, Flip angle = 75°, SENSE factor = 2, nominal voxel dimensions = 3 mm × 3 mm × 3 mm with 1 mm slice gap with 80 × 80 matrix and 37 slices; 130 dynamics for each run). Six four-minute task runs were acquired in five participants. The task runs were simple block design paradigms (six blocks with twenty-second off, twenty-second on; with an additional twenty second off block at the end of each run) of visual fixation alternating with either (a) full-field visual stimulation using an 8 Hz contrast-reversing black and white checkerboard or (b) full-field contrast-reversing black and white checkerboard visual stimulation with simultaneous sequential finger tapping (i.e., participants were instructed to tap their fingers sequentially at a comfortable pace whenever the checkerboard was seen). Visual and visuo-motor runs alternated, with the order counterbalanced among participants. Seven-minute resting state fMRI data using the same scanning parameters were obtained from the other fifteen subjects to compare FC measures during rest with the above tasks.
fMRI data analysis
Preprocessing (slice timing correction, motion correction, spatial normalization, intensity normalization, and smoothing with 6 mm Gaussian kernel) was performed using FSL26.
ICA connectivity
Group ICA was performed using the same method used for the simulated data. Using automatic dimensionality estimation with minimum description length (MDL) criteria27, ICA decomposed the BOLD fMRI data into fifty-five components (mean MDL = 55). Using the spatial distribution of the components in the grey matter, white matter and the cerebro-spinal fluid28, fourteen components were selected with anatomically plausible functional networks, and time courses consistent with hemodynamic modulation; remaining components were discarded as noise and nuisances (e.g. head motion & CSF pulsation).
ICA derived FC measures (WNC and BNC) were computed and contrasted with the same method used on the simulated data.
Seed-based connectivity
Two pipelines for preprocessing were performed for seed based connectivity. One preprocessing pipeline was identical to ICA preprocessing which included PCA dimensionality reduction and removal of noise components (Figure 1). The other preprocessing pipeline used for computing seed-based connectivity was typical preprocessing for seed based connectivity including regressing out motion, global, white matter and CSF signal29 (Figure 1) but without PCA dimensionality reduction or ICA-based noise components removal. Map similarity was calculated by spatial weighted correlation, the method used on the simulated data. SBC connectivity maps and FC metrics were obtained separately for each preprocessing pipeline and compared with ICA-derived connectivity maps and FC metrics.
Figure 1.
Data analysis processing pipeline. Functional connectivity measures were obtained separately on simulated and experimental data from three methods: ICA, seed-based connectivity using the same preprocessing as ICA and seed-based connectivity using typical preprocessing performed for seed-based connectivity approaches.
Results
Simulation: Seed based connectivity
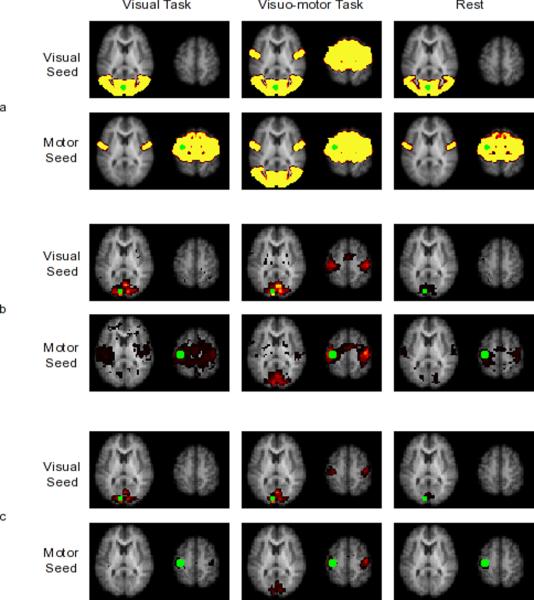
Thresholded connectivity maps of the visual seed and the motor seed for the three tasks are shown in Figure 2 panel a. During the visual run, the visual seed is connected to other regions in the visual cortex and the motor seed is connected to bilateral regions in the motor cortex. During the visuo-motor run, the visual seed appears connected to both regions in the visual cortex and regions in the motor cortex and similarly, the motor seed appears to be connected to regions in the motor cortex as well as the visual cortex.
Figure 2.
Seed based connectivity maps of primary visual cortex and primary motor cortex seeds (in green) from simulated data (panel a) and from experimental data using SBC on ICA-preprocessed data (panel b) and using SBC on SBC-preprocessed data (panel c). The three columns represent visual, visuo-motor and rest tasks, respectively. During visual task and rest, visual seed was connected only to regions in the visual cortex and the motor seed was connected only to regions in the motor cortex. During visuo-motor task, the visual seed was connected both to regions in the visual cortex and the motor cortex; the motor seed was connected both to regions in the motor cortex and the visual cortex. In the experimental data, the difference in the motor seed connectivity thresholded maps between different preprocessing methods was due to thresholding. Contrasting the two methods did not show significant difference (results not shown).
Simulation: ICA networks
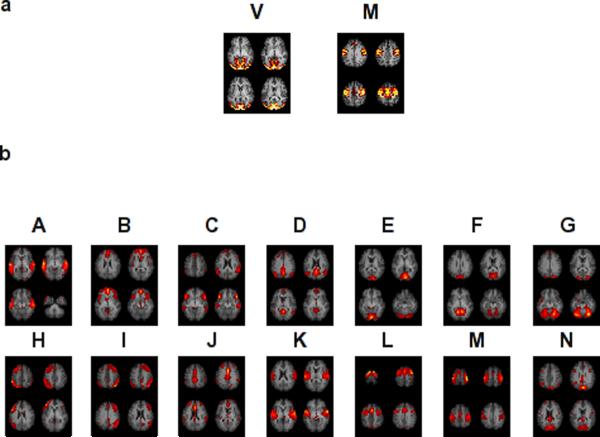
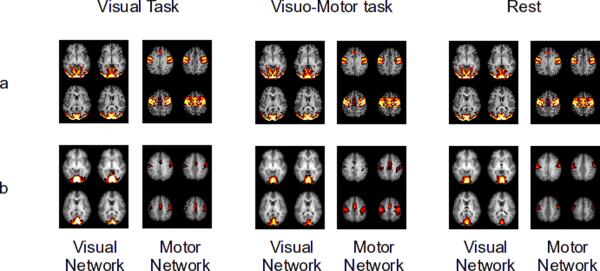
The two component maps obtained using spatial ICA on the simulated data are shown in Figure 3 panel a. ICA performed on the three tasks separately also showed similar component maps (Figure 4 panel a).
Figure 3.
Thresholded maps of neuro-physiologically relevant components obtained from group ICA on simulated (panel a) and experimental (panel b) data. The two components obtained from group ICA of simulated data are the V and M networks. The components labeled A-N are the fourteen components obtained from the experimental data whose peak locations are shown in Table 2.
Figure 4.
Group ICA thresholded component maps of the visual and motor network obtained by performing group ICA separately on visual task, visuo-motor task and rest. Figures are shown for simulated (panel a) and experimental data (panel b). In all three tasks ICA robustly separated the visual network from the motor network.
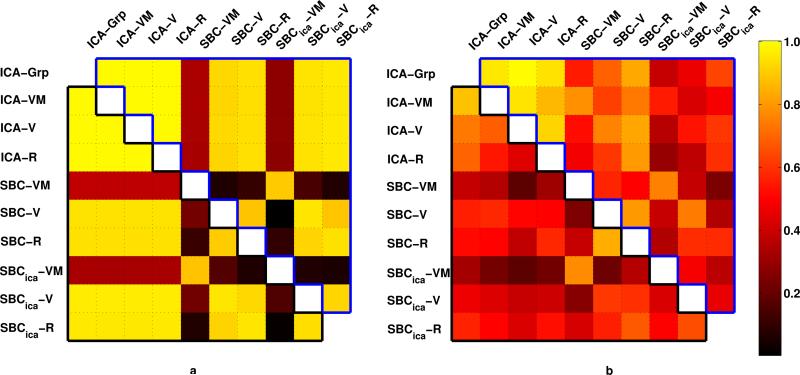
Quantitative comparisons performed by weighted spatial correlation of the unthresholded spatial maps are shown in Figure 5 panel a. As expected, high spatial correlation values are seen between pairs of visual networks (upper triangle of the matrix enclosed by blue) and pairs of motor networks (lower triangle of the matrix enclosed in black) obtained from all tasks and both methods, except while comparing maps obtained from seed-based method during visuo-motor task (rows 5, 8 and columns 5, 8).
Figure 5.
Similarity among connectivity maps shown for simulation (panel a) and experiment (panel b). Weighted spatial correlations between unthresholded visual (motor) connectivity maps obtained by different methods and tasks is shown in the upper (lower) triangle of the matrix. ICA connectivity maps obtained on each tasks (rows 1–4 and columns 1–4) were highly consistent in both the simulated data and the actual experiment. Consistency between SBC and ICA maps were higher during simulation than during the experiment. Visual network showed higher consistency than the motor network.
No WNC differences were found between the tasks. BNC between the two networks was significantly higher in visuo-motor run than in the visual run (p<0.0001) and in the resting run (p<0.0001). Quantitative comparison of SBC and ICA measures of FC between the motor seed and the visual seed revealing the relationship in Eq (5) is shown in Table 2.
Table 2.
FC between the visual seed region and the motor seed region during the three tasks derived using SBC and ICA on the simulated data.
| Task | SBC | Sum (WNC) | Sum (BNC) |
|---|---|---|---|
| Visual | −0.09 ± 0.12 | −0.14 ± 0.02 | 0.04 ± 0.12 |
| Visuo-motor | 0.89 ± 0.03 | −0.07 ± 0.00 | 0.96 ± 0.03 |
| Rest | −0.10 ± 0.13 | −0.07 ± 0.00 | −0.03 ± 0.14 |
SBC: Seed based connectivity; WNC: ICA-derived within network connectivity; BNC: ICA-derived between network connectivity; Values are shown as Mean ± Standard deviation.
Experiment: Seed-based connectivity
Thresholded connectivity maps of primary visual cortex seed and primary motor cortex seed during the visual, visuo-motor and rest conditions are shown in Figure 2 panels b and c. During the visual run, the primary visual seed is significantly connected only to regions within the visual cortex; the primary motor seed is significantly connected only to bilateral motor cortices. During the visuo-motor run, in addition to connectivity to the higher-order visual cortices, the primary visual seed appears to be connected to the supplementary motor area and the primary motor cortex; a similar connectivity map is observed for the primary motor cortex seed. During rest, connectivity is similar to the visual-only run: the visual seed is significantly connected only to regions within the visual cortex and the motor seed is significantly connected only to regions within the motor cortex. Apparent differences in SBC maps between the two preprocessing methods, are due to differences in threshold. Comparison by contrasting the two methods showed no significant difference (not shown) though higher sensitivity to connectivity is evident while using typical SBC preprocessing.
Experiment: ICA Networks
Cross-sectional images of the fourteen functional networks from group ICA of all the runs (visual, visuo-motor and rest) are shown in Figure 3. Peak locations of the network clusters and their anatomical labels are listed in Table 2. Network A peaks were located in superior and middle temporal gyrus in Brodmann area 42, 22 and 39 commonly associated with the ventral visual pathway. Network B peaks were found in medial frontal gyrus, bilateral insula including Brodmann area 9, 10 and 47. Network B has spatial pattern consistent with the salience network6. Network C peaks were found in bilateral inferior frontal gyrus, bilateral angular gyrus and bilateral middle temporal gyrus. Network D has a spatial pattern matching the “default-mode network”30 with peaks in the precuneus, inferior parietal lobules, and the ventromedial prefrontal cortex. Network E peaks were primarily in bilateral cuneus in Brodmann area 17 and related primary visual cortices, consistent with primary visual cortex (V1). Network F peak locations were around bilateral cuneus, lingual gyrus and cerebellum consistent with secondary visual cortex (V2). Network G peaks were in Brodmann area 19, in the cuneus and the occipital gyrus, consistent with visual association cortex (V3). Network H peaks were found in Broca's area, left dorsolateral prefrontal cortex, left ACC and left PCC suggesting a role in language processing. Network I has peaks corresponding to Network H in the right side of the brain including Wernicke's area and the mirror neuron system. Network J peaks were found in the anterior cingulate cortex, dorsal cingulate cortex (BA 24), anterior middle frontal gyrus and angular gyrus forming a cingulate network. Network K included Brodmann areas 6 and 42 suggesting a role in sensori-motor processing along with network E. Network L has peaks in the dorsolateral prefrontal cortex (Brodmann area 9) and premotor areas (Precentral gyrus, supplementary motor area). Network M has peaks in the supplementary motor area and motor cortex (Brodmann area 6) and is consistent with motor planning and execution. Peaks of Network N lie in cuneus, PCC and angular gyrus.
ICA performed on the three conditions separately yielded similar neuro-physiologically relevant functional networks in all three conditions. Figure 4 panel b shows the motor and the visual network derived by using ICA on the three conditions separately.
Quantitative Comparison of spatial maps
Weighted spatial correlation on the spatial maps is shown in Figure 5 for the visual networks (upper triangle of the matrix) and the motor network (lower triangle of the matrix). Similar to results from simulation but with higher variability, the networks show similarity across methods except for networks derived by seed-based methods during visuo-motor runs (rows 5,8 and columns 5,8). Spatial distribution of visual networks appear to be more robust across tasks and methods than motor networks. ICA performed on visual task, visuo-motor task, rest separately and on all tasks combined, consistently separated visual and motor networks (rows 1–4, columns 1–4). Seed-based methods using typical seed based preprocessing produced maps that more consistent with ICA-derived maps when compared to seed-based methods using ICA-like preprocessing.
Experiment: Within Network Connectivity
Connectivity within the visual network was higher during visual (p<0.0108) and visuo-motor (p<0.0138) task when compared to rest. Inter-task differences in WNC of the other networks did not reach significance after Bonferroni correction.
Experiment: Between-Network Connectivity
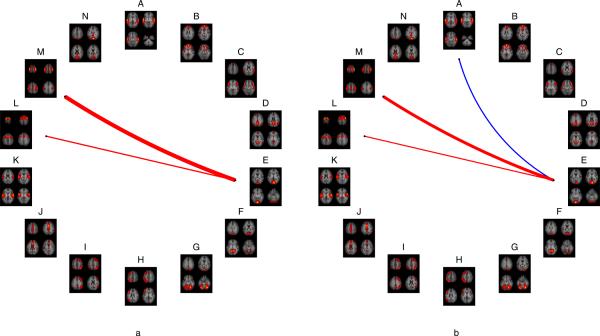
Connectivity between Network E and Network M (p<1e-8) and connectivity between Network E and Network L (p<0.0136) was significantly higher for the visuo-motor compared to the visual task. (Figure 6 panel a). Connectivities between Network E and Network M (p<1e-5) and between Network E and Network L (p<0.027) were significantly higher for the visuo-motor task compared to rest, while connectivity between Network E and Network A was significantly lower (p<0.0178) for the visuo-motor task compared to rest (Figure 6 panel b). No other BNC differences reached significance.
Figure 6.
BNC differences between visuo-motor and visual tasks (panel a) show that connectivity between networks E and M and between networks E and L were significantly higher during the visuo-motor task than during the visual task. BNC differences between visuo-motor task and Rest (panel b) showed connectivity between networks E and M and between networks E and L were significantly higher during the visuo-motor task than during rest. Connectivity between networks A and E was significantly lower during visuo-motor task than during rest. Thickness of lines are proportional to strength of connectivity difference.
Experiment: Quantitative comparison of SBC and ICA measures of FC
Connectivity between the motor seed and the visual seed, as computed using seed-based method and using ICA based measures (total WNC and total BNC) as described in Eq (4), are shown in Table 3. No significant difference between the two methods of preprocessing for the seed-based connectivity (SBC) was found (p<0.1781). As shown in Eq (4), the total WNC and total BNC added up to the total connectivity.
Table 3.
Peak locations and anatomical labels in standard space for the networks A through N obtained from group ICA on the experimental data
| MNI Coordinates | Anatomical Label | |
|---|---|---|
| Network A | −67,−33, −3 | L Middle Temporal Gyrus (BA 21) |
| +61,−27, −7 | R Middle Temporal Gyrus | |
| +63,−25, +9 | R Superior Temporal Gyrus (BA 42) | |
| −67,−13, +1 | L Superior Temporal Gyrus | |
| −55,−47, +1 | L Middle Temporal Gyrus (BA 22) | |
| −31,−17,−23 | L Parahippocampa Gyrus (BA) | |
| −63,−63, +9 | L Middle Temporal Gyrus (BA 39) | |
|
| ||
| Network B | −3,+47, −7 | L Medial Frontal Gyrus (BA 10) |
| −1,+31,+25 | L Anterior Cingulate | |
| −3,+47,+29 | L Medial Frontal Gyrus (BA 9) | |
| +41,+15, −7 | R Inferior Frontal Gyrus (BA 47) | |
| +31,+17,−11 | R Extra-Nuclear (BA 13) | |
|
| ||
| Network C | +49.+21, −7 | R Inferior Frontal Gyrus |
| +57,−49,+29 | R Supramarginal Gyrus | |
| −63,−35, −7 | L Middle Temporal Gyrus | |
| −3,+23,+57 | L Superior Frontal Gyrus (BA 8) | |
| +19,−91,−35 | R Uvula | |
|
| ||
| Network D | −3,−57,+17 | L Posterior Cingulate (BA 23) |
| −3,−65,+33 | L Precuneus | |
| +47,−69,+21 | R Middle Temporal Gyrus | |
| −3,+61,−11 | L Medial Frontal Gyrus (BA 11) | |
| −3,+57,+21 | L Medial Frontal Gyrus (BA 10) | |
|
| ||
| Network E | +3,−91, +5 | L Cuneus |
| −7,−95, −7 | L Lingual Gyrus | |
| +3,−97, +17 | R Cuneus (BA 18) | |
| +5,−87, +5 | L Cuneus (BA 17) | |
|
| ||
| Network F | −3,−85,+25 | L Cuneus |
| −17,−61, +1 | L Lingual Gyrus | |
| +1,−53, −3 | Culmen | |
| −13,−61, +1 | L Lingual Gyrus | |
| −59, +9, −7 | L Superior Temporal Gyrus (BA 22) | |
| −37,−67,−23 | L Declive | |
|
| ||
| Network G | +33,−69,−23 | R Declive |
| −39,−61,−19 | L Fusiform Gyrus (BA 37) | |
| −31,−97,+13 | L Middle Occipital Gyrus (BA 19) | |
| +25,−93,+25 | R Cuneus | |
| +13,−89,+41 | R Cuneus | |
| −33,−93, +1 | L Middle Occipital Gyrus | |
|
| ||
| Network H | −51,+31,+25 | L Middle Frontal Gyrus |
| −11,−49,+37 | L Precuneus (BA 31) | |
| −7,+31,+37 | L Medial Frontal Gyrus | |
| −9,+21,+41 | L Cingulate Gyrus (BA 32) | |
| −51,+37, +5 | L Inferior Frontal Gyrus (BA 45) | |
| −59,+11,+33 | L Inferior Frontal Gyrus (BA 9) | |
|
| ||
| Network I | +53,−59,+41 | R Inferior Parietal Lobule (BA 40) |
| +41,+21,+45 | R Middle Frontal Gyrus | |
| −3,+31,+41 | L Medial Frontal Gyrus (BA 6) | |
| +1,−45,+41 | L Cingulate cortex | |
| +29,+25,+53 | R Superior Frontal Gyrus | |
| +33,−77,+53 | R Superior Parietal lobule | |
| +61,−31,−11 | R Middle Temporal Gyrus | |
|
| ||
| Network J | −3, +9,+33 | L Cingulate Gyrus (BA 24) |
| −5,−35,+49 | L Paracentral Lobule (BA 5) | |
| −39,+37,+29 | L Middle Frontal Gyrus | |
| −59,+11, −7 | L Superior Temporal Gyrus (BA 22) | |
| +49,+13, −7 | R Superior Temporal Gyrus | |
| −23,−29,−19 | L Parahippocampa Gyrus (BA 35) | |
| +49,−49,+53 | R Inferior Parietal Lobule (BA 40) | |
|
| ||
| Network K | +61,−17, +9 | R Transverse Temporal Gyrus |
| −65,−19, +9 | L Transverse Temporal Gyrus | |
| −61, +3, −3 | L Superior Temporal Gyrus | |
| +57, −1, +1 | R Superior Temporal Gyrus | |
| +57, −1,+33 | R Precentral Gyrus (BA 6) | |
| +47, −5, −3 | R Insula | |
|
| ||
| Network L | −1, +7,+53 | L Superior Frontal Gyrus |
| −51, −1,+53 | L Precentral Gyrus | |
| +9, +5,+73 | R Superior Frontal Gyrus (BA 6) | |
| −59, +5,+37 | L Precentral Gyrus | |
| −43,+23, −3 | L Inferior Frontal Gyrus | |
| +33, +5, +5 | R Claustrum | |
| −27, +7, +1 | L Extra-Nuclear | |
| −19,−37,−47 | L Cerebelum | |
|
| ||
| Network M | −3,−13,+57 | L Medial Frontal Gyrus (BA 6) |
| +33,−37,+69 | R Postcentral Gyrus (BA 1) | |
| +29,−21,+69 | R Precentral Gyrus | |
| −15,−15,+77 | L Precentral Gyrus | |
| +17,−61,−23 | R Declive | |
| −27,−57,−23 | L Declive | |
| +27,−21,+69 | R Precentral Gyrus | |
| +41,−25,+57 | R Postcentral Gyrus (BA 3) | |
| −43,−25,+61 | L Postcentral Gyrus (BA 3) | |
|
| ||
| Network N | −1,−85,+33 | L Cuneus (BA 19) |
| −3,−33,+29 | L Cingulate Gyrus | |
| +41,−69,+49 | R Angular Gyrus | |
| −51,+5,+41 | L Middle Frontal Gyrus (BA 8) | |
| −43,−63,+37 | L Inferior Parietal Lobule | |
| −3,−33,+29 | L Cingulate Gyrus | |
| −67,−33, −7 | L Middle Temporal Gyrus (BA 21) | |
| −55,+23,−11 | L Inferior Frontal Gyrus (BA 47) | |
| +45,+19,−11 | R Inferior Frontal Gyrus | |
| +25,+59, −7 | R Superior Frontal Gyrus (BA 10) | |
| −39,+57,−11 | L Middle Frontal Gyrus (BA 11) | |
| −15, −3,−23 | L Parahippocampa Gyrus (BA 34) | |
The difference between the visuo-motor task and the visual task in the total BNC was significantly higher (p<7.4e-4) than the difference between the two tasks in the total WNC. Also, the difference between visuo-motor task and rest in the total BNC was significantly higher (p<5e-5) than the difference between the two tasks in the total WNC. The total WNC was not significantly different between visuo-motor and visual task (p<0.1548), or between visuo-motor task and rest (p=0.2813). The total BNC was significantly higher in visuo-motor task when compared to visual task (p=0.0031) and when compared to rest (p=4.7e-5).
During visuo-motor task, contribution of BNC to total connectivity was significantly higher (p<0.001) between the visual seed and the motor seed. (Table 2 and Figure 7). However, for the same task when computing FC between two voxels in the visual cortex, or between two voxels in the motor cortex, total WNC was found to be the bigger contributor (p<0.001) to total connectivity (Figure 4).
Figure 7.
Comparison of contribution of WNC and BNC to total connectivity during visuo-motor task. Connectivity between seeds that belong to different networks such as the visual and motor seed (left pair of bars) was primarily due to BNC, whereas connectivity between seeds within the same network, either visual (middle pair of bars) or motor (right pair of bars), was primarily due to WNC.
Discussion
Functional connectivity in BOLD fMRI was first introduced by Biswal et al.1 in 1995. Since, FC has been primarily investigated by using either seed-based connectivity1 or ICA derived connectivity13. Besides connectivity maps7,11,31,32 and FC between specific region pairs33–35, connectivity between functional networks have also been reported to be associated with disease12. FC is thought to be comprised of two subtypes: Intrinsic functional connectivity (IFC), which is task-independent1,36 and task-modulated functional connectivity17,37. Task modulated FC can include both connectivity induced in the brain due to task (e.g. connectivity between the visual and language network while reading) and externally induced co-activation due to different but simultaneous external stimuli (e.g. apparent connectivity between auditory network and visual face-processing network when listening to a song and simultaneously looking at pictures of faces). Dissecting FC in to intrinsic and task-modulated subtypes is nontrivial. Although FC measured during task-free resting state is considered to be representative of IFC, the measured FC is not purely IFC since the brain is never truly task-free. In this study we used externally induced co-activation to study task modulation of measures of FC. The relationship between FC measures that is derived and experimentally validated in this study should hold for all FC modulations.
Practical considerations
In this study, estimates of functional connectivity were obtained from simulated data and experimental data using two methods: seed-based temporal correlation, and spatial ICA. While comparing the two methods, several practical considerations have to be made.
Preprocessing
The typical preprocessing for the two methods are different, which may contribute to differences in FC measures. While performing group ICA using temporal concatenation, it is typically necessary to reduce the dimensionality of the data using PCA. In seed-based methods, typical preprocessing includes removal of nuisances from white matter, cerebro-spinal fluid, global signal and motion. To address this issue, we obtain FC metrics from SBC with typical SBC preprocessing, ICA with typical ICA preprocessing, and SBC with typical ICA preprocessing.
Thresholding
The statistical tests performed to threshold SBC spatial maps and ICA component maps arise from different queries on the underlying distribution. In seed based correlation, thresholding is performed by preventing false positives similar to the General Linear Model, whereas in ICA thresholding is performed to detect signal over the noise level. To avoid a problem in threshold mismatch, weighted spatial correlation values on unthresholded maps (higher values were given more weight) were computed to show degree of similarity in connectivity maps obtained from the two methods.
Number of components
While using the ICA method, the number of components estimated must be specified. Previous work has shown 8 to 10 functionally relevant networks20 by estimating a total of 20 or 30 components. More recent works have shown 20 functionally relevant networks or greater18. There exists the potential of deriving hundreds of sub-networks or regions using ICA. As the number of components increases for IC estimation, the networks break down to subnetworks and small regions. It is believed that the total number of networks or components is not determined by neurobiology but by experiment (such as magnet strength, acquisition methods, fMRI temporal and spatial resolution, estimation methods). It is possible to estimate networks at high dimensions and produce connectivity within and between components; however, the terminology of networks will have to be adjusted to account for sub-networks or regions. To obtain an optimal number of components in group ICA, we used the mean of the minimum description length (MDL) to estimate the number of components; this has proven sufficient to address our hypotheses of testing connectivity between the motor and visual networks.
Selection of components
Another practical issue in ICA is the segregation of components that have neuro-physiological origin from nuisance components (respiration, cardiac and motion induced artefacts). Several methods with some success have been proposed13,28,38–40. We used a combination of CORSICA28, power distribution in frequency domain and visual inspection to extract functionally relevant components.
Seed-based connectivity
While using seed-based methods, connectivity between two co-activating brain regions would be computed to be high irrespective of whether the two regions belonged to different intrinsically connected networks, i.e. seed-based correlation reports connectivity between any two synchronous voxels independent of their allegiance to intrinsically connected networks. Hence seed-based correlation has the same limitation as general linear model usage in task activation studies, in that activation of one functional network cannot be distinguished from co-activation of distinct networks41. The appearance of the motor cortices' connectivity to the primary visual seed region during the visuo-motor task shows that the two regions are synchronous during the particular task, but does not mean that the motor cortex and the visual cortex are connected as an intrinsic functional network. These connected regions are elements of a task activated ensemble6 rather than an intrinsic functional network.
ICA connectivity
ICA uses spatial independence to decompose data into components each with a spatial map and an associated time course. ICA component spatial maps have been used to study tasks and rest in BOLD fMRI for several years12,13,15–17. The ICA component spatial maps remain very similar for a wide variety of tasks in a large spectrum of the population18,19,24; which has been exploited by using group ICA for varying tasks and rest.
WNC
The spatial maps of the networks are assumed to be robust between tasks and hence inter-task differences in WNC are driven by the component time courses. As shown in Eq (7), the inter-task WNC difference can be compared using the power of the network time course. In the present experiment, we found increased connectivity within the visual cortex during tasks that engaged the entire visual network (full field visual stimulation). Likely due to low statistical power and non-involvement of the entire motor network in finger tapping, similar increase in motor network during motor task was not observed. We predict that increasing the sample size and performing a task that involves all regions of the motor network would reveal increased motor network WNC during motor tasks.
BNC
Since the components are derived using spatial independence, no assumption about temporal coherence of voxels in different components is made. To estimate connectivity between ICA derived networks, correlation between the time courses of network pairs was computed by Jafri et al12. Hence, ICA provides two measures of connectivity: Within network connectivity as seen in spatial maps and time course power, and connectivity between networks (BNC) estimated as correlation of time courses of network pairs.
In the present experiment, comparing BNC between tasks, and between task and rest, yielded significant differences only in networks of clear relevance to the task. Specifically, the increase in connectivity between Networks E (visual network) and M and L (motor networks) was reasonable, reflecting synchrony between visual and motor cortices during a visuo-motor task. The connectivity between visual ventral stream network and visual network is lost during the visuo-motor task compared to rest. This is likely due to specific stimulation of only the visual system during the task.
Changes in total connectivity between a motor seed and a visual seed from visual task to visuo-motor task is mainly due to changes in BNC rather than WNC as seen in Table 2 and Table 4. During visuo-motor task, contribution of WNC and BNC to total connectivity changed depending on the network allegiance of the seeds. While BNC was the greater contributor to total connectivity between seeds from distinct networks, WNC was the greater contributor to total connectivity between seeds within the same network.
Table 4.
FC between visual seed region and the motor seed region derived from seed based and ICA based methods during the three task states from the experimental data
| Task | Run | SBC | SBCICA | Sum (WNC) | Sum (BNC) |
|---|---|---|---|---|---|
| Visual | 1 | −0.11 | 0.45 | 0.34 | 0.10 |
| 2 | −0.06 | 0.26 | 0.26 | 0.00 | |
| 3 | −0.12 | 0.45 | 0.39 | 0.06 | |
| 4 | −0.25 | 0.08 | 0.8 | −0.72 | |
| 5 | −0.04 | 0.24 | 0.33 | −0.09 | |
|
| |||||
| Mean ± Std | −0.12 ± 0.08 | 0.29 ± 0.16 | 0.42 ± 0.22 | −0.12 ± 0.08 | |
|
| |||||
| Visuo-motor | 1 | 0.63 | 0.85 | 0.21 | 0.64 |
| 2 | 0.82 | 0.86 | 0.19 | 0.67 | |
| 3 | 0.68 | 0.87 | 0.17 | 0.70 | |
| 4 | 0.81 | 0.93 | 0.2 | 0.74 | |
| 5 | 0.71 | 0.86 | 0.22 | 0.64 | |
|
| |||||
| Mean ± Std | 0.73 ± 0.08 | 0.87 ± 0.03 | 0.20 ± 0.02 | 0.68 ± 0.04 | |
|
| |||||
| Rest | 6 | 0.02 | −0.36 | 0.17 | −0.53 |
| 7 | −0.07 | 0.42 | 0.25 | 0.17 | |
| 8 | −0.19 | −0.03 | 0.2 | −0.23 | |
| 9 | 0.23 | −0.02 | 0.31 | −0.34 | |
| 10 | 0.14 | −0.02 | 0.2 | −0.21 | |
| 11 | −0.25 | 0.33 | 0.23 | 0.10 | |
| 12 | −0.01 | 0.38 | 0.24 | 0.14 | |
| 13 | −0.03 | −0.15 | 0.23 | −0.38 | |
| 14 | 0.31 | 0.52 | 0.17 | 0.35 | |
| 15 | 0.21 | 0.4 | 0.35 | 0.05 | |
| 16 | −0.15 | 0.09 | 0.23 | −0.13 | |
| 17 | 0.21 | −0.11 | 0.17 | −0.29 | |
| 18 | −0.14 | 0.49 | 0.22 | 0.27 | |
| 19 | 0.27 | 0.71 | 0.21 | 0.50 | |
| 20 | −0.02 | −0.03 | 0.23 | −0.26 | |
|
| |||||
| Mean ± Std | 0.04 ± 0.18 | 0.17 ± 0.31 | 0.23 ± 0.05 | −0.05 ± 0.30 | |
SBC: Seed-based connectivity; SBCICA: Seed-based connectivity from ICA preprocessed data; WNC: ICA-derived within-network connectivity; BNC: ICA-derived between-network connectivity.
Hence, similar to comparing BNC of specific networks (Figure 6), WNC within each network can be compared. In addition, the contribution of WNC and BNC to total connectivity can also be computed. We propose that each of these additional FC measures may vary with task, or disease, and may serve as an additional biomarker to study brain function.
It is to be noted that the correction for multiple networks comparison used for WNC and BNC (not the spatial maps) was very stringent and probably masked subtle changes in WNC and BNC. A more appropriate correction such as permutation testing may be necessary while investigating WNC and BNC differences between tasks. However, that is beyond the scope of this paper.
Relationship between ICA and seed-based connectivity
Connectivity maps obtained using a seed voxel in the primary visual cortex showed connectivity of the seed to other regions in the primary visual cortex, the secondary visual cortex and some regions of the higher order visual processing during all three conditions. During the visuo-motor task, in addition to this connectivity, the seed was correlated with the premotor and motor cortices. Connectivity maps obtained using a seed voxel in the primary motor cortex showed connectivity of the seed to other regions in the primary motor cortex and to premotor areas during all three conditions. During the visuo-motor task, in addition to this connectivity, the seed was correlated to the visual cortices. Group ICA consistently separated the visual network and the motor network in all three tasks. Connectivity between the visual and the motor networks was significantly stronger during the visuo-motor run than during the visual run or rest. The above results were observed in both simulated and experimental data.
Since in both methods functional connectivity was inferred from thresholded spatial maps, and the threshold used in the two methods are different due to underlying statistical tests, weighted spatial correlation on unthresholded connectivity maps was computed between visual (or motor) maps obtained for each task in both methods (Figure 5). The figure shows that the primary visual (and motor) maps are robustly estimated in pooled group ICA and in individual task group ICA (rows 1–4 and columns 1–4) in both simulated and experimental data. As expected, lower values are observed in row 5, row 8, column 5 and 8 where SBC maps during visuo-motor task is compared with others. SBC maps appear to be more consistent with ICA networks in simulated data, compared to experimental data. This is potentially due to lack of specificity of the atlas-based seed across subjects in the experimental data. Differences between the two preprocessing pathways in SBC derived maps are evident. The typical preprocessing used for SBC which includes nuisance removal (white matter, CSF, global signal), appears to be more consistent with ICA derived maps than SBC maps derived from ICA preprocessed data (which includes dimensionality reduction and denoising by removing nuisance components). In all comparisons, the primary visual network appears to be more consistent than the motor network. This may be due to higher SNR or higher synchrony within the entire primary visual cortex compared to the entire motor cortex.
For a quantitative comparison of FC measures, as shown in Table 4, connectivity computed using seed-based method and ICA-derived total connectivity computed as the sum of WNCs and BNCs are identical. However, differences between the two preprocessing methods for SBC measure are evident, exposing the significance of preprocessing methods. Typical SBC preprocessing (including regression of global, white matter and CSF signals) produced connectivity maps that are more consistent with ICA derived intrinsic connectivity maps. However, the total connectivity derived using typical SBC preprocessing is considerably (though not significantly) different. This difference is primarily due to ICA specific preprocessing (dimensionality reduction and ICA-based denoising) and not SBC specific preprocessing such as global, white matter and CSF signal regression (results not shown). While denoising using ICA is neurobiologically justified, the PCA dimensionality reduction is not. Hence, methods to perform group ICA without dimensionality reduction may improve consistency between the two preprocessing pipelines.
Conclusions
The purpose of this study was to elucidate the relationship between seed correlation and ICA, the two predominant methods used for calculating FC from fMRI data. Spatial distribution of the network maps obtained using seed-based methods and ICA-based methods have been shown to yield similar but not identical results21. The differences in the measures of functional connectivity have not been compared between the two methods.
When using seed-based correlation during a task (or state) that co-activates two brain networks, voxels from both networks will appear to be connected. Seed-based correlation thus does not reveal information about intrinsically connected networks and their interactions, but reveals functional connectivity of a brain region for the specific experimental brain state. On the other hand, ICA identifies each network distinctly and consistently, and provides metrics of connectivity between networks. A brain region may be part of several ICA derived networks, and a query on a specific brain region will involve investigating all those networks and their interactions with other functional brain networks. Hence this relationship shows that ICA methods are able to distinguish intrinsic connectivity from task modulated connectivity, whereas seed-based methods cannot.
In summary, while seed based connectivity provides a single metric of FC, ICA, in addition to providing total FC, decomposes total FC into connectivity within each network and connectivity between pairs of networks. Thus, the relationship between the seed & ICA approaches to FC is similar to the relationship between the general linear model (GLM) and ICA approaches for computing activation, summarized by Friston et al41 as the distinction between “modes” and “models”: The GLM detects voxels respecting a user-specified temporal model, while ICA yields networks of brain regions displaying synchronous signals or “modes”. As seed-based correlation is essentially a GLM using the time course of the seed voxel, seed-based FC is essentially a map of the “model” specified by the seed voxel, while ICA based FC distinguishes brain “modes” and the temporal relationships between them.
Acknowledgments
The authors thank Dr. Bennett Landmann for help with acquisition of resting state data. The authors also thank Mr. Joseph S. Gillen, Ms. Terri Brawner, Ms. Kathleen Kahl, and Ms. Ivana Kusevic for experimental assistance. This publication was made possible by grant support from NIH-NCRR P41-RR15241. The National Center for Research Resources (NCRR) is a component of the National Institutes of Health (NIH). The contents of the paper are solely the responsibility of the authors and do not necessarily represent the official view of NCRR or NIH. Equipment used in the study is manufactured by Philips. Dr. van Zijl is a paid lecturer for Philips Medical Systems. Dr. van Zijl is the inventor of technology that is licensed to Philips.
Footnotes
This arrangement has been approved by Johns Hopkins University in accordance with its conflict of interest policies.
References
- 1.Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic Resonance in Medicine: Official Journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 1995 October;34(4):537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- 2.Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America. 2005 July 5;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Stein T, Moritz C, Quigley M, Cordes D, Haughton V, Meyerand E. Functional connectivity in the thalamus and hippocampus studied with functional MR imaging. AJNR. American Journal of Neuroradiology. 2000 September;21(8):1397–1401. [PMC free article] [PubMed] [Google Scholar]
- 4.Xiong J, Parsons LM, Gao JH, Fox PT. Interregional connectivity to primary motor cortex revealed using MRI resting state images. Human Brain Mapping. 1999;8(2–3):151–156. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<151::AID-HBM13>3.0.CO;2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kelly AMC, Uddin LQ, Biswal BB, Castellanos FX, Milham MP. Competition between functional brain networks mediates behavioral variability. NeuroImage. 2008 January 1;39(1):527–537. doi: 10.1016/j.neuroimage.2007.08.008. [DOI] [PubMed] [Google Scholar]
- 6.Seeley WW, Menon V, Schatzberg AF, Keller J, Glover GH, Kenna H, Reiss AL, Greicius MD. Dissociable intrinsic connectivity networks for salience processing and executive control. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2007 February 28;27(9):2349–2356. doi: 10.1523/JNEUROSCI.5587-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Garrity AG, Pearlson GD, McKiernan K, Lloyd D, Kiehl KA, Calhoun VD. Aberrant “default mode” functional connectivity in schizophrenia. The American Journal of Psychiatry. 2007 March;164(3):450–457. doi: 10.1176/ajp.2007.164.3.450. [DOI] [PubMed] [Google Scholar]
- 8.Greicius MD, Flores BH, Menon V, Glover GH, Solvason HB, Kenna H, Reiss AL, Schatzberg AF. Resting-state functional connectivity in major depression: abnormally increased contributions from subgenual cingulate cortex and thalamus. Biological Psychiatry. 2007 September 1;62(5):429–437. doi: 10.1016/j.biopsych.2006.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Greicius M. Resting-state functional connectivity in neuropsychiatric disorders. Current Opinion in Neurology. 2008 August;21(4):424–430. doi: 10.1097/WCO.0b013e328306f2c5. [DOI] [PubMed] [Google Scholar]
- 10.Greicius MD, Srivastava G, Reiss AL, Menon V. Default-mode network activity distinguishes Alzheimer's disease from healthy aging: evidence from functional MRI. Proceedings of the National Academy of Sciences of the United States of America. 2004 March 30;101(13):4637–4642. doi: 10.1073/pnas.0308627101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kennedy DP, Courchesne E. The intrinsic functional organization of the brain is altered in autism. NeuroImage. 2008 February 15;39(4):1877–1885. doi: 10.1016/j.neuroimage.2007.10.052. [DOI] [PubMed] [Google Scholar]
- 12.Jafri MJ, Pearlson GD, Stevens M, Calhoun VD. A method for functional network connectivity among spatially independent resting-state components in schizophrenia. NeuroImage. 2008 February 15;39(4):1666–1681. doi: 10.1016/j.neuroimage.2007.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van de Ven VG, Formisano E, Prvulovic D, Roeder CH, Linden DEJ. Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest. Human Brain Mapping. 2004 July;22(3):165–178. doi: 10.1002/hbm.20022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Calhoun VD, Adali T, Pearlson GD, Pekar JJ. A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping. 2001 November;14(3):140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.McKeown MJ, Jung TP, Makeig S, Brown G, Kindermann SS, Lee TW, Sejnowski TJ. Spatially independent activity patterns in functional MRI data during the stroop color-naming task. Proceedings of the National Academy of Sciences of the United States of America. 1998 February 3;95(3):803–810. doi: 10.1073/pnas.95.3.803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Calhoun VD, Pekar JJ, Pearlson GD. Alcohol intoxication effects on simulated driving: exploring alcohol-dose effects on brain activation using functional MRI. Neuropsychopharmacology: Official Publication of the American College of Neuropsychopharmacology. 2004 November;29(11):2097–2017. doi: 10.1038/sj.npp.1300543. [DOI] [PubMed] [Google Scholar]
- 17.Calhoun VD, Pekar JJ, McGinty VB, Adali T, Watson TD, Pearlson GD. Different activation dynamics in multiple neural systems during simulated driving. Human Brain Mapping. 2002 July;16(3):158–167. doi: 10.1002/hbm.10032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, et al. Correspondence of the brain's functional architecture during activation and rest. Proceedings of the National Academy of Sciences of the United States of America. 2009 August 4;106(31):13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shehzad Z, Kelly AMC, Reiss PT, Gee DG, Gotimer K, Uddin LQ, Lee SH, Margulies DS, Roy AK, Biswal BB, et al. The resting brain: unconstrained yet reliable. Cerebral Cortex (New York, N.Y.: 1991) 2009 October;19(10):2209–2229. doi: 10.1093/cercor/bhn256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.De Luca M, Beckmann CF, De Stefano N, Matthews PM, Smith SM. fMRI resting state networks define distinct modes of long-distance interactions in the human brain. NeuroImage. 2006 February 15;29(4):1359–1367. doi: 10.1016/j.neuroimage.2005.08.035. [DOI] [PubMed] [Google Scholar]
- 21.Van Dijk KRA, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. Journal of Neurophysiology. 2010 January;103(1):297–321. doi: 10.1152/jn.00783.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, Sejnowski TJ. Analysis of fMRI data by blind separation into independent spatial components. Human Brain Mapping. 1998;6(3):160–188. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Beckmann CF, Smith SM. Tensorial extensions of independent component analysis for multisubject FMRI analysis. NeuroImage. 2005 March;25(1):294–311. doi: 10.1016/j.neuroimage.2004.10.043. [DOI] [PubMed] [Google Scholar]
- 24.Damoiseaux JS, Rombouts S, Barkhof F, Scheltens P, Stam CJ, Smith SM, Beckmann CF. Consistent resting-state networks across healthy subjects. Proceedings of the National Academy of Sciences. 2006;103(37):13848. doi: 10.1073/pnas.0601417103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fisher RA. On the `probable error' of a coefficient of correlation deduced from a small sample. Metron. 1921;1:3–32. [Google Scholar]
- 26.Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23(Suppl 1):S208–219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 27.Li YO, Adali T, Calhoun VD. Estimating the number of independent components for functional magnetic resonance imaging data. Human brain mapping. 2007;28(11):1251–1266. doi: 10.1002/hbm.20359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Perlbarg V, Bellec P, Anton J, Pélégrini-Issac M, Doyon J, Benali H. CORSICA: correction of structured noise in fMRI by automatic identification of ICA components. Magnetic Resonance Imaging. 2007 January;25(1):35–46. doi: 10.1016/j.mri.2006.09.042. [DOI] [PubMed] [Google Scholar]
- 29.Behzadi Y, Restom K, Liau J, Liu TT. A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. NeuroImage. 2007 August 1;37(1):90–101. doi: 10.1016/j.neuroimage.2007.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proceedings of the National Academy of Sciences of the United States of America. 2001 January 16;98(2):676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Boly M, Phillips C, Tshibanda L, Vanhaudenhuyse A, Schabus M, Dang-Vu TT, Moonen G, Hustinx R, Maquet P, Laureys S. Intrinsic brain activity in altered states of consciousness: how conscious is the default mode of brain function? Annals of the New York Academy of Sciences. 2008;1129:119–129. doi: 10.1196/annals.1417.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Damoiseaux JS, Beckmann CF, Arigita EJS, Barkhof F, Scheltens P, Stam CJ, Smith SM, Rombouts SARB. Reduced resting-state brain activity in the “default network” in normal aging. Cerebral Cortex (New York, N.Y.: 1991) 2008 August;18(8):1856–1864. doi: 10.1093/cercor/bhm207. [DOI] [PubMed] [Google Scholar]
- 33.Fair DA, Bathula D, Mills KL, Dias TGC, Blythe MS, Zhang D, Snyder AZ, Raichle ME, Stevens AA, Nigg JT, et al. Maturing thalamocortical functional connectivity across development. Frontiers in Systems Neuroscience. 2010;4:10. doi: 10.3389/fnsys.2010.00010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fair DA, Cohen AL, Power JD, Dosenbach NUF, Church JA, Miezin FM, Schlaggar BL, Petersen SE. Functional brain networks develop from a “local to distributed” organization. PLoS Computational Biology. 2009 May;5(5):e1000381. doi: 10.1371/journal.pcbi.1000381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Castellanos FX, Margulies DS, Kelly C, Uddin LQ, Ghaffari M, Kirsch A, Shaw D, Shehzad Z, Di Martino A, Biswal B, et al. Cingulate-precuneus interactions: a new locus of dysfunction in adult attention-deficit/hyperactivity disorder. Biological Psychiatry. 2008 February 1;63(3):332–337. doi: 10.1016/j.biopsych.2007.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fox MD, Snyder AZ, Zacks JM, Raichle ME. Coherent spontaneous activity accounts for trial-to-trial variability in human evoked brain responses. Nat Neurosci. 2006 January;9(1):23–25. doi: 10.1038/nn1616. [DOI] [PubMed] [Google Scholar]
- 37.Arfanakis K, Cordes D, Haughton VM, Moritz CH, Quigley MA, Meyerand ME. Combining independent component analysis and correlation analysis to probe interregional connectivity in fMRI task activation datasets. Magnetic resonance imaging. 2000;18(8):921–930. doi: 10.1016/s0730-725x(00)00190-9. [DOI] [PubMed] [Google Scholar]
- 38.De Martino F, Gentile F, Esposito F, Balsi M, Di Salle F, Goebel R, Formisano E. Classification of fMRI independent components using IC-fingerprints and support vector machine classifiers. NeuroImage. 2007 January 1;34(1):177–194. doi: 10.1016/j.neuroimage.2006.08.041. [DOI] [PubMed] [Google Scholar]
- 39.Tohka J, Foerde K, Aron AR, Tom SM, Toga AW, Poldrack RA. Automatic independent component labeling for artifact removal in fMRI. NeuroImage. 2008 February 1;39(3):1227–1245. doi: 10.1016/j.neuroimage.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zeng W, Qiu A, Chodkowski B, Pekar JJ. Spatial and temporal reproducibility-based ranking of the independent components of BOLD fMRI data. NeuroImage. 2009 July 15;46(4):1041–1054. doi: 10.1016/j.neuroimage.2009.02.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Friston KJ, Price CJ, Fletcher P, Moore C, Frackowiak RS, Dolan RJ. The trouble with cognitive subtraction. NeuroImage. 1996 October;4(2):97–104. doi: 10.1006/nimg.1996.0033. [DOI] [PubMed] [Google Scholar]