Localized Harmonic Motion Imaging for Focused Ultrasound Surgery Targeting

Abstract

Recently, an in vivo real-time ultrasound-based monitoring technique that uses localized harmonic motion (LHM) to detect changes in tissues during focused ultrasound surgery (FUS) has been proposed to control the exposure. This technique can potentially be used as well for targeting imaging. In the present study we evaluated the potential of using LHM to detect changes in stiffness and the feasibility of using it for imaging purposes in phantoms and in vivo tumor detection. A single-element FUS transducer (80 mm focal length, 100 mm diameter, 1.485 MHz) was used for inducing a localized harmonic motion and a separate ultrasound diagnostic transducer excited by a pulser/receiver (5 kHz PRF, 5 MHz) was used to track motion. The motion was estimated using cross-correlation techniques on the acquired RF signal. Silicon phantom studies were performed in order to determine the size of inclusion that was possible to detect using this technique. Inclusions were discerned from the surroundings as a reduction on LHM amplitude and it was possible to depict inclusions as small as 4 mm. The amplitude of the induced LHM was always lower at the inclusions as compared with the one obtained at the surroundings. Ten New Zealand rabbits had VX2 tumors implanted on their thighs and LHM was induced and measured at the tumor region. Tumors (as small as 10 mm in length and 4 mm in width) were discerned from the surroundings as a reduction on LHM amplitude.

INTRODUCTION

Palpation is a technique broadly used by practitioners to assess the texture of a patient’s tissue and assess tenderness through tissue deformation. Its value as a diagnostic tool for cancer comes from the high sensitivity of changes in mechanical properties of tumor tissues from the surrounding tissues (Krouskop et al. 1998). In recent years, there have been a multitude of techniques for the estimation of mechanical properties to develop new imaging modalities for the detection of tumors.

In particular, ultrasound imaging of tissue elastic properties has been widely investigated since it can provide a low cost imaging tool for tissue elastic properties. It can also offer more flexibility than palpation since deeper tissues can be imaged to obtain their mechanical properties. One field where the imaging of mechanical properties of tissues is of particular interest is focused ultrasound surgery (FUS). FUS is a non-invasive image-guided therapy that can treat regions within the body through thermal coagulation (Leslie and Kennedy. 2006). Magnetic Resonance Imaging (MRI) is currently the only FDA-approved method for targeting and control FUS treatments in the U.S.A. However, MRI guidance cost is high, it can be contraindicated for some patients with metallic implants or oversized, requires building infrastructure and finding compatible materials for the treatment. All this makes the search of alternative imaging techniques an important goal. The changes in elastic parameters between malignant and surrounding tissues can provide means to identify tumor targets and it can also be used to ascertain coagulated tissues after FUS treatment.

Several ultrasound-based methods have been developed to estimate tissue stiffness. Acoustic radiation force impulse imaging (ARFI) uses a localized, impulsive radiation force to excite the target tissues and the generated displacements are followed by using ultrasonic correlation-based methods to evaluate stiffness (Nightingale et al. 2002, Nightingale et al. 2003). ARFI has been successfully used to visualize tumor (Cho et al. 2010, Zhai et al. 2010) and thermal lesions (Fahey et al. 2005, Fahey et al. 2004) ex vivo, in vivo and in clinic allowing determination of location, shape, relative size through time and malignancy. Vibro-acoustography or ultrasound-stimulated acoustic emission (USAE) employs the superposition of ultrasound beams to exert a varying force on the tissues. In response, tissues vibrate in a pattern determined by their viscoelastic properties. The acoustic emission field resulting from the object vibration is detected using a hydrophone and used to form an image that represents both the ultrasonic and low-frequency (kHz range) mechanical characteristics of the object (Fatemi and Greenleaf. 1999). USAE has been used to detect mass lesions in breast (Fatemi and Greenleaf. 1999) and it has been proposed to guide therapy (Mitri et al. 2009, Mitri et al. 2008). Sonoelastography produces strain images by continuously compressing tissues while the ultrasound RF signal is acquired and by calculating displacements (Ophir et al. 1999). Sonoelastography has been used for tumor and thermal ablation evaluation (Garra et al. 1997, Curiel et al. 2005, Souchon et al. 2003, Varghese et al. 2002). Supersonic shear imaging (SSI) uses ultrasonic focused beams to remotely generate mechanical vibration sources radiating low-frequency shear waves inside tissues. By using an ultrafast scanner it is possible to image the propagation of the shear wave and with inversion algorithms it is possible to map the shear elasticity of the medium to form an image (Bercoff et al. 2004b). SSI has been used to image tumor and thermal lesions (Bercoff et al. 2004a, Athanasiou et al. 2010).

On this paper we propose the use of another ultrasound-based technique to image tissues with different stiffness. By remotely applying an oscillatory and harmonically varying radiation force, a localized harmonic motion (LHM) can be induced within the tissues. This localized harmonic motion can be measured using a separate ultrasound beam and acquiring ultrasound RF signals during the motion (Konofagou and Hynynen. 2003, Heikkila and Hynynen. 2006). The advantage of this technique is that the motion is localized and provides information of the tissues at the focus with less influence of the neighboring structures. Also, since the LHM is induced by a FUS transducer, this technique has been successfully used during a thermal exposure to detect and control coagulation in vitro (Maleke and Konofagou 2008) and in vivo (Maleke and Konofagou 2010a, Curiel et al. 2009a, Curiel et al. 2009b, Heikkila et al. 2008). LHM has been proposed for mapping differences in stiffness in order to generate images in a simulation study validated with in vitro phantoms and ex vivo tissues (Maleke et al. 2010).

In the present study we propose to use the LHM method for mapping local characteristics of the tissues as a targeting tool for thermal coagulation treatments. We used LHM to perform imaging and evaluated the feasibility and sensitivity of these images to detect changes in stiffness in phantoms with single and multiple inclusions, as well as in tumors in vivo. Experiments on phantoms and VX2 tumors in vivo were performed in order to validate the technique.

MATERIALS AND METHODS

Localized Harmonic Motion (LHM) Induction

A single-element Focused Ultrasound (FUS) transducer with a central frequency of 1.485 MHz, a focal length of 80 mm and a diameter of 100 mm, 0.8 mm full width at half maximum intensity, and a 14 mm diameter central hole was used for inducing the localized harmonic motion.

To induce the localized harmonic motion the FUS transducer was excited at its central frequency by amplitude-modulated signals with a modulation frequency of 75 Hz. An arbitrary waveform generator card (CompuGen 4300, Gage, Lockport, IL, USA) was used to obtain the modulated signal that was then amplified (3100L, E&I, Rochester, NY, USA). The 75 Hz modulation frequency was chosen as a tradeoff between the LHM amplitude and the time needed to obtain a measurement. It has been shown that the lower the LHM frequency the higher the obtained amplitude (Curiel et al 2009a). At the same time, the lower the frequency the longer the time needed to establish the harmonic motion and to obtain a full cycle of the motion to determine the amplitude (Heikkila and Hynynen 2006).

For all measurements we induced 5 periods of the LHM with a 5 s delay between measurements (1% duty cycle) to minimize tissue heating as previously described (Curiel et al. 2009b). The acoustical power measured during the LHM induction was between 30 and 40W.

Displacements Tracking

A separate circular-element diagnostic ultrasound transducer with a central frequency of 5 MHz, a focal length of 47 mm, a 20 mm diameter, and 50% bandwidth at −3 dB in power (PZT 5, 1–3 piezocomposite, Imasonic, Besançon, France) was used to track tissue motion. The transducer was mounted through the central hole of the FUS transducer and its focal volume was aligned to that of the FUS transducer using a needle hydrophone (0.075 mm diameter, Precision Acoustics, Dorset, UK). Since the FUS transducer had a central hole of 14 mm in diameter the diagnostic transducer blocked some of the FUS beam propagation to the focus.

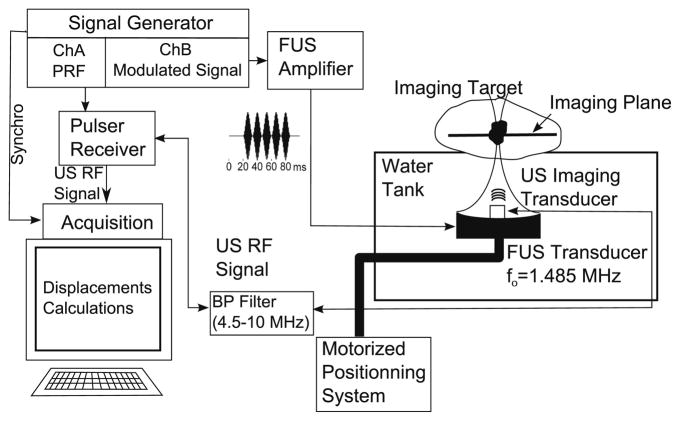
The diagnostic transducer was excited by a pulser/receiver (DPR300, JSR Ultrasonics, Pittsford, NY, USA) at a 5 kHz pulse repetition frequency. The received radio-frequency (RF) signal was first filtered using a band-pass filter with a lower cutoff frequency of 4.5 MHz and an upper cutoff frequency of 10 MHz to remove signal contamination generated by the FUS transducer. The band-pass filter eliminated the noise caused by the FUS transducer at the central frequency and its harmonics (below to the 4^th and above the 6^th). The RF signal was then amplified by a low-noise RF amplifier (0.2–400 MHz MITEQ, New York, NY, USA) and acquired using a digitizer card (ATS860, Alazartech, Montreal, QC, Canada). In order to synchronize the acquisition and the generation of the LHM, the arbitrary function generator clock was used as external clock for the acquisition card and as a trigger for the pulser/receiver. This ensured that no jitter was present on the acquired RF signals. A schematic of the system is shown in Fig. 1.

Fig. 1.

Schematic for the excitation and acquisition of the localized harmonic motion. An imaging ultrasound transducer was placed at the centre of a focused ultrasound (FUS) transducer excited with a modulated signal. The radio-frequency (RF) signal obtained was acquired and used for calculation of the target displacement.

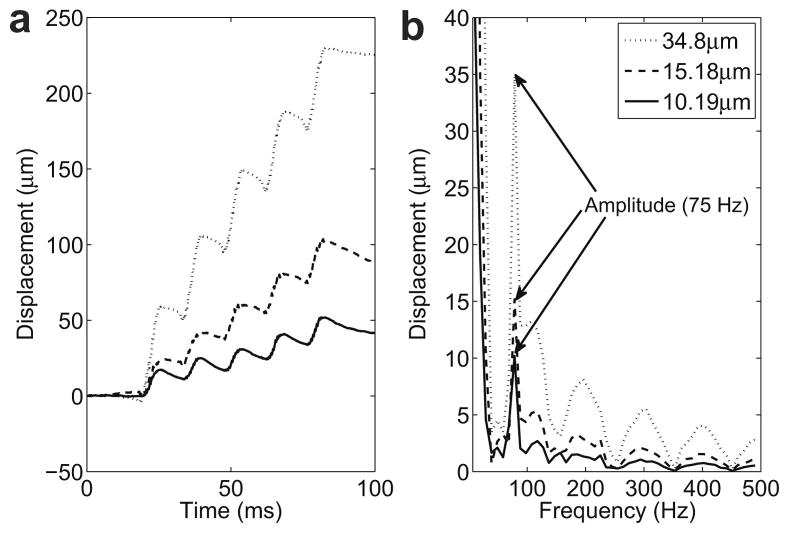
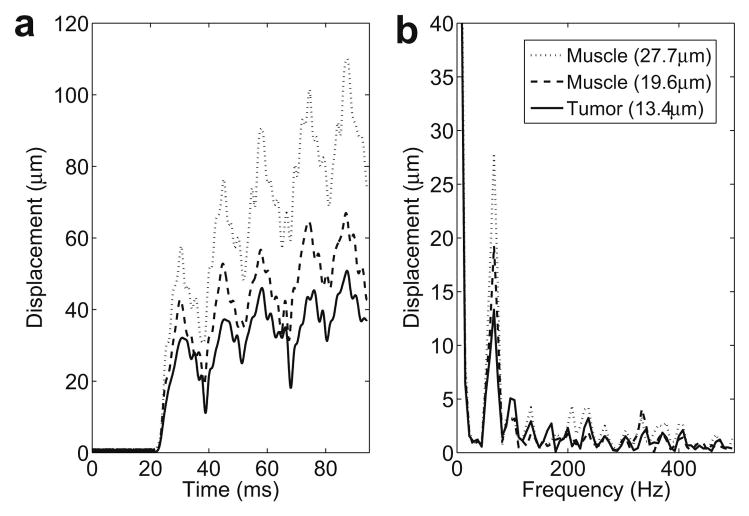
The RF signal was acquired for a total duration of 100 ms and the FUS transducer excitation was started 20 ms after the acquisition. After acquisition of the RF signals, a digital notch filter was used to filter the harmonics of the FUS frequency that were within the band pass of the filter (4^th, 5^th and 6^th). Tissue displacements were calculated at the focus of the FUS transducer using cross-correlation techniques over the acquired RF signals with a 3 mm window and 1.5 mm window shift. Five periods of the LHM were induced 20 ms after starting the acquisition. This produced each time a calculated displacement with no motion for 20 ms before the LHM. Fig. 2(a) shows an example for the displacements obtained on a phantom at three locations with different hardness. The displacements show a static (or very low frequency) component which is more important for higher amplitude motion (softer targets) which is consistent with simulation data previously reported by Heikkila et al. (2008).

Fig. 2.

Localized harmonic motion (LHM) induced on a phantom (RTV6166, 20% part A, 80% part B) with a modulation frequency of 75 Hz. Five periods of the LHM were induced 20 ms after starting the acquisition and RF lines were acquired for a total of 100ms: (a) displacements calculated from the beginning of the acquisition and (b) frequency spectrum of the displacements with a peak at 75Hz (modulation frequency).

A fast Fourier transform (FFT) was calculated on the displacements. Finally, the amplitude of the motion was obtained from the modulus of the FFT coefficient corresponding to the modulation frequency of 75 Hz. The frequency spectrum and the amplitude value obtained for the displacements corresponding to the three cases in Fig. 2(a) are shown in Fig. 2(b). The peak at 75 Hz corresponds to the induced harmonic motion and this was the value used as the amplitude of the motion for the images. The large peak at low frequency is caused by the static component in the displacements. The higher frequency peaks in the spectrum were caused by the sharp slope when the radiation force is applied as compared with the slower relaxation when the force is stopped, making the displacements curve approach to a saw-tooth shape therefore generating higher frequencies in the FFT.

Image Formation

In order to obtain an image we mounted the transducer assembly into a motorized arm that was controlled to perform a raster grid and induce LHM displacements at different locations each location generating a pixel in the final image. LHM displacements measurements were repeated 5 times at each location and the final LHM amplitude value mapped in the images was obtained as the average LHM amplitude of the 5 repetitions. The final images were obtained after 2x2 median filtering of the LHM amplitudes in the grid. The averaging of 5 measurements helped reducing noise on the final calculated amplitude. The median filtering was applied to increase the SNR of the final image as it has been shown by other groups for tissue elastic properties imaging (Souchon et al. 2003).

Phantom Study

Silicon phantom studies were performed in order to determine the hardness difference, size of inclusion and inclusion spacing that was possible to detect.

Room-temperature-vulcanizing (RTV) silicon (RTV6166, two-part silicone, Momentive Performance Materials, New York, NY, USA) was used to make all the phantoms. By varying the proportions of part A and B on the silicon mix before vulcanization it was possible to vary the obtained hardness. This two-part silicone has a behavior similar to soft tissues in the linear range to at least 30% strain (Kerdok et al. 2003, Ottensmeyer. 2001). For this silicon mix, a proportion of part A to part B of 40:60 presents a Young modulus of 7.63kPa while a 30:70 mix is harder with a modulus of 15.3kPa (Kerdok et al. 2003, Ottensmeyer. 2001, Ottensmeyer. 2002). Reported values of Young modulus for muscle tissue vary between 6.2 to 790kPa depending on the measure technique (Duck. 1990), the direction of the fibers and the tissues being tense or relaxed. Relaxed tissues along the fibers have a reported Young modulus of 6.2kPa which is close to the value obtained for the 40:60 silicon phantoms.

The silicon mix was poured into a cylindrical mold of 200 mm diameter by 40 mm in height and heated at 100 °C for 1 hour to attain vulcanization. In order to create inclusions within the phantom, we introduced cylindrical glass rods at the centre of the mold before pouring the mix and the rods we extracted after vulcanization. Finally, to obtain a harder inclusion, a silicon mix with different proportions in part A and B was poured in the void and vulcanized. For scattering purposes, acid-washed glass beads (particle size <106 μm, Sigma-Aldrich, Oakville, ON, Canada) at a concentration of 2% by weight were added to the silicon mix before vulcanization in both the main phantom and the inclusions.

LHM was induced and amplitudes were obtained within 41x41 mm grids with 1 mm spatial step and each grid was repeated 5 times.

In order to determine the smallest inclusion that was possible to detect, a first set of phantoms was made and imaged where the diameter of the inclusion was varied from 2 to 8 mm. Different Part A to part B silicon proportions for the inclusions (20:80; 30:70) and the surrounding silicon (40:60; 50:50) were tested.

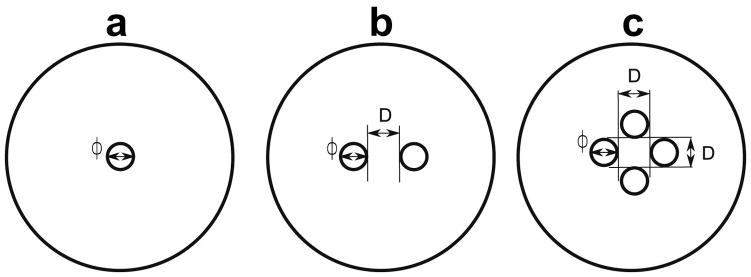
A second set of phantoms was imaged to evaluate the feasibility of detecting multiple inclusions with different spacing between inclusions. Part A to part B silicon proportion was 20:80 for the inclusions and 40:60 for the surrounding silicon. Phantoms with two and four inclusions of 5 mm in diameter were made with different spacing between them (Table 1 and Fig. 3).

Table 1.

Expected and measured dimensions for the inclusions in the phantoms

Expected					Measured
# of inclusions	φ (mm)	D (mm)	Area (mm2)	Fig.	# of inclusions	φ (mm)	D (mm)	Area (mm2)
1	2	-	3.1	3(a)	NV(a)	NV(a)	-	NV(a)
1	3	-	7.1	3(a)	NV(a)	NV(a)	-	NV(a)
1	4	-	12.6	3(a)	1	5.0±1.2	-	19
1	5	-	19.6	3(a)	1	5.5±0.4	-	20
1	7	-	38.5	3(a)	1	8.5±0.7	-	54
1	8	-	50.3	3(a)	1	9.0±0.5	-	56
2	5	0	39.2	3(b)	1	5.1±0.8	0	64
2	5	2.5	39.2	3(b)	2	5.7±1.2	2	47
2	5	5	39.2	3(b)	2	6.8±1.6	5	41
2	5	9	39.2	3(b)	2	6.9±1.4	10	49
4	5	5	78.4	3(c)	1	17.9±2.4	0	131
4	5	9	78.4	3(c)	4	7.3±2.0	8.5	102
4	5	15	78.4	3(c)	4	5.7±1.2	13.5	83

^(a)The inclusion was not visible

Fig. 3.

Schematic for phantoms with: (a) single inclusion of diameter φ, (b) two inclusions of diameter φ and space between inclusions of D, and (c) four inclusions of diameter φ and space between inclusions of D.

Two readers delineated the inclusion in the images and determined the number of detected inclusions (#). The readers were blinded to the structure of the phantom corresponding to the image. After manual delineation by the two readers, the area (A), diameter (φ) and space between inclusions (D) were obtained from the readers manual delineation using in-house processing with Matlab (The Mathworks Inc, R2009b, Natick, MA, USA). The area (A) was obtained as the number of pixels identified as part of the inclusion multiplied by the area of the pixel (1 mm²). The diameter (φ) was determined as the major axis of the delineated region. The space between inclusions (D) was calculated as the average distance between two or more distinct regions.

Animal experiments

After ethics approval from the animal care committee, ten New Zealand White rabbits (male, average weight 3.5 kg) were injected with VX2 cells in one thigh (1x10⁶ cells diluted in 0.6 ml of phosphate-buffered saline). One week post-injection, animals were anesthetized using ketamine (50 mg/kg) and xylazine (10 mg/kg), and then lay on top of the water tank in a lateral, decubitus position with its depilated thigh in front of the transducer assembly and in contact with the water bath. The anesthetic dose injection was repeated approximately once per hour. The animal was placed in a magnetic resonance imaging scanner and imaging was obtained to locate the tumor. Fast Spin Echo images (256x256, TE/TR=9.03/500, FOV=16cm, Slice=2 mm, ETL=4, 3NEX) were performed to locate the tumor and for comparison with the LHM images.

The transducer assembly used for LHM induction was mounted on a motorized MRI-compatible positioning system (Chopra et al. 2008) and aligned with the MRI imaging. The assembly was moved to the centre of the tumor and tissue motion was induced at each point of a 30x30 mm grid at 1 mm steps. At each point of the grid, measurements of the LHM amplitude were obtained 5 times. After scanning the animal was euthanized using a single dose of pentobarbital sodium (2ml/4.5kg).

Following LHM image formation, the dimensions of the observed tumor were obtained after delineation of the low LHM amplitude area by two different readers. The readers were blinded to the MR image corresponding to the LHM image. After manual delineation by the readers, the area (A) and diameter (φ) were calculated using in-house processing using Matlab (The Mathworks Inc, R2009b, Natick, MA, USA). The area (A) was obtained as the number of pixels inside the manually delineated region multiplied by the area of the pixel (1 mm²), the length or long diameter (φ_L) was determined as the major axis of the delineated region and the width or short diameter (φ_S) was the short axis of the delineated region. Dimensions for the observed tumor in the MR images were obtained using the same processing.

RESULTS

Phantoms

The displacement induced at three different locations on phantoms is shown in Fig. 2(a). The five induced cycles can be observed as well as the static component previously described by (Heikkila and Hynynen. 2006, Heikkila et al. 2008). The spectrum of this displacement in Fig. 2(b) shows the expected peak at the modulation frequency (75 Hz). Higher frequency components appear as well in these displacements caused by the sharp tooth-like shape of the obtained curve.

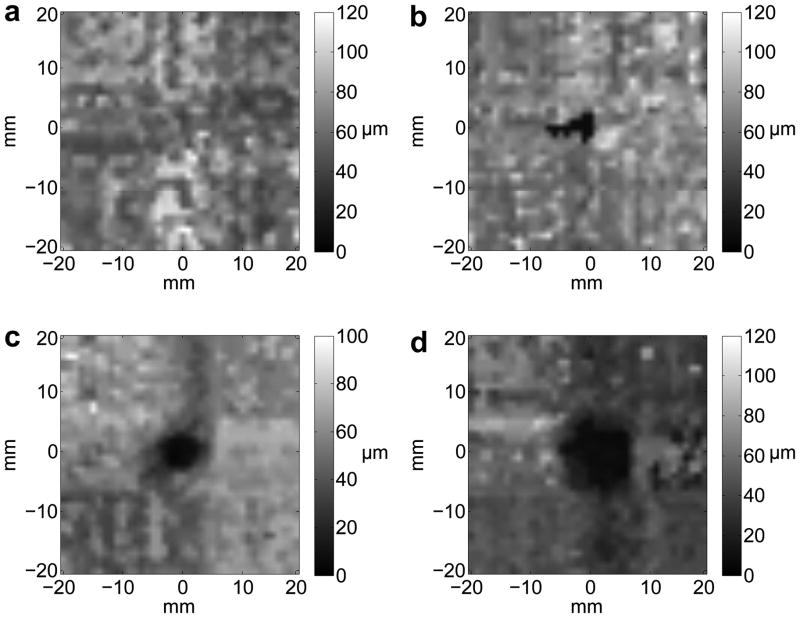
The LHM amplitude in the inclusions was 6.9±1.6μm when the motion was induced with an acoustic power of 28W and 9.6±1.9μm with an acoustic power of 37W. The amplitude in the surroundings was 52.3±20.3μm for an acoustic power of 28W and 68.4±23.2μm for 37W. The amplitude was significantly lower in inclusions (harder regions) as compared to softer surroundings for both acoustic powers (p<0.0001, T-test). Fig. 4 shows examples of images obtained for phantoms with individual inclusions where we can see that the 2 mm single inclusion in 4(a) is not visible, whereas inclusions above 4 mm in diameter could be detected as shown in 4(b) and 4(c) for a 5 mm and an 8 mm inclusion respectively.

Fig. 4.

Images obtained from LHM amplitudes (at 75 Hz) registered on a 40x40 mm grid with a 1 mm step on silicon phantoms with a 20:80 inclusion and 40:60 surroundings. All phantoms had a single inclusion with diameter: (a) 2 mm, (b) 4 mm, (c) 5 mm and (d) 8 mm. Total scan time was 67 min.

Fig. 5 shows images obtained for multiple inclusion phantoms. Two and four inclusions of 5 mm in diameter were located with different spacing between their centers. The two inclusions are clearly discernible in Fig. 5(a) and 5(b) but they are observed as a single object when the borders of the inclusions touch as it is shown in 5(c). The four inclusions can be seen in Fig. 5(d) and 5(e) but they blend and are detected as a single inclusion in 5(f) when the borders of the inclusions touched.

Fig. 5.

Images obtained from LHM amplitudes at the frequency of 75 Hz registered on a 40x40 mm grid with a 1 mm step on silicon phantoms with a 20:80 inclusion and 40:60 surroundings. Phantoms had multiple inclusions with 5 mm diameter: (a) 2 inclusions separated by 9 mm, (b) 2 inclusions separated by 5 mm, (c) 2 inclusions with no space between them, (d) 4 inclusions separated by 15 mm, (e) 4 inclusions separated by 9 mm, and (f) 4 inclusions separated by 5 mm (borders touching).

The results of the measurements obtained from the figures and a summary of the expected and measured values are shown in Table 1. Inclusions with a diameter less than 4 mm were not visible (marked as NV). For the detected inclusions the diameter and the area were larger than the expected values. The distances between multiple inclusions could be accurately determined except when the inclusions borders were touching.

The LHM amplitude obtained in the inclusions and surroundings as a function of the proportion Part A: Part B of the phantoms was measured and it is shown in Table 2. The values shown are the average of the LHM amplitude for all phantoms either inside (inclusion) or outside (surroundings) the area as delineated by the two readers. The amplitude of the LHM was consistently lower (9.6±1.9 μm) for inclusions compared to surroundings (68.4±23.2 μm). The amplitude was also reduced for areas where the silicon mix was harder. The softer the silicon mix, the higher the standard deviation was for the amplitude values. The LHM amplitude increased as well for higher acoustical power. Table 3 shows the values of the amplitude for two different values of power for inclusions and surroundings.

Table 2.

Local harmonic motion amplitude obtained in silicon phantoms for inclusions and surroundings with different Part A:Part B proportions and an acoustic power of 37W

Surroundings (Part A:Part B)	Inclusion (Part A:PartB)	LHM amplitude at the inclusion (μm)	LHM amplitude in the surroundings (μm)
50:50	30:70	15.1±2.6	73.0±40.8
40:60	20:80	9.6±1.9	68.4±23.2

Table 3.

Local harmonic motion amplitude obtained in silicon phantoms for two different acoustic power values for inclusions at a proportion of 20:80 and surroundings at 40:60

Acoustic Power (W)	LHM amplitude at the inclusion (μm)	LHM amplitude in the surroundings (μm)
28	6.9±1.6	52.3±20.3
37	9.6±1.9	68.4±23.2

Animal experiments

Fig. 6(a) shows the calculated displacements for the induced LHM at three different locations on a rabbit thigh, two of them were being located on the muscle and one on the tumor. The static component observed on the phantoms is also present in vivo as it can be observed on the spectrum in Fig. 6(b). The calculated displacements presented a less smooth curve compared to the phantom studies and this translated into more high frequency components as it can be observed on the spectrum in Fig. 6(b). The spectrum shows more peaks at frequencies higher than 75 Hz as compared with the phantoms (Fig. 2(b)) and the associated amplitude for those peaks is also higher.

Fig. 6.

LHM induced on rabbit thigh at three different locations with a modulation frequency of 75 Hz. Five periods of the LHM were induced 20 ms after starting the acquisition: (a) displacements calculated from the beginning of the acquisition and (b) frequency spectrum of the displacements with a peak at 75Hz (modulation frequency).

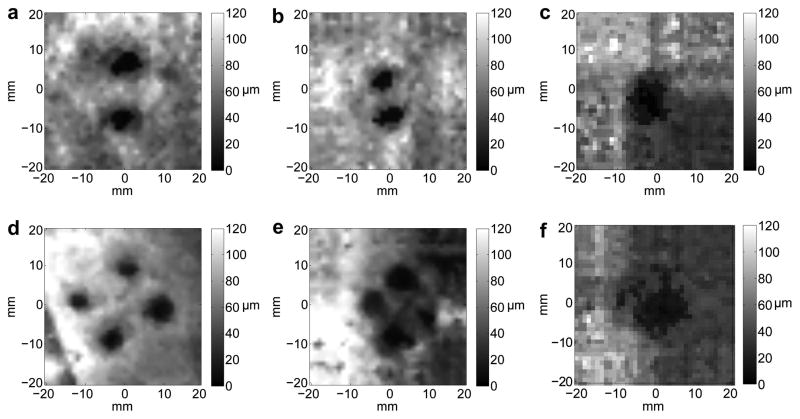
The average amplitude of the LHM registered within the tumor was 5.7±1.3μm and 19.5±5.8μm in the surrounding muscle. Tumors were discerned from the surrounding based on the reduction in the LHM amplitude and the images were matched to MRI results. Since tumors have an increased stiffness compared to the surrounding tissues, a reduction in LHM amplitude was expected from the phantoms results. The average dimensions for the tumors on LHM images were 17.8±7.6 mm in length or long axis diameter (φ_L) and 4.7±0.9 mm in width or short axis diameter (φ_S). The smallest value obtained for the width was 4.1 mm (see Table 4) and the standard deviation of 0.9 mm was explained by the spread of values [4.1 – 6.7 mm]. Fig. 7 shows the LHM mapping made at the same location as the VX2 tumor was located under MRI. The correspondent MR image for the tumor is shown below. The darker regions in the LHM mappings are consistent with the tumor on the MR images. The shape of the detected region matched the MR images. In two cases it was not possible to detect the tumor in the LHM images.

Table 4.

Measured dimensions for VX2 tumors

MRI				LHM
	φL (mm)	φS (mm)	Area (mm2)	φL (mm)	φS (mm)	Area (mm2)	LHM amplitude at tumor (μm)	LHM amplitude at surrounding tissues (μm)
1	15.1±1.3	4±0.3	46±7	13.2±1.5	4.3±0.8	27±2	6.3±0.3	15.4±5.8
2	9±0.8	2.8±0.1	18±3	NV(a)	NV(a)	NV(a)	NV(a)	NV(a)
3	10.7±0.8	3.6±0.2	28±2	NV(a)	NV(a)	NV(a)	NV(a)	NV(a)
4	12.5±1.8	4.9±0.9	44±2	11.9±1.8	4.1±0.6	16±2	3±0.7	10.5±7.7
5	17.1±2.1	6±0.2	54±7	12.3±1	5.1±0.3	35±3	2.8±1.1	20.1±8.2
6	10.5±2.3	4±0.2	32±3	12±1	4.3±0.1	36±2	3.4±0.3	21.6±5.3
7	16.3±2.3	4.6±0.1	56±8	13.5±1.5	4.1±0.3	34±4	3.2±0.2	17.1±4.2
8	23.5±2.2	4.1±1	45±1	23.4±1.8	4.7±0.5	28±15	12.6±1.5	26.6±4.4
9	43.9±2.7	7.5±0.1	252±30	30.5±2.3	4.7±0.9	85±10	6±1.2	20.6±5.8
10	31.5±4.6	10.4±1.6	242±28	26.3±1.9	6.7±0.2	130±15	8.2±4.6	24±5.4

^(a)The tumor was not visible

Fig. 7.

In vivo images obtained from LHM amplitudes at the frequency of 75 Hz registered on a 30x30 mm grid with a 1 mm step on VX2 tumors implanted in rabbit muscles. Three different cases are shown with (a), (b) and (c) being the LHM images and (d), (e) and (f) their corresponding magnetic resonance (MR) images. Total scan time was 38 min.

Table 4 shows the results for the different measurements obtained from the tumor images. The dimensions obtained from LHM images matched well the observed MRI images. LHM tumor sizes were generally smaller than those obtained from MR images (average length of 17.8±7.6 mm for LHM and 19±11 mm for MRI; average width of 4.7±0.9 mm for LHM and 5.2±2.3 mm for MRI) but the difference was not statistically significant (p=0.1 for length and p=0.11 for width, T-test).

DISCUSSION AND CONCLUSION

Images obtained by mapping the LHM amplitude were successfully achieved for phantoms and tumors in vivo. It was possible to detect harder structures as small as 4 mm (either inclusions or tumors) as a significant reduction on the LHM amplitude (p<0.001).

In phantoms it was possible to use LHM measurements to detect hard inclusions for single and multiple inclusions and to differentiate them as long as their margins were not in contact. It was possible to detect individual inclusions as small as 4 mm. Multiple inclusions were individually identified on the images as long as their borders were not contiguous. When multiple inclusions were touching, the images showed them as a single inclusion. This could be explained by effects of neighboring harder regions that reduces the amplitude of the motion that can be obtained, translating into a larger area in the image.

The changes in LHM amplitude registered in harder inclusions were enough to detect inclusions as small as 4 mm in diameter. This shows the potential of using LHM amplitude as an imaging tool. We expected to be able to detect smaller structures using this technique since the acoustic beam width of the transducer was narrow enough to induce localized motion in small structures. There are two explanations to this limitation: the use of a large step size that can cause aliasing in the images, and the low power. The step size was kept large in order to keep the acquisition time manageable, but it can be reduced with an optimized system. The power was limited to reduce the risk of heating, which was observed and limited in previous applications for LHM induction (Curiel et al. 2009b).

In some of the silicon phantom images other structures were observed close to the inclusions (i.e. Fig. 5(d)). These were observed as regions with lower amplitude in the motion that can be related with harder regions. For those particular phantoms we cut the silicon after imaging and found regions of harder silicon at the location where the low amplitude was observed in the images. The appearance of these regions was explained by the fabrication process of the phantom. When the glass rods were extracted after vulcanization of the phantom, fractures were created in these phantoms that were later filled by the harder silicon mix.

For the phantom studies the LHM was induced and measured in grids that were repeated 5 times. The measurements were very reproducible and showed a small standard deviation. However, for in vivo experiments, this repeatability was more challenging and we had to induce the LHM five times at the same location before moving to the next in order to reduce the variability. This was explained by possible small movements from the animal between two grids since the whole acquisition could take up to 8 minutes per grid. The averaging of 5 measurements helped reducing this noise. As well, using a 2-D median filter increased the SNR of the images and helped the readers find the stiffer areas but this came at the cost of resolution (Souchon et al. 2003).

In vivo images were successfully obtained and the tumors could be detected in the majority of the cases. In two cases the LHM images did not show a region with lower amplitude that could be related with the MR image. The tumors were implanted in muscle and they grew along the muscular fibers showing an elongated narrow shape. For the two tumors that could not be detected on LHM images, the observed tumor in the MRI presented a length lower than 10 mm and a width smaller than 4 mm. The limit for detection of the tumor seems to be related to the 4 mm width, which is the size of the smallest inclusion that could be detected in phantoms.

The measurements obtained from the LHM in vivo images generally underestimated the regions delineated in the MR images. This can be explained by the surroundings of the tumor not being hard enough to significantly reduce the amplitude of the induced motion. It is also known that T2-weighted images may include the surrounding tissue edema caused by the tumor and thus may be overestimates of the actual tumor size. However, the difference between the LHM and MRI was small (6%), not statistically significant (p=0.1) and within the resolution of the measurement systems.

The amplitude of the LHM motion in both the tumors and muscle were lower than the one obtained for the inclusions and surroundings in the phantoms. The average LHM amplitude for the silicon inclusions was 1.7 times the one measured at the tumors and the LHM amplitude for the surrounding silicon was 3.5 times the one obtained for the muscle. The Young modulus of the surrounding silicon phantom was 7.63kPa and the modulus for muscle has been reported between 6.2 and 790kPa. The lower LHM amplitude can be explained by an actual Young modulus that could be higher for the rabbit muscle than for the phantoms, causing the amplitude of the induced motion to be lower. We can presume from the lower LHM amplitude that the tumor had a higher Young modulus than the inclusions as well.

For in vivo experiments we obtained displacements that were less smooth than the ones observed for phantoms. This could have been caused by small movements that caused changes on the RF signal and therefore de-correlation leading to incorrect displacement calculations. The effect of these points was more high frequency components on the displacements spectrum. The averaging of 5 measurements per point helped reducing this effect on the final calculated amplitude for the images.

The main source of error for the technique came from any changes in the RF signal that caused de-correlation as it has previously been reported (Curiel et al. 2009b). These include out-of-plane movements while inducing the LHM and acoustic noise generated by the FUS transducer. We minimized these errors by acquiring at high PRF for which very small movements are tracked every time. In addition, relatively short measuring times (100 ms) make the technique less sensitive to large and usually slower movements like breathing, blood flow and digestive tract. For fast-moving organs these movements could be an issue and should be studied.

The experiments were performed with a laboratory system. An optimized system should perform better with reduced noise. A specific design of FUS and diagnostic transducers to avoid noise between them should improve the performance. As well, ameliorating the filtering and processing should help obtaining better images.

A practical limitation for the system was the total acquisition time for a full LHM map. Each point needs a minimum of 100ms for the harmonic excitation leading to a total of 800s (13 min) for a 40x40 grid with 5 repetitions. When adding the communication and file processing we obtained a 500ms time per point, and therefore a 40x40 scan with 5 repetitions totaled 4000s (67 min). This total scan time can be reduced by better processing and control, but the excitation will still need a 100ms minimum per point. One way of further reducing the acquisition time is to work with lower number of LHM excitations per point as well as using higher modulation frequencies. Since higher frequencies leads to lower LHM amplitude (Curiel et al. 2009a), the sensitivity of the imaging for higher frequencies should be investigated further.