Taxonomic variation in size–density relationships challenges the notion of energy equivalence

Abstract

The relationship between body mass and abundance is a major focus for research in macroecology. The form of this relationship has been suggested to reflect the partitioning of energy among species. We revisit classical datasets to show that size–density relationships vary systematically among taxonomic groups, with most variation occurring at the order level. We use this knowledge to make a novel test of the ‘energy equivalence rule’, at the taxonomic scale appropriate for the data. We find no obvious relationship between order-specific exponents for abundance and metabolic rate, although most orders show substantially shallower (less negative) scaling than predicted by energy equivalence. This finding implies greater energy flux among larger-bodied animals, with the largest species using two orders of magnitude more energy than the smallest. Our results reject the traditional interpretation of energy equivalence as a predictive rule. However, some variation in size–density exponents is consistent with a model of geometric constraints on foraging.

1. Introduction

The observation that ‘big things are rare’ is one of the most prevalent patterns in ecology. Damuth [1,2] showed that the size–density relationship (SDR) followed a power-law, with scaling exponent close to −3/4: this pattern has become known as ‘Damuth's Rule’ [3]. Damuth realized that his exponent is the inverse of Kleiber's metabolic scaling exponent, thus suggesting an energetic basis for population density. This energetic paradigm is strengthened by the observation that SDRs get tighter once resource density, a proxy for energy available, is controlled for [4]. Nee et al. [5] reported a pattern consistent with Damuth's rule among British birds, and coined the phrase ‘energetic equivalence rule’ (henceforth energy equivalence) for the independence of mass and the notional rate of energy flux per unit area (also known as population energy use), estimated as the product of population density and individual metabolic rate.

Considerable variation in SDRs has been reported in the literature, much of which is attributable to the spatial scale of observation [3,6]. Local SDRs, measured among coexisting species, often form triangular relationships with power-law exponents significantly shallower than Damuth's rule, suggesting that energy flux increases with size and rejecting energy equivalence [7–9]. Global SDRs tend to show tighter fits, perhaps because they tend to span a larger range of body masses [3,6], but show a range of exponents. Surprisingly little attention has been devoted to explain this variation [10]. Recently, it has become clear that substantial variation exists around 3/4 power metabolic scaling [11–13], raising the possibility that scaling exponents for abundance and metabolic rate covary in a manner consistent with energetic equivalence. Carbone et al. [14] showed that deviations from Damuth's Rule might arise even when energy flux and mass are independent. Specifically, they predicted shallower abundance scaling for organisms foraging in three-dimensional habitats (as a simple consequence of converting a three-dimensional distribution of animals to a two-dimensional measure of abundance) and steeper (more negative) SDRs among predators where the prey of larger species form larger groups [14]. A combination of these factors might therefore lead to a wide range of abundance scaling exponents that are still consistent with energy equivalence.

Here, we provide a systematic description of the nature and magnitude of the variation in the global SDR, using data spanning 12 orders of magnitude in body size. Specifically, we test whether the SDR varies systematically among taxa, and whether the data support Damuth's exponent of −3/4 (after accounting for any heterogeneity). We then test energy equivalence by comparing taxon-specific scaling exponents for abundance and metabolic rate, rather than the overall mean values used in previous studies.

2. Material and methods

Abundance was measured as individual density (km⁻²). Data came from Damuth ([2], 700 species) and Cotgreave & Harvey ([15], 491 bird species). We did not augment these classical datasets with new data in order that our results are directly comparable with the original studies. We used standard sources to assign species to phylum, class, order and family. Data were log-transformed prior to analysis (base e) and log body mass data were centred on zero.

We used linear mixed-effects models to partition the variance in abundance into taxonomic components, to explore the variation in SDRs and to estimate the mean scaling exponent. Following Isaac & Carbone [13], we fitted a series of models in which the slope (scaling exponent) and intercept (normalization constant) varied among taxonomic groups (phylum, class, order and family) as random effects. This hierarchical approach (cf. [16]) allowed us to model variation in SDRs without prior expectation of what taxonomic level would exhibit variation, while also accounting for variation in mean abundance among taxa that may be owing to trophic level or mode of thermoregulation [2].

We first fitted 16 ‘universal’ models, each of which had a single slope but different combinations of intercept terms. Next, we sequentially added terms for random slopes at each taxonomic level (see [13] for more details). At each step, we used Akaike's information criterion (AIC) to compare the fit of candidate models with the best-fitting model from the previous step, until all candidates led to an increase in AIC. Parameters were estimated by restricted maximum likelihood using the lme4 package [17] v. 0.999375-28 in R 2.10.1. We inferred support for these models using Akaike weights [18], which are based on the AIC scores for all models in the candidate set.

We then tested whether scaling exponents for abundance and metabolic rate covary in accordance with energetic equivalence (i.e. whether they cancel out). We extracted taxon-specific SDRs from the best-fitting model (following [13]) and matched these with metabolic scaling exponents for the same taxa (using data from [13]).

3. Results

We found strong evidence for heterogeneity in the SDR. Five models make up the 95 per cent ‘confidence set’, all of which have a different slope for each order: several also have slopes that vary at other taxonomic levels (table 1). Universal (single-slope) models are poorly supported by these analyses: the Akaike weight for the best-fitting universal model is less than 1 per cent. The model-averaged slope (scaling exponent) is −0.583, which is considerably shallower than the predicted value of −3/4.

Table 1.

Mixed-effect models of the SDR among 1191 species. (Rank denotes the rank fit among 27 candidate models (only 1 of 15 ‘universal’ models is shown). Slope and intercept columns indicate the taxonomic levels at which each parameter varied (P = phylum, C = class, O = order and F = family). Mass denotes the overall mean scaling exponent; weight is the Akaike model weight; and cumWt is the cumulative sum of model weights.)

rank	slope effects				intercept effects				mass	AIC	∂AIC	weight	cumWt
1			O		P	C	O	F	−0.578	5067.12	0	0.454	0.454
2			O		P	C		F	−0.591	5068.33	1.21	0.247	0.701
3		C	O		P	C	O	F	−0.600	5069.67	2.55	0.127	0.828
4			O	F	P	C	O	F	−0.579	5070.65	3.54	0.077	0.905
5	P		O		P	C	O	F	−0.559	5070.78	3.67	0.073	0.978
6			O			C	O	F	−0.589	5075.32	8.20	0.008	0.985
7a					P	C	O	F	−0.545	5075.55	8.43	0.007	0.992
8		C			P	C	O	F	−0.580	5075.90	8.79	0.006	0.997
9	P				P	C	O	F	−0.518	5078.74	11.63	0.001	0.999
10				F	P	C	O	F	−0.549	5079.05	11.93	0.001	1
12			O		P	C	O		−0.594	5103.95	36.83	0	1
18			O		P		O	F	−0.551	5137.73	70.62	0	1

^aBest-fitting ‘universal’ model.

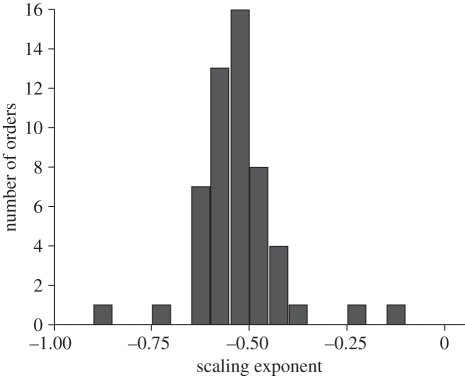
Further analyses are based on the overall best-fitting model. Strikingly, the structure of this model is identical to the best-fitting model of metabolic scaling reported by Isaac & Carbone [13]. The mean scaling exponent (−0.578) is significantly shallower than −3/4 (t = 3.95, p = 0.001), with 95 confidence intervals (CIs) close to −1/2 and −2/3 (−0.49, −0.66). However, the large order-level variance (0.0239) predicts that 5 per cent of orders should lie outside the range of −0.28 to −0.88 (figure 1).

Figure 1.

Histogram of taxon-specific scaling exponents for 54 orders, extracted from the best-fitting model.

We repeated these analyses using two subsets of the data: first excluding the birds and second using only mammals. In both cases, we found substantial support for the model with order-specific slopes, with a similar mean exponent (−0.57, −0.54, respectively).

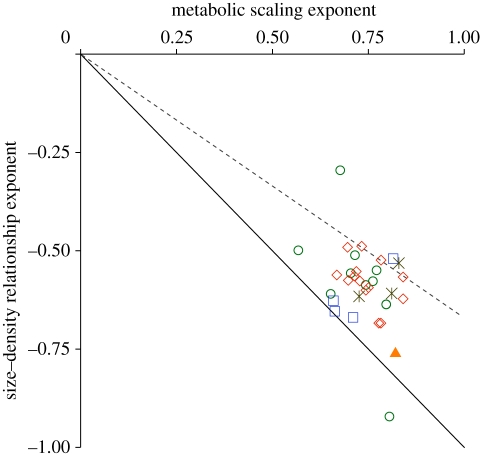
Our results indicate that SDRs are generally shallower than predicted by energy equivalence, indicating that populations of bigger animals use more energy than small animal populations. This finding is not dependent on our conclusion that SDRs are heterogeneous among orders (see the best universal model, table 1). Scaling exponents for abundance and metabolic rate do not appear to covary in any systematic way, let alone in a manner consistent with energy equivalence (figure 2). Just eight out of 32 orders lie within 0.1 units of the energy equivalence line, and 11 orders are more than 0.2 units away. Just one order, the Carnivora, shows steeper scaling of abundance than metabolic rate. The full set of order-specific scaling exponents is presented in the electronic supplementary material.

Figure 2.

Exponents of the SDR for 32 orders (y-axis), extracted from the best-fitting model, plotted against order-specific metabolic scaling exponents (x-axis). The solid and dashed lines indicate the expectation of the energetic equivalence rule in two- and three-dimensional foraging habitats, respectively. Green circles, mammals; red diamonds, birds; orange triangle, lizards; blue squares, fishes; black asterisks, invertebrates.

4. Discussion

We have presented a comprehensive analysis of global SDRs and revealed substantial variation among taxa. Our taxon-specific estimates of the SDR exponent facilitated a test of energy equivalence at the most appropriate scale for the data. Our results indicate that the SDR exponent, on average, is far shallower than predicted by Damuth's Rule. This finding adds to a growing body of evidence that SDRs commonly have exponents between −0.5 and −0.6 [7,8,10,16]. Moreover, the pattern among individual orders reveals no obvious tendency for steeper SDR exponents to be associated with steeper metabolic scaling, as expected under energy equivalence. Taken at face value, the results suggest that energy flux increases by 48 per cent for an order of magnitude increase in body mass, and that populations of elephant-sized animals use 124 times more energy per unit area than populations of copepod-sized animals (the smallest species in our dataset). These findings present a strong challenge to the notion of energy equivalence as an ecological ‘rule’ with any kind of predictive power.

Our results contradict the pioneering work of Damuth [1,2], using the same data. Damuth grouped his data into broad categories and fitted separate regressions to each. We suspect that such groups are ecologically heterogeneous and contain taxa that differ substantially in mean abundance, leading to slope estimates that are confounded by intercept effects (differences in the mean). This is borne out by a simple variance components analysis on our dataset: although most variation in abundance is found at high taxonomic levels (56% among phyla, 23% among classes), the order (5%) and family (4%) components are highly significant. We did not include a genus term in our models, but note that McGill [16] found significant variance in the abundance of North American bird genera.

The alternative explanation for our results is that energy equivalence does hold, but that other factors have shaped the SDR patterns. Some of the variation in SDR exponents is consistent with a model of geometric constraints on foraging behaviour [14]: virtually all orders fall between the predictions for two- and three-dimensional habitats (figure 2). Habitat dimensionality appears particularly effective at predicting the relative positions of fish orders: the largely benthic Cypriniformes, Perciformes and Siluriformes all lie close to the two-dimensional prediction, while the pelagic Salmoniformes lie close to the three-dimensional prediction. The extreme position of the Carnivora is also predicted by the geometric model, based on the existence of a prey-grouping effect [14]. The geometric model, however, cannot explain the extreme shallow scaling of abundance in Rodentia (−0.30), where energy flux appears to be genuinely skewed in favour of large-bodied species. However, we caution against making inferences about relative energy flux from these results, because support for the geometric model is entirely post hoc and qualitative. Formal quantitative testing would be challenging, given the heterogeneity in foraging behaviour within orders [11] and the fact that few organisms are genuinely three-dimensional in foraging behaviour. Unfortunately, the overlapping nature of these predictions makes it difficult to draw firm conclusions [19], but the patterns illustrate the potential value of scaling theories that incorporate a richer variety of ecological processes.