A modified bacterial one-hybrid system yields improved quantitative models of transcription factor specificity

Abstract

We examine the use of high-throughput sequencing on binding sites recovered using a bacterial one-hybrid (B1H) system and find that improved models of transcription factor (TF) binding specificity can be obtained compared to standard methods of sequencing a small subset of the selected clones. We can obtain even more accurate binding models using a modified version of B1H selection method with constrained variation (CV-B1H). However, achieving these improved models using CV-B1H data required the development of a new method of analysis—GRaMS (Growth Rate Modeling of Specificity)—that estimates bacterial growth rates as a function of the quality of the recognition sequence. We benchmark these different methods of motif discovery using Zif268, a well-characterized C₂H₂ zinc-finger TF on both a 28 bp randomized library for the standard B1H method and on 6 bp randomized library for the CV-B1H method for which 45 different experimental conditions were tested: five time points and three different IPTG and 3-AT concentrations. We find that GRaMS analysis is robust to the different experimental parameters whereas other analysis methods give widely varying results depending on the conditions of the experiment. Finally, we demonstrate that the CV-B1H assay can be performed in liquid media, which produces recognition models that are similar in quality to sequences recovered from selection on solid media.

INTRODUCTION

Determining the specificity of transcription factors (TFs) is an important step in elucidating regulatory networks. It is also an essential step in developing rules describing the relationship between the protein sequence of a TF and its preferred binding sites, which can be used to predict the specificities of uncharacterized TFs and to design TFs with novel specificities. Traditionally, determining the specificity of a TF was a slow and laborious process. Recent technological advances have greatly increased the rate at which new TFs can be analyzed (1). One new method, MITOMI (2,3), provides good estimates of binding affinities to different DNA sequences in a moderately high-throughput format, including a recent advance that allows affinity measurements for all possible 8-long (8-mer) binding sites. Protein binding microarrays (PBMs) were first described ∼10 years ago, and recently have been implemented in a format that allows all 10-mers to be included in the analysis (4–6). Cognate site identification (CSI) is a related technique with similar capabilities (7–9). Systematic evolution of ligands by exponential enrichment (SELEX) has long been used to determine the specificity of TFs, but initially it was used in a low-throughput manner that only returned the consensus sequence and some measure of the variability tolerated at different positions (10–13). Several years ago, it was coupled with a serial analysis of gene expression (SAGE) method to create a moderate throughput method that greatly increased the accuracy of specificity determination (14). In the last year, SELEX has been scaled up to utilize next generation sequencing methods and is now capable of determining highly accurate specificities for TFs (15–17). One advantage of SELEX over the other methods is that it is capable of analyzing binding sites of essentially any length; the only limitation is that the library of potential binding sites is limited to ∼10¹² and the number of sites that can be sequenced is ∼10⁸, both of which are much greater than all possible 10-mers (10⁶ different sequences), the limit of methods such as PBM.

Another method to determine the binding specificities of TFs is a bacterial one-hybrid (B1H) system (18–20). In this approach a TF is expressed in Escherichia coli fused to the ω subunit of RNA Polymerase. This turns any DNA binding protein into an activator of transcription. A library of randomized binding sites is located upstream of a weak promoter driving expression of a selectable gene. Under appropriate growth conditions only sites with high affinity for the TF will survive selection. As with SELEX, this approach has the advantage that binding sites of any size can be studied, the only limitation being that the library size is constrained by the transformation efficiency of bacteria, which is ∼10⁸ individual sequences. Another advantage of this approach is that the TF does not have to be purified, or expressed in vitro; any TF that can be functionally expressed in E. coli can be assayed with this method making it rapid and easy to use. It can also be used with TFs that have very low specificity by fusing them to two fingers of a zinc-finger protein to create a chimeric protein with sufficient specificity and affinity for function within the B1H system (20). Previously binding sites were sequenced from a small number of surviving colonies, typically 20–40, and a model of the specificity of the TF would be inferred using a motif finding program (20,21), such as Consensus (22) or MEME (23).

Regardless of the method employed, the goal is to obtain an accurate quantitative model of the specificity of the TF. In this article, we test several different variations of the B1H method, including different approaches to analyzing the data, using the well-characterized Zif268 zinc-finger protein as the standard for comparison. We find that the standard B1H method, which employs a large randomized library and determines the binding sites from a few selected colonies, has reasonable accuracy which can be further improved by the application of high-throughput sequencing methods that determine the frequencies of selected binding sites across the distribution from high affinity to low affinity. We also show that using a library with limited variability, in which part of the binding site is fixed and the other part randomized, combined with high-throughput sequencing allows us to measure the growth rate of colonies containing each site in the library. An algorithm that models the relationship between binding energy and growth rate can then further increase the accuracy of the quantitative specificity model. We call this experimental approach CV-B1H for ‘constrained variation B1H’ and the analysis method GRaMS for ‘Growth Rate Modeling of Specificity’ and we compare its performance under many different experimental protocols to other experimental and analysis methods. Overall we show that CV-B1H is an inexpensive, fast and easy method for accurately determining the specificity of a TF, where optimal results are obtained when the data are analyzed using an appropriate model that accounts for the dynamic growth of cells.

METHODS

Zif268 B1H selections

All of the B1H binding site selections were performed as described previously using an ω-Zif268 fusion protein expressed from a UV2 promoter in the plasmid pB1H2ω (20). Zif268 was used for these experiments because it has been thoroughly characterized by a number of other methods allowing comparison of the recognition models we obtain to its previously defined specificity.

Randomized 28 bp binding site library

Four independent B1H binding site selections for Zif268 were performed using a 28-bp randomized library in pH3U3 reporter vector as previously described (20). Approximately 2 × 10⁷ co-transformed cells containing the library and the ω-Zif268 expression plasmid were plated under each selection condition on selective media plate containing 0, 2 (replicated) or 5 mM 3-AT and 10 μM IPTG. These selections were incubated at 37°C for 36–48 h following which surviving cells were washed off the plate as a pool. The plasmid DNA from the pooled colonies was isolated. Library regions from the recovered reporter plasmids were PCR amplified, adaptor ligated with barcodes identifying each selection, and the library for Illumina sequencing was prepared as previously described (24). The initial 28 bp library was also Illumina-sequenced where ∼10⁷ reads were obtained to provide a background model for subsequent motif analysis.

Randomized 6 bp binding site library

The binding site library (GCGGCCACTGGGCAGCTGGCCANNNNAAAAATNNNNNNGCGGTACCTAGGTTCTTCGAATTC) cloned between the EcoRI and NotI sites in pH3U3 contains two different randomized regions: a 6 bp element (bold underlined) that is associated with the four 3′-bases of the Zif268 recognition sequence (GCGG, underlined) and a 4 bp randomized region (italics) that serves as an internal control to identify sequences that may be enriched in the selections or preparation for sequencing sample due to jackpot effects. We did not observe any evidence of a jackpot effect. Auto-activating clones within this library were removed by 5-FOA counter selection as previously described (20). Approximately 10⁶ co-transformed cells containing the library and the ω-Zif268-expression plasmid were plated under each selection condition on selective media plates containing 0.5, 1 or 2 mM 3-AT and 0, 10 or 50 μM IPTG, where these selections were incubated at 37°C for 4, 8, 12, 18 or 24 h. This was a total of 45 independent selections. At the desired time-point surviving cells were washed off the plate as a pool. Isolated plasmid DNA from the pooled cells was prepared for Illumina sequencing as for the 28 bp library. Using barcodes for each experiment, sequences from all 45 experiments were obtained from a single Illumina sequencing lane that contained over 15 million reads, leading to an average of about 300 000 binding sites per experiment. There are only 4096 different 6-mer sites so this quantity of sequences is sufficient for good coverage of all possible binding sites. We also performed CV-B1H from the same initial library in liquid media with 5 mM 3-AT and 50 μM IPTG. After 4 h the cells were pelleted, plasmids isolated and they were prepared for Illumina sequencing as with the experiments on plates. We independently sequenced the counter selected library, which was the input to each of the binding site selection experiments, to define the initial frequency of each 6-mer. More than 16 million reads were obtained and every 6-mer was observed at least 472 times. This allowed us to determine the enrichment of each site after selection. The sequences from each data set are available at http://ural.wustl.edu/htb1h_zif68 and from the GEO database (GSE26767).

Binding site modeling using existing programs

We model the binding energy of Zif268 for any sequence using a position weight matrix (PWM) (25). We used four different motif discovery methods on the different data sets. BioProspector (26) was used on both the 28 bp data sets with a site size of 10 bp and on the 6 bp data sets with a site size of 6 bp. For the 6 bp data set, the orientation was fixed whereas for the 28 bp data sets sites could be discovered in either orientation. A third-order Markov model, based on the sequences of the respective initial libraries, was used for the background model. MEME (23) was run only on the 28 bp data sets because it requires sites longer than 6 bp for motif analysis. The 3000 most abundant 28-mers served as the input to MEME with each sequence being used only once in the input set. Sites were allowed to occur in either orientation. BEEML (16) requires the alignment of the binding sites for motif analysis, so it was used only on the 6 bp data sets with the background model derived from the 6-mer counts in the initial library. On the 6 bp data sets, we also tested a simple log-odds method that determines the value of each PWM element from the ratio of the observed frequency of each base at each position in the aligned binding sites to the observed frequency of each base at each position in the initial library (from the randomized region). We also tested the accuracy obtained from the consensus sequence, GCGTGGGCGG, where its energy is set to zero and the optimal mismatch energy (over all possible integer values) is two.

Binding site modeling based on growth rate analysis

We model protein–DNA binding using a biophysical model described previously (16). Briefly, the probability that the sequence S_i is bound at equilibrium is:

(1)

where K_d is the dissociation constant and square brackets indicate concentrations. It is convenient to express the energy of binding, E_i, relative to the Gibbs free energy of binding to a reference sequence; we use the consensus sequence, in units of RT, with its energy defined as, E_ref = 0:

(2)

where

(3)

and

(4)

Binding sites with E_i = μ have a binding probability of one-half.

In order to grow and replicate, cells must express sufficient His3 enzyme to meet their histidine requirements. We define the growth rate of an allele as the number of doublings that a cell possessing it undergoes each hour during exponential growth phase. The equation

(5)

describes the exponential growth of a colony, where t is the number of hours, N_i(t) is the final number of cells possessing site S_i present at time t, r_i is the growth rate for cells containing that site in doublings per hour and N_i(0) is the initial number of cells with that site at time zero.

Histidine is a rate limiting reagent, and we make the simplifying assumption that the amount of histidine is directly proportional to the occupancy of the His3 promoter by the TF (up to some saturating level) and that the growth rate, r_i, of cells possessing S_i is directly proportional to the amount of histidine produced, up to a level where it is no longer limiting. The relationship between binding energy of the TF for site S_i and the growth rate is then:

(6)

where M is the maximum growth rate for these cells under the same conditions but with histidine not being limiting. Supplementary Figure S1A shows a simulated ideal experiment where the counts for each sequence depend on the binding energies as described in the biophysical model of the preceding equations. Data taken at different time points will fall on different curves, but when converted to growth rates all of the data sets converge to a common curve describing the relationship between growth rate and binding energy (Supplementary Figure S1B).

We are only able to determine the frequency of each allele from the Illumina reads. In order to convert these frequencies into numbers of cells, we need to know the initial number of cells plated, n_I, and the final number of cells on the plate, n_F, at time t. The growth rates determined by the frequencies at time t will be off by a constant

(7)

such that

(8)

where f_i(t) is the frequency of site S_i at time t and f_i(0) is the initial frequency of S_i before selection. We refer to the quantity

(9)

as the enrichment of site S_i at time t. For a given experiment, every growth rate will be off by the same constant. If we assume that the minimum growth rate is zero (cells may not divide but they do not disappear from the plate), we can determine the constant by assuming the plateau of high energy binding sites represents a growth rate of zero. For the remainder of the paper, including all of the figures, the calculated growth rates for each site have been adjusted such that the median of the high energy plateau is defined as zero.

For a given PWM, the predicted growth rates,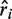, depends on the energy model via:

(10)

where 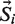is the encoded sequence, S_i and 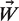is the PWM. In this analysis, M was fixed to the maximum growth rate for each data set. We use the Levenberg-Marquardt algorithm (27–29) in a program called GRaMS to perform a least squares fit between the measured and predicted growth rates in order to find the optimum PWM.

Assessment of different protocols and analysis methods

For each experimental data set and each analysis method we obtain a PWM. We adjust the elements such that those corresponding to the reference sequence are assigned zero, and the other elements are estimates of the binding energy differences for each other base at each position in the binding site, as proposed by Berg and von Hippel (24). We determine the accuracy of each method by measuring, using the squared Pearson correlation coefficient (R²), how well it predicts the binding data from a single-round SELEX experiment (16). In that experiment a large library of random 10-mers were bound to Zif268 and the bound fraction as well as the initial library were Illumina sequenced. For each PWM, the values of µ and a non-specific binding energy, E_ns, are found that maximize the fit for that model so that the comparisons are strictly between how well the PWMs capture the energy differences for each base at each position. BEEML (16) was developed specifically to model that SELEX data so we determined its R² value when trained on the SELEX data directly as the maximum that any other PWM could be expected to obtain. This was 0.93 and 0.96 for the 10 bp PWMs and 6 bp PWMs, respectively. The remaining variance is probably due to experimental noise as well as binding energy contributions not captured by the simple PWM which are known to exist but be small for Zif268 (30).

RESULTS

Selections from 28 bp library

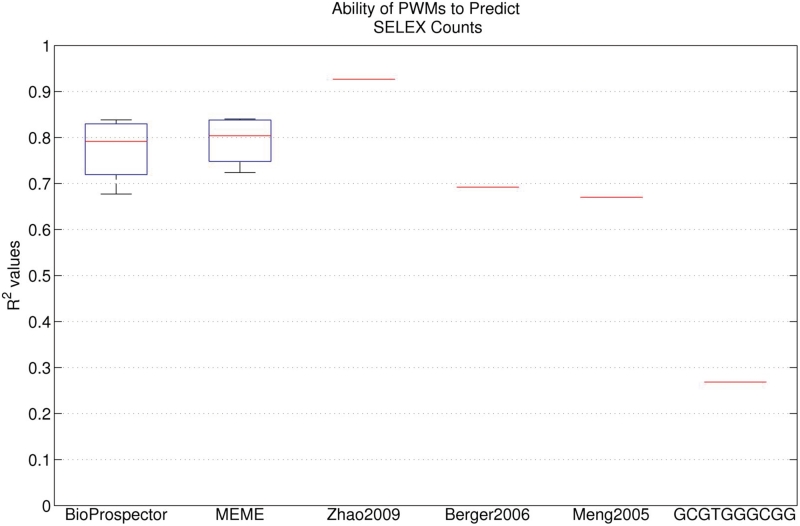
We first characterized how well the PWM obtained from the 28 bp library can predict the zif268 SELEX data. The PWM from Meng et al. (2005), which was based on only 17 sequences from selected colonies, gives an R²= 0.67. This is nearly as high as that obtained from a Zif268 PWM obtained from PBM data (R²= 0.69) (4) and is much better than simply using a consensus sequence (GCGTGGGCGG) to predict quantitative binding affinities, which gives an R²= 0.27. We next tested whether using high-throughput sequencing methods when applied to the B1H selected clones would provide a motif with even higher accuracy. We collected all of the cells on the plate from a selection using Zif268, which includes the large colonies, small colonies and even individual cells that have not divided, purified the binding site plasmids and subjected the entire mixture to Illumina sequencing. We did this for four different growth conditions and obtained between 117 475 and 928 304 sequences from each selection (after removing poor quality reads that did not match the fixed sequences flanking the library). We used BioProspector and MEME to obtain alignments and PWMs from each data set, and then used those PWMs to predict the SELEX data. The results from both motif discovery methods were nearly identical, with median R² of 0.79 and 0.80 for BioProspector and MEME, respectively (Figure 1). This is a significant improvement over the PWM based on only 17 sequences. We also tested how many reads are required to obtain that accuracy by randomly selecting subsets of sequences of various sizes from our data sets. We found that the maximum accuracy was achieved by both BioProspector and MEME analyses with a population of about 3000 reads. Thus, a large number of different B1H binding site selections can be multiplexed together in a single Illumina lane to minimize sequencing costs, while still obtaining good recognition models for each experiment.

Figure 1.

Box plot showing the ability of the set of MEME and BioProspector motifs learned from the four 28 bp B1H data sets to predict the SELEX data. For each PWM, R² was calculated to determine the correlation between the predicted and observed SELEX counts. The performance of three PWMs from the literature is also shown. Zhao2009, Berger2006 and Meng2005 were learned from SELEX, PBM and B1H data, respectively. The GCGTGGGCGG consensus sequence PWM was constructed using an optimal mismatch penalty term.

Selections from 6 bp library

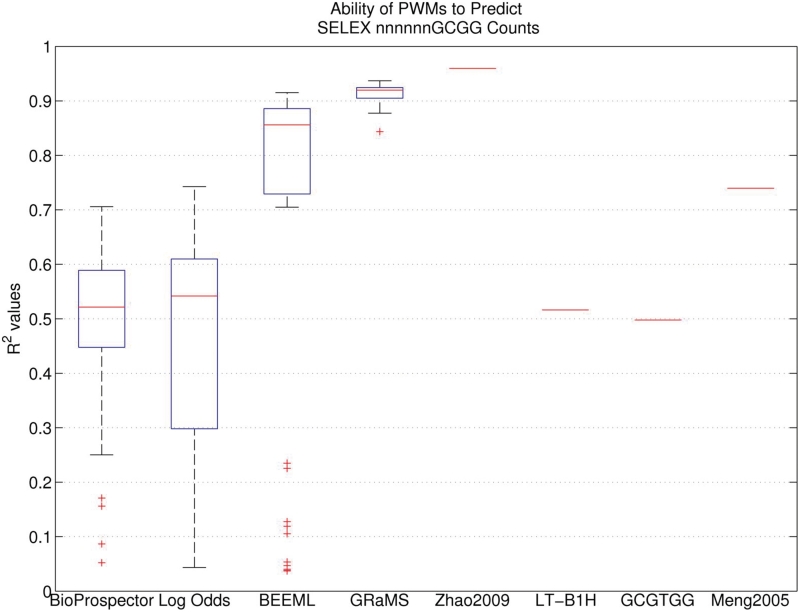
While quite good, those R² values still leave considerable room for improvement. We next tested whether we could get further improvement by fixing part of the binding site, in this case 4 bp, and only randomizing the remaining 6 bp for our B1H binding site selections. This eliminates problems related to aligning the binding sites because the TF should always prefer the orientation and position that overlaps the fixed region; we found no exceptions to that expectation in the analysis of the data that was generated. Moreover, because there are only 4096 different 6 bp sequences, we can obtain good frequency estimates for all binding sites in both the initial library and in the selected sites while at the same time multiplexing many different experiments in a single Illumina lane. We averaged about 300 000 reads for each of 45 different selections that explore a range of different selection conditions (3-AT, IPTG and incubation time). Motif comparisons for data generated from these experiments were made to the subset of Zif268 SELEX data that contained the GCGG sequence in the last four positions on the binding site, to be consistent with the constraints in our selections. The BEEML PWM predicts the SELEX data (that it was trained on) with an R²= 0.96, which is the maximum we would expect from any other method trained on alternative data sets. The simple consensus sequence, with optimal mismatch penalty, predicts the SELEX data with an R²= 0.50 and the 6 bp segment of the previous B1H Zif268 PWM (18) fits with R²= 0.74 (Figure 2). We performed a traditional B1H experiment on this library, picking and sequencing just 22 colonies, and the resulting PWM had an R² of only 0.52, much worse than the previous PWM from a 28 bp library. Equally unexpected was that BioProspector and log-odds analyses on the various 6 bp experiments were highly variable and generally much poorer than for the 28 bp library. The median values of R² were only 0.52 and 0.54 for BioProspector and log-odds, respectively and the maximum values were only 0.71 and 0.74 (Figure 2). Motifs generated from selections with short incubation times displayed the worst performance, but none of the experimental conditions performed very well on this library.

Figure 2.

Boxplot showing the ability of the 45 PWMs produced by each analysis method using each B1H data set as training data to predict the SELEX nnnnnnGCGG data. For each model, R² was calculated to determine the correlation between the predicted and observed SELEX counts. The performance of four individual PWMs is also indicated. Two of these PWMs, Zhao2009 and Meng2005, were obtained from published SELEX and B1H studies respectively; the first six positions of these PWMs were used. The LT-B1H PWM was learned from 22 sequences obtained from a CV-B1H experiment. The GCGTGG consensus sequence PWM was constructed using an optimal mismatch penalty term.

We think these results are explained by the fact that the initial library, which has been counter selected to remove autoactivating sequences, has a very low proportion of the consensus binding site and some other closely related sites. Their low initial frequencies ensure that even after the 24 h time selections they have not become the most abundant sites, therefore leading to PWMs with sub-optimal parameters. Although both the log-odds method and BioProspector take the initial library into account through their background estimates, those are only based on the total composition, in the case of log-odds, or a third-order Markov model, neither of which really captures the explicit deficiency of specific binding sites, some of which are high-affinity sites. We, therefore, tested the BEEML program on the 45 data sets. It takes into account each specific binding site in both the initial and selected libraries and, based on a biophysical model for enrichment based on affinity, does a nonlinear regression to find the optimal parameters for a PWM. While its performance is still quite poor on the earliest time points, its median R² is 0.86 and its best is 0.92, both significantly better than the other methods (Figure 2). This level of performance makes BEEML analysis of the 6 bp CV-B1H data even better than the BioProspector and MEME performance on the 28 bp high-throughput B1H data sets (Figure 1).

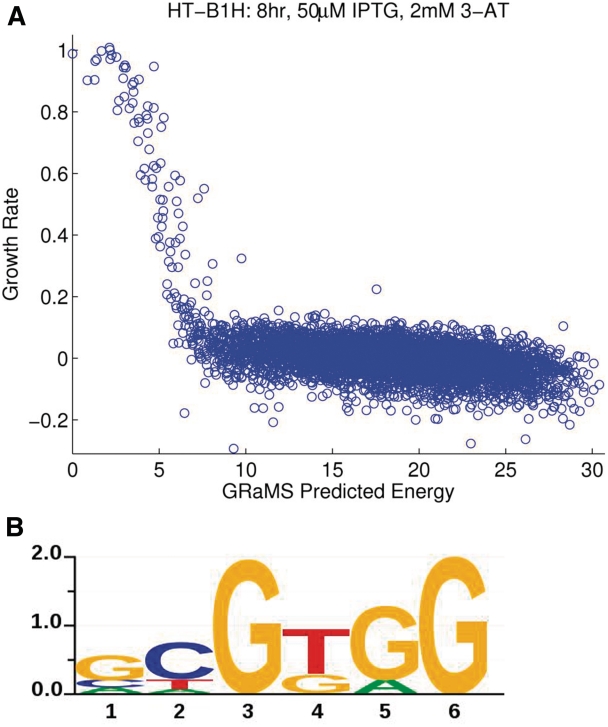
Since we expect the differences in binding energies for different sites to affect their relative growth rates, we developed GRaMS to obtain optimal PWMs for CV-B1H data according to the model described in ‘Methods’ section. Supplementary Figure S1 shows, for ideal simulated data, how the occurrences of difference binding sites at various time points fall on different lines, but when converted to growth rates they all converge to a single line that shows the relationship between growth rate and binding energy. Figure 3A shows the results from one experiment (8 h, 50 μM IPTG, 2 mM 3-AT) where the binding energies are the predictions from the GRaMS model (Figure 3B). Supplementary Figure S2 shows the same curve for all 45 data sets. While obviously noisier than the simulated data, the curves are all very similar and are consistent with our model. Supplementary Figure S3 shows the logos for all 45 data sets. Note that the models are very similar indicating that with GRaMS analysis the resulting models are relatively insensitive to the exact experimental protocol. Motifs from the 4 h time points are still the least accurate and those from the late time points have slightly reduced accuracy probably due to the onset of colony saturation for the highest affinity binding sites. At the earlier times points increased stringency, using higher concentrations of 3-AT, improved the quality of the motifs somewhat but the results are not much affected by the concentration of IPTG. In contrast, Supplementary Figure S4 shows the Logos for the 45 different PWMs obtained by BioProspector. While overall they are not too bad, they are more variable between different conditions and none fit the SELEX data as well as the GRaMS models.

Figure 3.

Results of CV-B1H on Zif268 analyzed with GRaMS. (A) Plot of predicted energies versus growth rates per 6-mer. The GRaMS PWM (8 h, 50 μM IPTG, 2 mM 3-AT) was used to predict the energies. The growth rates (shifted so that the median value is zero) are from the 8 h, 50 μM IPTG, 2 mM 3-AT data set used to estimate the GRaMS PWM. (B) Sequence logo for the GRaMS PWM obtained from the same data set. The y-axis indicates the information content of each position in bits. Sequence logos were produced using in-house software, svgSeqLogo, written by RGC.

Using GRaMS, we obtained R² values with a median of 0.92 (Figure 2) and with a maximum value of 0.94, nearly as good as the maximum expected. The entire range is from 0.84 to 0.94, again indicating that the models are relatively insensitive to the exact experimental protocol. Only one sample gave an R² as low as 0.84, with the next lowest value being 0.88. On average, the lowest R² values were obtained using GRaMS models trained on the 4 h data sets. None of the methods performed particularly well on these data sets, but GRaMS performed the best (Supplementary Figure S5). On data sets from the later time points, the R² values ranged from 0.89 to 0.94 with a median of 0.92 (Supplementary Table S1).

The largest difference between the logos from GRaMS (Supplementary Figure S2) and from BioProspector (Supplementary Figure S3) is at position 5, where BioProspector nearly always shows a slight preference for A over G, whereas GRaMS has a somewhat larger preference for G over A, which is consistent with the SELEX data. This difference can be attributed to bias in the initial library (probably due to the counter selection), which contains many more sequences with A at position 5 than with G. Even after selection up to 24 h, A remains the most common base in each data set, which causes the BioProspector PWM to prefer A. But the growth rate of sites with G in position 5 is, on average, greater than for those with A, so GRaMS infers the higher affinity for G. Presumably BioProspector would perform better if the initial library were less biased, as we observed in the 28 bp library, but one advantage of GRaMS is that it takes the bias into account directly through its background model and so is not strongly influenced by it.

We also performed CV-B1H in liquid culture and found that similar models could be obtained. Supplementary Figure S6 shows the motif obtained through GRaMS analysis after 4 h of growth which attained an R²= 0.93 on the SELEX quantitative predictions. This may be the most straightforward method to employ for selections in practice but we have not examined its performance in detail as we have with the plate growth method. Performing the B1H assay in liquid media has the potential artifact that the cells with low affinity sites may be able to grow using histidine made in excess by other cells, although this should not be a major limitation at early time points when the cell densities are very low.

Given that GRaMS performed so well with CV-B1H data, we wondered whether it would also improve the models obtained from the 28 bp B1H experiments. One limitation is that GRaMS does not generate a native alignment of binding sites from a population of selected sequences, it requires an existing alignment to generate a binding motif. Consequently, we generated PWMs with GRaMS using the aligned sites generated by BioProspector and MEME, and we used for the background model the counts of 10-mers from the input 28 bp library. This provided almost no improvement over the original MEME and BioProspector models, where the median R² values increased by only 0.01 for both sets (data not shown). We think this stems from several factors including: an incomplete sampling of the binding sites, especially the low affinity sites, in the BioProspector and MEME alignments; an incomplete sampling of the sequences in the initial library for the construction of the background model; and the influence on the activity of a sequence by its distance from the promoter, which is evident in the strong preferences for the recovery of binding sites at specific registers in the randomized sequences, that is not accounted for within the current GRaMS model. Therefore as currently implemented, GRaMS does not provide an improved analysis method for general B1H experiments, even with high-throughput sequencing data, but with the appropriate experimental design, as in the CV-B1H experiments, it can be used to obtain highly accurate, quantitative models of TF specificity.

DISCUSSION

The B1H assay has proven to be a robust technique applicable to a wide variety of different TF families. For instance, it has recently been successfully applied to more than 200 different Drosophila TFs from a variety of different families (i.e. pfam families: bZIP_1, bZIP_2, CBF_beta, Fork_head, HLH, HMG_box, PAX, RHD, Runt, zf-C2H2 and zf-C4) (31). We find that applying massively parallel sequencing methods to all of the selected binding sites on an entire plate can lead to more accurate, quantitative models of TF specificity. The new models are more accurate than those obtained from the same library when sequencing only a few selected colonies, as might be expected. These new models are also slightly better than those obtained from PBM experiments on Zif268. Despite the increased accuracy from the high-throughput sequencing there remains substantial room for improvement. We show that by constraining the variability in the library, which eliminates ambiguities in the alignment of the sites and allows for deep sampling of the population, very accurate models can be obtained. However, even when using the CV-B1H protocol, the accuracy of the resulting motifs depends on the data analysis method employed. By measuring growth rates of cells across the distribution from high affinity to low affinity sites and using a biophysical model for the relationship between growth rate and binding energy, GRaMS is able to obtain more accurate models from B1H data than any other approach we tested. This approach is fairly insensitive to the exact B1H protocol used and we obtained good models under all of the variations that we tested except for the very early time point (4 h). From selections in liquid culture, we were able to obtain a good model even after only 4 h of growth. Increased 3-AT concentrations, which increase the stringency of the selection, increased the accuracy of the resulting model slightly on average. The IPTG concentration had little effect, although 10 and 50 μM were slightly better than zero, on average.

We have used some simplifying assumptions in our biophysical model, but the fact that we consistently get good PWMs suggests that the assumptions are reasonable. In particular, we have not used a coupling factor, referred to as λ by Berg and von Hippel (32,33) that relates the binding energy to the functional activity of a binding site. In essence, we assume λ = 1, which is within the range of 0.5 to 1.5 that they found for several natural systems. If we empirically determine a λ for each of our PWMs that convert them to the optimal PWM for Zif268, we find that it decreases at late times, but we think this is best explained by the saturation effects of the faster growing colonies beginning to reach their maximum size. For early time points, and for most conditions, assuming λ = 1 appears to be a good approximation. It is unclear whether this relationship will hold true for other TFs, but the fact that the TFs analyzed by this approach use the ω-fusion as the means of coupling DNA binding to transcriptional activation suggests that assuming λ = 1 is likely to be reasonable in general.

AVAILABILITY

The sequences from each data set are available at http://ural.wustl.edu/htb1h_zif68 and via GEO (accession GSE26767). GRaMS was implemented as a MATLAB program and is available for download from http://ural.wustl.edu/resources.html#Software.

ACCESSION NUMBERS

GEO, GSE26767.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: National Institutes of Health (R24GM078369, R01HG004744 and R01HG00249).

Conflict of interest statement. None declared.