Abstract
This paper compares the structural approach to economic policy analysis with the program evaluation approach. It offers a third way to do policy analysis that combines the best features of both approaches. We illustrate the value of this alternative approach by making the implicit economics of LATE explicit, thereby extending the interpretability and range of policy questions that LATE can answer.
Keywords: Marschak’s Maxim, generalized Roy model, structural methods, reduced form methods, program evaluation, policy evaluation, instrumental variables, LATE
1 Introduction
Few topics in economics evoke more passion than discussions about the correct way to do empirical policy analysis.1 These discussions are sometimes framed as conflicts between “structural” and “reduced form” approaches.2 In current usage, “structural” is taken to mean parametric, explicitly formulated, empirical economic models.
“Reduced form” has multiple and sometimes conflicting meanings. One strand of the reduced form approach uses explicit economic models to motivate and interpret empirical analyses and approximates the economic models using simple econometric techniques. Harberger (1964), Shimer and Werning (2008), Chetty (2009), and Einav et al. (2009) are good examples of this approach. Chetty (2009) surveys a large literature in this tradition.
Another strand is the “program evaluation” approach surveyed in Imbens and Wooldridge (2009). This approach focuses on “effects” defined by experiments or surrogates for experiments as the objects of interest, and not the parameters of explicit economic models. It often leaves implicit the economics and policy relevance of the output from its procedures. This paper compares structural and program evaluation approaches—the contrast between the economic parameters featured in the structural approach and the “effects” featured in the program evaluation approach.
Explicit structural models facilitate policy analysis. However, after 60 years of experience with fitting explicit structural models on a variety of data sources, empirical economists have come to appreciate the practical difficulties that arise in identifying, and precisely estimating, the parameters of fully specified structural models that can answer a wide variety of policy questions. There have been many demonstrations of the sensitivity of estimates of structural models to assumptions about functional forms and distributions of unobservables. Liu (1960), Hendry (1980), Sims (1980), and Leamer (1983) gave early warnings about the fragility of standard econometric estimates of explicit economic models. Killingsworth and Heckman (1986) and Pencavel (1986) summarize structural estimates of the effects of taxes and wages on labor supply and report estimates from the literature that are sometimes absurd. Lewis (1986) reports the sensitivity of structural estimates of the causal effect of unionism on wages to the use of alternative methodologies and reports many estimates that are incredibly large. An influential paper by LaLonde (1986) is widely interpreted as having demonstrated that standard structural estimation methods applied to non-experimental data cannot duplicate the estimates obtained from a job training experiment.
These and other studies reported in the literature more than 20 years ago fueled the flight of many empirical economists from structural models, even though Heckman and Hotz (1989) cautioned that many applications of the structural approach by those comparing structural estimates with experimental estimates did not perform specification tests to see if the estimated structural models were concordant with the pre-program data. They show that when such tests are performed, the surviving structural models closely match the estimates produced from the experiment analyzed by LaLonde, findings duplicated for other experiments (see Todd and Wolpin, 2006, Attanasio, Meghir, and Santiago, 2009, Attanasio, Meghir, and Santiago, 2009, and the discussion in Keane, Todd, and Wolpin, 2010).
The perceived failures of the structural methods of the 1970s and 1980s produced two different methodological responses.3 One response—the “program evaluation” approach—was a retreat to statistics, away from the use of explicit economic models either in formulating economic policy questions or in suggesting frameworks for estimating models to answer such questions. The second response was development of a more robust version of the structural approach.
The program evaluation approach replaces the traditional paradigm of economic policy evaluation with the paradigm of the randomized controlled trial. In place of economic models of counterfactuals, practitioners of this approach embrace a statistical model of experiments due to Neyman (1923) and Cox (1958) that was popularized by Rubin (1974, 1978, 1986) and Holland (1986). In this approach, the parameters of interest are defined as summaries of the outputs of experimental interventions. This is more than just a metaphorical usage. Rubin and Holland argue that causal effects are defined only if an experiment can be performed.4 This conflation of the separate tasks of defining causality and identifying causal parameters from data is a signature feature of the program evaluation approach. It is the consequence of the absence of clearly formulated economic models. The probability limits of estimators, and not the parameters of well-defined economic models, are often used to define causal effects or policy effects.
The retreat to statistics in the program evaluation literature left a lot of economics behind. A big loss was the abandonment of economic choice theory. Important distinctions about ex ante and ex post outcomes and subjective and objective evaluations that are central to structural econometrics were forgotten.
The influence of the program evaluation approach is widespread. It is now commonplace for many empirical economists to use the language of “treatment” and “control” to describe the comparisons made in empirical policy studies.
The structural response to the perceived failures of the 1970s and 1980s structural models has focused on nonparametric identification and estimation of well-posed economic models within which to conduct policy analyses. This line of work preserves the goals of the Cowles Commission pioneers of the structural approach — to estimate models that can make forecasts for a range of widely different policies and criteria. It is more explicit than the program evaluation approach in articulating economic models. It embraces developments in dynamic economics, game theory, auction theory, and the theory of mechanism design. The richness of the theoretical models (in contrast to the intuitive “effects” promoted in the program evaluation literature) make the fruit of this approach more intellectually interesting. It also produces estimates that cumulate across studies.5
On the negative side of the ledger on structural estimation, the often complex computational methods that are required to implement this approach make it less transparent. Replication and sensitivity analyses are often more difficult in this approach than in the program evaluation approach. Economists advocating the program evaluation approach dismiss the structural approach as overly complex and not “credible,” focusing on the statistical and computational properties of estimators as the measure of the credibility of procedures (see, e.g., Angrist and Pischke, 2008, 2010).6
An important paper by Marschak (1953) suggests a middle ground between these two camps, and is a motivation for the present paper. Writing in the early 1950s during the first wave of structural econometrics, Marschak noted that for many problems of policy analysis, it is not necessary to identify or estimate fully specified structural models—the goal of structural analysis as conceived by the Cowles pioneers and successor generations of structural economists. Marschak’s Maxim suggests that economists should solve well-posed economic problems with minimal assumptions. All that is required to conduct many policy analyses or to answer many well-posed economic questions are policy invariant combinations of the structural parameters that are often much easier to identify than the individual parameters themselves and that do not require knowledge of individual structural parameters. This approach advocates transparency and empirical robustness as does the program evaluation approach, but it also focuses attention on answering clearly stated economic and policy questions.
This approach is often less computationally intensive and focuses on a more limited range of policy questions than the very large range of policy questions contemplated by the Cowles pioneers. The computationally less demanding models, more transparent sources of identifiability and the relative ease of performing replication and sensitivity analyses give credibility to this approach. At the same time, this approach improves on the program evaluation approach by producing estimates that have clear economic and policy relevance.
The plan of this paper is as follows. In the next section, I review the range of questions that arise in evaluating economic policies and how the program evaluation approach and the structural approach address them. I use the Roy model (1951) and its extensions as examples of widely-used and prototypical structural models. In the following section, I apply Marschak’s Maxim to the analysis of the Roy model. This produces an empirical approach that simplifies policy analysis for a certain class of policies. It links the Roy model to the Local Average Treatment (LATE) framework of Imbens and Angrist (1994). This approach facilitates the interpretation of what LATE and extends the range of questions LATE answers. The final section of the paper summarizes the argument.
This paper is not a position piece for or against any particular statistical methodology. It is about the interpretability of estimates and their policy relevance. It is an exploration of how to get the most out of the data using economics to define the questions of interest and statistics to help answer them.
2 The Structural Versus the Program Evaluation Approach to Evaluating Economic Policies
Policy analysis is all about identifying counterfactual states. Counterfactual policy states are possible outcomes in different hypothetical states of the world. An example is the set of outcomes of the same persons in different tax regimes. Causal comparisons entail contrasts between outcomes in alternative possible states holding factors other than the features of the policy being analyzed the same across the contrasts. Thus the person subject to a particular policy is the same as the person who is not, except for treatment status and, possibly, the outcome associated with treatment status.
The concept of causality at the individual level is based on the notion of controlled variation — variation in treatment holding other factors constant. This is Alfred Marshall’s (1890) ceteris paribus clause which has been the operational definition of causality in economics for over a century.7 It is distinct from other notions of causality sometimes used in economics that are based on prediction (e.g. Granger, 1969, and Sims, 1972).8
There are two distinct tasks in causal inference and policy analysis: (a) Defining counterfactuals and (b) Identifying causal models from data. Table 1 delineates the two distinct problems.
Table 1.
Two Distinct Tasks that Arise in the Analysis of Causal Models
| Task | Description | Requirements |
|---|---|---|
| 1 | Defining the Set of Hypotheticals or Counterfactuals |
A Well-specified Economic Theory |
| 2 | Identifying Causal Parameters from Data | Mathematical Analysis of Point or Set Identification Joined With Estimation and Testing Theory |
The first task entails the application of economic models. Models are descriptions of hypothetical worlds obtained by varying — hypothetically — the factors determining outcomes. Models may be motivated by empirical evidence, and they may crystalize evidence. They are, however, abstract representations of the evidence with an internal logic of their own.
The second task is inference from data. It requires solving the identification problem including solving practical problems of inference from empirical samples.9 Economists sometimes differ over what constitutes admissible data for examining any policy question, what prior information should be used and how the prior information should be used. There are no sharp rules to settle these differences.
Part of the controversy surrounding the construction of policy counterfactuals for evaluating policies is a consequence of analysts being unclear about the two distinct tasks represented in Table 1 and sometimes confusing them. Particular methods of estimation (e.g., randomization, matching or instrumental variable estimation) have become associated with the definition of “causal parameters”, because issues of definition and identification are often conflated.
The structural econometric approach to policy evaluation separates these two tasks and emphasizes the role of models in defining hypotheticals and causal effects. Some statisticians reject the use of models in defining causality and seek an assumption-free approach to causal inference and policy analysis (see, e.g., Tukey, 1986).
Any estimator makes assumptions (often implicit) about the behavior of the agents being analyzed. For example, the ability of a randomized controlled trial to identify parameters of interest depends on assumptions about the behavior of the agents being subject to randomization.10 The structural approach is explicit about these assumptions. The program evaluation approach is often not. Some economists confuse the absence of explicit statements of assumptions with the absence of assumptions.11
The “causal models” advocated in the program evaluation literature are motivated by the experiment as an ideal. They do not clearly specify the theoretical mechanisms determining the set of possible counterfactual outcomes, how hypothetical counterfactuals are realized or how hypothetical interventions are implemented except to compare “randomized” with “nonrandomized” interventions. They focus on outcomes, leaving the model for selecting outcomes and the preferences of agents over expected outcomes unspecified.
The emphasis on randomization or its surrogates, like matching or instrumental variables, rules out a variety of alternative channels of identification of policy effects from data. The emphasis on randomization has practical consequences leading to the conflation of Task 1 with Task 2 in Table 1. Since a randomized protocol is used to define the parameters of interest, this practice sometimes leads to the confusion that randomization is the only way — or at least the best way — to identify causal parameters from data.
The models in the program evaluation literature do not specify the sources of randomness generating variability among agents, i.e., they do not specify why otherwise observationally identical people make different choices. They do not distinguish what is in the agent’s information set from what is in the observing economist’s information set, although the distinction is fundamental in justifying the properties of any estimator for solving selection and evaluation problems. They do not allow for interpersonal interactions inside and outside of markets in determining outcomes that are at the heart of game theory, general equilibrium theory, and models of social interactions and contagion (see,e.g., Aguirregebaria and Mira, 2010; Brown and Matzkin, 1996; Brock and Durlauf, 2001; Durlauf and Young, 2001; Manski, 1993; Tamer, 2003).
The goal of the structural econometrics literature, like the goal of all science, is to understand the causal mechanisms producing effects so that one can use empirical versions of models to forecast the effects of interventions never previously experienced, to calculate a variety of policy counterfactuals and to use theory to guide choices of estimators to interpret evidence and to cumulate evidence across studies. These activities require models for understanding “causes of effects” in contrast to the program evaluation literature that focuses only on the “effects of causes” (Holland, 1986).
Before turning to a specific comparison of the two approaches, it is useful to review the variety of questions that arise in policy analysis. What are the economically interesting questions? The success or failure of any methodology hinges on how well it answers substantive policy questions. Thus, it is helpful to have a list in front of us to examine which questions are addressed or ignored by different approaches.
2.1 Policy Evaluation Problems and Criteria of Interest
Three broad classes of policy evaluation problems arise in economics. Policy evaluation problem one is:
P1 Evaluating the Impacts of Implemented Interventions on Outcomes Including Their Impacts on the Well-Being of the Treated and Society at Large
It is useful to distinguish objective or public outcomes that can in principle be measured by all external observers from “subjective” outcomes that are the evaluations of the agents experiencing treatment (e.g. patients) or the agents prescribing treatment (e.g., physicians). Objective outcomes are intrinsically ex post (“after the fact”) in nature. The literature on program evaluation focuses on ex post objective outcomes.
The structural literature studies both subjective and objective outcomes. Subjective outcomes can be ex ante (“anticipated”) or ex post. The outcome of a medical trial produces both a cure rate and the pain and suffering of the patient. Ex ante anticipated pain and suffering from a procedure may be different from ex post realized pain and suffering. A similar distinction arises in an analysis of the returns to schooling. Monetary returns are only part of total benefits which include important elements of psychic cost.12 Ex ante evaluations of outcomes by agents may differ from their ex post evaluations. Thus in advance of going to school, students may have expectations about rewards and costs that differ from their realizations. Expected rewards govern responses to market incentives. The impacts in P1 include individual level or population level counterfactuals and their valuations. “Well-being” in P1 includes the valuations of the outcomes of interventions by the agents being analyzed or other parties (e.g., the parents of the agent or “society” at large). They may be ex ante or ex post, and both are of interest in evaluating policy. Regret and anticipation are important aspects of public approval of policies.
P1 is the problem of internal validity. It is the problem of identifying the impacts of an intervention conducted in a given environment. Solving just this problem can be a challenging task and good answers are valuable. However, most economic policy evaluation is conducted with an eye toward the future and toward informing decisions about new policies and applications of old policies to new environments.
There is a second problem frequently encountered in policy analysis.
P2 Forecasting the Impacts (Constructing Counterfactual States) of Interventions Implemented in One Environment in Other Environments, Including Impacts on Well-Being
This is the problem of external validity: taking a treatment parameter or a set of parameters identified in one environment to another environment.13
The most ambitious problem is forecasting the effects of a new policy, never previously experienced:
P3 Forecasting the Impacts of Interventions (Constructing Counterfactual States Associated with Interventions) Never Historically Experienced, Including Their Impacts on Well-Being
P3 is a problem that economic policy analysts have to solve daily. Structural econometrics addresses this question. The program evaluation approach does not.
2.2 A Prototypical Economic Model for Policy Evaluation
Abstract discussions of policy evaluation problems become very tedious very fast. To be specific and to keep the discussion focused, consider the following version of the Roy model, which is a useful framework for policy evaluation.14 The Roy model and its extensions undergird a huge literature in microeconometrics.15 It was applications of the Roy model that fueled the flight from structural econometrics in the 1980s.
The Roy model is a model of hypothetical outcomes. Economic theory defines the space of possible counterfactual outcomes. It also specifies agent decision rules. It executes Task 1 of Table 1.
Roy (1951) considered an economy where agents face two potential outcomes (Y0, Y1) with distribution FY0,Y1(y0, y1) where “0” refers to the no treatment state and “1” refers to the treated state and (y0, y1) are particular values of random variables (Y0, Y1). More generally, the set of potential outcomes is where is the set of indices of potential outcomes. In the Roy model . I focus on two outcome models to simplify the exposition. In the application of Gronau (1974) and Heckman (1974), Y0 is the value of nonmarket time, and Y1 is the value of market time. In Willis and Rosen (1979), Y0 is the present value of high school earnings, and Y1 is the present value of college earnings. In the application of Tunali (2000), Y0 and Y1 are incomes in two regions. The central question recognized in this literature is that analysts observe either Y0 or Y1, but not both, for any person. In the program evaluation literature, this is called the evaluation problem.
In addition to this problem, there is the selection problem. The values of Y0 or Y1 that are observed are not necessarily a random sample of the potential Y0 or Y1 distributions. In the original Roy model, an agent selects into sector 1 if Y1 > Y0. Let D be an indicator or dummy variable. Then
| (1) |
where “1” is a function that is 1 if the condition in the argument holds and is 0 otherwise.
A variety of more general decision rules have been considered in the structural literature. A simple generalization of the Roy model adds cost C. This can be thought of as a cost of moving from “0” to “1”, e.g., tuition in the Willis-Rosen model, costs of work in the Gronau-Heckman model, or costs of migration in the Tunali model. The decision rule becomes
| (2) |
This framework defines a set of counterfactual outcomes and costs (Y0, Y1, C) with distribution FY0,Y1,C(y0, y1, c) and a mechanism for selecting which element of (Y0, Y1) is observed for any person. The outcome observed for any person, Y , can be written as
| (3) |
This representation is the Quandt (1958, 1972) switching regression framework.
Agents may make their choices under imperfect information. Let denote the agent’s information. In advance of participation, the agent may be uncertain about all components of (Y0, Y1, C). The expected benefit is . Then
| (4) |
Moreover, the decision maker selecting “treatment” may be different than the person who experiences the outcomes (Y0, Y1). Thus parents may make schooling decisions for their children; doctors may make treatment decisions for patients. More generally, decisions to participate may entail joint approval of all parties.16
The ex post objective outcomes are (Y0, Y1). The ex ante outcomes are and . The ex ante subjective evaluation is ID. The ex post subjective evaluation is Y1 − Y0 − C. Agents may regret their choices because realizations may differ from anticipations.
The ex ante vs. ex post distinction is essential for understanding behavior. In environments of uncertainty, agent choices are made in terms of ex ante calculations. Yet the treatment effect literature largely reports ex post returns. For example, the recent literature on the returns to schooling reports ex post returns (Autor, Katz, and Kearney, 2005; Katz and Autor, 1999; Katz and Murphy, 1992). Yet it is the analysis of ex ante returns that is needed to understand why, over time, responses to increases in ex post returns to schooling have been so sluggish.17
Carneiro, Hansen, and Heckman (2001, 2003), Cunha, Heckman, and Navarro (2005, 2006) and Cunha and Heckman (2007) develop econometric methods for distinguishing ex ante from ex post evaluations of social programs. Abbring and Heckman (2007) provide an extensive survey of this literature.18
In the language of the program evaluation literature, Y1 − Y0 is the individual level treatment effect. It is also the Marshallian ceteris paribus causal effect. Because of the evaluation problem, it is generally impossible to identify individual level treatment effects (Task 2). Even if it were possible, Y1 − Y0 does not reveal the ex ante subjective evaluation ID or the ex post assessment Y1 − Y0 − C.
Economic policies can operate through changing (Y0, Y1) or through changing C. Thus, in the college going example, policies may reduce tuition costs or reduce commuting costs (Card, 2001). They may tax future earnings. The structural approach considers policies affecting both returns and costs.19
2.3 Population Parameters of Interest
Because it is generally impossible to identify individual-level treatment effects, analysts typically seek to identify parameters defined at the population level. Conventional parameters include the Average Treatment effect (ATE = E(Y1 − Y0)), the effect of Treatment on The Treated (TT = E(Y1 − Y0 | D = 1)), or the effect of Treatment on the Untreated (TUT = E(Y1 − Y0 | D = 0)).
However, in addressing economic policy evaluation questions, a variety of other population level parameters are often more interesting. In positive political economy, the fraction of the population that perceives a benefit from treatment is of interest. This is called the voting criterion and is
In gauging support for a policy in place, the percentage of the population that ex post perceives a benefit may also be of interest: Pr(Y1 − Y0 − C > 0).
More generally, for evaluation of the distribution of welfare, knowledge of the ex ante and ex post joint distributions of outcomes are of interest.20 Because of the evaluation problem, it is very difficult to identify the joint distribution because we generally do not observe Y0 and Y1 together. This problem plagues all methodologies including social experiments.21
Determining marginal returns to a policy is a central goal of economic analysis. In the generalized Roy model, the margin is specified by people who are indifferent between “1” and “0”, i.e., those for whom ID = 0. The mean effect of treatment for those at the margin of indifference is
I discuss approaches for identifying this parameter in Section 3.
2.4 Treatment Effects Versus Policy Effects
Different policies can affect treatment choices and outcomes differently. Each of the population-level treatment effects discussed in the previous subsection can be defined for different policy regimes. Economists are often more interested in the effects of policies on outcomes than in conventional treatment effects.
To illustrate this point, consider the Policy Relevant Treatment Effect (Heckman and Vytlacil, 2001c) which extends the Average Treatment Effect by accounting for voluntary participation in programs. It is designed to address problems P2 and P3. Let “b” represent a baseline policy (“before”) and “a” represent a policy being evaluated (“after”). Let Ya be the outcome under policy a, while Yb is the outcome under the baseline. () and () are outcomes under the two policy regimes.
Policy invariance facilitates the job of answering problems P2 and P3. If some parameters are invariant to policy changes, they can be safely transported to different policy environments. Structural econometricians search for policy invariant “deep parameters” that can be used to forecast policy changes.22
Under one commonly invoked form of policy invariance, policies keep the potential outcomes unchanged for each person: , , but affect costs (Ca ≠ Cb).23 A tuition policy in the absence of general equilibrium effects is an example. Invariance of this type rules out social effects including peer effects and general equilibrium effects. Let Da and Db be the choice taken under each policy regime. Invoking invariance of potential outcomes, the observed outcomes under each policy regime are Ya = Y1Da+Y0(1−Da) and Yb = Y1Db+Y0(1−Db). The Policy Relevant Treatment Effect (PRTE) is
This is the Benthamite comparison of aggregate outcomes under policies “a” and “b”.24 PRTE extends ATE by recognizing that policies affect incentives to participate (C) but do not force people to participate. Only if C is very large under b and very small under a, so there is universal nonparticipation under b and universal participation under a, would ATE and PRTE be the same parameter.
2.5 The Structural Approach Versus the Program Evaluation Approach
The recent literature on program evaluation in economics draws on a model of counterfactuals and causality attributed to Donald Rubin by Paul Holland (1986).25 It defines causality using experimental manipulations and thereby creates the impression in the minds of many followers of this approach that random assignment is the most convincing way to identify causal models.
Neyman and Rubin postulate counterfactuals .26 They do not develop choice mechanisms that determine which outcome is selected or the subjective evaluations of treatments. There is no discussion of the mechanisms producing the outcomes studied or the relationship between outcomes and choice mechanisms.
Rubin (1986) invokes a portion of the traditional econometric invariance assumptions developed by Hurwicz (1962).27 Since he does not develop models for choice or subjective evaluations, he does not consider the more general invariance conditions for both objective and subjective evaluations that are features of the structural literature.28 The range of issues covered by the two approaches is given in Table 2.29
Table 2.
Comparison of the Aspects of Evaluating Social Policies that are Covered by the Neyman-Rubin Approach and the Structural Approach
| Neyman-Rubin Frame- work |
Structural Framework | |
|---|---|---|
| Counterfactuals for objective outcomes (Y0, Y1) | Yes | Yes |
| Agent valuations of subjective outcomes (ID) | No (choice-mechanism implicit) |
Yes |
| Models for the causes of potential outcomes | No | Yes |
| Ex ante versus ex post counterfactuals | No | Yes |
| Treatment assignment rules that recognize the vol- untary nature of participation |
No | Yes |
| Social interactions, general equilibrium effects and contagion |
No (assumed away) | Yes (modeled) |
| Internal validity (problem P1) | Yes | Yes |
| External validity (problem P2) | No | Yes |
| Forecasting effects of new policies (problem P3) | No | Yes |
| Distributional treatment effects | Noa | Yes (for the general case) |
| Analyze relationship between outcomes and choice equations |
No (implicit) | Yes (explicit) |
An exception is the special case of common ranks of individuals across counterfactual states: “rank invariance.” See the discussion in Abbring and Heckman (2007).
The Neyman-Rubin model does not consider many issues discussed in structural econometrics. It is at best an incomplete introduction to some of the important issues in evaluating social policies.30 The analysis in Rubin’s 1974 and 1978 papers is a dichotomy between randomization and non-randomization, and not an explicit treatment of particular selection mechanisms in the non-randomized case as is developed in the structural literature.
The statisticians who have had the greatest impact on the program evaluation literature in economics conflate the two tasks stated in Table 1. The discussion of Holland (1986) illustrates this point and the central role of the randomized controlled trial to the Holland-Rubin analysis. After explicating the “Rubin model,” Holland makes a very revealing claim: there can be no causal effect of gender on earnings because analysts cannot randomly assign gender. This statement confuses the act of defining a causal effect (a purely mental act performed within a model) with empirical difficulties in estimating it.31 The local average treatment effect “LATE” parameter of Imbens and Angrist (1994), discussed in Section 3, follows in this tradition and uses instrumental variables as surrogates for randomization. LATE is defined by an instrument and conflates tasks 1 and 2 of Table 1. In Section 3, I present a framework that defines the LATE parameter within the generalized Roy model discussed in Subsection 2.2 that separates issues of definition of parameters from issues of identification.
2.6 Identifying Policy Parameters
The structural approach to policy evaluation addresses policy evaluation questions P1-P3 by estimating models for Y0, Y1, and C in different economic environments. Commonly used specifications write
| (5) |
32 where (X, Z) are observed by the analyst, and U0, U1, UC are unobserved. Economic theory specifies the ingredients in Z and X. In general, there is no “objective” way to choose these conditioning variables. Any argument for inclusion or exclusion of variables has to be made by an appeal to theory — implicit or explicit.
To simplify notation, I define Z to include all of X. Variables in Z not in X are instruments. Write where and . In this notation, choice equation (3) can be expressed as
| (6) |
In the early literature that implemented this approach μ0(X), μ1(X), and μC(Z) were assumed to be linear in the parameters, and the unobservables were assumed to be normal and distributed independently of X and Z.
The caricature of the structural approach in the recent program evaluation literature is that linearity and normality are essential to this approach. In truth, the essential aspect of the structural approach is joint modeling of outcome and choice equations. Structural econometricians have developed nonparametric identification analyses for the Roy and generalized Roy models. See Heckman and Honoré (1990), Heckman (1990), Ahn and Powell (1993), Andrews and Schafgans (1998), and Das, Newey, and Vella (2003). The field has moved well beyond the parametric functional forms used in the early papers that were the targets of the 1980’s criticism. Traditional distributional and parametric assumptions are relaxed in the recent structural econometric literature. (See Ackerberg, Benkard, Berry, and Pakes, 2007; Athey and Haile, 2007; Matzkin, 1992, 1993, 1994, 2007, 2010a,b; Powell, 1994; Vella, 1998; Abbring and Heckman, 2007; and Keane et al., 2010; for reviews.)
As an illustration of the benefits of the structural approach for solving policy problem P3, consider the analysis of college choice by Cameron and Taber (2004). Suppose that one seeks to know the effects of increases in the expected gross returns to college on college choices. From equation (6), if one knows the effects of variations in tuition (C) on college choices, one can use the choice outcomes associated with variations in C to accurately predict the response to changes of equal magnitude (in opposite sign) in expected mean gross returns, even if returns to schooling have never varied in the past.
2.7 Marschak’s Maxim and the Relationship Between the Structural Economics Literature and the Program Evaluation Literature: A Synthesis
Structural models make explicit the preferences and constraints which govern individual decisions, the rules of interaction among agents in market and social settings, and the sources of variability across agents. These features facilitate finding answers to policy questions P1–P3. They are absent from the program evaluation literature.
At the same time, that literature makes fewer statistical assumptions in terms of independence, functional form, exclusion and distributional assumptions than the standard structural estimation literature in econometrics. This is an attractive feature of the program evaluation approach.33 The greater simplicity of its estimation schemes fosters transparency, replicability, and sensitivity analyses.34 While the structural economics literature has advanced greatly in recent years in terms of producing a robust version of its product, it is an unpleasant fact that fully-specified structural models are often harder to compute. It is more difficult to replicate the estimates from them and to test the sensitivity of estimates to assumptions.
The two approaches can be reconciled by noting that for many policy questions, it is not necessary to identify fully specified models to answer a range of policy questions. It is often sufficient to identify policy-invariant combinations of structural parameters. These combinations are often much easier to identify (i.e., require fewer and weaker assumptions), and do not require knowledge of the particular individual structural parameters that form the combination.
Marschak (1953) recognized that the answers to many policy evaluation questions do not require knowledge of all of the component parts of full structural models. I call this principle Marschak’s Maxim in honor of his insight. Consider estimating the marginal effect of policy expansions. The traditional structural approach identifies the component parts of E(Y1 − Y0 | ID = 0) constructed from estimates of the parameters of equations (5) and (6) and assembles them to estimate the marginal effect of the policy expansion (see Björklund and Moffitt, 1987).
In the next section, I exposit an approach that is consistent with Marschak’s Maxim that directly identifies the combination of parameters that define E(Y1 − Y0 | ID = 0) to solve policy problems, rather than identifying the component parts of the structural model and building it up from the components. Marschak’s Maxim is an application of Occam’s Razor to policy evaluation.35
3 Using Economics to Interpret What LATE Estimates and to Make It Useful For Evaluating a Broad Range of Policies
This section presents an example of an approach to policy evaluation that implements Marschak’s Maxim in the context of LATE. It makes the implicit economics in LATE explicit and thereby expands the range of policy questions that LATE can address.
In the economic theory of policy evaluation, a comparison between marginal benefits and marginal costs determines the optimal size of social programs. For example, to evaluate the optimality of a policy that promotes expansion in college attendance, analysts need to estimate the return to college for the marginal student, and compare it to the marginal cost of the policy. This task requires that analysts identify marginal returns.
In the spirit of the program evaluation literature, in the following discussion, I ignore general equilibrium effects, and I do not emphasize the ex ante and ex post distinction. Both topics are addressed in many papers in the structural approach. To simplify the notation, I keep the conditioning variables X implicit unless it clarifies matters by making them explicit. I follow standard conventions and denote random variables by capital letters and their realizations by the corresponding lower case letters. Thus Z = z means that random variable Z takes the value z. Z is a vector with K components, Z = (Z1, … , ZK). zj means a particular realization of Z, i.e., . I assume for simplicity that all means are finite.
The equation for ex post outcome Y as a function of participation status is
| (7) |
where D is a dummy variable indicating participation in a program, β is the individual return to participation or treatment effect and ε is an error term that is unobserved by the analyst. Equation (7) is one representation of the Quandt switching regression model (3). In terms of counterfactual notation, α = μ0, ε = U0 and Y0 = μ0 + ε, and β = (Y1 − Y0) = μ1 − μ0 + U1 − U0.
Estimating marginal returns to a policy that changes D is a relatively simple task if the effect of the policy is the same for everyone (conditional on X). This is the case when U1 − U0 = 0, and ε = U0 = U1. In this case, the mean marginal and average returns are the same for all people with the same X.
The recent literature on policy evaluation allows for the possibility that β varies among people even after conditioning on X. Denoting the mean of β by , the outcome equation can be written as
| (8) |
where .36 If β is uncorrelated with D, the only new econometric problem that arises in the analysis of (8) that is not present in the traditional analysis of (7) is that the error term is heteroscedastic. As in the case where β is a common parameter shared by everyone with the same X, the main econometric problem for inference about is that D is correlated with ε.37
β is statistically independent of D if, given X, agents cannot anticipate their ex post idiosyncratic gains from participation so is independent of D because it is not in the agent’s information set . Another reason why β might be independent of D is that agents know , but do not act on it in choosing D. In both cases, mean marginal returns are the same as mean average returns. Under standard conditions, application of instrumental variables identifies .38 One does not have to specify the model by which D is selected. All valid instruments identify .
The recent literature analyzes the less conventional case where agents know and make choices about D with at least partial knowledge of β = Y1 − Y0, and the agent knows more about Y1 − Y0 than what is in the observing economists’ conditioning set (X, Z). Instrumental variables (IV) do not in general estimate and instrumental variables estimators using different instruments have different probability limits.39 Structural selection models can estimate the distribution of β (and hence ) and answer a range of the public policy evaluation questions discussed in Section 2 but under assumptions that are held to be “incredible” in the program evaluation literature.40 Angrist and Pischke (2008, 2010) offer the Local Average Treatment Effect (LATE) as a “credible” alternative to structural methods.
Under the conditions reviewed in the next subsection, Imbens and Angrist (1994) show that instrumental variable estimators identify LATE, which measures the mean gross return to treatment for individuals induced into treatment by a change in an instrument. The LATE parameter is widely interpreted as estimating the mean return at the margin defined by manipulation of the instrument.
In general, LATE is not the same as , but it might be all that is needed to evaluate any particular policy. The key question is “what question does LATE answer?” Unfortunately, the people induced to go into state 1 (D = 1) by a change in any particular instrument need not be the same as the people induced to go to state 1 by policy changes other than those corresponding exactly to the variation in the instrument. A desired policy effect may not directly correspond to the variation captured by the IV. The people induced to change state by the instrument are not identified in LATE. Widely held intuitions about what IV identifies break down in this case since different instruments identify different parameters. Moreover, if there is a vector of instruments that generates choices and the components of the vector are intercorrelated, IV estimates using the components of Z as instruments, one at a time, do not, in general, identify the policy effect corresponding to varying that instrument, keeping all other instruments fixed, the ceteris paribus effect of the change in the instrument. Recent research that builds on and improves LATE shows how to use the generalized Roy model implicit in LATE to estimate the mean marginal returns to alternative ways of producing marginal expansions of programs when variation in the available instruments does not correspond exactly to the variation induced by proposed policies.41 This research also enables analysts to determine the people who are affected by changes in instruments. I first review LATE and then consider recent extensions of it.
3.1 LATE
LATE is defined by the variation of an instrument. The instrument in LATE plays the role of a randomized assignment. Indeed, randomized assignment is an instrument.42 Using the notation of Section 2, Y0 and Y1 are potential ex post outcomes. Instrument Z assumes values in . D(z) is an indicator of hypothetical choice representing what choice the individual would have made had the individual’s Z been exogenously set to z. D(z) = 1 if the person chooses (is assigned to) 1. D(z) = 0, otherwise. One can think of the values of z as fixed by an experiment or by some other mechanism independent of (Y0, Y1). All policies are assumed to operate through their effects on Z. It is assumed that Z can be varied conditional on X.
Imbens and Angrist (1994) make three assumptions to define LATE. Their first assumption is an instrumental variables assumption formulated in terms of a model of counterfactuals:
where “⫫” denotes independence, and A ⫫ B | X means A is independent of B conditional on X. are random variables defined over the population. Assumption (IA-1) states that the values of potential outcomes and potential choices are independent of Z (conditioning on X).
Imbens and Angrist also assume a rank condition:
This says that the distribution of P(Z) = Pr(D = 1 | Z) is nondegenerate conditional on X.
To make IV identify a treatment effect, they invoke a monotonicity condition on the D(z) at the individual level.
This condition is a statement across people. z1 and z2 are two different values of vector Z. Fixing the instrument at two values z1 and z2 moves choices across people in the same direction (either in favor of 1 or against it). This condition does not require that for any other two values of Z, say z3 and z4, the direction of the inequalities on D(z3) and D(z4) have to be ordered in the same direction as they are for D(z1) and D(z2). It only requires that the direction of the inequalities are the same across people. Thus for any person, D(z) need not be monotonic in z.43
Under these conditions, Imbens and Angrist establish that for two distinct values of Z, z1 and z2, IV applied to (7) identifies
if the change from z1 to z2 induces people into the program (D(z2) ≥ D(z1)).44 This is the mean return to participation in the program for people induced to switch treatment status by the change from z1 to z2.45
LATE does not identify which people are induced to change their treatment status by the change in the instrument. It also leaves unanswered many of the policy questions discussed in Section 2. For example, if a proposed program changes the same components of vector Z as used to identify LATE but at different values of Z (say z4, z3), LATE(z2,z1) does not identify LATE(z4, z3). If the policy operates on different components of Z than are used to identify LATE, one cannot safely use LATE to identify marginal returns to the policy. LATE answers a version of policy problem P1 for objective outcomes, but ignores P2 and P3. It does not, in general, identify treatment on the treated, ATE or the other parameters discussed in Section 2.
3.2 Making Explicit the Implicit Economics of LATE
In a fundamental paper, Vytlacil (2002) shows that the LATE model is equivalent to a nonparametric version of the generalized Roy model. The Imbens-Angrist conditions imply the generalized Roy model, and the generalized Roy model implies the LATE model. Vytlacil’s analysis is the basis for defining LATE abstractly within a well-posed economic model and separating the task of definition (Task 1 of Table 1) from the task of identification (Task 2 of Table 1). Vytlacil’s analysis clarifies the implicit economic assumptions of LATE, what features of the generalized Roy model LATE estimates, and what policy questions LATE addresses. It also extends the range of policy questions that LATE can answer.
By Vytlacil’s theorem, the Imbens-Angrist conditions imply (and are implied by) a continuous latent variable discrete choice model, which represents the individual’s decision to enroll in the program being studied. Recall that ID (in equation (4)) is the net benefit to the individual of enrolling in the program. A person takes treatment D = 1 (e.g., goes to college) if ID > 0; otherwise D = 0. Vytlacil shows that the treatment choice equation underlying LATE can be expressed in terms of observed (Z) and unobserved (V) variables that can be represented by equation (6): ID = μD(Z) − V and D = 1 if ID > 0; D = 0 otherwise, where V is a continuous random variable with distribution function FV .46 μD(Z) is defined in the discussion preceding equation (6). V may depend on U0 and U1 in a general way.47
LATE assumes that (U0, U1, V) are independent of Z given X. This relaxes the independence assumption (between X and the unobservables) that was frequently maintained in the early structural literature. The counterfactual choice indicator is generated by choice equation (6): D(z) = 1(μD(z) > V). This representation makes explicit the implicit random variable (V) used to define D(z) in the analysis of Imbens and Angrist, and the independence between Z and V that is part of condition (IA-1).
The additive separability between μD(Z) and V in the latent index model (6) plays an essential role in LATE. Model (6) is far from the most general possible representation of choices. If choice responses to variations in Z are heterogeneous in a general way, the same change in Z could lead some persons toward and other persons away from participation in the program, and the separability between μD(Z) and V in (6) would break down. Another way to say this is that monotonicity condition (IA-3) would be violated.48
To understand the economic model implicit in LATE, let P(z) denote the probability of taking treatment (e.g., attending college, D = 1) conditional on Z = z: P (z) ≡ Pr(D = 1|Z = z). From equation (6), P(z) = Pr(μD(z) > V) = FV(μD(z)). P(z) is a monotonic transformation of the mean utility function μD(z) in discrete choice theory. P(z) is sometimes called the propensity score.
Define random variable UD = FV(V), which is uniformly distributed over the interval [0, 1] and thus the pth quantile of UD is p, i.e., the proportion of UD that is p or lower. Different values of UD correspond to different quantiles of V. We can rewrite (6) using FV(μD(Z)) = P(Z) so that
| (9) |
From the estimated propensity score, one can identify the ex ante net benefit ID up to scale. Thus, one can determine for each value of Z = z, what proportion of people perceive that they will benefit from the program and the intensity of their benefit. Using the nonparametric identification analyses of Cosslett (1983), Manski (1988), Klein and Spady (1993), and Matzkin (1992, 1993, 1994, 2007), one can nonparametrically identify the distribution of V and the mean valuation μD(Z) (up to scale).49 Thus, from agent choices, one can supplement the information in LATE and ascertain ex ante subjective evaluations.
As a consequence of Vytlacil’s theorem, the LATE assumptions imply the selection model representation (i.e., the generalized Roy model) and using the selection model representation, one can establish that E(Y | Z = z) = E(Y | P(Z) = P(z)). Under the LATE assumptions, Z enters the model only through its effect on P(Z). This property is called index sufficiency where P(Z) is the index. It is a central property of the LATE model.
As a consequence of Vytlacil’s theorem, one can define LATE(z2, z1) using the latent variable UD and the values taken by P(Z) when Z = z1 and Z = z2. To do so, I use the property that the Z enter the model only through P(Z).
| (10) |
This is the mean gross return to persons whose UD ∈ [P(z1), P(z2)].50
The LATE parameter can be defined within the generalized Roy model, without reference to an instrument. Thus the LATE produced by economic theory can be expressed as
| (11) |
the mean gross return to persons whose . This is a theoretical construct (Task 1). Proceeding in this fashion, we separate Task 1 of Table 1 from Task 2. A choice of two values of Z (z1 and z2) picks specific values of [] that identify the model-generated LATE from data (say Pr(D = 1 | Z = z1) = p1 = uD and ). This is Task 2.
3.2.1 The Surplus From Treatment and the Marginal Treatment Effect
Using Vytlacil’s theorem, it is possible to understand more deeply what economic questions LATE answers. Toward that end, it is useful to introduce the Marginal Treatment Effect (MTE) and show how it can be used to unify the literature on treatment effects and to make explicit the economic content of LATE.
For P(Z) = p, the mean gross gain of moving from “0” to “1” for people with UD less than or equal to p is
| (12) |
51 The first equality follows from the LATE assumption that (Y0, Y1) are independent of the instruments Z (IA-1) and hence any functions of Z. The second equality follows from the definition of the propensity score. The mean gross gain in the population (or gross surplus S(p)) that arises from participation in the program for people whose UD is at or below p is the product of the gain to people whose UD is at or below p and the proportion of people whose UD is at or below p: E(Y1 − Y0 | p ≥ UD)p = S(p).
Using Vytlacil’s theorem, we can move from the theory (Task 1 of Table 1) to the data (Task 2 of Table 1) to identify the gross surplus S(p). The mean of Y given P(Z) = p depends on the gross surplus:
| (13) |
We can identify the left-hand side of (13) for all values of p in the support of P(Z).52 This is Task 2 in Table 1. It is not necessary to impose functional forms to obtain this expression, and one can avoid one of the criticisms directed against 1980’s structural econometrics. The surplus can be defined for all values of p ∈ [0, 1] whether or not the model is identified.
If p is increased by a small change in z, some people near the margin of indifference who chose not to participate in the program would now choose to participate. Small variations in p identify the mean marginal gross return to a policy expansion that changes P(Z). Formally, the marginal increment in outcomes is
| (14) |
53 This is the mean marginal gross return to treatment for persons indifferent between participation in the program or not at mean scale utility level p = UD, and it is also the marginal change in the gross surplus. The sample analogue of (14) is the local instrumental variable (LIV) estimator of Heckman and Vytlacil (1999, 2005).54 Adopting a nonparametric approach to estimating E(Y | P(Z) = p) avoids extrapolation outside of the sample support of P(Z) and produces a data sensitive structural analysis.
A generalization of this parameter defined for other points of evaluation of uD is the Marginal Treatment Effect (MTE):
This parameter is very useful in understanding how to go from IV estimates to policy effects and in interpreting the economics of LATE.55 Recall that UD is a uniform random variable in the interval [0, 1], so that MTE for different uD values shows how the mean gross returns to the program vary with different quantiles of the unobserved component of the utility of participation, UD.
Expression (13) can be simplified to
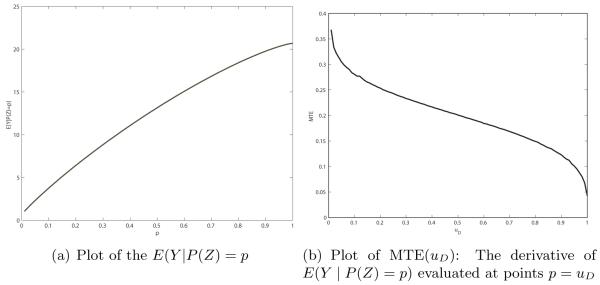
| (15) |
where . Figure 1 plots E(Y | P(Z) = p) (Figure 1(a)) and its derivative (Figure 1(b)) using values derived from a model discussed in Heckman and Vytlacil (2005). In this analysis, E(Y | P(Z) = p) increases at a diminishing rate in p, so MTE(uD) is decreasing in uD, i.e., there are diminishing returns to the marginal entrants attracted into the program by increasing P(z).
Figure 1.
Plots of E(Y|P(Z) = p) and the MTE derived from E(Y|P(Z) = p)
Source: Heckman and Vytlacil (2005)
Notice from (14) that persons with larger values of P(z) identify the return for those with larger values of UD, i.e., values of UD that make persons less likely to participate in the program. This is so because marginal increases in P(z) at high levels of P(z) induce those individuals with high UD values into treatment. This is a consequence of the economic choice model (9). Those with low values of UD already participate in the program for low values of P(z) = p. A marginal increase in P(z) starting from a high value has no effect on the participation decision of those with low values of UD. From LIV, it is possible to identify returns at all quantiles of UD within the support of the distribution of P(Z) to determine which persons (identified by the quantile of the unobserved component of the desire to take the treatment, UD) are induced to go into the treatment (D = 1) by a marginal change in P(z), i.e., analysts can define the margins of choice traced out by variations in different instruments as they shift P(z). This clarifies what empirical versions of LATE identify by showing that all instruments operate through P(z), and variations around different levels of P(z) identify different stretches of the MTE. I now develop this point.
3.2.2 The Fundamental Role of the Choice Probability in Understanding What Instrumental Variables Estimate When β Depends on D
For any two values of p, say p1 and p2, generated by two different values of Z, where p2 > p1,
where the last expression follows from the fact that Pr(p1 ≤ UD ≤ p2) = p2 − p1. Thus,
This expression can be obtained directly from equation (15). From the definition of LATE,
| (16) |
Thus LATE is the chord of the gross surplus function over the interval [p1, p2]. The model-generated LATE approximates MTE(uD) over an interval. By the mean value theorem, LATE(p2, p1) = MTE(uD(p2, p1)) where uD(p2, p1) is a point of evaluation and uD(p2, p1) ∈ [p1, p2]. The model-generated LATE can be identified if there are values of Z, say and such that and . Under standard regularity conditions
If we partition the support of uD into M discrete and exhaustive intervals
where uD,0 = 0 and uD,M = 1, we can define
where ηj = uD,j − uD,j−1. Thus
| (17) |
which is the counterpart to expression (15) when p = 1. It shows how mean income can be represented as a sum of incremental gross surpluses above E(Y0).
These expressions are derived from an underlying theoretical model. Whether or not the components can be identified from the data depends on the support of Pr(D = 1 | Z). If Pr(D = 1 | Z = z) assumes values at only a discrete set of support points, say p1 < p2 < ⋯ < pL, we can only identify LATE in intervals with boundaries defined by uD,ℓ = pℓ, ℓ = 1, … , L.
MTE(uD) and the model-generated LATE (10) are structural parameters in the sense that changes in Z (conditional on X) do not affect MTE(uD) or theoretical LATE. They are invariant with respect to all policy changes that operate through Z. Conditional on X, one can transport MTE and the derived theoretical LATEs across different policy environments and different data sets. These policy invariant parameters implement Marschak’s Maxim since they are defined for combinations of the parameters of the generalized Roy model. Instead of separately estimating the components of the selection model presented in Section 2.6, one can identify an interpretable marginal gross benefit function by using the derivative of E(Y | P(Z) = p).
This deeper understanding of LATE facilitates its use in answering out-of-sample policy question P3 for policies that operate through changing Z. Thus if one computes a LATE for any two pairs of values Z = z1, and Z = z2, with associated probabilities Pr(D = 1 | Z = z1) = P(z1) = p1 and Pr(D = 1 | Z = z2) = P(z2) = p2, one can use it to evaluate any other pair of policies and such that
and
Thus, one can use an empirical LATE determined for one set of instrument configurations to identify outcomes for other sets of instrument configurations that produce the same p1 and p2, i.e., one can compare any policy described by with any policy and not just the policies associated with z1 and z2 that identify the sample LATE. This is a powerful result and enables analysts to solve policy evaluation question P3 to evaluate new policies never previously implemented if they can be cast in terms of variations in P(Z) over the empirical support on Z.56
Variation in different components of Z produce variation in P(Z). Analysts can aggregate the variation in different components of Z into the induced variation in P(Z) to trace out MTE(uD) over more of the support of uD than would be possible using variation in any particular component of Z. The structural approach enables analysts to determine what stretches of the MTE different instruments identify and to determine the margin of UD identified by the variation in an instrument.
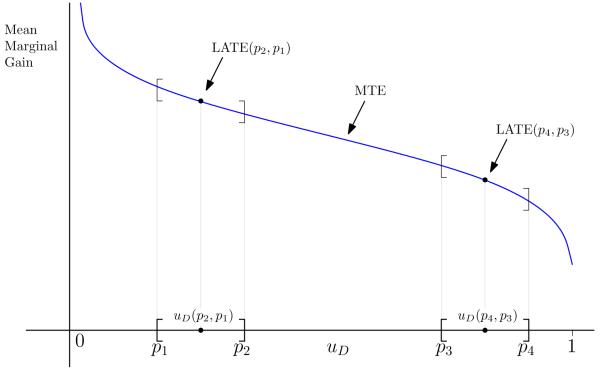
Figure 2 reproduces the MTE displayed in Figure 1(b) on a different scale. Consider values of instruments that are associated with P(z) = p2 and P(z) = p1 They identify the MTE at a value of uD in the interval uD ∈ [p1, p2], as depicted in the graph. This is LATE(p2, p1). If there is continuous variation in Z it could be used to trace out the entire interval of MTE for P(Z) ∈ [p1, p2], using LIV. Independent of any instrument, we can define the LATE and MTE using the underlying economic model. In this fashion, we separate the task of definition of parameters from the task of identifying them.
Figure 2.
MTE as a function of uD: What sections of the MTE different values of the instruments and different instruments approximate.
Instruments associated with higher values of P(Z), [p3, p4], identify the LATE in a different stretch of the MTE associated with higher values of uD. Thus different instruments can identify different parameters. Continuous instruments can identify entire stretches of the MTE while discrete instruments define the MTE at discrete points of the support (i.e., the LATE associated with the interval defined by the values assumed by P(Z)). As a consequence of Vytlacil’s Theorem, one can identify the intervals of uD implicit in using LATEs formed using different instruments.
If the MTE does not depend on uD, E(Y | P(Z) = p) = E(Y0) + (μ1 − μ0)p, and all instruments identify the same parameter: . In this case, MTE is a flat line parallel to the uD axis. This is the case traditionally assumed in the analysis of instrumental variables.
A test of whether MTE(uD) depends on uD, or a test of nonlinearity of E(Y | P(Z) = p) in p, is a test of the whether different instruments estimate the same parameter.57 The LATE model and its extensions overturn the logic of the Durbin (1954)–Wu (1973)–Hausman (1978) test for overidentification. Variability among the estimates from IV estimators based on different instruments may have nothing to do with the validity of any particular instrument, but may just depend on what stretch of the MTE they approximate.
3.3 All Treatment Effects Are Weighted Averages of the MTE
Using the economics implicit in LATE unifies and interprets the literature on treatment effects. All of the conventional treatment effects featured in the program evaluation literature can be written as weighted averages of the MTE or the structural LATEs where the weights can be estimated from the data over the sample support of P(Z). Thus for treatment effect e,
| (18) |
where he(uD) is a weighting function. For ATE, he(uD) = 1 and . Using the linearity of the integral, one can always break (18) into a sum of components over the intervals [uD,0, uD,1), [uD,1, uD,2), …, [uD,M−1, uD,M] to obtain
where uD,j > uD,j−1 > uD,j−2 > ⋯. By the mean value theorem,58 we may express each of the integrals in the sum as
for some . From (16) we obtain
Thus we may write expression (18) as
where . In the special case of ATE, and
where ηj = uD,j − uD,j−1.
The Policy Relevant Treatment Effect (PRTE), defined in Section 2, is
where , and is the distribution of P(Z) under policy b, and is the distribution of P(Z) under policy a.59 Using the mean value theorem, one can generate a counterpart expression in terms of LATEs.
The PRTE weights MTE(uD) by the change in the distribution of the probabilities of participation at different values of uD.60 Thus for a typical MTE as graphed in Figure 1(a), if a policy shifts the distribution of participants toward low uD values, it generates a positive PRTE, since MTE(uD) is higher for low uD values than it is for high uD values.
Notice that the same MTE(uD) can be used to evaluate the impacts of a variety of different policies. MTE(uD) is a structural function since it is invariant across policies that affect the distribution of the P(Z) but not the distribution of the potential ex post outcomes. We can evaluate the effect of new policies never previously experienced if we can characterize the distributions of P(Z) for those policies.
Table 3 displays the weights of the MTE that produce the traditional treatment parameters. All of the weights can be estimated from the distribution P(Z).61 There are corresponding expressions for the case of discrete support for P(Z) that can be obtained using the mean value theorem. The weights integrate to 1. When β is independent of D, MTE(uD) does not depend on , so all treatment parameters equal .
Table 3.
MTE Weights For Different Treatment Parameter and IVs. (Fp is the distribution of P. fP is its density.)
| Treatment Parameter Weights | |
|
| |
| IV Weights | for P(Z) as an instrument |
| for a general instrument J(Z)*, a function of Z | |
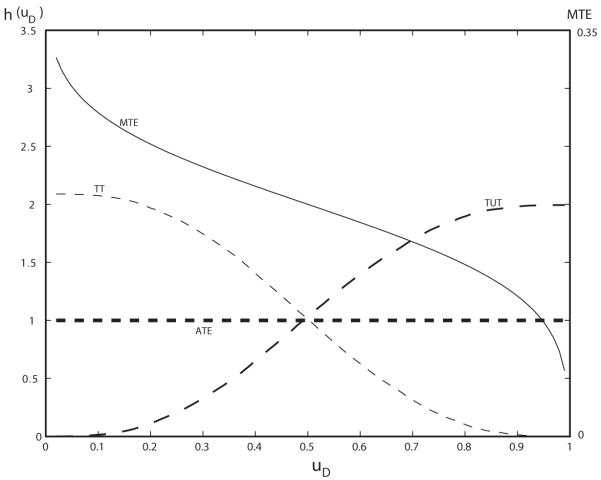
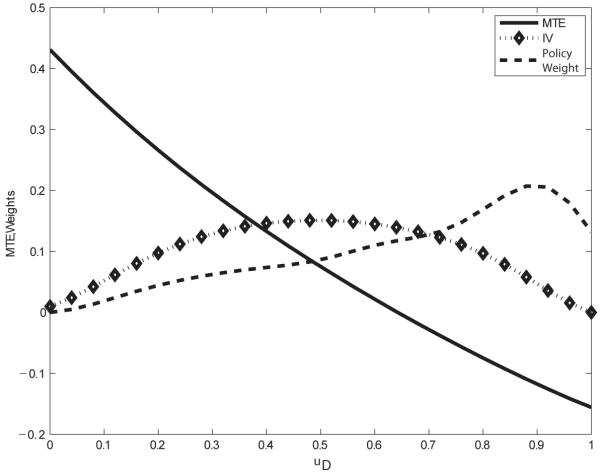
Figure 3 plots an MTE taken from the analysis of Heckman and Vytlacil (2005) and the weights for MTE associated with ATE, TT, and TUT for a case where β is not independent of D. ATE weights uD evenly. TT oversamples low values of uD (associated with persons more likely to participate in the program). TUT oversamples high uD. In this example, because MTE(uD) is decreasing in uD, TT > ATE > TUT.
Figure 3.
MTE and the weights for the marginal treatment effect for different parameters for the model graphed in Figure 1
Source: Heckman and Vytlacil (2005)
3.4 What Does Conventional IV estimate?
In most empirical studies, more than the two values of Z are used to construct IV estimates. For this case, Imbens and Angrist (1994) use weights developed by Yitzhaki (1989) to express IV as a weighted average of component LATEs defined for different values of the instruments. The weights used by Imbens-Angrist are positive for each component LATE for the special instrument they consider (P(Z) or some monotonic function of P(Z)). Since MTE(uD) may change sign over the interval uD ∈ [0, 1], the IV may be negative even if some portion of the MTE(uD) is positive. For general instruments that are not monotonic functions of P(Z), the output of IV is even more ambiguous. The IV weights can be negative over regions of uD ∈ [0, 1]. Thus an IV based on general instruments may have a sign opposite to the true causal effect as defined by the MTE. Even if each component of LATE is positive, in the general case IV can be negative. Negative components of MTE(uD) weighted by negative weights can generate a positive IV.
This analysis is constructive because the weights can be identified from the data. Analysts can ascertain whether or not the weights are negative and over what regions of uD. In this subsection I analyze the case where P(Z) is the instrument and the weights are positive. I analyze the general case in section 3.6 below.
To understand what IV identifies, consider a linear regression approximation of E (Y | P(Z) = p):
62 where
b is the same as the IV estimate of “the Effect” of D on Y using P(Z) as an instrument since Cov(P(Z), D) = Var(P(Z)).63
Using condition (IA-1) (in particular that P(Z) is independent of Y0), and expression (15), we obtain
| (19) |
Note that when MTE(uD) is constant in so that β is independent of D, the numerator of the preceding expression simplifies to
so . This is the traditional result for IV. In this case, the marginal surplus is the same as the average surplus for all values of p. Expression (19) arises because D depends on β (=Y1−Y0), something assumed away in traditional applications of IV. As a consequence, in general, the marginal surplus is not the average surplus.
An explicit expression for the numerator of (19) is
Reversing the order of the integration of the terms on the right-hand side and respecting the requirement that 0 < uD < p < 1, we obtain
where
64,65 An alternative expression for the weight is as the mean of left truncated P(Z):
which shows that the weight on the MTE(uD) is non-negative for all uD.
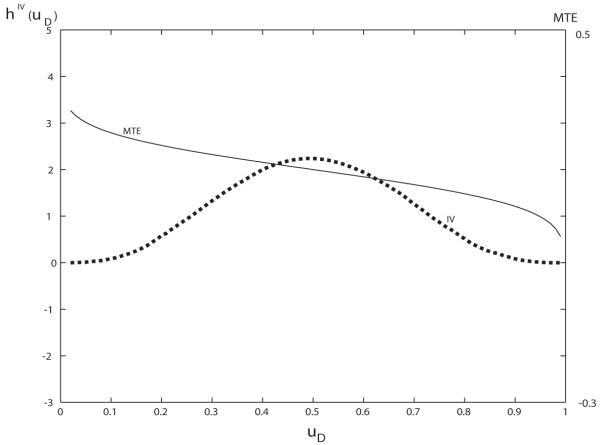
The weights can be estimated from the sample distribution of P(Z). The weights for P(Z) as an instrument have a distinctive profile. It is readily verified that they are non-negative, reach a peak at the mean of the distribution of P(Z), and are zero at the extremes uD = 0 and uD = 1. The weights integrate to 1.66 Figure 4 plots the IV weights and the MTE from a study by Heckman and Vytlacil (2005). Comparing the IV weights with the weights for different treatment effects enables analysts to determine how closely IV approximates any particular mean treatment effect.
Figure 4.
The MTE and IV weights as a function of uD.
Source: Heckman and Vytlacil (2005).
For discrete valued instruments mapped into P(z1) = p1 < P(z2) = p2 < ⋯ < P(zL) = pL,
where and fP(pt) is the probability that P(Z) = pt. For a proof, see Heckman, Urzua, and Vytlacil (2006) or Appendix B.
3.5 The Problem of Limited Support
Before turning to the analysis of general instruments, I consider the problem of limited support for P(Z) for the special instrument P(Z) used by Imbens and Angrist. Analysis of this simple case establishes principles that apply to more general instruments. While the various treatment parameters can be defined from the generalized Roy model, they may not necessarily be identified from the data. Both the nonparametric structural approach and the nonparametric program evaluation approach avoid the problem of extrapolating estimates outside the support of the data.67 The early literature in structural econometrics imposed strong functional forms (typically linearity) to obtain estimates.68 P(Z) may not be identified over the full unit interval. Thus the lowest sample value of P(Z) may exceed zero and the largest value of P(Z) may be less than 1.
In addition, P(Z) may only assume discrete values. This limits the identifiability of MTE. In this case, only LATE over intervals of uD ∈ [0, 1] can be identified from the values of P(Z) = P(z) associated with the discrete instruments.69
One approach to this problem developed by Manski (1990, 1995, 2003) is to produce bounds on the treatment effects. Heckman and Vytlacil (1999, 2000, 2001a,b, 2007b) develop specific bounds for the generalized Roy model that underlies the LATE model. The bounds developed in the literature are for conventional treatment effects and not for policy effects.
Carneiro, Heckman, and Vytlacil (2010) consider an alternative approach based on marginal policy changes. Many proposed policy changes are incremental in nature, and a marginal version of the PRTE is all that is required to answer questions of economic interest. When some instruments are continuous, it is possible under the conditions in their paper to identify a marginal version of PRTE (MPRTE). MPRTE is in the form of representation (18) where the weights can be identified from the data and the support requirements are more limited than the conditions required to identify PRTE for large changes in policies. Their paper presents a derivation of the weights for classes of policy expansions.70 Application of these data sensitive nonparametric approaches enables analysts to avoid one source of instability of the estimates of policy effects that plagued 1980s econometrics.
3.6 More General Instruments
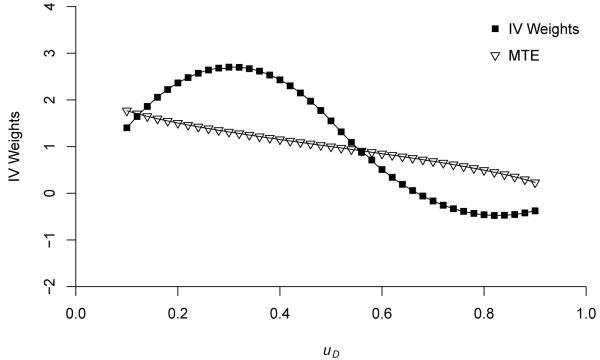
Typically, economists use a variety of instruments one at a time and not just P(Z) or some function of P(Z), or some function of P(Z), as an instrument and compare the resulting estimates (see, e.g, Card, 1999, 2001). When there is selection on the basis of gross gains 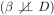 so that the marginal gross surplus is not the same as the average gross surplus, different instruments identify different parameters. IV is a weighted average of MTEs where the weights integrate to 1 and can be estimated from sample data. However, in the case of general instruments, the weights can be negative over stretches of uD.
so that the marginal gross surplus is not the same as the average gross surplus, different instruments identify different parameters. IV is a weighted average of MTEs where the weights integrate to 1 and can be estimated from sample data. However, in the case of general instruments, the weights can be negative over stretches of uD.
Consider using the first component of Z, Z1, as an instrument for D in equation (7). Suppose that Z contains two or more elements (Z = (Z1, … , ZK), K ≥ 2). The economics implicit in LATE informs us that Z determines the distribution of Y through P(Z). Any correlation between Y and Z1 arises from the statistical dependence between Z1 and P(Z) operating to determine Y .
The IV estimator based on Z1 is
Note, however, that choices (and hence Y) are generated by the full vector of Z operating through P(Z). The analyst may only use Z1 as an instrument but the underlying economic model informs us that the full vector of Z determines observed Y . Conditioning only on Z1 leaves uncontrolled the influence of the other elements of Z on Y . This is a new phenomenon in IV that would not be present if D did not depend on β(= Y1 − Y0). An IV based on Z1 identifies an effect of Z1 on Y as it operates directly through Z1 (Z1 changing P(Z1, … , ZK)) holding other elements in Z constant and indirectly through the effect of Z1 as it covaries with (Z2, … , ZK), and how those variables affect Y through their effect on P(Z).
A linear regression analogy helps to fix ideas. Suppose that outcome Q can be expressed as a linear function of W = (W1, … , WL), an L-dimensional regressor:
where E(ε | W) = 0. If we regress Q only on W1, we obtain in the limit the standard omitted variable result that the estimated “effect” of W1 on Q is
| (20) |
where φ1 is the ceteris paribus direct effect of W1 on Q and the summation captures the rest of the effect (the effect on Q of W1 operating through covariation between W1 and the other values Wℓ, ℓ ≠ 1). An analogous problem arises in using one instrument at a time to identify “the Effect” of Z1.
Thus if the analyst does not condition on the other elements of Z in using Z1 as an instrument, the margin identified by variations of Z1 does not in general correspond to variations arising solely from variations in Z1, holding the other instruments constant. The margin of choice implicitly defined by the variation in Z1 is difficult to interpret and depends on the parameters of the generalized Roy model generating outcomes as well as on the sample dependence between instrument Z1 and P(Z). Thus an IV based on Z1 mixes causal effects with sample dependence effects among the correlated regressors.71 In a study of college going, if Z1 and Z2 are tuition and distance to college, respectively, the instrument Z1 identifies the direct effect of variation in tuition on college attendance and the effect of distance to college on college attendance as distance covaries with tuition in the sample used by the analyst. This is not the ceteris paribus effect of a variation in tuition. It does not correspond to the answer needed to predict the effects of a policy that operates solely through an effect on tuition. In models in which D depends on β, the traditional instrumental variable argument that analysts do not need a model for D and can ignore other possible determinants of D other than the instrument being used, breaks down. To interpret which margin is identified by different instruments requires that the analyst specify and account for all of the Z that form P(Z). Since different economists may disagree on the contents of Z, different economists using Z1 on the same data will obtain the same point estimate but may disagree about the interpretation of the margin identified by variation in Z1.
To establish these points, note that as a consequence of Vytlacil’s theorem, Z enters the distribution of Y only through P(Z). Thus the conditional distribution of Y given Z1 = z1 operates through the effect of Z1 as it affects P(Z). That is a key insight from Vytlacil’s theorem. Thus
where gP(Z)|Z1 (p, z1) is the conditional density of P(Z) given Z1 = z1.72 Putting all of these ingredients together, and using (15), we obtain
Using this expression to compute , we obtain
This expression integrates the argument in the numerator with respect to uD, p, and z1 in that order. Reversing the order of integration to integrate with respect to p, z1, and uD in that order, we obtain
where
The weight integrates to 1 but can be negative over stretches of uD.73 At the extremes (uD = 0, 1), the weights are zero.
An illuminating way to represent this weight is
As uD is increased, the censored (by the condition P(Z) > uD) mean of (Z1 − E(Z1)) may switch sign, and hence the weights may be negative over certain ranges. Thus the IV estimator may have a sign opposite to the true causal effect (defined by the MTE).
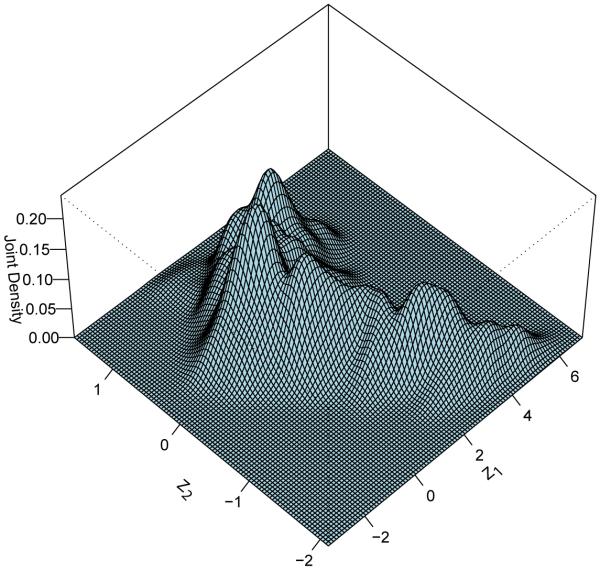
Figure 6 illustrates this possibility for the distribution of the data Z = (Z1, Z2) shown in Figure 5, where Z is continuously distributed. The support of the data only permits identification of P(Z) over the interval [0.1, 0.9]. Thus none of the conventional treatment parameters is identified. From LIV, we can identify the MTE over the interval [0.1, 0.9]. We can also identify the weights over this interval. For values of uD > 0.65, the weights are negative in this example. Thus it is possible that the IV based on Z1 can be negative even if the MTE is everywhere positive. Table 4, taken from Heckman, Urzua, and Vytlacil (2006) shows how three different distributions of Z for the same underlying policy-invariant model with the same ATE can produce very different IV estimates.
Figure 6.
MTE and IV weights for a general instrument Z1, a component of Z = (Z1, Z2).
Figure 5.
Joint density of instruments Z = (Z1, Z2)
Table 4.
IV estimator for three different distributions of Z but the same generalized Roy model.
| Data Distribution | IV | ATE |
|---|---|---|
| 1 | 0.434 | 0.2 |
| 2 | 0.078 | 0.2 |
| 3 | −2.261 | 0.2 |
This analysis elucidates the benefits and limitations of the method of randomized controlled experiments. Experiments that manipulate Z1 independently of other components of Z isolate the effects of Z1 on outcomes in comparison with the effects obtained by sample variation in Z1 correlated with other components of Z. Neither set of variations may identify the returns to any given policy unless the experimentally induced variation corresponds exactly to the variation induced by the policy. Economists can use experimental variation to identify the MTE. The features of a proposed policy are described by its effects on the PRTE weights as it affects the distribution of P(Z). Proceeding in this way, one can use experiments to address a range of questions beyond the effects directly identified by the experiment.
Using the implicit economic theory underlying LATE, economists can do better than just report an IV estimate. We can be data sensitive but not at the mercy of the data. We can determine the MTE (or LATEs) over the identified regions of uD in the empirical P(Z). We can also determine the weights over the empirical support of P(Z) to determine whether they are negative or positive. We can bound estimates of the unidentified parameters. (See Heckman and Vytlacil, 1999, 2001a,b, 2007b.) We can construct the effects of policy changes for new policies that stay within the support of P(Z) (see Carneiro, Heckman, and Vytlacil, 2010).
3.7 Policy Effects, Treatment Effects, and IV
A main lesson of this paper is that policy effects are not generally the same as treatment effects and, in general, neither are produced from IV estimators. Since randomized assignments of components of Z are instruments, this analysis also applies to the output of randomized experiments. The economic approach to policy evaluation formulates policy questions using well-defined economic models. It then uses whatever statistical tools it takes to answer those questions. Policy questions and not statistical methods drive analyses. Well-posed economic models are scarce in the program evaluation approach. Thus in contrast to the structural approach, it features statistical methods over economic content. “Credibility” in the program evaluation literature is assessed by statistical properties of estimators and not economic content or policy relevance.
We can do better than hoping that an instrument or an estimator answers policy problems. By recovering economic primitives, we can distinguish the objects various estimators identify from the objects needed to address policy problems and can address those problems. Constructing the PRTE is an example of this approach.74
Figure 7, taken from an analysis of the returns to attending college by Carneiro, Heckman, and Vytlacil (2009), plots the estimated weights for MTE from a marginal change in policy that proportionally expands the probability of attending college for everyone. The figure also plots the estimated MTE and the IV weight using P(Z) as an instrument. The IV weights and the policy weights are very different. The policy weights oversample high values of uD compared to the IV weights. Since the MTE is declining in uD, this translates into an IV estimate of .095 compared to a marginal policy effect of .015.75 The IV estimate would suggest a substantial mean marginal gross return. The true marginal policy effect is much lower. Since the MTE can be estimated (or approximated) from the data and the policy weights constructed from the data, one can produce more accurate policy forecasts using the economics of the model.
Figure 7.
MTE and Weights for IV and MPRTE in the Carneiro-Heckman-Vytlacil (2009) Analysis of the Wage Returns to College.
Source: Carneiro, Heckman, and Vytlacil (2009).
Notes: The scale of the y-axis is the scale of the MTE, not the scale of the weights, which are scaled to fit the picture. The IV is P(Z).
3.8 Multiple Choices
Imbens and Angrist analyze a two choice model. Heckman, Urzua, and Vytlacil (2006, 2010) and Heckman and Vytlacil (2007b) extend their analysis to an ordered choice model and to general unordered choice models.76
In the special case where the analyst seeks to estimate the mean return to those induced into a choice state by a change in an instrument compared to their next best option, the LATE framework remains useful (see Heckman, Urzua, and Vytlacil, 2006, 2010; Heckman and Vytlacil, 2007b). If, however, one is interested in identifying the mean returns to any pair of outcomes, unaided IV will not do the job. Structural methods are required.
In general unordered choice models, agents attracted into a state by a change in an instrument come from many origin states, so there are many margins of choice. Structural models can identify the gains arising from choices at these separate margins. This is a difficult task for IV without invoking structural assumptions. Structural models can also identify the fraction of persons induced into a state coming from each origin state. IV alone cannot. See Heckman and Urzua (2010).
4 Conclusions
This paper compares the structural approach to empirical policy analysis with the program evaluation approach. It offers a third way to do policy analysis that combines the best features of both approaches. This paper does not endorse or attack any particular statistical methodology. Economists are fortunate to have a rich menu of estimation methods from which to choose.
This paper advocates placing the economic and policy questions being addressed front and center. Economic theory helps to sharpen statements of policy questions. Modern advances in statistics can make the theory useful in addressing these questions. A better approach is to use the economics to frame the questions and the statistics to help address them.
Both the program evaluation approach and the structural approach have desirable features. Program evaluation approaches are generally computationally simpler than structural approaches, and it is often easier to conduct sensitivity and replication analyses with them. Identification of program effects is often more transparent than identification of structural parameters. At the same time, the economic questions answered and the policy relevance of the treatment effects featured in the program evaluation approach are often very unclear. Structural approaches produce more interpretable parameters that are better suited to conduct counterfactual policy analyses.
The third way advocated in this essay is to use Marschak’s Maxim to identify the policy relevant combinations of structural parameters that answer well-posed policy and economic questions. This approach often simplifies the burden of computation, facilitates replication and sensitivity analyses, and makes identification more transparent. At the same time, application of this approach forces analysts to clearly state the goals of the policy analysis — something many economists (structural or program evaluation) have difficulty doing. That discipline is an added bonus of this approach.
I have illustrated this approach by using the economics implicit in LATE to interpret the margins of choice identified by instrument variation and to extend the range of questions LATE can answer. This analysis is a prototype of the value of a closer integration of theory and robust statistical methods to evaluate public policy.
Appendices
A Derivation of the Weights for PRTE
Preliminary Remarks
Recall that, if for two random variables J and K for 0 ≤ j ≤ 1 and 0 ≤ k ≤ 1, with density fJ,K(j, k)
the value of the integral for the region 0 < j < k < 1
Derivation
We can write
because P(Z) ⫫ UD, Y1, Y0 | X.
Thus
Interchanging the limits of each integral
By a parallel argument for
Subtracting the first expression from the second expression we obtain the expression in the text
B IV For Discrete Instruments
Suppose that the support of the distribution of P(Z) contains a finite number of values p1 < p2 < ⋯ < pK. The support of the instrument Z1 is also discrete, taking I distinct values. E(Z1|P(Z) > uD) is constant in uD for uD within any (pℓ, pℓ+1) interval, and Pr(P(Z) > uD) is constant in uD for uD within any (pℓ, pℓ+1) interval. Let λℓ denote the weight on the LATE for the interval (pℓ, pℓ+1).
Under monotonicity condition (IA-3),
Let be the ith smallest value of the support of Z1:
| (21) |
Footnotes
See the essays in the symposium “Con out of Economics,” Journal of Economic Perspectives, Vol. 24, No. 2, Spring 2010 (Angrist and Pischke, 2010; Einav and Levin, 2010; Keane, 2010; Leamer, 2010; Nevo and Whinston, 2010; Sims, 2010; Stock, 2010).
Heckman and Vytlacil (2007a) discuss the concept of structure and reduced form as defined by the pioneering Cowles Commission econometricians who developed the first rigorous framework for inference and policy analysis. This concept received its clearest statement in a classic paper by Hurwicz (1962). A structural relationship in its original usage is a relationship invariant to a class of policy interventions and can be used to make valid policy forecasts for policies in that class. The explicit parametrizations used in the modern version of the “structural” literature are intended to represent policy invariant parameters. Reduced forms are one representation of a structure that represent endogenous variables in terms of exogenous variables. Current meanings of “structure” and “reduced form” have changed greatly from their original meanings, but that is not the point of this essay.
Throughout this essay, I consider methodologies that conduct primary empirical analyses. I do not discuss calibration. Practitioners of the calibration approach use well-posed economic models but typically use estimates of key parameters taken from the literature with all of the attendant problems that the parameters utilized are not necessarily appropriate for the model being calibrated. For discussions of calibration, see Hansen and Heckman (1996), Kydland and Prescott (1996), and Sims (1996).
For a recent statement of this position, see Berk, Li, and Hickman (2005).
Matzkin (2007) provides a valuable overview of the literature. See also Ackerberg, Benkard, Berry, and Pakes (2007) and Athey and Haile (2007) for developments in IO and auction theory respectively. See Abbring and Heckman (2007) for discussion of identification of models of dynamic discrete choice and Aguirregebaria and Mira (2010) for a survey of computational methods.
For brevity, in this paper my emphasis is on microeconometric approaches. There are parallel developments and dichotomies in the macro time series and policy evaluation literatures. See Heckman (2000) for a discussion of that literature.
See Heckman (2000) for a discussion of the intellectual history of causality in economics.
Holland (1986) makes useful distinctions among commonly used definitions of causality. Cartwright (2004) discusses a variety of definitions of causality from a philosopher’s perspective.
Many econometricians, but not all, distinguish the task of identification from the task of inference. In this distinction, identification is about recovering parameters from population data distributions, where sampling variation is not an issue, and inference is about properties of sampling distributions.
For example, risk-averse agents may not participate in randomized controlled trials. For discussion of this and other examples, see Heckman (1992) and Heckman and Smith (1995).
Rosenzweig and Wolpin (2000) present a catalogue of examples of this practice.
See, e.g., Becker (1964) and Cunha, Heckman, and Navarro (2005).
See, e.g., Campbell and Stanley (1963), Heckman, LaLonde, and Smith (1999), or Shadish, Cook, and Campbell (2002).
Heckman (2008) and Heckman and Vytlacil (2007a,b) present general discussions of the policy evaluation problem.
See Heckman (2001) and Heckman and Vytlacil (2007a,b) for surveys. See also Vella (1998) and Keane, Todd, and Wolpin (2010).
See Poirier (1980) and Farber (1983).
The econometrician may possess a different information set, . Choice probabilities computed against one information set are not generally the same as those computed against another information set. Operating with hindsight, the econometrician may be privy to some information not available to agents when they make their choices.
Manski (2004) surveys a rich literature on the elicitation of expectations.
See, e.g., Heckman, Lochner, and Taber (1998a,b,c), Duflo (2004), Lise, Seitz, and Smith (2005, 2006), Albrecht, Van den Berg, and Vroman (2009), or Lee and Wolpin (2006).
See Heckman, Smith, and Clements (1997) and Abbring and Heckman (2007) for discussions of these parameters.
See Abbring and Heckman (2007) for discussions of alternative approaches to identify or bounding these joint distributions.
Frisch (1933, translated in 2009) considered these notion under the concept of “autonomy.” See Marschak (1953) and Hurwicz (1962) who develop refinements of this concept.
If potential outcomes are not policy invariant, one would work with () and ().
See, e.g., Imbens and Wooldridge (2009).
in the Roy example.
He calls it “SUTVA” for Stable Unit Treatment Value Assumption.
See, e.g., Heckman (2008) or Heckman and Vytlacil (2007a,b) for discussions of these conditions.
Not every paper in the empirical structural literature addresses all of the issues in Table 2 in deriving its estimates, but most papers in this tradition are explicit in noting which questions are not addressed.
It is a mark of their detachment from economics that advocates of the program evaluation approach in economics claim that Marshall’s ceteris paribus concept (Marshall, 1890) for defining causality was developed in a 1974 paper by Rubin, and that they also attribute versions of the Cowles Commission policy invariance assumptions to Rubin.
As another example of the same point, Rubin denies that it is possible to define a causal Effect of sex on intelligence because a randomization cannot in principle be performed. “Without treatment definitions that specify actions to be performed on experimental units, I cannot unambiguously discuss causal effects of treatments” (Rubin, 1978, p. 39). In this and many other passages in the statistics literature, a causal effect is defined by a randomization. Issues of definition and identification are confused. This confusion continues to flourish in the literature in applied statistics. For example, Berk, Li, and Hickman (2005) echo Rubin and Holland by insisting that if an experiment cannot “in principle” be performed, a causal effect cannot be defined.
μ1(X) = E(Y1 | X); μ0(X) = E(Y0 | X); μC(Z) = E(C | Z).
A recent exception to this robust approach is the analysis of Angrist and Pischke (2008) who claim that policy evaluation models should be based on linear-in-parameter estimating equations.
Manski (1995, 2003) has developed an elaborate methodology for sensitivity analysis in the program evaluation literature for certain classes of data.
Heckman and Robb (1985) apply a version of Marschak’s Maxim to methods in program evaluation. Thus matching can identify the average treatment effect or treatment on the untreated without identifying the component parts of equations (5) and (6).
I assume that the mean is finite: E|β| < ∞.
If this problem is solved, it is possible to estimate the distribution of β (see, e.g., Heckman and Smith, 1998).
Matching and selection methods also identify under their assumed conditions. Regression discontinuity methods are a local version of instrumental variables (Hahn, Todd, and Van der Klaauw, 2001, and Heckman and Vytlacil, 2007b).
See Heckman and Robb (1985, p. 196); Heckman (1997); Heckman, Schmierer, and Urzua (2010).
See Abbring and Heckman (2007) for a survey of methods for estimating and bounding the distribution of β.
See Heckman and Vytlacil (2005, 2007a,b), Heckman, Urzua, and Vytlacil (2006), and Carneiro et al. (2009, 2010)
For this reason, Heckman, Urzua, and Vytlacil (2006) call this condition “uniformity.”
This expression is easily modified to cover the opposite case where the change in Z reduces program participation. (IA-3) rules out both cases arising at the same time.
If “monotonicity” were not invoked, changes in Z from z1 to z2 could induce two way flows.
Recall that I keep the X implicit, but it is implicitly conditioned on throughout this paper.
In the original Roy model (1951) V = −(U0 − U1).
See Heckman, Urzua, and Vytlacil (2006) for a discussion of this case. An example is μD(Z) = γZ, where γ varies among people so that the same change in Z can produce differences among people in choice responses to variations in Z in addition to the variation produced by V .
The scale is the standard deviation of V , σV .
Because UD is a continuous random variable, the distinction between strict and weak inequalities is irrelevant in defining the expressions in section 3 of this paper.
The mean net gain is E(Y1 − Y0 − C | p ≥ UD).
The support of a random variable is the region where it has positive density.
For any two random variables M, N with density f(m, n) where m and n are realizations of M and N, where N is a uniform random variable in the interval , where , where . In the expression in the text, M = Y1 − Y0 and N = UD.
Chalak, Schennach, and White (2010) develop the sampling properties of this estimator under general conditions.
MTE was introduced into the literature on policy evaluation by Björklund and Moffitt (1987) and extended in Heckman and Vytlacil (1999, 2001b, 2005, 2007b).
We only require Y observations for each value of P(Z) = p for each p in the target population, not values of Y for all Z. Assuming data on (Y, D, Z) triples, a completely nonparametric approach to identifying P(Z) would require that all LATEs required to answer P3 would already be identified in the sample used to address P1 and identify P(Z), i.e., there is no distinction between P1 and P3. However, one can imagine cases where the analyst has access to a richer set of data on (D, Z) where data on Y are not available. Using the index sufficiency property, analysts can determine E(Y | Z = z*) = E(Y | P(Z) = P(z*)), even if no Y is observed for a Z = z*, so long as there is some value of Z = z** in the sample such that P(z*) = P(z**). Moreover, if one adopts a parametric functional form for P(Z), one can answer a much wider range of P3 questions. The same is true if a nonparametric P(Z) is available from another sample. Structural invariance would justify combination of information across samples.
See Heckman, Schmierer, and Urzua (2010) for a formal development of these tests and some Monte Carlo evidence on their performance.
The PRTE can be interpreted as an economically more explicit version of Stock’s (1989) nonparametric policy analysis parameter for a class of policy interventions with explicit agent preferences where the policies evaluated operate solely on agent choice sets.
I discuss the relationship between MTE and IV in the next subsection. For the general case, knowledge of the joint distribution of Z, P(Z) is required.
E* (M | N) denotes linear projection, i.e., the linear regression of M on N.
D(Z) = P(Z) + τ where E(τ | P(Z)) = 0, thus .
This result is due to Yitzhaki (1989) and is elaborated in Heckman, Urzua, and Vytlacil (2006) and Heckman and Vytlacil (2007a). The Yitzhaki paper is posted at the website for Heckman, Urzua, and Vytlacil (2006).
Under the conditions of Fubini’s theorem, it is valid to reverse the order of the integration. See the discussion in the preliminary remarks of Appendix A.
Angrist and Pischke (2010) are exceptions. They advocate use of linear equations in estimating treatment effects.
As did the program evaluation literature. See Barnow, Cain, and Goldberger (1980).
Bounds for MTE and LATE in the case of limited support are presented in Heckman and Vytlacil (1999, 2001a,b, 2007b). Manski (1990, 1995, 2003) presents bounds for a wide array of models.
Ichimura and Taber (2002) develop an alternative local approach that does not exploit the structure of the generalized Roy model that underlies LATE.
Relationships that combine sample and structural relationships were called “mongrel” relationships by the early structural econometricians (see Klein (1953)).
An alternative approach developed in Heckman and Vytlacil (2005) constructs combinations of instruments using sample data on Z that address specific policy questions.
These estimated effects are statistically significantly different from each other (see Carneiro, Heckman, and Vytlacil, 2009).
Angrist and Imbens (1995) propose an ordered choice version of their 1994 paper. As shown by Heckman, Urzua, and Vytlacil (2006) and Heckman and Vytlacil (2007b), their proposed extension has some unsatisfactory features which can be removed by using an extension of the generalized Roy model to an ordered choice model using the choice framework of Cunha, Heckman, and Navarro (2007) and Carneiro, Hansen, and Heckman (2003).
References
- Abbring JH, Heckman JJ. Econometric evaluation of social programs, part III: Distributional treatment effects, dynamic treatment effects, dynamic discrete choice, and general equilibrium policy evaluation. In: Heckman J, Leamer E, editors. Handbook of Econometrics. 6B. Elsevier; Amsterdam: 2007. pp. 5145–5303. [Google Scholar]
- Ackerberg D, Benkard CL, Berry S, Pakes A. Econometric tools for analyzing market outcomes. In: Heckman JJ, Leamer EE, editors. Handbook of Econometrics. 6A. Elsevier Science; 2007. pp. 4171–4276. [Google Scholar]
- Aguirregebaria V, Mira P. Dynamic discrete choice structural models: A survey. Forthcoming in Journal of Econometrics. 2010 [Google Scholar]
- Ahn H, Powell J. Semiparametric estimation of censored selection models with a nonparametric selection mechanism. Journal of Econometrics. 1993 July;58(1-2):3–29. [Google Scholar]
- Albrecht J, Van den Berg GJ, Vroman S. The aggregate labor market effects of the Swedish knowledge lift program. Review of Economic Dynamics. 2009 January;21(1):129–146. [Google Scholar]
- Andrews DW, Schafgans MM. Semiparametric estimation of the intercept of a sample selection model. Review of Economic Studies. 1998 July;65(3):497–517. [Google Scholar]
- Angrist JD, Imbens GW. Two-stage least squares estimation of average causal effects in models with variable treatment intensity. Journal of the American Statistical Association. 1995 June;90(430):431–442. [Google Scholar]
- Angrist JD, Pischke J-S. Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton University Press; Princeton: 2008. [Google Scholar]
- Angrist JD, Pischke J-S. The credibility revolution in empirical economics: How better research design is taking the con out of econometrics. Journal of Economic Perspectives. 2010 Spring24(2):3–30. [Google Scholar]
- Athey S, Haile PA. Nonparametric approaches to auctions. In: Heckman JJ, Leamer EE, editors. Handbook of Econometrics. 6A. Elsevier; Amsterdam: 2007. pp. 3847–3965. [Google Scholar]
- Attanasio O, Meghir C, Santiago A. Educational choices in Mexico: Using a structural model and a randomised experiment to evaluate PROGRESA. IFS/EDEPO Working Paper. 2009 [Google Scholar]
- Autor DH, Katz LF, Kearney MS. Trends in U.S. wage inequality: Re-assessing the revisionists; Working Paper 11627; National Bureau of Economic Research. 2005. [Google Scholar]
- Barnow BS, Cain GG, Goldberger AS. Issues in the analysis of selectivity bias. In: Stromsdorfer E, Farkas G, editors. Evaluation Studies. Vol. 5. Sage Publications; Beverly Hills, California: 1980. pp. 42–59. [Google Scholar]
- Becker GS. Human Capital: A Theoretical and Empirical Analysis, with Special Reference to Education. National Bureau of Economic Research; New York: 1964. distributed by Columbia University Press. [Google Scholar]
- Berk R, Li A, Hickman LJ. Statistical difficulties in determining the role of race in capital cases: A re-analysis of data from the state of Maryland. Journal of Quantitative Criminology. 2005 December;21(4):365–390. [Google Scholar]
- Björklund A, Moffitt R. The estimation of wage gains and welfare gains in self-selection. Review of Economics and Statistics. 1987 February;69(1):42–49. [Google Scholar]
- Brock WA, Durlauf SN. Interactions-based models. In: Heckman JJ, Leamer E, editors. Handbook of Econometrics. Vol. 5. North-Holland; New York: 2001. pp. 3463–3568. [Google Scholar]
- Brown DJ, Matzkin RL. Testable restrictions on the equilibrium manifold. Econometrica. 1996;64(6):1249–1262. [Google Scholar]
- Cameron SV, Taber C. Estimation of educational borrowing constraints using returns to schooling. Journal of Political Economy. 2004 February;112(1):132–182. [Google Scholar]
- Campbell DT, Stanley JC. Experimental and Quasi-Experimental Designs for Research. Rand McNally; Chicago: 1963. [Google Scholar]
- Card D. The causal effect of education on earnings. In: Ashenfelter O, Card D, editors. Handbook of Labor Economics. Vol. 5. North-Holland; New York: 1999. pp. 1801–1863. [Google Scholar]
- Card D. Estimating the return to schooling: Progress on some persistent econometric problems. Econometrica. 2001 September;69(5):1127–1160. [Google Scholar]
- Carneiro P, Hansen K, Heckman JJ. Removing the veil of ignorance in assessing the distributional impacts of social policies. Swedish Economic Policy Review. 2001 Fall8(2):273–301. [Google Scholar]
- Carneiro P, Hansen K, Heckman JJ. Estimating distributions of treatment effects with an application to the returns to schooling and measurement of the effects of uncertainty on college choice. International Economic Review. 2003 May;44(2):361–422. [Google Scholar]
- Carneiro P, Heckman JJ, Vytlacil EJ. Estimating marginal returns to education. American Economic Review. 2009 doi: 10.1257/aer.101.6.2754. Under revision. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carneiro P, Heckman JJ, Vytlacil EJ. Evaluating marginal policy changes and the average effect of treatment for individuals at the margin. Econometrica. 2010 January;78(1):377–394. doi: 10.3982/ECTA7089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cartwright N. Causation: One word many things. Philosophy of Science. 2004 December;71(4):805–819. [Google Scholar]
- Chalak K, Schennach S, White H. Local indirect least squares and average marginal effects in nonseparable structural systems; Working Papers in Economics 680; Boston College Department of Economics; 2010. [Google Scholar]
- Chetty R. Sufficient statistics for welfare analysis: A bridge between structural and reduced-form methods. Annual Review of Economics. 2009;1:451–488. [Google Scholar]
- Cosslett SR. Distribution-free maximum likelihood estimator of the binary choice model. Econometrica. 1983 May;51(3):765–82. [Google Scholar]
- Cox DR. Planning of Experiments. Wiley; New York: 1958. [Google Scholar]
- Cunha F, Heckman JJ. The evolution of uncertainty in labor earnings in the U.S. economy. University of Chicago; 2007. Unpublished manuscript. Under revision. [Google Scholar]
- Cunha F, Heckman JJ, Navarro S. Separating uncertainty from heterogeneity in life cycle earnings, The 2004 Hicks Lecture. Oxford Economic Papers. 2005 April;57(2):191–261. [Google Scholar]
- Cunha F, Heckman JJ, Navarro S. Counterfactual analysis of inequality and social mobility. In: Morgan SL, Grusky DB, Fields GS, editors. Mobility and Inequality: Frontiers of Research in Sociology and Economics. Stanford University Press; Stanford, CA: 2006. pp. 290–348. Chapter 4. [Google Scholar]
- Cunha F, Heckman JJ, Navarro S. The identification and economic content of ordered choice models with stochastic cutoffs. International Economic Review. 2007 November;48(4):1273–1309. [Google Scholar]
- Das M, Newey WK, Vella F. Nonparametric estimation of sample selection models. The Review of Economic Studies. 2003 January;70(1):33–58. [Google Scholar]
- Duflo E. The medium run effects of educational expansion: Evidence from a large school construction program in Indonesia. Journal of Development Economics. 2004 June;74(1):163–197. Special Issue. [Google Scholar]
- Durbin J. Errors in variables. Review of the International Statistical Institute. 1954;22:23–32. [Google Scholar]
- Durlauf SN, Young HP. Social Dynamics. MIT Press; Cambridge, MA: 2001. [Google Scholar]
- Einav L, Finkelstein A, Cullen MR. SIEPR Discussion Paper 08-046. 2009. Estimating welfare in insurance markets using variation in price. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einav L, Levin J. Empirical industrial organization: A progress report. Journal of Economic Perspectives. 2010 Spring24(2):145–162. [Google Scholar]
- Farber HS. The determination of the union status of workers. Econometrica. 1983 September;51(5):1417–1437. [Google Scholar]
- Frisch R. Problems and Methods of Econometrics: The Poincaré Lectures of Ragnar Frisch, 1933 (Routledge Studies in the History of Economics) Routledge; New York, New York: Jul, 2009. [Google Scholar]
- Granger CWJ. Investigating causal relations by econometric models and crossspectral methods. Econometrica. 1969 August;37(3):424–438. [Google Scholar]
- Gronau R. Wage comparisons – a selectivity bias. Journal of Political Economy. 1974 November-December;82(6):1119–43. [Google Scholar]
- Hahn J, Todd PE, Van der Klaauw W. Identification and estimation of treatment effects with a regression-discontinuity design. Econometrica. 2001 January;69(1):201–209. [Google Scholar]
- Hansen LP, Heckman JJ. The empirical foundations of calibration. Journal of Economic Perspectives. 1996 Winter10(1):87–104. [Google Scholar]
- Harberger A. The measurement of waste. American Economic Review. 1964;54:58–76. [Google Scholar]
- Hausman JA. Specification tests in econometrics. Econometrica. 1978 November;46(6):1251–1272. [Google Scholar]
- Heckman JJ. Shadow prices, market wages, and labor supply. Econometrica. 1974 July;42(4):679–694. [Google Scholar]
- Heckman JJ. Varieties of selection bias. American Economic Review. 1990 May;80(2):313–318. [Google Scholar]
- Heckman JJ. Haavelmo and the birth of modern econometrics: A review of The History of Econometric Ideas by Mary Morgan. Journal of Economic Literature. 1992 June;30(2):876–886. [Google Scholar]
- Heckman JJ. Randomization as an instrumental variable. Review of Economics and Statistics. 1996 May;78(2):336–340. [Google Scholar]
- Heckman JJ. Instrumental variables: A study of implicit behavioral assumptions used in making program evaluations. Journal of Human Resources. 1997 Summer;32(3):441–462. Addendum published vol. 33 no. 1 (Winter 1998) [Google Scholar]
- Heckman JJ. Causal parameters and policy analysis in economics: A twentieth century retrospective. Quarterly Journal of Economics. 2000 February;115(1):45–97. [Google Scholar]
- Heckman JJ. Micro data, heterogeneity, and the evaluation of public policy: Nobel lecture. Journal of Political Economy. 2001 August;109(4):673–748. [Google Scholar]
- Heckman JJ. Econometric causality. International Statistical Review. 2008 April;76(1):1–27. [Google Scholar]
- Heckman JJ, Honoré BE. The empirical content of the Roy model. Econometrica. 1990 September;58(5):1121–1149. [Google Scholar]
- Heckman JJ, Hotz VJ. Choosing among alternative nonexperimental methods for estimating the impact of social programs: The case of Manpower Training. Journal of the American Statistical Association. 1989 December;84(408):862–874. Rejoinder also published in Vol. 84, No. 408, (Dec. 1989) [Google Scholar]
- Heckman JJ, LaLonde RJ, Smith JA. The economics and econometrics of active labor market programs. In: Ashenfelter O, Card D, editors. Handbook of Labor Economics. 3A. North-Holland; New York: 1999. pp. 1865–2097. Chapter 31. [Google Scholar]
- Heckman JJ, Lochner LJ, Taber C. Explaining rising wage inequality: Explorations with a dynamic general equilibrium model of labor earnings with heterogeneous agents. Review of Economic Dynamics. 1998a January;1(1):1–58. [Google Scholar]
- Heckman JJ, Lochner LJ, Taber C. General-equilibrium treatment effects: A study of tuition policy. American Economic Review. 1998b May;88(2):381–386. [Google Scholar]
- Heckman JJ, Lochner LJ, Taber C. Tax policy and human-capital formation. American Economic Review. 1998c May;88(2):293–297. [Google Scholar]
- Heckman JJ, Robb R. Alternative methods for evaluating the impact of interventions: An overview. Journal of Econometrics. 1985 October-November;30(1-2):239–267. [Google Scholar]
- Heckman JJ, Schmierer D, Urzua S. Testing the correlated random coefficient model. Journal of Econometrics. 2010 doi: 10.1016/j.jeconom.2010.01.005. Forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman JJ, Smith JA. Assessing the case for social experiments. Journal of Economic Perspectives. 1995 Spring9(2):85–110. [Google Scholar]
- Heckman JJ, Smith JA. Evaluating the welfare state. In: Strom S, editor. Econometrics and Economic Theory in the Twentieth Century: The Ragnar Frisch Centennial Symposium. Cambridge University Press; New York: 1998. pp. 241–318. [Google Scholar]
- Heckman JJ, Smith JA, Clements N. Making the most out of programme evaluations and social experiments: Accounting for heterogeneity in programme impacts. Review of Economic Studies. 1997 October;64(221):487–536. [Google Scholar]
- Heckman JJ, Urzua S. Comparing IV with structural models: What simple IV can and cannot identify. Journal of Econometrics. 2010 May;156(1):27–37. doi: 10.1016/j.jeconom.2009.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman JJ, Urzua S, Vytlacil EJ. Understanding instrumental variables in models with essential heterogeneity. Review of Economics and Statistics. 2006;88(3):389–432. [Google Scholar]
- Heckman JJ, Urzua S, Vytlacil EJ. Instrumental variables in models with multiple outcomes: The general unordered case. Les Annales d’Economie et de Statistique. 2010;90 In press. [Google Scholar]
- Heckman JJ, Vytlacil EJ. Local instrumental variables and latent variable models for identifying and bounding treatment effects. Proceedings of the National Academy of Sciences. 1999 April;96(8):4730–4734. doi: 10.1073/pnas.96.8.4730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman JJ, Vytlacil EJ. The relationship between treatment parameters within a latent variable framework. Economics Letters. 2000 January;66(1):33–39. [Google Scholar]
- Heckman JJ, Vytlacil EJ. Instrumental variables, selection models, and tight bounds on the average treatment effect. In: Lechner M, Pfeiffer F, editors. Econometric Evaluation of Labour Market Policies. Center for European Economic Research; New York: 2001a. pp. 1–15. [Google Scholar]
- Heckman JJ, Vytlacil EJ, Hsiao C. Local instrumental variables. In: Morimune K, Powell JL, editors. Nonlinear Statistical Modeling: Proceedings of the Thirteenth International Symposium in Economic Theory and Econometrics: Essays in Honor of Takeshi Amemiya. Cambridge University Press; New York: 2001b. pp. 1–46. [Google Scholar]
- Heckman JJ, Vytlacil EJ. Policy-relevant treatment effects. American Economic Review. 2001c May;91(2):107–111. [Google Scholar]
- Heckman JJ, Vytlacil EJ. Structural equations, treatment effects and econometric policy evaluation. Econometrica. 2005 May;73(3):669–738. [Google Scholar]
- Heckman JJ, Vytlacil EJ. Econometric evaluation of social programs, part I: Causal models, structural models and econometric policy evaluation. In: Heckman J, Leamer E, editors. Handbook of Econometrics. 6B. Elsevier; Amsterdam: 2007a. pp. 4779–4874. [Google Scholar]
- Heckman JJ, Vytlacil EJ. Econometric evaluation of social programs, part II: Using the marginal treatment effect to organize alternative economic estimators to evaluate social programs and to forecast their effects in new environments. In: Heckman J, Leamer E, editors. Handbook of Econometrics. 6B. Elsevier; Amsterdam: 2007b. pp. 4875–5144. [Google Scholar]
- Hendry DF. Econometrics — alchemy or science? Economica. 1980;47(188):387–406. [Google Scholar]
- Holland PW. Statistics and causal inference. Journal of the American Statistical Association. 1986 December;81(396):945–960. [Google Scholar]
- Hurwicz L. On the structural form of interdependent systems. In: Nagel E, Suppes P, Tarski A, editors. Logic, Methodology and Philosophy of Science. Stanford University Press; 1962. pp. 232–239. [Google Scholar]
- Ichimura H, Taber C. Semiparametric reduced-form estimation of tuition subsidies. American Economic Review. 2002 May;92(2):286–292. [Google Scholar]
- Imbens GW, Angrist JD. Identification and estimation of local average treatment effects. Econometrica. 1994 March;62(2):467–475. [Google Scholar]
- Imbens GW, Wooldridge JM. Recent developments in the econometrics of program evaluation. Journal of Economic Literature. 2009 March;47(1):5–86. [Google Scholar]
- Katz LF, Autor DH. Changes in the wage structure and earnings inequality. In: Ashenfelter O, Card D, editors. Handbook of Labor Economics. Vol. 3. North-Holland; New York: 1999. pp. 1463–1555. Chapter 26. [Google Scholar]
- Katz LF, Murphy KM. Changes in relative wages, 1963-1987: Supply and demand factors. Quarterly Journal of Economics. 1992 February;107(1):35–78. [Google Scholar]
- Keane MP. A structural perspective on the experimentalist school. Journal of Economic Perspectives. 2010 Spring24(2):47–58. [Google Scholar]
- Keane MP, Todd PE, Wolpin KI. Forthcoming in Handbook of Labor Economics. II 2010. The structural estimation of behavioral models: Discrete choice dynamic programming methods and applications. [Google Scholar]
- Killingsworth MR, Heckman JJ. Female labor supply: A survey. In: Ashenfelter OC, Layard R, editors. Handbook of Labor Economics. Vol. 1. Elsevier; Amsterdam, The Netherlands: 1986. pp. 103–204. Chapter 2. [Google Scholar]
- Klein LR. A Textbook of Econometrics. Row, Peterson and Co.; Evanston: 1953. [Google Scholar]
- Klein RW, Spady RH. An efficient semiparametric estimator for binary response models. Econometrica. 1993 March;61(2):387–421. [Google Scholar]
- Kydland FE, Prescott EC. The computational experiment: An econometric tool. Journal of Economic Perspectives. 1996 Winter10(1):69–85. [Google Scholar]
- LaLonde RJ. Evaluating the econometric evaluations of training programs with experimental data. American Economic Review. 1986 September;76(4):604–620. [Google Scholar]
- Leamer E. Lets take the con out of econometrics. American Economic Review. 1983;73(1):31–43. [Google Scholar]
- Leamer EE. Tantalus on the road to asymptopia. Journal of Economic Perspectives. 2010 Spring24(2):31–46. [Google Scholar]
- Lee D, Wolpin KI. Intersectoral labor mobility and the growth of the service sector. Econometrica. 2006 January;74(1):1–40. [Google Scholar]
- Lewis HG. Union Relative Wage Effects: A Survey. University of Chicago Press; Chicago: 1986. [Google Scholar]
- Lise J, Seitz S, Smith J. Equilibrium policy experiments and the evaluation of social programs; Working Paper 1076; Queen’s University, Department of Economics, Kingston, Ontario. 2005. [Google Scholar]
- Lise J, Seitz S, Smith J. Evaluating search and matching models using experimental data; Working paper 1074; Queen’s University, Department of Economics, Kingston, Ontario. 2006. [Google Scholar]
- Liu T. Underidentification, structural estimation, and forecasting. Econometrica. 1960;28:855–865. [Google Scholar]
- Manski CF. Identification of binary response models. Journal of the American Statistical Association. 1988 September;83(403):729–738. [Google Scholar]
- Manski CF. Nonparametric bounds on treatment effects. American Economic Review. 1990 May;80(2):319–323. [Google Scholar]
- Manski CF. Identification of endogenous social effects: The reflection problem. Review of Economic Studies. 1993 July;60(3):531–542. [Google Scholar]
- Manski CF. Identification Problems in the Social Sciences. Harvard University Press; Cambridge, MA: 1995. [Google Scholar]
- Manski CF. Partial Identification of Probability Distributions. Springer-Verlag; New York: 2003. [Google Scholar]
- Manski CF. Measuring expectations. Econometrica. 2004 September;72(5):1329–1376. [Google Scholar]
- Marschak J. Economic measurements for policy and prediction. In: Hood W, Koopmans T, editors. Studies in Econometric Method. Wiley; New York: 1953. pp. 1–26. [Google Scholar]
- Marshall A. Principles of Economics. Macmillan and Company; New York: 1890. [Google Scholar]
- Matzkin RL. Nonparametric and distribution-free estimation of the binary threshold crossing and the binary choice models. Econometrica. 1992 March;60(2):239–270. [Google Scholar]
- Matzkin RL. Nonparametric identification and estimation of polychotomous choice models. Journal of Econometrics. 1993 July;58(1-2):137–168. [Google Scholar]
- Matzkin RL. Restrictions of economic theory in nonparametric methods. In: Engle R, McFadden D, editors. Handbook of Econometrics. Vol. 4. North-Holland; New York: 1994. pp. 2523–58. [Google Scholar]
- Matzkin RL. Nonparametric identification. In: Heckman J, Leamer E, editors. Handbook of Econometrics. 6B. Elsevier; Amsterdam: 2007. [Google Scholar]
- Matzkin RL. Estimation of nonparametric models with simultaneity. UCLA, Department of Economics: Feb, 2010a. Unpublished manuscript. [Google Scholar]
- Matzkin RL. Identification in nonparametric limited dependent variable models with simultaneity and unobserved heterogeneity. UCLA, Department of Economics: Jan, 2010b. Unpublished manuscript. [Google Scholar]
- Nevo A, Whinston MD. Taking the dogma out of econometrics: Structural modeling and credible inference. Journal of Economic Perspectives. 2010 Spring24(2):69–82. [Google Scholar]
- Neyman J. Statistical problems in agricultural experiments. Journal of the Royal Statistical Society II (Supplement) 1923;(2):107–180. [Google Scholar]
- Pencavel J. Labor supply of men. In: Ashenfelter O, Layard R, editors. Handbook of Labor Economics. Vol. 1. North-Holland; Amsterdam: 1986. pp. 3–102. [Google Scholar]
- Poirier DJ. Partial observability in bivariate probit models. Journal of Econometrics. 1980;12(2):209–217. [Google Scholar]
- Powell JL. Estimation of semiparametric models. In: Engle R, McFadden D, editors. Handbook of Econometrics. Vol. 4. Elsevier; Amsterdam: 1994. pp. 2443–2521. [Google Scholar]
- Quandt RE. The estimation of the parameters of a linear regression system obeying two separate regimes. Journal of the American Statistical Association. 1958 December;53(284):873–880. [Google Scholar]
- Quandt RE. A new approach to estimating switching regressions. Journal of the American Statistical Association. 1972 June;67(338):306–310. [Google Scholar]
- Rosenzweig MR, Wolpin KI. Natural ”natural experiments” in economics. Journal of Economic Literature. 2000 December;38(4):827–874. [Google Scholar]
- Roy A. Some thoughts on the distribution of earnings. Oxford Economic Papers. 1951 June;3(2):135–146. [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974 October;66(5):688–701. [Google Scholar]
- Rubin DB. Bayesian inference for causal effects: The role of randomization. Annals of Statistics. 1978 January;6(1):34–58. [Google Scholar]
- Rubin DB. Statistics and causal inference: Comment: Which ifs have causal answers. Journal of the American Statistical Association. 1986;81(396):961–962. [Google Scholar]
- Shadish WR, Cook TD, Campbell DT. Experimental and Quasi-Experimental Designs for Generalized Causal Inference. Houghton Mifflin; Boston, MA: 2002. [Google Scholar]
- Shimer R, Werning I. Liquidity and insurance for the unemployed. American Economic Review. 2008;98(5):1922–1942. [Google Scholar]
- Sims CA. Money, income, and causality. American Economic Review. 1972 September;62(4):540–552. [Google Scholar]
- Sims CA. Macroeconomics and reality. Econometrica. 1980 January;48(1):1–48. [Google Scholar]
- Sims CA. Macroeconomics and methodology. Journal of Economic Perspectives. 1996;10(1):105–120. [Google Scholar]
- Sims CA. But economics is not an experimental science. Journal of Economic Perspectives. 2010 Spring24(2):59–68. [Google Scholar]
- Stock JH. Nonparametric policy analysis. Journal of the American Statistical Association. 1989 June;84(406):565–575. [Google Scholar]
- Stock JH. The other transformation in econometric practice: Robust tools for inference. Journal of Economic Perspectives. 2010 Spring24(2):83–94. [Google Scholar]
- Tamer E. Incomplete simultaneous discrete response model with multiple equilibria. Review of Economic Studies. 2003 January;70(1):147–165. [Google Scholar]
- Todd P, Wolpin KI. Assessing the impact of a school subsidy program in mexico using experimental data to validate a dynamic behavioral model of child schooling. American Economic Review. 2006;96(5):1384–1417. doi: 10.1257/aer.96.5.1384. [DOI] [PubMed] [Google Scholar]
- Tukey JW. Comments on alternative methods for solving the problem of selection bias in evaluating the impact of treatments on outcomes. In: Wainer H, editor. Drawing Inferences from Self-Selected Samples. Springer-Verlag; New York: 1986. pp. 108–110. Reprinted in 2000, Mahwah, NJ: Lawrence Erlbaum Associates. [Google Scholar]
- Tunali I. Rationality of migration. International Economic Review. 2000 November;41(4):893–920. [Google Scholar]
- Vella F. Estimating models with sample selection bias: A survey. Journal of Human Resources. 1998 Winter33(1):127–169. [Google Scholar]
- Vytlacil EJ. Independence, monotonicity, and latent index models: An equivalence result. Econometrica. 2002 January;70(1):331–341. [Google Scholar]
- Willis RJ, Rosen S. Education and self-selection. Journal of Political Economy. 1979 October;87(5, Part 2):S7–S36. [Google Scholar]
- Wu D. Alternative tests of independence between stochastic regressors and disturbances. Econometrica. 1973 July;41(4):733–750. [Google Scholar]
- Yitzhaki S. On using linear regression in welfare economics; Working Paper 217; Department of Economics, Hebrew University. 1989. [Google Scholar]